
A
D
H
I
J
C
F
E
G
B
K
L
M
x
O
2
O
3
O
4
O
1
O
5
O
6
O
7
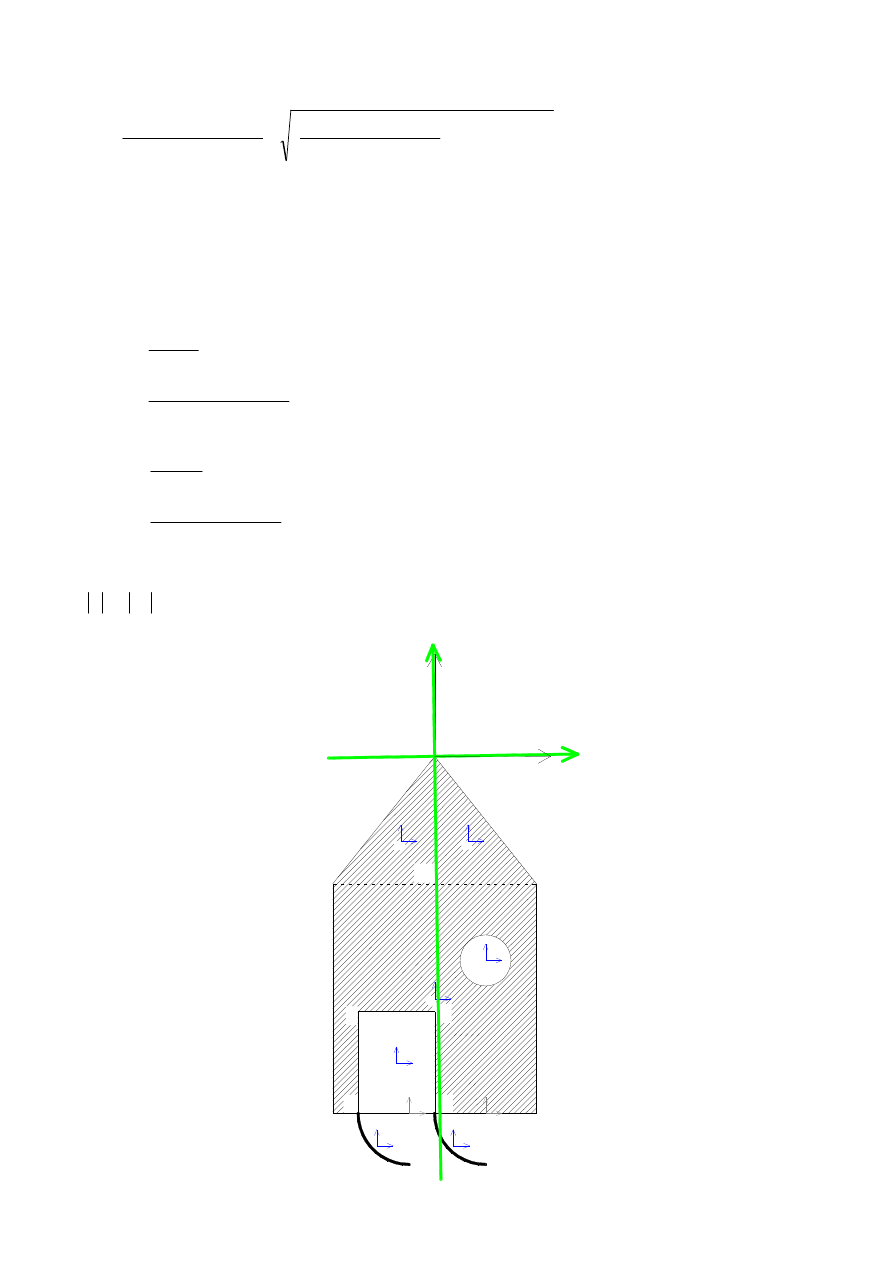
Dla zadanej figury płaskiej o gęstości
ρ
=1 wyznaczyć główne osie i momenty bezwładności
w punkcie A.
Podział na obszary:
Prostokąt BCDE + Trójkąt EMA + Trójkąt MDA – Prostokąt FGHI – Koło L + Łuk FJ + Łuk GK
(Łuk FJ , Łuk GK – ćwiartka okręgu)
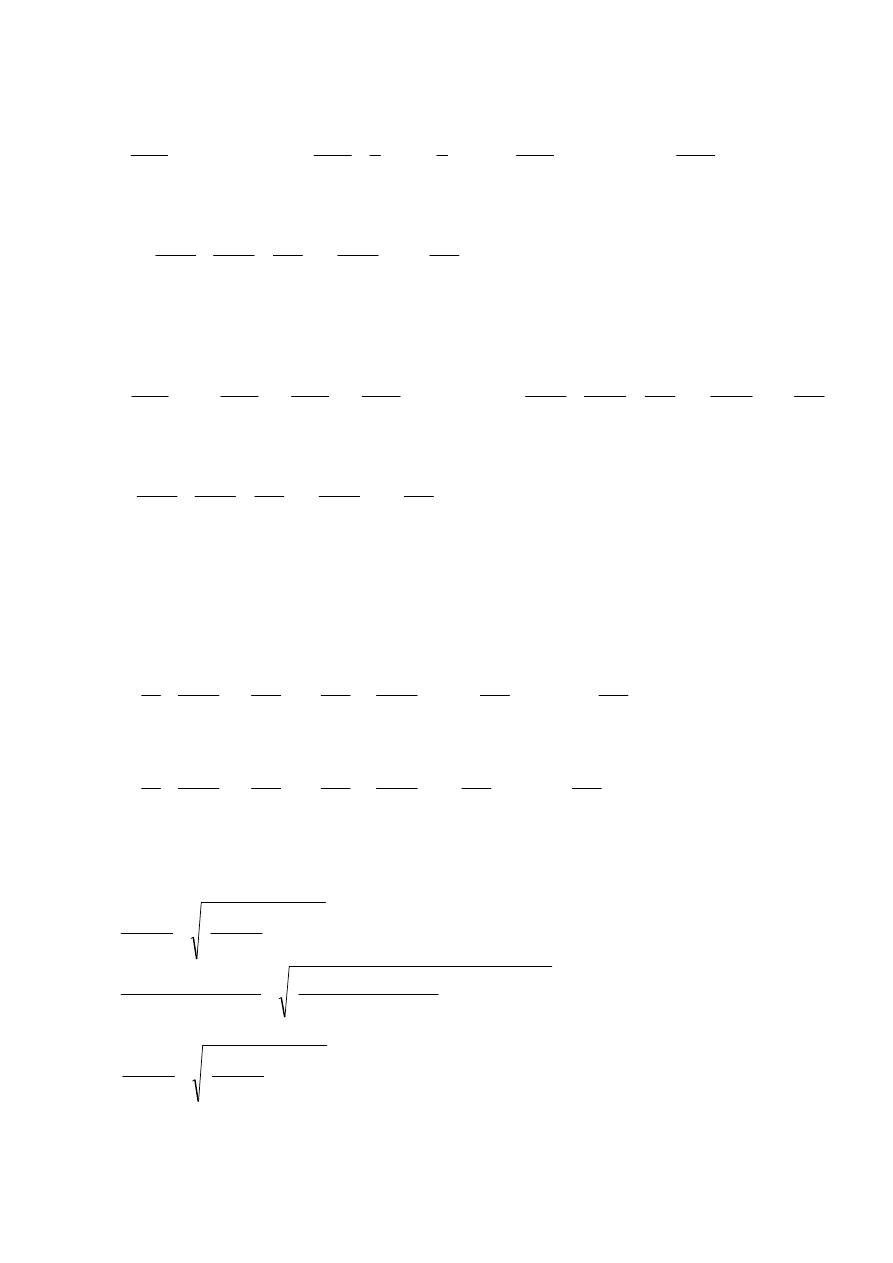
BCDE
EMA, MDA
FGHI
L
( )
( )
( )
+
⋅
⋅
+
⋅
−
⋅
⋅
+
⋅
−
⋅
⋅
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
=
2
2
4
2
3
2
3
2
3
8
1
4
1
12
3
4
12
3
4
5
3
2
4
5
2
1
36
4
5
2
5
,
9
8
9
12
8
9
π
π
x
I
FJ , GK
⋅
+
⋅
⋅
+
⋅
⋅
⋅
−
⋅
⋅
+
2
2
3
2
2
14
4
2
2
2
2
4
2
2
4
2
2
π
π
π
π
π
223
,
6756
=
x
I
BCDE EMA, MDA FGHI
L FJ
( )
+
⋅
+
⋅
⋅
+
⋅
⋅
⋅
−
⋅
+
⋅
⋅
+
⋅
−
⋅
−
⋅
⋅
+
⋅
=
2
2
3
2
2
4
3
3
3
2
2
1
4
2
2
2
2
4
2
2
4
2
2
1
4
1
3
4
3
12
5
4
2
12
9
8
π
π
π
π
π
π
π
y
I
GK
⋅
−
⋅
⋅
+
⋅
⋅
⋅
−
⋅
+
2
2
3
2
2
2
4
2
2
2
2
4
2
2
4
2
π
π
π
π
π
256
,
408
=
y
I
BCDE EMA, MDA FGHI
L
[
]
( )( )
[
]
+
−
⋅
⋅
+
−
−
⋅
−
⋅
⋅
+
−
+
=
2
8
1
0
)
12
(
)
5
,
1
(
3
4
0
0
0
2
π
z
D
FJ
+
⋅
+
−
⋅
⋅
+
−
⋅
⋅
+
⋅
−
⋅
⋅
−
⋅
⋅
−
+
π
π
π
π
π
π
2
2
14
2
2
1
4
2
2
2
2
2
2
4
2
2
2
2
3
GK
⋅
+
−
⋅
⋅
−
⋅
⋅
+
⋅
−
⋅
⋅
−
⋅
⋅
−
+
π
π
π
π
π
π
2
2
14
2
2
2
4
2
2
2
2
2
2
4
2
2
2
2
3
717
,
93
−
=
z
D
Główne momenty bezwładności w punkcie A:
2
2
1
2
2
z
y
x
y
x
D
I
I
I
I
I
+
−
+
+
=
2
2
1
)
717
,
93
(
2
256
,
408
223
,
6756
2
256
,
408
223
,
6756
−
+
−
+
+
=
I
606
,
6757
1
=
I
2
2
2
2
2
z
y
x
y
x
D
I
I
I
I
I
+
−
−
+
=
A
D
H
I
J
C
F
E
G
B
K
L
M
x
y
O
2
O
3
O
4
O
1
O
5
O
6
O
7
1
2
2
2
2
)
717
,
93
(
2
256
,
408
223
,
6756
2
256
,
408
223
,
6756
−
+
−
−
+
=
I
873
,
406
2
=
I
Sprawdzenie:
2
1
I
I
I
I
y
x
+
=
+
2
1
2
I
I
D
I
I
z
y
x
⋅
=
−
⋅
Główne osie bezwładności w punkcie A:
1
1
tan
I
I
D
y
z
−
=
α
⇒
−
−
=
606
,
6757
256
,
408
717
,
93
tan
1
α
°
=
85
,
0
1
α
2
2
tan
I
I
D
y
z
−
=
α
⇒
−
−
=
873
,
406
256
,
408
717
,
93
tan
2
α
°
−
=
15
,
89
2
α
Sprawdzenie:
°
=
+
90
2
1
α
α
Wyszukiwarka
Podobne podstrony:
IIsem 7 g mas 2
Brymora Kaczyński Logistyka wytwórni mas bitumicznych ppt
Spektrometria mas NMAZ
oznaczanie mas molowych
14 06 Wytwornie mas bitumicznych i betoniarnie
MAS wszystkie pytania testowe 2007
,Analiza chemicznych zanieczyszczeń środowiska , Zasada powstawania widma mas
pogarda mas IV
Bunt mas
PrzeglÄ…d mas plastycznych, ortografia dla dzieci
spoleczenstwo mas - Mills, Studia (europeistyka), nauka o polityce, Teoria polityki, ćwiczenia 14
teoria sportu wyklady IIsem
MAS e przyklad roz id 281198 Nieznany
prawo dzialania mas
La costa mas lejana
Ruchy grawitacyjne mas skalnych geografia
więcej podobnych podstron