1.

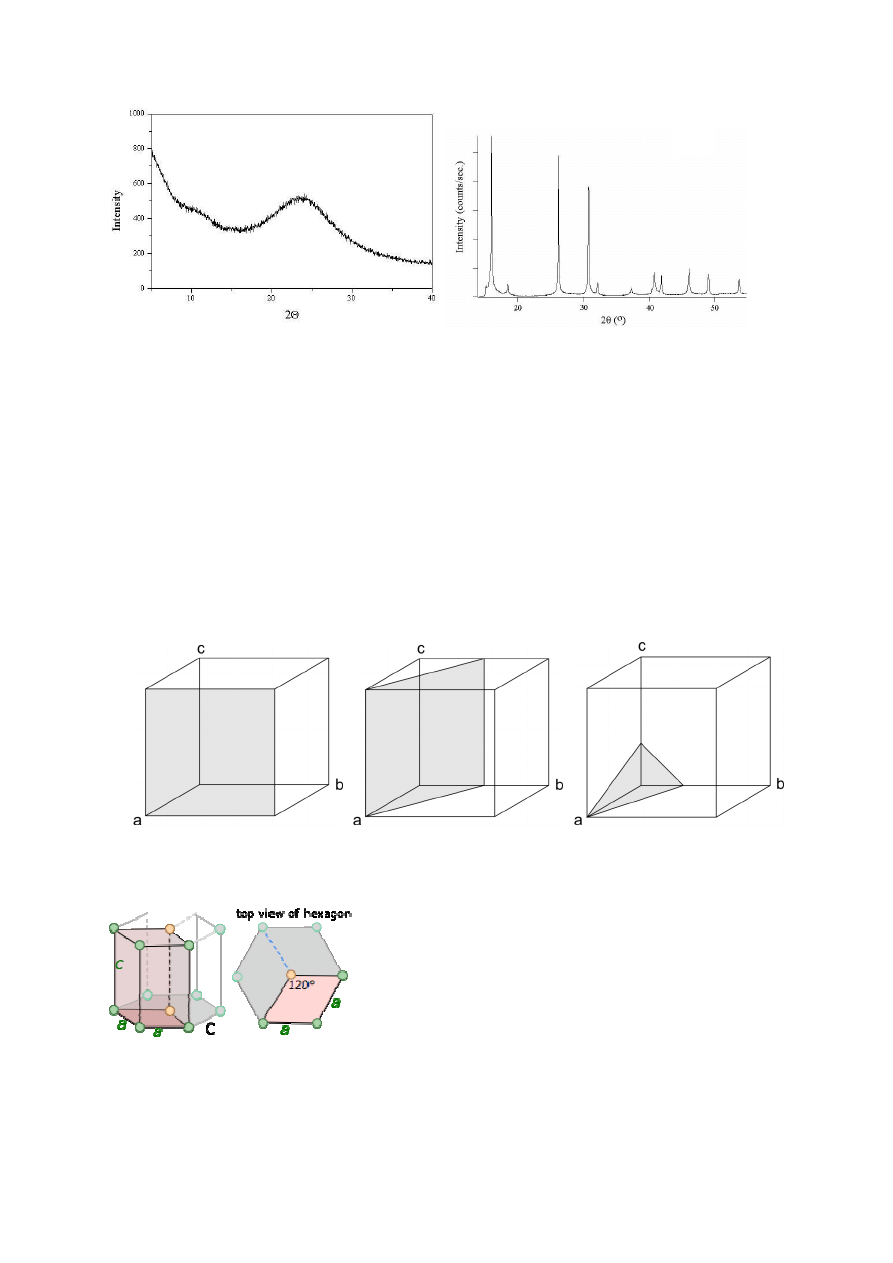
Na podanych rysunkach zamieszczono dyfraktogramy ciał stałych. Co można powiedzieć o

strukturze krystalicznej tych materiałów? Odpowiedź uzasadnij. (1)

Kryształ - ciało stałe dające dyskretny obraz dyfrakcyjny. Zatem materiał, którego dyfraktogram

jest oznaczony jako B ma strukturę krystaliczną, a materiał o którego dyfraktogram jest oznaczony

jako A nie ma struktury krystalicznej.

2.

Które z podanych ciał stałych nie są przewodnikami elektrycznymi? Mg(s), C(grafit), I

2

(s), H

2

O(s)

(1)

I

2

(s), H

2

O(s)

3.

Podaj co najmniej trzy charakterystyczne właściwości kryształów kowalencyjnych. (1

)

twarde, wysoka temperatura topnienia, słabe przewodnictwo cieplne i elektryczne

4.

Jakie są indeksy (hkl) płaszczyzn krystalograficznych na załączonych rysunkach? (1)

5.

Narysuj kształt komórki elementarnej heksagonalnego układu krystalograficznego, zaznaczając

symbolicznie charakterystyczne kąty i długości. (1)

a=b≠c, α=β=90, γ≠120

Należy pamiętać, że komórka elementarna to równoległościan (tylko sześć ścian).

6.

Narysuj ułożenie atomów w układzie regularnym w komórce ściennie centrowanej oraz podaj

ilość atomów w takiej komórce wraz z uzasadnieniem. (1)

A

B

A

B

C

100

120

133

4 atomy w komórce = 8x1/8 + 6x1/2

7.

Podaj, na podstawie obliczeń, krytyczny stosunek promienia kationu (r

k

) do promienia anionu (r

a

)

dla koordynacji sześciennej. (2)

2(r

k

+ r

a

) = 2r

a

3

2r

k

+ 2r

a

- 2r

a

3

= 0

r

k

= r

a

(

3

– 1)

r

k

/r

a

=

3

– 1 = 0.732

8.

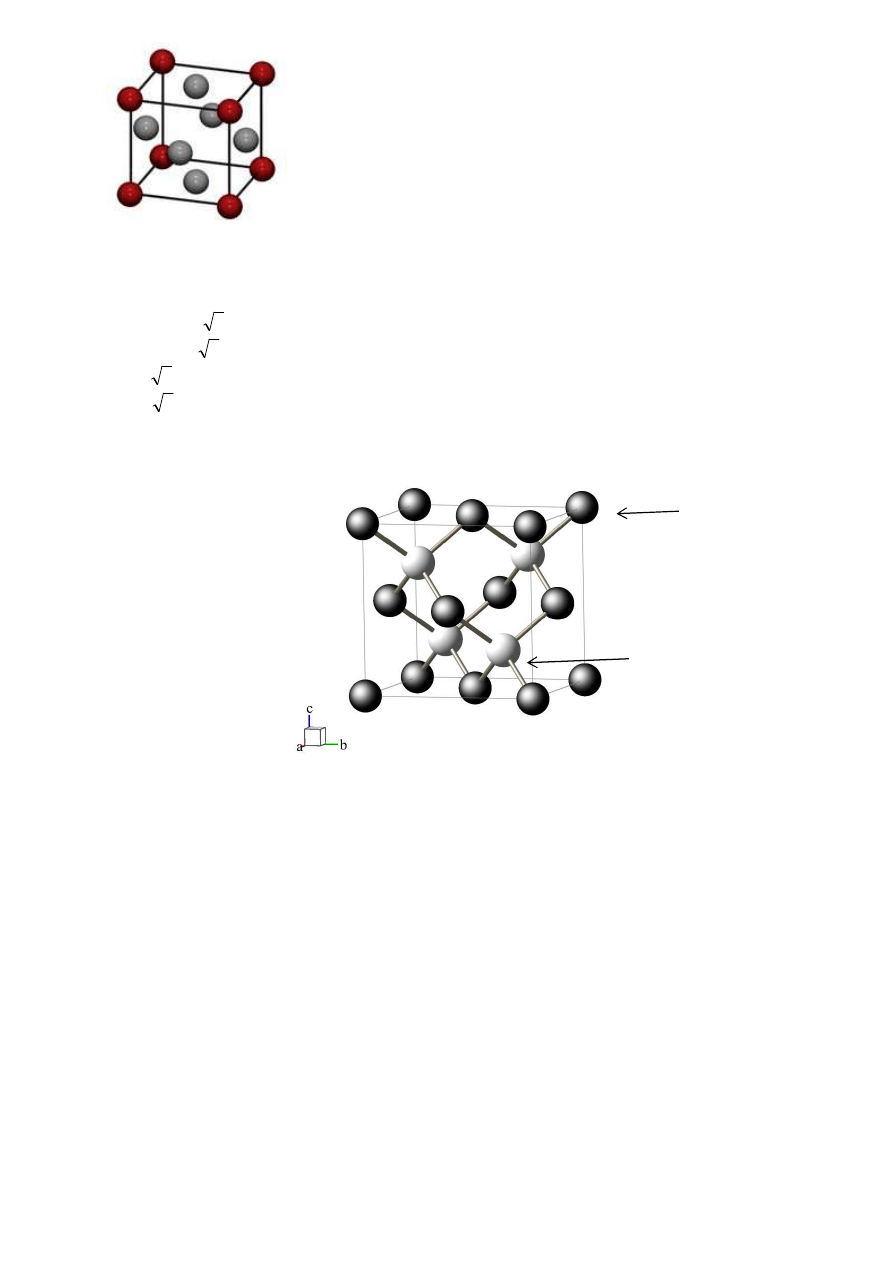
Na podstawie poniższego rysunku uzasadnij, że stechiometria sfalerytu (ZnS) jest zgodna z jego

strukturą krystaliczną. (1)

Stechiometrię związku można określić na podstawie ilości atomów w komórce elementarnej.

Należy zwrócić uwagę na położenie atomów (naroża – 1/8 atomu, ściany – 1/2 atomu, krawędzie

1/4 atomu, wnętrze równoległościanu 1 cały atom): Zn – 8x1/8 + 6x1/2 = 4 atomy ; S – 4 całe = 4

atomy: Zn

4

S

4

-> ZnS

Alternatywnie, można stwierdzić, że jony Zn

2+

na rysunku tworzą komórką ściennie centrowaną.

Baza w postaci Zn – S w połączeniu z siecią regularną z komórką FCC, przedstawioną na rysunku,

umożliwia odtworzenia struktury krystalicznej z zachowaniem proporcji 1:1 cynku i siarki.

9.

W której z poniższych struktur liczba koordynacyjna kationów i anionów w strukturze gęstego

upakowania jest taka sama? (1)

a.

Jony Cl

–

tworzą strukturę typu FCC i jony Na

+

zajmują wszystkie luki oktaedryczne w

komórce elementarnej.

b.

Jony Ca

2+

tworzą strukturę typu FCC i jony F

–

zajmują wszystkie osiem luk

tetraedrycznych w komórce elementarnej.

c.

Jony O

2–

tworzą strukturę typu FCC i jony Na

+

zajmują wszystkie osiem luk

tetraedrycznych w komórce elementarnej.

d.

Jony S

2–

tworzą strukturę typu FCC i jony Zn

2+

zajmują co drugą lukę tetraedryczną w

komórce elementarnej.

Zn

2+

S

2-

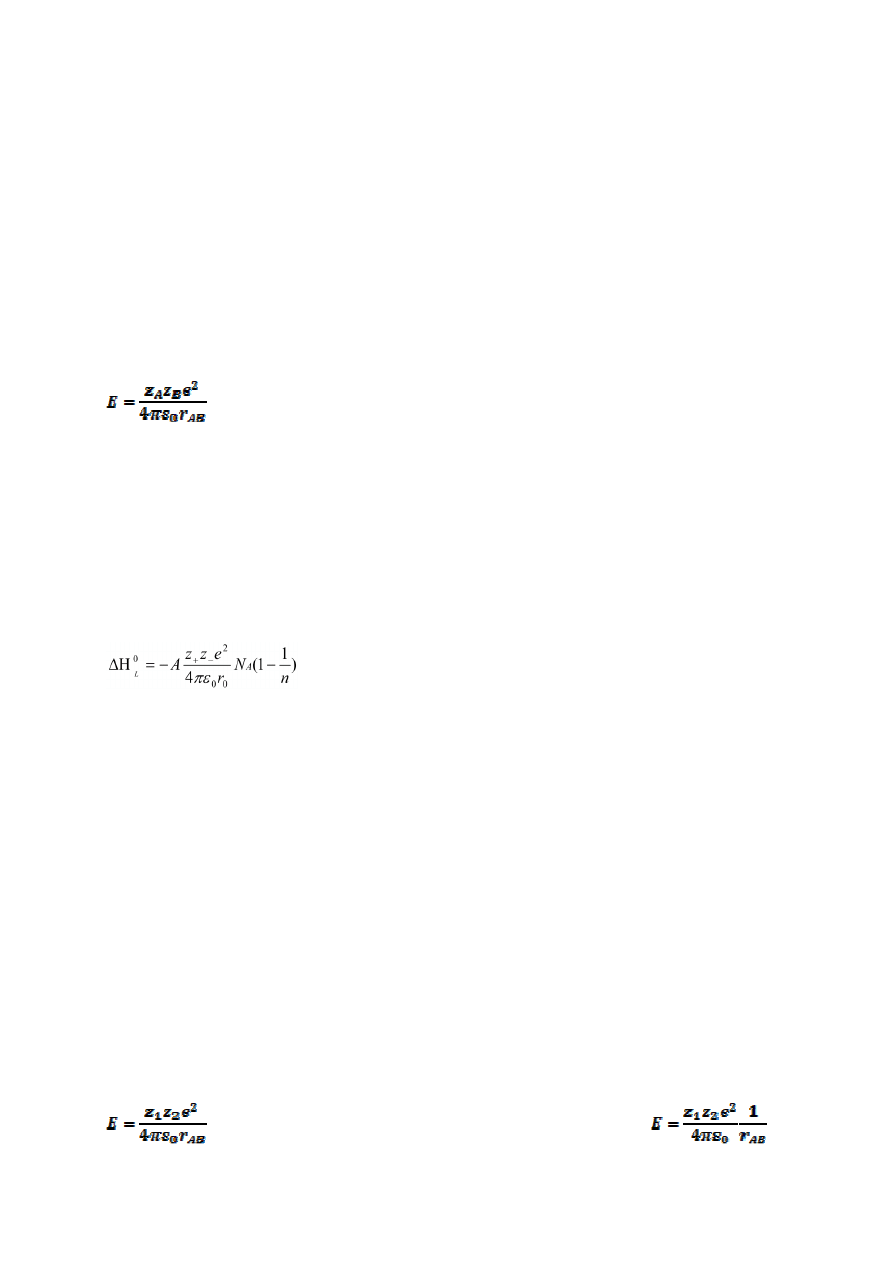
10.

Srebro tworzy sieć typu FCC i na podstawie pomiarów dyfrakcyjnych wykazano, że długość boku

komórki elementarnej wynosi 408,6 pm. Oblicz gęstość srebra (masa atomowa Ag wynosi

107,9 u). (2)

Z – 4 atomy na komórkę elementarną

a – długość boku komórki elementarnej [pm]

M

Ag

– masa atomowa Ag [u == g/mol]

Gęstość = Z * M

Ag

/a

3

N

A

Gęstość = 10.5 g/cm

3

11.

Który w podanych związków charakteryzuje się największą energią sieciową? Odpowiedź

uzasadnij uwzględniając oddziaływania elektrostatyczne pomiędzy jonami. LiF, NaF, CaF

2

, AlF

3

(1)

AlF

3

– największa energia przyciągania Coulombowskiego, największy ładunek z (iloczyn wynosi 3).

O wiele większy wpływ ładunku jonu na energię oddziaływania niż odległość pomiędzy jonami.

12.

Wapno, CaO, krystalizuje strukturze soli kamiennej. Oszacuj energię sieciową dla CaO. Wykładnik

Borna wynosi 8. (2)

Ca – 100 pm (dla LK = 6)
O – 140 pm (dla LK = 6)
A – 1,74756 dla soli kamiennej (NaCl);
n = 8

E = -3527 kJ/mol

13.

Oszacuj wartość energii sieciowej dla MgCl

2

na podstawie Cyklu Borna-Habera. (2)

ΔH

f

= ΔH

(sub)

+ IE

(1)

+ IE

(2)

+ ΔH

(dys)

- 2EA + U

(latt)

U

(latt)

= ΔH

f

- ΔH

(sub)

- IE

(1)

- IE

(2)

- ΔH

(dys)

+ 2EA

= -614.6 - 148 - 738 - 1450 - 243 + 2(349) kJ molˉ¹

= -2495.6 kJ molˉ¹

U

(latt)

= -2495.6 kJ molˉ¹

1. Musimy uwzględnić obydwie energie jonizacji magnezu.
2. Zgodnie z definicją podaną na kartce z danymi tablicowymi

powinowactwo elektronowe jest to energia

potrzebna do usunięcia elektronu z pojedynczo naładowanego anionu: X

–

= X + e. Bardziej ogólnie można

zapisać, że powinowactwo elektronowe = E

koniec

– E

początek

, w przypadku kiedy dodatkowy elektron jest

przyłączony do atomu lub cząsteczki. Oznacza to, że do obliczeń z cyklu Borna-Habera należy wziąć ujemną
wartość powinowactwa elektronowego. Wartość tą bierzemy dwukrotnie – dla każdego atomu chloru.

14.

Podaj wartość stałej Madelunga dla pary jonów A

+

B

-

. (1)

; ilość najbliższych sąsiadów w odległości 1r

AB

wynosi 1, zatem

, a

stała wynosi 1. Również w strukturach 3D każda para jonów liczona jest tylko raz.

15.

Podaj i uzasadnij obliczeniami wartość stałej Madelunga dla atomów zaznaczonych strzałką na

poniższym rysunku, uwzględniając wszystkie narysowane atomy. Różne kolory oznaczają jony o

różnym znaku, narysowany wielościan to sześcian. Czy na podstawie obliczonej wartości stałej

Madelunga można coś powiedzieć o względnej reaktywności ty jonów (uzasadnij)? Jeśli tak, to

co? (2+1)

Rozwiązanie podobnie jak w grupie 2.