Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
1/5
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
29:
A
NALYTICKÁ GEOMETRIA
1. príklad (301/Pr. 2)
Zadanie: Ur
č
te vzdialenos
ť
mimobežiek p, q, pri
č
om:
:
p
R
t
t
z
t
y
t
x
∈
−
=
+
=
+
=
;
9
2
3
7
:
q
R
s
s
z
s
y
s
x
∈
+
=
+
=
−
=
;
3
1
2
1
7
3
Riešenie:
[
]
[
]
3
,
2
,
7
u
;
1
,
2
,
1
u
q
p
−
=
−
=
pq
=
XY
H
ľ
adáme body
Y
X,
také, že
q
p
q
p
⊥
∧
⊥
∧
∈
∧
∈
XY
XY
Y
X
, takže
(
)
(
)
[
]
[ ] (
)
R
k
k
k
k
∈
⋅
=
⋅
=
×
⋅
=
⇒
⊥
∧
⊥
4
,
1
,
2
16
,
4
,
8
u
u
u
u
u
u
u
q
p
XY
q
XY
p
XY
Pre smerový vektor
XY
zárove
ň
platí:
[
] [
]
t
s
t
s
t
s
t
s
t
s
t
s
+
+
−
−
+
−
−
−
−
=
+
−
+
−
−
+
−
−
−
=
=
3
8
,
2
2
2
,
7
4
9
3
1
,
2
3
2
1
,
7
7
3
XY
u
XY
Teraz dostávame tri rovnice o troch neznámych:
2
;
0
4
3
8
2
2
2
2
7
4
−
=
=
=
=
+
+
−
=
−
+
−
=
−
−
−
k
t
s
k
t
s
k
t
s
k
t
s
Do parametrických vyjadrení mimobežiek dosadíme hodnoty
s
a
t
a dostaneme body
[
]
7,3,9
X
a
[
]
3,1,1
Y
.
21
2
84
64
4
16
XY
=
=
+
+
=
=
pq
Vzdialenos
ť
mimobežiek
q
p
,
je
21
2
.
2. príklad (303/1)
Zadanie: Je daná rovina
0
6
3
2
:
=
−
−
+
z
y
x
α
a priamka
R
t
t
z
t
y
t
x
p
∈
+
=
+
=
−
=
,
3
4
,
2
2
,
1
:
.
a) Ur
č
te prienik priamky
p
a roviny
α
.
b) Napíšte parametrické vyjadrenie pravouhlého priemetu priamky
p
do roviny
α
.
Riešenie:
[
]
1
,
3
,
2
n
−
=
α
[
]
3
,
2
,
1
u
−
=
p
a)
α
α
,
0
1
n
u
p
p
⇒
≠
=
⋅
nie sú rovnobežné
α
,
p
⇒
sú rôznobežné
{ }
α
∩
=
p
P
Súradnice P:

Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
2/5
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
29:
A
NALYTICKÁ GEOMETRIA
( ) (
) (
)
[
]
10
,
6
,
1
P
2
0
6
3
4
6
6
2
2
0
6
3
4
2
2
3
1
2
−
⇒
=
=
−
−
−
+
+
−
=
−
+
−
+
+
−
t
t
t
t
t
t
t
Prienik priamky
p
a roviny
α
je bod
[
]
10
,
6
,
1
P
−
.
b)
[
]
1,2,4
A
;
A
p
∈
:
A
k
k
α
k
⇒
∈
∧
⊥
R
s
s
z
s
y
s
x
∈
−
=
+
=
+
=
;
4
3
2
2
1
{ }
α
∩
=
k
K
A
Súradnice
A
K
:
(
) (
) (
)
⇒
=
=
−
+
−
+
+
+
=
−
−
−
+
+
+
7
27
,
7
17
,
7
9
A
7
1
0
6
4
9
6
4
2
0
6
4
3
2
3
2
1
2
K
s
s
s
s
s
s
s
:
PA
K
R
k
k
z
k
y
k
x
∈
−
=
−
=
+
−
=
;
7
43
10
7
25
6
7
16
1
:
PA
K
R
k
k
z
k
y
k
x
∈
−
=
−
=
+
−
=
;
43
10
25
6
16
1
Kolmý priemet priamky
p
do roviny
α
je priamka
K
PA
.
3. príklad (303/3)
Zadanie: Napíšte rovnicu priamky
q
, ktorá prechádza bodom
[ ]
3
,
5
A
a zviera s priamkou
0
1
3
:
=
−
+
y
x
p
uhol
°
=
60
α
.
Riešenie:
0
:
=
+
+
c
by
ax
q
2
1
60
cos
=
°
3
1
3
n
n
n
n
2
2
+
⋅
+
+
=
⋅
⋅
=
b
a
b
a
p
q
p
q
1
2
2
3
b
a
b
a
+
+
=
b
a
3
+
2
2
b
a
+
=
2
2
3
3
2
b
ab
a
+
+
2
2
b
a
+
=
2
2
3
2
b
ab
+
0
=
(
)
b
a
b
+
⋅
3
2
0
=
⇓

Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
3/5
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
29:
A
NALYTICKÁ GEOMETRIA
0
=
b
3
a
b
−
=
∨
[ ]
0
,
n
a
q
=
[
]
3
,
n
a
a
q
−
=
∨
[ ]
0
,
1
n
=
q
[ ]
3
,
1
n
−
=
∨
q
0
:
=
+
c
x
q
0
3
:
=
+
−
∨
c
y
x
q
0
5
:
A
=
+
∈
c
q
0
3
5
:
=
+
−
∈
∨
c
q
A
5
−
=
c
2
−
=
∨
c
Rovnice
priamok
2
1
, q
q
prechádzajúcich
bodom
[ ]
3
,
5
A
a zvierajúcich
s priamkou
0
1
3
:
=
−
+
y
x
p
uhol
°
=
60
α
sú
0
5
:
1
=
−
x
q
a
0
2
3
:
2
=
−
−
y
x
q
.
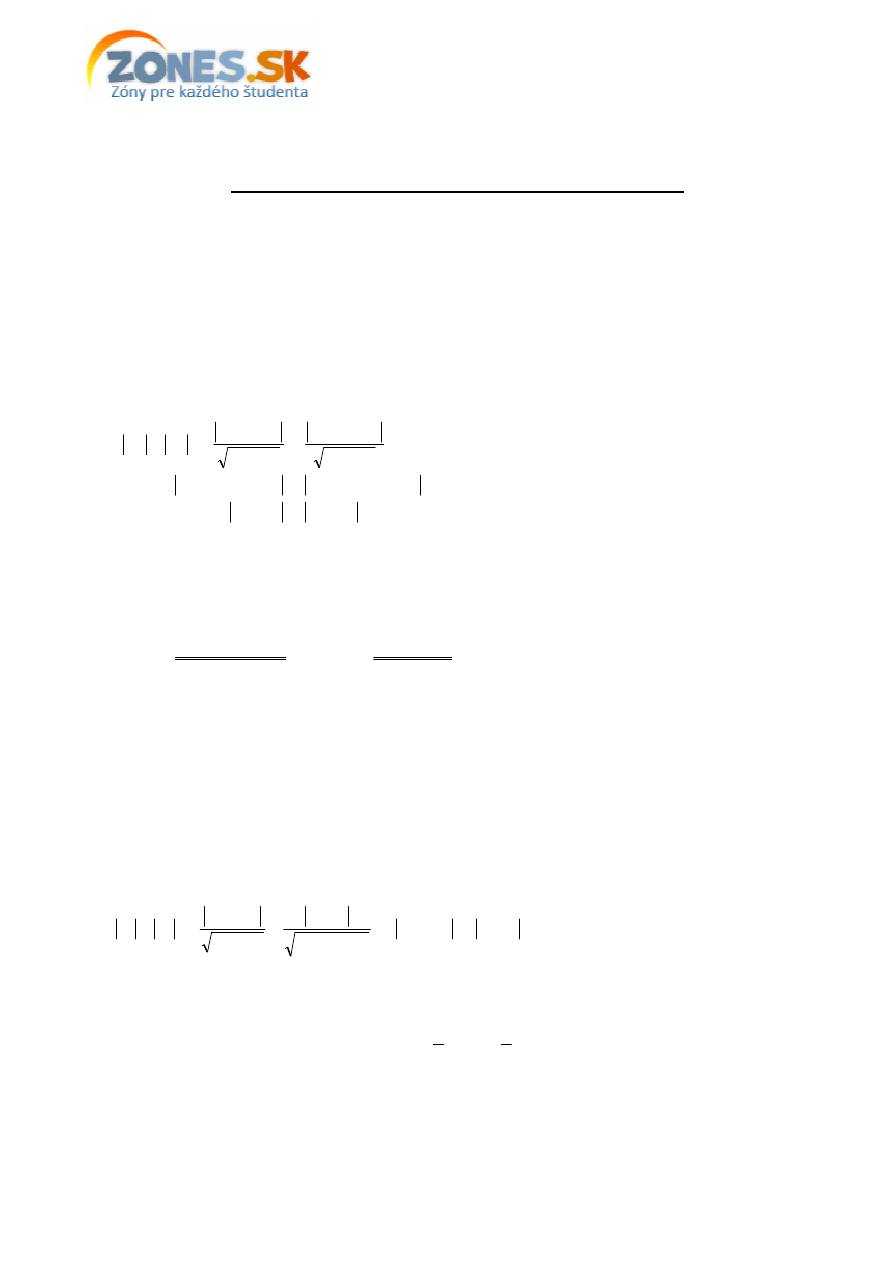
Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
4/5
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
29:
A
NALYTICKÁ GEOMETRIA
4. príklad (303/6)
Zadanie: Sú dané body
[
] [ ] [ ]
3,7
B
,
1
5,
A
,
2,3
M
−
−
. Nájdite všetky priamky, ktoré prechádzajú bodom
M
a majú od bodov
B
A,
rovnakú vzdialenos
ť
.
Riešenie:
0
:
=
+
+
c
by
ax
p
b
a
c
c
b
a
p
3
2
0
3
2
M
−
=
⇒
=
+
+
−
⇒
∈
2
2
5
Bp
Ap
b
a
c
b
a
+
+
−
⇒
=
2
2
7
3
b
a
c
b
a
+
+
+
=
b
a
b
a
3
2
5
−
+
−
b
a
b
a
3
2
7
3
−
+
+
=
b
a
4
7
−
b
a
4
5
+
=
⇓
b
a
8
2
=
0
12
=
∨
a
1
4
=
=
b
a
∨
1
0
=
=
b
a
0
4
:
=
+
+
c
y
x
p
0
:
=
+
∨
c
y
p
0
5
4
:
M
=
+
+
⇒
∈
y
x
p
p
0
3
:
M
=
−
⇒
∈
∨
y
p
p
Priamky, ktoré prechádzajú bodom
M
a majú od bodov
B
A,
rovnakú vzdialenos
ť
sú:
0
5
4
:
1
=
+
+
y
x
p
a
0
3
:
2
=
−
y
p
.
5. príklad (304/10)
Zadanie: Ur
č
te rovnice dvoch navzájom kolmých priamok, ktoré prechádzajú bodom
[ ]
1
,
7
A
a od
za
č
iatku súradnej sústavy majú rovnakú vzdialenos
ť
.
Riešenie:
⇒
⊥
q
p
0
:
=
+
+
c
by
ax
p
,
0
:
=
+
−
d
ay
bx
q
b
a
c
c
b
a
p
−
−
=
⇒
=
+
+
⇒
∈
7
0
7
A
b
a
d
d
a
b
q
7
0
7
A
−
=
⇒
=
+
−
⇒
∈
( )
b
a
a
b
b
a
b
a
b
a
−
−
⇒
−
+
−
=
+
−
−
⇒
=
7
7
7
0q
0p
2
2
2
2
b
a
7
−
=
⇓
b
a
b
a
7
7
−
=
+
a
b
b
a
−
=
+
∨
7
7
b
a
8
6
−
=
b
a
6
8
=
∨
b
a
3
4
−
=
b
a
4
3
=
∨
0
4
3
:
0
3
4
:
=
+
−
−
=
+
−
d
y
x
q
c
y
x
p
∨
0
3
4
:
0
4
3
:
=
+
−
=
+
+
d
y
x
q
c
y
x
p
0
3
4
:
0
4
3
:
=
+
−
=
+
+
c
y
x
p
d
y
x
q
∨
0
3
4
:
0
4
3
:
=
+
−
=
+
+
d
y
x
q
c
y
x
p

Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
5/5
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
29:
A
NALYTICKÁ GEOMETRIA
0
4
3
:
=
+
+
c
y
x
p
,
0
3
4
:
=
+
−
d
y
x
q
0
25
4
3
:
A
=
−
+
⇒
∈
y
x
p
p
0
25
3
4
:
A
=
−
−
⇒
∈
y
x
q
q
Rovnice dvoch navzájom kolmých priamok, ktoré prechádzajú bodom
[ ]
1
,
7
A
a od za
č
iatku súradnej
sústavy majú rovnakú vzdialenos
ť
sú
0
25
4
3
:
=
−
+
y
x
p
a
0
25
3
4
:
=
−
−
y
x
q
.
Wyszukiwarka
Podobne podstrony:
10 ANALYTICKA GEOMETRIE
Analyticka geometria
geometria w płaszczyźnie
GEOMETRIA
GEOMETRIA OBLICZENIOWA I
lec6a Geometric and Brightness Image Interpolation 17
Geometria wykreślna Ćwiczenie 8
Algebra liniowa i geometria kolokwia AGH 2012 13
Geometria wykreślna przenikanie brył2
GK 9 Przekształcenia geometryczne
Zynel M Geometria elementarna id 106714
Geometria Wykreślna wykłady
Geometria krzywych i powierzchn Nieznany
Geometria W 1 2
geometria analityczna
Co to jest teoria względności podstawy geometryczne
więcej podobnych podstron