ZESTAW 5. Granica i ciągłość funkcji
Zadanie 5.1. Obliczyć następujące granice (o ile istnieją)
a)
1
2
)
1
(
lim
2
1
−
−
−
→
x
x
x
x
b)
1
5
6
1
8
lim
2
3
2
1
+
−
−
→
x
x
x
x
c)
)
1
3
1
1
(
lim
3
1
x
x
x
−
−
−
→
d)
2
3
2
1
lim
4
−
−
+
→
x
x
x
e)
9
1
2
13
lim
2
3
−
+
−
+
→
x
x
x
x
f)
x
x
x
3
sin
5
sin
lim
0
→
g)
2
0
1
cos
lim
x
x
x
−
→
h)
2
0
cos
1
lim
x
x
x
−
→
i)
2
1
1
lim
2
2
x
x
x
x
−
+
∞
→
j)
x
x
x
1
sin
lim
∞
→
k)
)
1
3
(
lim
+
−
+
∞
→
x
x
x
l)
)
1
1
(
lim
2
2
x
x
x
x
x
+
−
−
+
+
∞
→
m)
1
1
2
3
2
lim
+
∞
→
+
+
x
x
x
x
n)
5
2
1
2
1
3
lim
−
∞
→
+
−
x
x
x
x
o)
x
x
x
1
sin
lim
0
→
p)
1
1
lim
3
2
1
−
−
→
x
x
x
q)
1
3
3
2
lim
+
+
∞
→
x
x
x
x
r)
1
3
1
3
4
lim
+
−∞
→
−
+
x
x
x
Zadanie 5.2. Obliczyć granice jednostronne funkcji f w punkcie
0
x
, jeżeli:
a)
3
,
3
1
)
(
0
=
−
=
x
x
x
f
b)
3
,
3
1
)
(
0
=
−
=
x
x
x
f
c)
3
,
)
3
(
1
)
(
0
2
=
−
=
x
x
x
f
d)
1
,
1
1
)
(
0
=
−
+
=
x
x
x
x
f
e)
2
,
4
1
)
(
0
2
=
−
=
x
x
x
f
f)
1
,
2
)
(
0
1
1
=
=
−
x
x
f
x
g)
2
,
4
)
(
0
4
1
2
=
=
−
x
x
f
x
h)
2
,
e
)
(
0
4
1
2
−
=
=
−
x
x
f
x
i)
0
,
e
1
)
(
0
1
=
−
=
x
x
x
f
x
Zadanie 5.3.
Obliczaj
ą
c granice jednostronne zbada
ć
, czy istniej
ą
granice
a)
1
1
lim
1
−
+
→
x
x
x
b)
2
3
1
|
1
|
lim
x
x
x
x
−
−
→
c)
2
1
1
1
e
lim
x
x
−
→
d)
|
|
sin
lim
0
x
x
x
→
e)
1
1
]
[
lim
2
−
+
→
x
x
x
Zadanie 5.4.
Zbada
ć
ci
ą
gło
ść
funkcji f
a)
>
−
≤
+
=
+
0
dla
)
2
(
0
dla
1
3
)
(
2
1
x
x
x
x
f
x
b)
≥
−
<
−
=
0
dla
1
2
0
dla
1
2
)
(
x
x
x
x
f
x
c)
=
≠
=
−
1
dla
0
1
dla
e
)
(
1
x
x
x
f
x
x
d)
−
=
−
−
≠
+
+
=
1
dla
1
1
dla
|
1
|
)
(
2
x
x
x
x
x
x
f

e)
=
≠
=
0
dla
0
0
dla
1
cos
)
(
x
x
x
x
x
f
f)
=
≠
=
0
dla
0
0
dla
1
sin
)
(
x
x
x
x
f
Zadanie 5.5.
Sprawdzi
ć
, czy mo
ż
na dobra
ć
warto
ś
ci parametrów a i b tak, aby funkcja
f :
Ñ
→
Ñ
była ci
ą
gła, je
ż
eli
a)
>
−
≤
+
=
+
0
dla
)
(
0
dla
5
2
)
(
2
2
x
x
a
x
x
f
x
b)
>
−
≤
+
=
−
2
dla
|
2
|
2
dla
1
3
)
(
2
x
x
a
x
x
f
x
c)
≥
−
<
<
−
+
−
≤
+
=
+
1
dla
)
2
(
1
1
dla
1
dla
1
2
)
(
2
1
x
x
x
b
ax
x
x
f
x
d)
>
≤
≤
−
+
−
<
−
−
=
0
dla
sin
0
1
dla
2
3
1
dla
1
)
(
x
x
bx
x
x
x
x
a
x
f
ZESTAW 6. Pochodna funkcji. Reguła de l’Hospitala
Zadanie 6.1. Korzystając z definicji obliczyć pochodną funkcji f w punkcie
0
x
a)
2
,
4
2
)
(
0
2
3
=
−
+
=
x
x
x
x
f
b)
1
,
)
(
0
3
=
=
−
x
x
x
f
c)
4
,
)
(
0
=
=
x
x
x
x
f
Zadanie 6.2. Obliczyć pochodne następujących funkcji
a)
4
)
(
=
x
f
b)
x
x
x
x
x
f
+
−
+
=
2
2
)
(
3
c)
2
4
3
4
)
(
x
x
x
f
−
=
d)
x
x
x
f
−
+
=
1
3
4
)
(
e)
2
4
)
(
2
2
+
=
x
x
x
f
f)
1
3
)
(
4
−
=
x
x
f
g)
3
)
(
+
=
x
x
x
f
h)
)
2
)(
1
(
)
(
1
−
+
=
−
x
x
x
f
i)
)
2
(
4
)
(
3
3
x
x
x
f
−
=
j)
x
x
x
x
f
e
)
1
(
)
(
2
+
=
k)
5
4
)
(
+
=
x
x
f
l)
x
x
x
f
3
4
)
(
=
m)
x
x
x
f
ln
)
(
=
n)
3
ln
2
2
)
(
+
−
=
x
x
x
f
o)
x
x
x
f
+
=
2
ln
4
)
(
p)
x
x
f
2
log
)
(
2
=
r)
x
x
x
f
cos
sin
)
(
+
=
s)
x
x
x
f
cos
)
(
3
=
t)
x
x
x
f
sin
)
(
=
u)
x
x
x
x
x
f
cos
sin
cos
sin
)
(
−
+
=
v)
2
3
sin
2
)
(
2
+
=
x
x
x
f
w)
x
x
x
f
arcsin
)
(
+
=
x)
x
x
x
f
arccos
arcsin
)
(
+
=
y)
x
x
x
f
arctg
)
(
=
z)
x
x
x
f
+
−
=
1
1
)
(
aa)
)
e
1
e
ln(
)
(
x
x
x
f
+
+
=
ab)
5
2
e
)
(
−
=
x
x
f
ac)
x
x
x
f
−
=
1
sin
)
(
ad)
4
2
)
3
2
(
)
(
−
=
x
x
f
ae)
6
2
1
1
)
(
+
+
=
x
x
x
f
af)
3
ln
1
ln
)
(
+
=
x
x
x
f
ag)
)
5
3
cos(
)
(
2
x
x
x
f
+
=
ah)
x
x
f
5
sin
)
(
=
ai)
3
2
5
1
3
)
(
x
x
x
f
+
=
aj)
1
2
3
)
3
4
(
)
(
+
⋅
+
=
x
x
x
f
ak)
)
sin
1
(
)
(
3
x
x
x
f
+
=
Zadanie 6.3.
Obliczy
ć
pochodne
f
′
,
f
′′
,
f
′′′
dla podanych funkcji
a)
x
x
x
f
ln
)
(
2
=
b)
x
x
x
f
sin
)
4
(
)
(
3
+
=
c)
2
)
(
2
+
=
x
x
f
Zadanie 6.4.
Korzystaj
ą
c z reguły de l’Hospitala obliczy
ć
nast
ę
puj
ą
ce granice
a)
8
4
lim
3
2
2
−
−
→
x
x
x
b)
x
x
x
)
1
ln(
lim
0
+
→
c)
2
0
1
lim
x
x
e
x
x
−
−
→
d)
x
x
x
ln
lim
0
+
→
e)
e
1
ln
lim
e
−
−
→
x
x
x
f)
)
1
e
(
lim
1
−
−∞
→
x
x
x
g)
4
0
cos
1
lim
x
x
x
−
→
h)
x
x
x
x
cos
sin
lim
0
→
i)
3
2
ln
lim
x
x
x
∞
→
PDF Created with deskPDF PDF Writer - Trial :: http://www.docudesk.com

j)
x
x
x
e
lim
∞
→
k)
−
−
+
→
x
x
x
x
ln
1
1
lim
1
l)
x
x
x
ln
1
)
1
(
lim
−
+
→
m)
2
1
0
)
1
(
lim
x
x
x
+
+
→
n)
1
1
)
1
2
(
lim
+
+
∞
→
x
x
x
o)
)
ln
(
lim
2
x
x
x
−
∞
→
PDF Created with deskPDF PDF Writer - Trial :: http://www.docudesk.com

Zestaw 7 Badanie przebiegu zmienności funkcji
Zadanie 7.1 Znaleźć asymptoty funkcji:
a) f(x)=
x
x
−
−
5
7
4
b) f(x)=
2
1
1
x
−
c) f(x)=
3
2
2
+
x
x
d) f(x) =
4
2
2
3
−
+
x
x
x
e) f(x)=
1
2
+
x
x
f) f(x)=
9
2
3
−
−
x
x
g) f(x)=
x
x
2
2
1
+
+
h) f(x)=
x
x 2
1+
i) f(x)=
x
x
sin
j) f(x)=
x
e
x
−
2
Zadanie 7.2 Wyznaczyć przedziały monotoniczności funkcji:
a) f(x)= 2x 3 + 10x- 18 b) f(x)=2x 3 - 9x 2 +12x +2 c) f(x)=
4
2
+
x
x
d) f(x)=
2
2
1
2
3
+
+
x
x
e) f(x)= xe
x
2
−
f) f(x)= x- ln(1+x) g) f(x)=(x 2 - 4 )e
x
−
Zadanie 7.3 Wyznaczyć ekstrema funkcji:
a) f(x)= 2x 3 - 15x 2 + 36x – 14 b) f(x)= x 4 + 4x – 2 c) f(x)= x 3 + 3x 2 -9x -2
d) f(x)= x 4 + 4x 2 - 2 e) f(x)=
4
2
+
x
x
f) f(x)=
4
1
x 4 -
2
1
x 2
g) f(x)=
(
)
x
x
2
2
1−
h) f(x)= x - x i) f(x)= e
x + e x
−
j) f(x)=
1
2
4
2
+
+
x
x
k) f(x)=
1
2
2
+
x
x
Zadanie 7.4 Znaleźć najmniejszą i największą wartość funkcji w przedziałach:
a) f(x)= x 2 - 2x +3 , x∈[-2,5]
b) f(x)= 2x 3 - 3x 2 -36x- 8, x∈[-3, 6]
c) f(x)= -x 3 -3x 2 -9x + 21, x∈[-4, 2]
d) f(x)= -4x 3 +6x 2 +24x -3, x∈[0, 3]

e) f(x)= 2x 3 +21x 2 +36x -4, x∈[-2, 1]
f) f(x)= x- 2 x , x∈[0,5]
g) f(x)= x 2 lnx, x∈[1,e]
h) f(x)=
2
1
−
+
x
x
, x∈[3, 5]
i) f(x)=
4
2
1
2
+
+
x
x
, x∈[-1, 1]
j) f(x)=
2
2
3
2
2
+
−
x
x
, x∈[-1, 1]
Zadanie 7.5 Wyznaczyć punkty przegięcia, przedziały wypukłości i wklęsłości funkcji:
a) f(x)= 4
x
-4x 3 +8x 2
b) f(x)= 3
4
x +7x +1
c) f(x)=
4
x -12x 3 +48x 2
d) f(x)= 5
4
x +2x 3 +x 2
e) f(x)= -2
4
x -4x +5
f) f(x)=
2
2
3
3
3
2
12
4
x
x
x
+
−
g) f(x)=
2
2
+
x
x
h) f(x)= xe
x
−
i) f(x)=
x
x
ln
Zadanie 7.6 Zbadać przebieg zmienności funkcji i sporządzić wykresy funkcji:
a) f(x)= x 3 -3x 2 +4 b) f(x)=
(
) (
)
2
2
1
+
−
x
x
c) f(x)=
2
1 x
x
−
d) f(x)=
1
3
−
x
x
e) f(x)= x
1
−
x
f) f(x)=
x
x −
g) f(x)=
x
x
ln
h) f(x)= e
2
x
−
i) f(x)=
1
+
x
x
e
j) f(x)=
1
2
+
x
x
k) f(x)=
2
5
+
−
x
x
l) f(x)= x
3
+
x
x
Zadanie 7.7 Uzupełnić komentarze, wypełnić tabelkę i narysować wykres funkcji:
x∈(- ∞ , 4) ∪ (4, + ∞ )
+∞
=
−∞
→
)
(
lim
x
f
x
0
)
(
4
lim
=
→
−
x
f
x
+∞
=
→
+
)
(
4
lim
x
f
x
+∞
=
+∞
→
)
(
lim
x
f
x
+∞
=
−∞
→
x
x
f
x
)
(
lim
1
)
(
lim
=
+∞
→
x
x
f
x
(
)
0
)
(
lim
=
−
+∞
→
x
x
f
x
3
0
)
(
−
=
⇔
=
x
x
f
)
,
7
(
)
4
,
2
(
0
)
(
'
+∞
∪
∈
⇔
>
x
x
f

)
7
,
4
(
)
2
,
(
0
)
(
'
∪
−∞
∈
⇔
<
x
x
f
7
2
0
)
(
'
=
∨
=
⇔
=
x
x
x
f
)
,
4
(
)
4
,
(
0
)
(
"
+∞
∪
−∞
∈
⇔
>
x
x
f
f(2)= -2, f(7)=9
Zestaw 8 Całka nieoznaczona
Zadanie 8.1 Obliczyć:
a)
dx
x
x
x
∫
−
+
−
2
5
2
4
3
b)
dx
e
x
x
x
x
∫
+
−
+
−
−
2
3
4
6
5
7
9
4
c)
dx
x
x
x
∫
+
−
5
3
2
7 4
6
d)
dx
x
∫
3 4
e)
dx
x
x
x
x
∫
+
3
5 4
3 2
f)
dx
x
x
x
∫
−
6
4
3
g)
dx
x
x
∫
+
1
2
h)
dx
x
e
x
e
∫
−
−
1
1
2
i)
dx
x
x
x
∫
−
+
−
3
9
6
2
j)
dx
x
x
x
∫
−
sin
cos
2
cos
k)
dx
x
2
2
sin
∫
l)
∫
x
x
dx
2
cos
2
sin
Zadanie 8.2 Stosując metodę podstawiania obliczyć:
a)
dx
x
x
7
6
2
∫
+
b)
dx
x
x
−
∫
7
3
2
c)
dx
x
∫
−
5
4
d)
dx
x
x
∫
−
2
2
e)
dx
x
x
∫
+ 2
4
f)
dx
x
x
∫
+ 2
3
g)
dx
x
x
x
∫
+
+
6
3
2
2
h)
dx
x
x
∫
−
5
5
2
4
i)
dx
x
x
∫
+
5
6
2
5
j)
dx
x
∫
+
1
2
1
k)
dx
x
x
∫
ln
l)
dx
x
x
∫
ln
1
m)
dx
x
e
∫
+
−
9
4
n)
∫
+
−
dx
x
xe
8
2
o)
dx
x
x
e
∫
2
1
p)
dx
x
e
x
e
∫
+
1
4
q)
dx
x
x
e
x
e
∫
+
+
5
1
5
5
r)
dx
x
e
x
e
∫
+ 6
1
3
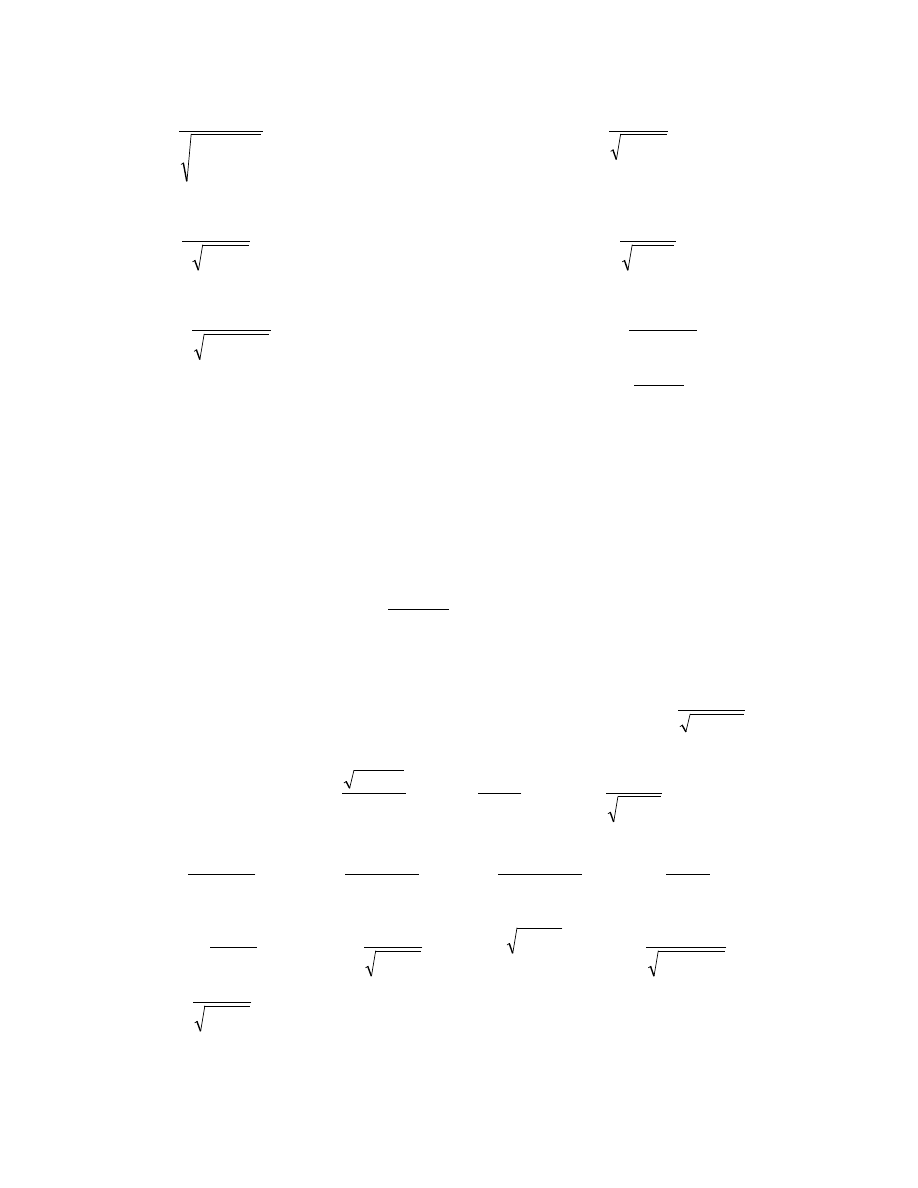
s)
dx
x
x
∫
−
3
2
1
3
t)
∫
−
9
2
x
xdx
u)
∫
−
2
2
x
x
dx
v)
∫
− 8
1
3
x
dx
x
w)
∫
−
+
−
x
e
dx
x
e
4
4
4
x)
∫
+
x
xdx
cos
5
1
sin
y)
∫
xdx
x
cos
sin
z)
dx
x
x
∫
ln
sin
Zadanie 8.3 Całkując przez części, obliczyć:
a)
dx
x
xe
∫
b)
dx
x
e
x
∫
2
c)
dx
x
e
x
∫
+
5
2
d)
dx
x
e
x
∫
+
1
3
e)
∫
xdx
ln
f)
∫
xdx
x
ln
g)
xdx
x
ln
3
∫
h)
xdx
x
e
sin
∫
i)
xdx
x
e
cos
∫
j)
∫
xdx
x
sin
2
k)
(
)
dx
x
x
e
x
∫
−
2
1
Zadanie 8.4 Obliczyć:
a)
∫
xdx
2
cos
b)
∫
xdx
2
sin
c)
∫
xdx
x
cos
5
sin
d)
∫
+
x
xdx
sin
1
cos
e)
dx
x
x
∫
+ 2
1
ln
f)
dx
x
x
∫
+
ln
2
g)
∫
+
1
4
x
xdx
h)
dx
x
x
∫
− 6
1
2
i)
dx
x
x
x
∫
+
+
−
1
2
1
3
j)
dx
x
∫
+
2
3
2
1
k)
dx
x
x
x
∫
−
+
+
10
3
2
6
4
l)
dx
x
∫
−
1
4
2
m)
dx
x
∫
+ 2
4
2
n)
dx
x
∫
− 2
5
1
o)
dx
x
∫
− 2
5
p)
dx
x
x
∫
−
+
2
1
1
q)
dx
x
∫
−
3
2
1
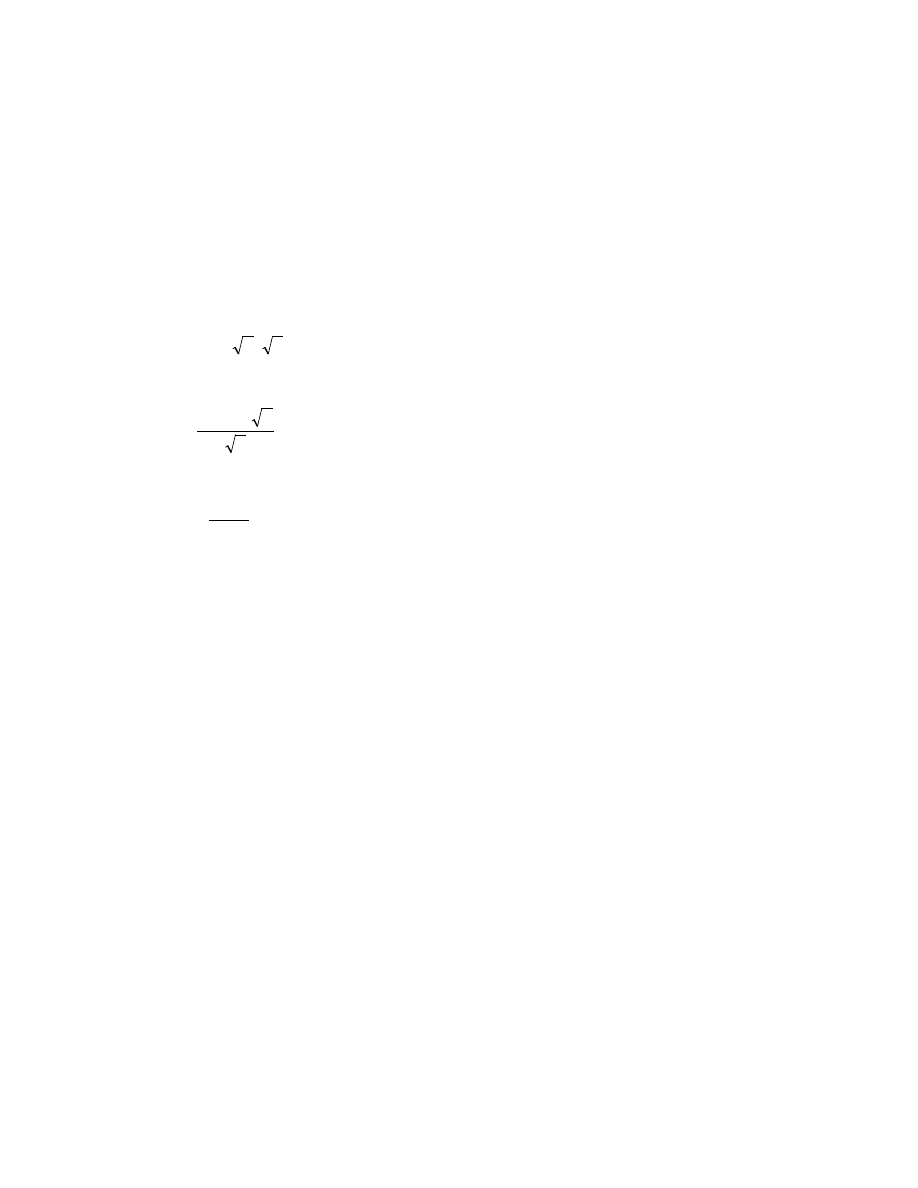
Zestaw 9 Całki oznaczone
Zadanie 9.1 Obliczyć całki oznaczone
a)
(
)
∫
−
−
2
1
7
3
dx
x
b)
∫
−
−
+
3
3
4
8
2
5
dx
x
x
c)
(
)(
)
∫
+
−
1
0
3
3
2
dx
x
x
x
x
d)
∫
+
2
1
3
3
2
2
dx
x
x
x
e)
∫
−
−
+
2
4
1
2
1
dx
x
f)
∫
+
4
3
3
2
dx
x
e
g)
∫
−
⋅
1
0
5
5
2
dx
x
e
x
h)
∫
+
⋅
1
0
4
2
3
dx
x
e
x
i)
∫
−
−
0
1
dx
x
xe
j)
∫
⋅
e
xdx
x
1
ln
k)
∫
⋅
3
1
2
ln xdx
x
Zadanie 9.2 Obliczyć pole obszaru ograniczonego krzywymi:
a)
x
y
x
y
5
,
2
=
=
b)
x
y
x
y
4
,
3
=
=
c)
2
2
2
,
x
y
x
y
−
=
=

d)
2
,
2
+
=
=
x
y
x
y
e)
4
,
1
,
0
,
5
4
2
=
=
=
−
−
=
x
x
y
x
x
y
f)
4
2
,
6
2
+
=
+
+
−
=
x
y
x
x
y
g)
4
17
,
1
+
−
=
=
x
y
x
y
h)
0
,
4
,
3
,
2
1
=
=
=
−
=
y
x
x
x
y
i)
0
,
2
,
0
,
1
1
=
=
=
+
−
=
y
x
x
x
y
j)
2
2
,
1
25
16
x
y
x
y
=
+
=
k)
,
3
2
2
3
x
x
x
y
−
−
=
x=1, x=2, y=0
l)
1
,
,
=
=
=
−
x
e
y
e
y
x
x
m)
2
2
4
,
4
x
y
x
y
−
=
−
=
n)
x
x
y
3
2
+
−
=
, x=1, x=2, y=0
o)
14
5
2
+
+
−
=
x
x
y
,
6
5
2
+
−
=
x
x
y
Zadanie 9.3 Obliczyć długość łuku
a)
2
2x
y =
,
1
0
≤
≤
x
b)
2
2
x
e
y =
,
2
ln
0
≤
≤
x
c)
x
x
y =
,
4
0
≤
≤
x
Zadanie 9.4 Obliczyć objętość bryły powstałej z obrotu wokół osi OX
a)
2
sin
3
x
y =
w przedziale
[
]
π
,
0
b)
x
e
y
2
2
=
w przedziale [0,1]
c)
x
y
cos
=
w przedziale
−
2
;
2
π
π
Zadanie 9.5 Obliczyć pole powierzchni obrotowej powstałej z obrotu
wokół
osi OX wykresu funkcji:
a)
x
y
cos
=
w przedziale
−
2
;
2
π
π

b)
x
y
2
=
w przedziale [0;1]
c)
x
y
sin
=
w przedziale [0;
π
]
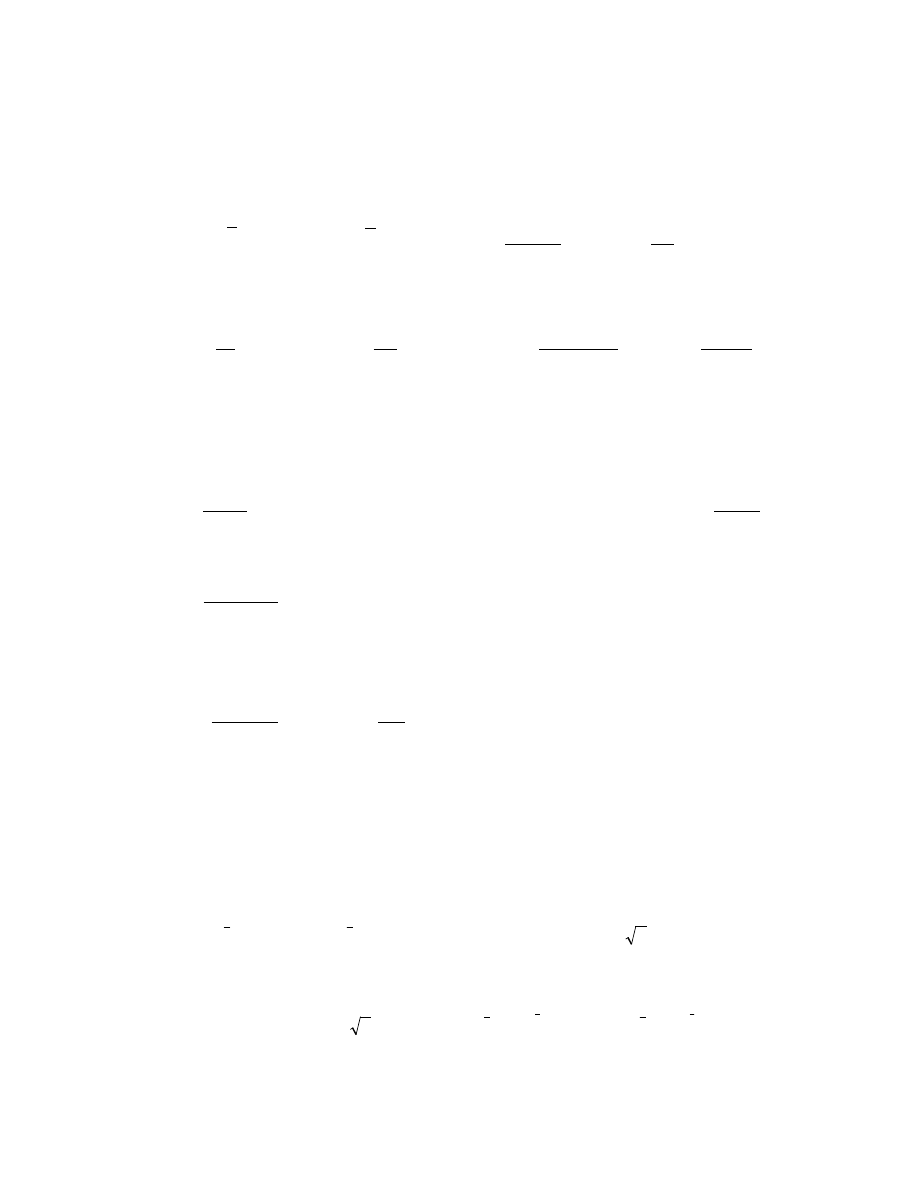
Zestaw 10 Całki niewłaściwe
Zadanie 10.1 Obliczyć całki niewłaściwe:
a)
dx
x
∫
−
−
1
2
3
1
b)
dx
x
∫
−
1
0
2
1
c)
(
)
∫
−
3
0
3
2
x
dx
d)
dx
x
∫
1
0
2
1
e)
∫
∞
+
1
x
dx
f)
dx
x
∫
∞
+
1
2
1
g)
∫
∞
+
∞
−
+
+
9
4
2
x
x
dx
h)
∫
∞
+
2
2
ln
x
x
dx
i)
∫
∞
+
∞
−
+
2
1
x
dx
j)
∫
∞
+
−
0
dx
x
e
k)
dx
x
arctgx
∫
∞
+
+
0
2
1
l)
∫
∞
+
−
2
2
9
2
2
x
xdx
m)
∫
−
1
0
2
5
3
x
x
dx
n)
dx
e
x
x
∫
1
3
ln
Zadanie 10.2 Obliczyć całki:
a)
dx
xe
x
∫
∞
−
0
2
b)
dx
e
x
x
∫
∞
−
0
2
5
c)
dx
e
x
x
∫
∞
−
0
6
d)
dx
e
x
x
x
∫
∞
−
0
3
e)
dx
e
x
x
∫
∞
−
0
4
5
f)
dx
e
x
x
x
∫
∞
−
0
2
3
g)
(
)
dx
x
x
∫
−
1
0
2
1
2
3
1
h)
(
)
dx
x
x
∫
−
1
0
2
1
2
1
1

i)
(
)
dx
x
x
∫
−
1
0
4
6
1
j)
(
)
dx
x
x
∫
−
3
1
0
8
5
3
1
k)
(
)
dx
x
x
∫
−
5
0
12
5
5
l)
(
)
dx
x
x
∫
−
1
0
5
3
1
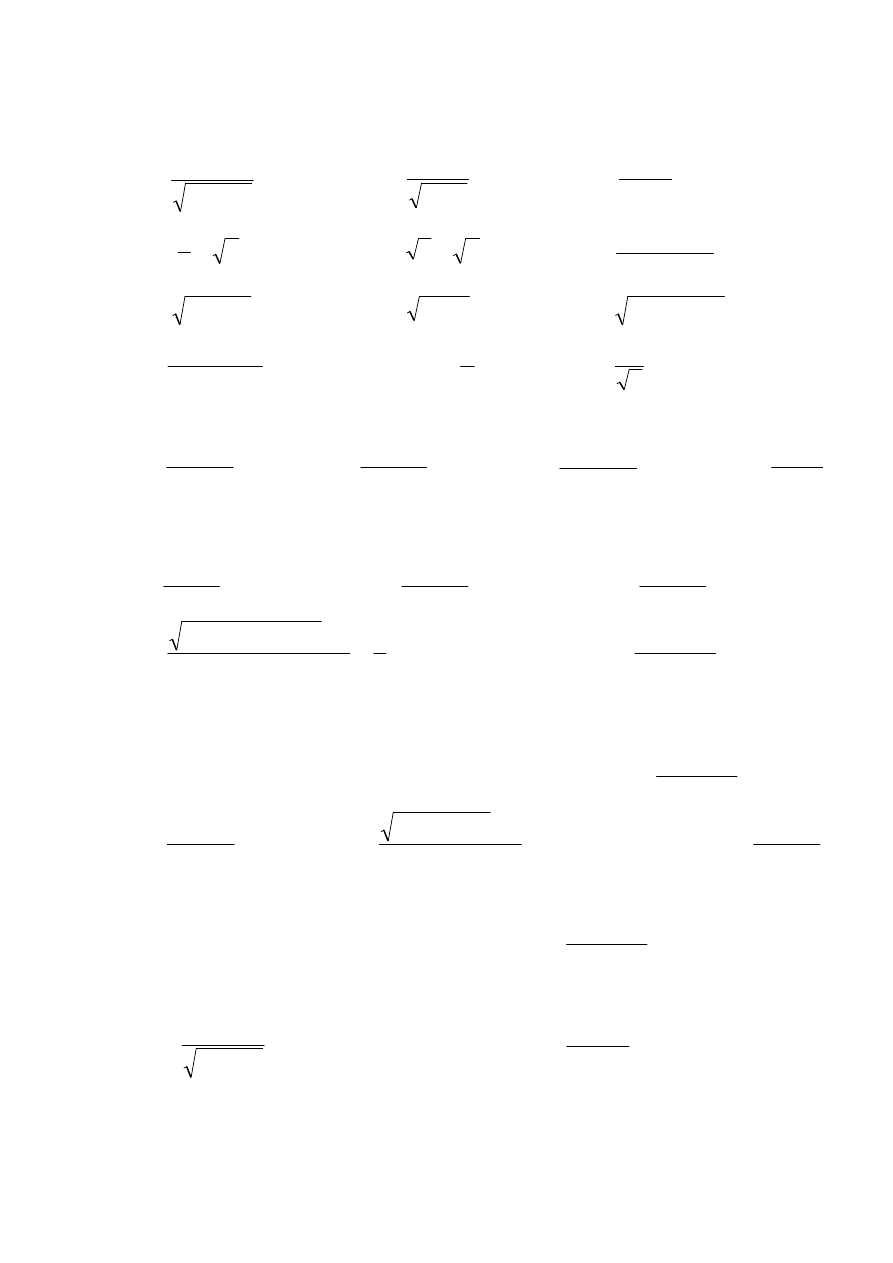
ZESTAW 11. Funkcje wielu zmiennych – granice i ciągłość oraz pochodne cząstkowe
Zadanie 11.1. Wyznaczyć dziedzinę funkcji
)
,
(
y
x
f
i przedstawić ją graficznie
a)
2
2
1
)
,
(
y
x
y
x
f
+
=
b)
y
x
y
x
f
+
=
1
)
,
(
c)
)
ln(
1
)
,
(
xy
y
x
f
=
d)
y
x
y
x
f
+
=
1
)
,
(
e)
y
x
y
x
f
+
=
)
,
(
f)
2
)
,
(
2
2
−
+
=
y
x
x
y
x
f
g)
2
2
)
,
(
y
x
y
x
f
−
=
h)
1
)
,
(
2
−
=
x
y
x
f
i)
2
2
4
)
,
(
y
x
y
x
f
−
−
=
j)
3
2
ln
)
,
(
2
−
−
=
x
x
y
y
x
f
k)
y
x
y
x
f
arcsin
)
,
(
=
l)
)
3
2
ln(
1
)
,
(
+
−
=
y
x
y
x
f
Zadanie 11.2. Wykazać, że nie istnieją następujące granice:
a)
2
2
)
0
,
0
(
)
,
(
lim
y
x
xy
y
x
+
→
b)
2
2
2
)
0
,
0
(
)
,
(
lim
y
x
x
y
x
+
→
c)
2
2
2
2
)
0
,
0
(
)
,
(
2
lim
y
x
y
x
y
x
−
+
→
d)
1
lim
2
6
)
1
,
0
(
)
,
(
−
→
y
x
y
x
Zadanie 11.3. Pokazać, że
a)
1
1
lim
2
)
0
,
1
(
)
,
(
=
+
→
y
x
y
x
b)
0
lim
2
2
3
)
0
,
0
(
)
,
(
=
+
→
y
x
x
y
x
c)
0
lim
2
2
4
4
)
0
,
0
(
)
,
(
=
+
−
→
y
x
y
x
y
x
d)
2
1
)
2
(
1
1
)
2
(
lim
2
2
2
2
)
2
,
0
(
)
,
(
=
−
+
−
+
−
+
→
y
x
y
x
y
x
e)
1
1
e
lim
2
2
)
0
,
0
(
)
,
(
2
2
=
+
−
+
→
y
x
y
x
y
x
Zadanie 11.4. Obliczyć następujące granice:
a)
)
2
(
lim
)
0
,
0
(
)
,
(
y
x
y
x
+
→
b)
)
(
lim
2
2
)
0
,
0
(
)
,
(
y
x
y
x
+
→
c)
2
2
)
0
,
0
(
)
,
(
1
e
lim
2
2
y
x
y
x
y
x
+
−
+
→
d)
y
x
y
x
y
x
+
−
+
→
1
e
lim
)
0
,
0
(
)
,
(
e)
2
2
2
2
)
0
,
0
(
)
,
(
3
9
lim
y
x
y
x
y
x
+
−
+
+
→
f)
2
2
2
2
)
0
,
0
(
)
,
(
1
ln
)
(
lim
y
x
y
x
y
x
+
+
→
Zadanie 11.5. Zbadać ciągłość funkcji f w punkcie (0,0)
a)
=
≠
+
=
)
0
,
0
(
)
,
(
gdy
0
)
0
,
0
(
)
,
(
gdy
)
,
(
2
2
y
x
y
x
y
x
y
x
f
b)
=
≠
+
−
=
+
)
0
,
0
(
)
,
(
gdy
1
)
0
,
0
(
)
,
(
gdy
1
e
)
,
(
2
2
2
2
y
x
y
x
y
x
y
x
f
y
x
c)
=
≠
+
−
=
+
)
0
,
0
(
)
,
(
gdy
0
)
0
,
0
(
)
,
(
gdy
1
e
)
,
(
4
4
4
4
y
x
y
x
y
x
y
x
f
y
x
d)
=
≠
=
−
−
)
0
,
0
(
)
,
(
gdy
3
)
0
,
0
(
)
,
(
gdy
e
3
6
)
,
(
1
2
y
x
y
x
y
x-
y
x
f
y
x
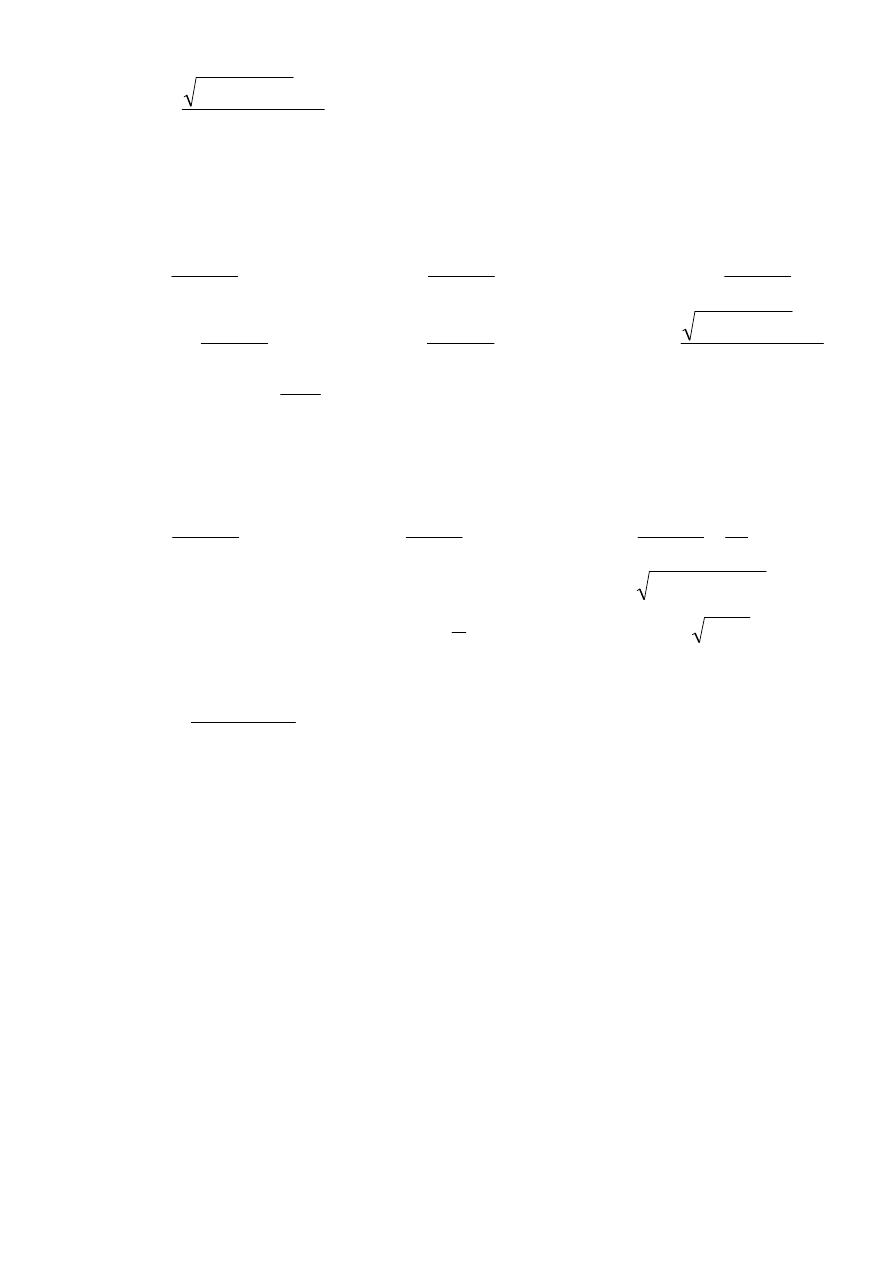
e)
=
≠
+
−
+
+
=
)
0
,
0
(
)
,
(
gdy
2
)
0
,
0
(
)
,
(
gdy
3
9
)
,
(
2
2
2
2
y
x
y
x
y
x
y
x
y
x
f
.
Zadanie 11.6. Zbadać, czy podane funkcje można tak określić w punkcie (0,0), aby były
ciągłe w tym punkcie.
a)
2
2
2
)
,
(
y
x
x
y
x
f
+
=
b)
2
2
4
)
,
(
y
x
x
y
x
f
+
=
c)
2
2
1
sin
)
,
(
y
x
x
y
x
f
+
=
d)
2
2
1
sin
)
,
(
y
x
y
x
f
+
=
e)
y
x
y
x
f
y
x
+
−
=
+
1
e
)
,
(
f)
2
2
2
2
3
9
)
,
(
y
x
y
x
y
x
f
+
−
+
+
=
g)
2
2
1
2
2
)
1
(
)
,
(
y
x
y
x
y
x
f
+
+
+
=
Zadanie 11.7. Wyznaczyć pochodne cząstkowe rzędu pierwszego dla podanych funkcji:
a)
3
2
5
3
)
,
(
xy
y
x
y
x
f
+
=
b)
x
y
y
x
f
5
sin
)
,
(
=
c)
))
sin(
2
(
)
,
(
y
x
y
e
y
x
f
x
+
+
=
d)
2
2
3
)
,
(
y
x
x
y
x
f
+
=
e)
y
x
y
x
y
x
f
+
−
=
2
)
,
(
f)
xy
y
x
y
xy
y
x
f
1
2
)
,
(
2
+
+
−
=
g)
y
x
y
x
f
+
=
2
2
3
)
,
(
h)
)
5
ln(
)
,
(
2
y
x
y
x
f
−
=
i)
2
2
2
)
,
(
xy
x
x
y
x
f
−
+
=
j)
x
x
y
x
f
y
ln
)
,
(
+
=
k)
x
y
y
x
f
arctg
)
,
(
=
l)
)
ln(
)
,
(
y
x
y
y
x
f
+
−
=
m)
z
y
xyz
z
y
x
f
3
2
3
)
,
,
(
+
=
n)
xz
z
z
y
z
y
x
f
y
x
2
e
)
1
ln(
)
,
,
(
3
−
+
−
=
+
o)
2
3
2
)
,
,
(
z
xy
z
xy
e
z
y
x
f
x
−
−
=
p)
)
3
ln(
2
5
)
,
,
(
2
xyz
y
x
z
x
z
y
x
f
+
−
+
+
=
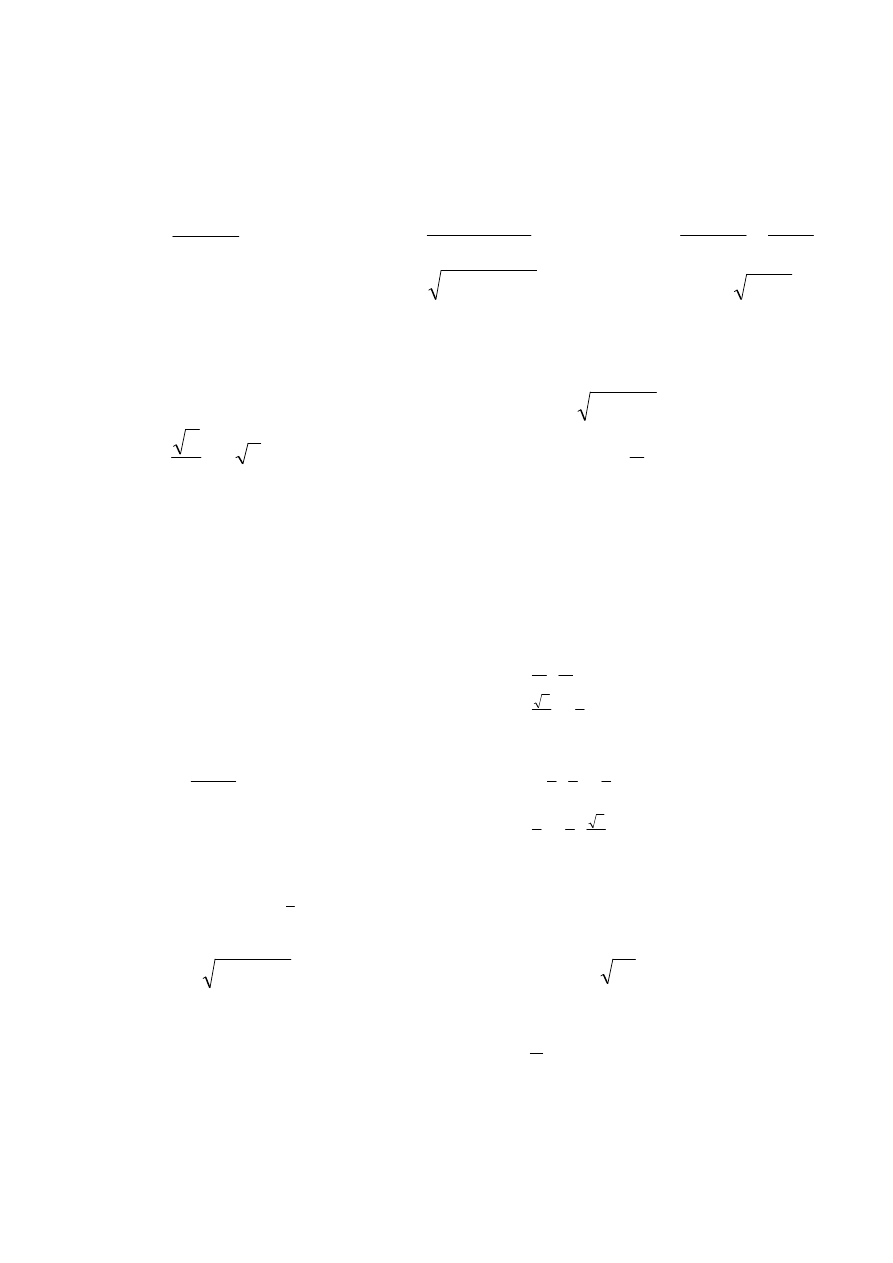
ZESTAW 12. Pochodne cząstkowe (cd.) i ekstrema funkcji wielu zmiennych
Zadanie 12.1. Wyznaczyć wszystkie pochodne cząstkowe rzędu drugiego podanych
funkcji:
a)
3
2
5
3
)
,
(
xy
y
x
y
x
f
+
=
b)
x
y
y
x
f
3
sin
3
)
,
(
=
c)
y
x
y
x
f
3
2
e
)
,
(
−
=
d)
2
2
3
)
,
(
y
x
x
y
x
f
+
=
e)
x
xy
xy
y
x
y
x
f
−
+
=
3
2
5
3
)
,
(
f)
y
x
x
xy
y
y
x
f
−
+
+
=
1
2
)
,
(
2
g)
)
3
2
ln(
)
,
(
2
y
x
y
x
f
−
=
h)
3
2
5
3
)
,
(
y
y
x
y
x
f
+
=
i)
)
ln(
)
,
(
y
x
x
y
x
f
−
+
=
j)
z
xy
z
x
z
y
x
f
3
2
5
3
)
,
,
(
+
=
k)
z
xy
z
x
z
y
x
f
3
2
5
)
2
ln(
3
)
,
,
(
+
+
=
Zadanie 12.2. Znaleźć gradienty podanych funkcji we wskazanych punktach:
a)
y
x
y
x
y
x
f
sin
)
,
(
3
2
−
=
,
P
0
=(
−
2,0) b)
2
2
)
,
(
y
x
y
x
f
−
=
, P
0
=(
−
5,3)
c)
x
y
x
y
y
x
f
+
=
)
,
(
, P
0
=(1,1) d)
x
y
y
x
y
x
f
+
=
2
)
,
(
, P
0
=(
−
2,1)
e)
3
2
5
3
)
,
(
xy
y
x
y
x
f
+
=
P
0
=(2,
−
3) f)
xy
y
x
f
arctg
)
,
(
=
P
0
=(
−
1,2)
g)
z
y
xyz
z
y
x
f
3
2
3
)
,
,
(
+
=
P
0
=(2,
−
1,3)
h)
xz
z
z
y
z
y
x
f
y
x
2
e
)
1
ln(
)
,
,
(
3
−
+
−
=
+
P
0
=(1,1,
−
2)
Zadanie 12.3. Obliczyć pochodne kierunkowe funkcji we wskazanych punktach i
kierunkach
a)
2
2
)
,
(
y
x
y
x
f
+
=
,
)
4
,
3
(
0
−
=
P
]
,
[
13
5
13
12
=
u
b)
y
x
y
x
f
sin
cos
)
,
(
=
,
)
0
,
(
0
π
=
P
]
,
[
2
1
2
3
−
=
u
c)
xy
y
x
f
arctg
)
,
(
=
,
)
1
,
1
(
0
=
P
]
1
,
1
[
=
u
d)
y
z
x
z
z
y
x
f
+
−
=
)
,
,
(
)
3
,
0
,
1
(
0
−
=
P
]
,
,
[
7
2
7
3
7
6
−
−
=
u
e)
xyz
z
y
x
f
e
)
,
,
(
=
)
1
,
1
,
1
(
0
−
−
=
P
]
,
,
[
4
3
4
3
2
1
−
=
u
Zadanie 12.4. Wyznaczyć ekstrema funkcji:
a)
3
3
1
2
2
8
4
)
,
(
y
x
y
x
y
x
f
−
+
=
b)
3
2
3
15
3
3
)
,
(
y
x
y
x
x
y
x
f
−
−
+
=
c)
xy
y
x
y
x
f
3
)
,
(
3
3
−
+
=
d)
2
2
4
4
2
4
2
)
,
(
y
xy
x
y
x
y
x
f
−
+
−
+
=
e)
2
2
3
2
)
,
(
y
x
y
x
f
+
−
=
f)
y
y
x
y
x
f
e
)
(
)
,
(
2
+
=
g)
x
y
x
y
x
f
e
)
2
(
)
,
(
2
+
=
h)
)
2
(
e
)
,
(
2
2
y
x
y
x
f
y
x
−
=
−
i)
2
2
)
2
ln(
)
,
(
y
x
y
x
y
x
f
−
−
+
=
j)
)
ln(
2
)
,
(
2
y
x
x
y
x
f
−
+
=

Zadanie 12.5. Wyznaczyć ekstrema lokalne funkcji uwikłanych
)
(x
y
y
=
określonych
równaniami:
a)
0
1
2
2
2
2
=
+
−
−
+
y
x
y
x
b)
0
3
2
e
=
−
+
−
y
xy
xy
c)
0
1
6
2
3
2
2
2
=
+
−
−
−
−
y
x
y
xy
x
d)
0
3
3
3
=
+
+
xy
y
x
e)
xy
y
x
4
2
4
=
+
f)
6
)
(
2
2
2
=
+
+
+
y
x
y
x
g)
0
2
2
4
=
−
−
−
y
y
x
x
h)
0
2
2
2
2
4
=
+
+
−
−
y
y
x
y
x
x
Wyszukiwarka
Podobne podstrony:
Geometria krzywych i powierzchni, zestaw 9
Geometria krzywych i powierzchni, zestaw 11
Geometria krzywych i powierzchni zestaw 9
Geometria krzywych i powierzchni, zestaw 8
Geometria krzywych i powierzchni zestaw 11
Geometria krzywych i powierzchni zestaw 7
Geometria krzywych i powierzchni zestaw 14
Geometria krzywych i powierzchni zestaw 8
Geometria krzywych i powierzchni, zestaw 7
Geometria krzywych i powierzchni, zestaw 13
Geometria krzywych i powierzchni, zestaw 10
Geometria krzywych i powierzchni, zestaw 12
Geometria krzywych i powierzchni, zestaw 9
Geometria krzywych i powierzchni, zestaw 11
03 PO Geometria 2013id 4609 Nieznany (2)
geometria-krzywe-i-powierzchnie-notatki-z-wykladu 3
GEOMETRIA 2 id 189404 Nieznany
Geometria i Grafika Inzynierska Nieznany (2)
więcej podobnych podstron