Materiały pomocnicze do ćwiczeń z przedmiotu:

Termodynamika techniczna

Rozdział 1

Gazy jako czynnik termodynamiczny

mgr inż. Agnieszka Sadłowska-Sałęga

Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 1

mgr inż. Agnieszka Sadłowska-Sałęga

3

1 Gaz jako czynnik termodynamiczny

Gaz doskonały (idealny) jest to abstrakcyjny, matematyczny model gazu, spełniający na-

stępujące warunki:

 brak oddziaływań międzycząsteczkowych z wyjątkiem odpychania w momencie zderzeń cząste-

czek;

 objętość cząsteczek jest znikoma w stosunku do objętości gazu;

 zderzenia cząsteczek są doskonale sprężyste;

 cząsteczki znajdują się w ciągłym chaotycznym ruchu.

Gaz doskonały posiada stałe ciepło właściwe (niezależne od temperatury i ciśnienia), nie zmienia

stanu skupienia. Można go traktować jako zbiór cząstek stanowiących punkty materialne. Ściśle

podporządkowuje się następującym prawom gazowym:

1. Boyle’a i Mariotte’a;

2. Gay-Lussaca;

3. Avogadra.

Gaz półdoskonały stosuje się do wyżej wymienionych trzech praw, ale jego ciepło właściwe

nie jest stałe i zależy od temperatury.

Gaz rzeczywisty – pojęcie termodynamiczne oznaczające gaz, który nie zachowuje się ściśle

zgodnie z prawami ustalonymi dla gazu doskonałego. W praktyce są to wszystkie gazy istniejące w

realnym świecie, aczkolwiek przybliżenie gazu doskonałego może w wielu warunkach być do nich

z powodzeniem zastosowane. Przybliżenie to zawodzi jednak w skrajnych warunkach, oraz gdy

istnieje potrzeba dokonania bardzo dokładnych obliczeń w warunkach zbliżonych do normalnych.

Należy zwrócić uwagę na to że gazy rzeczywiste znajdujące się pod niezbyt dużymi ciśnieniami

i w temperaturach znacznie wyższych od temperatur, w których mogłyby być bez zmiany ciśnienia

zmienione w ciecz, a zarazem niższych od tych, w których dysocjacja odgrywałaby dużą rolę, mają

własności bardzo zbliżone od własności gazów półdoskonałych. Stosując wtedy do nich prawa

Boyle'a i Mariotte'a, Gay-Lussaca, Avogadra i wynikające z tych praw wzory popełniamy tylko

małe błędy. Stosowanie zaś omawianych praw gazowych bardzo ułatwia nam obliczenia.

Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 1

mgr inż. Agnieszka Sadłowska-Sałęga

4

Jako gazy półdoskonałe traktować więc można suche powietrze, azot, tlen, hel, metan i wiele

innych gazów znajdujących się pod ciśnieniem nie przekraczającym 4 MPa w temperaturach panu-

jących u nas zwykle w zimie i w lecie, a tym bardziej temperaturach wyższych. Natomiast nie wol-

no traktować jako gazów półdoskonałych tlenu zawartego w butli pod ciśnieniem 15 MPa (za wy-

sokie ciśnienie), pary wodnej wytworzonej w kotle parowym (w kotłach niskoprężnych temperatura

tej pary jest często równa lub niewiele wyższa od temperatury, w której można zamienić ją na ciecz,

para zaś wyprodukowana w nowoczesnych kotłach wysokoprężnych ma za duże ciśnienie) itd.

[Wilk. 1998].

Jeżeli w rozpatrywanym przez nas zagadnieniu ciepło właściwe gazu zmienia się bardzo mało

lub jeżeli chodzi nam tylko o obliczenia orientacyjne, to często nie tylko stosujemy omawiane tu

prawa gazowe, ale zakładamy jeszcze dodatkowo, że ciepło właściwe danego gazu jest niezmienne

– czyli traktujemy gaz jako doskonały.

1.1 Prawa gazowe

1.1.1 Prawo Boyle'a-Mariotte'a

1

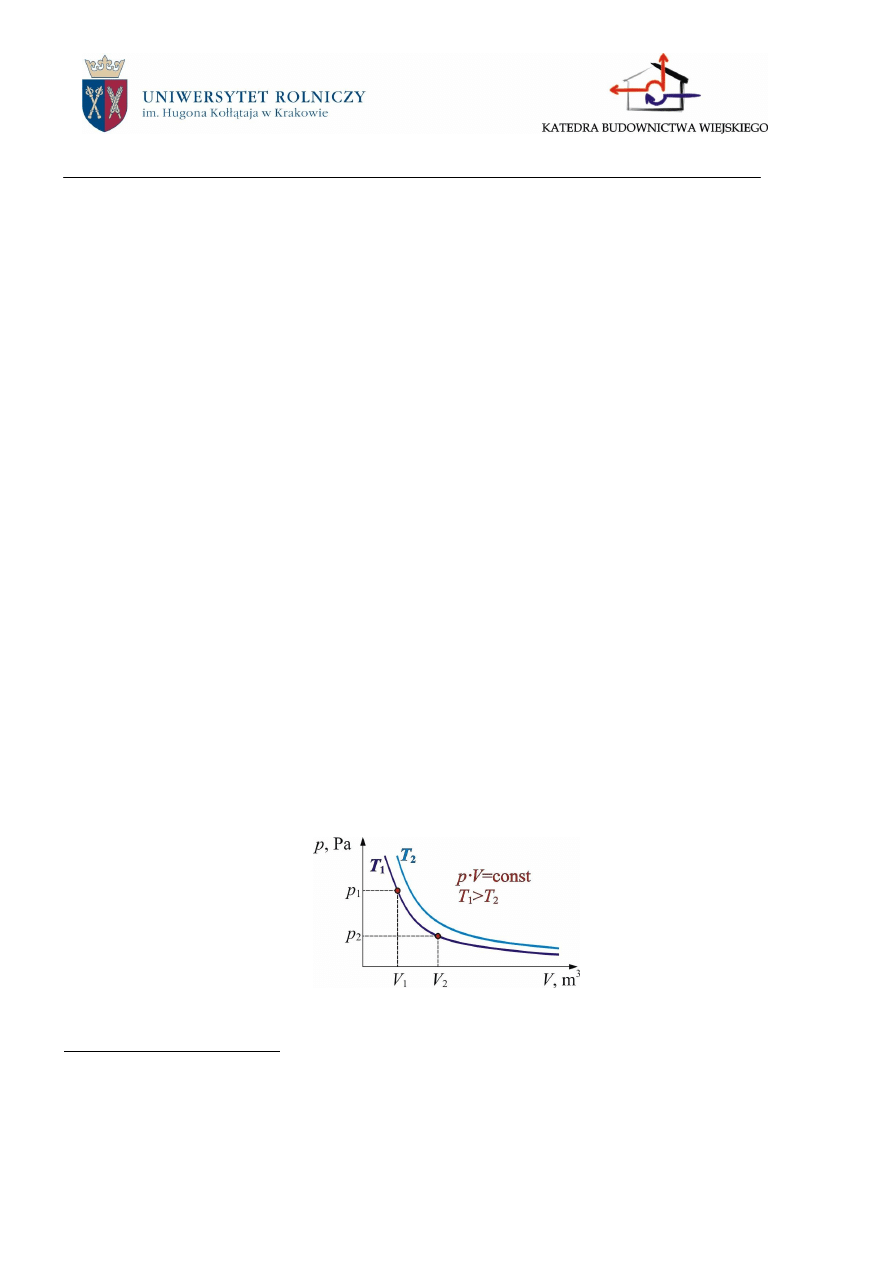
Prawo Boyle'a-Mariotte'a dotyczy zachowania gazu doskonałego w przemianie izotermicznej:

Jeżeli temperatura gazu nie zmienia się, to iloczyn jego ciśnienia bezwzględnego i objętości jest

wielkością stałą.

Gdy T = const:

const.



V

p

(1.1)

1

Prawo Boyle'a-Mariotte'a, zwane też (głównie w krajach anglosaskich) prawem Boyle'a, a prawem Mariotte'a we

Francji, zostało podane w1662 r. przez irlandzkiego naukowca Roberta Boyle'a, a niezależnie od niego w 1676 r.
przez Francuza Edme Mariotte'a.

Rys.1.1. Graficzna interpretacja prawa Boyle'a-Mariotte'a

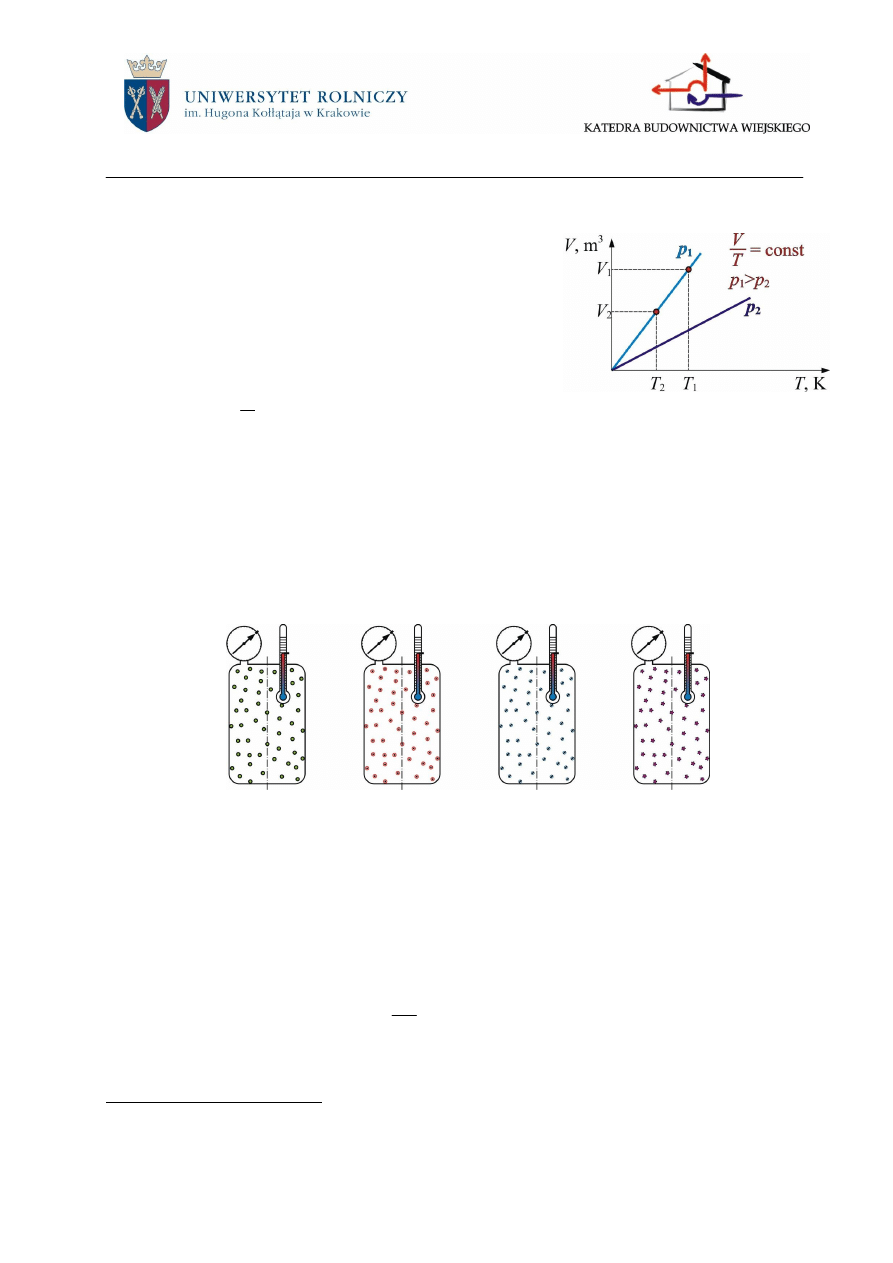
Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 1

mgr inż. Agnieszka Sadłowska-Sałęga

5

1.1.2 Prawo Gay-Lussaca

2

Prawo Gay-Lussaca opisuje przemianę izobaryczną

gazu doskonałego: Jeżeli ciśnienie gazu jest stałe, to jego

objętość zmienia się wprost proporcjonalnie do temperatury

wyrażonej w kelwinach.

Gdy p = const:

const.



T

V

(1.2)

1.1.3 Prawo Avogadra

Prawo Avogadra (hipoteza Avogadra) jest prawem przybliżonym, którego zakres stosowalno-

ści zależy od podobieństwa porównywanych gazów rzeczywistych do gazu doskonałego.

W tych samych warunkach fizycznych tj. w takiej samej temperaturze i pod takim samym ci-

śnieniem, w równych objętościach różnych gazów znajduje się taka sama liczba cząsteczek.

Rys.1.3. Graficzna interpretacja prawa Avogadra

1.2 Równanie stanu gazu doskonałego i półdoskonałego

1.2.1 Ciepło właściwe

Pojemność cieplna (C) jest to różniczkowa ilość ciepła zaabsorbowanego przez układ (dQ),

niezbędna do zmiany temperatury układu jest proporcjonalna do tej zmiany temperatury (dT).

.

dT

dQ

C

]

K

J

[

1







(1.3)

2

Prawo to odkrył J.A. Charles na podstawie doświadczeń rozpoczętych w 1787 r. a ostatecznie sformułował

Gay-Lussac na podstawie opublikowanych przez siebie danych w 1802 r.

Rys.1.2. Graficzna interpretacja prawa

Gay-Lussaca

Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 1

mgr inż. Agnieszka Sadłowska-Sałęga

6

Pojemność cieplna przypadająca na jednostkę masy to ciepło właściwe a na 1 mol to molowe ciepło

właściwe.

Kilogramowym ciepłem właściwym (c) nazywamy ilość ciepła potrzebną do ogrzania 1 kg

ciała o 1 stopień. W układzie jednostek SI ma ono wymiar J·kg

-1

·K

-1

.

Molowym ciepłem właściwym (Mc) nazywamy ilość ciepła potrzebną do ogrzania 1 mol cia-

ła o 1 stopień. W układzie jednostek SI ma ono wymiar J·mol

-1

·K

-1

.

Pojemność cieplna C jest związana z ciepłem właściwym oraz molowym ciepłem właściwym

poprzez proste zależności:

];

K

J

[

1









m

c

C

(1.4)





];

K

J

[

1









n

Mc

C

(1.5)

gdzie:
m

–

masa substancji, [kg];

n

–

liczba moli substancji, [mol].

Molowe ciepło właściwe, zwane czasem molową pojemnością cieplną, łączy z ciepłem właściwym

zależność opisana następującym wzorem:





];

K

mol

[J

1

1













c

M

Mc

(1.5)

gdzie:
M

–

masa molowa substancji, [kg·mol

-1

].

Ściśliwość gazów powoduje, że inną ilość ciepła należy dostarczyć ogrzewając gaz o 1 K przy

niezmiennym ciśnieniu, a inną – przy niezmiennej objętości. Z tego powodu, dla gazów, rozróżnić

należy ciepło właściwe przy stałym ciśnieniu (c

p

) i ciepło właściwe przy stałej objętości (c

v

).

Ciepło właściwe gazów doskonałych nie zależy od temperatury.

Analogicznie do ciepła właściwego molowe ciepło właściwe, w przypadku gazów, rozróż-

niamy molowe ciepło właściwe przy stałym ciśnieniu (Mc

p

) oraz molowe ciepło właściwe przy

stałym ciśnieniu (Mc

v

).

Ciepło właściwe przemiany realizowanej przy stałym ciśnieniu jest większe, niż ciepło wła-

ściwe przemiany realizowanej przy stałej objętości. Stosunek obu tych wielkości jest wykładni-

kiem adiabaty (κ):

Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 1

mgr inż. Agnieszka Sadłowska-Sałęga

7









.

Mc

Mc

c

c

v

p

v

p







(1.6)

W tabeli 1.1. podano wartości molowego ciepła właściwego przy stałym ciśnieniu oraz stałej

objętości dla gazów doskonałych.

Tab.1.1. Molowe ciepło właściwe gazów doskonałych [Wilk]

Gazy

(Mc

p

)

[J·kmol

-1

·K

-1

]

(Mc

v

)

[J·kmol

-1

·K

-1

]



1-atmomowe

20 800

12 500

1,7

2-atmomowe

29 100

20 800

1,40

3- i więcej atmomowe

33 300

24 900

1,33

1.2.2 Stała gazowa

Uniwersalna stała gazowa (RM) – stała fizyczna równa pracy wykonanej przez 1 mol gazu

doskonałego podgrzewanego o 1 kelwin podczas przemiany izobarycznej. Wartość uniwersalnej

stałej gazowej nie zależy od rodzaju gazu, dla każdego gazu jest jednakowa i wynosi:





.

,

,

RM

1

1

K

mol

J

000015

0

314472

8













Dla gazu doskonałego, uniwersalna stała gazowa jest równa różnicy molowego ciepła właściwego

przy stałej objętości oraz przy ciśnieniu:













].

K

mol

[J

1

1













v

p

Mc

Mc

RM

(1.7)

gdzie:
(Mc

p

) –

molowe ciepło właściwe przy stałym ciśnieniu, [J·mol

-1

·K

-1

];

(Mc

v

)

molowe ciepło właściwe przy stałej objętości, [J·mol

-1

·K

-1

].

Indywidualna stała gazowa (R) – stała fizyczna równa pracy wykonanej przez 1 kg gazu

podgrzewanego o 1 kelwin podczas przemiany izobarycznej. Wartość indywidualnej stałej gazowej

jest zależna wyłącznie od masy molowej gazu i można ją wyliczyć z zależności:





].

K

kg

[J

1

1











M

RM

R

(1.8)

gdzie:
M

–

masa molowa substancji, [kg·mol

-1

].

Uwaga!

W literaturze można spotkać również inne oznaczenia ciepła właściwego oraz stałych gazo-

wych:

Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 1

mgr inż. Agnieszka Sadłowska-Sałęga

8

 molowe ciepło właściwe: C

m

, C

m

, C;

 uniwersalna stała gazowa R  indywidualna stała gazowa r.

W tabeli 1.2 Podano wartości indywidualnej stałej gazowej dla wybranych gazów.

Tab.1.2. Wartości indywidualnej stałej gazowej dla niektórych gazów

c

p

c

v

Rodzaj gazu

Znak chemiczny

R

[J·kg

-1

·K

-1

]

[J·kg

-1

·K

-1

]

Acetylen

C

2

H

2

319,6

1511

1216

Amoniak

NH

3

488,18

2060

1571

Azot

N

2

296,8

1038

742,7

Dwutlenek siarki

SO

2

129,8

586

478,6

Dwutlenek węgla

CO

2

188,8

802

630,1

Etan

C

2

H

6

276,7

1729

1445

Etylen

C

2

H

4

296,6

1612

1290

Hel

He

2078,0

5234

3161

Metan

CH

4

518,7

2160

1637

Powietrze

—

287,0

1006

716

Tlen

O

2

259,8

917

656,5

Tlenek węgla

CÓ

296,9

1047

743,2

Wodór

H

2

4124,2

14225

10111

Znając indywidualną stałą gazową oraz wykładnik adiabaty wartości ciepła właściwego przy

stałym ciśnieniu oraz stałej objętości obliczyć można również z następujących zależności:

;

K

kg

J

1

1

1















R

c

p





(1.9)

;

K

kg

J

1

1

1

1















R

c

v



(1.10)

1.2.3 Równanie Clapeyrona – równanie stanu gazu doskonałego

Na podstawie praw Boyle’a i Mariotte’a i Gay-Lussaca wyprowadzone zostało równanie sta-

nu gazu

3

opisujące związek pomiędzy temperaturą, ciśnieniem i objętością gazu doskonałego, a w

sposób przybliżony opisujący gazy rzeczywiste:

;

T

R

m

V

p









(1.11)

;

T

R

v

p







(1.11a)

3

Równanie stanu gazu sformułowane zostało w 1834 roku przez Benoîta Clapeyrona.

Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 1

mgr inż. Agnieszka Sadłowska-Sałęga

9





;

T

RM

n

V

p









(1.11b)

gdzie:
m

–

masa gazu, [kg];

n

–

liczba moli gazu , [mol];

p

–

ciśnienie gazu, [Pa];

R

–

indywidualna stała gazowa, [J·kg

-1

·K

-1

];

RM

–

uniwersalna stała gazowa (RM = 8,314 J·mol

-1

·K

-1

), [J·mol

-1

·K

-1

];

T

–

temperatura gazu, [K];

V

–

objętość gazu, [m

3

];

v

–

objętość właściwa gazu, [m

3

·kg

-1

].