CHARAKTERYSTYKI STATYCZNE PRZETWORNIKÓW POMIAROWYCH 

 

Transport informacji w postaci sygnału wykazuje wiele podobieństw do trans-

portu energii, stanowiącej jego nośnik. W szczególności transportowi energii zawsze 

towarzyszy jej rozpraszanie (straty). Podobnie rozpraszaniu (bezpowrotnej stracie) 

ulega część informacji zawartej w przekazywanym sygnale. Straty te, nazywane 

inaczej zniekształceniami sygnału, w klasycznej teorii metrologii odpowiadają pojęcia 

błędów pomiarowych. Minimalizacja błędów pomiarowych sprowadza się, więc do 

zapobiegania zniekształceniom sygnału w aparaturze pomiarowej. Współczesna 

aparatura pomiarowa najczęściej posługuje się sygnałem, w którym nośnikiem ener-

getycznym jest energia elektryczna. Zakładając,  że zestaw aparatury (tor pomiaro-

wy) do danego zadania pomiarowego jest funkcjonalnie prawidłowy (nie popełniono 

błędów przy opracowaniu zasady pomiaru, metody pomiarowej itp.) oraz, że 

sprawne są poszczególne człony zestawu - na ogół odrębne przyrządy, we własnych 

obudowach, tzw. „przyrządy uniwersalne” - ewentualnych zniekształceń sygnału 

należy upatrywać w połączeniach pomiędzy członami.  

Każdy pomiar realizuje się w pewien sposób przez porównanie wielkości mierzonej 

względem określonego wzorca. Istnieje jednak wiele metod osiągnięcia tego celu, 

1.  Metodą bezpośrednia wykonywania pomiaru jest to metoda, za pomocą, 

której uzyskuje się wartość wielkości mierzonej bezpośrednio, bez potrzeby 

dodatkowych obliczeń opartych na zależności funkcjonalnej wielkości mie-

rzonej od innych wielkości bezpośrednio mierzonych. W tej metodzie wszyst-

kie obliczenia wykonywane są wewnątrz przyrządu. 

2.  Metoda pośrednia wykonywania pomiaru jest to taka metoda, w której ba-

dany parametr uzyskuje się przez wykorzystanie "pośrednich" wielkości o 

różnych wymiarach, które są powiązane ze sobą funkcjonalnie w pewien 

sposób. Przykładem metody pośredniej może być pomiar odległości przez 

pomiar czasu przejścia impulsu promieniowania np. świetlnego. 

3.  Metoda porównawcza wykonywania pomiaru jest to taka metoda pomiaro-

wa, która opiera się na porównaniu wartości wielkości mierzonej z wartością 

znaną tej samej wielkości lub ze znaną wartością innej wielkości, która wyka-

Strona 1 

 

zuje zależność funkcyjną od wielkości mierzonej. W tej metoda można wy-

różnić następujące metody pomiarowe: 

a.  Metoda bezpośredniego porównania  

b.  Metoda wychyłowa  

c.  Metoda różnicowa  

d.  Metoda zerowa  

e.  Metoda komplementarna (uzupełnienia)  

f. 

Metoda rezonansowa

 

Własności wejściowe i wyjściowe przyrządów - członów aparatury 

 

Przetwornik pomiarowy stanowi względnie wyodrębniony zespół elementów, które 

służą do przetwarzania - z określoną dokładnością i według określonego prawa -

wartości wielkości mierzonej (albo wielkości już przetworzonej z wielkości mierzonej) 

na wartość innej wielkości lub inną wartość tej samej wielkości. 

Sygnały wnoszące informacje do przetworników pomiarowych nazywa się sygnała-

mi wejściowymi.  Powodują one powstanie na wyjściu przetworników sygnałów 

wyjściowych. 

Elementy składowe przetworników. Przetworniki zbudowane są z trzech rodzajów 

elementów podstawowych: 

1.  Elementy powodujące straty energii rozpraszanej na energię cieplną; 

2.  Elementy magazynujące energię w postaci kinetycznej; 

3.  Elementy magazynujące energię w postaci potencjalnej. 

 

Układ pomiarowy. Przez połączenie przetworników współpracujących w procesie 

pomiaru powstaje układ pomiarowy tworzący  łańcuch odbioru i przetwarzania 

informacji pomiarowych o wielkości mierzonej. 

Przetworniki pomiarowe zostały zdefiniowane jako urządzenia przetwarzające 

energię. Biorąc pod uwagę rodzaje energii na wejściach przetworników pomiaro-

wych, można wyróżnić kilka najważniejszych typów przetworników: 

 

Mechaniczne 

 

Chemiczne 

 

Magnetyczne 

Strona 2 

 

 

Elektryczne 

 

Optyczne 

 

Termiczne 

 

Akustyczne 

 

Nuklearne 

Biorąc pod uwagę postać przetwarzanego sygnału przetworniki dzielimy na:  

 

Analogowe A/A. 

 

Cyfrowe C/C.  

 

Analogowo-cyfrowe A/C.  

 

Cyfrowo-analogowe C/A. 

 

Nie wnikając w tym miejscu, w sposób przetwarzania sygnału wewnątrz przyrządu 

pomiarowego, prawidłowe połączenia przyrządów pomiarowych w zestawy, można 

uzyskać jedynie w oparciu o znajomość parametrów wejściowych i wyjściowych 

poszczególnych aparatów. Parametry te są zawarte w dokumentacji technicznej 

przyrządów, czasem są umieszczane na ich obudowie a niektóre są objęte normali-

zacją. 

Parametry wejściowe 

 

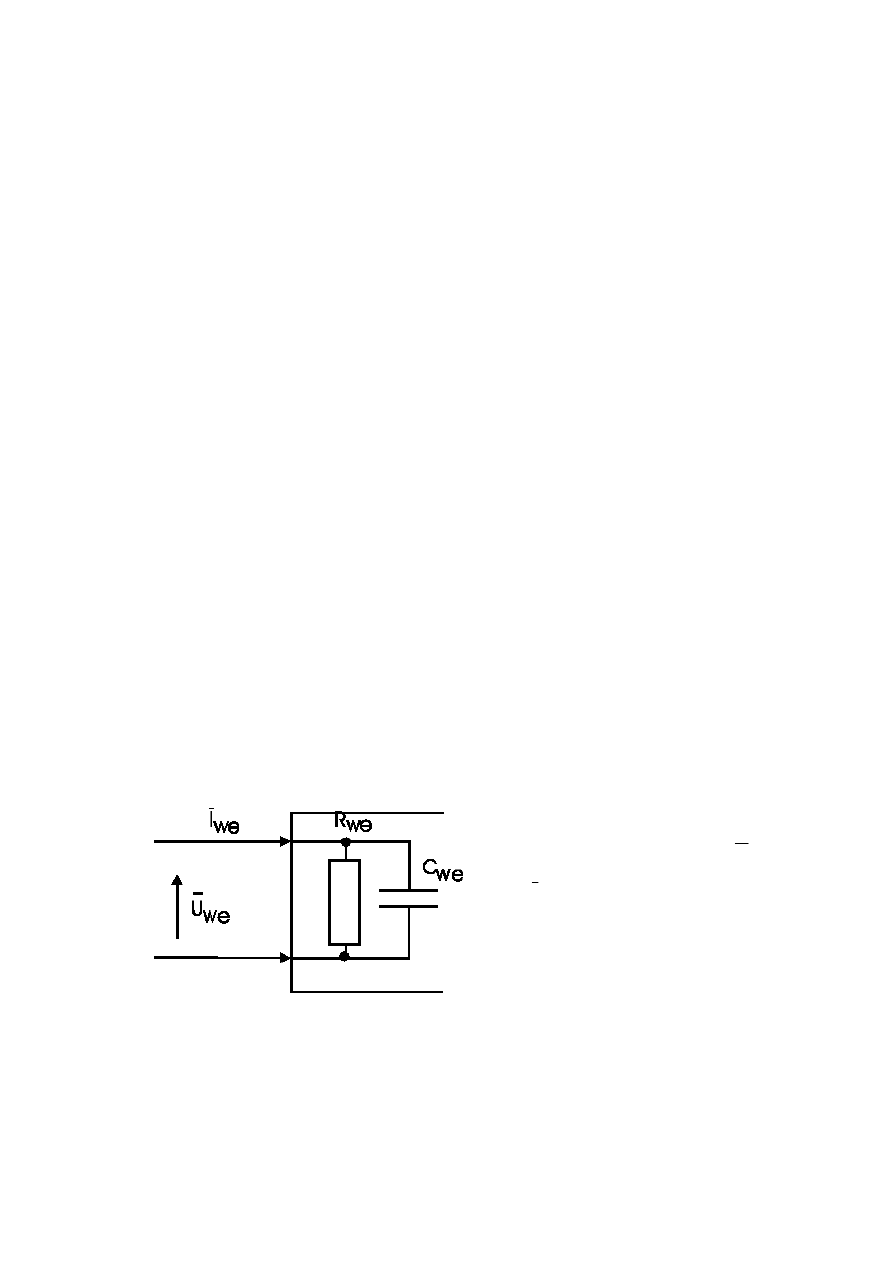
Rysunek 1 przedstawia układ 

zastępczy wejścia, słuszny dla 

większości przyrządów 

pomiarowych. Wartość 

we

U lub  

we

I   (są one związane uogólnio-

nym prawem Ohma) jest 

parametrem sygnału wejścio-

wego zawierającym informacje. 

Wartość ta podawana jest 

zwykle jako skuteczna (RMS), 

szczytowa lub amplituda 

 

 

 

 

 

 

 

 

Rys.1 Schemat zastępczy układu wejścia

 

Strona 3 

 

napięcia.  R

we

 jest rezystancją wejściową (opornością czynną przyrządu widzianego 

od strony zacisków wejściowych), C

we

 jest pojemnością wejściową. 

Parametry wyjściowe  

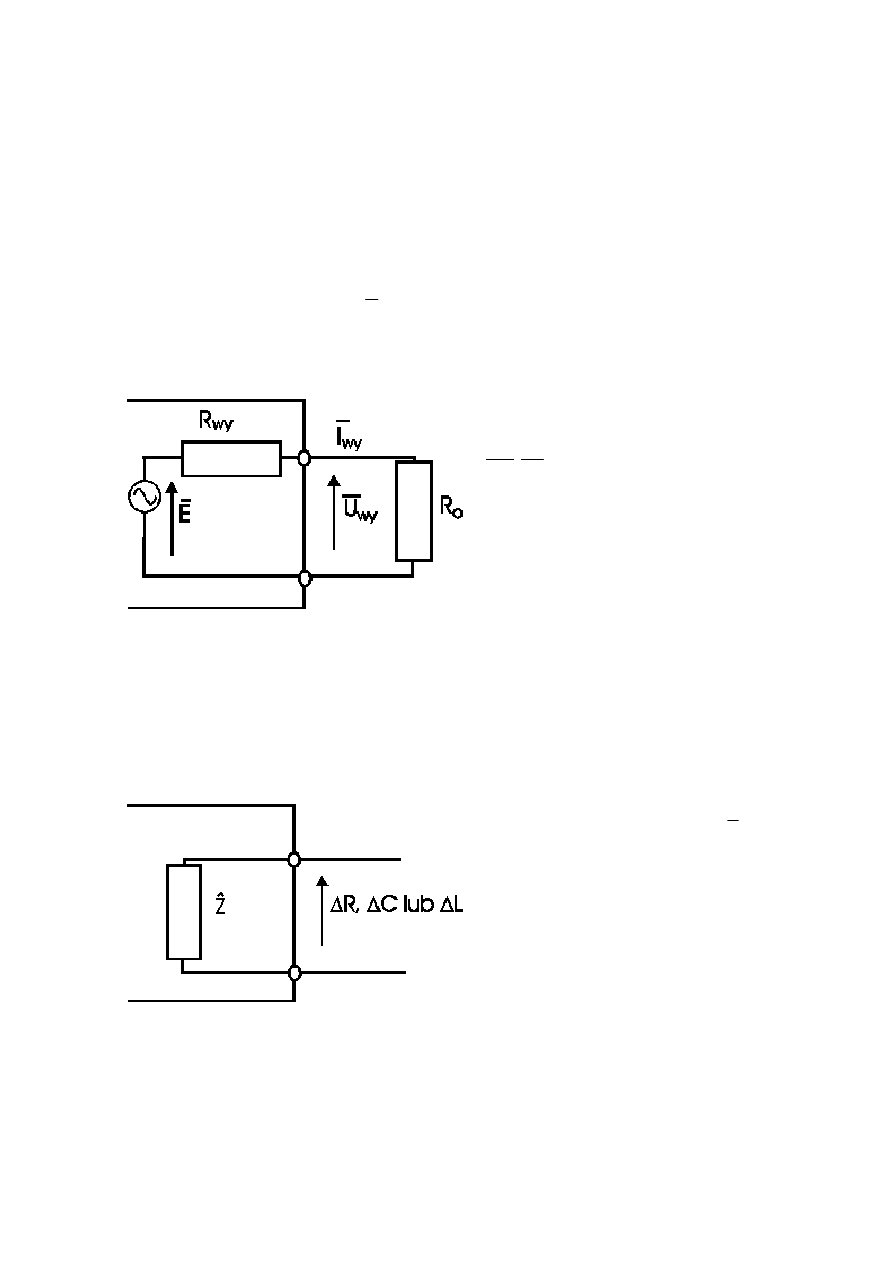
Jeden z możliwych wariantów układu zastępczego „czynnego” wyjścia przyrządu 

przedstawia rysunku 2 (wyjściem czynnym nazywamy wyjście, z którego może być 

czerpana energia elektryczna).  E  jest siłą elektromotoryczną  źródła napięciowego, 

szeregowa rezystancja R

wy

 - rezystancją wyjściową urządzenia.  R

o

 czyli oporność 

obciążenia reprezentuje rezystancję 

wejściową urządzenia współpracują-

cego z wyjściem przyrządu. Wartości 

U

I

wy

wy

,

  są parametrami sygnału 

wyjściowego zawierające informacje. 

Zasadniczo inny jest układ zastępczy 

tzw. wyjścia biernego (parametrycz-

nego). Przyrządy posiadające takie 

wyjście nie generują w swoim 

wnętrzu energii elektrycznej a więc nie wytwarzają sygnału. Informacja pojawia się 

na takim wyjściu w postaci zmiany któregoś z parametrów obwodu (rezystancji, 

pojemności lub indukcyjności) i może być przekształcona w sygnał dopiero w 

następnym członie aparatury, odpowiednio skonstruowanym. Schemat zastępczy 

wyjścia parametrycznego przedsta-

wia ogólnie rys. 3, gdzie   jest 

uogólnioną zastępczą impedancją 

wyjściową układu. 

 

 

 

 

 

 

 

 

Rys.2. Schemat zastępczy czynnego układu wyjściowego 

 

 

 

 

 

 

 

 

Rys.3. Schemat układu wyjściowego parametrycznego 

Z

 

 

 

 

 

Strona 4 

 

Własności przejściowe przyrządów 

Prawidłowe przetwarzanie sygnałów wewnątrz przyrządu (między jego wej-

ściem a wyjściem) odbywa się zawsze tylko w pewnych granicach zmian sygnału 

wejściowego. Najistotniejsze są dwa ograniczenia opisane niżej.  

Ograniczenia wynikające z kształtu charakterystyki statycznej  

 

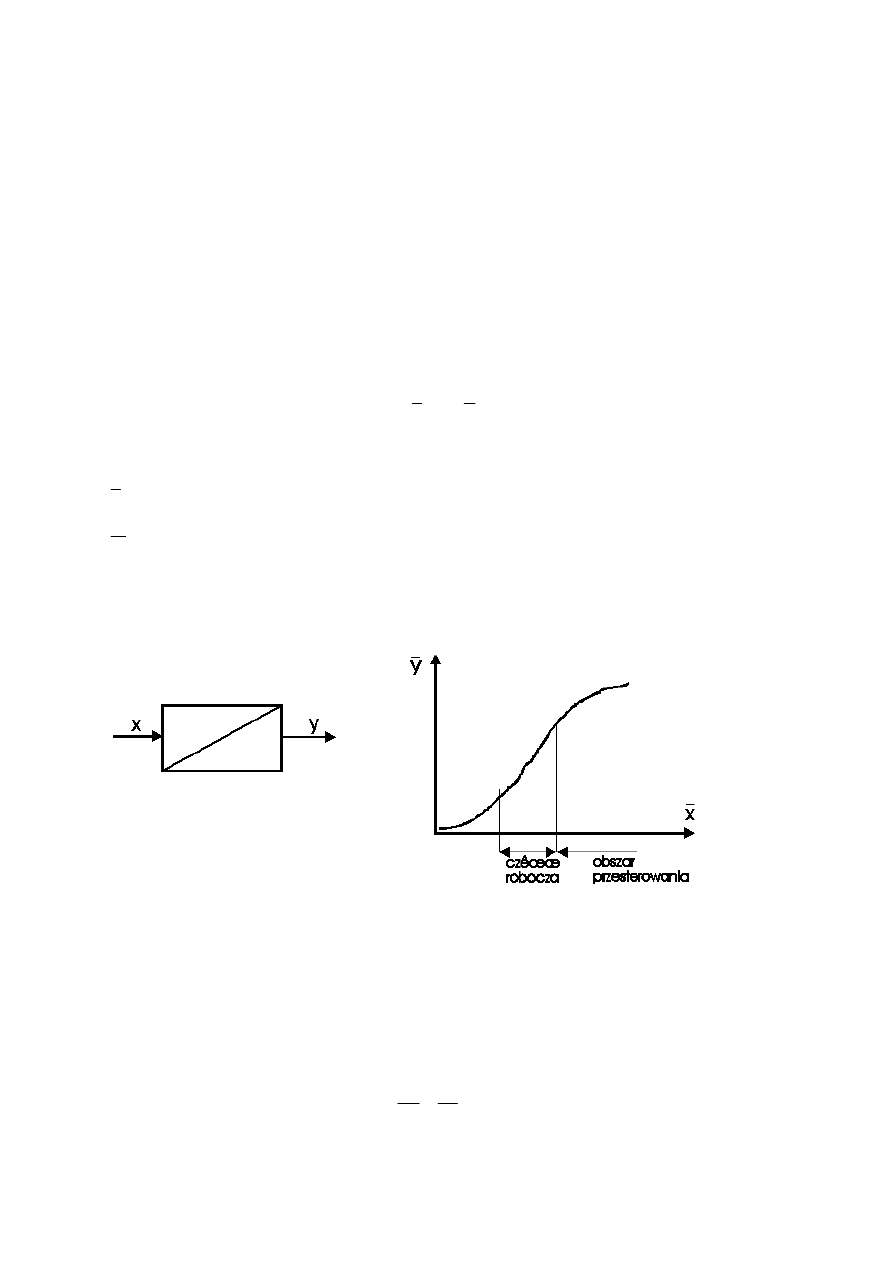
Statyczną funkcją przetwarzania przyrządu nazywamy zależność przedstawioną 

graficznie jako charakterystykę statyczną ( rys. 4)  

)

(X

f

Y

=

 

gdzie:   

Y  - istotna z punktu widzenia zawartości informacji cecha sygnału wyjściowego, 

X  - istotna z punktu widzenia zawartości informacji cecha sygnału wejściowego. 

 

 

 

 

 

 

 

 

 

 

Rys.  4 Charakterystyka statyczna przyrządu 

 

Część robocza charakterystyki statycznej jest zwykle prostoliniowa. 

Czułość statyczna - granica stosunku przyrostu wielkości wyjściowej do wywołują-

cego tę zmianę przyrostu wielkości wejściowej: 

α

tg

dx

dy

x

y

S

x

=

=

∆

∆

=

→

∆

0

lim

 

Strona 5 

 

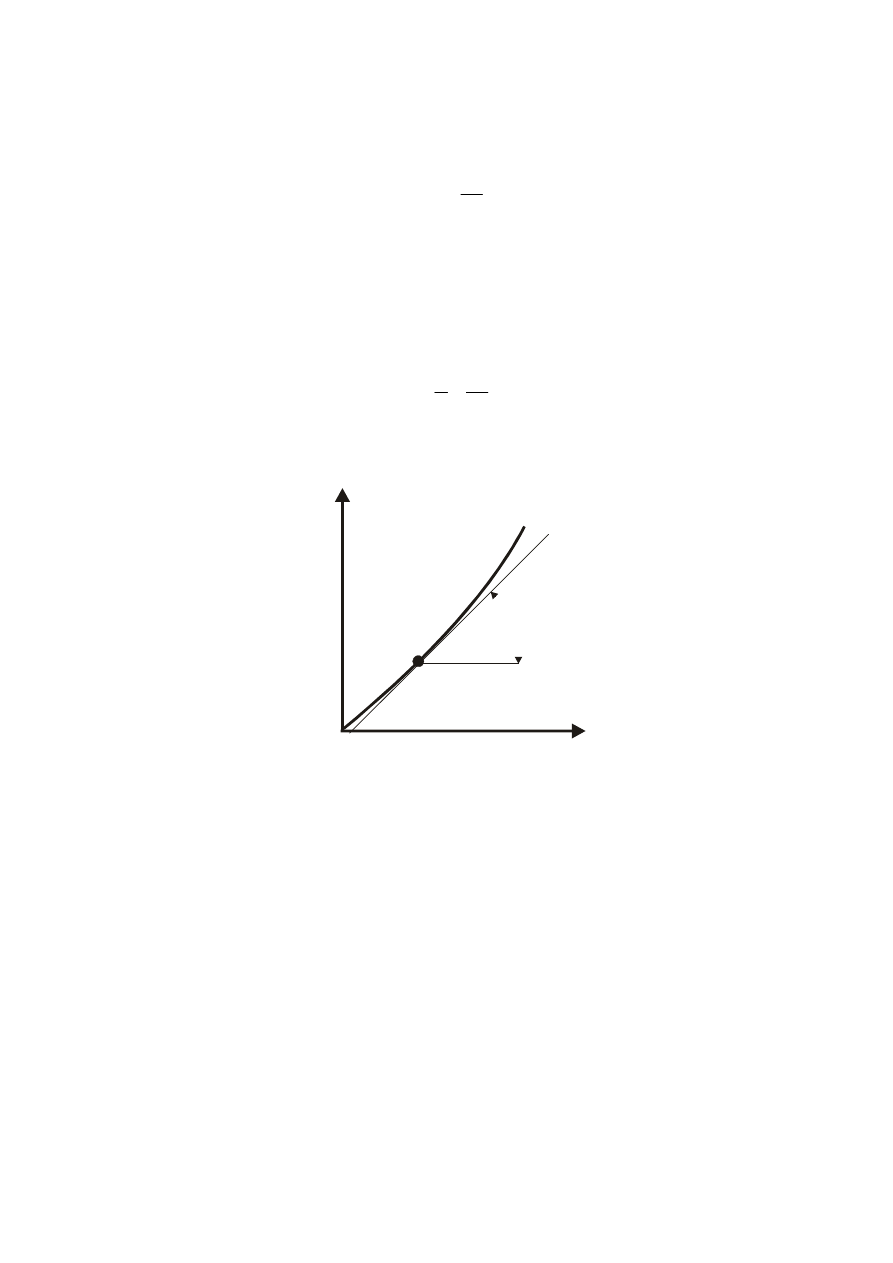
W praktyce z wystarczającą dokładnością przyjmuje się jako czułość stosunek skoń-

czonych przyrostów odpowiednich wielkości: 

x

y

S

∆

∆

≈

 

Czułość statyczna jest wielkością mianowaną. Wymiar czułości zależy od wielkości 

wejściowej i wyjściowej przetwornika (np. termoelement: V/K;). Jest ona wielkością 

stałą w całym zakresie pomiarowym jedynie dla przyrządów o liniowej charakterysty-

ce przetwarzania. Odwrotność czułości nazywana jest stałą przyrządu: 

y

x

S

C

∆

∆

=

=

1

 

 

Y

X

S=tga

 

 

Rys.5 Geometryczna interpretacja czułości statycznej: 

 

 

 

 

 

 

 

 

 

 

Jeżeli idealna funkcja przetwarzania jest prosta przechodząca przez początek 

układu współrzędnych i „S” jest stałe w całym zakresie wielkości wejściowej „X” to 

przetwornik nazywamy liniowym. Uchyby statyczne przetwornika (błędy przetwa-

rzania). Różnica między charakterystyką statyczną idealną a rzeczywistą jest miarą 

dokładności przetwornika w stanie statycznym. 

Strona 6 

 

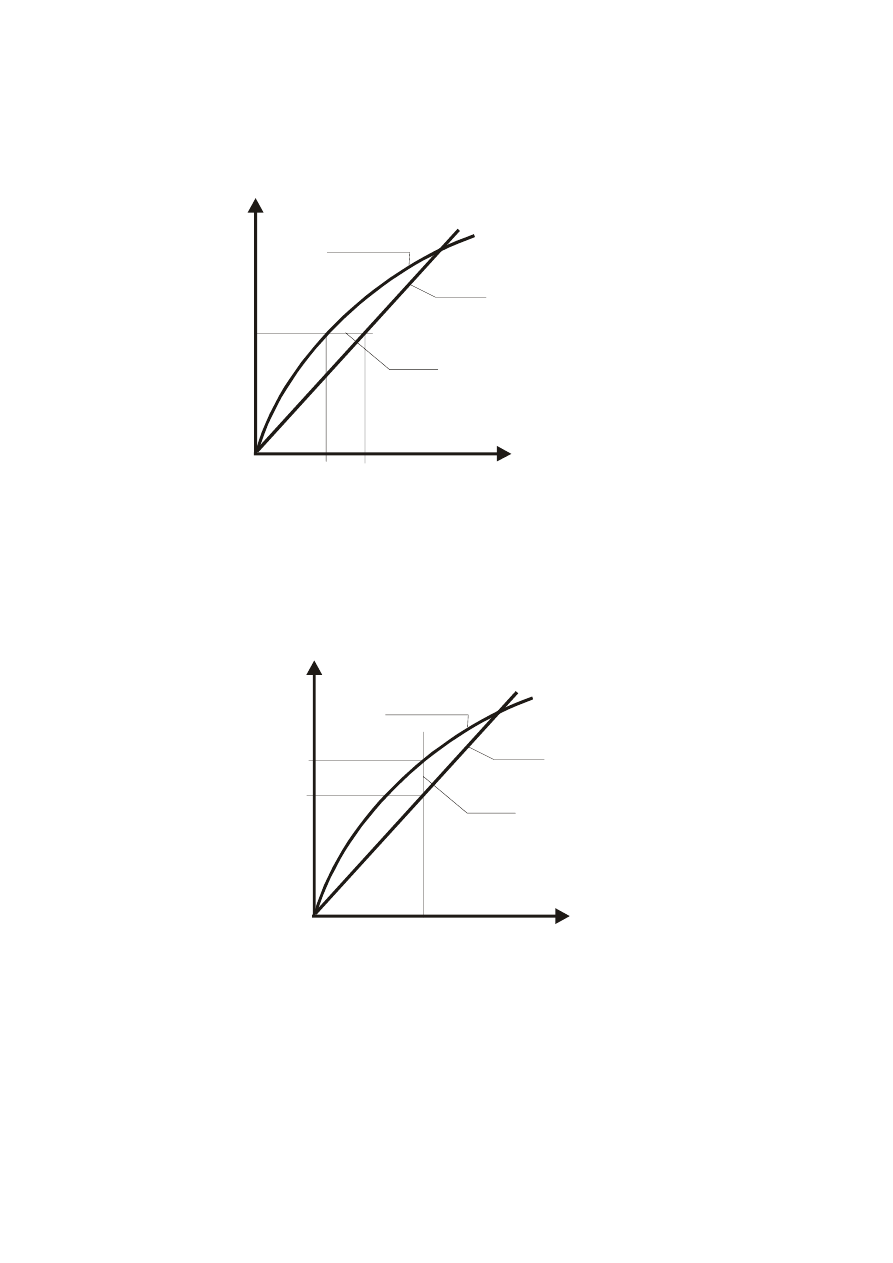
Uchyb bezwzględny odniesiony do wejścia:  

e

rzeczywist

e

idea

x

x

x

−

=

∆

ln

. 

 

 

 

 

 

 

 

 

 

Uchyb statyczny bez-

względny odniesiony do wyjścia:

 

Y

X

idealna

rzeczywista

X

rzeczywiste

X

idealne

DX

 

Rys.  6. 

Charakterystyka statyczna 

rzeczywista i idealnego przetwornika pomiarowego z 

zaznaczeniem uchybu odniesionego do wejścia

 

e

idea

e

rzeczywisy

y

y

y

ln

−

=

∆

 

Y

X

idealna

rzeczywista

Y

rzeczywiste

Y

idealne

DY

 

Rys. 7. 

Charakterystyka statyczna rzeczywista i 

idealnego przetwornika pomiarowego z zaznaczeniem 

uchybu odniesionego do wyjścia

 

 

Strona 7 

 

 

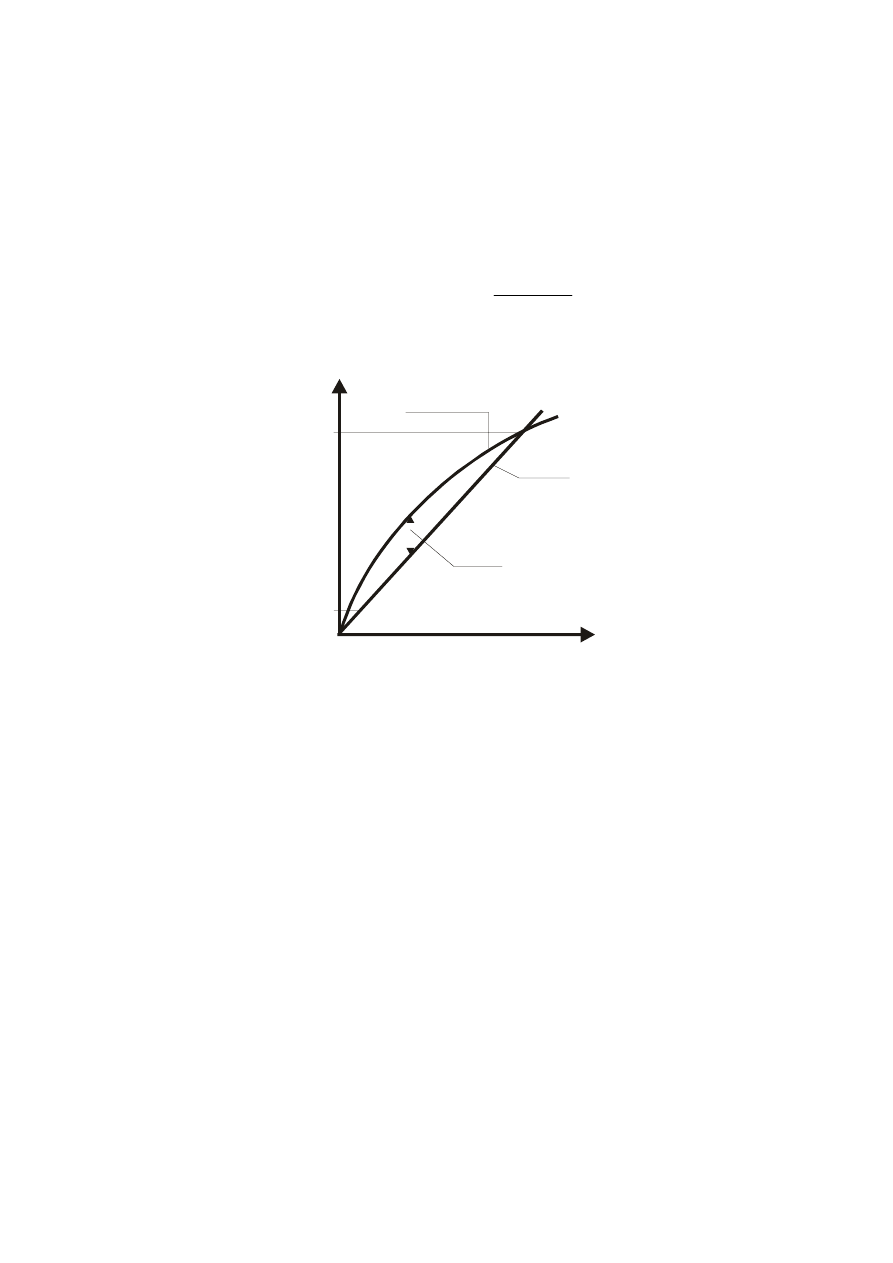
Jako miarę nieliniowości przyjmuje się często maksymalne odchylenie rzeczywistej 

charakterystyki przetwarzania od charakterystyki idealnej w postaci linii prostej. 

Używa się zwykle miary względnej:

 

min

max

max

y

y

y

sci

nieliniowo

blad

−

∆

=

 

 

 

 

 

 

 

 

 

 

 

Zakres pomiarowy - zakres zmian wartości wielkości wejściowej, dla  których 

odpowiednie wartości wielkości wyjściowej przetwornika, otrzymane w normalnych 

warunkach użytkowania i z jednego tylko pomiaru, nie powinny być obarczone 

błędem większym od granicznego błędu dopuszczalnego. 

Y

X

idealna

rzeczywista

Y

max

Y

min

DY

max

 

Rys.  8. 

Interpretacja graficzna błędu nieliniowości

 

 

 

 

8 

 

Y

X

Y

zn

Y=f(X)

Idealna

charakterystyka

statyczna

Niejednoznaczność

przetwarzania
odniesiona do

wyjścia

Próg czułości

odniesiony do

wejścia

Próg czułości

odniesiony do

wyjścia

Niejednoznaczność

przetwarzania
odniesiona do

wejścia

X

zn

 

Rys.  9. 

Charakterystyka statyczna przetwornika z 

zaznaczonymi jej charakterystycznymi parametrami.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

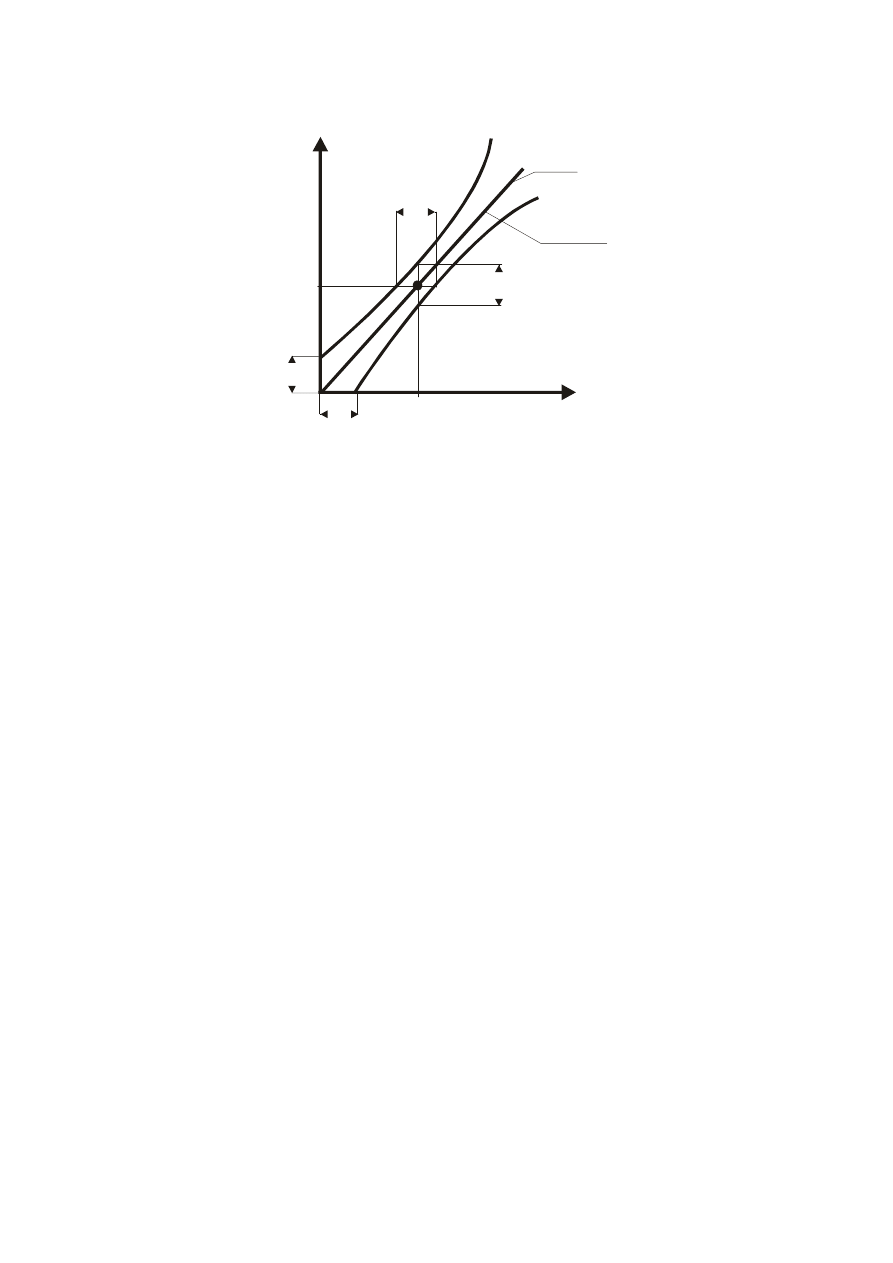
Aproksymacja charakterystyki statycznej przetwornika 

 

 Z 

reguły do większości charakterystyk przetworników pomiarowych – liniowych 

da się zastosować przeliczanie wyniku pomiaru x na wartość  y według zależności 

liniowej  y=ax+b. Zastosowanie przyrządu, który można przeskalować zgodnie z 

zależnością y=ax+b pozwala na poprawne przesunięcie punktu zerowego, ale wynik 

pomiaru obarczony jest dodatkowo tzw. błędem aproksymacji wynikającym z 

aproksymacji funkcji nieliniowej funkcją liniową. Często odstępstwo charakterystyki 

przetwornika od funkcji liniowej nazywane jest błędem nieliniowości. (wartość błędu 

aproksymacji odpowiada wartości błędu nieliniowości). Ilustrację błędu aproksymacji 

(nieliniowości) w czasie tej aproksymacji podano na rys. 10. 

 

9 

 

 

Rys.  10. 

Nieliniowa charakterystyka y=f(x) przetwornika i aproksymująca ją prosta y=ax

 

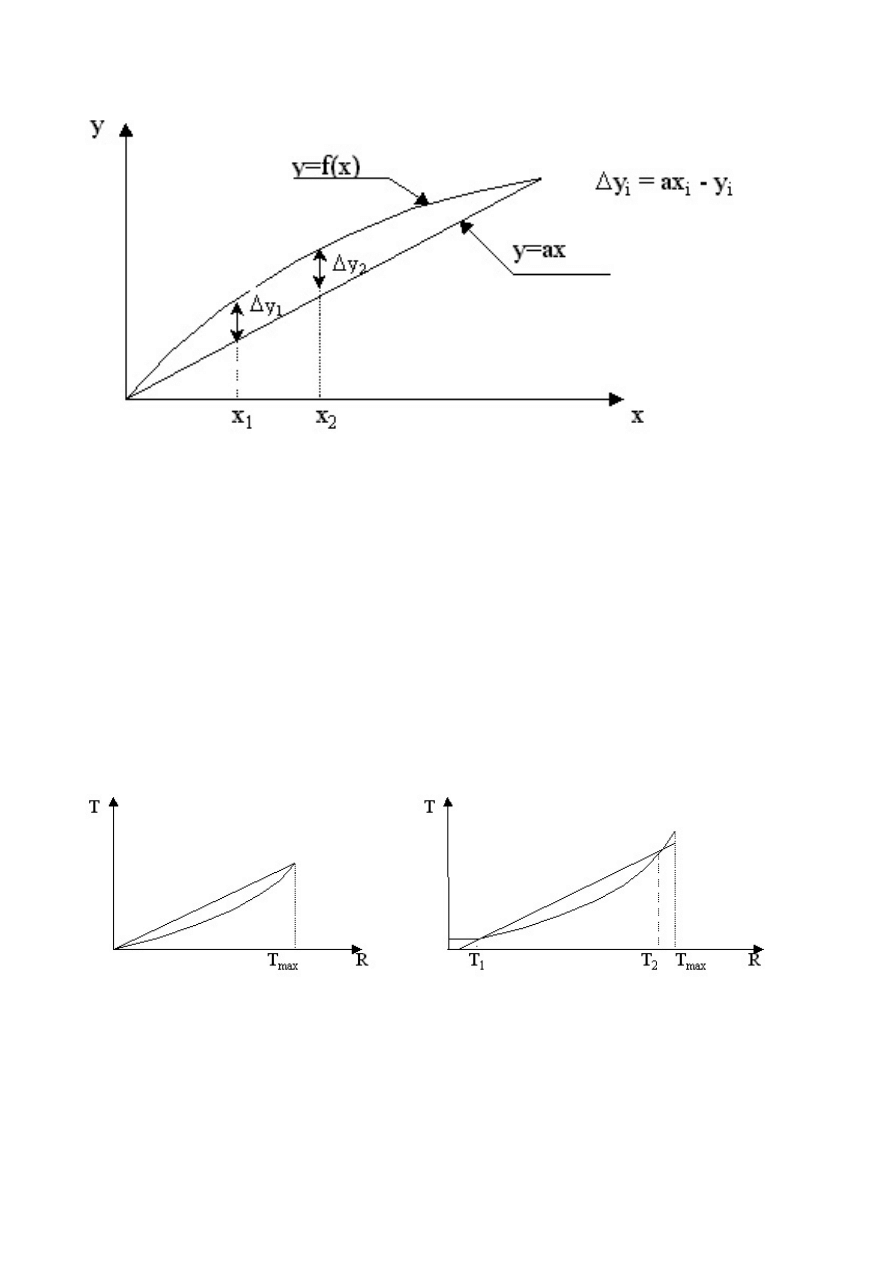
Mając do dyspozycji np. programowany przyrząd który można przeskalować zgodnie 

z funkcją  T=A*R+C należy wyznaczyć współczynniki  A i  C tak, aby wynik cyfrowy 

odpowiadał wartości mierzonej dla dwóch wybranych punktów np. T=0 i  T=T

max

. Tak 

przeskalowany przyrząd wskazywać będzie wartości T=0 i T=T

max

 z błędem wynika-

jącym z niedokładności czujnika i z niedokładności przyrządu. Pozostałe wartości z 

przedziału 0 do T

max  

obarczone będą dodatkowo błędem wynikającym z ewentualnej 

nieliniowości charakterystyki samego przetwornika T=f(R). Minimalizację  błędu 

pochodzącego z nieliniowości charakterystyki można uzyskać aproksymując funkcję 

T = f(R) inną prostą (rys. 11b) 

 

 

Rys.  11. 

Aproksymacja charakterystyki nieliniowej prostą łączącą punkty wyznaczające zakres 

pomiarowy – rys. po lewej stronie. Aproksymacja charakterystyki nieliniowej prostą minimalizującą 
błąd nieliniowości – rys. po prawej stronie.

 

  

Do 

określenia współczynników prostej T=A*R+C, która minimalizowałaby 

błędy nieliniowości można zastosować tzw. metodę najmniejszych kwadratów. 

 

10