Pracownia Fizyki Współczesnej Instytutu Fizyki PŁ

1

Ćwiczenie 523

Dyfrakcja elektronów na polikrystalicznej warstwie grafitu

Przed zapoznaniem się z instrukcją i przystąpieniem do wykonywania ćwiczenia należy opanować następujący
materiał teoretyczny (z dowolnego podręcznika spośród podanych na końcu instrukcji):
1. Dualizm korpuskularno-falowy; postulat de Broglie'a.
2. Mono- i polikrystaliczna struktura ciał stałych.
3. Dyfrakcja promieniowania na kryształach, wzór Braggów-Wulfa.
4. Sieć przestrzenna grafitu.

Cel ćwiczenia

Celem ćwiczenia jest obserwacja zjawiska dyfrakcji elektronów i pomiar odległości międzypłaszczyznowych

w graficie.

Opis zjawiska

Luis de Broglie wysunął postulat, zgodnie z którym z cząstką materialną o pędzie p można związać falę o

długości

p

h

=

λ

(1)

gdzie h oznacza stałą Plancka.

Z postulatu tego wynika, że wiązka rozpędzonych cząstek, np. elektronów stanowi falę, która powinna ulegać

załamaniu, dyfrakcji i interferencji w taki sam sposób jak fale innych rodzajów. Podobnie jak każda fala, także
„fala” elektronów, padając na odpowiednio dobraną do swej długości siatkę dyfrakcyjną, tworzyć będzie maksima
i minima interferencyjne.

Elektronom rozpędzonym w polu elektrycznym napięciem kilku kilowoltów odpowiadają fale materii o

długościach 10

−10

m – 10

−12

m. Rolę siatki dyfrakcyjnej o odpowiedniej dla nich stałej pełni sieć krystaliczna. Płaska

fala elektronów o długości

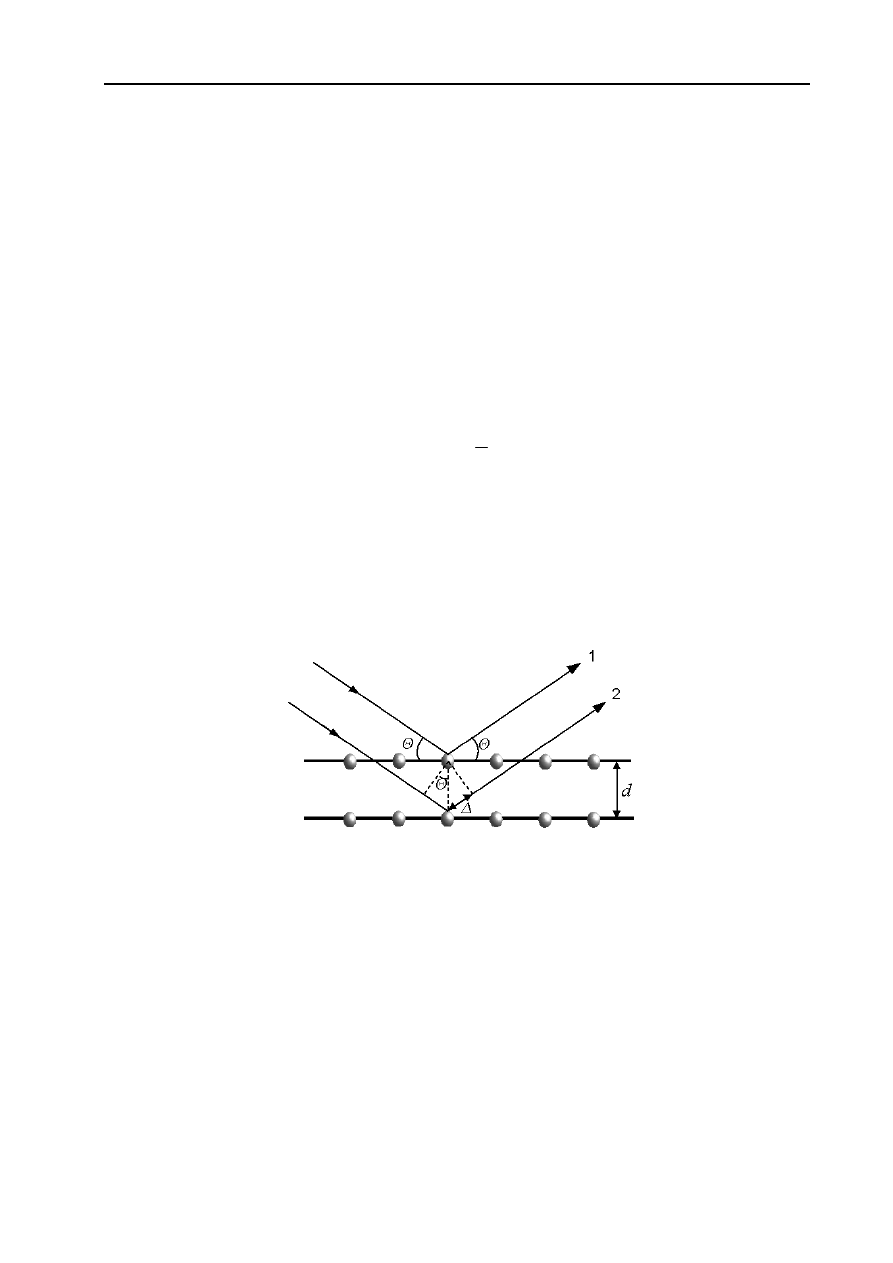
λ padając na kryształ ulega odbiciu od jego płaszczyzn sieciowych (rys. 1). Jeżeli różnica

dróg 2

∆ przebytych przez promienie odbite 1 i 2 wynosi nλ (gdzie n = 1, 2, 3, ...) to promienie te docierają

Rys. 1. Odbicie promieni elektronów od płaszczyzn sieciowych kryształu

do ekranu (lub innego detektora) w zgodnych fazach dając maksimum interferencyjne. Z rysunku 1 wynika, że

Θ

=

∆

sin

d

, a zatem warunkiem uzyskania maksimum interferencyjnego jest spełnienie równania:

λ

=

Θ n

d sin

2

(2)

Równanie (2) zwane jest równaniem Braggów-Wulfa i zostało pierwotnie wyprowadzone dla promieniowania
rentgenowskiego. Oddziaływanie wiązki elektronów z siecią krystaliczną przebiega zatem analogicznie, jak fali
promieniowania rentgenowskiego i opisane jest równaniem (2).

Układ pomiarowy

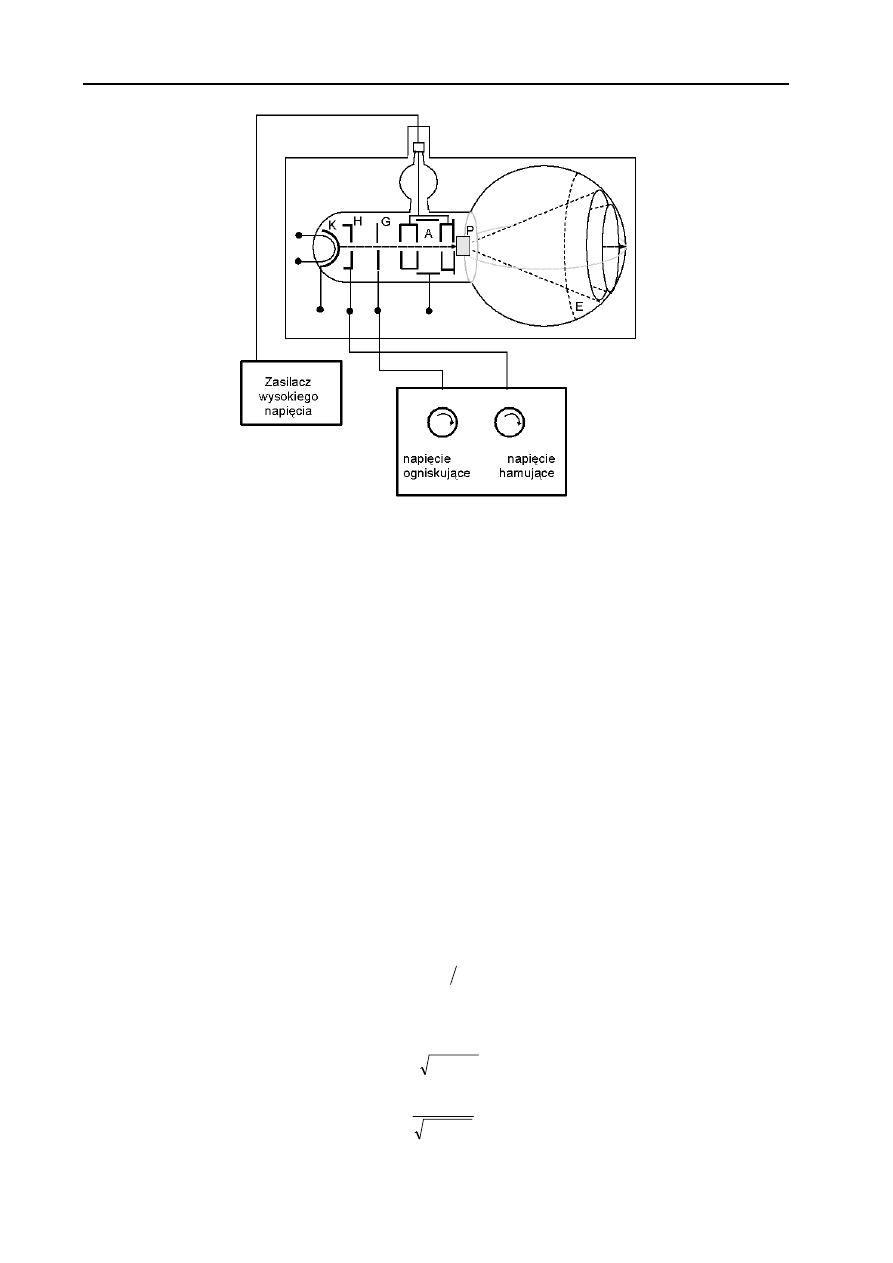
Schemat aparatury stosowanej w ćwiczeniu przedstawia rysunek 2. Jego zasadniczą częścią jest szklana

lampa próżniowa, w której znajdują się katoda K będąca źródłem elektronów, cylinder Wehnelta H służący do
regulacji natężenia wiązki elektronów, elektrody ogniskujące wiązkę G, anoda A, próbka grafitu polikrystalicznego
P, na której następuje ugięcie elektronów oraz ekran pokryty luminoforem E, na którym widoczny jest ślad wiązki
ugiętej.

Pracownia Fizyki Współczesnej Instytutu Fizyki PŁ

2

Rys. 2. Schemat aparatury stosowanej w ćwiczeniu; K – katoda, H – cylinder Wehnelta,

G – elektrody ogniskujące wiązkę, A – anoda, P – próbka, E – ekran

Wiązka elektronów wybiegająca z katody K zostaje przyspieszona w polu elektrycznym wytworzonym

pomiędzy katodą i anodą. Elektrony padając na warstwę polikrystalicznego grafitu ulegają odbiciu od płaszczyzn
sieciowych a następnie padają na ekran luminescencyjny powodując jego świecenie. Badana próbka grafitu ma
strukturę polikrystaliczną, co oznacza, że znajdują się w niej obszary (krystality), w których płaszczyzny sieciowe są
różnie zorientowane w stosunku do kierunku padającej wiązki elektronów. Jeżeli badana próbka nie posiada tekstury
(tj. wyróżnionego kierunku ułożenia krystalitów), krystality rozłożone są w niej chaotycznie a płaszczyzny sieciowe
tworzą kąty od 0 do 90 stopni z kierunkiem wiązki padającej. Wśród wszystkich krystalitów składających się na
próbkę znajdują się takie, w których dla pewnych zespołów płaszczyzn sieciowych spełniony jest warunek
wzmocnienia (2). Część wiązki padającej, która zostaje odbita od tych płaszczyzn tworzy wiązkę odbitą w kształcie
stożka. Obrazem tego stożka na ekranie lampy jest okrąg (rys. 2). Jeżeli warunek (2) spełniony jest dla 2 (lub więcej)
zespołów płaszczyzn o różnych odległościach międzypłaszczyznowych to elektrony odbite od próbki tworzą 2 (lub
więcej) stożków interferencyjnych o różnych kątach rozwarcia i dają na ekranie 2 (lub więcej) okręgów o różnych
promieniach.

W skład zestawu wchodzą ponadto zasilacz wysokiego napięcia i układ regulacji wiązki. Na obudowie lampy

umieszczona jest skala służąca do pomiaru kąta ugięcia wiązki elektronów.

Metoda pomiaru

Jeżeli pomiędzy katodę i anodę lampy przyłożone zostanie napięcie U

A

to energia kinetyczna elektronów

docierających do anody wynosić będzie

A

K

eU

E

=

(3)

gdzie e jest ładunkiem elektronu. Z drugiej strony

m

p

E

K

2

2

=

(4)

gdzie p oznacza pęd elektronu a m jego masę spoczynkową (dla napięć anodowych stosowanych w ćwiczeniu można
pominąć efekty relatywistyczne). Z obu tych wzorów można wyznaczyć pęd elektronów docierających do warstwy
grafitu:

A

meU

p

2

=

. (5)

Zgodnie z zależnością (1) odpowiada mu więc długość fali elektronów równa

A

meU

h

2

=

λ

. (6)

Pracownia Fizyki Współczesnej Instytutu Fizyki PŁ

3

Aby fala o tej długości dała maksimum interferencyjne przy odbiciu od zespołu płaszczyzn sieciowych odległych od
siebie o d to zgodnie z warunkami (2) i (6) spełnione musi być równanie

A

meU

nh

d

2

sin

2

=

Θ

. (7)

Mierząc kąt

Θ i znając rząd interferencji n można obliczyć odległości płaszczyzn sieciowych, od których nastąpiło

odbicie. Ponieważ jasność obrazu interferencyjnego szybko maleje wraz ze wzrostem rzędu interferencji, co w
niezaciemnionym pomieszczeniu praktycznie uniemożliwia zobaczenie okręgów odpowiadających n > 1, należy
przyjąć, że obserwowane okręgi odpowiadają rzędowi n = 1.

Z równania (7) wynika, że zależność sin

Θ od

A

U

1

jest funkcją liniową a współczynnik nachylenia tej

prostej wynosi

me

d

h

a

2

2

=

(8)

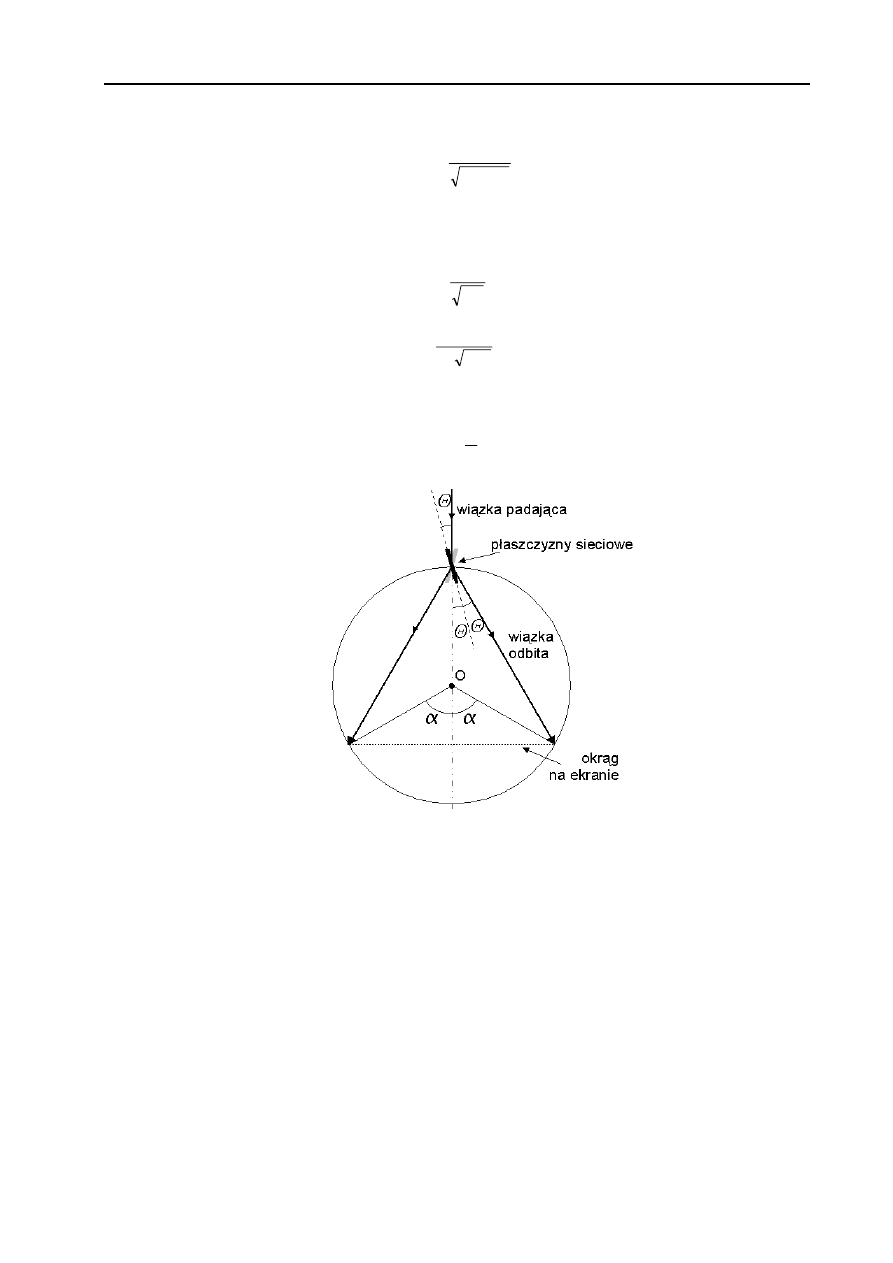
Za pomocą skali kątowej umieszczonej na obudowie lampy można zmierzyć kąt

α odpowiadający szerokości

kątowej otrzymanych na ekranie okręgów. Ponieważ oś skali kątowej przechodzi przez środek lampy (punkt O na
rysunku 3) to pomiędzy kątami

α i Θ istnieje zależność:

4

α

=

Θ

(9)

Rys. 3. Sposób pomiaru kąta ugięcia

Kolejność czynności

UWAGA: włączenie układu pomiarowego do sieci i jego pierwsza regulacja musi być przeprowadzona pod
kontrolą dyżurnego inżyniera lub osoby prowadzącej zajęcia!
1. Włączyć zasilacz napięcia hamującego i ogniskującego.
2. Odczekać około 5 minut aż katoda lampy dostatecznie się rozgrzeje.
3. Włączyć zasilacz napięcia anodowego.
4. Ustawić napięcie anodowe na wartość 4 kV.
5. Napięcie hamujące ustawić tak, aby na ekranie otrzymać wyraźne, ale niezbyt jaskrawe okręgi.
6. Napięcie ogniskujące ustawić w taki sposób, aby okręgi miały ostre krawędzie (bez poświaty).
7. Za pomocą skali kątowej zmierzyć szerokość kątową każdego z otrzymanych okręgów tj. kąty

α

1

i

α

2

. Sposób

pomiaru uzgodnić z prowadzącym zajęcia.

8. Powtórzyć pomiary według punktów 4 - 7 zwiększając napięcie anodowe każdorazowo o 0,5 kV aż do

maksymalnego napięcia 9 kV. Na czas regulacji napięcia anodowego zmniejszać jasność obrazu do minimum.

9. Niezwłocznie po zakończeniu pomiarów wyłączyć najpierw zasilacz napięcia anodowego a następnie zasilacz

napięć hamującego i ogniskującego.

Pracownia Fizyki Współczesnej Instytutu Fizyki PŁ

4

Opracowanie sprawozdania

1. Metodą najmniejszych kwadratów obliczyć parametry liniowych zależności

(

)

A

U

1

f

sin

=

Θ

dla obu okręgów

oraz błędy jakimi są one obarczone.

2. Sporządzić wykresy zależności

(

)

A

U

1

f

sin

=

Θ

i nanieść na nie proste obliczone w punkcie 1.

3. Obliczyć odległości międzypłaszczyznowe d według wzoru (8).
4. Obliczyć błędy wielkości d metodą różniczki zupełnej. Wpływ błędów wyznaczenia stałych h, e, m na błąd

wielkości d pominąć.

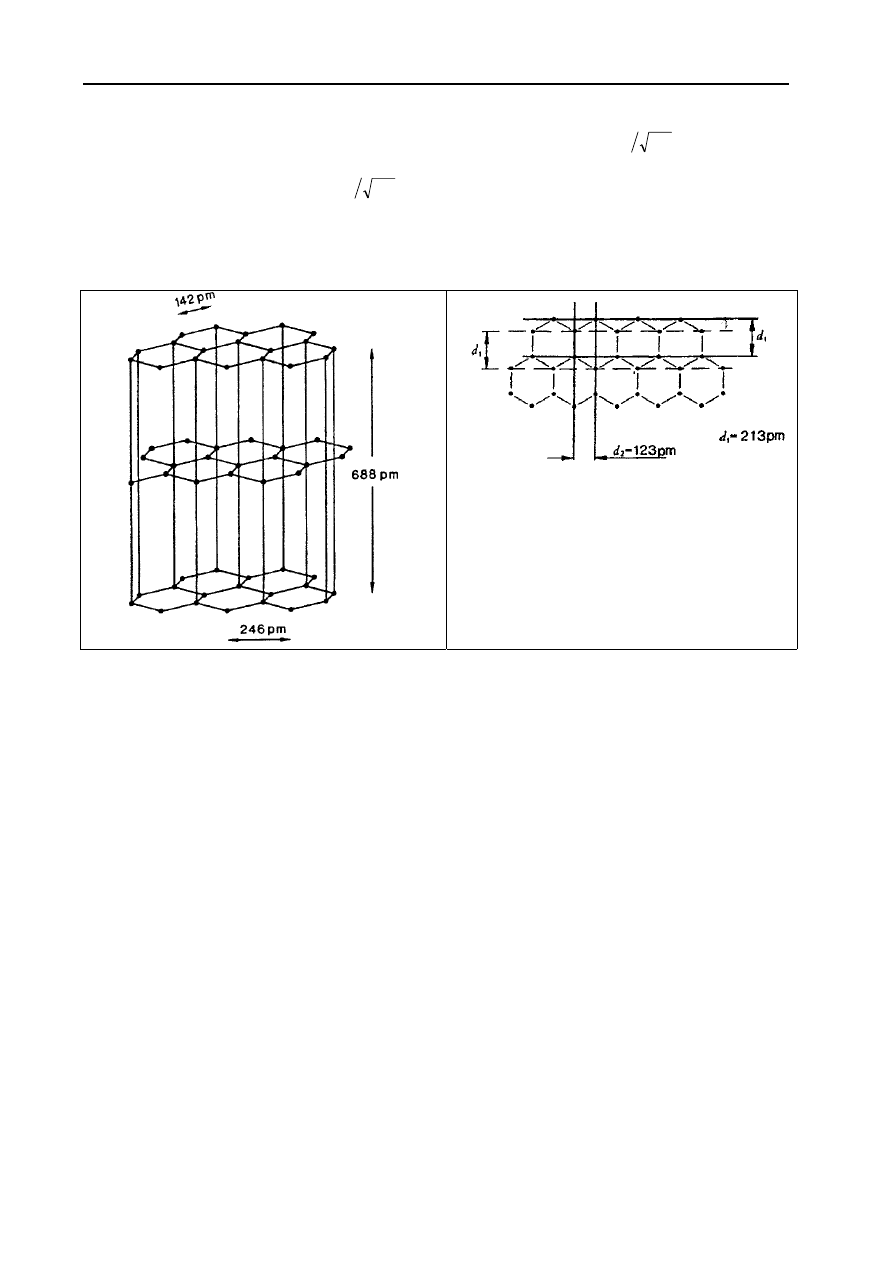
5. Przedyskutować wyniki wykorzystując rysunek 4.

Rys. 4. Odległości płaszczyzn sieciowych w graficie

Literatura
[1] V. Acosta, C. L. Cowan, B. J. Graham, Podstawy fizyki współczesnej, PWN, Warszawa, 1981.
[2] J. Massalski, Fizyka dla inżynierów, t. 2, WNT, Warszawa, 1977.
[3] Sz. Szczeniowski, Fizyka doświadczalna, cz. 5, PWN, Warszawa, 1980.
[4] R. Resnick, D. Halliday, Fizyka, t. II, PWN, Warszawa, 1997.

Więcej wiadomości na tematy związane z ćwiczeniem można znaleźć w podręcznikach:

Z. Bojarski, M. Gigla, K. Stróż, M.

Surowiec, Krystalografia. Podręcznik wspomagany komputerowo,

PWN, Warszawa, 1996.

Z. Trzaska-Durski,

H. Trzaska-Durska,

Podstawy krystalografii strukturalnej i rentgenowskiej,

PWN, Warszawa, 1994.