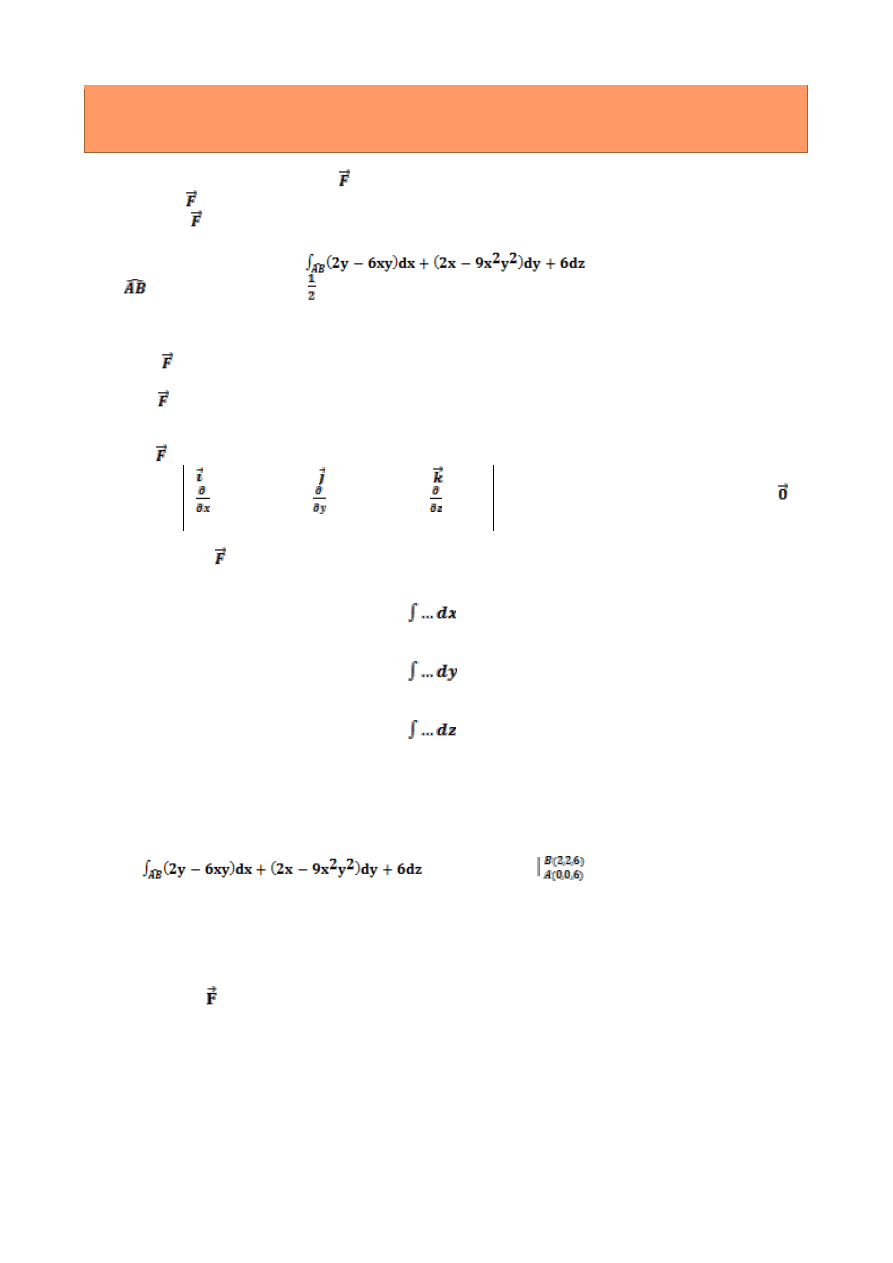
Egzamin 

 

 

 

 

 

 

 

 

 

rok 2008/2009

 

 

 

Zadanie 1:

 Dane jest pole wektorowe  =[2y-6xy

3

,2x-9x

2

y

2

,6]. 

a) 

Obliczyć div  . 

b) 

Wykazać, że   jest polem potencjalnym oraz wyznaczyć jego potencjał. 

c) 

Obliczyć całkę 

, 

gdzie 

 

jest łukiem krzywej {y =  x

2

, z = 6} 

łączącym punkty A(0,0,6) i B(2,2,6). 

 

Rozwiązanie:

  

a) 

Dywergencja wyraża się następującym wzorem: 

div   = P

x 

+ Q

y 

+ R

z

 

Obliczam dywergencję danego pola: 
div  = -6y

3

-18x

2

y 

≠ 0 → oznacza to, że pole jest źródłowe. 

 

b) 

Aby wykazać, że dane pole jest potencjalne należy najpierw obliczyć rotacje pola: 

rot  = 

 
= [0-0,-(0-0),2-18xy

2

-2+18xy

2

] = [0,0,0] =    

 
 

zatem pole   jest potencjalne. 

 

Wyznaczam 

potencjał: 

   

f

x

=2y-6xy

3

     

 

 

/

 

  f=2xy-3x

2

y

3

+C(y,z)    

 

/'

y 

  f

y

=2x-9x

2

y

2

+C'(y,z)=2x-9x

2

y

2

 

  C'(y,z)=0   

 

 

 

/

 

  C(y,z)=A(z) 
   f=2xy-3x

2

y

3

+A(z)     

 

/'

z

 

   f

z

=A'(z)=6      

 

 

/

    

   A(z)=6z+B 
    
  Zatem f(x,y,z)=2xy-3x

2

y

3

+6z+B 

 

c) 

obliczam całkę: 

 

= (2xy-3x

2

y

3

+6z)

  

= 8 

– 96 + 36 - 36 = -88

 

 
 
 
 
 
 

Odpowiedź:

 

Pole    

jest źródłowe, potencjalne o potencjale równym 2xy-3x

2

y

3

+6z+B. 

Wartością całki jest 

liczba -88.

 

 

 

Autor:

 

Weronika Rozłonkowska

  

grupa 

10 

 

26.10.2013 

                                                            

                                                        

2y-6xy

3                         

2x-9x

2

y

2                          

6