1

1. Czym rózni sie opis materii na poziomie
makroskopowym i na poziomie
mikroskopowym?
OPIS MAKROSKOPOWY
Materia jest „ciagła”. Prostymi metodami
fizycznymi można ją dzielić na dowolnie małe
cześci.
Cechy charakterystyczne : stan skupienia,
masa, objetość, gęstość, przewodnictwo
cieplne,elektryczne; lepkość, kolor, zdolnosc
do pzremian fizycznych i chemicznych,
wytrzymałość mechaniczna
OPIS MIKROSKOPOWY
Materia nie jest „ciągła”. Składa sie z atomów
(jednostek materii) pomiedzy atomami jest
próżnia

2. Jakie znamy rodzaje promianiowania
jądrowego, jak możemy je
scharakteryzować?
Atomy niektórych pierwiastków samoistnie
wyrzucają z siebie jakieś cząstki, które w rózny
sposób zachpwują się w polu elektrycznym i
magnatycznym , takie promianiowanie
nazywamy JĄDROWYM.
α– strumień jąder helu 42 He, cechuje się małą
przenikliwością
β -strumie elektronów lub pozytronów, silnie
pochłaniany przez materię, jest zatrzymywany
przez aluminiową blachę
γ- promieniowanie o energii kwantu większej
niż 10 keV , jest silnie przenikliwe ,
pochłaniane przez ołów

3. Jakie sa podstawowe składniki materii, w
jaki sposób dzielimy cząstki elementarne?
BOZONY(mezony, nośniki oddziaływań) –
spin całkowity
FERMIONY ( leptony, bariony) – spin
połówkowy

4. Jak przebiega rozpad swobodnego
nautronu?
Neutron w stanie wolnym jest nietrwały,
rozpada sie wg. schematu:
10n→11p + 0-1e + ~v
Neuton zbudowany jest z 2 kwadków dolnych
d i jednego górnego u

5. Na czym polegał eksperyment z czastkami
alfa i folia ze złota? Jakie wnioski mozna
wyciagnac z tego eksperymentu? (
eksperyment Rutherforda)
Eksperyment polegał na skierowaniu zródła
czastek alfa na złota folię. Jedna na 8000
czastek alfa została odbita pod dużym katem.
WNISEK: w atomach obecne sa jądra, w
kórych jest skupiona prawie cała amsa atomu ,
poza tym atom jest „pusty”

6. Jak jest rola protonów i neutronów w
jądrze atomowym? Jakie są warunki
trwałości jądra atomowego?
Protony oraz neutrony tworzą jądro atomowe.
W nim skupiona jest praktycznie cała masa
atomu. Gdy w jądrze są przynajmniej dwa
protony do stabilności potrzebny jest
przynajmniej jeden neutron. Neutrony w jądrze
zapewniają jego stabilność. Najbardziej
stabilnymi są jądra o zbliżonej liczbie
protonów i neutronów.

7. Jakie są skutki wypromieniowania
określonego rodzaju promieniowania
jądrowego dla jądra atomowego, które je
wypromieniowało?
Skutkiem jest, w przypadku różnych
promieniowań: emisja pozytonu, elektronu,
jądra helu, protonu bądź neutronu, emisja
promieniowania gamma (pozbycie się
nadmiaru energii), jak również zmiana liczby
protonów w jądrze atomu.

8. Jakie są na poziomie atomowym skutki
oddziaływania promieniowania jądrowego z
materią?
W zależności od typu i własności
promieniowania, czyli jego energii, zasięgu,
ładunku, materia, którą owo promieniowanie
napotyka na swej drodze, reaguje inaczej. Na
podstawie opisanych w rozdziale 3 typów
promieniowania, najogólniej można podzielić
promieniowanie jonizujące na dwie kategorie.
Do pierwszej z nich należy promieniowanie, w
którym nośnikiem energii są ciężkie cząstki
naładowane lub prędkie elektrony. Cząstki te
poprzez swój ładunek elektryczny,
bezpośrednio siłą coulombowską, oddziałują w
sposób ciągły z elektronami obecnymi w
środowisku, przez które przechodzą.
Do drugiej kategorii zalicza się
promieniowanie γ, X oraz neutrony, które nie
podlegają siłom coulombowskim, ponieważ nie
mają ładunku elektrycznego. W tych
przypadkach musi najpierw zajść
oddziaływanie (często angażujące jądra
atomów środowiska), w którym całkowita lub
częściowa energia przekazana jest wtórnej
cząstce naładowanej. Jeżeli to pierwotne
oddziaływanie nie zajdzie wewnątrz
określonego obszaru materii, promieniowanie
tej kategorii może przeniknąć, nie
pozostawiając żadnego śladu. W przypadku
obu rodzajów promieniowania w efekcie
końcowym całkowita lub częściowa energia

przekazana jest bezpośrednio lub za
pośrednictwem cząstki wtórnej elektronom
środowiska. Elektrony atomów absorbujących
promieniowanie mogą być przenoszone na
wyższe poziomy energetyczne, co oznacza
wzbudzenie atomu lub mogą być z nich
całkowicie usunięte, co odpowiada jonizacji.
Zwykle mamy do czynienia z sytuacją, w której
absorbowana energia wystarcza do jonizacji
wielu atomów

9. W jaki sposób jądro atomowe może
zmniejszyć stosunek liczby protonów do
liczby neutronów?
Poprzez rozpad alfa, beta - i pochłonięcie
promieniowania neutronowego

10. W jaki sposób powstają sztuczne źródła
promieniotwórcze?
1. Aparaturę rentgenowską lub inną, lecz
wytwarzającą promie-niowanie jonizujące na
podobnej zasadzie. W aparaturze tego typu
promieniowanie rentgenowskie jest
wytwarzane przez ha-mowanie na metalowych
elektrodach lub szklanych ekranach strumienia
elektronów rozpędzanych uprzednio w silnym
polu elektrycznym, zazwyczaj w odpowiedniej
komorze próżniowej. Aparatura tego typu to
przede wszystkim lampy rentgenowskie, a
także kineskopy telewizyjne, prostowniki
próżniowe, beta-trony, akceleratory itp.
2. Izotopy promieniotwórcze. Izotopami
nazywane są atomy pier-wiastków, które mają
tę samą liczbę protonów w jądrze atomu, a
różną liczbę neutronów. Izotopy tego samego
pierwiastka mają te same właściwości
chemiczne, różnią się jedynie masą atomową.

11. Jak powstaje i czym się charakteryzuje
reakcja łańcuchowa?
Reakcja łańcuchowa to ciąg szeregów
przebiegających samorzutnie po ich
zainicjowaniu. Będzie ona zachodziła po
zbombardowaniu neutronami jądra 235U.
Podczas tego procesu wydzielane są nowe
neutrony zdolne do rozszczepiania kolejnych
jąder. Reakcja ta przebiega bardzo szybko i
podczas jej trwania wydzielane są duże ilości
energii.

12. Jak ilościowo opisujemy szybkość
rozpadu promieniotwórczego? Jakie
parametry są z nim związane?
Szybkość rozpadu promieniotwórczego jest
określona równaniem różniczkowym, którego
rozwiązaniem jest funkcja N(t). dN/dt=kN(t),
gdzie k jest stałą rozpadu. Po rozdzieleniu
zmiennych otrzymujemy: dN/N=kdt. Po
obliczeniu całki oznaczonej w granicach od N0
w czasie t=0 do N po czasie t otrzymamy: N=
N0e-kt co daje nam t=1/k*ln(N0/N). Gdy
N=N0/2 mamy wzór na czas połowicznego
rozpadu: t1/2=1/k*ln(2N0 /N0).

13. Jak jest zdefiniowana i skąd pochodzi
energia wiązania nukleonów w jądrze
atomowym.
Energia wiązania jest to energia potrzebna do
rozdzielnia jadra atomowego na protony i
neutrony. Im większa energia tym trwalsze
jądro. Suma mas wszystkich nukleonów w
jądrze jest większa niż masa całego jądra
utworzonego z tych nukleonów. Różnicę
między tymi masami nazywamy deficytem
masy i oznaczamy delta m. Ta brakująca masa
jest równa energii wiązania nukleonów zgodnie
ze wzorem Einsteina: delta E = delta m*c2.

14.Oblicz energię wydzielającą się przy
powstawaniu 10 jąder atomowych berylu:
mBe=9.012182u
mp=1,007825u
Mn=1,008665u

1u=931,494MeV
Zatem energia wiązania dla 1 jadra wynosi:
0,062443*931,494=58,16MeV
A dla 10 jader: 10*58,16=581,6MeV

15.Co to są i jakie znamy szeregi
promieniotwórcze:
Szereg promieniotwórczy – szereg nuklidów
promieniotwórczych przekształcających się
kolejno jedne w drugie na drodze rozpadów
promieniotwórczych. Kolejne produkty
rozpadów promieniotwórczych tworzą szereg,
który rozpoczyna się izotopem
promieniotwórczym o długim okresie
półtrwania, a kończy izotopem trwałym
(niepromieniotwórczym).
Rodzaje:
1.uranowo-radowy
2.uranowo-aktynowy
3.szereg torowy
4.szereg neptunowy

16.Opisać przebieg poszczególnych zmian w
szeregu uranowo-radowym (uranowo-
aktynowym , torowym, neptunowym)
SZEREG URANOWO-RADOWY:
Szereg rozpoczyna się izotopem uranu 238U o
okresie półtrwania wynoszącym 4,5 miliarda
lat, a kończy na stabilnym ołowiu 206Pb.
Szereg opisuje wzór 4n + 2 i należy do niego

16 nuklidów, między innymi: 238U, 234U,
226Ra, 222Rn, 210Po, 210Pb.
nuklid
typ rozpadu
czas połowicznego rozpadu
uwolniona energia, MeV
produkt rozpadu
U 238
α
4,51•109 lat
4,270
Th 234
Th 234
β-
24.10 d
0,273
Pa 234
Pa 234
β-
1,18 min
2,197
U 234
U 234
α
2,44∙105 lat
4.859
Th 230
Th 230
α
7,50∙104 lat
4,770
Ra 226
Ra 226
α
1599 lat
4,871
Rn 222
Rn 222
α
3,823 d
5,590
Po 218
Po 218
α
3,05 min
6,88
Pb 214
Pb 214
β-
26,8 min
1,024
Bi 214
Bi 214
β- 99,98%
α 0,02%
19,7 min
3,272
5,617
Po 214
Tl 210
Po 214
α
0,162 ms
7,883
Pb 210
Tl 210
β-
1,32 min
5,484
Pb 210
Pb 210
β-
22,3 lat
0,064
Bi 210
Bi 210
β- 99,99987%
α 0,00013%
5,0 d
1,426
5,982
Po 210
Tl 206
Po 210
α
138,375 d
5,407
Pb 206
Pb 206
.
Trwały
.
.

SZEREG URANOWO-AKTYNOWY:
Szereg rozpoczyna się izotopem uranu 235U o
okresie półtrwania wynoszącym 700 milionów
lat a kończy na stabilnym ołowiu 207Pb.
Szereg opisuje wzór 4n + 3 i należy do niego
14 nuklidów, między innymi: 235U, 231Pa,
223Ra.
nuklid
typ rozpadu
czas połowicznego rozpadu
uwolniona energia, MeV
produkt rozpadu
U 235
α
6,96•108 lat
4,678
Th 231
Th 231
β-
25,64 h
0,391

Pa 231
Pa 231
α
32760 lat
5,150
Ac 227
Ac 227
β- 98,62%
α 1,38%
21,772 lata
0,045
5.042
Th 227
Fr 223
Th 227
α
18,72 d
6,147
Ra 223
Fr 223
β-
21,8 min
1,149
Ra 223
Ra 223
α
11,434 d
5,979
Rn 219
Rn 219
α
3,920 s
6,946
Po 215
Po 215
α 99,99977%
β- 0,00023%
1,78 ms
7,527
0,715
Pb 211
At 215
Pb 211
β-
36,1 min
1,367
Bi 211
Bi 211
α 99,724%
β- 0,276%
2,15 min
6,751
0,575
Tl 207
Po 211
Po 211
α
510 ms
7,595
Pb 207
Tl 207
β-
4,79 min
1,418
Pb 207
Pb 207
.
Trwały
.
.
SZEREG TOROWY:
Szereg rozpoczyna się izotopem toru 232Th o
okresie półtrwania wynoszącym 14 miliardów
lat, a kończy stabilnym ołowiem 208Pb. Szereg
jest opisanym wzorem 4n + 0, należy do niego
12 nuklidów, między innymi: 232Th, 228Th,
228Ra, 220Rn.
nuklid
typ rozpadu
czas połowicznego rozpadu
uwolniona energia, MeV
produkt rozpadu
Th 232
α
1,405•1010 lat
4,081
Ra 228
Ra 228
β-
5,75 lat
0,046
Ac 228
Ac 228
β-
6,13 h
2,124
Th 228
Th 228
α
1,913 lat
5,520
Ra 224
Ra 224
α
3,64 d
5,789
Rn 220
Rn 220
α
54,5 s
6,404
Po 216
Po 216
α
0,158 s

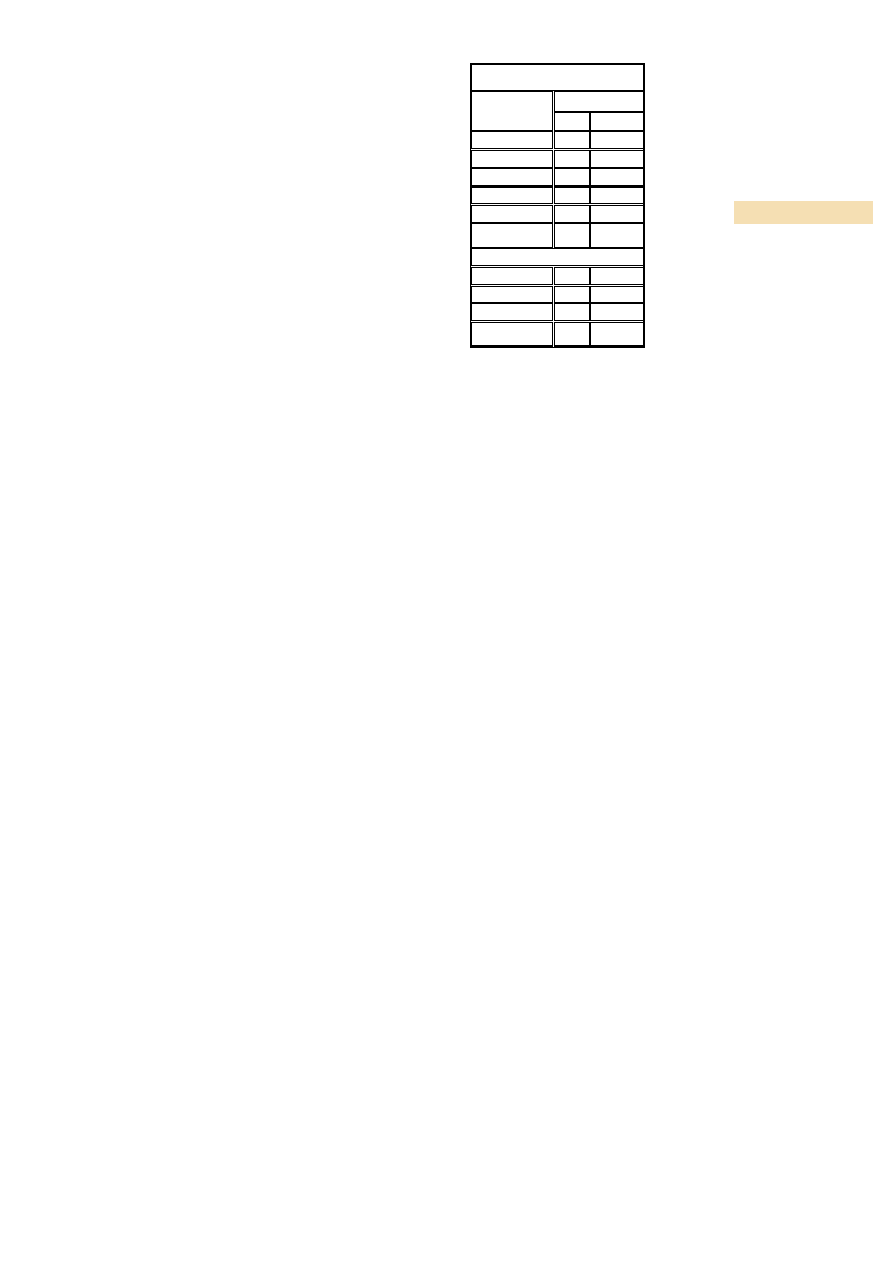
2

6,906
Pb 212
Pb 212
β-
10,64 h
0,570
Bi 212
Bi 212
β- 64,06%
α 35,94%
60,55 min
2,252
6,208
Po 212
Tl 208
Po 212
α
3∙10-7 s
8,955
Pb 208
Tl 208
β-
3,0 min
4,999
Pb 208
Pb 208
.
Trwały



SZEREG NEPTUNOWY:
Szereg rozpoczyna się izotopem neptunu
237Np o okresie półtrwania 2,1 miliona lat, a
kończy na stabilnym bizmucie 209Bi. Szereg
opisany jest wzorem 4n + 1 i należy do niego
13 nuklidów, między innymi: 237Np, 233U,
229Th.
Szereg neptunowy występuje jedynie w wyniku
sztucznego otrzymywania (naświetlanie uranu
strumieniem neutronów). Okres półtrwania
neptunu jest około 2000 razy krótszy od wieku
Ziemi przez co zostały jedynie niewykrywalne
jego ilości. Obecnie w rudach uranowych
występuje go ok. 1,8∙10-12% (2 atomy neptunu
na bilion atomów uranu).
nuklid
typ rozpadu
czas połowicznego rozpadu
uwolniona energia, MeV
produkt rozpadu
Np 237
α
2,14•106 lat
4,959
Pa 233
Pa 233
β-
27,0 d
0,571
U 233
U 233
α
1,59•105 lat
4,909
Th 229
Th 229
α
7340 lat
5,168
Ra 225
Ra 225
α
14,8 d
0,36
Ac 225
Ac 225
α
10 d
5,935
Fr 221
Fr 221
α
4,8 min
6,3
At 217
At 217
α
32,3 ms
7,0
Bi 213
Bi 213
β-
α
46 min
.
5,87
Po 213
Tl 209
Po 213
α
4,2∙10-6 s
.
Pb 209
Tl 209
β-
2,2 min
3,99
Pb 209
Pb 209
β-
3,25 h
0,644
Bi 209
Bi 209

.
quasi trwały*
.
.
*Izotop 209Bi, choć często opisywany jako
trwały, ma okres połowicznego rozpadu
1,9·1019 lat, a produktem jego rozpadu α jest
205Tl. Tak długi okres rozpadu (setki milionów
razy dłuższy od wieku wszechświata) pozwala
traktować bizmut jako praktycznie trwały.

17. W jaki sposób przebiega synteza He w
gwiazdach:
Reakcje termojądrowe w gwiazdach:
I.Cykl protonowy:
Cykl rozpoczyna fuzja dwóch protonów, która
jest możliwa, gdy mają one dostatecznie dużą
energię, by pokonać barierę kulombowską.
Zbliżenie protonów jest możliwe także dzięki
znanemu z mechaniki kwantowej efektowi
tunelowemu, którego prawdopodobieństwo
zajścia zależy od energii kinetycznej protonów
i rośnie wraz z nią. Tempo przebiegu tej reakcji
w temperaturze Słońca jest rzędu 109 lat. Z
powodu powolności tej reakcji Słońce nadal
świeci - w przeciwnym wypadku reakcje
przebiegały by na tyle szybko, że wodór
zostałby w gwieździe wyczerpany.
Do wytworzenia jąder helu z czterech jąder
wodoru może dojść w wyniku różnych reakcji
jądrowych. Stosuje się podział na trzy
zazębiające się cykle: ppI, ppII i ppIII.
1. Cykl ppI
Pierwsze zachodzące reakcje składają się na
tzw. cykl ppI. W wyniku fuzji dwóch jąder
wodoru 1H (dwóch protonów) powstaje jądro
deuteru 2D, pozyton i neutrino elektronowe.
Pozyton natychmiast anihiluje z elektronem i
zostają wypromieniowane dwa kwanty
promieniowania gamma. Następnie jądro
deuteru 2D łączy się z jądrem wodorem 1H
tworząc jądro helu 3He. Dodatkowo zostaje
wypromieniowany kwant promieniowania
gamma.
Cykl ppI kończy reakcja fuzji dwóch jąder helu
3He w efekcie której powstają jądro helu 4He i
dwa jądra wodoru 1H, Zachodzi on głównie w
przedziale temperatur 107<T<1,4107K. W
temperaturze T<107 K produkowane jest
niewiele jąder helu.
2. Cykl ppII
W przedziale temperatur 1,4107<T<2,3107K
dominuje cykl ppII. Po dwóch pierwszych
reakcjach cyklu ppI dochodzi do syntezy helu
3He z helem 4He. Wytworzone zostaje jądro
berylu 7Be i kwant promieniowania gamma.
Nietrwałe jądro berylu 7Be szybko wychwytuje
elektron i tworzy się jądro litu 7Li i neutrino
elektronowe.
Następnie w wyniku reakcji litu 7Li i jądra
wodoru 1H powstają dwa jądra helu 4He.
3. Cykl ppIII
W temperaturze T>2,3107K, po pierwszej
reakcji cyklu ppII może zamiast reakcji
wychwytu elektronu przez jądro berylu zajść
fuzja wodoru i berylu w wyniku której
powstaje jądro boru 8B i kwant
promieniowania gamma.
Jądro boru 8B szybko wychwytuje elektron i
rozpada się na jądro berylu 8Be, pozyton i
neutrino elektronowe. Wzbudzone jądro berylu
8Be rozpada się na dwa jądra helu 4He
emitując energię 18,072 MeV.
Cykl ppIII nie jest istotnym źródłem energii w
Słońcu, ale generuje on wysokoenergetyczne
neutrina (do 14.06 MeV), z którymi związany
był problem neutrin słonecznych.
4. Energia
W wyniku każdego z cyklów ppI, ppII, ppIII z
czterech jąder wodoru powstaje jedno jądro
helu i dwa neutrina. Energia uwalniana w tych
reakcjach wynosi 26,74 MeV, ale neutrina
unoszą jej część. W cyklu ppI neutrina unoszą
1,9% , w cyklu ppII 3,9% i w cyklu ppIII -
27,3% energii całkowitej.

II.Cykl węglowo-azotowo-tlenowy:
Cykl węglowo-azotowo-tlenowy (CNO) - cykl
przemian jąder atomowych, których efektem
jest przemiana wodoru w hel oraz powstawanie
dużych ilości energii. Jest źródłem energii dla
masywnych gwiazd, ponieważ może zachodzić
tylko w bardzo dużych temperaturach (rzędu 20
milionów kelwinów).

W wyniku takiego cyklu reakcji następuje
przemiana czterech protonów w jądro helu i
uwolnienie energii: 41H → 4He + energia.
Węgiel-12 działa tu tylko jako katalizator i nie
ulega zużyciu, zatem nie potrzeba go w dużych
ilościach. Powstaje on natomiast w wyniku
oddziaływania ze sobą trzech jąder 4He,
zwanych też cząstkami alfa. W gwieździe
posiadającej dość zapasów wodoru
oddziaływanie to występuje sporadycznie.
Zaczyna jednak odgrywać coraz większą rolę,
gdy cały wodór zostanie zużyty i gwiazda staje
się tzw. czerwonym olbrzymem. To właśnie
przemiana helu w węgiel jest wtedy głównym
źródłem energii.
W cyklu CNO, raz na tysiąc reakcji, w wyniku
połączenia azotu-15 z protonem, powstaje jądro
tlenu-16 i foton (nie powstaje cząstka alfa). Ale
nawet w tym przypadku po kilku przemianach

otrzymujemy jądro helu, a azot powraca do
cyklu.

Szczegółowy przebieg cyklu

Reakcja1)

Wydzielona energia2)

w MeV w

12C + p → 13N + γ

1,944

14,4

13N → 13C + e+

2,22

16,5

13C + p → 14N

7,551

52

14N + p → 15O + γ 7,297

46,9

15O → 15N + e+

2,754

17,7

15N + p → 12C +
4He

4,966

30,1

raz na tysiąc reakcji zachodzi

15N + p → 16O + γ

16O + p → 17F + γ

17F → 17O + e+

17O + p → 14N +
4He

17A. Zdefiniuj pojecie amsy atomowej
pierwiastka chemicznego?
MASA ATOMOWA PIERWIASTKA
Artmetyczba srednia ważona mas atomów
nuklidów, gdzie wagami sa udziały masowe,
wyrazonaw [u]
1u=1/12 masy atomu 12C = 1,66057*10-27
Opisz prawa Rydberga okreslające mozliwe
długosci fal w widmie emijyjnym wodoru.?

Rydberg wykazał, że długości fal w liniach
widma wodoru mozna wyrazić równaniem.
λ - długość fali emisyjnej
l-stała równa 2 (dla seri Balmera)
n- liczba całkowita ≥3
R- stała ryderga

R=1,09677*10-7 m-1

18. Czym róznią sie i od czego zaleza
poszczególne serie widmowe w widmie
promieniowania elektromagnetycznego
wydzielanego przez atom wodoru?
Mamy pare serii widm emisyjnych wodoru.
Różnice w nich wynikaja z róznych zakresów
długosci fali swiatła ,w którym dane widmo
ejst widzialne. Wywyłuje to rónice w wartości
stałej l.
Seria Balmera –leży w swietle widzialnym, l=2
Seria Lymana- lezy w nadfiolecie, l=1
Seria Paschena – lezy w podczerwieni, l=3
Seria Bracketta – ley w podczerwieni, l=4

19. Wyznacz promień dla n-tej orbity Bohra,
dla elektronu w atomie wodoru.
r=n2*(h/4*Π2*e2*m*k)
r=0,5292*n2*10-8 cm
r- promień orbity m
n-liczba porządkowa orbity
e- łądunek elektyczny elektronu 1,60217 * 10-
19 C
m- masa elektronu 9,10938 *10-31 kg
k- stała oddziaływania elektrostatycznego w
próżni
h- stała Plancka 6,62607 *10-34 J*s

20. Jak przebiegał i czego dowodził
eksperyment Franck'a Hertz'a?
Eksperyment Franck'a Hertz'a.
Para rtęci jest przezroczysta, gdy elektrony
mają niską energię.
Gdy elektrony osiągną energię minimalną
4,9eV (energia fotonu o dł. fali 254nm) to gaz
zaczyna świecić.
Dowodzi to, że istnieją stany wzbudzone dla
rtęci.

21. Scharakteryzuj model Bohra-
Sommerfelda.
Orbity elektronów – okręgi i elipsy
elektrony poruszają się jedynie po niektórych,
dozwolonych okręgach i elipsach
liczba poboczna kwantowa l (określa kształt,
„spłaszczenie” orbity), przyjmuje wartości
l=0,1,n-1
elektrony poruszające się po 2 orbitach o
jednakowej liczbie n, ale posiadających różne
kształty, różnią się nieco energiami
zbiór orbit o tym samym n – powłoka
n = 1 -> K
n = 2 -> L
n = 3 -> M
magnetyczna liczba kwantowa (ml) określa
orientację (położenie w przestrzeni) orbit,
przyjmuje wartości (2*l+1)
ml = -l , ... , -1 , 0 , 1 , .... , l
zbiór orbit o tych samych n i l – podpowłoka
l = 0 -> s
l = 1 -> p
l = 2 -> d
magnetyczna spinowa liczba kwantowa (ms),
przyjmuje wartości: ½ i - ½

22. Jakie znaczenie ma zakaz Pauliego, gdy
jest on zastosowany do elektronów w
atomie?
W atomie nie może być dwóch elektronów w
tym samym stanie, tzn. że w atomie nie może
być 2 elektronów o takich samych 4 liczbach
kwantowych (n, l, ml, ms)

23. Jak zakaz Pauliego wpływa na
pojemność poszczególnych powłok i
podpowłok elektronowych?

Maksymalna liczba elektronów dla podpowłok
wynosi: s - 2, p - 6, d - 10, f – 14

24. Czym charakteryzuje się i jak opisujemy
prostą falę sinusoidalną rozchodzącą się w
ośrodku jednowymiarowym?
Fala sinusoidalna powstaje wówczas, gdy
ośrodek jest pobudzany cyklicznie do drgań.
Chwilowe wychylenie cząsteczki ośrodka
uczestniczącej w ruchu falowym zależy
zarówno od czasu, jak i położenia tej
cząsteczki.
Parametrami charakterystycznymi fali są:
prędkość rozprzestrzeniania się, u [m/s];
amplituda; A [wymiar – różnie]; długość fali
[m]; częstotliwość drgań f, v [1/s]; okres drgań,
T [s]; energia [J].

25. Opisz podstawowe zjawiska związane z
rozchodzeniem się fali (lub fal) w ośrodku.
prostoliniowe rozchodzenie się fali w
ośrodkach jednorodnych;
odbicie – po dojściu do granicy ośrodków fale
zmieniają kierunek poruszając się nadal w tym
samym ośrodku. Odbicie może dawać obraz
lustrzany lub być rozmyte, zachowując tylko
właściwości fali, ale nie dokładny obraz jej
źródła;
załamanie – na granicy ośrodków fala
przechodząc do ośrodka, w którym porusza się
z inną prędkością, zmienia kierunek swego
biegu. Zmiana prędkości powoduje zmianę
długości fali, a częstotliwość pozostaje stała.
dyfrakcja – uginanie się fali na krawędziach,
czego skutkiem jest zdolność do omijania
przeszkód mniejszych niż długość fali, oraz
powstawanie pasków dyfrakcyjnych po
przejściu fali przez wąską szczelinę albo
przeszkodę.

26. Jakie są falowe właściwości
promieniowania elektromagnetycznego?
Promieniowanie elektromagnetyczne
demonstruje swe właściwości falowe
zachowując się jak każda fala, ulegając
interferencji, dyfrakcji, spełnia prawo odbicia i
załamania. W wyniku superpozycji fal
elektromagnetycznych może powstać fala
stojąca.
Jednak niektóre właściwości promieniowania
elektromagnetycznego (szczególnie jego
oddziaływanie z materią) zależą od długości
fali (częstotliwości promieniowania) i dlatego
dokonano podziału promieniowania
elektromagnetycznego na zakresy ze względu
na jego częstotliwość.
Właściwości:
Mogą uginać się przy przejściu przez
przeszkodę;
Mogą oddziaływać ze sobą – wzmacniać się
lub wygaszać;
Konieczne jest wprowadzenie pojęcia kwantu
energii promieniowania elektromagnetycznego;
Określone zachowania promieniowania
elektromagnetycznego każą nam myśleć o nim
jak o strumieniu cząstek.

27. Co to jest kwant energii promieniowania
elektromagnetycznego i jak go wyrażamy?
Kwant energii – jest to energia jednego fotonu
padającego światła, absorbowana przez jeden
fotoelektron katody. Promieniowanie
elektromagnetyczne jest więc wysyłane i
pochłaniane w określonych porcjach
(kwantach) energii zależnych od częstości
promieniowania, które obecnie nazywamy
fotonami. Promieniowanie zachowuje się jak
strumień cząstek.
Energia całkowita fotoelektronu jest równa:
hv=Ek+W (gdzie W to praca przejścia
potrzebna do uwolnienia fotoelektronu z
metalu, a Ek to energia kinetyczna elektronu
zmieniana na energię potencjalną w polu
hamowania).

28. Na czym polega zjawisko fotoelektryczne
(zewnętrzne) i jakie wnioski z niego
wynikają?

Nr powłoki

Maksymalna ilość
elektronów

1

2

2

8

3

18

4

32

5

50

3

Efekt fotoelektryczny - zjawisko fizyczne
polegające na emisji elektronów z powierzchni
przedmiotu (substancji) pod wpływem światła
(zjawisko fotoelektryczne zwane również
zjawiskiem fotoelektrycznym zewnętrznym dla
odróżnienia od wewnętrznego).
Emitowane w zjawisku fotoelektrycznym
elektrony nazywa się czasem fotoelektronami.
Energia kinetyczna fotoelektronów nie zależy
od natężenia światła a jedynie od jego
częstotliwości.
Zjawisko to odkrył Hertz w 1887r.

29. Wyznacz energię kinetyczną elektronu
wybitego z płytki potasowej, jeśli długość fali
promieniowania wynosi 400nm, a praca
wyjścia dla potasu wynosi 223kJ/mol.
(h=6,62*10-34 J/s)
h=6,62*10-34 J/s
c=299792458 m/s
λ=400nm=400*10^-9m
W=223kj/mol=223000J/mol
223000J – 6,02214179*1023 cząst.
X – 1 cząst.
X=3,703001486*10-19 J
Ek=hν-W
Ek=(hc)/λ – X
Ek=1,258563694*10^-19 J
(najprawdopodobniej w dżulach)

30. Na czym polega zjawisko Comptona,
związane z przejściem promieniowania
rentgenowskiego przez płytkę grafitową?
Jakie wnioski z niego wynikają?
Zjawisko Comptona polega na rozpraszaniu
promieniowania rentgenowskiego na swo-
bodnych elektronach, w wyniku czego pro-
mieniowanie rozproszone ma większą długość
fali niż promieniowanie padające.
Aby to zjawisko wyjaśnić, należy założyć, że
miało miejsce sprężyste zderzenie dwóch
poruszających się cząstek: fotonu i elektronu,
podczas którego spełniona była zasada
zachowania energii i pędu. W czasie zderzenia
foton przekazuje część swojej energii i pędu
elektronowi, stąd wzrost długości fali
rozproszonego fotonu (zmiana długości fali
promieniowania zależna od kąta rozpraszania).
Zjawisko Comptona stanowi potwierdzenie
korpuskularnej natury promieniowania
elektromagnetycznego.

31. Co dla opisu zachowania się elektronów
w atomie oznacza zasada nieoznaczoności
Heisenberga?
Nie można jednocześnie dokładnie zmierzyć
dwóch sprzężonych ze sobą
(komplementarnych) wielkości fizycznych, np.
pewnej składowej położenia i odpowiadającej
jej składowej pędu cząstki.



x - niepewność pomiaru współrzędnej po-

łożenia;



px - niepewność pomiaru odpowiedniej

składowej pędu.
h- stała Plancka
Z zasady nieoznaczoności wynika, że im
dokładniej wyznaczy się jedną wielkość (np.
położenie lub energię), tym mniej dokładnie
zostanie określona ta druga wielkość
(odpowiednio: składowa pędu lub czas).
Zasada nieoznaczoności jest konsekwencją
dualizmu korpuskularno-falowego i stosuje się
ją do wszystkich obiektów, które wykazują
dwoistą naturę.
Nie jest możliwe jednoczesne dokładne
określenie położenia elektronu w atomie i jego
pędu w danej chwili.

32. Czego dotyczy i jak zapisujemy hipotezę
de Broglie’a?
Według de Broglie'a nie tylko fotonom, lecz
wszystkim cząstkom można przypisać
jednocześnie naturę korpuskularną i falową.
Przypuszczenie to zostało potwierdzone
eksperymentalnie (np. dyfrakcja i interferencja
elektronów, neutronów, atomów helu,
cząsteczek wodoru).
Każdej poruszającej się cząstce może być
zatem przypisywana odpowiednia fala materii,
zwana falą de Broglie'a, której długość



jest

uzależniona od pędu p cząstki:
h - stała Plancka.
h= 6,02



10-34 J



s

33. W jaki sposób wyprowadzamy równanie
Schrodingera z ogólnego równania ruchu
falowego?
7-10 slajd z wykładu VI (chyba nie ma sensu
żeby to wszystko tutaj przepisywać)

34. Jakie warunki musi spełnić funkcja
falowa będąca rozwiązaniem r.
Schrodinegra, aby mogła być wykorzystana
do opisu zachowania się elektronu w atomie?
Funkcja Ѱ –musi być: ciągła i skończona. Jeśli
x ∞ to Ѱ 0
Funkcja Ѱ –musi być znormalizowana:
Ѱ2dv=1

35. W jaki sposób energia elektronu zależy
od liczb kwantowych w przypadku atomu
zawierający tylko jeden elektron?
Energia elektronu może przyjmować tylko
wartości określone główną liczbą kwantową.

36.Co to są części radialne i kątowe funkcji
falowych i jak je uzyskujemy?
Część radialna -pokazuje zależność
prawdopodobieństwa napotkania elektronu w
atomie w stanie podstawowym w funkcji
odległości od jądra (prawdopodobieństwo
napotkania elektronu w at. w zależności od
długości promienia r). Czyli podaje
prawdopodobieństwo napotkania elektronu w
objętości zawartej pomiędzy powierzchnią kuli
o promieniu r, a powierzchnią kuli o promieniu
r+dr. Wykres części radialnej funkcji
przedstawia tą funkcję jako funkcję promienia
r.
Część kątowa- określa prawdopodobieństwo
znalezienia elektronu w danym kierunku w
przestrzeni. Miarą tego prawdopodobieństwa
jest odległość między początkiem układu
współrzędnych i punktem przecięcia prostej
poprowadzonej pod danym kątem z wykresem
funkcji. Aby przedstawić graficznie jej
przebieg, kreślimy we wszystkich kierunkach
w przestrzeni promienie wodzące wychodzące
z początku układu współrzędnych. Na każdym
z tych promieni odkładamy następnie odcinek o
określonej długości. Końce odcinków tworzą
jedna lub więcej powierzchni zamkniętych,
które można łatwo narysować, są to kontury
orbitalu.

37. Jaki jest związek między wartością
funkcji falowej w określonym miejscu w
przestrzeni a prawdopodobieństwem
znalezienia tam elektronu?
Wartość funkcji falowej dla danych
parametrów (w określonym miejscu w
przestrzeni) nazywa się amplituda
prawdopodobieństwa, a kwadrat jej modułu jest
proporcjonalny do gęstości
prawdopodobieństwa znalezienia elektronu w
danym punkcie w przestrzeni.

38. Co to jest gęstość prawdopodobieństwa
znalezienia elektronu i jaki jest jej związek z
rozwiązaniami równania Shondlingera
Gęstość prawdopodobieństwa znalezienia
elektronu to wielkość opisująca
prawdopodobieństwo znalezienia elektronu w
danym miejscu. Zależy ona od kwadratu
modułu funkcji falowej elektronu, która jest
rozwiązaniem równania Schodingera.
39. Jaki mają przebieg i od jakich
parametrów zależą części kątowe funkcji
falowej dla elektronu w atomie wodoru?
Części kątowe funkcji falowej dla elektronu w
atomie wodoru zależą od dwóch liczb
kwantowych l i m (orbitalnej i magnetycznej).
Dla wszystkich kierunków w przestrzeni
funkcja ma taką samą wartość, czyli promienie
wodzące mają taka sama długość, gdyż
odpowiada ona wartości funkcji. Końce tych
promieni wodzących tworzą sferę
(powierzchnię kuli).

40. Jak zależy prawdopodobieństwo
znalezienia elektronu od odległości od jądra
atomowego w zależności od wartości licz
kwantowych?
Im większa odległość od jadra atomowego tym
mniejsze prawdopodobieństwo znalezienia
elektronu. Im większe wartości mają liczby
kwantowe tym większy jest obszar orbitalny,
czyli zwiększa się odległość od jądra, a wraz z
większą odległością maleje
prawdopodobieństwo znalezienia elektronu.

41. JAKIE SĄ KSZTAŁTY ORBITALI
NALEŻĄCYCH DO POWŁOKI L?
L,M,N to powłoki na których występują
elektrony o podobnej energii. Elektrony z danej
powłoki rozmieszczone są na podpowłokach. I
właśnie w tych podpowłokach znajdują się
elektrony, które poruszają się w przestrzeni o
określonym kształcie - i to są właśnie orbitale.
*tak poprawnie to orbital jest funkcją falową,
której kształt opisuje przestrzeń występowania
elektronu. Orbital s przyjmuje kształt sferyczny
orbital p jest ich 3 są to tj. osómki
ukierunkowane wzdłuż osi ox, oy,oz. Orbital d
to tj.konczynka.

42. W jaki sposób energia elektronu zależy
od liczb kwantowych w przypadku atomów
zawierających wiele elektronów?
Istotna różnica pomiędzy atomami wodoru a
AT. Wieloelektronowymi polega na tym że w
pierwszym przypadku o energii decyduje
wyłącznie główna liczba kwantowa n, podczas
gdy w drugim wpływ na energie ma również
liczba kwantowa l. Zwraca się uwagę na fakt,
że w miarę wzrostu liczby kwantowej n
zachodzą na siebie poziomy energetyczne.
Poziom elektronowy odpowiadający w atomie
wodoru liczbie kwantowej n, rozszczepia się
zatem w at. Wieloelektrodowym na tyle
nowych blisko siebie położonych poziomów,
ile różnych wartości może przyjąć ( przy tej
samej liczbie kwantowej n) liczba kwantowa n
. atomy wieloelektrodowe są w związku z tym
bogatsze o dozwolone poziomy energetyczne
niż atom wodoru. Poszczególnym poziomom
odpowiada natomiast mniejsza liczba orbitali
czyli jak mówimy zmniejsza się degeneracja
poziomów energetycznych. Im większa liczba
kwantowa n tym większa energia orbitalu i tym

słabiej związany jest elektron w atomie. Jądro
w tym atomie przyciąga silniej elektrony
zmniejszając ich energię. W atomie wodoru nie
występuje odpychanie wieć wszystkie orbitale
mają jednakową energię. W atomach
wieloelektrodowych jednak odpychanie
powoduje iż en. Elektronu w orbitalu 2p jest
większa niż w 2s.

43. Czego dotyczy i jak brzmi AUFBAŁ?
Konstruując konfigurację elektronowe stanu
podstawowego korzystamy z reguły zwaną
zasadą rozbudowy powłok czyli zasady
Aufbau. Dotyczy ona kolejności obsadzania
orbitali atomowych. Po każdym dodaniu
jednego elektronu przesuwamy się o jedno
miejsce w prawo. Po zakończeniu jednego
okresu rozpoczynamy następny.

44. Jakie konsekwencje dla konfiguracji
elektronów w atomie mają zasady
PAULIEGO i HUNDAE
W atomie nie mogą występować elektrony
które nie różnią się przynajmniej jedną liczbą
kwantową. Z tej reguły zwanej ZAKAZEM
PAULIEGO wynika że jeden orbital o liczbach
kwantowych n, l, oraz m może opisywać
zachowanie się co najwyżej dwóch elektronów,
a mianowicie tych różniących się spinową
liczbą kwantową która przyjmuje dwie
wartości. Dowolny orbital może być osadzony
przez najwyżej dwa elektorny. Jeżeli w
podpowłoce dostępnych jest kilka orbitali
elektrony obsadzają puste orbitale zanim
utworzą parę w jednym z orbitali. Orbitale
zdegenerowane a więc orbitale o takiej samej
energii, przyporządkowywane są kolejno
elektronom w taki sposób by liczba
niesparowanych elektronów w stanie
podstawowym atomu była możliwie
największa. To twierdzenie zwane REGUŁĄ
HUNDA umożliwia rozstrzygnięcie w jaki
sposób są przyporządkowane elektronom np.
orbitale 2p. Znając wymienione zasady
możemy prześledzic strukturę powłok
elektronowych atomów poszczególnych
pierwiastków. Elektrony obsadzają orbitale w
taki sposób by całkowita energia atomu była
najmniejsza. Zostaje to osiągnięte przez
obsadzenie orbitali o najmniejszej energii
dzięki właśnie regule Pauliego.

45. Jak definiujemy energię jonizacji i jak
ona zależy od położenia w układzie
okresowym?
Energią jonizacji pierwiastka(Ej) nazywa się
minimum energii jaką należy użyć by oderwać
elektron od atomu tego pierwiastka w stanie
gazowym.
Energia jonizacji:
-wyraźny wzrost w okresie
-spadek w grupie
E.J. I- usunięcie pierwszego elektronu
E.J.II- usunięcie drugiego elektronu
E.J.III- usunięcie trzeciego elektronu
E.J.I< E.J.II< E.J.III (MJ/mol; eV/atom)

46. W jaki sposób opisuje się powstawanie
orbitali molekularnych?
Orbital molekularny (inaczej: cząsteczkowy,
skrót: MO) jest funkcją, opisującą stan
elektronu w cząsteczce, w ramach teorii orbitali
molekularnych. Zwykle przedstawia się go jako
kombinację orbitali atomowych - "zwykłych"
bądź zhybrydyzowanych.
Orbitale molekularne dzieli się głównie na:
zlokalizowane, np. H-O w H2O
zdelokalizowane, np. w cząsteczce benzenu
C6H6
Jednakże każdą funkcję falową elektronów w
cząsteczce można przedstawić jako wyznacznik
Slatera orbitali totalnie zdelokalizowanych lub
całkiem zlokalizowanych.
Zarówno jedne, jak i drugie mogą być:
wiążące (stabilizują cząsteczkę)
antywiążące (destablilizują cząsteczkę, są
oznaczane gwiazdką [*])
niewiążące (są obojętne przy oznaczaniu
trwałości cząsteczki)
Przykłady orbitali molekularnych:
σs-s - wszystkie MO utworzone z orbitali s to
wiązania σ
σs-p - wiązanie powstałe przez czołowe
nakładanie się orbitali s i p
σs-sp3 - wiązanie pomiędzy orbitalem s, a
hybrydą sp3, jak np. w CH4 - metanie
πp-p - wiązanie π może występować tylko z
orbitalami innymi niż s, czyli p, d i f.
πp-p* antywiążący orbital π
δ - orbital powstały przez boczne nakładanie
się dwóch orbitali d, lub orbitalu d z orbitalem
π*, posiada dokładnie dwie płaszczyzny
węzłowe zawierające oś wiązania
W wiązaniu σ występuje czołowe nakladanie
się orbitali, a w wiązaniu π - boczne.

47. Jakie są różnice pomiędzy orbitalami
atomowymi i cząsteczkowymi?
Różnice:
-w atomie pole potencjalne(pudło potencjału)-
jednego jądra;
w cząsteczce dwóch jąder o odległości R .
-w cząsteczce: stare rozwiązania(orbitale
atomowe) nowe rozwiązania(orbitale
cząsteczkowe)

48. Jakie są cechy wspólne orbitali
atomowych i cząsteczkowych?
-Funkcja falowa elektronu w tym polu
-dopuszczalne rozwiązania-orbitale
dopuszczalne energię elektronu w atomie
-rozmieszczenie gęstości prawdopodobieństwa
znalezienia elektronu w atomie

49. Jak energia orbitali molekularnych
zależy od odległości pomiedzy atomami?
Elektrony znajdujące sie w atomie( na ostatniej
powłoce bo te tylko biorą udział w reakcji)
mają wyższą energie wtedy kiedy są bliżej
innych atomów(ligandów ) to powoduje wzrost
energi całego atomu( układu).

50. Opisz przypadki tworzenia cząsteczki
dwuatomowej homojądrowej dla
pierwiastków ktróch powłoką walencyjną
jest powłoka K(L)
Weźmy H2. Ma on 2 elektrony na powłoce K.
Orbital 1s z jednego atomu wodoru oraz 1s z
drugiego nakładają sie na siebie tworząc
wspólny orbital wiążący sigma1s na którym
znajdują sie 2 elektrony. Taki stan zapewnia
niższą energię w więc wiekszą trwałość.
Następną cząsteczką homojądrową będzie Li2.
Posiada on 2 elektrony na powłoce K i jeden na
L.
Jest to podobny przykład jak dla wodoru jednak
tutaj mamy doczynienia z nakładaniem sie
orbitali typu 2s
Konfigurację dla cząsteczki litu możemy
zapisać następująco
[Li2]=KK(sigma2s)2
K-to orbital 1s
Z przytoczonych tutaj rozważań należy
zauważyć że w tworzeniu orbitali
cząsteczkowych biorą udział tylko orbitalami
powłoki walenyjnej i elektronami znajdujacymi
się na niej.

51. Scharakteryzuj możliwe kształty orbitali
wiążących i antywiążących powstającyh w w
yniku nakładania się orbitali atomowych
jednakowego typu
Patrz Bielański str. 128 ( naprawde nie wiem co
mam tu innego napisać:P)

52. Opisz efekty nakładania sie orbitali
atomowych odmiennych typów
Im większa liczba atomowa tym dalsze
powłoki są obsadzane przez elektrony np. dla
litu powłoka ta to s a dla boru to już p.
Zaczynają być obsadzane orbitale antywiążące
tzn energia się zwiększa a trwałość maleje.

53. W jaki sposób poziomy energetyczne
orbitali cząsteczkowych homojądrowych
cząsteczek pierwiastków okresu drugiego
zależą od liczby atomowej?
Homojądrowe cząsteczki pierwiastków okresu
drugiego to: Li2, Be2, B2, C2, N2, O2, F2. W
tej kolejności liczba atomowa wzrasta.
Normalna kolejność poziomów energetycznych
to sigma2s, sigma*2s, pi2p, sigma2p, pi*2p,
sigma*2p. Przy O2 (Z=8) kolejność się zmienia
i inna kolejność obejmuje O2 i F2 i jest to:
sigma2s, sigma*2s, sigma2p, pi2p, pi*2p,
sigma*2p.

54. Określ (zapisz i przedstaw na diagramie)
konfigurację elektronową cząsteczki Li2
(Be2, B2, C2, N2, O2, F2). (wszystkie
przykłady w wykładzie VIII rozrysowane).
Li2
Li: 1s2 2s2
[Li2]: 1s2 1s2 sigma2s2
[Li2]: [He] [He] sigma2s2
[Li2]: K K sigma2s2 może byc różny zapis
RW = 1/2 (4-2) = 1
B2, C2, N2, O2 i F2 analogicznie.
Be2 --> w przypadku berylu 1s2 2s2 mamy
sytuację podobną jak w He. Tyle samo
elektronów na orbitalu antywiążącym co na
wiążącym. Efekt antywiążący będzie większy
niż efekt wiążący. RW = 0. Uniemożliwia to
powstanie trwałej cząsteczki Be2.

55. Wyjaśnij na podstawie wyglądu i
charyzmy p. Żukowskiego dlaczego jest
starym kawalerem.

56. Jak różnica poziomów energetycznych
orbitali atomowych wpływa na powstawanie
orbitali cząsteczkowych w cząsteczkach
heterojądrowych?
Wspólna para elektronowa jest przyciągana
przez oba atomy, choć różnice w
elektroujemności powodują, że orbital
molekularny nie jest symetryczny.

57. Co to jest moment dipolowy i jak go
wyznaczamy?
Moment dipol występuje w cząsteczkach w
przypadku nierównomiernego rozmieszczenia
ładunku dodatniego i ujemnego w
cząsteczkach. Są to tzw. cząsteczki polarne
czyli biegunowe. Wielkość momentu
dipolowego określa iloczyn ładunku i
odległości między biegunami w cząsteczce
dwubiegunowej. Moment dipolowy wyraża się
w tzw. Debajach. Moment dipolowy odnosi się
do obiektow makroskopowych, ukladow

4

wieloatomowych lub do pojedynczego
wiązania. Moment dipolowy jest wielkoscia
wektorowa, wypadkowy moment dipolowy dla
obiektow zlozonych jest suma wektorowa.
Wartosc momentu dipolowego decyduje o
wielu wlasciwosciach związku chemicznego
m=e*l
gdzie: m - moment dipolowy
e - wielkość ładunku
l - odległość między biegunami dipolu

58. Jak okreslac wartość momentu
dipolowego dla dowolnego wiązania
pomiędzy A-B ?
Rozwiązania MO  rozkład gestosci
elektronowej, metoda bardzo trudna.
Przypisac pewne wartości pierwiastkom A i B
Xa i Xb tak aby roznica dawala moment
dipolowy wyrażony w Debajach

59. Zdefiniuj pojęcie elektroujemności.
Elektroujemność, elektronegatywność.
Zdolność atomów danego pierwiastka do
przyciągania elektronów.
To miara tendencji do przyciągania elektronów
przez atomy danego pierwiastka gdy tworzy on
związek chemiczny z atomami innego
pierwiastka. Bardziej elektroujemny
pierwiastek „sciaga” do siebie elektrony
tworzące wiązanie z atomem mniej
elektroujemnym co prowadzi do polaryzacji
wiązania. W skrajnym przypadku gdy
elektroujemności obu pierwiastków bardzo się
różnią (np. chlor i sód) dochodzi do pełnego
przeskoku elektronów na bardziej
elektroujemny atom co prowadzi do powstania
wiązania jonowego, Według R.S. Mullikena,
wartość elektroujemności jest średnią
arytmetyczną z powinowactwa elektronowego i
pierwszej energii jonizacji. Elektroujemność
rośnie w okresie a maleje w grupie. Największa
dla fluoru, tlenu, azotu, chloru (niemetale).
Najmniejsza Cs, Fr.

60. Opisz sposób tworzenia skali
elektroujemności wg Maullikena.
Skala Mullikena
Skalą biorącą pod uwagę rzeczywisty stan
atomu w danej cząsteczce, a więc liczbę i
rodzaj wiązań w jakich uczestniczy atom w
danym momencie, jest skala Mullikena. W
skali tej jednak pierwiastki mają zmienną
elektroujemność, zależną od tego w jakim
związku występują, więc jest ona trudna do
stosowania w praktyce.

61. Opisz sposób tworzenia skali
elektroujemności wg Allereda i Rochowa
Skala Allreda-Rochowa
Inną skalę zaproponowali Allred i Rochow ,
którzy obliczyli elektroujemność na podstawie
liczby atomowej i efektywnego promienia
walencyjnego atomów. Różnice między skalą
Allreda i Paulinga dochodzą do 0,5.

62. W jaki sposób elektroujemność zmienia
się w układzie okresowym?
Elektroujemność rośnie w okresach od strony
lewej do prawej. W grupach zmniejsz się przy
przejściu od pierwiastków o mniejszych
liczbach atomowych do pierwiastków o
większych liczbach atomowych. Wodoru nie
zaliczamy do litowców, ponieważ jego
elektroujemność znacznie różni się od
elektroujemności innych pierwiastków
pierwszej grupy układu okresowego. Skala
wprowadzona przez Linusa Paulinga ułatwia
określenie rodzaju wiązań występujących
między atomami pierwiastków.Według skali
wprowadzonej przez Linusa Paulinga
największą elektroujemność ma fluor (4,0), a
najmniejszą frans (0,7). Dużą wartość
elektroujemności wykazują niemetale,
natomiast metale charakteryzują się małymi
wartościami elektroujemności.Elektroujemność
rośnie ze wzrostem liczby atomowej w
okresach i maleje w grupach układu
okresowego.

63. Na czym polega hybrydyzacja orbitali
atomowych w atomie centralnym cząsteczki?
Hybrydyzacja to zabieg matematyczny
polegający na kombinacji liniowej
walencyjnych orbitali atomowych tego samego
atomu. Otrzymane zhybrydyzowane orbitale są
mieszaninami (hybrydami) orbitali
wyjściowych i charakteryzują się jednakowym
kształtem konturu i energią (co odróżnia je od
orbitali, z których powstały). Typ hybrydyzacji
określa, które walencyjne orbitale atomowe
zostały poddane matematycznemu
przekształceniu, a jednocześnie wyznacza
rozmieszczenie przestrzenne powstałych
hybryd. Hybrydy w przestrzeni ułożone są w
sposób gwarantujący ich minimalne
oddziaływania.

64. Opisz wybrane 4 typy hybrydyzacji:

typ
hybrydyzacji

liczba i ułożenie
hybryd

nazwa
hybrydyzacji

sp
(wymieszanie
jednego
orbitalu s i p)

dwie hybrydy
ułożone liniowo

hybrydyzacja
dygonalna

sp2

trzy hybrydy
skierowane do
naroży trójkąta
równobocznego,
leżące w jednej
płaszczyźnie

hybrydyzacja
trygonalna

sp3

cztery hybrydy
skierowane do
naroży tetraedru

hybrydyzacja
tetragonalna

dsp2 cztery hybrydy skierowane od środka ku
wierzchołkom kwadratu h.kwadratowa

Hybrydyzacja
sp

Hybrydyzacja
sp2

Hybrydyzacja
sp3

65. Porównaj orbitale powstające w wyniku
hybrydyzacji z odpowiednimi orbitalami, z
których powstały:
Orbitale powstające w wyniku hybrydyzacji
mają takie same właściwości, odpowiada im
taka sama energia i taki sam kształt, ale ta
energia i kształt są inne niż orbitali z których
powstały.

66. Scharakteryzuj możliwe kształty
cząsteczek, jeśli w atomie centralnym
zachodzi hybrydyzacja sp3 :
Tetraedr (109 stopni) - CH4 (liczba WP =0)
Piramida trygonalna (107 stopni) -NH3 (liczba
WP =1)
Kątowa (105 stopni)- H2O (liczba WP =0)

67. Scharakteryzuj możliwe kształty
cząsteczek, jeśli w atomie centralnie
zachodzi hybrydyzacja sp2 :
Trójkąt równoboczny – NO2- (liczba WP =1)
Trójkąt równoramienny – BCl2 (liczba WP =0)
Kryształ lodu dzięki wiązaniom wodorowym
ma strukturę heksagonalną- lód Ih Jego
komórka elementarna (najmniejszy fragment
powtarzający się w sieci krystalicznej) ma
kształt graniastosłupa o podstawie sześciokąta.
Stąd kryształy lodu mają sześciokrotną oś
symetrii co przesądza o kształcie płatków
śniegu.
Płatki śniegu powstają w chmurach, gdzie
znajduje się duże nasycenie pary wodnej. Gdy
temperatura staje się ujemna i znajdzie się
jakieś centrum krystalizacji na przykład
drobinka kurzu lub pyłek kwiatowy i to na nim
rozpoczyna się kondensacja cząsteczek wody i
tworzenie kryształu Tworzące się płatki mogą
mieć, zależnie od temperatury i wilgotności
powietrza różne kształty. Najpierw wszystkie
kryształki lodu rosną tak samo, formując
sześcian foremny. W czasie podróży płatka
śniegu w kierunku powierzchni ziemi zmienia
się zarówno wilgotność, jak i temperatura
otoczenia. Na wystających krawędziach mogą
się tworzyć nowe kryształy inaczej ustawione
w przestrzeni niż wcześniejsze formy.
Zachowana jest jednak symetria bowiem
odległość pomiędzy ramionami śniegowej
gwiazdki jest na tyle mała, że każde z ramion
rośnie praktycznie w tej samej temperaturze i
wilgotności. W bardzo niskich temperaturach,
poniżej -20°C brak jest w padającym śniegu
wymyślnych kształtów podobnych do
gwiazdek. Na ziemskich biegunach pada śnieg
w kształcie kolumienek czy płaskich płytek o
podstawie sześciokąta. Największe i
najpiękniejsze śnieżynki powstają w przedziale
temperatur od -10°C do -20°C przy dużej
wilgotności powietrza. Generalnie, im wyższa
wilgotność, tym kryształki lodu mają bardziej
złożone kształty.

Ponieważ woda w niejednakowym stopniu
przepuszcza promienie różnych barw będące
składowymi światła białego, światło barwy
czerwonej i żółtej zostanie dość silnie
pochłonięte nawet przez cienkie warstwy
wody, ale już niebieskie i fioletowe znacznie
słabiej. Tak więc światło przenikające coraz
głębiej nabiera wyraźnego
zielonkawoniebieskiego koloru. Promienie
niebieskie są słabo pochłaniane przez wodę,
natomiast silnie się w niej rozpraszają, zostają
najszybciej skierowane w górę i dzięki
niewielkiemu pochłanianiu nie osłabną tak
bardzo jak promienie innych kolorów.

68. Scharakteryzuj możliwe kształty
cząsteczek, jeśli w atomie centralnym
zachodzi hybrydyzacja z udziałem orbitali
podpowłoki d
bipiramida trygonalna
bipiramida tetragonalna
bipiramida pentagonalna

69.  Opisz metode VSEPR i podaj
przykłady jej zastosowania
Teoria VSEPR zakłada, że pary elektronów są
rozmieszczone wokół atomu centralnego tak,
aby siły wzajemnego odpychania były
możliwie jak najmniejsze, przy czym w
sumarycznym efekcie wszystkich odpychań
istotny jest udział wolnych (niewiążących) i
wiążących par elektronowych. Najsłabiej
odpychają się pary wiążące, potem para
wiążąca z wolną parą elektronową, a najsilniej
dwie wolne pary elektronowe. Inaczej mówiąc,
jeżeli odległości par decydujących o geometrii
cząsteczki są maksymalne, to w zależności od
liczby tych par powstają pewne
uprzywilejowane struktury o
charakterystycznym rozmieszczeniu wolnych i
wiążących par elektronowych na wyróżnionych
kierunkach wokół atomu centralnego.

Regularne kształty cząsteczek powstają tylko
wtedy, gdy wszystkie pary elektronów
wiążących zostaną wykorzystane do związania
takich samych atomów. Występowanie w
cząsteczce różnych ligandów wokół atomu
centralnego i niewiążących par elektronowych
zaburza idealne struktury, np. wraz z rosnącą
liczbą wolnych par elektronowych może
następować zmiana kąta wiązania.
Zastosowanie:
poszukiwanie kształtu niewielkich, zwykle
nieorganicznych cząsteczek

70. Opisz możliwe geometrie cząsteczek dla
których liczba przestrzenna przypisana do
atomu centralnego wynosi 3, 4, 5, 6
Dla liczby przestrzennej równej 3:
Powstałe trzy orbitale shybrydyzowane sp2
układają się na płaszczyźnie, a kąty między
nimi wynoszą ok. 120o. Cząsteczka z atomem
centralnym o takiej hybrydyzacji ma budowę
płaską, trygonalną. Hybrydyzację sp2 można
przypisać atomom węgla w graficie i w
pierścieniach aromatycznych, a także w
węglowodorach zawierających podwójne
wiązanie.
Dla liczby przestrzennej równej 4:
powstają cztery orbitale zhybrydyzowane sp3 o
jednakowej uśrednionej energii, ułożone w
przestrzeni ku wierzchołkom czworościanu
foremnego. Cząsteczka z atomem centralnym o
takiej hybrydyzacji ma budowę przestrzenną w
kształcie czworościanu (tetraedru) foremnego.
Hybrydyzację sp3 można przypisać atomom
węgla w diamencie, we wszystkich alkanach i
cykloalkanach oraz atomowi tlenu w cząsteczce
wody, czy atomowi azotu w cząsteczce
amoniaku.

71. Charakteryzuj budowę cząsteczki C2H6
(lub C2H4, C2H2)
Cząsteczka C2H6
Zbudowana z ośmiu atomów. Wiązanie
pomiędzy atomami węgla: C – C typu σ, węgle
czterowartościowe, w hybrydyzacji sp3.

Cząsteczka C2H4
Zbudowana z sześciu atomów. Wiązanie
podwójne pomiędzy atomami węgla. Wyróżnia
się wiązanie C – C typu σ oraz wiązanie C – C
typu π, słabsze niż wiązanie σ. Cztery wiązania
C – H typu σ. Węgle czterowartościowe w
hybrydyzacji sp2. Cząsteczka jest bardziej
reaktywna w porównaniu z cząsteczką etanu.
Możliwe usztywnienie cząsteczki, czyli
podstawienie dodatkowymi atomami lub
grupami atomów.

Cząsteczka C2H2
Zbudowana z czterech atomów. Wiązanie
potrójne pomiędzy atomami węgla. Wyróżnia
się wiązanie C – C typu σ oraz dwa wiązania C
– C typu π. Węgle czterowartościowe w
hybrydyzacji sp. Cząsteczka reaktywna,
nienasycona. Istnieje możliwość przyłączania
atomów lub cząstek.

72. Jakie są różnice pomiędzy wiązaniem
kowalencyjnym zlokalizowanym a
zdelokalizowanym?
Wiązanie chemiczne zlokalizowane łączy oba
atomy sąsiadujące ze sobą, natomiast wiązanie
chemiczne zdelokalizowane obejmuje kilka
atomów.

73. Opisz budowę cząsteczki O3 (lub CO2,
BF3, C3O2, C4H6, C6H6).
Cząsteczka O3
Atom centralny – O. Hybrydyzacja sp2.
Cząsteczka wygięta. Wiązania są jednakowe.
Jedna wolna para elektronowa. 18 elektronów
walencyjnych.

Cząsteczka CO2
Atom centralny – C. Hybrydyzacja sp.
Cząsteczka liniowa. Atom węgla w środku a
odległości do atomów tlenu są takie same. Nie
posiada wolnych par elektronowych. 16
elektronów walencyjnych.

Cząsteczka BF3
Atom centralny – B. Hybrydyzacja sp2.
Cząsteczka trygonalna płaska. Nie posiada

wolnych par elektronowych. 24 elektrony
walencyjne.

Cząsteczka C3O2
Cząsteczka liniowa wzdłuż osi OX. Węgle
czterowartościowe w hybrydyzacji sp. 24
elektrony walencyjne.

Cząsteczka C4H6
Węgle czterowartościowe w hybrydyzacji sp2.
Posiada 22 elektrony walencyjne. Zawiera 3
wiązania C – C typu σ oraz 6 wiązań C – H
typu σ.
Cząsteczka C6H6
Węgle czterowartościowe w hybrydyzacji sp2.
Posiada 30 elektrony walencyjne. Istnieje w
niej 6 wiązań C – C typu σ i drugie 6 wiązań C
– H typu σ.

74. Jakie są charakterystyczne właściwości
cząsteczek związków organicznych, w
których występują orbitale
zdelokalizowane?
Właściwości fizyczne:
Delokalizacja prowadzi do powstania szeregu
orbitali położonych blisko siebie (w skali
energii). Powoduje to, że cząstki mogą
absorbować kwanty promieniowania
elektromagnetycznego o stosunkowo małej
energii (w zakresie światła widzialnego).

Właściwości chemiczne:
- sprzężenie prowadzi do aromatyczności
(związki cykliczne)
- możliwość powstawania wiązań
koordynacyjnych
- mogą wychwytywać wolne elektrony,
dezaktywując wolne rodniki
- mogą transportować elektrony w
makrocząsteczkach.

75. Jak różnice w budowie odmian
alotropowych węgla wpływają na ich
właściwości?
Różnice w budowie odmian alotropowych
węgla sprawiają że mają one całkiem odmienne
właściwości. Poszczególne odmiany różnią się
między sobą jeśli chodzi o twardość, łupliwość,
przewodnictwo elektryczne, cieplne, czy też
gęstość.

76. Jakie są warunki powstawania wiązań
wodorowych?
Wiązanie wodorowe powstaje między
cząsteczkami związków zbudowanych z atomu
wodoru (zgromadzony cząstkowy ładunek
dodatni) połączonego z innym silnie
elektroujemnym pierwiastkiem posiadającym
niewiążące pary elektronowe (zgromadzony
cząstkowy ładunek ujemny). Atom jest
związany kowalentnie z atomami F,O,N. Przy
H(-) występuje wiązanie spolaryzowane (+).
Druga cząsteczka musi posiadać wolne pary
elektronowe przy F,O,N. Atomy biorące udział
w tworzeniu wiązania wodorowego mogą
należeć do tej samej cząsteczki lub innych
cząsteczek.

77. Opisz budowę HF2-
Jon HF2- powstaje przez połączenie F+HF.
Wiązania w nim występujące są równocenne.
Nakładają się na siebie równocześnie 3
orbitale.

78. Opisz przypadki powstawanie mostków
wodorowych między cząsteczkami związków
organicznych.
Mostki wodorowe tworzą się np. w DNA
łącząc ze soba dwie nici tego kwasu.
Mostki wodorowe pomiędzy zasadowymi
połączeniami azotowymi (a) cytozyna-
guanidyna (trzy mostki wodorowe) (b) tymina
adenina (dwa mostki wodorowe). Występuja w
alkoholach R-OH, fenolach Ar-OH, kwasach
organicznych R-COOH i aldehydach R-CHO.
Powstaja w stosunkowo dużych cząsteczkach.

79. Opisz przypadki powstawania mostków
wodorowych między cząsteczkami związków
nieorganicznych.
H2O, NH3, HF- silne wiązania wodorowe.
Powstaja tak jak w zad 5….

80. Jak obecność wiązań wodorowych
wpływa na właściwości fizyczne substancji? (
ciepło parowania, temperatura wrzenia)
Im więcej mostków siarczkowych tym
mniejsze ciepło parowania. Mostkom
zawdzięcza swoje dziwne właściwości woda,
one są odpowiedzialne za stały stan skupienia
wielu związków, one determinują drugo- i
trzeciorzędową strukturę białek i odgrywają
zasadniczą
rolę w kształtowaniu ich właściwości.
Wysoka temp wrzenia, np. fluorowodoru

81. Przykladowe proste ligandy i spos w jaki
lacza sie z atomem centralnym w zwiazku
kompleksowym.
Ligand w związku kompleksowym jest zawsze
donorem pary elektronowej.
Może on być dawcą jednej pary elektronowej i
wtedy zajmuje jedno miejsce
koordynacyjne taki ligand nazywamy ligandem
jednopozycyjnym np. Cl-, CN-, OH-, NH3.

5

82. Podstawowe cechy budowy zwiazkow
kompleksowych:
Związki kompleksowe jest to specyficzna
grupa związków złożona z:
− rdzenia (jednego lub kilku); rdzeń takiego
związku stanowi najczęściej
jon metalu przejściowego lub ciężkiego metalu
grupy głównej,
− ligandów – skoordynowanych przez atom
centralny jonów lub cząsteczek
elektroobojętnych ułożonych w ściśle
określonym porządku wokół jonu
centralnego.
Rdzeniem (atomem centralnym) jest zwykle
atom lub jon o strukturze
elektronowej umożliwiającej przyjęcie par
elektronowych i wytworzenie wiązania
koordynacyjnego, w którym jest akceptorem
elektronów. Ligandami są cząsteczki
lub jony dysponujące wolnymi parami
elektronów, które odgrywają rolę donorów
par elektronowych. W wyniku utworzenia
związku kompleksowego atom centralny
uzyskuje konfiguracje elektronową
najbliższego gazu szlachetnego (lub zbliżoną).
Liczbę ligandów w cząsteczce podaje liczba
koordynacyjna.

Związki kompleksowe możemy podzielić:
ze względu na ładunek sfery koordynacyjnej
na:
− kationowe,
− anionowe,
ze względu na strukturę elektronową jonu
centralnego na:
− przenikowe – związki koordynacyjne, w
których jon centralny przyjmuje
konfigurację elektronową gazu szlachetnego,
− przylegowe – związki koordynacyjne, w
których jon centralny nie ma
konfiguracji elektronowej gazu szlachetnego,
ze względu na liczbę jonów centralnych na:
− jednordzeniowe,
− wielordzeniowe,
ze względu na szybkość wymiany ligandów na:
− labilne – szybko wymieniające ligandy,
− bierne – wolno wymieniające ligandy.

83. Charakterystyka budowy ligandow
wielokleszczowych na przykladach
rozniacych sie iloscia mozliwych wiazan
Ligandy zawierające dwa lub wiecej atomów, z
których każdy moze jednocześnie utworzyc
dwuelektronowe wiązanie donorowe z tym
samym atomem metalu, noszą nazwę ligandów
wielokleszczowych
(wielofunkcyjnych) lub chelatowych, gdyż
chwytają one niejako kation miedzy dwa lub
wiecej atomów donorowych.
Ligandy dwukoordynacyjne, np.
Ligandy trój, cztero, a nawet
sześciokoordynacyjne, przykład - kwas
etylenodwuaminoczterooctowy
Zwiazek kompleksowy chelatowy (chelat)
Liczba ligandów otaczających bezpośrednio
jon centralny nazywa się liczbą koordynacyjną
i zwykle wynosi 2, 4, 6, 8.
Ponieważ ładunek drobiny kompleksowej jest
algebraiczną sumą ładunków jonu centralnego
oraz ligandów, więc może ona być kationem
[Cu(NH3)2]+ lub anionem [Zn(CN)4]2- lub
cząsteczką elektrycznie obojętną Ni(CO)4,
PtCl2(NH3)2.
Ligand może posiadać dwa lub więcej atomów
będących donorem pary
elektronowej. Taki ligand zajmuje odpowiednio
więcej miejsc koordynacyjnych
wokół jonu centralnego. Nazywamy go
ligandem wielopozycyjnym lub chelatowym

(kleszczowym). Do najpopularniejszych
ligandów dwupozycyjnych należą: diaminy,
difosfiny i dietery, (etylenodiamina (en)
2,2’bipirydyl (bpy), dimetryloglioksym
(dmg), anion kwasu szczawiowego (ox)) które
tworzą z metalem trwałe pierścienie.
Do najpopularniejszych ligandów
trójkleszczowych należy: dietylenotriamina
(dien),
czterokleszczowych – trietylenotetraamina
(yrien) a sześciokleszczowych anion
kwasu etylenodiaminotetraoctowego (EDTA).
Przykładem kompleksu wielokleszczowego jest
hemoglobina.

84. Czym jest EDTA i jakie ma zastosowania
?
EDTA (kwas etylenodiaminotetraoctowy, kwas
wersenowy, komplekson II) – organiczny
związek chemiczny kwas polikarboksylowy i
jednocześnie α-aminokwas. Z mocnymi
zasadami tworzy sole werseniany. Jest szeroko
stosowanym czynnikiem kompleksującym
wiele kationów metali, takich jak Ca2+, Mg2+
czy Fe3+. Zazwyczaj stosowany w postaci soli
disodowej (wersenian disodowy) ze względu na
jej większą rozpuszczalność w wodzie (tzw.
komplekson III).
Jego skrót pochodzi od nazwy angielskiej:
EthyleneDiamineTetraacetic Acid.
Ważnym zastosowaniem EDTA jest
maskowanie jonów metali, takich jak bizmut,
chrom(III), cynk, cyrkon, glin, kadm, kobalt,
magnez, miedź, nikiel, ołów, tor, wanad i

żelazo(III), które jest możliwe na skutek
tworzenia kompleksów chelatowych z jonami
metali. Własności chelatujące EDTA są na tyle
silne, że tworzy ona kompleksy nawet z
berylowcami.
kompleks chelatowy EDTA z jonem metalu M.
Zastosowania EDTA
-odczynnik kompleksujący w chemii
analitycznej
-środek konserwujący żywność (wiązanie
kationów metali ciężkich - kofaktorów
niepożądanych enzymów)
-składnik roztworów buforowych
-zapobieganie pozaustrojowemu krzepnięciu
krwi (wiązanie jonów wapnia)
-stosowany jako odtrutka w zatruciach
metalami ciężkimi
-stosowany w nawozach mikroelementowych
-inhibitor metaloproteaz

85. Kiedy występuje i na czym polega
izomeria optyczna w kompleksach
oktaedrycznych?
Zgodnie z definicją izomerami optycznymi są
cząsteczki, które mają się do siebie tak, jak
obraz i jego zwierciadlane odbicie. Takie
cząsteczki nazywane są enacjomerami.
Enacjomery różnią się pod wzgledem
skręcalności optycznej.
Taką właściwość posiadają pewne typy
kompleksów oktaedrycznych. Do
najważniejszych enancjomerów
oktaedrycznych należą kompleksy zawierające
dwa lub trzy ligandy kleszczowe, tj. typu M(L-
L)2X2 oraz kompleksy typu M(L-L)3.
Przykłady na rysunkach poniżej.

86. Omów oddziaływanie pola ligandów na
orbitale d atomu centralnego
Sześć wiążących orbitali molekularnych
występujących w kompleksach oktaedrycznych
jest wypełnionych przez elektrony ligandów
natomiast elektrony metalu przejściowego z
orbitali d zajmują orbitale niewiążące lub
antywiążące. Różnica w w energii pomiędzy
orbitalem niewiążącym a antywiążącym dla
kompleksu o geometrii oktaedru opisywana jest
jako ΔO, jej wartość zależy od rodzaju
oddziaływań orbitali π ligandów z orbitalami d
jonu centralnego. Jak przedstawiono w
poprzednim paragrafie ligandy π-donorowe
prowadzą do spadku wartości ΔO i są
nazywane ligandami słabego pola natomiast
ligandy π-akceptorowe zwiększają wartość ΔO
i nazywane są ligandami silnego pola. Ligandy
nie uczestniczące w formowaniu wiązań π
mogą mieć różnorodny wpływ na wartość ΔO.

Wartość ΔO ma znaczący wpływ na strukturę
elektronową jonów metali o konfiguracjach d –
d . W przypadku wymienionych konfiguracji
niewiążące i antywiążące orbitale molekularne
mogą zostać wypełnione na dwa sposoby: w
pierwszym najpierw dochodzi do wypełnienia
orbitali niewiążących a dopiero później
zapełniane są orbitale antywiążące. Tego
rodzaju kompleksy, z uwagi na brak lub małą
liczbę niesparowanych elektronów nazywa się
kompleksami niskospinowymi. Jeżeli natomiast
obserwuje się równomierne wypełnianie obu
typów orbitali przez elektrony to powstały
kompleks nazywany jest kompleksem
wysokospinowym z uwagi na dużą liczbę
niesparowanych elektronów. Niska wartość ΔO
może zostać przezwyciężona przez stabilizację
energetyczną wynikłą z braku odpychania się
parujących elektronów w kompleksach
wysokospinowych. W przypadku wysokiej
wartości ΔO energia parowania spinów staje
się zaniedbywalnie mała w porównaniu do
spadku energii wynikającego z formowania się
stanów niskospinowych

Spinowość cząsteczki ma wpływ na własności
makroskopowe związku koordynacyjnego
ponieważ obecność niesparowanych
elektronów powoduje paramegnetyczność
związku.

87. Pzedstaw zależność energi jonizacji od
położenia pierwiastka w układzie
okresowym
Energia odpowiadająca energii potrzebnej do
usunięcia jednego elektronu z obojętnej
cząsteczki lub atomu zwana jest energią
jonizacji. Wyróżniamy pierwszą energię
jonizacji, drugą energię jonizacji, itd., które
odpowiadają usunięciu pierwszego, drugiego,
trzeciego, itd. elektronu. Energia jonizacja
wyznaczana jest za pośrednictwem pomiarów
spektroskopowych i wyrażamy ją w eV/atom.
Pierwsza energia jonizacji określa energię
konieczną do oderwania z obojętnego atomu,
bądź cząsteczki jednego elektronu. Można więc
stwierdzić, że im bliżej jądra znajduje się
elektron (im mniejszy jest promień atomowy),
tym większa jest energia potrzebna do jego
oderwania. W obrębie okresu promień
atomowy zmniejsza się przy przejściu od
strony lewej do prawej, więc energia jonizacji
zwiększa się w tym samym kierunku i dla
gazów szlachetnych, które posiadają w swojej
powłoce walencyjnej oktet elektronowy, osiąga
największą wartość. W grupach układu
okresowego energia jonizacji maleje ze

wzrostem liczby atomowej (ze zwiększeniem
się liczby powłok elektronowych i wzrostem
promieni atomowych). Druga, trzecia, czwarta,
itd. energia jonizacji ma wartość większą niż
pierwsza, ponieważ do oderwania drugiego,
trzeciego i kolejnych elektronów z jonu
posiadającego ładunek dodatni konieczna jest
znacznie większa energia.

88. Zdefiniuj powinowactwo elektronowe i
opisz jego zmienność w układzie okresowym
Powinowactwo elektronowe to wielkość
charakteryzująca zdolność atomu (lub
cząsteczki) do przyłączania elektronu i
tworzenia jonu ujemnego (anionu). Ilościowo
określa się je jako energię, która wydziela się w
wyniku tego procesu. Tradycyjnie energię tę
podaje się w elektronowoltach (eV).
Powinowactwo elektronowe jest pośrednią
miarą elektroujemności pierwiastków
chemicznych. Czym większa wartość
powinowactwa tym większa elektroujemność
pierwiastka.
Miarą powinowactwa elektronowego jest
energia wydzielona podczas przyłączenia
jednego elektronu do cząsteczki lub atomu i
utworzenia jednoujemnego anionu.
Przyłączeniu kolejnych elektronów odpowiada
drugie, trzecie, czwarte, itd. powinowactwo
elektronowe. Największe powinowactwo mają
atomy pierwiastków o największej
elektroujemności. Powinowactwo elektronowe
jest efektem energetycznym, który towarzyszy
przyłączaniu jednego dodatkowego elektronu
do powłoki walencyjnej danego atomu. Zatem
im mniejszy jest promień atomowy, tym
większe jest powinowactwo elektronowe,
ponieważ tym mocniejsze jest oddziaływanie
dodatnio naładowanego jądra na elektron. W
obrębie grupy obserwuje się zwiększanie
promieni atomowych i zmniejszanie
powinowactwa elektronowego ze wzrostem
liczby atomowej. Natomiast w obrębie okresu
idąc od strony lewej do prawej zauważa się
zmniejszanie promieni atomowych oraz wzrost
powinowactwa elektronowego.

89.Opisz oddziaływanie pary jonów
tworzących strukturę ciała stałego.
Atomy (cząsteczki ) tworzące ciało stałe
oddziałują ze sobą tak, że tworzą sztywną
strukturę. Siły istniejące między nimi mają tę
własność, że na dużych odległościach są
przyciągające, zaś na małych - odpychające.
Wskutek tego odległości między atomami
ustalają się tak, że atomy przyjmują położenia
równowagowe. Oznacza to, że energia
potencjalna V każdego atomu osiąga w tych
punktach wartość minimalną. Oddziaływania
między atomami lub cząsteczkami mogą być
różnego pochodzenia, zależnie od rodzaju
atomów (cząsteczek), czyli od rodzaju
pierwiastka (związku chemicznego). Siły
wiązania można podzielić na pięć grup:
jonowe, kowalencyjne, metaliczne, wodorowe i
van der Waalsa.

90. czym jest i od czego zależy energia
sieciowa.
Energia sieciowa kryształu, energia jaka należy
dostarczyć, by jeden mol danej substancji
krystalicznej rozłożyć na atomy lub jony
znajdujące się w nieskończenie dużych
odległościach od siebie. Energia sieciowa
kryształu jest miarą spójności kryształu, zależą
od niej - temperatura topnienia, rozszerzalność
cieplna, ściśliwość, rozpuszczalność i inne
charakterystyczne wielkości.
Dla kryształu utworzonego z jonów o
wartościowościach z- i z+ energia sieciowa
kryształu Uo wyraża się wzorem: U0 = -
(N0Az-z+e2/r0)·(1-1/n), gdzie: N0 - stała
Avogadra, e - ładunek elektronu, A - stała
Madelunga, zależna od typu struktury
krystalicznej, r0 - odległość dwóch sąsiednich
jonów przeciwnego znaku w krysztale, n -
wykładnik Borna zależny od ściśliwości
kryształu.

91. Jaka jest zależność makroskopowych
właściwości substancji o budowie jonowej od
jej cech na poziomie atomowym?
Przepraszam nie znalazłam odpowiedzi na to
pytanie uzupełnię je jak tylko będę mogła
otworzyc wykład albo wczesniej jeśli gdzies
znajde.

ROZWIĄZANIA NIEKTÓRYCH ZADAŃ
OBLICZENIOWYCH:
III 8
Oblicz energie wydzielającą się przy
powstawaniu 10 jader atomowych 9 4Be. mBe
= 9,012182u, mp = 1,007825u, mn =
1,008665u.

Energie musimy wyliczyc ze znanego wzoru
ΔE = Δm*c2, gdzie Δm to deficyt masy, a c to
predkosc swiatla. Deficyt masy wyraza się
wzorem Δm = Z*Mp + N*Mn – mjadra, gdzie
Z – liczba protonow, N – liczba neutronow (A-
Z). W przypadku tego zadania mamy:
Δm = (4*mp + 5*mn – mj) *10
10 – mamy 10 jader
Δm = (4*1,007825 + 5*1,008665 -
9,012182)*10 = 0,62443 [u]

1u = 1,6605387313*10-27kg
0,62443u = 1,03689*10-27
ΔE = 1,03689*10-27* (299 792 458)2 =
9,319*10-11 [kg*m2/s2 = J]

Odp: Energia wydzielona przy powstaniu 10
jader boru wynosi 9,319*10-11 J.

IV 5
Wyznacz energie calkowita elektronu dla n-tej
orbity Bohra, dla elektronu w atomie wodoru
(należy wykorzystac postulaty Bohra).
Postulaty Bohra:
Ze wszystkich możliwych klasycznych orbit
kołowych dozwolone są tylko takie, na których
wartość momentu pędu elektronu jest całkowitą
wielokrotnością stałej Plancka h podzielonej
przez 2π:

mVr = nh/2π = n* ħ

gdzie m - masa elektronu, V - prędkość
elektronu, r - promień orbity elektronu, n -
główna liczba kwantowa będąca liczbą
całkowitą większą bądź równą 1, h - stała
Plancka h = 6,63·10-34 Js, ħ = h/2π = 1,05·10-
34 Js.
Orbity Bohra nazwane zostały orbitami
stacjonarnymi: znajdujące się na nich elektrony
nie promieniowały z założenia. Promienie orbit
stacjonarnych mogą przybierać jedynie ściśle
określone, dyskretne wartości, dlatego orbity
stacjonarne określa się mianem
skwantowanych. Liczba n, nazwana główną
liczbą kwantową, określa numer orbity
stacjonarnej elektronów w atomie liczonej od
orbity o najmniejszym promieniu.
Emisja lub absorpcja energii następuje tylko
podczas przejścia elektronu z jednej orbity
stacjonarnej na drugą, a energia
wypromieniowanego bądź pochłoniętego
kwantu promieniowania elektromagnetycznego
równa jest wartości bezwzględnej różnicy
energii stanu końcowego Ek i początkowego
Ep:
|Ek – Ep| = hν
gdzie ν – częstotliwość wyemitowanej bądź
pochłoniętej fali elektromagnetycznej.



Na podstawie założeń Bohra można wyznaczyć
promienie orbit stacjonarnych.
W atomie wodoru H na elektron o masie m
poruszający się po orbicie kołowej wokół jądra
działa siła dośrodkowa:
F = mV2/r
gdzie F - siła dośrodkowa, m - masa elektronu,
V - prędkość elektronu, r - promień orbity
elektronu.
Siła ta wynika z oddziaływania
coulombowskiego między ładunkami elektronu
i jądra:
F = e2/(4 π ε0 r2)
gdzie F - siła oddziaływania elektronu z jądrem
atomowym, e - ładunek elementarny e = -
1,6·10–19 C, ε0 - przenikalność elektryczna
próżni ε0 = 8,85·10-12 F/m, r – odległość
między elektronem a jądrem atomowym.

Przekształcając wzór z pierwszego postulatu
Bohra: mVr = nh/2π, uzyskuje się wzór na
prędkość elektronu na dowolnej orbicie
stacjonarnej:
V = nh/(2 πrm)
Podstawiając otrzymany wzór do zależności
siły dośrodkowej i siły Coulomba otrzymuje się
wzór na promień dowolnej orbity elektronu w
atomie wodoru:
rn = ε0 h2n2/(πme2)
gdzie rn – promień n-tej orbity elektronu, ε0 –
przenikalność elektryczna próżni, h – stała
Plancka, n – główna liczba kwantowa, m –
masa elektronu, e – ładunek elementarny.
Stosując podobną analogię można wyznaczyć
całkowitą energię elektronu znajdującego się na
dowolnej orbicie stacjonarnej. Energia
całkowita elektronu w atomie wodoru jest sumą
jego energii kinetycznej:
Ek = mV2/2
I potencjalnej:
Ep = -e2/ (4 π ε0 r)
Energia calkowita jest suma tych energii:
Ec = Ek + Ep = mV2/2 - e2/ (4 π ε0 r)
Po wykorzystaniu w powyższym wzorze
zależności opisanej w pierwszym postulacie
Bohra otrzymuje się ostateczny wzór na
energię całkowitą elektronu znajdującego się na
n-tej orbicie atomu wodoru:

En = -me4/ (8h2 ε02)*1/n2

V 6
Wyznacz energie kinetyczna elektronu
wybitego z plytki potasowej, jeśli dlugosc fali
promieniowania wynosi 400nm, a praca
wyjscia dla potasu wynosi 223 kJ/mol.
(h=6,62*10-34 J/s).

Energia calkowita elektronu jest opisana
wzorem:
Ec = Ek + W
Gdzie Ec = hν = h*c/λ, czyli:
Ek = h*c/λ – W

6

W = 223 kJ/mol
1 mol = 6,022 * 10 23 czast.
W = 3,7031 *10-22 kJ = 3,7031 *10-19 J
λ = 400nm = 400 *10-9 m

Ek = (6,626 * 10-34* 299 792 458/400*10-9) –
3,7031*10-19
Ek = 1.26296 * 10-19 J

Odp: Energia kinetyczna tego elektronu wynosi
1,26296 * 10-19 J.











1. Czym rózni sie opis materii na poziomie
makroskopowym i na poziomie
mikroskopowym?
2. Jakie znamy rodzaje promianiowania
jądrowego, jak możemy je
scharakteryzować?
3. Jakie sa podstawowe składniki materii, w
jaki sposób dzielimy cząstki elementarne?
4. Jak przebiega rozpad swobodnego
nautronu?
5. Na czym polegał eksperyment z czastkami
alfa i folia ze złota? Jakie wnioski mozna
wyciagnac z tego eksperymentu? (
eksperyment Rutherforda)
6. Jak jest rola protonów i neutronów w
jądrze atomowym? Jakie są warunki
trwałości jądra atomowego?
7. Jakie są skutki wypromieniowania
określonego rodzaju promieniowania
jądrowego dla jądra atomowego, które je
wypromieniowało?
8. Jakie są na poziomie atomowym skutki
oddziaływania promieniowania jądrowego z
materią?
9. W jaki sposób jądro atomowe może
zmniejszyć stosunek liczby protonów do
liczby neutronów?
10. W jaki sposób powstają sztuczne źródła
promieniotwórcze?
11. Jak powstaje i czym się charakteryzuje
reakcja łańcuchowa?
12. Jak ilościowo opisujemy szybkość
rozpadu promieniotwórczego? Jakie
parametry są z nim związane?
13. Jak jest zdefiniowana i skąd pochodzi
energia wiązania nukleonów w jądrze
atomowym.
14.Oblicz energię wydzielającą się przy
powstawaniu 10 jąder atomowych berylu:
15.Co to są i jakie znamy szeregi
promieniotwórcze:
16.Opisać przebieg poszczególnych zmian w
szeregu uranowo-radowym (uranowo-
aktynowym , torowym, neptunowym)
17. W jaki sposób przebiega synteza He w
gwiazdach:
17A. Zdefiniuj pojecie amsy atomowej
pierwiastka chemicznego?
18. Czym róznią sie i od czego zaleza
poszczególne serie widmowe w widmie
promieniowania elektromagnetycznego
wydzielanego przez atom wodoru?
19. Wyznacz promień dla n-tej orbity Bohra,
dla elektronu w atomie wodoru.
20. Jak przebiegał i czego dowodził
eksperyment Franck'a Hertz'a?
21. Scharakteryzuj model Bohra-
Sommerfelda.
22. Jakie znaczenie ma zakaz Pauliego, gdy
jest on zastosowany do elektronów w
atomie?
23. Jak zakaz Pauliego wpływa na
pojemność poszczególnych powłok i
podpowłok elektronowych?
24. Czym charakteryzuje się i jak opisujemy
prostą falę sinusoidalną rozchodzącą się w
ośrodku jednowymiarowym?
25. Opisz podstawowe zjawiska związane z
rozchodzeniem się fali (lub fal) w ośrodku.
prostoliniowe rozchodzenie się fali w
ośrodkach jednorodnych;
26. Jakie są falowe właściwości
promieniowania elektromagnetycznego?
27. Co to jest kwant energii promieniowania
elektromagnetycznego i jak go wyrażamy?
28. Na czym polega zjawisko fotoelektryczne
(zewnętrzne) i jakie wnioski z niego
wynikają?
29. Wyznacz energię kinetyczną elektronu
wybitego z płytki potasowej, jeśli długość fali
promieniowania wynosi 400nm, a praca
wyjścia dla potasu wynosi 223kJ/mol.
(h=6,62*10-34 J/s)
30. Na czym polega zjawisko Comptona,
związane z przejściem promieniowania
rentgenowskiego przez płytkę grafitową?
Jakie wnioski z niego wynikają?
31. Co dla opisu zachowania się elektronów
w atomie oznacza zasada nieoznaczoności
Heisenberga?
32. Czego dotyczy i jak zapisujemy hipotezę
de Broglie’a?

33. W jaki sposób wyprowadzamy równanie
Schrodingera z ogólnego równania ruchu
falowego?
34. Jakie warunki musi spełnić funkcja
falowa będąca rozwiązaniem r.
Schrodinegra, aby mogła być wykorzystana
do opisu zachowania się elektronu w atomie?
35. W jaki sposób energia elektronu zależy
od liczb kwantowych w przypadku atomu
zawierający tylko jeden elektron?
36.Co to są części radialne i kątowe funkcji
falowych i jak je uzyskujemy?
37. Jaki jest związek między wartością
funkcji falowej w określonym miejscu w
przestrzeni a prawdopodobieństwem
znalezienia tam elektronu?
38. Co to jest gęstość prawdopodobieństwa
znalezienia elektronu i jaki jest jej związek z
rozwiązaniami równania Shondlingera
39. Jaki mają przebieg i od jakich
parametrów zależą części kątowe funkcji
falowej dla elektronu w atomie wodoru?
40. Jak zależy prawdopodobieństwo
znalezienia elektronu od odległości od jądra
atomowego w zależności od wartości licz
kwantowych?
41. JAKIE SĄ KSZTAŁTY ORBITALI
NALEŻĄCYCH DO POWŁOKI L?
42. W jaki sposób energia elektronu zależy
od liczb kwantowych w przypadku atomów
zawierających wiele elektronów?
43. Czego dotyczy i jak brzmi AUFBAŁ?
44. Jakie konsekwencje dla konfiguracji
elektronów w atomie mają zasady
PAULIEGO i HUNDAE
45. Jak definiujemy energię jonizacji i jak
ona zależy od położenia w układzie
okresowym?
46. W jaki sposób opisuje się powstawanie
orbitali molekularnych?
47. Jakie są różnice pomiędzy orbitalami
atomowymi i cząsteczkowymi?
48. Jakie są cechy wspólne orbitali
atomowych i cząsteczkowych?
49. Jak energia orbitali molekularnych
zależy od odległości pomiedzy atomami?
50. Opisz przypadki tworzenia cząsteczki
dwuatomowej homojądrowej dla
pierwiastków ktróch powłoką walencyjną
jest powłoka K(L)
51. Scharakteryzuj możliwe kształty orbitali
wiążących i antywiążących powstającyh w w
yniku nakładania się orbitali atomowych
jednakowego typu
52. Opisz efekty nakładania sie orbitali
atomowych odmiennych typów
53. W jaki sposób poziomy energetyczne
orbitali cząsteczkowych homojądrowych
cząsteczek pierwiastków okresu drugiego
zależą od liczby atomowej?
54. Określ (zapisz i przedstaw na diagramie)
konfigurację elektronową cząsteczki Li2
(Be2, B2, C2, N2, O2, F2). (wszystkie
przykłady w wykładzie VIII rozrysowane).
Li2
55. Wyjaśnij na podstawie wyglądu i
charyzmy p. Żukowskiego dlaczego jest
starym kawalerem.
56. Jak różnica poziomów energetycznych
orbitali atomowych wpływa na powstawanie
orbitali cząsteczkowych w cząsteczkach
heterojądrowych?
57. Co to jest moment dipolowy i jak go
wyznaczamy?
58. Jak okreslac wartość momentu
dipolowego dla dowolnego wiązania
pomiędzy A-B ?
59. Zdefiniuj pojęcie elektroujemności.
60. Opisz sposób tworzenia skali
elektroujemności wg Maullikena.
61. Opisz sposób tworzenia skali
elektroujemności wg Allereda i Rochowa
62. W jaki sposób elektroujemność zmienia
się w układzie okresowym?
63. Na czym polega hybrydyzacja orbitali
atomowych w atomie centralnym cząsteczki?
64. Opisz wybrane 4 typy hybrydyzacji:
65. Porównaj orbitale powstające w wyniku
hybrydyzacji z odpowiednimi orbitalami, z
których powstały:
66. Scharakteryzuj możliwe kształty
cząsteczek, jeśli w atomie centralnym
zachodzi hybrydyzacja sp3 :
67. Scharakteryzuj możliwe kształty
cząsteczek, jeśli w atomie centralnie
zachodzi hybrydyzacja sp2 :
68. Scharakteryzuj możliwe kształty
cząsteczek, jeśli w atomie centralnym
zachodzi hybrydyzacja z udziałem orbitali
podpowłoki d
69.  Opisz metode VSEPR i podaj
przykłady jej zastosowania
70. Opisz możliwe geometrie cząsteczek dla
których liczba przestrzenna przypisana do
atomu centralnego wynosi 3, 4, 5, 6
71. Charakteryzuj budowę cząsteczki C2H6
(lub C2H4, C2H2)
72. Jakie są różnice pomiędzy wiązaniem
kowalencyjnym zlokalizowanym a
zdelokalizowanym?
73. Opisz budowę cząsteczki O3 (lub CO2,
BF3, C3O2, C4H6, C6H6).
74. Jakie są charakterystyczne właściwości
cząsteczek związków organicznych, w

których występują orbitale
zdelokalizowane?
75. Jak różnice w budowie odmian
alotropowych węgla wpływają na ich
właściwości?
76. Jakie są warunki powstawania wiązań
wodorowych?
77. Opisz budowę HF2-
78. Opisz przypadki powstawanie mostków
wodorowych między cząsteczkami związków
organicznych.
79. Opisz przypadki powstawania mostków
wodorowych między cząsteczkami związków
nieorganicznych.
80. Jak obecność wiązań wodorowych
wpływa na właściwości fizyczne substancji? (
ciepło parowania, temperatura wrzenia)
81. Przykladowe proste ligandy i spos w jaki
lacza sie z atomem centralnym w zwiazku
kompleksowym.
82. Podstawowe cechy budowy zwiazkow
kompleksowych:
83. Charakterystyka budowy ligandow
wielokleszczowych na przykladach
rozniacych sie iloscia mozliwych wiazan
84. Czym jest EDTA i jakie ma zastosowania
?
85. Kiedy występuje i na czym polega
izomeria optyczna w kompleksach
oktaedrycznych?
86. Omów oddziaływanie pola ligandów na
orbitale d atomu centralnego
87. Pzedstaw zależność energi jonizacji od
położenia pierwiastka w układzie
okresowym
88. Zdefiniuj powinowactwo elektronowe i
opisz jego zmienność w układzie okresowym
89.Opisz oddziaływanie pary jonów
tworzących strukturę ciała stałego.
90. czym jest i od czego zależy energia
sieciowa.
91. Jaka jest zależność makroskopowych
właściwości substancji o budowie jonowej od
jej cech na poziomie atomowym?

ROZWIĄZANIA NIEKTÓRYCH ZADAŃ
OBLICZENIOWYCH: