ELEMENTY FIZYKI KWANTOWEJ I JĄDROWEJ

101. Ciało doskonale czarne (rozkład Plancka)
Ciałami doskonale czarnyminazywamy ciała, których powierzchnie absorbują całe

promieniowanie, jakie na nie pada (nie odbijają światła).
W praktyce ciała doskonale czarne realizuje się robiąc pudło z bardzo małym otworkiem i

wnętrze tego pudła pokrywa się sadzą (sadza ma bardzo dobre własności pochłaniania
promieniowania). Wówczas promieniowanie wpadające w ten otworek odbija się

wielokrotnie od powierzchni wewnętrznej pudła, a ponieważ ma ona bardzo mały
współczynnik odbicia, więc po kilkunastu odbiciach promieniowanie zostaje

zaabsorbowane przez pudło. Następnie obserwuje się otwór i mierzy rozkład widmowy
promieniowania, który jest jednakowy dla wszystkich ciał doskonale czarnych.
Całkowitą energię wysyłanego promieniowania w całym zakresie długości fal możemy
obliczyć sumując emisję dla wszystkich długości fal (calkując R

λ

po wszyskich długościach

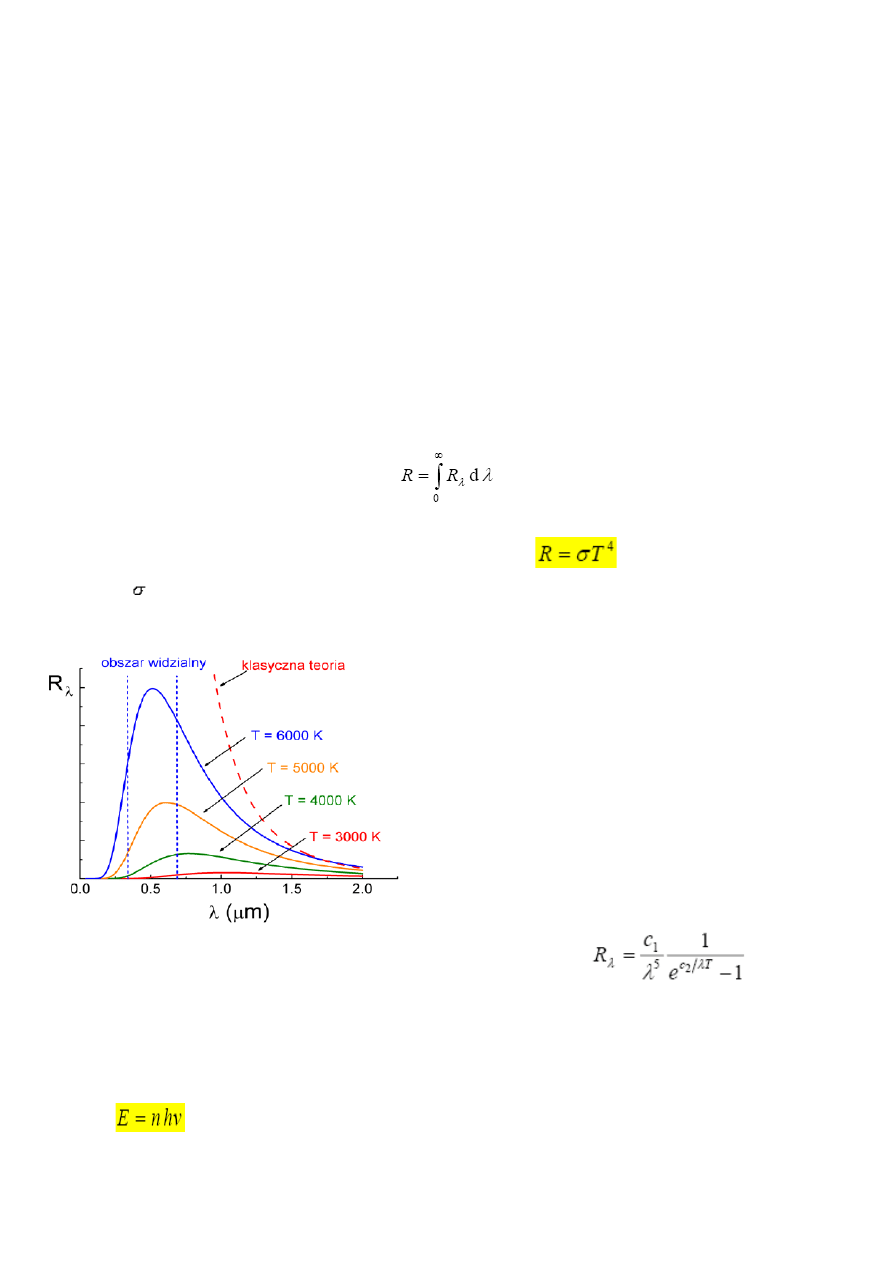
fal). Wielkość tą nazywamy całkowitą emisją energetyczną promieniowania R:

Emisja energetyczna promieniowania ciała doskonale czarnego zmienia się wraz z

temperaturą według prawa Stefana-Boltzmanna:

gdzie = 5,67,10

-8

W/m

2

K

4

jest stałą Stefana – Boltzmanna.

Zdolność emisyjna promieniowania dla ciała doskonale czarnego zmienia się z temperaturą

tak jak na rysunku:

Pokazane krzywe są zależa tylko od temperatury i
są całkowicie niezależne od materiału, kryształu i

wielkości.
Długość fali dla której przypada maksimum emisji

jest zgodnie z prawem Wiena odwrotnie
proporcjonalna do temperatury ciała.
Teoria klasyczna- widmowa zdolność emisyjna
wyliczona w oparciu o obliczoną wartość średniej

energii z prawa ekwipartycji energii. Sprzeczny z
rzeczywistością wynik rozważań klasycznych

nazywany jest „katastrofą w nadfiolecie”.
Teoria Plancka promieniowania we wnęce

Wzór Plancka dający wynik widmowej zdolnosci emisyjnej :
c

1

i c

2

- stałe wyznaczane doświadczalnie

Planck stwierdził, że w przypadku promieniowania ciała doskonale czarnego średnia
energia fal stojących jest funkcją częstotliwości. Założył on, że każdy atom zachowuje się

jak oscylator elektromagnetyczny posiadający charakterystyczną częstotliwość drgań.
Oscylatory te, wg Plancka, nie mogą mieć dowolnej energii, ale tylko ściśle określone

wartości dane wzorem:

h=6,63

.

10

-34

Js (stała Plancka), n- liczba kwantowania.

Oscylator wypromieniowuje energię kwantami (nie w sposób ciągły). Kwanty są emitowane
gdy oscylator przechodzi ze stanu o danej energii do drugiego o mniejszej energii.

Odpowiada to zmianie liczby kwantowej n o jedność, a w konsekwencji wypromieniowana
zostale eneria w ilości:

Oznacza to, że dopóki oscylator pozostaje w jedym ze swoich stanów kwantowych dopóty

ani nie emituje ani nie absorbuje energii. Mówimy, że znajduje się w stanie stacjonarnym.
102. Efekt fotoelektryczny, efekt Comptona, zjawisko kreacji par cząstek
Zjawisko uwalniania przez światło elektronów z powierzchni rozmaitych substancji
nazwane jest zjawiskiem fotoelektrycznym.

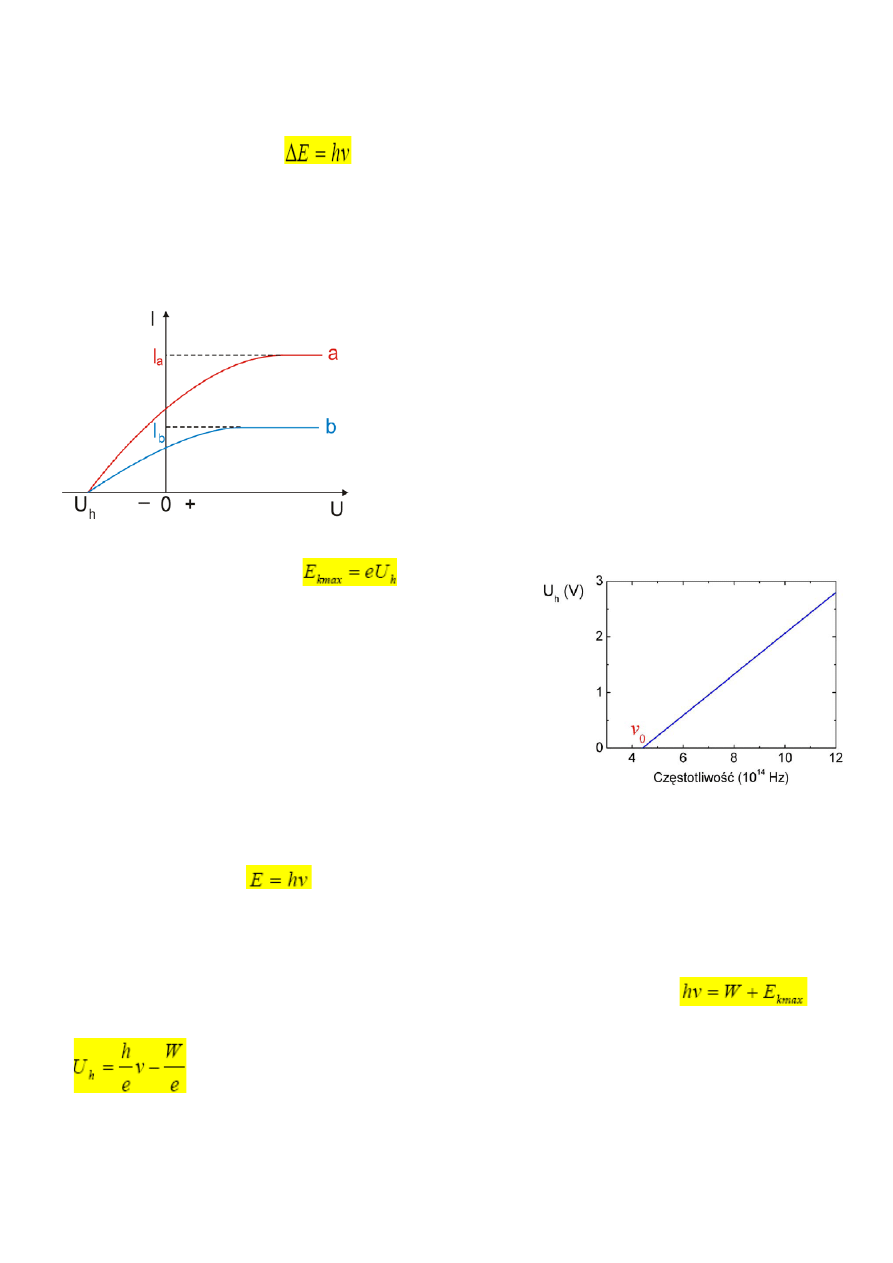
Jeśli wytworzymy pewną różnicę potencjałów pomiędzy
płytką A, z której uwalniane są elektrony, a płytką

zbierającą B, to zaobserwujemy przepływ prądu. Gdy U
jest dostatecznie duże, wtedy prąd fotoelektryczny

osiąga pewną wartość graniczną (prąd nasycenia).
Niektóre z elektronów dochodzą do elektrody B, pomimo

że pole elektryczne działa na ich ruch hamująco.
Jednakże gdy różnica potencjałów U jest dostatecznie

duża, równa wielkości U

h

zwanej napięciem hamującym,

wtedy prąd fotoelektryczny całkowicie zanika. Różnica
potencjałów U

h

pomnożona przez ładunek elektronu jest

miarą energii kinetycznej K

max

najszybszych

uwolnionych elektronów:
Krzywa b odpowiada dwukrotnie mniejszemu natężeniu
światła padającego niż krzywa a. Napięcie hamujące jest

niezależne od natężenia światła, natomiast natężenie
prądów nasycenia I

a

oraz I

b

są wprost proporcjonalne do

natężenia światła.
Zależność napięcia hamowania od częstotliwości światłą
padającego na powierzchnię sodu metalicznego jest

zależnością liniową. Isnieje pewna wartość progowa
częstotliwości v

o

, poniżej której zjawisko fotoelektryczne

nie występuje.
Einstein założył, że energia wiązki świetlnej rozchodzi się w przestrzeni w postaci

skończonych porcji (kwantów) energii zwanych fotonami. Energia pojedynczego fotonu
dana jest wzorem:

Einstein zapostulował, że kwanty światła rozchodzą się w

przestrzeni jak cząstki materii (wg Plancka jako fala elektromagnetyczna), i gdy foton

zderzy się z elektronem w metalu to może zostać przez elektron pochłonięty. Wówczas
energia fotonu zostanie przekazana elektronowi. Do wyrwania elektronu z metalu

potrzebna jest energia W (praca wyjścia). Energia hv fotonu, w części (W)
zostaje zużyta na wyrwanie elektronu z materiału, a ewentualny nadmiar

energii (hv – W) elektron otrzymuje w postaci energii kinetycznej.

Teoria Einsteina przewiduje liniową zależność pomiędzy napięciem

hamowania, a częstotliwoścą. Teoria fotonowa potwierdza fakty związane ze
zjawiskiem fotoelektrycznym, ale jest sprzeczna z teorią falową (dualizm

korpuskularnofalowy)

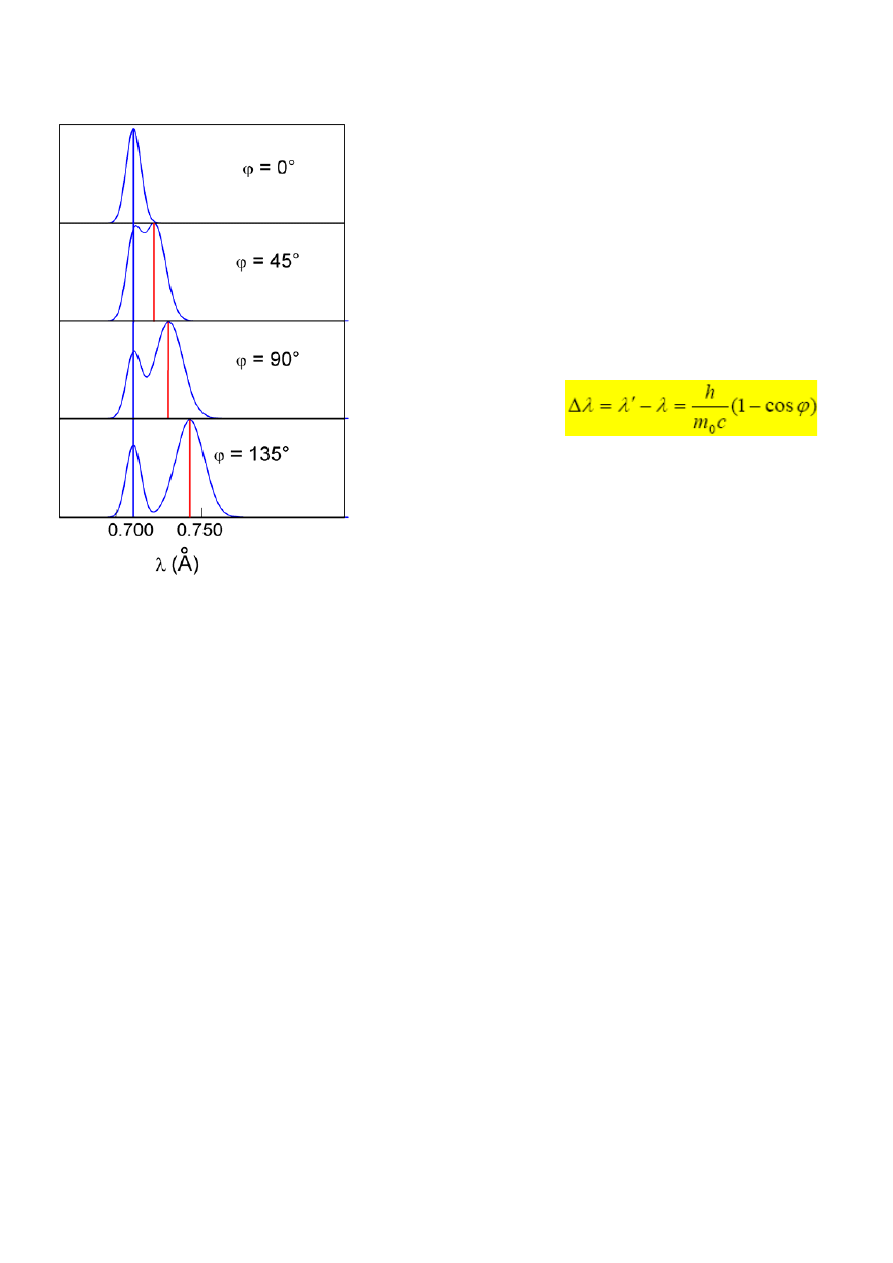
Efekt Comptona to doświadczenie związane z rozpraszaniem fal elektromagnetycznych

na swobodnych elektronach. Compton mieżył natężenie
wiązki rozproszonej pod różnymi kątami φ jako funkcję
długości fali λ. W promieniowaniu rozproszonym

występują dwie długości fal: jedna o długości λ
identycznej jak fala padająca i druga długości λ' większa

o Δλ. Jest to tzw. przesunięcie Comptona ( λ' zmienia
się wraz z kątem). Compton założył, że fotony zderzają

się z elektronami swobodnymi w bloku grafitu. W
wyniku zderzenia zmienia się kierunek poruszania się

fotonu oraz jego energia ( jej część została przekazana
elektronowi). Oznacza to zmianę częstotliwości oraz

długości fali. Stosując zasadę zachowania pędu oraz
zasadę zachowania energii otrzymujemy wyrażenie na

przesunięcie Comptona:
m

o

- masa elektronu

(spoczynkowa)
Przesunięcie Comptona zależy tylko od kąta

rozproszenia. Do obliczania energii kinetycznej
elektronu stosuje się wyrażenie relatywistyczne

ponieważ odrzucone elektrony mogą mieć prędkości
porównywalne z prędkością światła.

Zjawisko kreacji par cząstek- foton o wysokiej energii traci wskutek zderzenia z

jądrem całą swą energię hv i jej kosztem powstaje para cząstek - elektron i pozyton,
mających pewną energię kinetyczną. Pozyton jest cząstką o własnościach identycznych z

własnościami elektronu, z wyjątkiem znaku ładunku elektrycznego (i kierunku momentu
magnetycznego). W procesie tworzenia par energia przekazana jądru ulegającemu

odrzutowi jest zaniedbywalna, ponieważ jądro ma dużą masę. Obie cząstki mają jednakowe
energie spoczynkowe m

0

c

2

. Wyprodukowany pozyton ma nieco większą energię

kinetyczną, ponieważ w wyniku oddziaływania kulombowskiego wytworzonej pary z

dodatnio naładowanym jądrem występuje przyspieszenie pozytonu i hamowanie elektronu

.

Podstawowe prawa, które muszą być spełnione podczas oddziaływania to: prawo

zachowania całkowitej energii relatywistycznej, prawo zachowania pędu oraz prawo
zachowania ładunku. Mówimy, że proces kreacji par przebiega w polu jądra, czyli w polu

oddziaływania z jądrem. Minimalna energia fotonu, zwana inaczej energią progową,
potrzebna do wytworzenia pary cząstek, wynosi 2m

0

c

2

, czyli 1,02MeV, co odpowiada

długości fali 0,012Å. Jeżeli długość fali jest mniejsza, a tym samym energia jest większa od

energii progowej, to wytworzona para cząstek ma oprócz energii spoczynkowej również
pewną energię kinetyczną.
Ze zjawiskiem kreacji par ściśle związany jest proces odwrotny zwany anihilacją par. Polega
on na tym, że gdy spoczywające cząstki - elektron i pozyton - znajdują się blisko siebie,

wtedy łączą się ze sobą i ulegają anihilacji. W rezultacie następuje unicestwienie dwóch
cząstek materialnych, w miejsce których powstaje promieniowanie elektromagnetyczne.
W wyniku występowania zjawiska fotoelektrycznego oraz kreacji par zachodzi całkowita
absorpcja fotonów, natomiast zjawisko Comptona prowadzi do rozpraszania fotonów.

103. Model atomu Bohra (postulaty kwantowania)
Podstawową cechą modelu Bohra jest to, że umożliwia przewidywanie widm

promieniowania wysyłanego przez atomy.
W przeciwieństwie do widma ciągłego emitowanego na przykład przez powierzchnie ciał

ogrzanych do wysokich temperatur, widma promieniowania pierwiastków w postaci gazów
i par pobudzonych do świecenia na przykład za pomocą wyładowania elektrycznego, są

złożone z jasnych, ostrych linii, odpowiadających ściśle określonym długościom fal.

Promieniowanie wysyłane przez swobodne atomy (tzw. widmo emisyjne ) zawiera tylko

pewną liczbę długości fal. Takie widmo nazywamy widmem liniowym , a każdą z takich
składowych długości fal nazywana jest linią widmową.

Obok widm emisyjnych badano również widma absorpcyjne , tym razem obserwując
promieniowanie pochłaniane przez gazy zamiast emitowanego. Doświadczenia pokazują,

że pojedyncze atomy (cząsteczki) zarówno emitują jak i absorbują promieniowanie o ściśle
określonych długościach fali.

Niels Bohr zaproponował kwantowy model budowy atomu wodoru. Postulaty:

• elektron może poruszać się tylko po pewnych dozwolonych
orbitach.

• podobnie jak oscylatory Plancka, tak samo atom wodoru może
znajdować się tylko w ściśle określonych stacjonarnych stanach

energetycznych, w których, pomimo, że elektron doznaje
przyspieszenia (poruszając się po orbicie) nie wypromieniowuje

energii. Jego całkowita energia pozostaje stała.
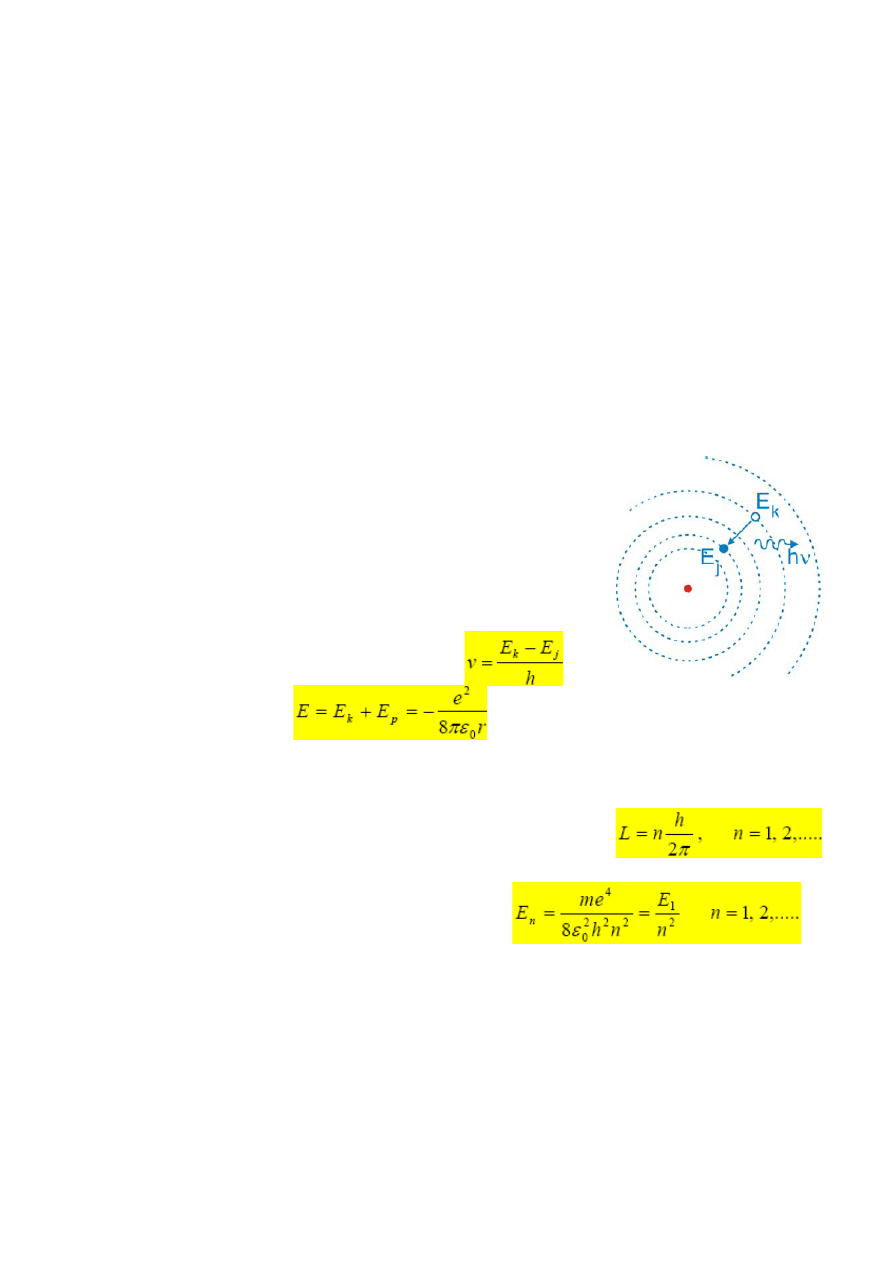
• promieniowanie elektromagnetyczne zostaje wysłane tylko

wtedy, gdy elektron poruszający się po swojej orbicie zmienia
swój ruch skokowo, tak że porusza się

następnie po orbicie o niższej energii.
Cęstotliwość emiptowanego promieniowania:

Całkowita enrgia ukłądu:

• elektron w atomie porusza się po orbicie kołowej pod wpływem przyciągania

kulombowskiego pomiędzy elektronem i jądrem i ruch ten podlega prawom mechaniki
klasycznej.

• elektron może poruszać się tylko po takich orbitach, dla których
moment pędu L jest równy całkowitej wielokrotności stałej

Plancka podzielonej przez 2π, (stała n jest liczbą kwantową).

Równanie przedstawia wartości energii dozwolonych
stanów stacjonarnych:

Wprowadzenie kwantowania orbitalnego momentu pędu elektronu prowadzi do

kwantowania jego energii całkowitej.

Serie widmowe wodoru:
Przejścia pomiędzy stanami stacjonarnymi i odpowiadające im linie widmowe tworzą serie

widmowe. Dana seria obejmuje promieniowanie emitowane przy przejściu elektronu z
poziomów wyższych na dany np. seria Balmera obejmuje przejścia ze stanów o n > 2 do

stanu o n = 2.
Tylko przejściom elektronu na drugą orbitę (seria Balmera) towarzyszy emisja

promieniowania z zakresu widzialnego. Seria Lymana obejmuje promieniowanie w
zakresie nadfioletu, a seria Paschena w podczerwieni.

104. Fale de Broglie'a i zasada nieoznaczności Heisenberga
W 1924 r. de Broglie zapostulował, że skoro światło ma dwoistą, falowo-cząstkową, naturę,
to także materia może mieć taką naturę. Posługując się klasyczną teorią
elektromagnetyzmu można pokazać, że światło o energii E ma
pęd p = E/c. Zatem foton (kwant światła) ma pęd równy:

De Broglie nie tylko zasugerował istnienie fal materii ale

również przewidział ich długość. Założył, że długość przewidywanych fal materii jest
określona tym samymzwiązkiem, który stosuje się do światła:
Eksperyment interferencyjny odsłania falowy charakter cząstek.
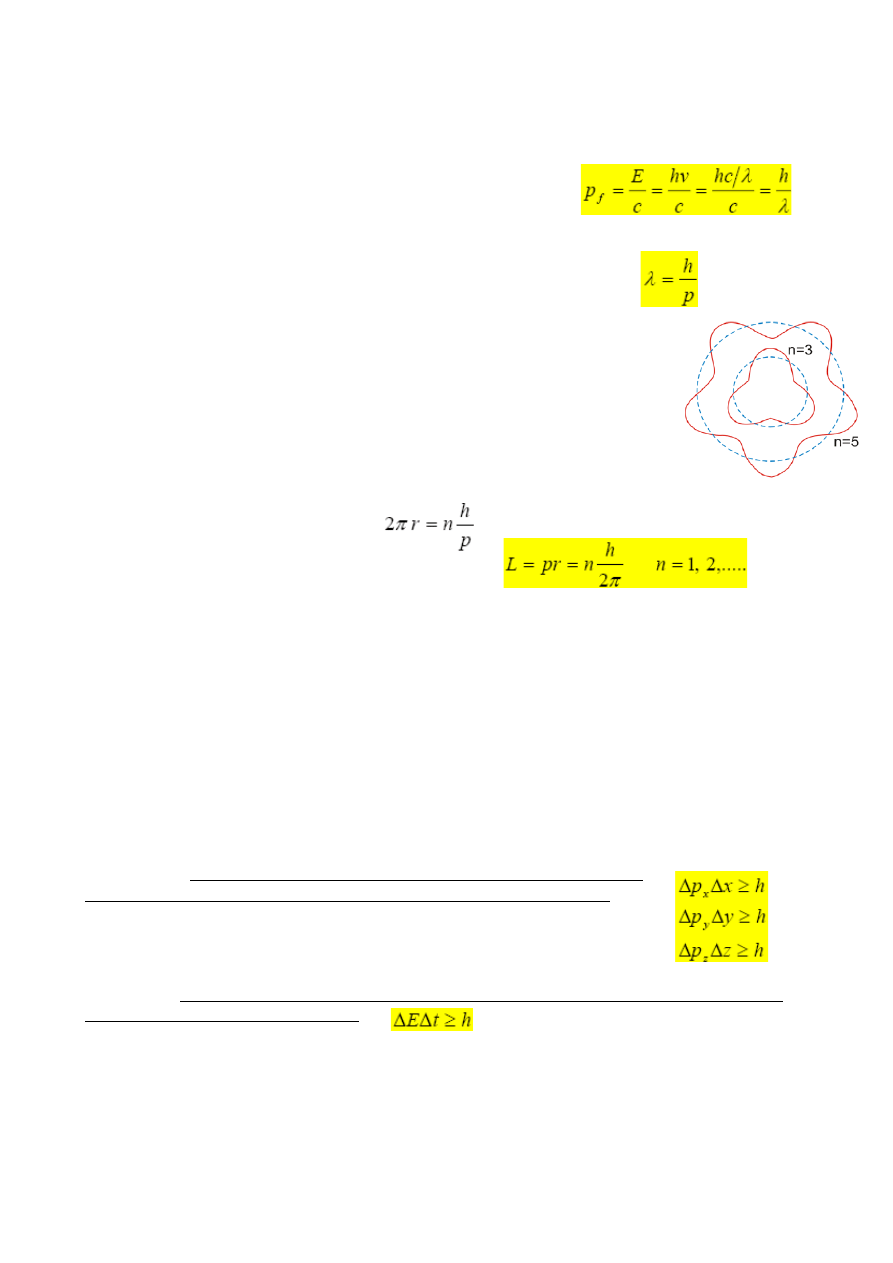
De Broglie przyjął, że elektron krążący wokół jądra po orbicie kołowej ze

stałą prędkością jest reprezentowany przez pewną falę materii - falę
elektronową. Ta fala, tak jak elektron, przebiega wielokrotnie wzdłuż orbity

kołowej, przy czym w każdym kolejnym okresie przebieg ulega dokładnemu
powtórzeniu, to znaczy fala jest zgodna w fazie z falami z poprzednich

obiegów. W przeciwnym razie powstająca fala wypadkowa miała by
natężenie równe zeru.
Ten warunek zgodności faz oznacza, że orbita musi na swym obwodzie
mieścić całkowitą liczbę długości fal de Broglie'a 2π r = nλ. Co w połączeniu z postulatem

de Broglie'a prowadzi do wyrażenia:

Stąd moment pendu elektronu:
Postulat de Broglie’a nie odpowiadał na pytanie jaką postać może mieć funkcja opisująca

fale materii - funkcja falowa , jak ją wyznaczyć oraz jaka jest jej interpretacja. Problem ten
został wyjaśniony przez Heisenberga i Schrödingera, którzy zaproponowali nowy sposób

opisu świata mikrocząstek - mechanikę kwantową.
Do pełniejszego opisu własności falowych materii należy posługiwać się funkcją falową ψ.

M. Born zasugerował, że wielkość | ψ |2 w dowolnym punkcie przedstawia miarę
prawdopodobieństwa, że cząstka znajdzie się w pobliżu tego punktu to znaczy w jakimś

obszarze wokół tego punktu np. w przedziale x, x+dx. Ta interpretacja funkcji ψ daje
statystyczny związek pomiędzy falą i związaną z nią cząstką. Nie mówimy gdzie cząstka jest

ale gdzie prawdopodobnie się znajdzie.
Zasada nieoznaczności Heisenberga
Pierwsza część tej zasady dotyczy jednoczesności pomiaru położenia i pędu (wyklucza ją).
Głosi ona, że iloczyn nieokreśloności pedu cząstki i nieokreśloności jej

położenia w danym kierunku jest zawsze większy od stałej Plancka. Im
dokładniej mierzymy pęd, tym bardziej rośnie nieoznaczność polozenia.

Druga część zasady nieoznaczności dotyczy pomiaru energii i czasu potrzebnego na jego

wykonanie. Jeżeli cząska posiada energię E, to dokładność jej wyznaczenia ΔE zależy od
czasu pomiaru Δt zgodnie z relacją:
Im dłużej cząstka jest w stanie o energi E tym dokładniej można wyznaczyć tą energię.
Zasada nieoznaczności stanowi podstawę stwierdzenia, że w fizyce kwantowej musimy

posługiwać się pojęciem prawdopodobieństwa.

105. Równanie Schrodingera
Równanie różniczkowe opisujące zachowanie się układu kwantowego w czasie i

przestrzeni. Rozwiązując je można znaleźć ścisłą postać funkcji falowej dla dowolnego
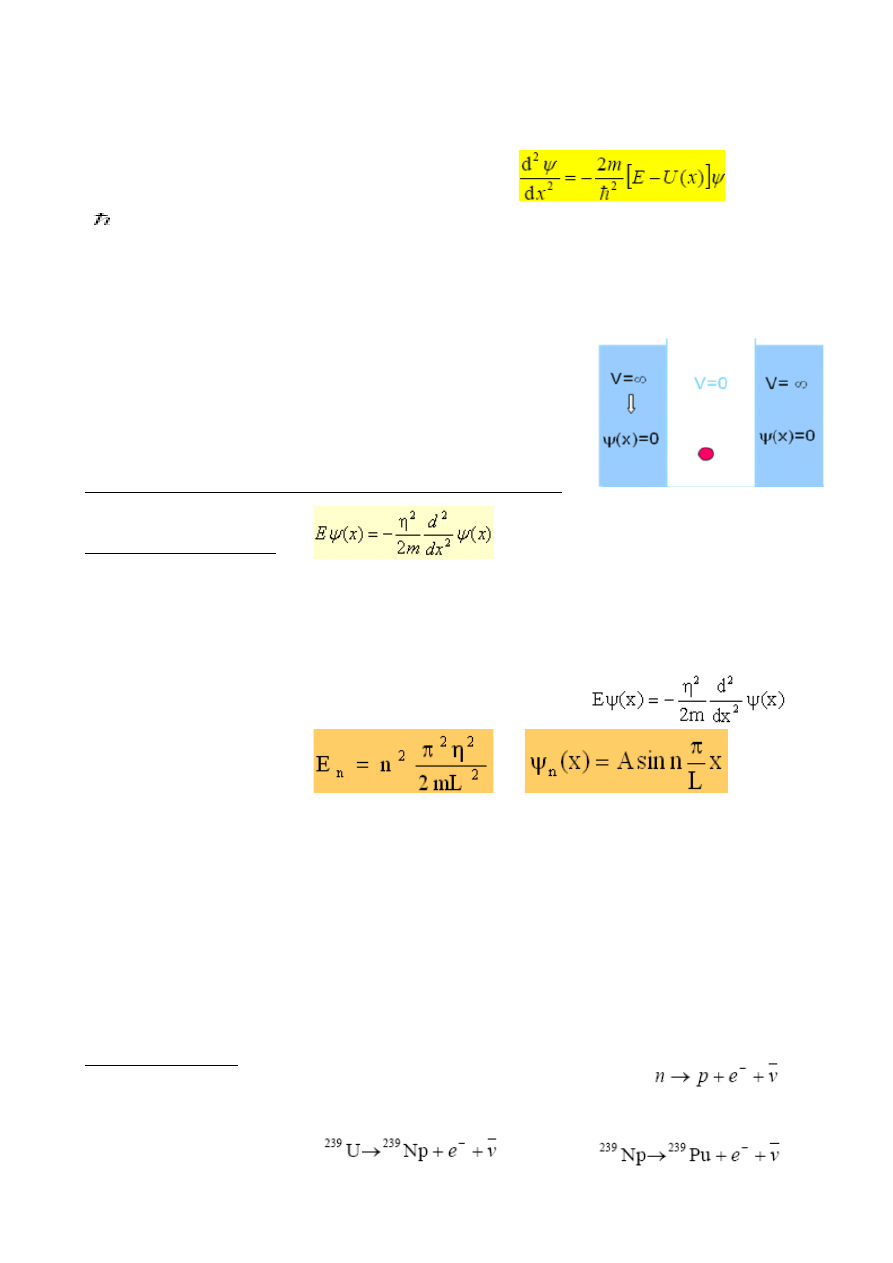
układu. W szczególności przyjmuje ono postać:

E – energia całkowita cząstki,
U(x) – energia potencjalna zależna od jej położenia,

= h/2π.

Zależność ta przedstawia najprostrzą formę równania Shroedingera, czyli równanie w

jednym wymiarze i niezależne od czasu. Jego rozwiązanie polega na znalezieniu postaci
funkcji falowej ψ i wartości energii cząstki E przy znanej działającej na cząstke sile zadanej

poprzez energię patecijalną U.

106. Studnia kwantowa (?)
ELEKTRON W NIESKOŃCZONEJ STUDNI POTENCJAŁU

Znaleźć możliwe energie E i odpowiadające im funkcje falowe
y(x) elektronu w nieskończonej studni potencjału.

ROZWIĄZANIE:

x<0 i x>LÞ V(x)=¥
Elektron nie może być w tym obszarze: y(x)=0 dla x<0 i x>L

lub
0<x<L Þ V(x)=0

Elektron jest swobodny.

Jeśli do studni potencjału „wrzuci” się wiele elektronów, to rozłożą się one tak, aby zakaz
Pauliego był spełniony.

Dozwolone energie (wartości własne energii)
Możliwe stany elektronu (funkcje własne)

Ponieważ wiadomo, że elektron nie może być w obszarze
nieskończonego potencjału, czyli y(x) =0 dla x<0 i x>L, to

rozwiązujemy tylko równanie dla elektronu swobodnego:

Odgadnięte rozwiązanie:

107. Promieniowanie alfa, beta, gamma, neutrony – własności

Promieniowanie alfa – promienie alfa (mało przenikliwe) to jądra helu. Rozpad alfa
występuje zazwyczaj w jądrach o Z>= 82. Polega ona na przemianie niestabilnego jądra w

nowe jądro przy emisji jądra

4

He tzw. cząstki alfa. Dla ciężkich jąder energia wiązania

pojedynczego nukleonu maleje ze wzrostem liczby masowej więc zmniejszenie liczby

nukleonó (w wyniku promieniowania alfa) prowadzi do powstania silniej związanego jądra.
Proces zachodzi samorzutnie bo jest kozystny energetycznie. Energia wyzwolona w czasie

rozpadu jest unoszona przez cząstkę alfa w postaci energii kinetycznej.
Promieniowanie beta – promienie beta to elektrony. Istnieje optymalna liczba

protonów i neutronów, które tworza stabilne jądra. Jądra, których ilość protonów Z różni
się od watrości odpowiadającej stabilnym jądrom o tej samej liczbie masowej A, mogą

zmieniać Z w kierunku jąder stabilnych poprzez rozpad beta.
Rozpad beta minus – jeżeli jądro ma większąod optymalnej liczbę

neutronów to w jadrze takim zachodzi przemiana neutronu w proton,
neutron n rozpada się na proton, elektron i antyneutrino. W takim

procesie liczba protonów Z wzrasta o jeden, a liczba nukleonów A pozostaje bez zmian.
Przykład: rozpad uranu

239

U:

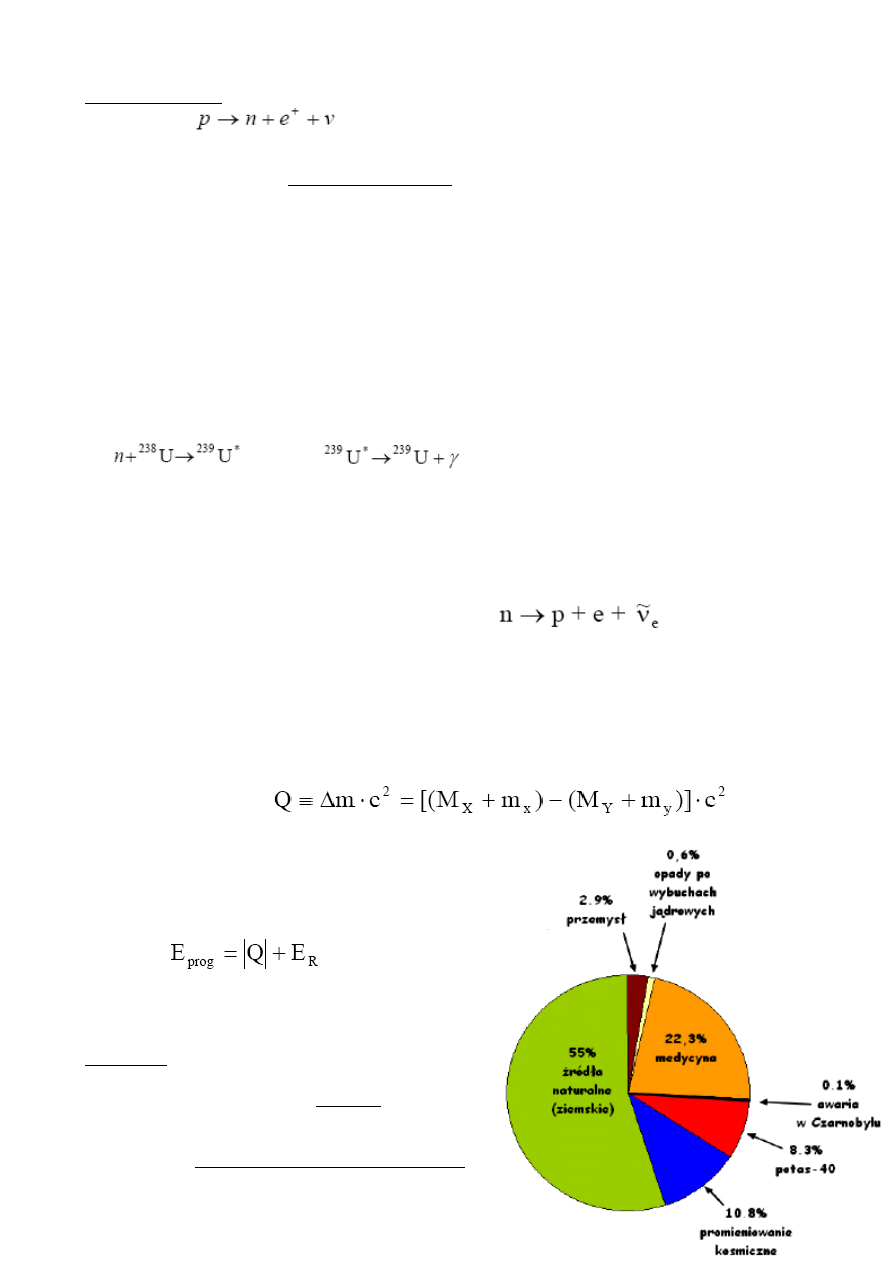
Rozpad beta plus – gdy jądro ma nadmiar protonów to zachodzi proces przemiany protonu
w neutron:

proton rozpada się na neutron, pozyton i neutrino. W

tym procesie liczba protonów Z maleje o jeden, a liczba

nukleonów pozostaje bez zmian.

Pierwiastki powstające w rozpadach alfa i beta są na ogół także promieniotwórcze i ulegają
dalszemu rozpadowi.

Promieniowanie gamma – rozpadom alfa i beta towarzyszy zazwyczaj emisja
wysokoenergetycznego promieniowania elektromagnetycznego – promieniowania gamma.

Ta samoczynna emisja fotonów następuje gdyjądra posiadające nadmiar energii, czyli
znajdujące się w stanie wzbudzonym przechodza do niższych stanów energetycznych.

Widmo promieniowania gamma ma charakter liniowy, tak jak charakterystyczne
promieniowanie X i bardzo wysoka energię, tysiące razy większą od energii fotonów

wysyłanych przez atomy.
Jądra w stanie wzbudzonym można również otrzymać za pomocą neutronów o małej

energii. Przykłąd: wiązka powolnych neutronów kierujemy na próbkę uranu 138U => część
neutronów zostaje wychwycona i powstają jądra uranu 239U* w stanie wzbudzonym. Takie

jądra przechodzą do stanu podstawowego emituja kwanty gamma. Przebieg procesu:

Emisji promieniowania gamma nie towarzyszy zmiana liczby masowej ani liczby atomowej.

Neutron – własności – neutron jest jednymz dwóch nukleonów w jądrze, jego masa to
1,674928(1)

.

10

-27

kg. Na wewnetrzna struktórę neutronu składaja się 3 kwarki: udd, dające

w sumie zerowy ładunek elektryczny. Pomimo braku ładunku elektrycznego (czyli braku
bezpośredniego oddziaływania elektromagnetycznegoz otoczeniem), neutron ma moment

magnetyczny równy -9,6491783(18)

.

10

-27

JT

-1

. Neutron jest cząska nietrwałą i rozpada się

ze średnim czasem życia (885,9s) wg schematu:

Neutrony mogą wywoływać szereg reakcji
jądrowych, których prawdopodobieństwo zajścia zalezy silnie od energi neutronó. Reakcje

z neutronami mogą być zarówno egzo-, jak i endotermiczne. W pierwszych ciepło reakcji Q
jest dodatnie, w drugich ujemne. Oznacza to, że w reakcjach pierwszego rodzaju wyzwala

się energia, do zajścia zaś reakcji drugiego typu energia musi być dostarczona przez
neutrony o odpowiedniej energii kinetycznej.

Obliczenie ciepła reakcji opiera się na rachunku mas spoczynkowych cząstek wchodzących
w reakcję. Dla reakcji, którą zapiszemy schematycznie jakos X(x,y)Y, ciepło rwakcji

definiujemy jako:
Dla Q<0 cząstka

bombardująca jądro utraci część swej energii na
energię odrzutu (E

R

) jądra, stąd też w wypadku

reakcji endoenergetycznych minimalna energia
wymagana dla ajścia reakcji, tzw. energia progowa

reakcji musi być sumą ciepła reakcji i energii
odrzutu:

108. Źródła, sposoby ochrony, detekcja
promieniowania

Źródła promieniowania można podzielić na:
zamknięte (gdy materoał promieniotwórczy jest

zamknięty w materii nieprominiującej i nie może się
przedostać do otoczenia) lub otwarte (gdy materiał

promieniotwórczy może przedostać się do
otoczenia).

Inny podział: naturalne źródła promieniowania

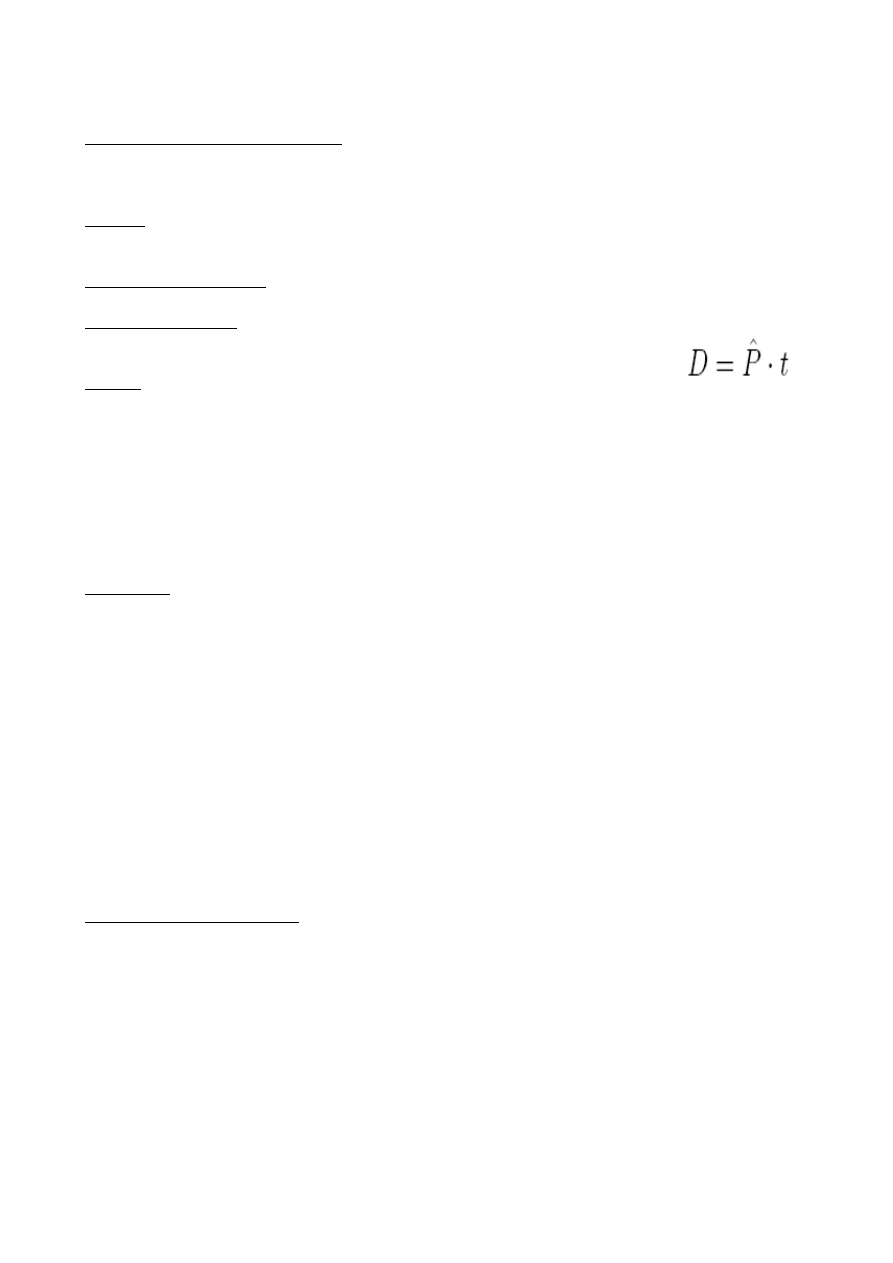
( promieniowanie kosmiczne, promieniowanie emitowane przez pierwiastki zawarte w
skorupie ziemskiej),

sztuczne źródła promieniowania ( aparatura rentgenowska, izotopy promieniotwórcze).
Sposoby ochrony – metody ochrony przed promieniowaniem różnia się w zalezności od

rodzaju promieniowania i żródła. Istnieją jednak podstawowe zasady dotyczące wszystkich
rodzajów źródeł oraz rodzajów promieniowania:

ALARA (As Low As Reasonably Achievable) podstawowa zasada mówiąca, że wszystkie
działania mają na celu ograniczenie kontaktu z materiałami promieniotwórczymi na tyle,

na ile jest to racjonalnie osiągalne.
Zwiększenie odległości – zawsze moc promieniowania maleje wraz z kwadratem odległości

od żródła.
Ograniczenie czasu – jedną z metod ograniczania otrzymanej dawki promieniowania jest

ograniczenie czasu przebywania w pobliżu materiału promieniotwórzcego:
gdzie D- dawka otrzymana, P – moc dawki.

Osłony – każdy rodzaj promieniowania wymaga dobrania odpowiedniej
osłony, tak aby była ona najbardziej efektywna. W przypadku promieniowania alfa

wystarczy kilka kartek papieru, a w przypadku beta stosunkowo cienka płyta aluminiowa.
Promieniowanie gamma jest bardzo przenikliwe, dlatego do jego zatrzymania używa się

osłon ołowiowych, które nadają się również do zatrzymywania promieniowania alfa i beta.
Nie można ich jednak stosować do zatrzymywania neutronów, ponieważ neutron

zderzający się z ciężkim jądrem osłony powoduje powstanie izotopów promieniotwórczych.
Dletego do zatrzymywania promieniowania neutronowego wykożystuje się bloki wodne,

parafine bądź bloki betonowe.maywane są na lekkich jądrach wodoru. W efekcie powstaje
promieniowanie gamma, które trzeba zatrzymać dodatkowymi osłonami.

Szczelność – ważnym elementem ochrony przed promieniowaniem w przypadku
wykorzystania żródeł w medycynie, przemyśle etc. jest zadbanie o ich szczelność.

Promieniowanie alfa oraz beta są mało przenikliwe jednak w przypadku przedostania się
do przewodu pokarmowego bądź dróg oddechowych mogą wywołać bardzo poważne

uszkodzenia.
Detekcja promieniowania – większość detektorów promieniowania jonizującego

opiera się na bardzo prostej zasadzie, promieniowanie jonizujące oddziałując z materiałem,
z którego wykonany jest detektor, powoduje powstanie pary elektron-jon, która ulega

separacji w polu elektrycznym. Następnie ilość ładunków jest zliczana i na jej podstawie
określana zostaje określona moc promieniowania jonizujacego, które spowodowało

jonizację ośrodka. Wady: efektywność kwantowa nie jest nigdy równa 100%. Istnieją
zawsze kwanty, które przechodząc przez ośrodek nie spowodują w nim jonizacji przez co

dla detektora pozostaną niezauważone. Promieniowanie alfa jest na tyle słabo przenikliwe,
że układ detekcyjny zamknięty wewnątrz obudowy nie jest w stanie go zarejestrować.

Dlatego, też stosuje się tzw. detektory okienkowe, w których występuje bezpośredni dostęp
do samego detektora.

Liczniki wypełnione gazem – bardzo powszechny rodzaj detektora. Gaz stanowi ośrodek, w
którym zchodzi detekcja promieniowania. Pole elektryczne przyłożone do elektrod

powoduje rozsunięcie pary elektron-jon. Przyspieszony elektron oraz jon trafiają na
przeciwległe elektrody. Odpowiedni układ mierzy powstały prąd elektryczny lub zlicza

poszczególne impulsy. W przypadku, gdy do elektrod podłączone jest stosunkowo
niewielkie napięcie w ośrodku następuje tylko jonizacja pierwotna. To znaczy

promieniowanie powoduje powstanie pary elektron-jon, jednakenergia kinetyczna
powstałych produktów jest na tyle mała, że nie może spowodować kolejnej jonizacji.

Produkty wędrują w stronę elektrod gdzie są zliczane. W przypadku większych napięć może
dojść do tzw. jonizacji wtórnej, kiedy to elektron powstały w wyniku jonizacji gazu ma

enerie kinetyczną na tyle dużą aby spowodować kolejną jonizację gazu. Gdy proces taki
powtarza się wielokrotnie dochodzi do powielenia elektronów zwanego wzmocnieniem

gazowym bądź też lawiną Townsenda. Do liczników wypełnionych gazem nalezą:

•

licznik Geigera-Mullera (liczba elektronów niezależna od napięcia na elektrodach,
możliwa identyfikacja rodzaju promieniowania, dostarcza jedynie informacji o ilości

czastek, dodatnie jony gromadzące się przy jednej z elektrod powodują spadek
napięcia, ograniczony czas działania z uwagi na degradację gazu, duża czułość,

mozliwość detekcji słabego promieniowania, prosty układ zliczający)

•

licznik proporcjonalny (detekcja dowolnego rodzaju promieniowania oraz jego

energii, wykorzystywanym gazem jest hel,argon lub trójfluorek boru, powstanie
swobodnych elektronów na drodze jonizacji wtórnej, interakcji fotoelektrycznych

oraz bombardowania elektrody przez dodatnio naładowane jony, możliwość
detekcji cząstek o nizkich energiach (<10 eV), ograniczony czas działania –

degradacja gazu)

•

kompra jonizacykna (sygnał wyjściowy proporcjonalny do energii cząstki, detekcja

silnego promieniowania (>10 eV), okienko dla cząstek alfa oraz beta,
wykorzystywanym ośrodkiem jest powietrze, skonstruowana z równoległych płyt

bądź z cylindra i umieszczonej wewnątrz elektrody, mozliwość detekcji neutronów.

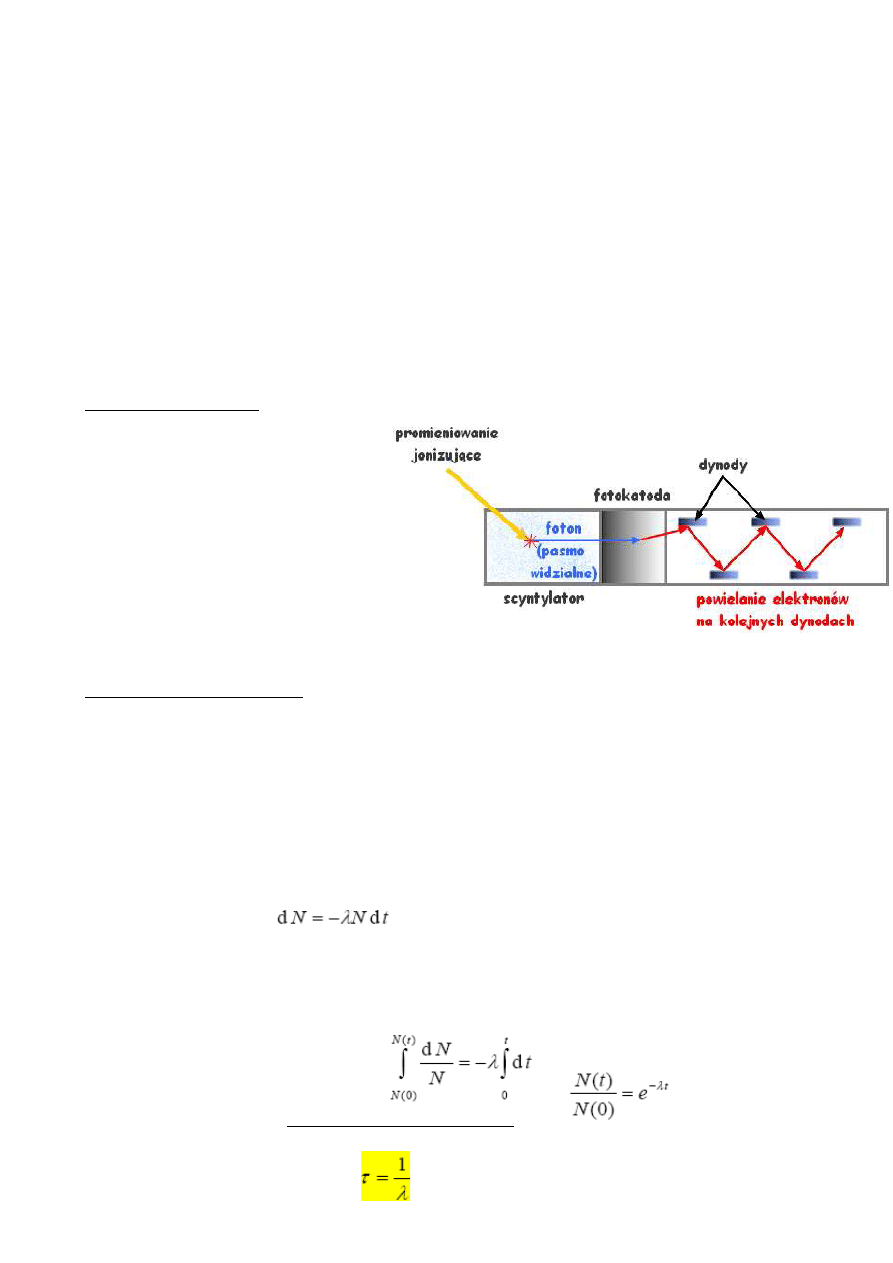
Liczniki scyntylacyjne – ze względu na budowe można je podzielić na trzy części:

scyntylator, w którym padające
promieniowanie jonizujące powoduje

przejście elektronów do stanu
wyższego, a następnie przy przejściu

elektronów do stanu nizszego
następuje emisja fotonu z pasma

światła widzialnego. Następnie foton
trafia na fotokatodę powodując

powstanie elektronów, te zaś
przyspieszane polem elektrycznym

trafiaja na kolejne dynody. Na każdej
z dynod następuje powielenie elekronów. Typowy układ składa się z 15 dynod. Różnica

potencjałów pomiędzy kolejnymi dynodami wynosi 80 – 120 V.
Liczniki półprzewodnikowe – przypominają w swoim działaniu komory jonizacyjne.

Różnica polega na tym, że nie powstają w nich pary elektron-jon, lecz pary elektron-dziura.
Zaletą liczników półprzewodnikowych jest duża dokładność oraz rozdzielczość

energetyczna. Dzięki temu mozliwe jest bardzo dokladne rozróżnienie energii cząsek.

109. Prawo rozpadu, aktywność, osłabienie promieniowania przez osłony,
szeregi promieniotwórcze

Rozpatrujemy układ zawierający w chwili początkowej wiele jąder tego samego rodzaju,
które podlegaja rozpadowi promieniotwórczemu (alfa lub beta). Aby określić liczbę jąder,

któte nie uległy rozpadowi po czasie t. Przez N oznaczamy liczbę jąder w materiale, dN jest
liczbą jąder, które rozpadają się w czasie dt. Spodziewana liczba rozpadów w czasie dt jest

dana wyrażeniem:

gdzie λ jest stałą rozpadu. Określa ona prawdopodobieństwo rozpadu w jednostce czasu,
nie zależy od czynników zewnętrznych. Znak minus wynika z tąd, że dN jest liczbą ujemną

bo liczba jąder N maleje z czasem.
Liczba jąder rozpadających się w jednostce czasu jest proporcjonalna do aktualnej liczby

jąder N. Całkując powyższe równanie

otrzymujemy ostatecznie wykładnicze prawo rozpadu:
Często wytaża się N poprzez średni czas życia jąder τ, który z definicji jest równy

odwrotności stałej rozpadu λ :

Prawo rozpadu można zapisać więc również w postaci:

Do scharakteryzowania szybkości rozpadu uzywa się czasu połowicznego rozpadu T. jest to
czas, po którym liczba jąder danego rodzaju maleje do połowy. Stąd:

I ostatecznie:

Aktywność wyraża się wzorem:

Szeregi promieniotwórcze – ogromną większość pierwiastków wykazujących
naturalną promieniotwórczość można podzielić na 3 grupy, zwane szeregami

promieniotwórczymi. Każdy szereg promieniotwórczy rozpoczyna się od jednego z
występujących na ziemi pierwiastków, a wszystkie trzy szeregi kończą się na trwałych

izotopach ołowiu.
W szeregu uranu, rozpoczynającym się od izotopu uranu

238

92

U, występują izotopy, których

liczby masowe można opisać ogólnym wzorem 4n+2. Szereg ten kończy się na izotopie
ołowiu

206

82

Pb.

Szereg aktynu rozpoczyna się od izotopu uranu

235

92

U, zwanego aktynouranem, i kończy się

na izotopie ołowiu

207

82

Pb. Liczby masowe izotopów tego szeregu opisane są wzorem 4n+3.

Szereg toru rozpoczyna się od izotopu toru

232

90

Th i kończy izotopem ołowiu

208

82

Pb.

Liczby masowe w tym szeregu opisane są wzorem 4n.

110. Rozpad a rozszczepienie, reakcje łańcuchowe, reaktor, bomba A

Energia wiąznia na jeden nukleon wzrasta z liczba masową aż do A>50. Dzieje się tak
dlatego, że dany nukleon jest przyciągany przez coraz większa liczbę sasiednich nukleonów.

Jednak przy dalszym wzroście liczby nukleonów obserwujemy zmniejszanie energii
wiązania nukleonu w jadrze. Siły jądrowe mają bardzo krótki zasięg i jeżeli odległość

między dwoma nukleonami jest więkasza niż 2,5

.

10

-15

m to oddziaływanie pomiędzy nimi

jest słąbsze. Jądra zawierające duza liczbę nukleonów mają większe rozmiary i odległości

pomiędzy poszczególnymi nukleonami mogą być relatywnie duże, a stąd słabsze
przyciąganie pomiędzy nimi. Konsekwencją takich zmian energii wiązania ze wzrostem

liczby nukleonów w jądrze jest występowanie zjawiska rozszczepienia.
Jeżeli ciężkie jądro rozdzielimy na dwie części, to powstałe dwa mniejsze jądra są silniej

wiązane do jądra wyjsciowego, tzn. te dwie części mają masę mniejszą niż masa jądra
wyjściowego. Dzięki temu w reakcji rozszczepienia wydziela się energia. Źródłem energii

bomby atomowej i reaktora jądrowego są procesy rozszczepienia jądrowego.
Spontaniczne rozszczepienie naturalnego jądra jest an ogół mniej prawdopodobne niż

rozpad alfa tego jądra. Można jednak zwiększyć prawdopodobieństwo rozszczepienia
bombardując jądra neutronami o odpowiednio wysokiej energii. Właśnie takie neutrony

powodują reakcję rozszczepienia uranu

235

U i plutonu

239

Pu.

Pierwiastki lekkie zawierają w jądrze zbliżone ilości protonów i neutronów, podczas gdy w

pierwiastkach ciężkich przeważa liczba neutronó. Z związku z tym w reakcji rozszczepienia
powstaje na ogół kilka neutronów. W konsekwencji rozszczepienie jądrowe może stać się

procesem samopodtrzymującym w wyniku tzw. reakcji łańcuchowej. Jeżeli przynajmniej
jeden z powstałych neutronów wywoła kolejne rozszczepienie to proces będzie sam się

podtrzymywał. Ilość materiału powyżej, której spełniony jest powyższy warunek nazywamy
masą krytyczną. Jeżeli liczba rozszczepień na jednostkę czasu jest utrzymana na stałym

poziomie to mamy do czynienia z kontrolowaną reakcją łańcuchową.
Masa materiału rozszczepianego może być tez nadkrytyczna. Wówczas neutrony powstałe

w wyniku jednego rozszczepienia wywołują więcej niż jedną reakcję wtórną. Mamy do
czynienia z lawinową reakcją łańcuchową. Cała masa ndkrytyczna może być rozszczepiona

w bardzo krótkim czasie, t<0,001 s, ze względu na dużą prędkość neutronów (3

.

10

5

m/s).

tak eksploduje bomba atomowa. Najczęściej przygotowuje się kulę o masie nadkrytycznej

ale rozrzedzonej. Następnie otacza się ją klasycznymi ładunkami wybuchowymi, których

detonacja wywołuje wzrost ciśnienia zewnętrznego i gwałtowne zwiększenie gęstości
materiału (zmniejsza się objetość kuli). W konsekwencji osiągnięty zastaje stan

nadkrytyczny.
Urządzenia, w których prowadzone są kontrolowane reakcje łąńcuchowe, nazywamy

reaktorami jadrowymi. Ważnym elementem każdego reaktora są urządzenia
zabezpieczające przed niepożądanym wzrostem szybkości reakcji łańcuchowej i rozwojem

reakcji lawinowej. Najczęściej służą w tym celu pręty kadmowe. Prawdopodobieństwo
wychwytu neutronów przez jądra kadmu jest bardzo duże, totez wsuwając do reaktora

pręty kadmowe mażemy znacznie zmniejszyć liczbę neutronów powodujących
rozszczepienie. Energia cieplna wydzielająca się w reaktorze jest odprowadzana na

zewnątrz przez czynnik chłodzący – gaz lub ciecz przepływającą przez wnętrze reaktora.

111. Wykorzystanie promieniowania: metody izotopowe, znacznikowe,
datowanie

Różne izotopy tego samego pierwiastka mają takie same własności chemiczne. Zatem
zastąpienie w cząsteczce jednego izotopu innym nie zmienia jej funkcji. Natomiast

promieniowanie emitowane przez izotop umożliwia jego wykrycie, zlokalizowanie i
śledzenie ruchu, a nawet pomiar jego stężenia bez ingerencji z zewnątrz. Metoda

znaczników izotopowych pozwala zatem badać funkcjonowanie żywego organizmu,
poczynając od poszczególnych jego komórek po cały narząd. Wielu przełomowych odkryć

naukowych w drugiej połowie dwudziestego wieku dokonano dzięki wykorzystaniu
promieniotwórczości m.in. odkryto funkcjonowanie genotypu, metabolizm komórek,

fotosyntezę, mechanizm wysyłania chemicznych informacji (hormony, neuromediatory)
wewnątrz organizmu. Izotopy radioaktywne wykorzystywane są w medycynie nuklearnej,

zwłaszcza w obrazowaniu medycznym, aby poznać działanie leków, funkcjonowanie
mózgu, wykryć zaburzenia pracy serca, umiejscowić przerzuty nowotworowe itp.

Promieniowanie jonizujące może selektywnie niszczyć zrakowaciałe komórki i doprowadzić
do likwidacji nowotworu. Jest to radioterapia. Było to jedno z pierwszych zastosowań

promieniotwórczości po jej odkryciu.
Metody datowania wykorzystują rozpad izotopów promieniotwórczych w materiałach

lub przedmiotach poddawanych datowaniu. Oczywiście musi być znany okres
połowicznego rozpadu tych izotopów. Do oznaczania wieku przedmiotów nie

przekraczających 50.000 lat używa się najczęściej izotopu węgla-14. Inne metody
datowania, w których wykorzystuje się kombinacje różnych izotopów pozwalają określić

wiek zdarzeń opisujących historię Ziemi, jej klimatu i istot żywych, które ją zamieszkują do
tej pory.

Dwutlenek węgla (CO2) obecny w atmosferze zawiera stabilny węgiel-12 i bardzo niewielki
odsetek promieniotwórczego węgla-14 (którego okres połowicznego rozpadu wynosi 5730

lat), ciągle tworzonego przez promienie kosmiczne. Dwutlenek węgla znajdujący się w
atmosferze jest wchłaniany przez organizmy żywe (w procesach oddychania i fotosyntezy).

Kiedy żywy organizm umiera, znajdujący się w nim węgiel-14 przestaje być odnawiany. W
miarę jak izotop ten ulega rozpadowi jego zawartość w porównaniu z węglem-12 spada. W

ten sposób węgiel-14 pełni rolę swoistego "zegara"; im mniej go pozostaje, tym starsza jest
próbka pobrana do datowania.