Opracowanie ćwiczenia nr 7

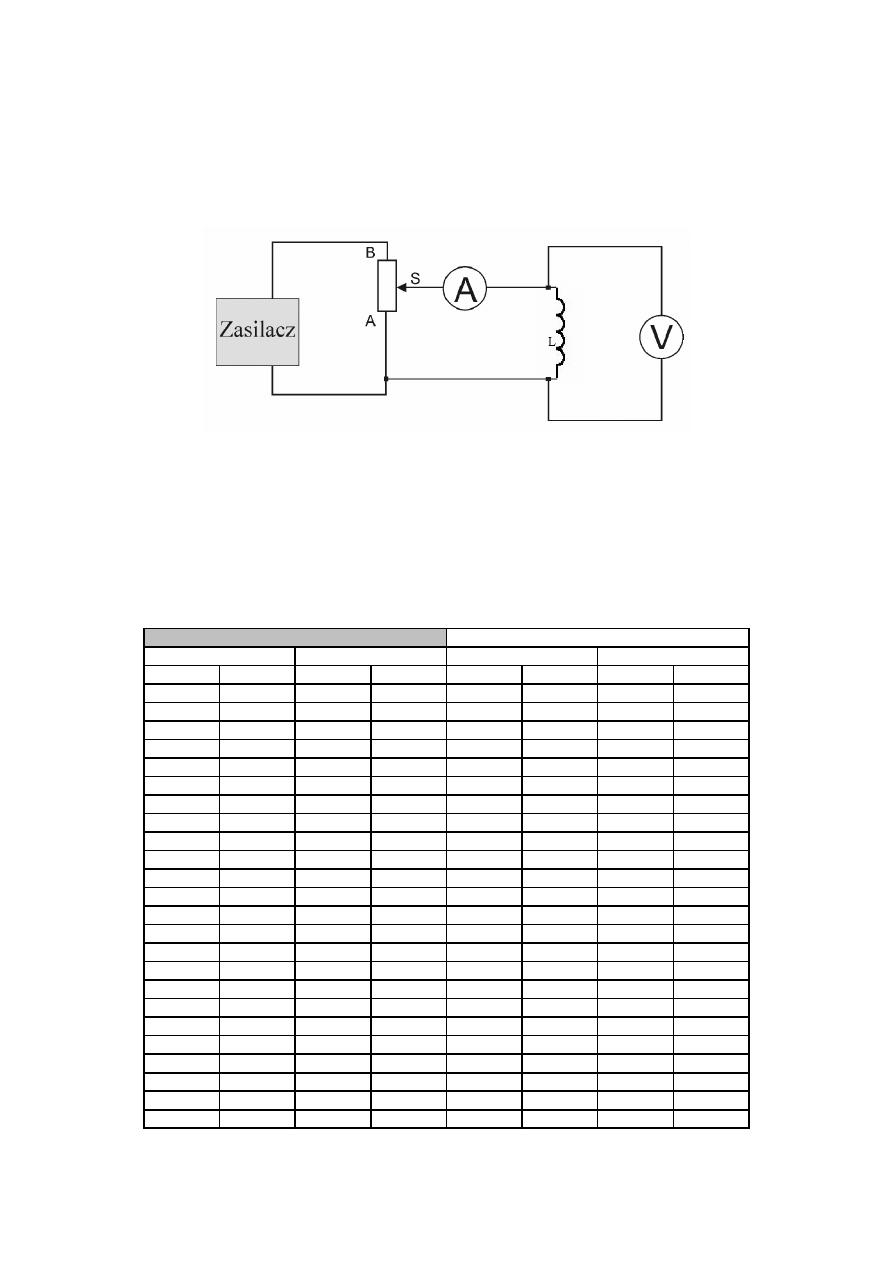
W ćwiczeniu badamy dwie różne cewki, mierząc przepływający przez nie prąd w funkcji
przyłożonego napięcia stałego lub zmiennego:

Napięcie na cewce regulowane jest za pośrednictwem ślizgacza „S” drutowego potencjometru
suwakowego. Woltomierz i amperomierz cyfrowy posiada przełączniki zakresu oraz rodzaju wielkości
mierzonej.
Do dyspozycji są dwa alternatywne źródła zasilania: zasilacz napięcia stałego 12V oraz transformator
napięcia zmiennego 220/12V 50Hz
Badane cewki nawinięte są na wspólnym rdzeniu.

Wyniki pomiarów:

U[V]

I[mA]

U[V]

I[mA]

U[V]

I[mA]

U[V]

I[mA]

0,49

16

0,54

1,30

0,48

34

0,54

3,00

1,00

33

1,04

2,40

1,00

71

1,05

5,60

1,54

50

1,51

3,40

1,52

109

1,52

7,70

1,97

64

2,07

4,50

2,01

143

2,05

9,90

2,48

80

2,51

5,20

2,50

178

2,57

11,90

3,00

97

3,07

6,20

3,01

214

3,02

13,50

3,49

113

3,54

6,90

3,50

249

3,53

15,30

3,99

129

4,02

7,60

4,05

281

4,00

16,70

4,49

144

4,55

8,40

4,51

320

4,51

18,30

5,01

161

5,03

9,10

5,03

356

5,05

20,00

5,59

177

5,55

9,80

5,51

390

5,53

21,40

6,00

193

6,06

10,50

6,03

426

6,05

22,70

6,50

209

6,50

11,10

6,45

455

6,50

24,00

7,00

225

7,00

11,80

7,01

495

7,01

25,30

7,55

242

7,49

12,40

7,59

534

7,53

26,60

8,03

258

8,01

13,00

8,02

563

8,01

27,80

8,51

273

8,54

13,70

8,53

599

8,54

29,10

8,96

287

9,03

14,20

9,00

631

9,02

30,20

9,49

303

9,52

14,80

9,48

663

9,56

31,30

10,08

322

10,00

15,40

10,06

702

10,05

32,40

10,59

337

10,51

16,00

10,48

730

10,47

33,40

11,09

357

11,08

16,60

11,03

760

11,05

34,70

11,47

367

11,59

17,20

11,57

802

11,53

35,60

12,02

382

12,07

17,70

12,12

836

12,07

36,60

Cewka 1

Cewka 2

Prąd stały

Prąd zmienny

Prąd stały

Prąd zmienny

ΔU = 0,01[V], ΔI = 1[mA] - dla prądu stałego i ΔI = 0,1[mA] - dla prądu zmiennego

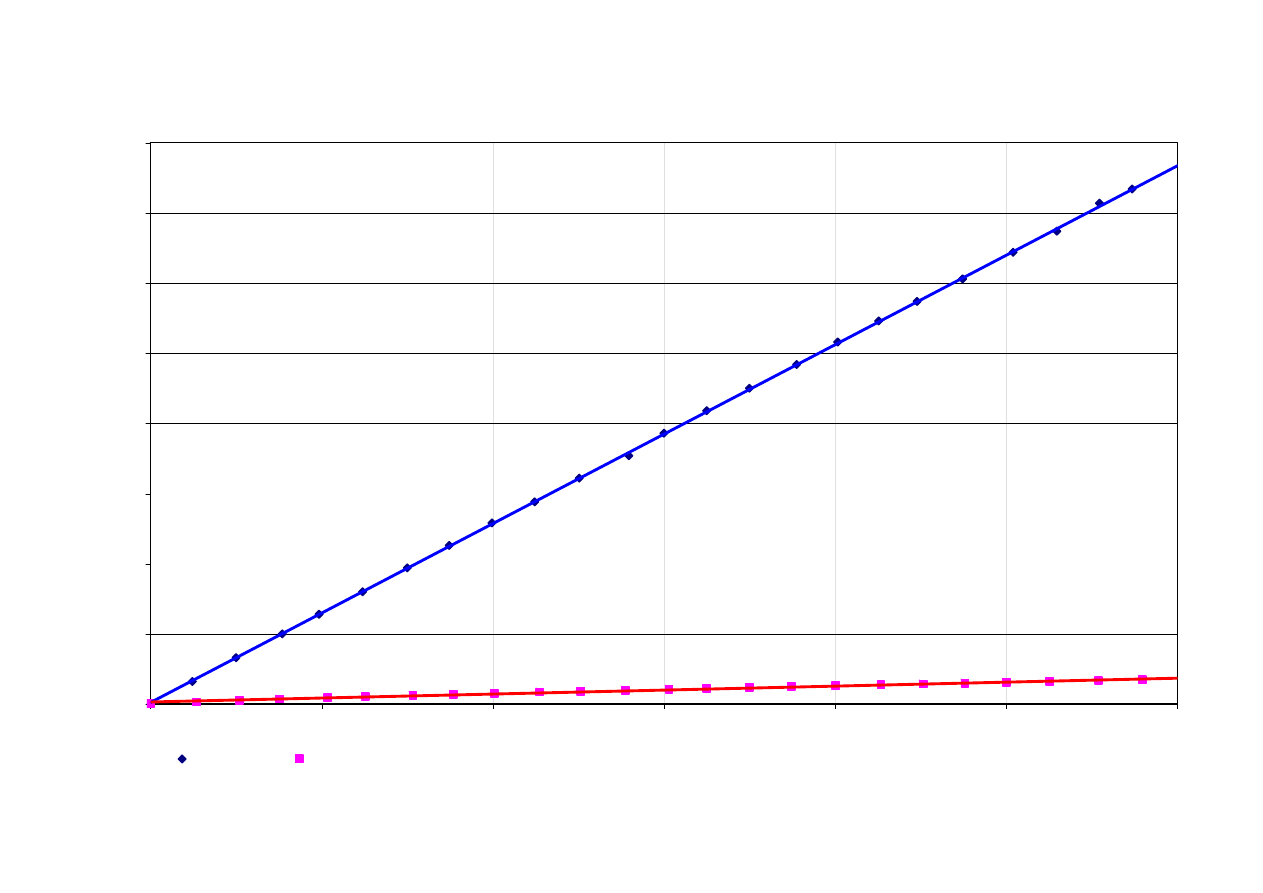
Cewka 1

y = 31,886x

y = 1,4127x

0

50

100

150

200

250

300

350

400

0,00

2,00

4,00

6,00

8,00

10,00

12,00

U[V]

I[m

A

]

Prąd stały

Prąd zmienny

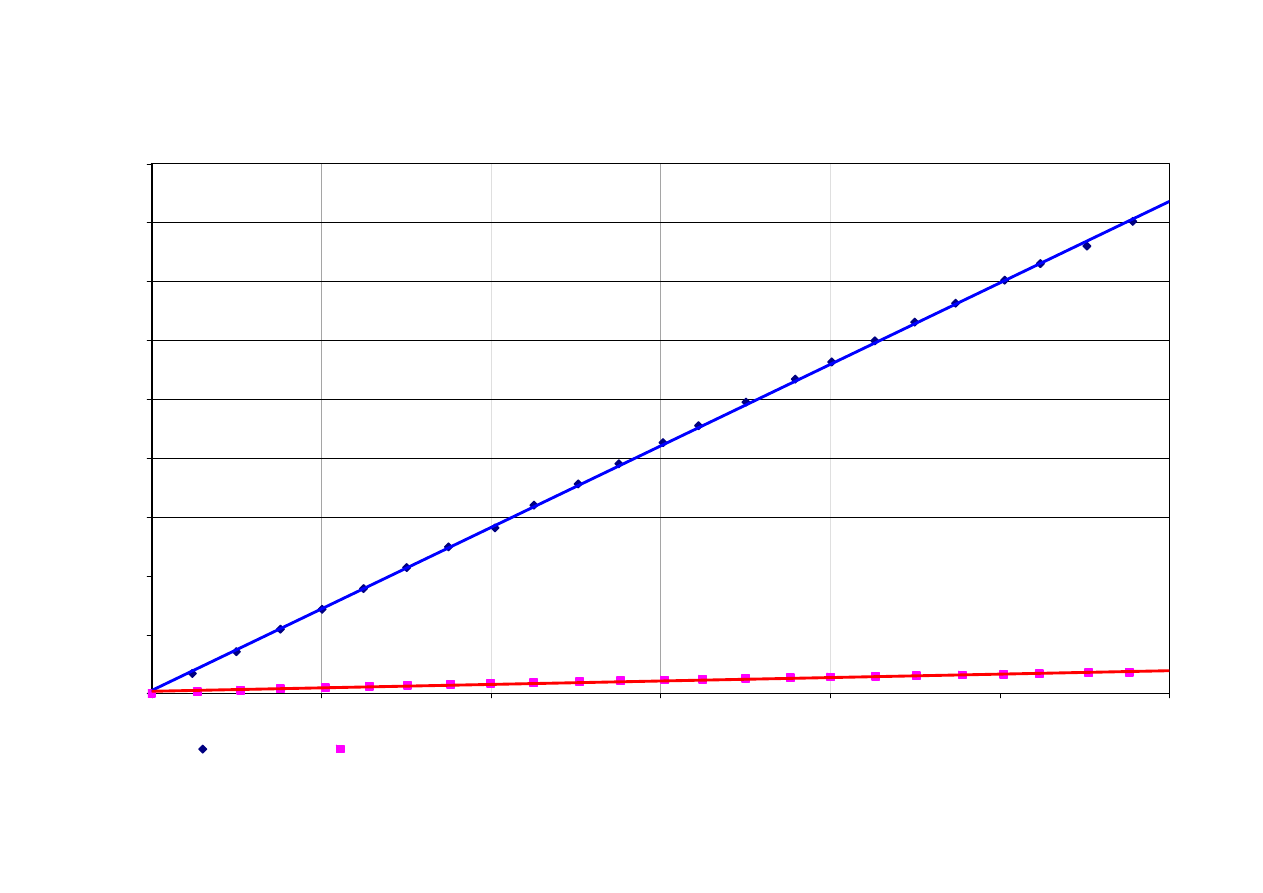
Cewka 2

y = 69,23x

y = 2,9026x

0

100

200

300

400

500

600

700

800

900

0,00

2,00

4,00

6,00

8,00

10,00

12,00

U[V]

I[

mA

]

Prąd stały

Prąd zmienny

Opracowanie wyników:

Posługując się metodą najmniejszych kwadratów dopasowujemy dane doświadczalne do funkcji
liniowej I(U)=G*U, gdzie G jest konduktancją (w przypadku prądu stałego) lub admitancją (w
przypadku prądu zmiennego) wtedy oznaczamy Y.
Korzystamy z wzorów:

1

1

1

2

2

1

1

n

n

n

i i

i

i

i

i

i

n

n

i

i

i

i

n

U I

U

I

a

n

U

U

=

=

=

=

=

−

=

⎛

⎞

− ⎜

⎟

⎝

⎠

∑

∑ ∑

∑

∑

Cewka 1

Prąd stały

Prąd zmienny

a=G

R

[ ]

Ω

a=Y

Z

[ ]

Ω

0,031886 31,36 0,001413 707,71

Cewka 2

Prąd stały

Prąd zmienny

a=G

R

[ ]

Ω

a=Y

Z

[ ]

Ω

0,06923 14,44 0,002903

344.47

Gdzie:
a – współczynnik kierunkowy prostej I(U) równy w przypadku prądu stałego G (konduktancji)
natomiast Y dla prądu zmiennego (admitancja)
G – kondunktancja
R – rezystancja
Y – admitancja
Z – impedancja

Wartość współczynnika samoindukcji cewki obliczymy przekształcając wzory

2

2

X

R

Z

+

=

(1)

C

L

X

X

X

−

=

w naszym przypadku X

C

=0, bo nie mamy żadnych kondensatorów stąd

L

X

X

=

(2)

L

X

L

ω

=

(3)

2 f

ω

π

=

(4)

Z wzorów (3) i (4) mamy:

2

L

L

X

X

L

f

ω

π

=

=

(5)

X

L

można obliczyć z wzoru (1) przy uwzględnieniu X

c

=0

2

2

R

Z

X

L

−

=

(6)

Ostatecznie z wzorów (5) i (6) mamy końcowy wzór:

f

R

Z

L

π

2

2

2

−

=

(7)

Stąd wartość indukcji dla cewki 1 wynosi L

1

=2,229[H] natomiast dla cewki 2 L

2

=1,125[H]

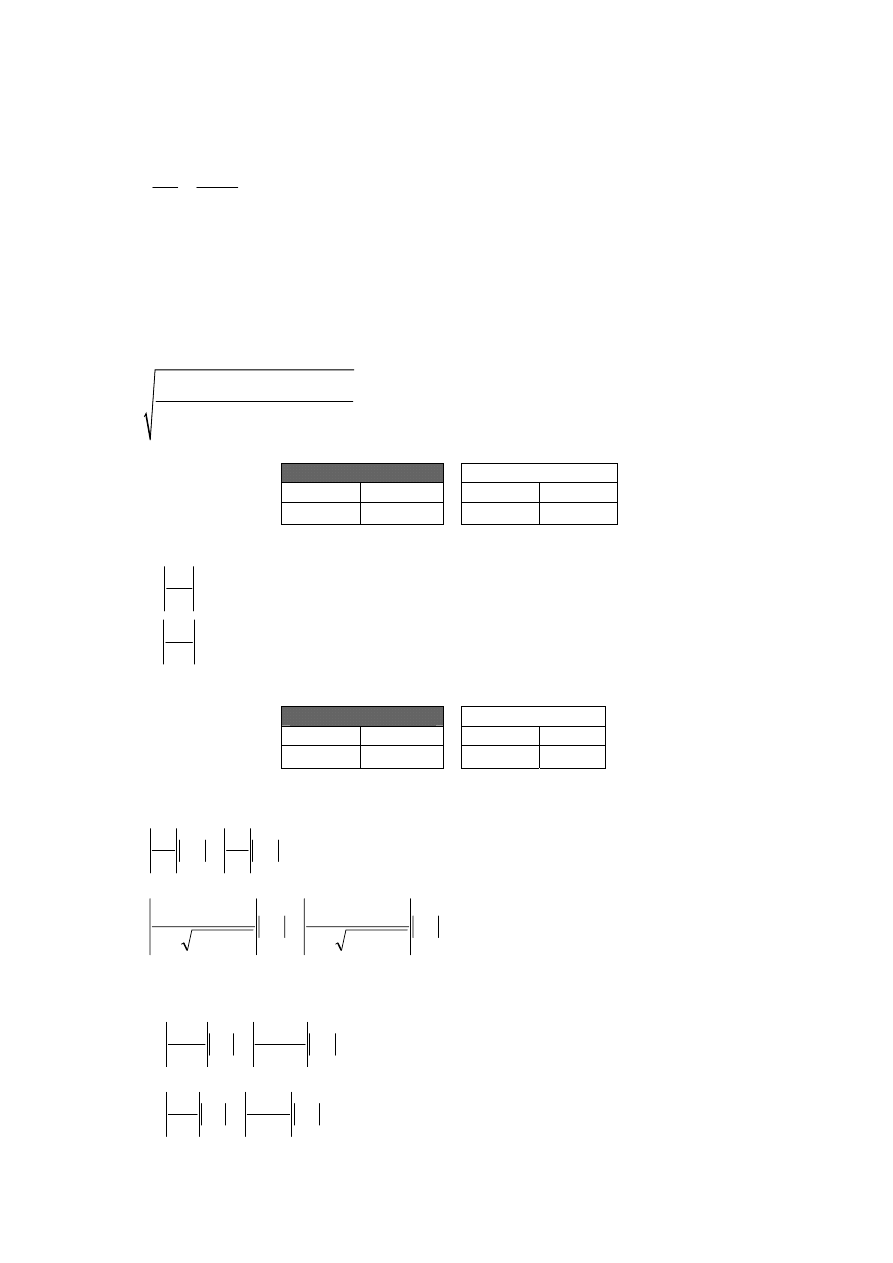
Mając dane L i R można obliczyć wartość tangensa kąta przesunięcia fazowego miedzy napięciem i
natężeniem prądu zmiennego korzystając z wzoru:

2

L

fL

tg

R

R

ω

π

ϕ

=

=

(8)

Stąd dla cewki 1

D

87,48

22,74

1

1

=

⇒

=

ϕ

ϕ

tg

natomiast dla cewki 2

D

87,66

24,50

2

2

=

⇒

=

ϕ

ϕ

tg

Niepewności pomiarowe:

Niepewność pomiaru konduktancji i admitancji dla obu cewek liczymy z wzoru:

(

)

(

)

(

)

2

2

2

2

i

i i

a

i

i

n

I

a

U I

n

n

U

U

δ

−

=

⎡

⎤

−

−

⎢

⎥

⎣

⎦

∑

∑

∑

∑

(9)

Cewka 1

Cewka

2

∆G

∆Y ∆G

∆Y

0,000061 0,000035 0,000221 0,000081

Niepewność wyznaczenia rezystancji i impedancji liczymy następująco:

G

G

R

R

Y

Y

Z

Z

Δ

=

Δ

Δ

=

Δ

(10)

Stąd

Cewka 1

Cewka

2

∆R

∆Z ∆R

∆Z

0,06 16,97

0,05 10,19

Błąd wyznaczenia wartości indukcyjności liczymy za pomocą różniczki zupełnej:

R

R

L

Z

Z

L

L

Δ

∂

∂

+

Δ

∂

∂

=

Δ

(11)

Zatem

R

R

Z

f

R

Z

R

Z

f

Z

L

Δ

−

−

+

Δ

−

=

Δ

2

2

2

2

2

2

π

π

(12)

ΔL

1

=0,054

ΔL

2

=0,032

Do wyznaczenia błędu tg

ϕ również stosujemy metodę różniczki zupełnej:

R

R

tg

L

L

tg

tg

Δ

∂

∂

−

+

Δ

∂

∂

=

Δ

ϕ

ϕ

ϕ

(13)

Stąd:

R

R

f

L

R

f

tg

Δ

−

+

Δ

=

Δ

2

2

2

π

π

ϕ

(14)

Δtgϕ

1

=0,57

⇒ϕ

1

=2,20

°

Δtgϕ

2

=0,78

⇒ϕ

2

=2,78

°

Podsumowanie:

Współczynnik samoindukcji cewki 1 wynosi L

1

=2,229

±0,054[H] natomiast cewki 2

L

2

=1,125

±0,032[H]

Kąt przesunięcia fazowego między napięciem i natężeniem wynosi odpowiednio:
ϕ

1

=87,48

±2,20° ϕ

2

=87,66

±2,78°

Powyższe błędy pomiarowe wynikają głównie z niedokładności przyrządów, jakimi posługiwaliśmy
się wykonując doświadczenie,.

Opracowali

Krzysztof Kawula

Michał Bogusz