W

W

Y

Y

K

K

Ł

Ł

A

A

D

D

 

 

1

1

4

4

 

 

R

R

U

U

C

C

H

H

 

 

T

T

U

U

R

R

B

B

U

U

L

L

E

E

N

N

T

T

N

N

Y

Y

 

 

–

–

 

 

C

C

.

.

D

D

.

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

“Gallery of Fluid Motion”-M. Samimy, K.S. Breuer

 

R

R

Ó

Ó

W

W

N

N

A

A

N

N

I

I

E

E

 

 

R

R

E

E

Y

Y

N

N

O

O

L

L

D

D

S

S

A

A

 

 

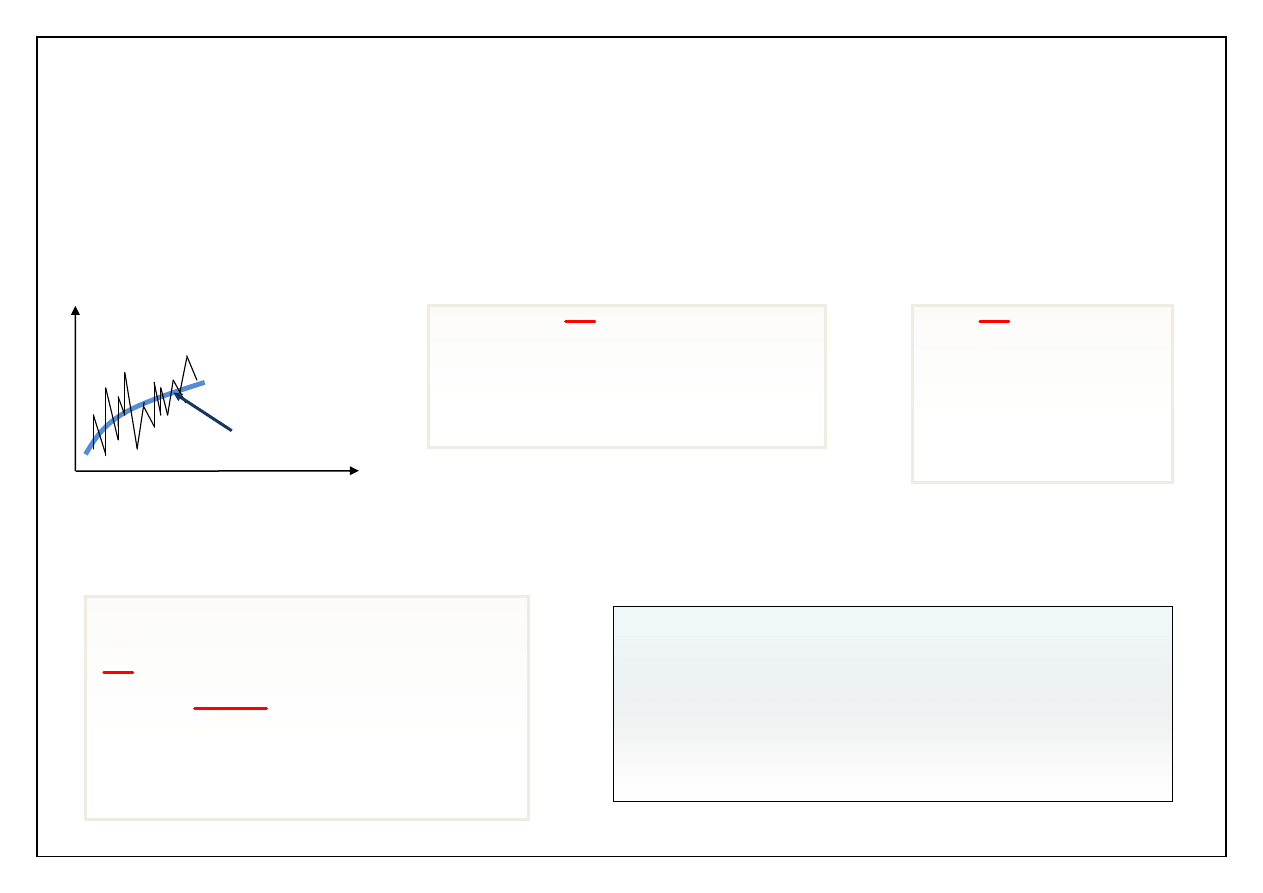
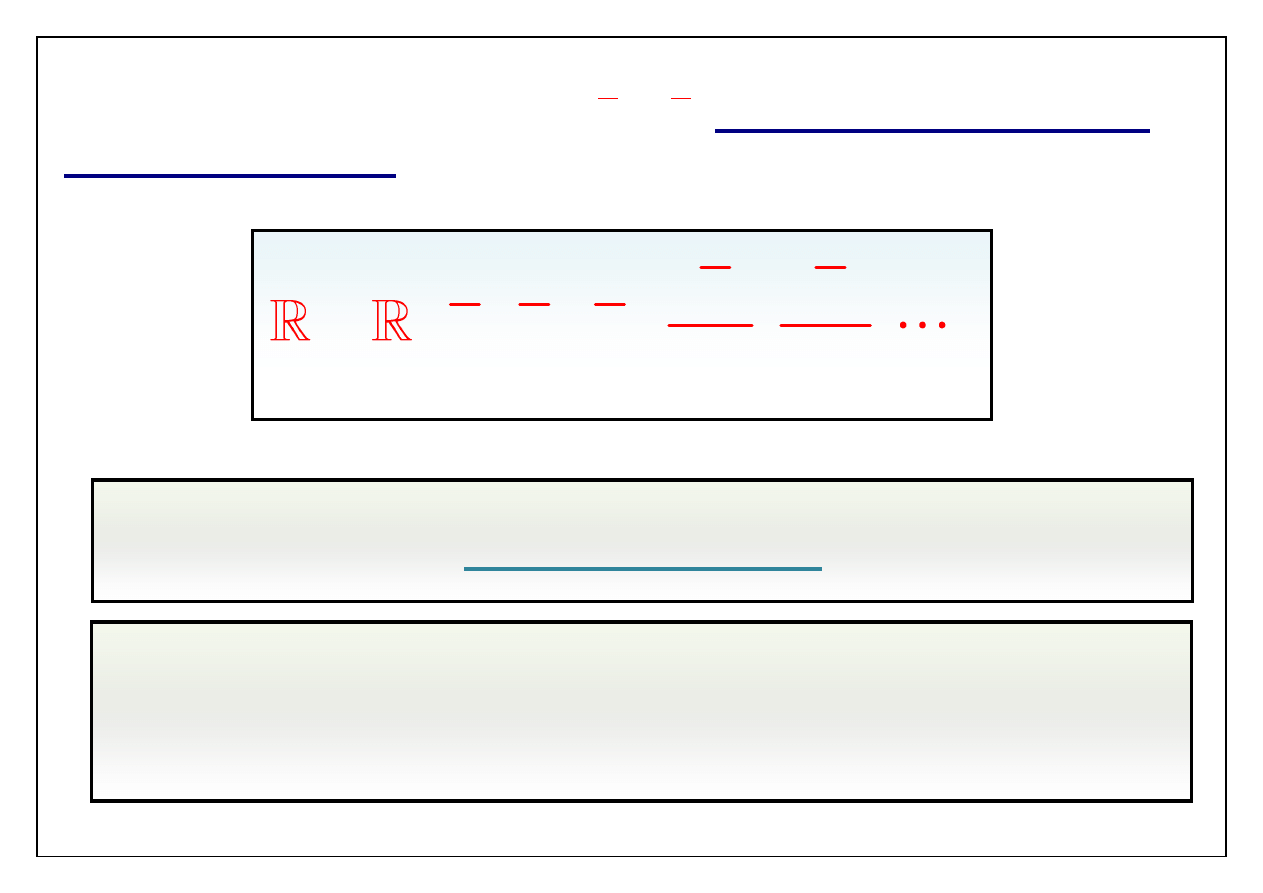
Dowolna wielkość w opisie ruchu turbulentnego może być 
przedstawiona w postaci wolnozmiennej „średniej” i 
szybkozmiennej, niewielkiej oscylacji. Oscylacja (= pulsacja = 
fluktuacja) jest wie

lkością losową. 

 

 

 
 
 
 
 
Definicja wartości średniej 
 
 
 
 
 
 

srednia

oscylacja

f

f

f







 

f 

czas 

średnia 

srednia

z oscylacji

f

0

 

 

 

t T

t T

1

f

f

d

2T

 









 

Czas uśredniania 2T powinien być 

większy od czasu charakteryzującego 

zmiany losowe i mniejszy od czasu, w 

którym istotnie zmienia się średnia 

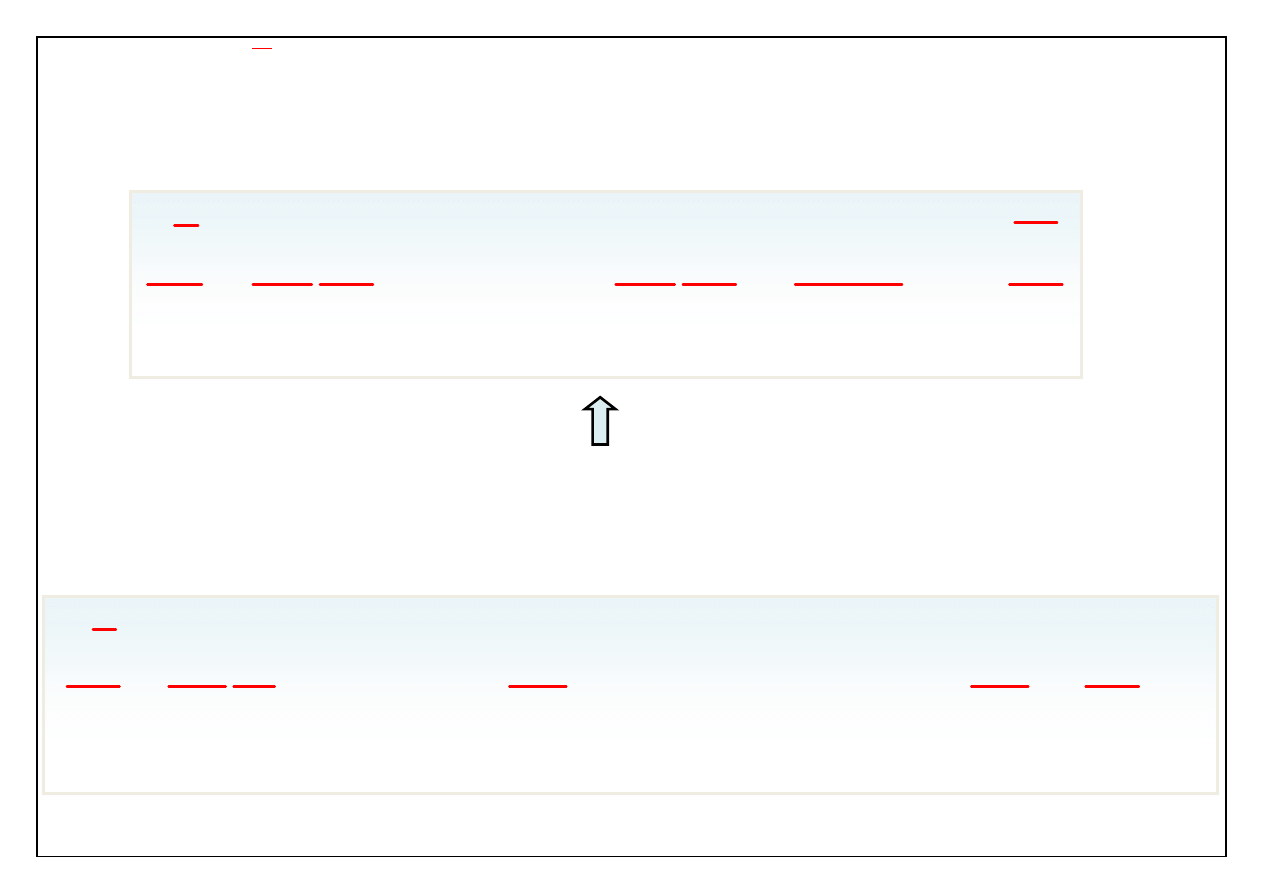
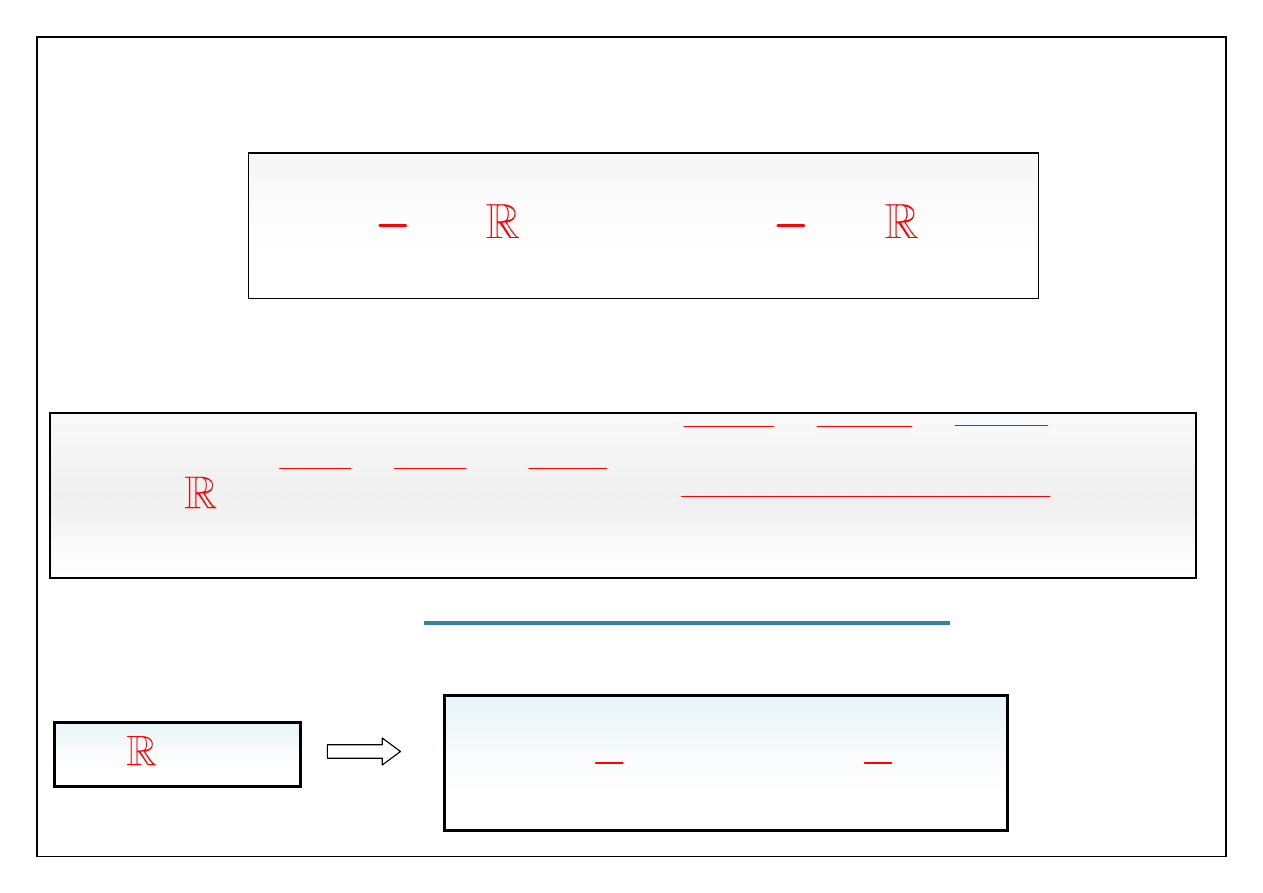
Pochodna 

f

 

jest funkcją miejsca i czasu.  

Pochodna średniej względem współrzędnej x ma postać:

 

 

 
 
 
 
 

Pochodna średniej względem położenia jest średnią pochodnej. 

 
Pochodną średniej względem czasu liczymy następująco: 

 

 

 

 

 

 

 

 

 

 





t T

t T

t T

t T

f

1

1

1

f

f ( ) d

f (t

T) f (t

T)

d

t

2T t

2T

2T

 









































 

t T

t T

t T

t T

f

1

1

f ( )

f

f ( ) d

d

x

2T x

2T x

x

x



 









































 

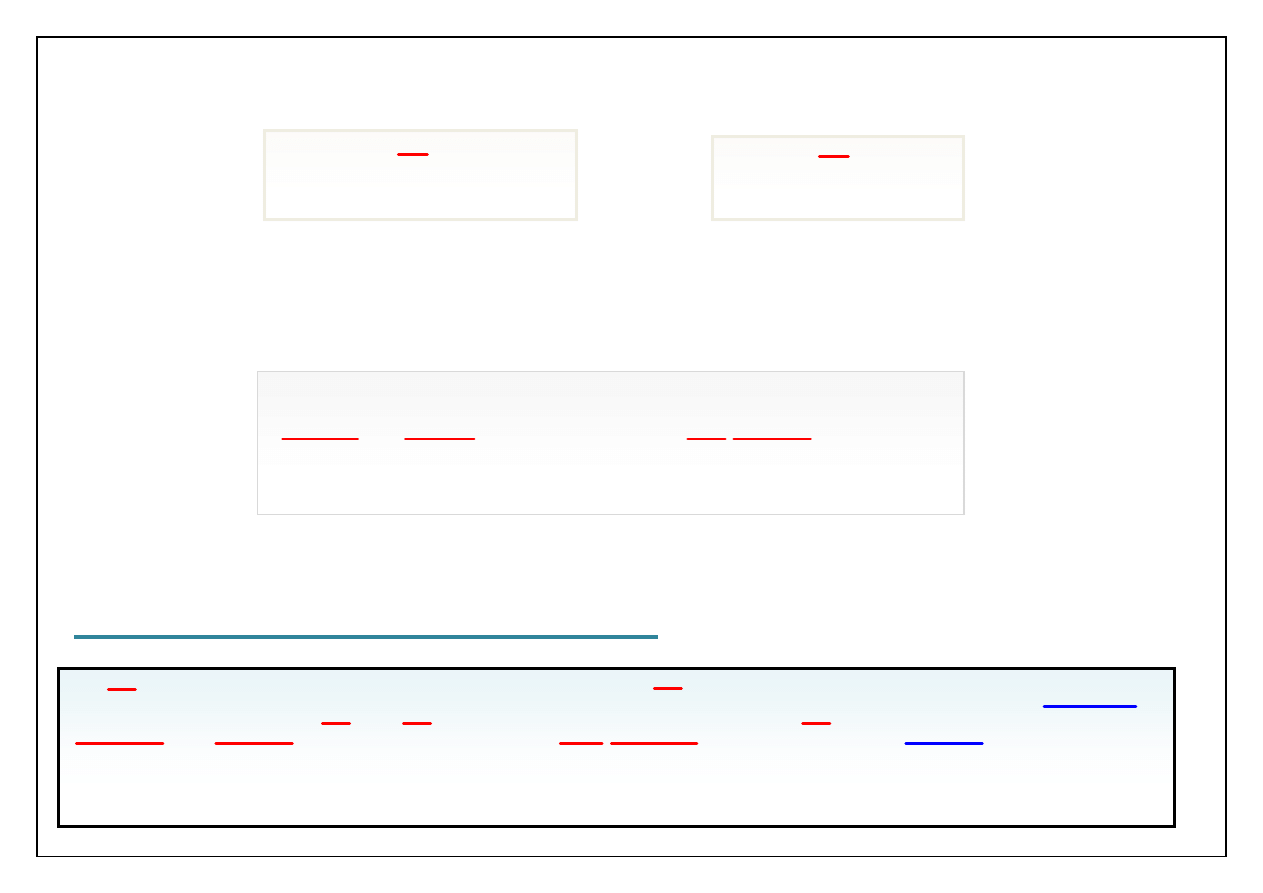
Przedstawmy prędkość i ciśnienie w postaci sum: 

 

 

 

 

 
 
Podstawmy  powyższe  zależności  do  równań  Naviera  –  Stokesa 
dla cieczy: 
 
 
 

 

 

W rezultacie otrzymujemy równanie, które nosi nazwę 
 

R

ównania Reynoldsa dla średnich 

 
 
 
 
 





k

k

i

k

i

k

v

1

p

v v

v

t

x

x













 

 







 









i

k

i

k

k

i

k

i

k

v

1

p

v v

v

v

v

t

x

x

x















 

  

















 

k

k

k

v

v

v







 

p

p

p



 

 

T

T

E

E

N

N

S

S

O

O

R

R

 

 

R

R

E

E

Y

Y

N

N

O

O

L

L

D

D

S

S

A

A

 

 

 
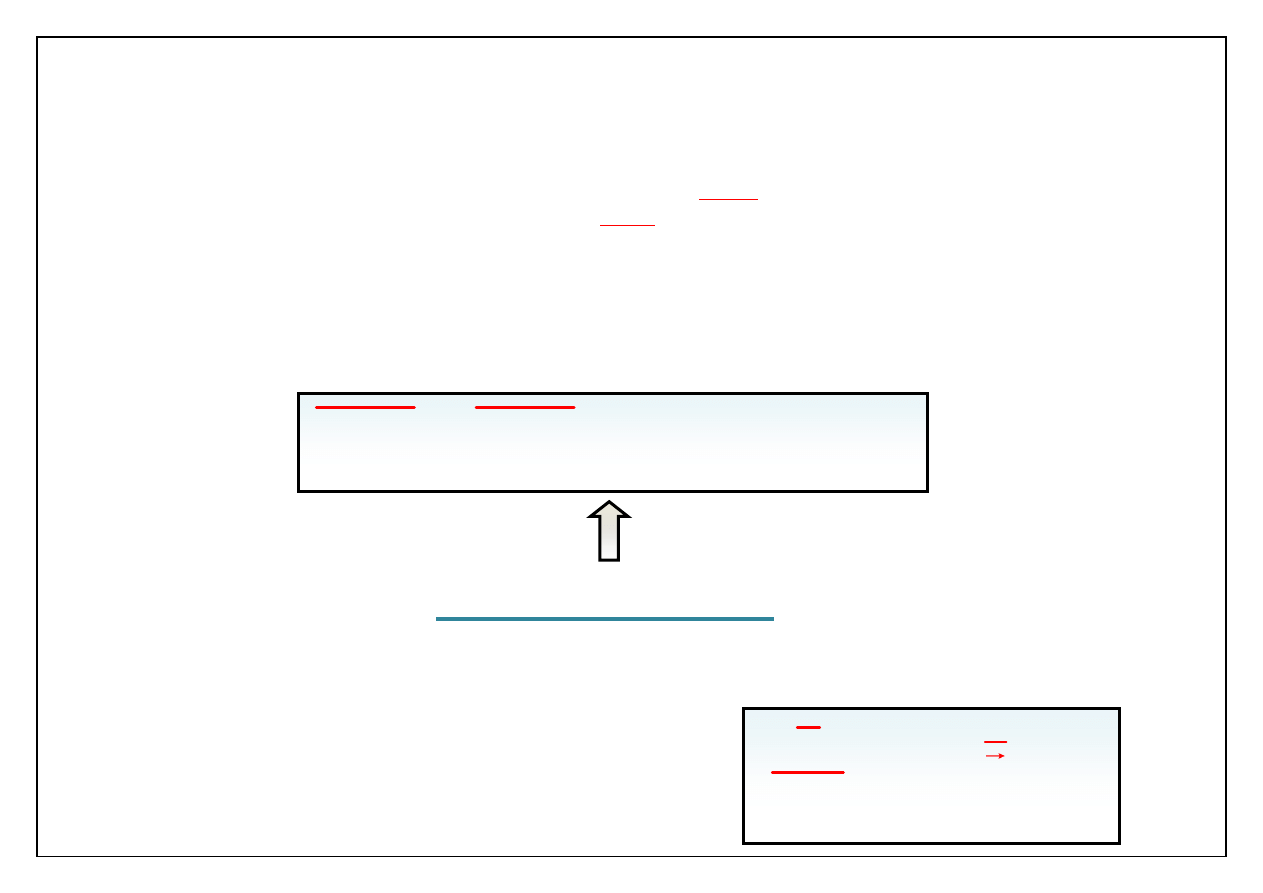
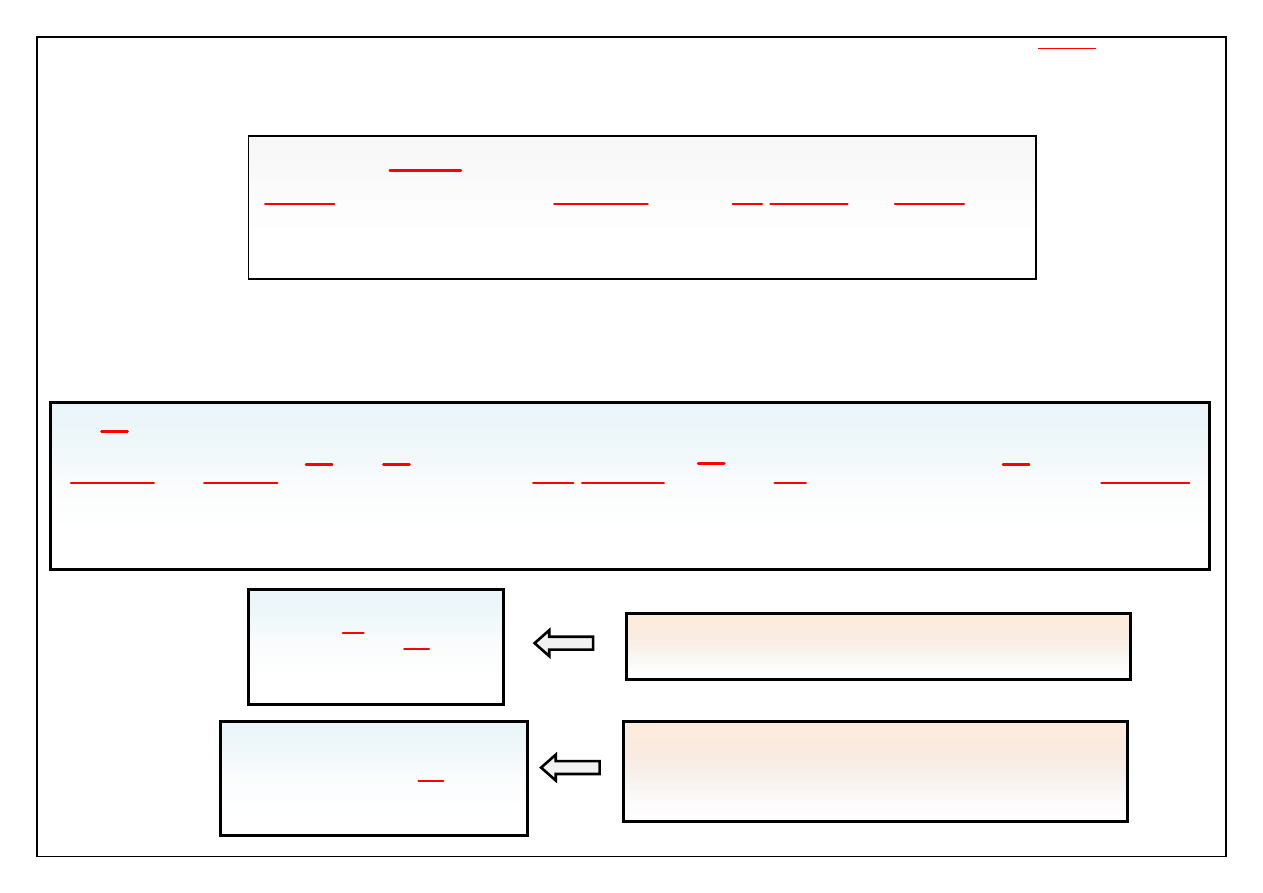
Zauważmy, że równanie Reynoldsa różni się od równania Naviera- 

Stokesa dodatkowym członem 

i

k

i

( v v )

x



 





 . 

 
Oznaczmy: 
 
 
 
 

 

Tensor Reynoldsa

 

 

 
 
Średnie spełniają równanie ciągłości 

 

ii

k

ik

i

ik

ki

v v

v v

R

R

 

 



 

 

 

 

k

k

v

diw v

0

x









 

 
Mamy układ opisujący średnie 

k

v

 i 

p

. 

Trzeba określić składowe 

tensora Reynoldsa. 
 
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

1

1

2

3

1

2

v

v

v , v , v ,

,

,

x

x









 











 



 

zależy od ruchu, a więc odpowiedni związek nie będzie 

wyrażał własności fizycznych płynu, lecz cechy ruchu!

 

Podanie powyższego  związku w jawnej formie nazywamy 

Hipotezą domknięcia

 

Zapiszmy 



 

w sposób następujący: 

 
 
 
 
 

Tr(



)  

- 

to ślad tensora Reynoldsa 

 

 

 
 

Gdzie  



 

nosi nazwę 

energii kinetycznej turbulencji 

 i jest to 

uśredniony kwadrat oscylacji turbulentnych. 
 
 

 

 
 

   

 

2

2

2

1

2

3

1 1

2

3

3

2

v

v

v

Tr( )

v v

v v

v v

2

2

2













 

 

 













 

 

 

ik

ik

ik

ik

1

1

R

Tr

R

Tr

3

3























 

Tr( )

2



 

 

ik

ik

ik

ik

2

2

R

R

3

3









 













 

W równaniu Reynoldsa występują pochodne wielkości

i

k

( v v )

 



.

 

Zatem 
 
 
 
 
Wstawmy to wyrażenie do równania Reynoldsa. Dostaniemy 
wtedy:  
 
 
 
 
 
gdzie  
 
 
 
 
 





t

ik

i

ik

k

i

i

k

i

R

2

v v

T

x

x

3 x

x











 





 











 





t

k

ik

k

i

k

i

k

i

v

T

1

2

v

v

p

v

t

x

x

3

x













 







 



  

















 

t

2

p

p

3



 

 

t

ik

ik

ik

2

T

R

3







 

ciśnienie turbulentne 

t

ensor naprężeń 

turbulentnych 

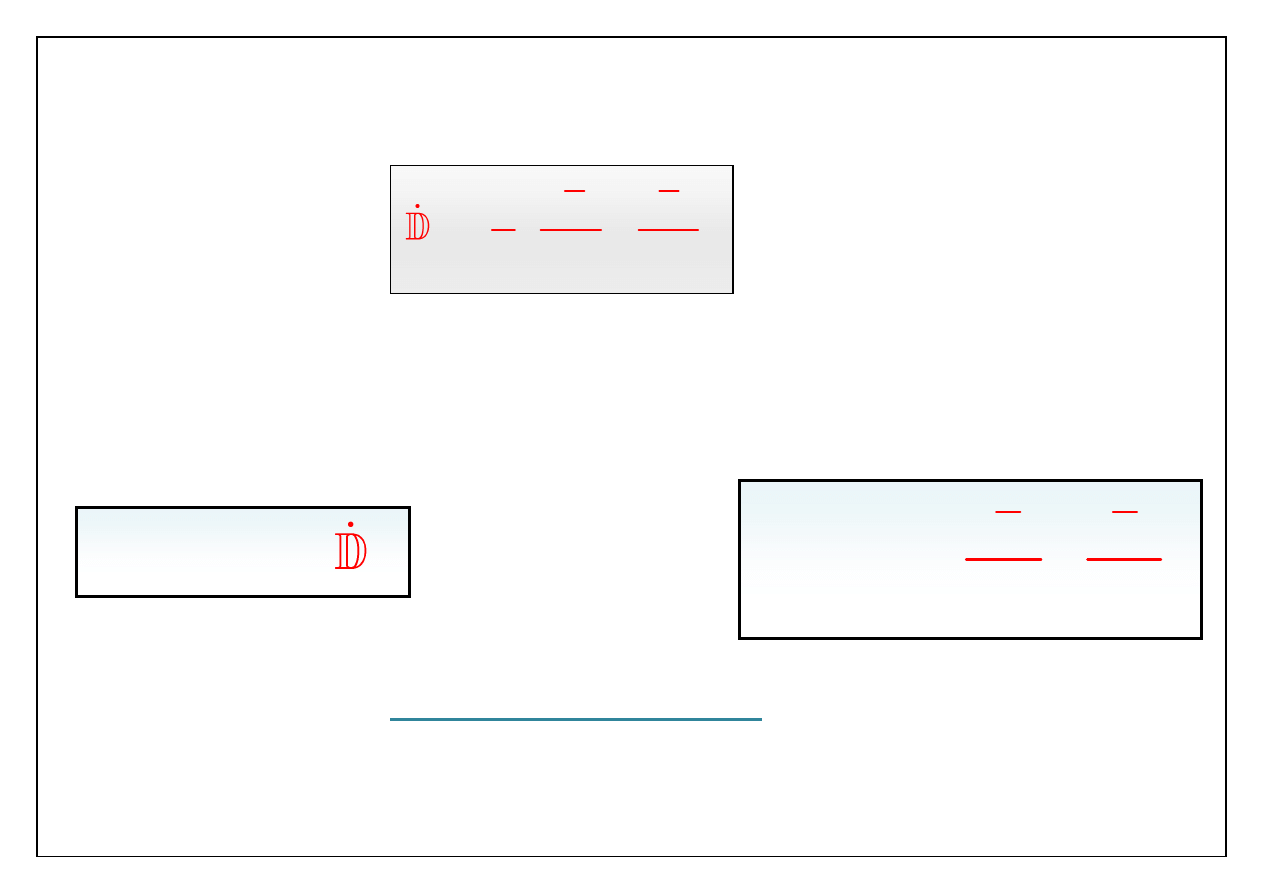
Można pokazać, ze tensor naprężeń turbulentnych ma zerowy 
ślad. Taki ślad ma też tensor określony następująco: 
 
 
 
 
 
 
Hipotezą wykorzystującą powszechnie w opisach ruchu 
turbulentnego jest równanie: 
 
 
 
 
 

µ

turb

 

– nazywa się 

lepkością turbulentną

 

i zależy od rodzaju  

 

 

  

ruchu, miejsca i „zwykłej” lepkości .

 

 
 

i

k

sr

k

i

v

v

1

2

x

x

























 

t

turb

sr

T

2







 

lub w składowych 

 

t

i

k

ik

turb

k

i

v

v

T

x

x



























 

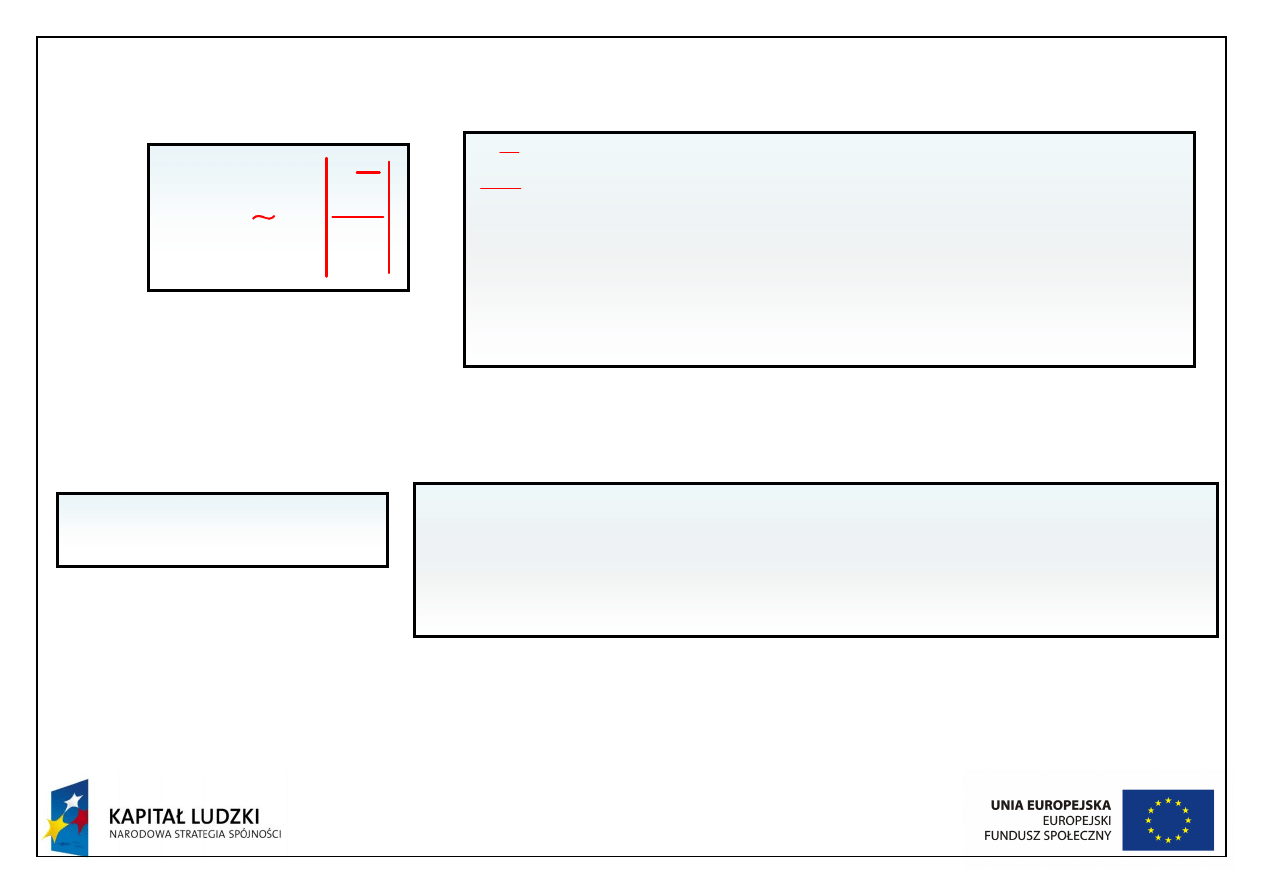
Gdyby udało się określić 

µ

turb

, to równania dla średnich 

prędkości i ciśnienia byłyby takie: 
 
 
 
 
 
 
 
 
 
 
 
 

Jeśli znamy 

µ

turb

  

to  z powyższego układu równań możemy 

wyznaczyć 

k

turb

v

i

p

 

 
 









k

k

i

turb

k

turb

sr ik

i

k

i

v

1

v

v

p

v

t

x

x

x



















 

  









 

i

i

v

0

x







 

równanie Reynoldsa 

równanie ciągłości dla średnich 

Hipotezy określające 

µ

turb

  : 

 

1. 

 

 
 
 
 
2. 

Hipoteza „

κ - ε

” 

 
 

 

 

 

 

 

 

κ 

i

 

ε

 

wynikają z 

dwu dodatkowych równań różniczkowych cząstkowych

 

 

 

 

2

turb

v

l

n






 

v

n




 - 

 pochodna w kierunku normalnym  

 

    

dominującej składowej prędkości 

 

l

- 

droga mieszania wyznaczana doświadczalnie

 

turb

turb

( , )





 



 

κ 

-  energia kinetyczna turbulencji

 

 

ε

 

– moc dyssypowana na ciepło skutkiem 

turbulencji