1

Hydrostatyka

– poziom rozszerzony

Zadanie 1. (11 pkt)

Źródło: CKE 01.2006 (PR), zad. 25.

Egzamin maturalny z fizyki i astronomii

3

Arkusz II

24.5 (2 pkt)

Jedna Īaróweczka przepaliáa siĊ. Oblicz, jakie napiĊcie nominalne powinna mieü nowa

Īarówka. W sprzedaĪy dostĊpne byáy jedynie Īaróweczki z napisami: 3 V oraz 0,21 W. Oblicz

opór zakupionej Īaróweczki Ğwiecącej w warunkach zgodnych z podanymi na niej

informacjami.

24.6 (3 pkt)

Nową ĪaróweczkĊ zamontowano do zestawu. Zapisz, jaki bĊdzie wpáyw nowej Īarówki na

jasnoĞü Ğwiecenia pozostaáych Īarówek. Uzasadnij swoje przewidywania dotyczące dziaáania

Īaróweczki po podáączeniu zestawu oĞwietleniowego do gniazdka (przepali siĊ czy bĊdzie

Ğwieciáa normalnie?).

Zadanie 25. Sáoik (11 pkt)

Podczas przygotowywania konfitur sáoiki wstawia siĊ do naczynia z wrzącą wodą, gdzie

osiągają temperaturĊ T

w

= 100°C. NastĊpnie zamyka siĊ szczelnie pokrywkĊ sáoika

(pozostawiając wewnątrz trochĊ powietrza) i wyciąga sáoik z wody do ostygniĊcia.

W dalszych rozwaĪaniach przyjmij, Īe w opisanych warunkach powietrze zamkniĊte w sáoiku

moĪemy traktowaü jak gaz doskonaáy. PomiĔ wpáyw ciĞnienia pary wodnej na ciĞnienie

wewnątrz sáoika oraz nie uwzglĊdniaj zmian objĊtoĞci sáoika i konfitur. Przyjmij ciĞnienie

atmosferyczne za równe p

0

= 1013 hPa.

25.1 (1 pkt)

Zapisz, jakiej przemianie gazowej ulega powietrze zamkniĊte w sáoiku w trakcie stygniĊcia,

zakáadając, Īe pokrywka nie ulega wygiĊciu.

4

Egzamin maturalny z fizyki i astronomii

Arkusz II

25.2 (2 pkt)

WykaĪ, Īe ciĞnienie powietrza wewnątrz sáoika po jego ostygniĊciu do temperatury otoczenia

równej T

0

= 20°C wynosi okoáo 795 hPa.

25.3 (2 pkt)

Oblicz, z jaką siáą po ostygniĊciu sáoika (nie bierz pod uwagĊ siáy wynikającej z dokrĊcenia

pokrywki) pokrywka jest dociskana do sáoika, jeĞli jej Ğrednica jest równa d = 8 cm.

25.4 (3 pkt)

Podczas morskiej wycieczki czĊĞciowo opróĪniony sáoik, (ale zamkniĊty pokrywką) potoczyá

siĊ po pokáadzie i wpadá do wody. Oblicz, jaka musi byü minimalna masa m przetworów

w sáoiku, aby po wpadniĊciu do wody morskiej zacząá tonąü. Masa pustego sáoika z zakrĊtką

wynosi M = 0,25 kg, a jego objĊtoĞü zewnĊtrzna V = 1,5 dm

3

. Przyjmij gĊstoĞü wody morskiej

przy powierzchni za równą

U

w

= 1025 kg/m

3

. PomiĔ wpáyw masy powietrza zamkniĊtego

w sáoiku na masĊ caáego sáoika.

Zadanie 1.1 (1 pkt)

Zadanie 1.2 (2 pkt)

Zadanie 1.3 (2 pkt)

2

4

Egzamin maturalny z fizyki i astronomii

Arkusz II

25.2 (2 pkt)

WykaĪ, Īe ciĞnienie powietrza wewnątrz sáoika po jego ostygniĊciu do temperatury otoczenia

równej T

0

= 20°C wynosi okoáo 795 hPa.

25.3 (2 pkt)

Oblicz, z jaką siáą po ostygniĊciu sáoika (nie bierz pod uwagĊ siáy wynikającej z dokrĊcenia

pokrywki) pokrywka jest dociskana do sáoika, jeĞli jej Ğrednica jest równa d = 8 cm.

25.4 (3 pkt)

Podczas morskiej wycieczki czĊĞciowo opróĪniony sáoik, (ale zamkniĊty pokrywką) potoczyá

siĊ po pokáadzie i wpadá do wody. Oblicz, jaka musi byü minimalna masa m przetworów

w sáoiku, aby po wpadniĊciu do wody morskiej zacząá tonąü. Masa pustego sáoika z zakrĊtką

wynosi M = 0,25 kg, a jego objĊtoĞü zewnĊtrzna V = 1,5 dm

3

. Przyjmij gĊstoĞü wody morskiej

przy powierzchni za równą

U

w

= 1025 kg/m

3

. PomiĔ wpáyw masy powietrza zamkniĊtego

w sáoiku na masĊ caáego sáoika.

Egzamin maturalny z fizyki i astronomii

5

Arkusz II

25.5 (2 pkt)

GĊstoĞü wody morskiej roĞnie wraz ze zwiĊkszaniem gáĊbokoĞci. Na powierzchni wynosi

1025 kg/m

3

, a na gáĊbokoĞci okoáo 1000 m osiąga wartoĞü 1028 kg/m

3

. Przy dalszym

wzroĞcie gáĊbokoĞci gĊstoĞü wody juĪ nie ulega zmianie. WyjaĞnij, jaki wpáyw na prĊdkoĞü

tonącego sáoika ma fakt, Īe gĊstoĞü wody morskiej roĞnie wraz z gáĊbokoĞcią. Przyjmij, Īe na

tonący sáoik dziaáa siáa oporu wody wprost proporcjonalna do wartoĞci prĊdkoĞci toniĊcia

sáoika.

25.6 (1 pkt)

Zapisz, jaka musi byü Ğrednia gĊstoĞü sáoika wraz z zamkniĊtą zawartoĞcią, aby mógá on

dotrzeü do dna morza, jeĞli gáĊbokoĞü w tym miejscu przekracza 1000 m.

Odp. ---------------------------------------------------------------------------------------------------------

---------------------------------------------------------------------------------------------------------------

Zadanie 26. Silnik elektryczny (10 pkt)

Silnik elektryczny na prąd staáy zasilany jest z baterii o SEM

İ

= 12 V. Podczas pracy silnika

przez jego uzwojenia páynie prąd o natĊĪeniu I = 2 A, natomiast gdy wirnik tego silnika jest

caákowicie zahamowany, przez jego uzwojenie páynie wiĊkszy prąd o natĊĪeniu I

0

= 3 A.

Opór wewnĊtrzny baterii pomijamy.

26. 1 (2 pkt)

W tym obwodzie wystĊpują siáy elektromotoryczne baterii i indukcji. OkreĞl i uzasadnij, czy

te SEM skierowane są zgodnie, czy przeciwnie (nie uwzglĊdniamy SEM samoindukcji).

Zadanie 1.4 (3 pkt)

Zadanie 1.2 (2 pkt)

Zadanie 1.6 (1 pkt)

3

Zadanie 2. (10 pkt)

Źródło: CKE 2010 (PR), zad. 6.

Egzamin maturalny z fizyki i astronomii

poziom rozszerzony

12

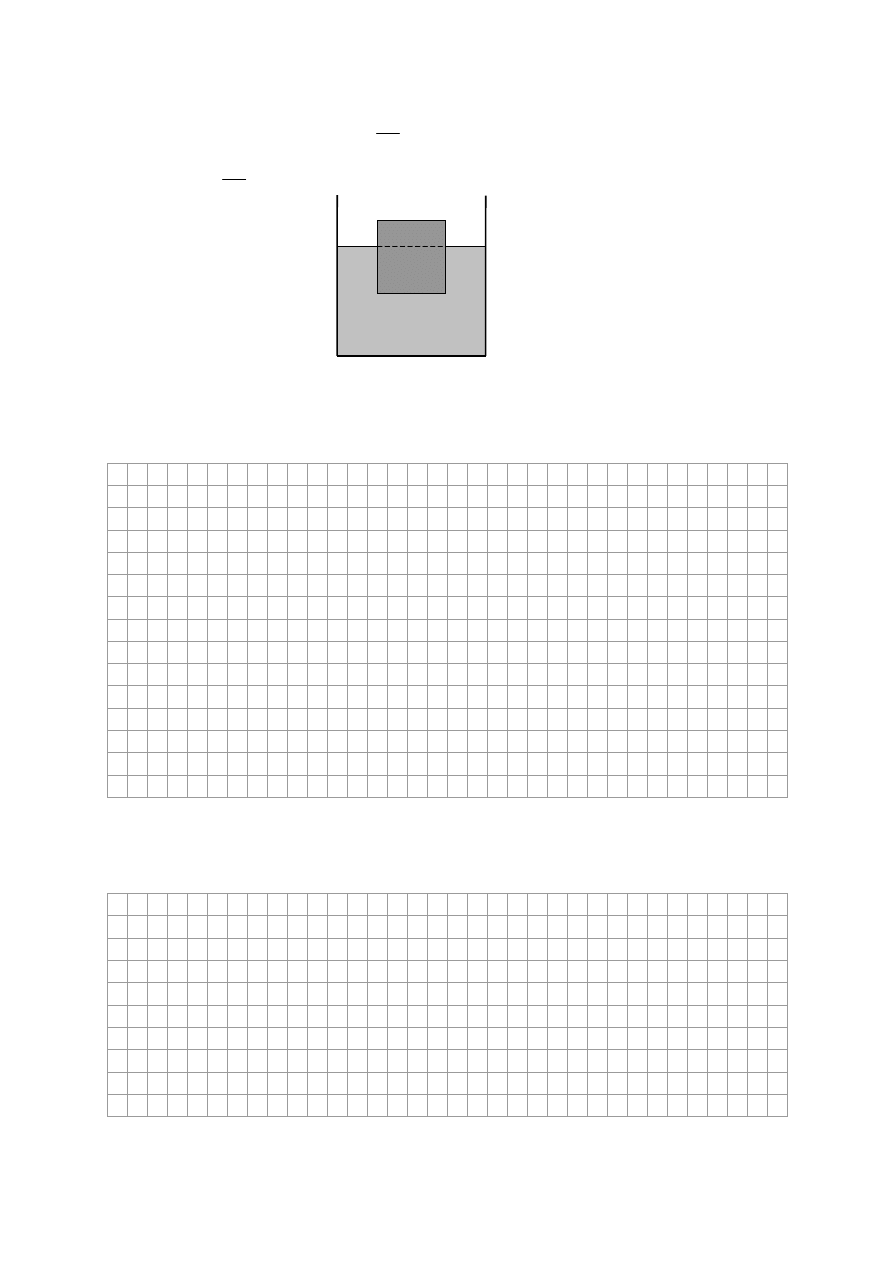
Zadanie 6. Siáa wyporu (10 pkt)

Drewniany szeĞcian o gĊstoĞci

3

900

m

kg

i boku a = 5 cm umieszczono w naczyniu z wodą

o gĊstoĞci

3

1000

m

kg

.

Zadanie 6.1 (3 pkt)

Oblicz stosunek objĊtoĞci czĊĞci wynurzonej (V

wyn

) do objĊtoĞci czĊĞci zanurzonej (V

zan

)

szeĞcianu páywającego w wodzie.

Zadanie 6.2 (3 pkt)

Oblicz najmniejszą wartoĞü siáy, której naleĪaáoby uĪyü, aby caáy szeĞcian znalazá siĊ

pod powierzchnią wody.

V

wyn

V

zan

Zadanie 2.1 (3 pkt)

Zadanie 2.2 (3 pkt)

4

Egzamin maturalny z fizyki i astronomii

poziom rozszerzony

13

Zadanie 6.3 (1 pkt)

SzeĞcian, opisany w treĞci zadania, wáoĪono do naczynia zawierającego wodĊ sáoną. Napisz,

czy zanurzenie szeĞcianu w sáonej wodzie zmieni siĊ w porównaniu z jego zanurzeniem

w wodzie sáodkiej. OdpowiedĨ krótko uzasadnij.

Zadanie 6.4 (3 pkt)

Do naczynia z wodą i páywającym w niej klockiem dolano oleju o gĊstoĞci

3

850

m

kg

, w taki

sposób, Īe górna krawĊdĨ klocka zrównaáa siĊ z powierzchnią oleju. Stwierdzono wtedy,
Īe w wodzie znalazáa siĊ czĊĞü klocka o wysokoĞci równej 1

a

3

. Oblicz wartoĞü siáy wyporu,

z jaką olej dziaáa na zanurzony w nim klocek.

Nr zadania

6.1 6.2 6.3 6.4

Maks. liczba pkt

3

3

1

3

Wypeánia

egzaminator Uzyskana liczba pkt

Zadanie 2.3 (1 pkt)

Zadanie 2.4 (3 pkt)