Teoretyczne Podstawy Informatyki

prowadz

ą

cy

dr hab. Krzysztof SZKATUŁA

Instytut Bada

ń

Systemowych PAN, docent

oraz

Politechnika Koszali

ń

ska, prof. PK

na podstawie materiałów Politechniki Koszali

ń

skiej

1

TEORETYCZNE PODSTAWY INFORMATYKI

Wymagania:

Algorytmy. Modele obliczeń, maszyny Turinga, obliczalność. Języki
formalne, gramatyki i automaty. Złożoność obliczeniowa, klasy
złożoności, NP-zupełność.

Wykłady:

1. Algorytmy. Dziedzina algorytmiczna. Termy i wyrażenia arytmetyczne.

Wyrażenia logiczne. Przykłady algorytmów.

2. Algorytmy. Procedury i rekursja. Przykłady algorytmów rekurencyjnych.

3. Poprawność algorytmów. Algorytm poprawny – semantyczna poprawność

algorytmów. Poprawność częściowa, własność określoności obliczeń,
własność stopu.

4. Poprawność algorytmów Dowodzenie poprawności częściowej - metoda

niezmienników Naur’a-Floyd’a. Dowodzenie własności stopu - metoda
liczników iteracji.

5. Sprawność algorytmów. Miary efektywności algorytmów. Złożoność

obliczeniowa algorytmów. Złożoność pesymistyczna i średnia. Dolne i górne
ograniczenie złożoności. Problemy algorytmicznie zamknięte i otwarte.

6. Klasyfikacja problemów algorytmicznych. Problemy łatwo-rozwiązywalne i

trudno-rozwiązywalne. Klasy problemów algorytmicznych: logarytmiczne,
wielomianowe, NP, NP-zupełne.

7. Klasyfikacja problemów algorytmicznych. Otwarte problemy związane z

klasyfikacją problemów algorytmicznych. Dowodzenie NP-zupełności.

8. Prymitywne modele algorytmiczne. Teza Churcha-Turinga. Maszyna

Turinga i jej warianty.

9. Prymitywne modele algorytmiczne. Przykłady implementacji wybranych

algorytmów.

10. Języki systemów informacyjnych. System informacyjny. Składania i

semantyka języka. Reguły przekształcania termów.

11. Języki systemów informacyjnych. Postać normalna termów. Dokładność i

efektywność języka.

12. Automaty. Układy sekwencyjne i kombinacyjne. Języki formalne. Język

wyrażeń regularnych. Automaty Rabina-Scotta. Automaty Meale’go i Moor’a.

13. Automaty. Realizacje automatów. Synteza abstrakcyjna z wykorzystaniem

charakterystyki wejście-wyjście.

2

14. Sieci Petriego. Definicja i klasyfikacje sieci Petriego. Reprezentacje

teoriomnogościowa, graficzna i macierzowa. Modelowanie - przykłady
zastosowań.

15. Sieci Petriego. Analiza właściwości – żywotność strukturalna i funkcjonalna.

Zjawiska blokady i konfuzji. Niezmienniki. Rozszerzenia sieci – czasowe,
kolorowane, stochastyczne.

Literatura

1. Banachowski L., Kreczmar A., Elementy analizy algorytmów. WNT, Warszawa

1982.

2. Majewski W., Albicki A., Algebraiczna teoria automatów. WNT, Warszawa

1980.

3. Pawlak Z., Systemy informacyjne (Podstawy teoretyczne). WNT, Warszawa

1983.

4.

Błażewicz J., Złożoność obliczeniowa w projektowaniu systemów
komputerowych. Wyd. Politechniki Poznańskiej, Poznań 1984.

5.

Starke P.K., Sieci Petri. Podstawy, teoria, zastosowania. PWN, Warszawa
1987.

3

TEORETYCZNE PODSTAWY INFORMATYKI

„Komputer zmusił nas do uporządkowania samych

siebie.,,,Zmusza nas do uprzedniego przemyślenia naszych

założeń i powoduje, że zdajemy sobie w ogóle sprawę z tego, że

przyjmujemy jakieś założenia.”

Peter Druckner

1. ALGORYTMY

• Algorytmy – rys historyczny, przykłady

• Dziedzina algorytmiczna

• Termy i wyrażenia arytmetyczne

• Wyrażenia logiczne

• Przykłady algorytmów

ALGORYTM

– źródłosłów

Abu Jafar Mukhammad ibin Musa al-Kwarizmi

(Mukhammad, ojciec Jafar’a, syn Moses’a, Kwarizmianin)

Al-Khorezmi

z Khorezm

(780 – 850) (Uzbekistan)

(Arytmetyka,

Algebra)

abu-aljabar

“Kitab al-jabr wal-muqabala”

źródło „Fihrist” – An-Nadin (987)

(The book of Aljabar and Almuqaba

– The book of Restoring and Equating)

Księga rekonstrukcji i bilansu

1 + 2 + 4 + ...+ 2

63

= (((16

2

)

2

)

2

)

2

= 18 446 744 073 709 551 615

Algorytm – przepis postępowania, w sposób automatyczny prowadzący do

rozwiązania określonego zadania.

Zakłada się, ze pewne pierwotne instrukcje tego przepisu są
wykonalne, to znaczy, że są one zdefiniowane i w algorytmie nie musi
się ich definiować, ale można ich używać.

4

Przykład

Mnożenie dwóch liczb naturalnych zapisanych w układzie dziesiętnym,
zakłada znajomość tabliczek dodawania i mnożenia cyfr dziesiętnych.

Budowa algorytmu zakłada zatem znajomość zbioru obiektów na
których ma działać zbiór wykorzystywanych w nim pierwotnych operacji.

Dziedzina algorytmiczna

- zbiór obiektów wraz z operacjami pierwotnymi

(A, f

1

,...,f

n

, r

1

,...,r

m

)

gdzie

A – zbiór niepusty

f

1

,...,f

n

– funkcje częściowo określone dla argumentów ze zbioru A i

przyjmujące wartości w zbiorze A

r

1

,...,r

m

– relacje zachodzące między elementami zbioru A

r

j

(x

1

,...,x

k

) – relacja k-argumentowa , r

j

⊆ A

k

f

j

(x

1

,...,x

k

) = x

k+1

– funkcja k-argumentowa częściowa

k+1-

argumentowa relacja, taka że dla ustalonego

(x

1

,...,x

k

) istnieje co najwyżej jeden element x

k+1

,

dla którego układ (x

1

,...,x

k

, x

k+1

) należy do tej relacji

Funkcja całkowita określona jest dla wszystkich
układów (x

1

,...,x

k

)

Przykład

Dziedziną algorytmiczna liczb całkowitych jest układ:

(Z , + , - , * , div , mod , = , >)

gdzie:

Z – zbiór liczb całkowitych

+ , - , * - dwuargumentowe całkowite funkcje dodawania, odejmowania i

mnożenia dwóch liczb całkowitych

`

= , > odpowiednio relacja równości i relacja porządku w zbiorze liczb

całkowitych

div, mod – częściowe funkcje dwuargumentowe określone dla par (n,m) gdy

m

≠0, dającymi odpowiednio iloraz i resztę z dzielenia n przez m

5

Przykład

Dziedzina algorytmiczna rachunku logicznego (Algebra

Boole’a)

(B ,

¬ , ∧ , ∨ , ⇒ , ⇔)

gdzie

B – zbiór wartości logicznych {false,true}
¬,∧,∨,⇒,⇔ - funkcje pierwotne zdefiniowane następująco:

¬(false) = true , ¬(true) = false

∧(true,true) = true , ∧(true,false) = ∧(false,true) = ∧(false,false) = false

∨(a,b) = ¬(∧(¬ (a),¬(b)))

⇒(a,b) = ∨(¬(a),b)

⇔(a,b) = ∧(⇒(a,b), ⇒(b,a))

Termy

Niech

(A, f

1

,...,f

n

, r

1

,...,r

m

)

będzie dziedziną algorytmiczną.

Term - napis języka (np. programowania), który definiuje algorytm polegający
na obliczeniu wartości funkcji pierwotnej danej dziedziny algorytmicznej, albo
superpozycji takich funkcji, a zatem spełniający warunki:

1) Każda stała i każda zmienna przyporządkowana danej dziedzinie

algorytmicznej jest termem.

2) Jeżeli f jest symbolem funkcji k-argumentowej oraz jeżeli t

1

,...,t

k

są

termami, to napis f(t

1

,...,t

k

) jest termem

3) Termem jest tylko taki napis, który można otrzymać stosując 1) lub 2)

Przykład

c , x , f(x) , f(d) , g(f(y),c)) , itp.

są termami

gdzie:

c, d – stałe
x, y – zmienne
f, g – symbole funkcji odpowiednio jedno i dwuargumentowej

Wykonanie termu, a więc algorytmu określonego przez term, polega na
obliczeniu jego wartości.

Przykład
W ramach dziedzin liczb całkowitych lub rzeczywistych termy nazywa się
wyrażeniami arytmetycznymi (definiującymi skończone ciągi operacji
arytmetycznych, które trzeba wykonać w określonej kolejności).

+(x,-(z,*(76.3,u)))

(x+(z-(76.3*u)))

x+z-76.3*u

6

Język definiujący napisy (algorytmy) obejmuje:

Stałe -

napisy, którym jest przyporządkowana jedna określona wartość –
element zbioru A, np. 0, -1, 00678, 315, itp. dla dziedziny liczb
całkowitych

Zmienne

-napisy, które mogą mieć przyporządkowaną dowolną wartość ze
zbioru A, np. var i,j,k: integer

re, im: real

itd.

Obliczenie wartości termu polega na obliczeniu wartości odpowiednich funkcji dla
określonych wartości stałych i wartości zmiennych.

Wartościowanie stałych – stałym odpowiadają pewne elementy zbioru A.
Wartościowanie zmiennych – określa funkcja

ν((x) , gdzie x – zmienna

Przykład

Jeżeli term jest stałą to jego wartością jest ta stała.

Jeżeli term jest zmienną, to jego wartość równa jest wartościowaniu
zmiennej.
Jeżeli term jest funkcją k-argumentową f(t

1

,...,t

k

) oraz funkcja g jest

określona to

ν(f(t

1

,...,t

k

) = g(

ν(t

1

),...,

ν(t

k

))

Przykład

Podstawienie

(przypisanie)

x := t , gdzie x – zmienna , t – term

Dla danego wartościowania

ν oblicza się wartość termu ν(t). Jeżeli

wartość ta jest należy do dziedziny algorytmicznej, do której jest
przyporządkowana zmienna x, to wartości zmiennej x można przypisać
(zastąpić) wartość

ν(t).

Przykład

Niech

a, b, c – zmienne, których początkowe wartości są równe

długościom boków trójkąta.
Algorytm obliczania pola trójkąta (ze wzoru Herona) definiują dwa
przypisania:

P:= (a + b + c)/2
S := sqrt(p*(p-a)*(p-b)*(p-c)

Algorytm ten można oczywiście zapisać korzystając z jednego
przypisania:

S := sqrt((a + b + c)*( b + c-a)*( a + c - b)*( a + b-c)/16)

Uwagi:

Porównaj

niezbędną do wykonania liczbę operacji dodawania,

mnożenia i pierwiastkowania.

Ile

algorytmów

rozwiązuje dany problem?

Jak

porównywać algorytmy?

7

Przykład

Traktując liczbę zespolona jako uporządkowana parę liczb rzeczywistych (a,b)
mnożenie dwóch liczb zespolonych (a,b)*(c,d) = (e,f) można określić przy
pomocy dwóch algorytmów:

a)

e:= a*c – b*d

f := a*d + b*c

b)

g := (a+b)*c ; h := a*(d-c) ; f:= g+h
h := b(*(d+c) ; e := g-h

Który z algorytmów jest lepszy?

Uwaga:

Termy postaci wyrażeń arytmetycznych oraz instrukcje podstawienia
umożliwiają definiowanie algorytmów najprostszej postaci (nie korzystających
z pierwotnych relacji danej dziedziny algorytmicznej) nie pozwalających
zmieniać kolejności wykonywanych czynności w zależności od aktualnego
wartościowania zmiennych, tzw. algorytmów liniowych.

Wyrażenia logiczne (wyrażenia boolowskie)

Zbiór napisów spełniających następujące warunki:

1) Każda stała logiczna i każda zmienna logiczna są wyrażeniami logicznymi

2) Jeżeli

t

1

,...t

k

są termami oraz r jest symbolem relacji k-argumentowej, to

r(t

1

,...,t

k

)

jest wyrażaniem logicznym.

3) Jeżeli

s, u

są wyrażeniami logicznymi, to napisy

¬s , s∧u , s∨u , s⇒u

, s

⇔u

są również wyrażeniami logicznymi

4) Wyrażeniem logicznym jest tylko ten napis, który można otrzymać stosując

1) – 3).

Przykłady algorytmów

Algorytm Euklidesa
Dane są dwie liczby całkowite dodatnie m i n. Należy wyznaczyć ich
największy wspólny dzielnik.

Z definicji NWD (największy wspólny dzielnik) oznacza największa dodatnią
liczbę całkowitą k taką, że k dzieli n i m (bez reszty).

8

Rozważmy

n = q*m + r

• r = 0

NWD(n,m) = m

• r > 0

NWD(n,m) = NWD(m,r)

n = 18 , m = 12

18 = 1*12 + 6

9*2 = 1*6*2 + 3*2

6*3 = 1*4*3*+ 2*3

n = 15 , m = 11

15 = 1*11 + 4

15*1 = 1*11*1 + 4*1

Uwaga:

Zatem zadanie poszukiwania NWD(n,m) można zastąpić zadaniem
NWD(m,r)

m

> r oznacza, ze liczba kroków algorytmu jest skończona

Warunek stopu n’ = q’*m’ + r’

,

r’ = 0 ; NWD = m’

Przykład

program euklid(input,output);

var r,n,m: integer;

begin read(n); read(m)

r:= n mod m;
while r

≠ 0 do

begin n:= m ; m := r ;

r := n mod m

end;
write(m)

end.

Przykład

n

m

r

420

825

420

825

420

405

420

405

15

505

15

0

Przykład

n

m

r

521

428

93

428

93

56

93

56

37

56

37

19

37

19

18

19

18

1

18

1 0

9

Sito Eratostenesa

Należy wygenerować wszystkie liczby pierwsze, nie większe od danej
liczby naturalnej n.

Rozważmy ciąg 2,...,n wszystkich liczb naturalnych od 2 do n.
Niech a

0

,a

1

,...,a

k

,a

k+1

,...,a

m

będzie podciągiem tego ciągu otrzymanym

w wyniku wykonania k-kroków tego algorytmu.

Dla k = 0 jest ciąg 2,3,...,n przy czym a

0

= 2.

W założeniu indukcyjnym przyjmuje się, że a

0

,a

1

,...,a

k

są kolejnymi

liczbami pierwszymi oraz a

k+1

,...,a

m

– wszystkimi liczbami naturalnymi i,

a

k

< i

≤

n, takimi, że żadna z liczb a

0

,a

1

,...,a

k

nie dzieli i.

W kolejnym kroku usuwa się z ciągu a

k+1

,...,a

m

wszystkie liczby

podzielne przez a

k

.

Otrzymuje się ciąg a

0

,a

1

,...,a

k

,a’

k+1

,...,a’

l

. Jeżeli ciąg a’

k+1

,...,a’

l

jest pusty

to STOP.

Uwagi:

Skończona liczba kroków postępowania.

Zastosowanie

algorytmu

Euklidesa

Przykład

2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31

2,

3, 5,7,9,11,12,13,15,17,19,21,23,25,27,29,31

2,3,

5, 7,11,13,17,19,23,25,29,31

2,3,5,

7, 11,13,17,19,23,29,31

2,3,5,7, 11, 13,17,19,23,29,31

.........................................................
2,3,5,7,11,13,17,19,23,29,31

Uwagi:

Generowanie kolejnych liczb pierwszych

Wzór Euklidesa

e

1

= 2, e

2

= 3

e

3

= e

1

* e

2

+1 = 7

e

4

= e

1

* e

2

* e

3

+1 = 43

e

5

= e

1

* e

2

* e

3

* e

4

+1 = 1087

...................................

e

k

= e

1

* e

2

* e

3

* e

k-1

+1

e

5

; e

6

????

Liczby Mersena

M

p

= 2

p

– 1 ,

p = 2,3,5, 7,13,17,19,31,67,127,257

p = 67 , 257 i 61, 89, 107 ????

10

2. Algorytmy

• Procedury i rekursja.

• Przykłady algorytmów rekurencyjnych.

program euklid(input,output);

var r,n,m: integer;

begin read(n); read(m)

r:= n mod m;
while r

≠ 0 do

begin n:= m ; m := r ; r := n mod m
end;
write(m)

end.

Procedura definiuje operacje (bloki – fragmenty algorytmów) wykorzystywane w
algorytmie. Procedura musi mieć nazwę oraz opis argumentów, na których będzie
działać.

Rodzajem procedury jest funkcja:

Przykład

p:= euklid2 (7,234) + q

Przykład

function euklid2 (n,m: integer);integer;

var r: integer;
begin r := n mod m;

while r

≠ 0 do

begin n := m ; m := r ; r := n mod m

end;

euklid2 := m

end.

procedure euklid1 (n,m: integer);

Parametry

formalne

typ

function euklid2 (n,m: integer);integer;

Parametry

formalne

typ

11

Komunikowanie się parametrów formalnych z aktualnymi:

• Przekazywanie przez wartość

• Przekazywanie przez zmienną

Przykład

procedure euklid3 (n,m: integer; var p: integer));integer;

var r: integer;
begin r := n mod m;

while r

≠ 0 do

begin n := m ; m := r ; r := n mod m

end;

p:= m

end.

Algorytmy rekurencyjne

Przykład a)

Dany jest ciąg a

1

,...,a

n

liczb całkowitych, dla n

≥

2. Należy wyznaczyć

największą i najmniejsza spośród tych liczb.

Ciąg liczb zadany jest przez tablicę a[1..n]. Aby znaleźć element
największy rozważmy ciąg jednoelementowy a[1]. Jego największy
element jest równy a[1].
Załóżmy, że a[j] jest największy w ciągu a[1],...,a[i-1]. Porównajmy a[i] z
a[j].

Jeżeli a[i] będzie większy od a[j], oznacza to, że a[i] jest największy w
ciągu a[1],...,1[i], należy zatem zmienić wartość zmiennej j na i.
W przeciwnym razie wartościowanie pozostaje bez zmiany.
Po wykonaniu iteracji aż do i = n, a[j] będzie wskazywało na największy
element w tym ciągu.

Dla wyznaczenia najmniejszego elementu relację > należy zastąpić
relacją <.

program maxmin 1 (input, output);

label 1,2,3; const n = 100;

var i,j,k: integer; a : array [1..n] of integer;

begin

for i:=1 to n do read(a[i]);

1: j:=1; for i :=2 to n do if a[i] > a[j] then j:=i;

2: k:=1; for i :=2 to n do if a[i] < a[k] then k:=i;

3: write(a[j]; write(a[k])

end.

12

Przykład b)

program maxmin 2 (input, output);

label 1,2; const n = 100;

var i,j,k: integer; a : array [1..n] of integer;

begin

for i:=1 to n do read(a[i]); j:=1 ; k:=1;

for i :=2 to n do

1:

if a[i] > a[j] then j:=i; else

if a[i] < a[k] then k:=i;

2:

write(a[j]; write(a[k])

end.

Uwagi:

Jakie są złożoności (koszty obliczeń) obu algorytmów?

Jakie diagramy przepływu (flowcharty) odpowiadają przedstawionym

algorytmom?

Algorytm

porządkowania elementów ciągu.

Jak maleje złożoność obliczeniowa algorytmu porządkowania elementów
ciągu przy zastosowaniu zasady dziel i zwyciężaj (ang. divide and conquer).

Podaj algorytm wyznaczający wartość F

n

, n tej liczby Fibonacciego, określonej

następującym wzorem rekurencyjnym:

F

0

= 1 , F

1

= 1

, F

n+1

= F

n

+ F

n-1

dla n

≥ 1.

3. Poprawność algorytmów

• algorytm poprawny – semantyczna poprawność algorytmów.

• poprawność częściowa,

• własność określoności obliczeń,

• własność stopu.

1. Czy ułożony program (zbudowany algorytm) rzeczywiście stanowi

rozwiązanie postawionego problemu?

2. Czy dla realizacji programu (dla potrzeb rozwiązania postawionego

problemu) wystarczy ta ilość czasu pracy komputera i ta ilość
miejsca pamięci, które można dla niego przeznaczyć?

3. Czy zmieniony program na każdym komputerze da te same wyniki,

co program przed modyfikacją?

13

Dana wejściowa algorytmu – wartość dostarczana do algorytmu z zewnątrz

(z programu wywołującego dany algorytm)

Przykład
W

programie

euklid wielkościami tymi są zmienne n i m. Ich wartości

ustalane są przy wykonywaniu instrukcji wejścia read(n) oraz read (m).

Wynik algorytmu – wartość, która algorytm przekazuje na zewnątrz

(do programu wywołującego dany algorytm)

Przykład
Wynikiem

programu euklid jest wartość zmiennej m, którą ten program

wypisuje przy wykonywaniu instrukcji write(m).

Z każdym algorytmem wiążą się warunki:

• Początkowy – podający ograniczenia na dane wejściowe algorytmu

• Końcowy – opisujący własności wyników algorytmu i ich związek z danymi

wejściowymi algorytmu.

Przykład

Dla programu euklid warunek początkowy może być sformułowany:

„wartości wczytywane na zmienne n i m są dodatnimi liczbami
całkowitymi”

warunek końcowy natomiast:

„wypisywana wartość jest największym wspólnym dzielnikiem
początkowych wartości n i m”

Niech dany algorytm K oraz para warunków opisujących jego działanie:

α- warunek początkowy oraz β– warunek końcowy

Algorytm K jest semantycznie poprawny względem warunków
początkowego

α i końcowego β , jeśli dla każdych danych

wejściowych spełniających warunek

α obliczenie algorytmu K

dochodzi do punktu końcowego oraz wartościowanie zmiennych
spełnia warunek

β.

Przykład

Niech instrukcja (algorytm):
for j:=1 to m do A[j] := B[j] , w której j i m są zmiennymi całkowitymi, n –
stałą całkowitą oraz A i B tablicami typu array[1..n] of integer.

14

Instrukcja ta jest poprawna względem warunków:

początkowego

„n > 0

∧ m ≤ n”

końcowego

„

∀j=1..m (A[j] = B[j]])”

Jest

również poprawna dla warunków

„n = m = 100”

„

Σ (i=1..n) A[i] = Σ (i=1..m) B[i]”

„n = m = 0”

„

∀ i=1..n (A[i]) = 5)”

Nie jest natomiast poprawna względem warunków:

„n > 0”

„

∀j=1..m (A[j] = B[j]])”

„

n > m”

∃ i=1..n (A[i] ≠ B[i])”

Uwagi:

• Dla każdego algorytmu można dobrać takie warunki, żeby algorytm był

poprawny względem tych warunków.

• Dla każdego algorytmu można dobrać takie warunki, żeby algorytm nie

był poprawny względem tych warunków.

• Warunki początkowy i końcowy zdeterminowane są przez nasze

postulaty, co algorytm ma liczyć.

Przykład

Niech dana instrukcja (algorytm):

begin i:= 0; while i

≠ u do i := i+1 end. i, u – zmienne rzeczywiste

dla u = -1 lub u = 0.5 - obliczenie instrukcji staje się nieskończone,

obliczanie jest skończone dla u spełniającego własność „u jest liczbą
naturalną”

Przykładowe warunki poprawne „u jest liczbą naturalną” oraz „u=i”

Przykładowe warunki nie poprawne „u>0” oraz „u=i”

15

Uwagi:

Niepoprawność algorytmu może być trojakiego rodzaju. Dla pewnych danych
wejściowych obliczenie algorytmu

• albo dochodzi do punktu końcowego, ale wyniki nie spełniają warunku

końcowego

• albo zatrzymuje się w punkcie niekońcowym tego algorytmu

• albo jest nieskończone

Poprawność algorytmu K względem warunków początkowego

α i końcowego

β dowodzi się zwykle przez pokazanie, że algorytm K ma następujące trzy
własności:

1) dla każdych danych wejściowych spełniających warunek początkowy

α

jeżeli obliczenie algorytmu K dochodzi do punktu końcowego, to
otrzymane wyniki spełniają warunek końcowy

β

2) dla każdych danych wejściowych spełniających warunek początkowy

α

obliczenie algorytmu K nie jest przerwane

3) dla każdych danych wejściowych spełniających warunek początkowy

α

obliczenie

α algorytmu K nie jest nieskończone.

Jeżeli zachodzi 1) wówczas algorytm K jest częściowo poprawny względem
warunku początkowego

α i końcowego β

Jeżeli zachodzi 2) wówczas algorytm K ma własność określoności obliczeń
względem warunku początkowego

α

Jeżeli zachodzi 3) wówczas algorytm K ma własność stopu względem
warunku początkowego

α

Poprawność algorytmu ustala się zatem dowodząc:

Częściowej poprawności,

Określoności obliczeń

Własności stopu

Podstawową metodą dowodzenia częściowej poprawności i określoności
algorytmów jest tzw. metoda niezmienników, w której opisywane są własności
wartościowań zmiennych otrzymywanych, gdy obliczenie algorytmu przechodzi przez
wyróżnione punkty tego algorytmu.

4 Poprawność algorytmów

• Dowodzenie poprawności częściowej - metoda niezmienników Naur’a-Floyd’a.

• Dowodzenie własności stopu - metoda liczników iteracji.

16

Dowodzenie poprawności częściowej

Przykład

procedure intdiv (x, y: integer; var q, r: integer);

label 1, 2, 3;

begin {

α: 0 ≤ ∧ 0 ≤ y}

1: q := 0; r := x;

2: while y

≤ r do

begin q := q+1; r:= r – y end;

3: {

β: x: = q*y + r ∧ 0 ≤ r < y}

end.

Należy wykazać, że dla każdego obliczenia algorytmu, które startuje z danymi
wejściowymi spełniającymi warunek

α, jeżeli obliczanie algorytmu dochodzi do końca

(do etykiety 3), to wartości zmiennych x, y, q oraz r spełniają warunek końcowy

β.

Trzeba zatem wykazać pewna własność obliczeń algorytmu, która łączy
zachodzenie pewnego warunku przy etykiecie 1 z zachodzeniem pewnego
warunku przy etykiecie 3.
Należy zatem skorzystać z tego co się dzieje miedzy etykietami 1 a 3; np. jaki
warunek spełniają wartości zmiennych x, y, q i r w punkcie pośrednim
oznaczonym etykieta 2.
Dokładniej: jaki warunek spełniają wartości zmiennych w chwili sprawdzania
warunku „y

≤

r” sterującego iteracją.

Rozważmy warunek:

γ: x= q*y + r ∧ 0 ≤ r ∧ 0 ≤ y

Uwagi:

Jeżeli obliczenie algorytmu startuje z danymi wejściowymi spełniającymi
warunek początkowy

α i dochodzi do punktu końcowego, to otrzymane wyniki

spełniają warunek końcowy

β – algorytm jest częściowo poprawny

Jeżeli algorytm nie jest poprawny względem rozważanych warunków, np. dla

x = y = 0

, wówczas obliczenie tego algorytmu jest nieskończone.

Wyróżniając pewne miejsca w algorytmie, przypisuje się do nich warunki na
wartościowanie zmiennych i wykazuje, że jeżeli początkowy stan obliczania
spełnia warunek początkowy, to ilekroć obliczanie algorytmu dochodzi do
wyróżnionego miejsca, zawsze przyporządkowany temu miejscu warunek jest
spełniony przez aktualne wartościowanie zmiennych.

17

W szczególności jeżeli obliczenie dochodzi do punktu końcowego to końcowe
wartościowanie zmiennych spełnia warunek końcowy algorytmu.

Postępując w ten sposób nie można stwierdzić, czy obliczenie algorytmu w
ogóle dochodzi do punktu końcowego. Stwierdza się tylko, że jeżeli dochodzi,
to jest spełniony warunek końcowy.
Wszystkie działania algorytmu są zawsze określone. Algorytm posiada
własność określoności obliczeń.

Dowodzenie własności stopu

Algorytm K ma własność stopu względem warunku początkowego

α, jeśli

dla każdych danych wejściowych spełniających warunek

α , obliczenie

algorytmu K nie jest nieskończone.

Przy dowodzeniu zwykle stosuje się jedną z metod:

• liczników iteracji

• malejących wielkości

Dowodzenie własności stopu algorytmów metoda liczników iteracji

Brak spełnienia warunku stopu, oprócz przypadków trywialnych, może
wystąpić przy realizacji instrukcji iteracyjnej.

Jak udowodnić więc, że przykładowy algorytm postaci:
„while

γ

do K” ma własność stopu względem warunku początkowego

α

Wprowadźmy dodatkową zmienną całkowitą l, nie występującą ani w warunku

γ

ani

w instrukcji K, zmienną służącą do obliczania liczby wykonań instrukcji iterowanej K.

Zmienna l nazywa się zwykle licznikiem iteracji „while

γ

do K”

Niech c będzie stała całkowitą (zazwyczaj c = 0 lub c = 1).
Równoważny algorytm ma postać:

M: begin

l:= c

while

γ

do

begin K; l:= l + 1 end

end

Szukamy wyrażenia arytmetycznego

τ , którego wartość w trakcie realizacji

algorytmu M ograniczałaby z góry wartość zmiennej l. Zakładamy, że wartości
zmiennych występujących w termie

τ nie są zmieniane w trakcie realizacji instrukcji

iterowanej begin K; l:= l + 1 end .

18

Skoro dla każdego obliczenia algorytmu M, które rozpoczyna się stanem
spełniającym warunek

α, przy każdym sprawdzaniu warunku iteracji

γ

warunek

τ

≥

l

jest spełniony i wartość

τ jest stała, więc liczba wykonań instrukcji iterowanej

begin K; l:= l + 1 end jest skończona.

Dowodzenie poprawności algorytmów rekurencyjnych

Stosowana jest indukcja względem wielkości danych wejściowych, dla których
algorytmy są realizowane. Nie zachodzi potrzeba dzielenia całego procesu
dowodzenia poprawności algorytmu na odrębne etapy weryfikacji własności
częściowej poprawności, określoności obliczeń i stopu.

function NWD(x,y: integer): integer

var r: integer;

begin {

α

: x > 0

∧

y > 0}

r:= x mod y;

if r = 0 then NWD := y else NWD := NWD(y,r)

{

β

: NWD = (x,y)}

end

(x,y) – oznacza największy wspólny dzielnik dodatnich liczb naturalnych x i y.

Dla wykazania, że funkcja NWD jest poprawna względem warunków

α i

β

wystarczy

wykazać, że dla każdych dodatnich wartości naturalnych x i y obliczenie wywołania
funkcji NWD(x,y) dochodzi do punktu końcowego z wartością NWD = (x,y)


4.

Sprawność algorytmów

.

• Miary efektywności algorytmów.

• Złożoność obliczeniowa algorytmów.

• Złożoność pesymistyczna i średnia.

• Dolne i górne ograniczenie złożoności.

• Problemy algorytmicznie zamknięte i otwarte.

Każde wykonanie algorytmu na komputerze wymaga pewnej ilości czasu pracy, jak
również pewnej ilości miejsca pamięci.

Przykład

Rozważmy algorytm, dla którego daną wejściową jest liczbą naturalna n i w
którym liczba jednostkowych operacji wykonywanych dla danej n wynosi n!
Zakładającym że komputer wykonuje średnio 10

5

jednostkowych operacji na

sekundę i że jest do wyłącznej dyspozycji przez 24 godziny algorytm ten może
być wykonany tylko dla danej wartości n

≤

13.

Dla

2

n

ograniczenie to zwiększa się do n

≤

33.

19

Przykład

Przyjmując wcześniejsze założenia, w przypadku algorytmów, których liczba

wykonywanych operacji określa funkcja wielomianowa od wartości danej

wejściowej (rozmiaru zadania), dla algorytmów wykonujących odpowiednio

n

3

,

n

2

, n*log(n)

operacji

w czasie 24 h komputer „poradzi” sobie odpowiednio z

n = 2000 ; 90 000 ; 250*10

6

.

Znajomość czasu działania algorytmu przydaje się również wtedy, gdy chcemy
wybrać najoszczędniejszy spośród algorytmów alternatywnych.

PROBLEM

- ALGORYTM

- KOMPUTER

komputer

algorytm

10

5

10

7

n!

13 16

2

n

33 42

n

3

2000 20

000

Przykład

Dane zadanie należy rozwiązać dla danej wejściowej n = 10 000 przy
użyciu komputera, który wykonuje średnio 10

5

jednostkowych operacji

na sekundę. Do dyspozycji są 4 algorytmy wykonujące dla danej n
odpowiednio n

3

, n

2

, n*log(n) jednostkowych operacji. Algorytmy te

wykonają zadanie odpowiednio w: 10

7

s. czyli ok. 115 dni, 17 minut i 13

sekund.

Pułapka wymiarowości

Problem

Dana jest para (X, c) , gdzie

X

-

zbiór

rozwiązań dopuszczalnych

c: X R - funkcja

celu

Należy znaleźć rozwiązanie x*

∈ X takie, że

c(x*) = min c(x)

x

∈ X

20

x – podzbiór zbioru {1, 2, 3,…,n};

2

n

x – permutacja zbioru {1, 2, 3,…,n};

n!

Czasy obliczeń: (jedno wyliczenie funkcji celu trwa 1

µs)

n

n

3

2

n

n!

10

0,001 s

0,001 s

3,6 s

20

0,008 s

1,05 s

771,5 stuleci

50

0,125 s

35,7 lat

9,6*10

48

stuleci

100 1

s

4,2*10

14

stuleci

3,0*10

142

stuleci

Wpływ wzrostu mocy obliczeniowej komputera na czasy obliczeń

Rozmiar największego problemu rozwiązywanego

w ciągu godziny

Przez obecny komputer

Przez komputer 1000

razy szybszy

n

3

N

1

10*N

1

2

n

N

2

≤ N

2

+ 10

n!

N

3

≤ N

3

+ 2 (przy n

3

> 10)

Miary efektywności algorytmów

o Funkcja kosztu (funkcja złożoności czasowej, pesymistyczna złożoność

czasowa)

o Złożoność średnia, złożoność pamięciowa

21

Dany algorytm K, dla którego zbiorem danych wejściowych jest zbiór D taki, że

dla każdej danej d ze zbioru D obliczenie algorytmu K dochodzi do punktu

końcowego.

Przez t(d) oznaczana jest liczba jednostkowych operacji wykonywanych przez

algorytm K dla danej wejściowej d ze zbioru D.

Odwzorowanie t jest funkcją ze zbioru danych D w zbiór liczb naturalnych

(tzw, pełna funkcja kosztu algorytmu K).

Przykład

Algorytm sprawdzający czy dana liczba naturalna n jest liczba pierwszą.

function prime(n: integer): Boolean;
label 1, 2, 3, 4;
var p: integer; B: Boolean;
begin {

α

: n > 0 }

1: p:= 2 ; B:= true;
2: while (p*p

≤

n)

∧

B do {(B

≡∀

(q=2..p-1) n mod q

≠

0)}

begin
3: if n mod p= 0 then B:= false; p := p+1
end;
4: prime := B

{

β

: (prime

≡

∀

(q=2..n-1) n mod q

≠

0)}

end.

Uwaga:

Przykłady operacji jednostkowych: podstawienie, skok,
dodawanie, itp.

Oszacowania liczb jednostkowych operacji wykonywanych przez instrukcje
odpowiadające poszczególnym etykietom:

1) – dokładnie 2 operacje jednostkowe
2) – co najwyżej 3

√n operacji jednostkowych

3) – co najwyżej 4(

√n - 1) +1 operacji jednostkowych

4) – dokładnie 1 operacja jednostkowa

Razem wykonywanych jest co najwyżej 7

√n jednostkowych operacji

Uwaga:

W przypadku gdy n jest liczba pierwsza wykonuje się dokładnie

t(n) = 7

√

n



- 1

operacji jednostkowych

W przypadku gdy n jest kwadratem liczby pierwszej

t(n) = 7

√

n



W przypadku gdy n jest liczbą parzysta wówczas

t(n) = 14

22

Niech X dowolny zbiór, a f i g funkcje przekształcające zbiór X w zbiór liczb
rzeczywistych.
Funkcja f jest co najwyżej rzędu funkcji g , f = O(g), jeśli istnieje stała c > 0 taka,
że nierówność |f(x)|

≤ c|g(x)| zachodzi dla prawie wszystkich x

∈

X .

Pełna funkcja kosztu algorytmu prime jest, co najwyżej rzędu

√

n,

tzn.

t(n) = O(

√

n)

Funkcja f jest dokładnie rzędu funkcji g , oznaczenie

f =

Θ

(g),

jeżeli istnieją stałe

c

1

, c

2

większe niż 0 jakie, że nierówności

c

1

|g(x)|

≤

|f(x)|

≤

c

2

|g(x)|

zachodzi dla

prawie wszystkich x

∈

X .

Ilustracja

Zbiór wszystkich ciągów o długości n

Uwaga

Dolne i górne ograniczenie złożoności obliczeniowej, złożoność
pesymistyczna.

3n

2

+ 8n + 4

n

2

Złożoność obliczeniowa algorytmu porządkowania

n

liczb jest

O(n

2

)

2n + 3

2nlogn + 4n + 3

3n

2

+ 8n + 4

23

Dokładniej:

Rozmiar problemu - długość ciągu kodującego binarnie wszystkie dane problemu.

(Praktycznie – liczba danych charakteryzujących problem)

Złożoność obliczeniowa algorytmu dla danego problemu o rozmiarze n – liczba

elementarnych operacji, które musi wykonać algorytm aby przy
najbardziej niesprzyjających danych rozwiązać problem o
rozmiarze n.

Uwaga

:

Przy analizie złożoności algorytmów (czasowej złożoności) zwykle rozważa się
tzw, operacje dominujące algorytmu.

Oprócz złożoności czasowej algorytmu rozważa się również złożoność
pamięciową.

Średnia złożoność czasowa – funkcja

T(w) =

Σ

Pr

w

(d) t(d

) odwzorowująca

|d|=w

zbiór rozmiarów danych W w zbiór liczb
rzeczywistych, gdzie:

Pr

w

(d)

– prawdopodobieństwo wystąpienia

na wejściu algorytmu danej d rozmiaru w

Przykład

Dane

wejściowe algorytmu tworzy liczba naturalna n i permutacja a zbioru

liczb

{1, 2, 3,…,n}. Przyjmujmy, że rozmiarem danej d = (n,a) jest n,

tzn. |d| = n.
Przyjmując, że każda permutacja n elementowa jest jednakowo
prawdopodobna, otrzymujemy

Pr

w

(d) = 1/n!

dla każdej danej

d

rozmiaru

n.

Problemy algorytmiczne zamknięte i otwarte

• Algorytm porządkowania liczb.

• Algorytm wyznaczania kolejnych liczb pierwszych

• Algorytm sprawdzania czy dana liczba naturalna jest liczbą pierwszą

• . . .

24

6. Klasyfikacja problemów algorytmicznych

• problemy łatwo i trudno rozwiązywalne

• klasy problemów algorytmicznych

Problemy łatwo i trudno rozwiązywalne

Przykład

(problem sortowania)

Dany jest zbiór {7, 5, 6, 1, 3, 4 , 2, 9, 8, 10}. Zbiór ten należy uporządkować

(posortować) od najmniejszego do największego elementu, tzn. {1, 2, 3 , 4 , 5

, 6 , 7 , 8 , 9 , 10}. Ile, w najgorszym przypadku, należy dokonać

elementarnych porównań i przestawień elementów zbioru, aby go

uporządkować?

Przyjmując zasadę porządkowania wg. algorytmu „bąbelkowego” liczba ta nie

przekracza

2

2

2

n

n

−

, gdzie n – liczność porządkowanego zbioru. Złożoności

obliczeniową tego problemu określa funkcja O(n

2

)

Przykład (problem plecakowy)

Dany jest zbiór A = {a

i

| i = 1,n} różnych typów towarów. Każda jednostka

danego typu towaru ma tę sama objętość g

i

(wagę w

i

) oraz cenę c

i

.

Dysponujemy plecakiem o pojemności G (możemy udźwignąć W).

Ile, jakich towarów należy załadować do plecaka aby wyjść z maksymalnym

zyskiem?

Przyjmując, że jednostek każdego towaru jest ta sama ilość m, liczba

wszystkich wariantów nie przekracza m

n

. Złożoności obliczeniową tego

problemu określa funkcja O(m

n

).

PROBLEMY

DECYZYJNE

OPTYMALIZACYJNE

PROBLEMY

TRUDNE

ŁATWE

(a)

(b)

25

Przykład (problem komiwojażera)

Komiwojażer, każdego dnia odwiedza n – miast. Dane są odległości d

i,j

pomiędzy każdą para miast i i j. Startując z wybranego miasta, należy

powrócić do niego przejeżdżając przez każde z pozostałych miast tylko jeden

raz.

Która z tras jest najkrótsza?

Liczba wszystkich tras, które trzeba sprawdzić nie przekracza (n-1)!

Złożoności obliczeniową tego problemu określa funkcja O(n!)

Problemy decyzyjne i optymalizacyjne.

Spotykane problemy dzielą się też na problemy decyzyjne i optymalizacyjne.

Przyjmując konwencję, wg., której każdy problem charakteryzuje trójka

(DANE, OGRANICZENIA, PYTANIE), za problem decyzyjny uznaje się taki, w

którym pytania są formułowane w taki sposób aby udzielana na nie odpowiedź

była postaci TAK lub NIE.

Z kolei za problem optymalizacyjny przyjmuje się taki, którego pytanie jest

sformułowane w taki sposób, aby udzielana na nie odpowiedź dotyczyła

ekstremum pewnej funkcji celu.

Z

każdym problemem optymalizacyjnym można związać problem decyzyjny.

Przykład

Problem plecakowy (problem optymalizacyjny)

Dany jest zbiór A = {a

i

| i = 1,n} różnych typów towarów. Każda jednostka

danego typu towaru ma tę sama objętość g

i

(wagę w

i

) oraz cenę c

i

.

Dysponujemy plecakiem o pojemności G (możemy udźwignąć W). Ile, jakich

towarów można załadować do plecaka aby wyjść z maksymalnym zyskiem?

Przestrzeń stanów (wartości zmiennej decyzyjnej) PS = N

0

x N

0

x...x N

0

obejmuje stan początkowy

X = (0, 0, ..., 0) oraz stan końcowy

X* = (x

1

,x

2

,...,x

n

) spełniający warunki funkcji celu, tzn.,

26

n

X*= max(

Σ x

i

c

i

)

i=1

n

Przy ograniczeniach

Σ x

i

g

i

≤ G

i=1

n

(

Σ x

i

w

i

≤ W )

i=1

Przykład

Problem plecakowy (problem decyzyjny)

Przy identycznym sformułowaniu i tych samych ograniczeniach funkcja celu
ma postać:

n

Σ x

i

c

i

≤ F

i=1

Uwaga

Zmniejszenie złożoności obliczeniowej można uzyskać bądź to poprzez
odpowiednie przedefiniowanie problemu, bądź też przeformułowanie problemu
(zmieniające strukturę danych).

Przykład

(Zasada dziel i zwyciężaj)

Zbiór danych jest dzielony na dwa rozłączne zbiory, prawie równoliczne, dla
których w dwóch następnych krokach są rozwiązywane podobne problemy.
Postępowanie takie pozwala zmniejszyć złożoność obliczeniową algorytmu.

Problem sortowania. Dany jest zbiór {7, 5, 6, 1, 3, 4 , 2, 9, 8, 10}. Zbiór ten
należy uporządkować (posortować) od najmniejszego do największego
elementu, tzn. {1, 2, 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10}.

Przyjmując zasadę porządkowania wg. algorytmu „bąbelkowego” złożoność
obliczeniowa dana jest funkcją n

2

/2 - n/2,

czyli: 100/2 -10/2 = 45 porównań.

W przypadku gdy zbiór ten wstępnie podzielimy na dwa, tzn. {7, 5, 6, 1, 3} ,
{4 , 2, 9, 8, 10} to na wynikową złożoność obliczeniową składają się trzy
składniki:
(n/2)

2

/2 - (n/2)/2 + (n/2)

2

/2 - (n/2)/2 +

n

a zatem

5

2

/2 - 5/2

+

5

2

/2 - 5/2

+

10

5

2

- 5 + 10 = 25 - 5 + 10 = 30 porównań.

27

Czy dalszy podział zbioru wyjściowego na 4 lub 6 podzbiorów zmniejszyłby
złożoność obliczeniową?

Problem –

Specyfikacja problemu

–

Algorytm

Schemat postępowania przy rozwiązywaniu problemów kombinatorycznych

Próba znalezienia algorytmu wielomianowego

sukces

brak

sukcesu

alg. o złożoności (n

k

)

próba

zmniejszenia

próba

wykazania

wykładnika

k

NP-zupełności

brak

sukcesu

sukces

konstrukcja

alg.

przybliżonego

Metody przeszukiwania

Metody deterministyczne (wolne od przypadku) są realizacjami schematu
ogólniejszego – metody prób i błędów.

Algorytm niedeterministycznych – algorytm realizujący techniki „prób i
błędów” składający się z dwóch faz: niedeterministycznej, polegającej na
odgadywaniu, i deterministycznej, polegającej na sprawdzaniu. Algorytm
niedeterministyczny ma złożoność wielomianową, gdy taka złożoności ma
odpowiednia procedura weryfikacji.

Klasy problemów

Klasa problemów typu P – klasa problemów rozpoznawania, które dadzą się

rozwiązać za pomocą wielomianowych algorytmów
deterministycznych.

28

Klasa problemów typu NP – klasa problemów rozpoznawania, które dadzą się

rozwiązać za pomocą wielomianowych algorytmów
niedeterministycznych.

Uwagi:

• P

⊂

NP

• Trudno sobie wyobrazić aby metodę prób i błędów – nawet prz założeniu

szybkiej weryfikacji hipotez - można było zawsze zastąpić szybkim
algorytmem deterministycznym. Stąd hipoteza:

P

≠

PN.

Problem NP-zupełny – problem należący do takiej klasy problemów, że jeżeli

udałoby się dla jednego problemu z tej klasy zbudować algorytm
wielomianowy to algorytm taki istniałby dla każdego pozostałego
problemu z tej klasy.
Gdyby natomiast wykazano, że nie istnieje algorytm wielomianowy dla
jednego, to nie istniałby dla każdego problemu z tej klasy.

NP – Nondeterministic Polynomial

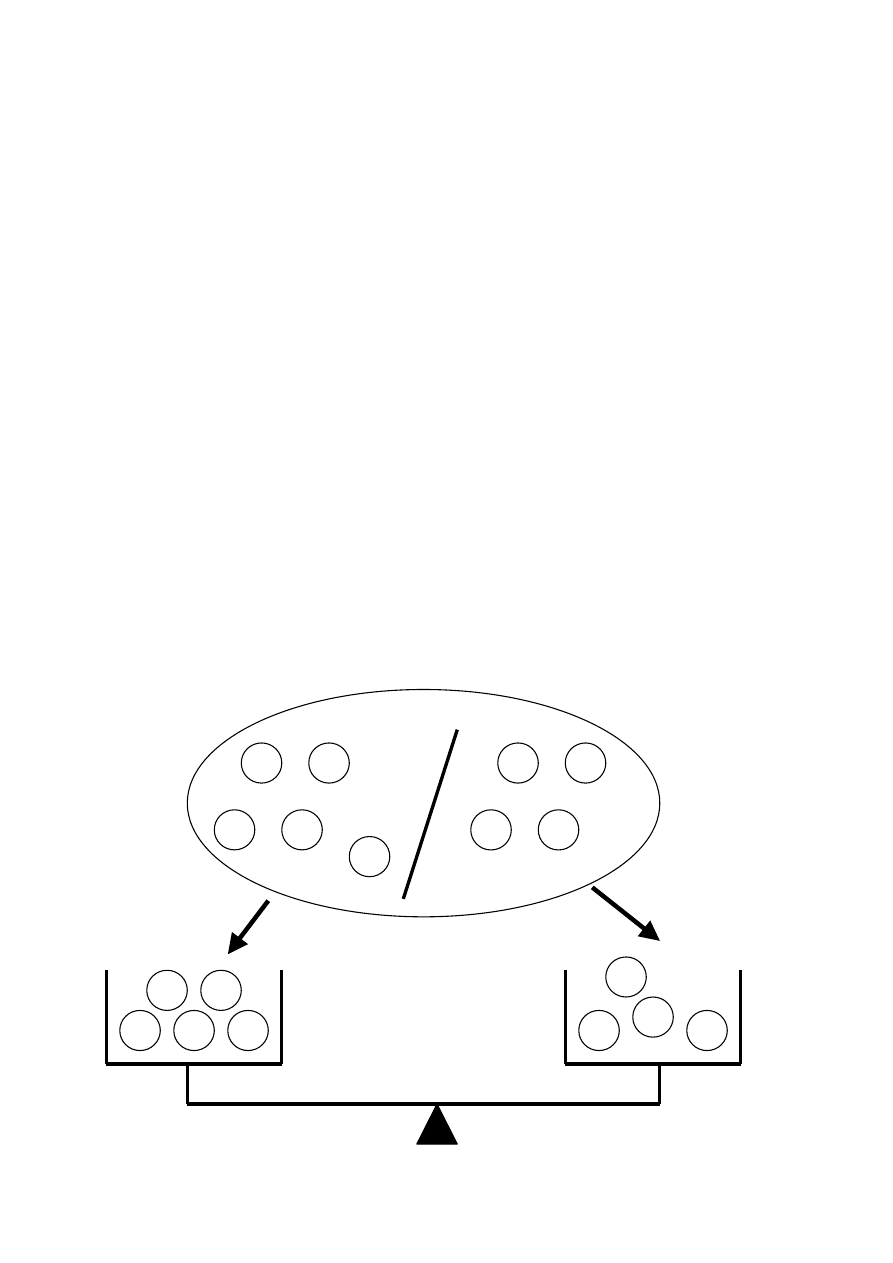
Przykład (najprostszy problem NP-zupełny)

Problem podziału n liczb naturalnych a

1

, a

2

, …, a

n

. Czy istnieje podzbiór

A

⊂ N = {1,2,3,…,n} taki, że

Σ

a

i

=

Σ

a

i

i

∈A i∈N\A

2

3

4

1

3

2

N = 9

N\A

A

3

2

2

3

4

1

3

3

2

3

5

3

29

Nikt nie podał algorytmu, którego liczba elementarnych kroków zależy wielomianowo
od liczby kulek n.

7. Klasyfikacja problemów algorytmicznych

• dowodzenie NP-zupełności

Metodyka dowodzenia NP-zupełnosci

1. Przejść z badanego problemu optymalizacyjnego

Π

1

na problem

decyzyjny.

Problem optymalizacyjny:

Znajdź x*

∈ X takie, że c(x*) = min c(x)

x

∈X

Problem decyzyjny:

Znajdź x*

∈ X takie, że c(x*) ≤ y

2. Wielomianowa weryfikacja:

Pokazać, że dla każdego rozwiązania x oraz „poziomu” y, sprawdzenie

„czy

x

∈ X

oraz

c(x*)

≤ y”

można wykonać algorytmem wielomianowym od rozmiaru badanego

problemu decyzyjnego

Π

1

.

3.

Znaleźć „zbliżony” do problemu

Π

1

, problem

Π

2

, o którym wiemy, że

jest NP-zupełny. Pokazać, że problem

Π

2

jest wielomianowo transformowany do

problemu

Π

1

.

D(

Π) -

zbiór wszystkich indywidualnych problemów (instancji),

problemu

Π

.

Y(

Π) -

zbiór tych instancji problemu

Π,

dla których odpowiedź brzmi

„TAK”;

Y(

Π) ⊂ D(Π)

.

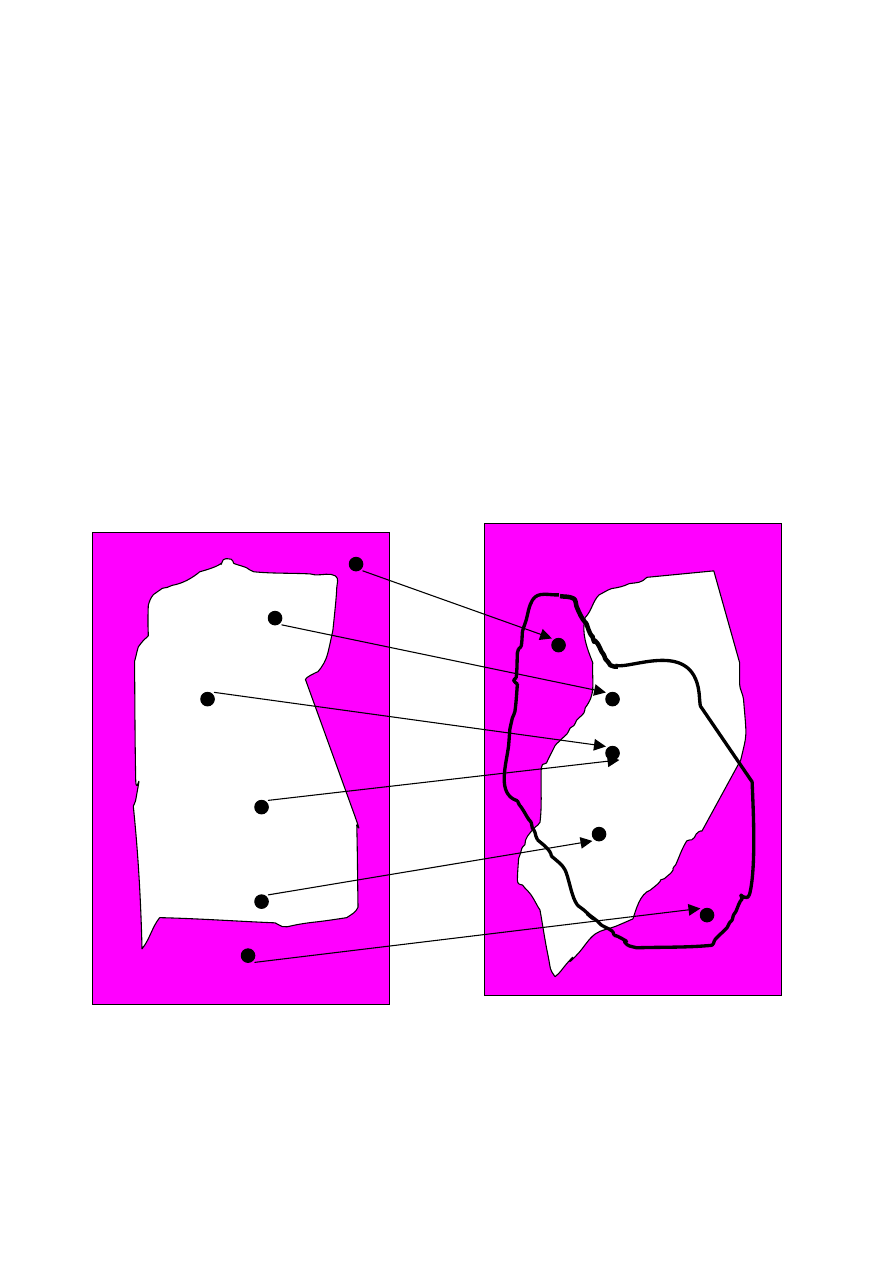
Transformacja wielomianowa pomiędzy problemami

Π

2

i

Π

1

.

f: D(

Π

2

) Æ D(

Π

1

)

30

• złożoność wyznaczenia wartości

f(I)

dla każdej instancji

I, I

∈ D(Π

2

),

jest ograniczona przez wielomian od rozmiaru tej instancji

• odpowiedź dla instancji I problemu

Π

2

brzmi „TAK” wtedy i tylko wtedy,

gdy dla instancji

f(I)

problemu

Π

1

też brzmi „TAK”

„TAK” dla I z

Π

2

⇔ „TAK” dla f(I) z Π

1

Ilustracja transformacji wielomianowej

Problem NP-zupełny

nasz

problem

D(

Π

2

)

D(

Π

1

)

Y(

Π

2

)

Y(

Π

1

)

31

Przykład

Problem

plecakowy

(załadunku)

Π

1

- n elementów (elementów N = {1, 2, 3,…,n} ); element j

∈ N jest

określony przez jego ciężar c

j

i wartość w

j

,

- ciężar plecaka po załadowaniu nie może przekroczyć C.

Należy tak załadować plecak, żeby miał największą wartość

Znaleźć podzbiór

A

⊂ N

taki, że

Σ w

i

Æ max

i

∈A

Σ c

i

≤ C

i

∈A

Problem decyzyjny

Czy istnieje dla poziomu W (zadanej dolnej wartości plecaka), podzbiór elementów
A

⊂ N taki, że

Σ w

i

≥

W

1)

i

∈A

Σ c

i

≤ C

2)

i

∈A

2. Wielomianowa weryfikacja:

Rozmiar problemu

Π

1

- n

Dla danego poziomu W oraz podzbioru

A

⊂ N

sprawdzenie, czy

zachodzą nierówności 1) i 2) wymaga

2(n-1) - dodawań
2

- porównań

Łącznie 2n elementarnych porównań

Oznacza to, że możliwa jest wielomianowa weryfikacja.

32

3. Wielomianowa transformacja

:

Znany jest problem NP-zupełny:

Problem podziału zbiór

Π

2

- n liczb naturalnych a

1

, a

2

, a

3

,…,a

n

Transformacja

Π

2

Π

2

wartość ciężar

S =

Σ a

j

Π

2

Π

2

Σ a

i

=

Σ a

i

⇔

Σ a

i

≥ ½ Σ a

i

i

∈A i∈N\A

i

∈A i∈N

Σ a

i

=

Σ a

i

i

∈A i∈N\A

Σ w

i

≥

W

i

∈A

Σ c

i

≤ C

i

∈A

Σ a

i

=

Σ a

i

i

∈A i∈N\A

Σ a

i

≥ ½ Σ a

i

i

∈A i∈N

Σ a

i

≤ ½ Σ a

i

i

∈A i∈N

a

1

a

2

.
.
.

a

n

w

1

c

1

w

2

c

2

.
.
.

w

n

c

n

w

1

=

c

1

= a

1

w

2

=

c

2

= a

2

.
.
.

w

n

= c

n

= a

n

f

W C

W = C = S/2

33

8. Prymitywne modele algorytmiczne.

- maszyna Turinga i jej warianty.
- przykłady implementacji wybranych algorytmów.

Turing zauważył, że każdy w pełni mechaniczny proces obliczeń
składa się z następujących operacji:

- odczytywanie symboli,
- wymazywanie i zapisywanie symboli
- zapamiętywanie i przenoszenie informacji

Obserwacje te doprowadziły do poniższej konstrukcji:

JEDNOTAŚMOWEJ DETERMINISTYCZNEJ MASZYNY TURINGA
(maszyny Turinga)

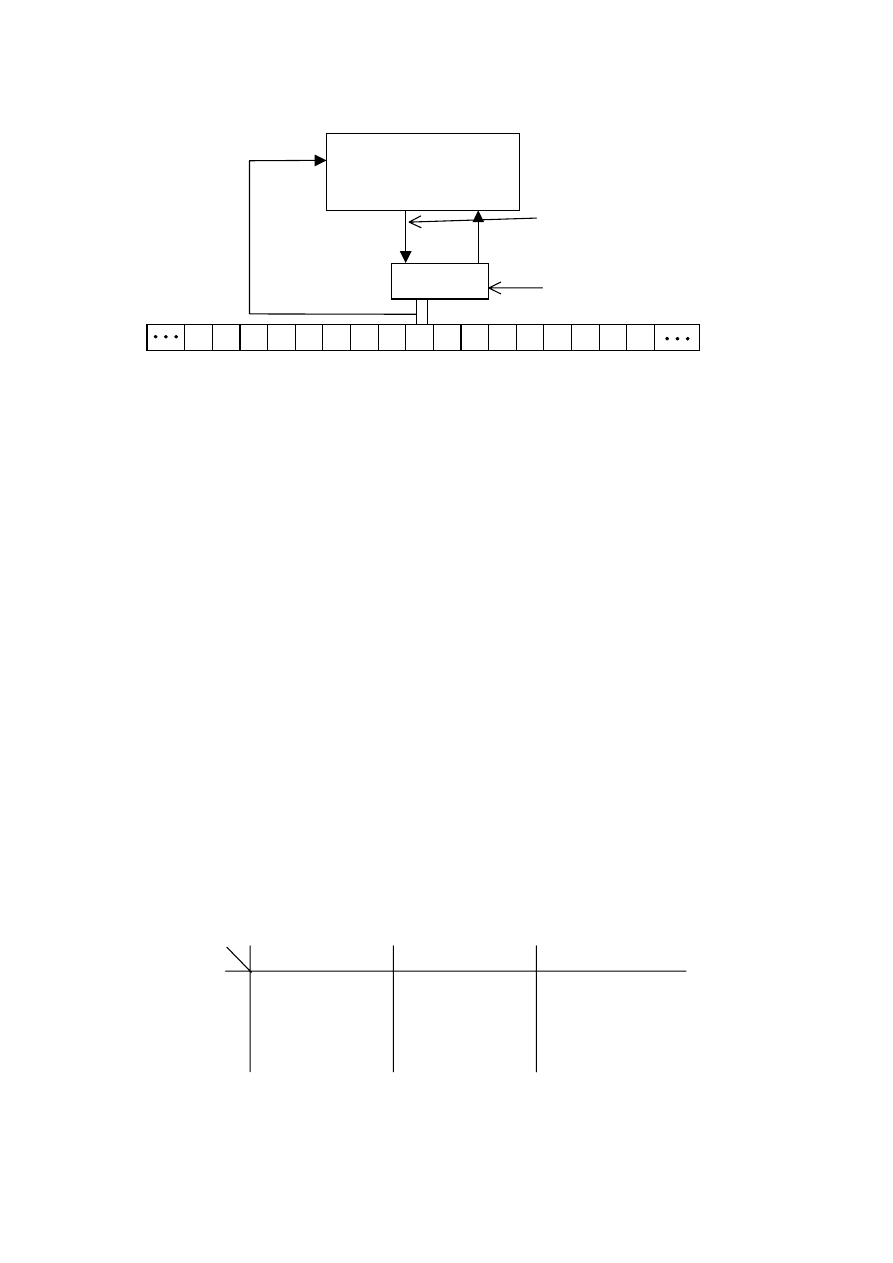
Maszyna Turinga – składa się z taśmy, głowicy pisząco-czytającej oraz urządzenia

sterującego.
Obustronnie nieskończona taśma podzielona jest na klatki, z których każda
zawiera najwyżej jeden symbol skończonego alfabetu, zwanego alfabetem
roboczym maszyny.
W dowolnym momencie prawie wszystkie klatki są puste – zawierają element
wyróżniony b (ang. blank – pusty).
Głowica ma w polu swojego działania zawsze dokładnie jedna klatkę.
Urządzenie sterujące pełni funkcje pamięcią; w każdym momencie znajduje
się ono w jednym ze skończonej liczby stanów.

Maszyna Turinga pracuje w czasie dyskretnym, tzn. kolejne ruchy numerowane

mogą być liczbami naturalnymi.
Każdy ruch jest jednoznacznie określony przez aktualny stan urządzenia
sterującego i odczyt głowicy.
Pojedynczy ruch składa się z trzech operacji:

- Symbol odczytywany przez głowicę może być zastąpiony nowym

symbolem,

- Urządzenie sterujące może przejść w nowy stan
- Głowica musi przesunąć się o jedną klatkę w lewo (L) lub w prawo (P)

W zbiorze stanów wyróżnia się stan początkowy S

o

(START) i stan końcowy (HALT).

Przejściu maszyny w stan {S

Y

, S

N

} (HALT), wyjątkowo, nie musi towarzyszyć

przesunięcie głowicy.

Maszyna Turinga znajduje się w konfiguracji początkowej, jeśli:

- Urządzenie sterujące znajduje się w stanie START
- Niepuste klatki tworzą skończony odcinek taśmy
- Głowica odczytuje zawartość pierwszej niepustej klatki.

Zawartość niepustej części taśmy w momencie rozpoczęcia obliczeń tworzy ciąg
zwany SŁOWEM wejściowym (lub DANYMI wejściowymi) maszyny.

34

Przykład

Rozważmy maszynę obliczająca funkcję

f(x) = x + 1

w układzie dwójkowym.

Oznacza to, że jeśli w konfiguracji początkowej niepusta część taśmy była
zapisem dwójkowym liczby

x

, to po zatrzymaniu niepusta część taśmy będzie

zapisem

x + 1

.

Symbol

Stan

0 1 b

START 0 START R 1 START R LEFT L

LEFT

1 HALT

0 LEFT L

1 HALT

Uwaga

START: Jeżeli odczytasz b, przesuń głowice w lewo i przejdź do LEFT; w

przeciwnym razie przesuń głowicę w prawo i powtórz START (szukanie
końca x).

LEFT: Jeżeli odczytasz 1, zastąp ją przez 0, przesuń głowicę w lewo i powtórz

LEFT, w przeciwnym razie symbol odczytany zastąp jedynką i
zatrzymaj się.

START ..b b1 1 b b...

START ...b b1 1 b b...

START

...b b1 1 b b...

LEFT

...b b1 1 b b...

LEFT

...b b 1 0 b b...

LEFT

...b b 0 0 b b...

START

...b 1 0 0 b b...

Złożoność maszyny Turinga - funkcja wyrażająca maksymalna liczbę ruchów

maszyny w zależności od rozmiaru danych wejściowych (tzn. liczby
klatek przez nie zajmowanych).

Maszyna Turinga jest automatem reagującym na sygnały wejściowe i zmieniającym
swój stan oraz wytwarzającym sygnał wyjściowy. Jest urządzeniem sterującym
ruchem głowicy zapisująco-odczytującej G, odbierającej sygnał wejściowy z komórek
taśmy T oraz programującym swoje działanie poprzez przekodowanie symboli
wejściowych i tworzenie nowych ciągów symboli

35

Działanie maszyny określa:

- Skończony zbiór symboli taśmy

Γ, podzbiór symboli wejściowych Σ oraz

wyróżniony symbol pusty b

- Skończony zbiór stanów S, zawierający wyróżniony stan początkowy S

0

i dwa

wyróżnione stany końcowe S

y

(odpowiedź tak) oraz S

n

(odpowiedź nie)

- Program maszyny zadany funkcją przejść

σ(S\{S

y

,S

n

}) x

Γ → S x Γ x {-1,1}

- Dane wejściowe stanowi słowo x

∈ Σ, elementy którego są w kolejnych

komórkach taśmy (w każdej komórce dokładnie jeden symbol). Pozostałe
komórki zawierają początkowo symbol pusty.

W chwili startu głowica odczytuje zawartość pierwszej komórki. Jeżeli
maszyna jest w stanie s

∈

S\{S

y

,S

n

} a w komórce nad którą znajduje się

głowica jest symbol

γ∈Γ

, to maszyna wykonuje czynność określoną przez

funkcję przejścia

σ

(S,

γ

) = (s’,

γ

’,

∆

). Oznacza to, że głowica w miejsce

symbolu

γ

wpisuje symbol

γ

’ , przesuwa się o jedną komórkę w lewo

∆ = -1, w

prawo

∆

= 1, stan maszyny zmienia się na s’. Wykonanie programu

realizowane jest do chwili, w której maszyna znajdzie się w jednym z dwóch
stanów S

y

lub S

n

.

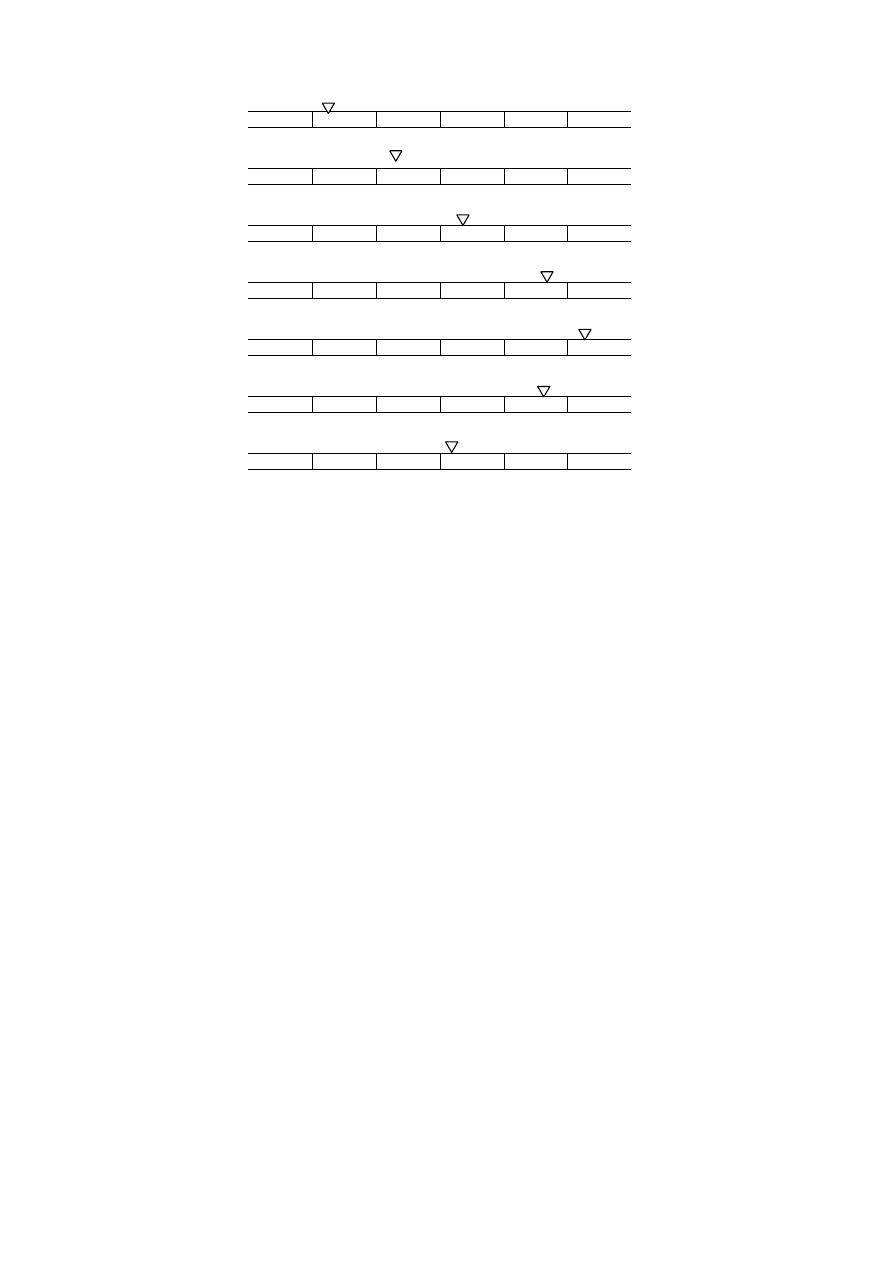
Przykład

Należy napisać program umożliwiający maszynie sprawdzanie czy dana liczba
naturalna jest liczbą parzystą. Łatwo zauważyć, że jeżeli liczbę te zapiszemy
w systemie dwójkowym to wystarczy sprawdzić czy ostatnia jej pozycja jest 0.
Przyjmijmy, że

Γ

= {0,1,b},

Σ

- {0,1} , S = {S

0

,S

1

,S

y

,S

n

}. Rozważmy program

zadany funkcją przejść.

Działanie programu przetestujmy na przykładzie liczby 13. W zapisie dwójkowym
mamy zatem słowo: 1101. Wykonanie programu zilustrowane zostało na rysunku.

Automat

S

∪{S

0

}

G

Τ

∆

Skończony

alfabet

symboli

Γ

Sterowanie (przesuwnie)

Drukowanie nowego

symbolu

S

S

0

S

1

x

0 1

b

(S

0

,0,+1)

(S

y

,b,-1)

(S

0

,1,+1)

(S

n

,b,-1)

(S

1

,b,-1)

(S

0

,b,+1)

36

W podobny sposób można zaproponować programy wykrywające
parzystość liczby, jej podzielność, itp.

Każda

maszyna Turinga jest abstrakcyjnym modelem jednofunkcyjnego komputera

o potencjalnie nieskończonej pamięci

NIEDETERMINISTYCZNA MASZYNA TURINGA – stan maszyny oraz odczyty

głowic nie określają ruchu w sposób jednoznaczny.
W szczególności, oznacza to, że maszyna rozpoczynając pracę nad
ustalonym słowem wejściowym, może przy pewnym wariancie obliczeń
zakończyć prace w stanie S

Y

, przy innym w stanie S

N

, albo też prowadzić

obliczenia w nieskończoność.

Problem stopu – Dana jest maszyna Turinga. Dla jakich danych wejściowych

praca tej maszyny zakończy się po skończonym czasie?

b 1 1 0 1 b

b 1 1 0 1 b

b 1 1 0 1 b

b 1 1 0 1 b

b 1 1 0 1 b

b 1 1 0 1 b

b 1 1 0 b b

S

0

S

0

S

0

S

0

S

0

S

1

S

n

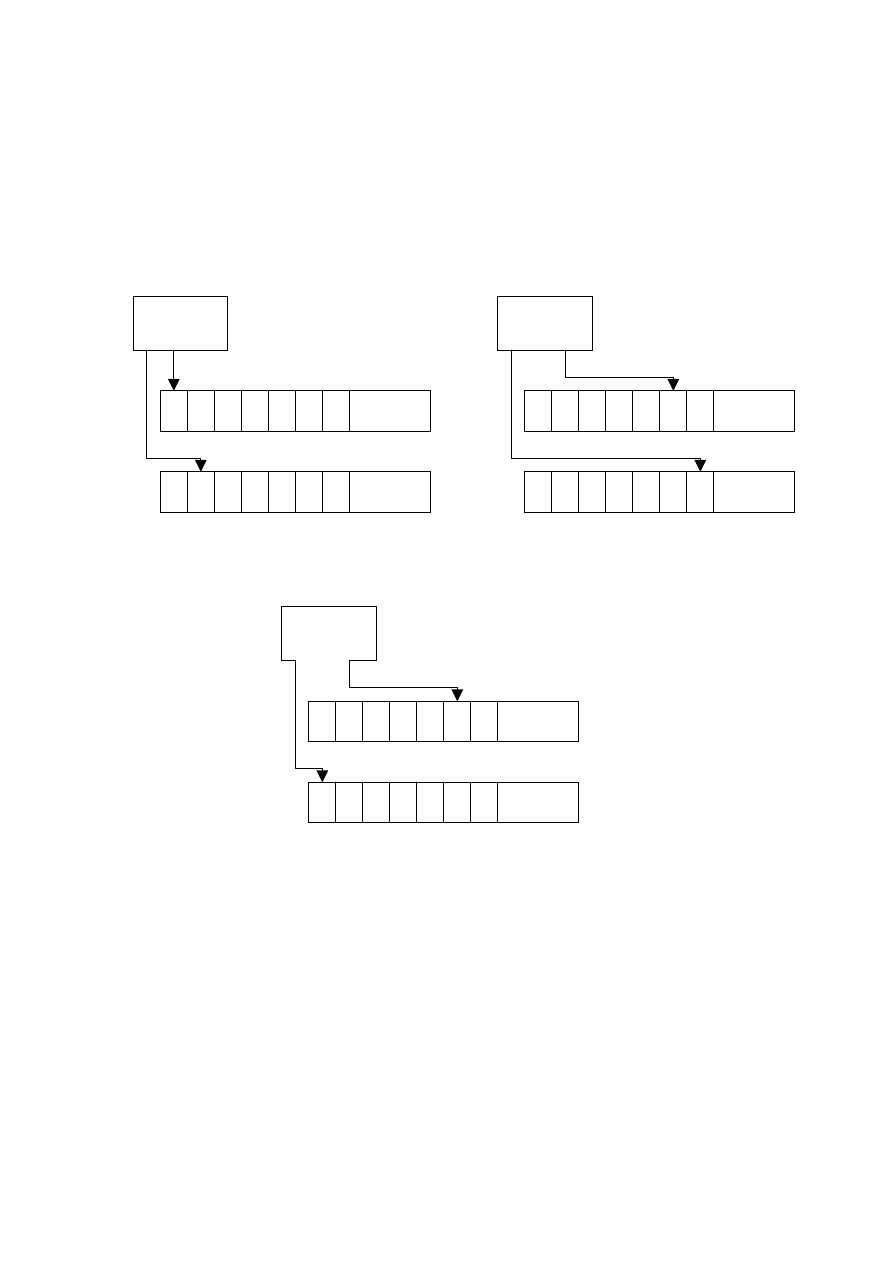
37

Dwutaśmowa maszyna Turinga

Przykład

Rozpoznawanie palindromów (słowa czytane tak samo od przodu jak i
od tyłu, np. Ala , 0100010) nad alfabetem

{0, 1}.

1. Pierwsza klatka taśmy 2 oznaczana jest specjalnym symbolem

X , i całe

słowo wejściowe jest kopiowane z taśmy 1 na taśmę 2.

2. Głowica taśmy 2 przesuwa się do symbolu

X

3. Iteracyjnie głowica taśmy 2 przesuwa się o jedna klatkę w prawo, a
głowica taśmy 1 o jedna klatkę w lewo oraz odpowiednie symbole czytane
przez głowice są porównywane.

Jeżeli słowo jest palindromem, maszyna przechodzi do stanu końcowego, w
przeciwnym razie maszyna znajdzie się w stanie, dla którego funkcja przejścia
jest już nie określona i nie może wykonać kolejnego kroku.

q

0 1 1 1 0 b b . . .

b b . . .

0 1 1 1 0 b b . .

q

x 0 1 1 1 0 b .

0 1 1 1 0 b b . .

q

x 0 1 1 1 0 b

38

9. PRYMITYWNE MODELE ALGORYTMICZNE.

- Teza Churcha-Turinga.

Problem stopu – Dana jest maszyna Turinga. Dla jakich danych wejściowych praca
tej maszyny zakończy się po skończonym czasie?

Twierdzenie Turinga o

NIEROZSTRZYGALNOŚCI PROBLEMU STOPU (1935)

Problem stopu dla dostatecznie skomplikowanej maszyny
Turinga jest nierozstrzygalny.

Przykład

Dane:

Równanie diofantyczne

n zmiennych.

Program: Generuj kolejno uporządkowane n-tki liczb całkowitych.

Zatrzymaj się jeśli któraś z nich okaże się rozwiązaniem
równania.

Uwaga

Rozstrzygnięcie problemu stopu w tym wypadku zakłada
umiejętność rozstrzygania istnienia rozwiązania całkowitego (dla
dowolnego równania diofantycznego).

Przykład

∃x ∀y (x=y ∧ x∨ y)

dziedzina liczb naturalnych / dziedzina liczb rzeczywistych

∀x ∃ y (y * y = x)

obie

dziedziny

Twierdzenie Tarskiego o

ROZSTRZYGALNOŚCI ELEMENTARNEJ ARYTMETYKI LICZB
RZECZYWISTYCH (1951)

Istnieje algorytm pozwalający o dowolnym zdaniu elementarnej
arytmetyki rozstrzygnąć czy jest ono prawdziwe w zbiorze liczb
rzeczywistych.

39

Twierdzenie Churcha o

NIEROZSTRZYGALNOŚCI ELEMENTARNEJ ARYTMETYKI LICZB
NATURALNYCH (1936)

Nie istnieje algorytm, który o dowolnym zdaniu elementarnej
arytmetyki pozwalałby rozstrzygać, czy jest ono prawdziwe w
zbiorze liczb naturalnych

Przykład

Czy równanie

x

2

– 2y

3

= 1

ma rozwiązanie w zbiorze liczb

całkowitych; wystarcza sprawdzić czy któreś z poniższych zdań jest
prawdziwe w zbiorze liczb naturalnych

∃x ∀y (

x

2

– 2y

3

= 1) ,

∀x ∀y (

x

2

– 2y

3

= 1)

Uwaga

Istnienie algorytmu oznacza teoretyczną rozstrzygalność problemu.

Twierdzenia Churcha i Turinga ukazują obiektywne ograniczenia metod
algorytmicznej – matematyki zautomatyzować się nie da.

Jaki jest zatem związek maszyny Turinga z intuicyjnym pojęciem algorytmu.

TEZA CHURCHA

W obrębie liczb naturalnych intuicyjne pojecie algorytmu
może być utożsamiane z pojęciem maszyny Turinga

Oznacza to, że każdy problem rozwiązywalny algorytmicznie może być rozwiązany
na pewnej maszynie Turinga. I oczywiście na odwrót.

Teza Churcha nie jest twierdzeniem: postuluje ona bowiem zgodność formalnej
definicji z intuicją. Oznacza to, że nigdy nie będziemy jej w stanie udowodnić z
zachowaniem rygorów matematycznej ścisłości.

40

10 JĘZYKI SYSTEMÓW INFORMACYJNYCH.

- System informacyjny.
- Składania i semantyka języka.
- Reguły przekształcania termów.

SYSTEM INFORMACYJNY

• Skończony zbiór obiektów X, i skończony zbiór atrybutów A.
• Z każdym atrybutem a

∈

A związany jest zbiór jego wartości V

a

nazywany

dziedziną atrybutu a.

• Przyjmuje się, że dziedzina każdego atrybutu jest co najmniej dwuelementowa

• System opisywany jest funkcją dwuargumentową g, która każdemu obiektowi

x

∈

X i atrybutowi a

∈

A przyporządkowuje wartość v należącą do dziedziny

V

a

atrybutu a.

System informacyjny jest czwórka uporządkowaną:

S = (X, A, V, g)

gdzie:
X – skończony zbiór obiektów
A – skończony zbiór atrybutów
V =

∪

V

a

(a

∈

A)

V

a

– dziedzina atrybutu a w systemie S

V

a

= { v

∈

V | dla których istnieje a

∈

X, takie że g(x,a) = v}

g – funkcja całkowita (określona dla wszystkich wartości argumentów x oraz a,

g: X x X

Æ

V ; przy czym g(x,a)

∈

V

a

dla każdego x

∈

X oraz a

∈

A.

Przykład

System informacyjny gdzie obiektami są ludzie a atrybutami ich nazwiska,
imiona, itd.

X NAZWISKO

IMIĘ MIEJSCE

URODZENIA

ROK
URODZENIA

STAN
CYWILNY

X

1

Kowalski Jan

Kraków 1958

kawaler

X

2

Nowak Jerzy Warszawa

1930

Wdowiec

X

3

Lipinski Gabriel Łódź 1960 żonaty

. . .

. . .

. . .

. . .

. . .

. . .

X

336

Baran

Łukasz Gdańsk 1977

kawaler

Deskryptor

– para (a,v), gdzie a – atrybut, v

∈

V

a

wartość atrybutu a należąca do

jego dziedziny.

Przykład

(NAZWISKO,Kowalski), (KOLOR OCZY, niebieski), itp.

41

Informacja

o obiekcie x w systemie S (równoważnie: dane o obiekcie)

g

x

(a) = g(x,a).

Informacją o obiekcie w danym systemie S jest po prostu zbiór wartości
wszystkich atrybutów obiektu w danym systemie.

Przykład

NAZWISKO IMIĘ MIEJSCE

URODZENIA

ROK
URODZENIA

STAN
CYWILNY

g

x2

Nowak Jerzy Warszawa

1930

Wdowiec

Opisem obiektu

x w systemie S nazywamy zbiór deskryptorów wyznaczany

przez informacje o obiekcie x.

WŁASNOŚCI SYSTEMÓW INFORMACYJNYCH

Oprócz pojęcia informacji o obiekcie systemu skorzystajmy z pojęcia informacji w
systemie.

Informacja w systemie - każda funkcja

ψ

o argumentach w zbiorze atrybutów A

oraz o wartościach należących do V, taka że

ψ

(a)

∈

V

a

Wszystkich możliwych (różnych) informacji w systemie jest

∏

card (V

a

)

a

∈

A

Przykład

Jeżeli w systemie występują trzy atrybuty

a

1

, a

2

, a

3

oraz atrybut

a

1

może

przyjmować dwie wartości, atrybut a

2

- trzy wartości, atrybut a

3

– również trzy

wartości, to system taki ma

2* 3* 3 = 18 różnych informacji.

Informacją w systemie mogą być np. opisy:

(a

1

,v

1

), (a

2

,v

2

), (a

3

,v

3

)

(a

1

,u

1

), (a

2

,u

2

), (a

3

,u

3

)

(a

1

,w

1

), (a

2

,w

2

), (a

3

,w

3

)

Uwaga

Każda informacja

ψ

wyznacza pewien zbiór obiektów X

ψ

, takich że

X

ψ

= {x

∈

X |

ψ

x

=

ψ

}

tzn. obiektów mających w systemie jednakowa informacje (jednakowy opis).

Przedmioty o tym samym opisie są nierozróżnialne w systemie S (są
identyczne).

Przykład

42

• Każda informacja dotyczy tylko jednego obiektu – systemy telefoniczne

• Danemu opisowi odpowiada kilka obiektów – systemy biblioteczne

• Danej informacji nie odpowiada żaden obiekt w systemie - informacja pusta

X

Ψ

=

∅

System informacyjny zupełny (kompletny) – gdy każda informacja jest nie pusta.


System informacyjny selektywny – gdy każdej informacji odpowiada co najwyżej

jeden obiekt.

Przykład

System informacji telefonicznej jest selektywny, natomiast system informacji
bibliotecznej (czy patentowej) jest na ogół nieselektywny.

Przykład

Niech system informacyjny S = (X,A,V,g), w którym

X = {x

1

, x

2

, x

3

, x

4

}

A = {a, b , c}
V

a

= {p

1

, p

2

}

V

b

= {q

1

, q

2

, q

=3

}

V

c

= {r

1

, r

2

, r

3

}

Funkcja g jest określona za pomocą tablicy

X a b c
x

1

p

1

q

2

r

1

x

2

p

1

q

3

r

2

x

3

p

1

q

2

r

1

x

4

p

2

q

1

r

3

Funkcja

ψ

taka, że

ψ

(a) = p

1

,

ψ

(b) = q

2

,

ψ

(c) = r

1

lub opis (a,p

1

), (b,q

2

), (c,r

1

)

jest informacją w systemie , oraz X

ψ

= {x

1,

x

3

}

Patrz tabela lub poniższe wyliczenia

X

ψ

= {x

∈

X | g

x

=

ψ

} =

= {x

∈

X |

∀

(a

∈

A) g

x

(a) =

ψ

(a)} =

=

∩

({x

∈

X | g(x,a) =

Ψ

(a)} =

a

∈

A)

= {x

∈

X | g(x,a) = p

1

}

∩

{x

∈

X | g(x,b) =q

2

}

∩

{x

∈

X | g(x,c) = r

1

} =

43

= {x

1

, x

2

, x

3

}

∩

{x

1

, x

3

}

∩

{x

1

, x

3

} =

= {x

1

, x

3

}.

System ten nie jest ani selektywny ani kompletny. Obiekty x

1

, x

3

mają jednakową

informację w tym samym systemie oraz istnieją w nim informacje, którym nie
odpowiadają żadne obiekty w systemie, np. (a,p

1

), (b,q

1

), (c,r

1

).

RÓWNOWAŻNOŚĆ OBIEKTÓW W SYSTEMIE

Wprowadźmy dwie relacje dwuargumentowe

Obiekty x,y

∈

X są nierozróżnialne w systemie S ze względu na atrybut a

∈

A

(symbolicznie x ~

a

y ) wtedy i tylko wtedy, gdy g

x

(a) = g

y

(a).

Obiekty x,y

∈

X są w systemie S nierozróżnialne ze względu na każdy atrybut a

∈

A

(albo krótko: są nie rozróżnialne w systemie S) symbolicznie x ~

S

y lub krótko x ~ y

wtedy i tylko wtedy, gdy g

x

= g

y

.

Przykład

Obiekty x

1

, x

4

są rozróżnialne ze względu na atrybut a, ponieważ

g

x1

(a) = g

x2

(a).

Natomiast obiekty x

1

, x

3

są nierozróżnialne ze względu na każdy atrybut

systemu, ponieważ g

x1

= g

x2

.

Własność

Dla każdego systemu informacyjnego S= {X, A , V, g} relacje ~

a

i ~ są

relacjami równoważności określonymi na zbiorze obiektów X i ponadto
spełniają one warunek

~

S

=

∩

~

a

(a

∈

A)

Uwaga

• Każda relacja równoważności dzieli zbiór, na którym jest określona, na

rozłączne klasy – bloki

• Bloki podziału wyznaczonego przez relację ~

S

nazywane są blokami

(zbiorami) elementarnymi systemu informacyjnego S.

Przykład

Niech system informacyjny S = (X, A, V, g), w którym

X = {x

1

, x

2

, x

3

, x

4

, x

5

, x

6

}

A = {a, b}
V

a

= {p

1

, p

2

}

V

b

= {q

1

, q

2

}

44

Funkcja g jest określona za pomocą tablicy

X a b
x

1

p

1

q

1

x

2

p

1

q

1

x

3

p

1

q

2

x

4

p

2

q

1

x

5

p

2

q

1

x

6

p

2

q

2

Występują zatem następujące podziały



Atrybut a dzieli zbiór X na bloki

B

1

= {x

1

, x

2

, x

3

}

B

2

= {x

4

, x

5 ,

x

6

}

Atrybut

b dzieli zbiór X na bloki

B

3

= {x

1

, x

2

, x

4

, x

5

}

B

4

= {x

3

,

x

6

}

Podział odpowiadający iloczynowi podziałów ~

a

i ~

b

składa się z bloków

B

5

= {x

1

, x

2

}

B

6

= {x

4

, x

5

}

B

7

= {x

3

}

B

8

= {x

6

}

Bloki B

5

– B

8

sa blokami elementarnymi

x

1

x

2

x

3

x

1

x

2

x

3

x

1

x

2

x

3

∩

=

x

4

x

5

x

6

x

4

x

5

x

6

x

4

x

5

x

6

~

a

~

b

~

a

∩ ~

b

45

Uwaga

Każdy system informacyjny wyznacza jednoznacznie pewien podział zbioru
obiektów (a więc pewną ich klasyfikację) i odwrotnie, każda klasyfikacja
obiektów oznacza pewien system informacyjny.

JĘZYKI SYSTEMÓW INFORMACYJNYCH

System informacyjny – języki zapytań

Pytania dotyczące zbiorów obiektów – pytania mnogościowe

Np. Podaj wszystkie książki z dziedziny

X, wydane po roku Y w języku Z.

Pytania dotyczące związków miedzy obiektami – pytania relacyjne.

Np. podaj wszystkich spadkobierców

X

Pytania dotyczące liczby elementów (zbiorów lub relacji) – pytania liczbowe

Np. Ile osób zna język angielski?

Pytania związane z koniecznością wykonania pewnych obliczeń – pytania

numeryczne.

Np. Podać średnie wynagrodzenie pracowników działu

X w roku Y.

Pytania wymagające sprawdzenia zachodzenia pewnych warunków (relacji pomiędzy
obiektami) – pytania logiczne.

Np. Czy

X jest autorem książki Y?

Język – jego konstrukcja może obejmować różne rodzaje pytań, może też dotyczyć

tylko jednego rodzaju pytań.

Rozważamy składnię języka na przykładzie pytań mnogościowych, tzn.
języka mnogościowego, którego odpowiedziami na pytania są pewne
zbiory obiektów systemu.

L

S

– język systemu informacyjnego S.

Składnię języka L

S

determinują reguły, według których budowane są wyrażenia

(termy) poprawne w tym języku.

Termy zbudowane są z symboli alfabetu, do którego należą:

1. deskryptory systemu, tj. pary symboli postaci (a,v), gdzie a

∈

A, v

∈

V

a

;

2. stałe 0, 1;
3. symbole operacji ~, * , + , Æ ,ÅÆ zwane odpowiednio: negacja, koniunkcją,

alternatywą, implikacją i równoważnością.

Symbole operacji można uważać za skróty spójników logicznych: „nie” , „i” ,
„lub” , „jeżeli…to”, „wtedy i tylko wtedy”.

46

Uwaga

W języku tym nie ma zmiennych, a jedynie stałe oraz symbole operacji.

Wyrażeniami poprawnymi (termami języka L

S

) są zatem dowolne stałe i deskryptory

połączone symbolami operacji, tzn.:

1. stałe 0 , 1 są termami
2. deskryptory systemu S, tj. pary stałych (a,v), a

∈

A, v

∈

V

a

są termami

3. jeżeli t , t’ są termami, to również termami są

~t , t

Æ

t’ ,

t + t’ ,

t

ÅÆ

t’

,

t * t’

Przykład

(NAZWISKO, Kowalski) inne oznaczenie (NAZWISKO = Kowalski)

(PŁEĆ=mężczyzna) * (WIEK=17)

Uwaga

Termy interpretowane są jako pytania. Zgodnie z wcześniej przyjętą intencją,
znaczeniem termu winien być pewien podzbiór zbioru obiektów, który stanowi
odpowiedź na pytanie reprezentowane przez term.

Znaczenie termów w systemie jest więc określone przez funkcję

σ

S

, której

argumentami są termy języka L

S

, wartościami zaś podzbiory obiektów systemu S.

Funkcja ta nazywana jest semantyką języka L

S

.

Gdy system S jest ustalony, zamiast

σ

S

stosowana będzie notacja

σ

.

Przykład

σ

S

(0) =

∅ ,

σ

S

(1) = X

σ

S

(a,v) = {x

∈X | Ψ

X

(A) = v}

σ

S

(~t) = X -

σ

S

(a,v)

σ

S

(t+t’) =

σ

S

(t)

∪ σ

S

(t’)

,

σ

S

(t*t’) =

σ

S

(t)

∩ σ

S

(t’)

σ

S

(tÆt’) = ~

σ

S

(t)

∪ σ

S

(t’)

σ

S

(tÅÆt’) =

σ

S

(tÆt’)

∩ σ

S

(tÅt’)

47

Np. 0 -

Odpowiedzią na pytanie reprezentowane przez stałą 0 jest zbiór
pusty.

1 - . . .

(OCZY=zielone) - zbiór wszystkich osób mających oczy zielone

~( OCZY=zielone)

- zbiór osób posiadających oczy o kolorze różnym
od zielonego

(OCZY=zielone)+(WZROST=170)

(OCZY=zielone)*(WZROST=170)

(STANOWISKO=mistrz)Æ(WYNAGRODZENIE=5000zł)

Przykład

(OCZY=niebieskie)Å Æ(WŁOSY=blond)

jeżeli odpowiedzią jest zbiór wszystkich obiektów systemu, tzn.

σ

S

[(OCZY=niebieskie)Å Æ(WŁOSY=blond)] = X

to zbiory osób mających niebieskie oczy oraz blond włosy są
identyczne tzn.

(OCZY=niebieskie) = (WŁOSY=blond)

Przykład

Niech

S będzie systemem informacyjnym

X a b c
x

1

v

1

w

1

u

2

x

2

v

2

w

1

u

3

x

3

v

1

w

2

u

1

x

4

v

1

w

2

u

1

x

5

v

2

w

2

u

3

x

6

v

1

w

1

u

3

Alfabet języka tworzą

• Stałe 0 , 1

• Symbole operacji ~, * , + , Æ ,ÅÆ

• Atrybuty a , b , c

• Wartości v

1

, v2 , w

1

, w

2

, w

3

,u

1

, u

2

, u

3

.

48

Rozważmy termy:

(a,v

1

) + (b,w

2

) * (c,u

2

)

~[(a,v

2

) * (a,v

1

)] + (c,u

3

)

(b,w

1

) + (c,u

1

)

(b,w

1

) Æ (c,u

3

)

(b,v

2

) ÅÆ (c,w

2

)

Znaczeniem tych termów są w systemie S następujące zbiory:

σ

S

((a,v

1

) + (b,w

2

) * (c,u

2

)) = {x

1

,x

3

,x

4

,x

6

}

∪ ({x

3

,x

4

,x

5

}

∩ {x

1

}) =

= {x

1

, x

3

, x

4

, x

6

}

σ

S

(~[(a,v

2

) * (a,v

1

)] + (c,u

3

)) = ~(

∅) ∪ {x

2

, x

5

, x

6

} = X

σ

S

((b,w

1

) + (c,u

1

)) = {x

1

, x

2

, x

6

}

∪ {x

3

,x

4

} = {x

1

, x

2

, x

3

,x

4

, x

5

}

σ

S

((b,w

1

) Æ (c,u

3

))= (X - {x

1

, x

2

, x

6

})

∪ {x

2

,x

5

,x

6

} = {x

2

, x

3

, x

4

, x

5

, x

6

}

σ

S

((a,v

1

) ÅÆ (b,w

3

))= {x

1

, x

3

, x

4

, x

6

}

∩ {x

1

, x

2

, x

6

} = {x

1

, x

6

}

Term

t języka L

S

jest prosty, gdy

t jest postaci:

(a

1,

v

1

) *

(a

2

,v

2

) * … * (a

n

,v

n

)

gdzie
a

1

,a

2

,..,a

n

– wszystkie atrybuty ze zbioru A

v

1

, v

2

, .. , v

n

- są pewnymi wartościami odpowiednio ze zbiorów

V

a1

, V

a2

, …,V

an

.

49

11

JĘZYKI SYSTEMÓW INFORMACYJNYCH.

- Postać normalna termów.
- Dokładność i efektywność języka.
- Termy proste maja następującą własność:

Własność

Jeżeli t jest termem prostym w języku L

S

, to

σ

S

(t) jest zbiorem

elementarnym w systemie S lub zbiorem pustym.

Przykład

(PŁEĆ=mężczyzna) * (WYNAGRODZENIE=duże) * (WIEK=młody)

Uwaga

Termy proste stanowią opisy klas równoważności relacji ~

S

(zbiorów

elementarnych).

Przykład

Dla systemu S określonego tabelką:

X a b
x

1

v

1

u

2

x

2

v

2

u

3

x

3

v

1

u

2

x

4

v

2

u

1

Termami prostymi w języku L

S

są

(a,v

1

) * (b,u

1

)

(a,v

1

) * (b,u

2

)

(a,v

1

) * (b,u

3

)

(a,v

2

) * (b,u

1

)

(a,v

2

) * (b,u

2

)

(a,v

2

) * (b,u

3

)

Wartości tych termów są następujące:

σ

S

((a,v

1

) * (b,u

1

))

=

∅

σ

S

((a,v

1

) * (b,u

2

))

= {x

1

,x

3

}

σ

S

((a,v

1

) * (b,u

3

))

=

∅

50

σ

S

((a,v

2

) * (b,u

1

))

= {x

4

}

σ

S

((a,v

1

) * (b,u

2

))

=

∅

σ

S

((a,v

1

) * (b,u

3

))

= {x

2

}

Zbiorami elementarnymi w systemie są:

{x

1

,x

3

} , {x

2

} , {x

4

}

Reguły przekształcania termów

(t + p) + s = t + (p +s)

(t * p) * s = t * (p * s)

t + p = p + t

t * p = p * t

t * (p +s) = t * p + t * s

. . .

~(t + p) = ~r * ~p
t + t = t
t + (t * s) = t
. . .
t

Æ

p = ~t + p

t

Å

Æ

p = t * p + ~t * ~p

t

Å

Æ

p = ~t

Å

Æ

~p

(a,v) * (a,u) = 0 , u,v

∈

V

a

, u

≠

v

dla każdego a

∈

A,

Każdy obiekt ma dokładnie jedną wartość każdego atrybutu ((jeżeli coś
ma kolor czerwony to nie ma innego)

Σ

(a,v) = 1

dla każdego

a

∈

A

v

∈

V

a

Każdy obiekt przyjmuje jedną z wartości każdego atrybutu. Jeśli
atrybutem jest KOLOR to każdy obiekt musi mieć jakiś kolor, który jest
wartością tego atrybutu.

~(a,v) =

Σ

(a , u) , u

≠

v ,

dla każdego

a

∈

A,

u

∈

V

a

Zamiast mówić, że obiekt nie ma jakiejś własności, można powiedzieć,
że ma on jedną z pozostałych własności

51

t

S

= 1 , t

S

– term charakterystyczny systemu S.

Z systemu wykluczone są elementy, których opisy nie występują jako
składniki termu charakterystycznego (termu będącego sumą niepustych
termów prostych).

POSTAĆ NORMALNA TERMÓW

Każdy term można przekształcić w term mu równoważny,
posiadający specjalną postać, zwaną postacią normalną –
pozwalającą każde pytanie przedstawić w jednolitej postaci,
umożliwiającej wygodny sposób znalezienia odpowiedzi.

Przykład

W systemie informacyjnym

X a b c
x

1

v

1

u

1

w

2

x

2

v

2

u

1

w

1

x

3

v

1

u

1

w

2

x

4

v

1

u

2

w

2

x

5

v

2

u

1

w

1

x

6

v

2

u

1

w

1

Istnieją trzy zbiory elementarne {x

1

,x

3

} , {x

2

, x

5

, x

6

} , {x

4

}

(a,v

1

) * (b,u

1

) * (c,w

2

)

(a,v

2

) * (b,u

1

) * (c,w

1

)

(a,v

1

) * (b,u

2

) * (c,w

2

)

Term

t

jest w postaci normalnej wtedy i tylko wtedy, kiedy

t = 0 , t = 1

lub

t = t

1

+ t

2

+ … t

k

, gdzie t

i

są termami prostymi.

Własność

Dla

każdego termu t istnieje term t’ w postaci normalnej równoważny

t.

Przykład

Sprowadź do postaci normalnej term (przyjmując, że system
informacyjny ma atrybuty a, b , c a zbiory ich wartości są
następujące):

52

V

a

={v

1

,v

2

} , V

b

={u

1

,u

2

} , V

c

={w

1

,w

2

}

t

1

= ~[(a,v

1

) * (b,u

2

)] + (b,u

1

)

Na podstawie reguły:

~(t * p) = ~t + ~p

Term t

1

można przedstawić w postaci:

t

2

= ~(a,v

1

) + ~(b,u

2

) + (b,u

1

)

Na podstawie reguły:

~(a,v) =

Σ (a , u) , u≠ v , dla każdego a∈A,

u

∈V

a

otrzymujemy:

t

3

= (a,v

2

) + (b,u

1

) + (b, u

1

)

Stosując do termu t

3

regułę:

t + t = t

Otrzymamy:

t

4

= (a,v

2

) + (b,u

1

)

Z kolei zgodnie z regułą :

Σ (a,v) = 1 dla każdego a∈A
v

∈V

a

Można zapisać:

(a,v

1

) + (a,v

2

) = 1

(b,u

1

) + (b,u

2

) = 1

(c,w

1

) + (c,w

2

) = 1

Na podstawie reguły:

t * 1 = t

Term t

4

można przedstawić w postaci:

t

5

= [(a,v

2

) + (b,u

1

)] * [(a,v

1

) + (a,v

2

)] * [(b,u

1

) + (b,u

2

)] *

* [(c,w

1

) + (c,w

2

)]

Zgodnie z kolei z regułami:
t * (p +s) = t * p + t * s ; t + (p *s) = (t + p) + (t + s)
t * t = t oraz (a,v) * (a,u) = 0 , u,v

∈V

a

, u

≠v dla każdego

a

∈A,

Otrzymuje się term:

53

t

6

= (a,v

1

) * (b,u

1

) + (c,w

1

) +

+

(a,v

1

) * (b,u

1

) + (c,w

2

) +

+

(a,v

1

) * (b,u

2

) + (c,w

1

) +

+

(a,v

1

) * (b,u

2

) + (c,w

2

) +

+

(a,v

2

) * (b,u

1

) + (c,w

1

) +

+

(a,v

2

) * (b,u

1

) + (c,w

2

) +

+

(a,v

2

) * (b,u

2

) + (c,w

1

) +

+

(a,v

2

) * (b,u

2

) + (c,w

2

)

Przykład

W systemie informacyjnym

X a b c
x

1

v

1

u

1

w

2

x

2

v

2

u

1

w

1

x

3

v

1

u

1

w

2

x

4

v

1

u

2

w

2

x

5

v

2

u

1

w

1

x

6

v

2

u

1

w

1

Istnieją trzy zbiory elementarne {x

1

,x

3

} , {x

2

, x

5

, x

6

} , {x

4

}

(a,v

1

) * (b,u

1

) * (c,w

2

)

(a,v

2

) * (b,u

1

) * (c,w

1

)

(a,v

1

) * (b,u

2

) * (c,w

2

)

którym odpowiadają termy proste

σ

S

[(a,v

1

) * (b,u

1

) * (c,w

2

)]

= {x

1

,x

3

}

σ

S

[(a,v

2

) * (b,u

1

) * (c,w

1

)]

= {x

2

,x

5

,x

6

}

σ

S

[(a,v

1

) * (b,u

2

) * (c,w

2

)]

= {x

4

}

natomiast wszystkie pozostałe termy proste są puste, tzn. odpowiadają im zbiory
puste.
A zatem

σ

S

(t

1

)

= {x

1

,x

3

,x

3

,x

4

,x

5

,x

6

} ,

tzn

. t

1

= 1.

Minimalna postać normalna termu t ze względu ma system S – postać , w której nie
występują termy puste.

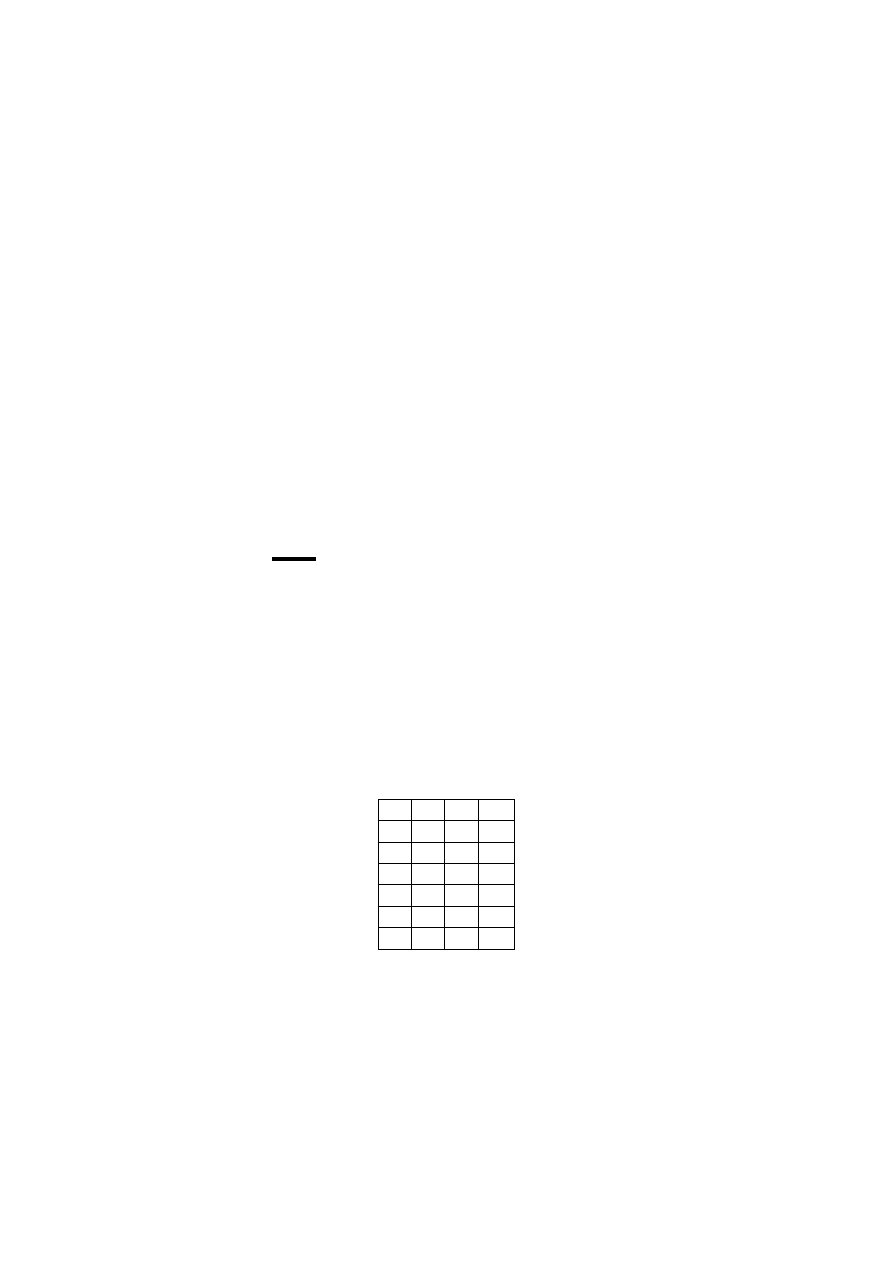
54

Uwaga

• Postać normalna mówi, że odpowiedź na dowolne pytanie jest zawsze sumą

teoriomnogościową pewnych zbiorów elementarnych.

• Wprowadzając pytanie w postaci normalnej, można łatwo znaleźć

odpowiadające każdemu termowi prostemu zbiory elementarne i w ten
sposób otrzymać odpowiedź na zadane pytanie.

DOKŁADNOŚĆ I EFEKTYWNOŚĆ JĘZYKA

Intuicyjnie – język dokładniejszy pozwala otrzymać więcej odpowiedzi niż jezyk mniej
dokładny.
Im więcej w systemie jest zbiorów elementarnych, tym więcej dostępnych jest
zbiorów opisywanych w tym systemie. W konsekwencji, w systemie dokładniejszym
istnieje więcej odpowiedzi niż w systemie mniej dokładnym.

Dokładność języka (języka zapytań) odnosi się do związanego z nim systemu
informacyjnego.

Dokładność systemu informacyjnego:

gdzie:

k – liczba bloków elementarnych w systemie
X – zbiór wszystkich obiektów w systemie informacyjnym S.

Oznacza stosunek liczby wszystkich podzbiorów opisywanych w systemie do liczby

wszystkich możliwych podzbiorów zbioru obiektów w systemie S.

Przykład

W systemie informacyjnym

X a b c
x

1

v

1

u

1

w

2

x

2

v

2

u

1

w

1

x

3

v

1

u

1

w

2

x

4

v

1

u

2

w

2

x

5

v

2

u

1

w

1

x

6

v

2

u

1

w

1

Istnieją trzy zbiory elementarne {x

1

,x

3

} , {x

2

, x

5

, x

6

} , {x

4

}

Można więc skonstruować 2

3

= 8 zbiorów opisywanych, tzn. możliwych jest w

systemie tylko 8 różnych odpowiedzi:

2

k

λ

S

=

= 2

k – card(X)

2

card(X)

55

∅
{x

4

}

{x

1

,x

3

}

{x

2

, x

5

, x

6

}

{x

1

,x

3

}

∪

{x

4

}

{x

2

, x

5

, x

6

}

∪

{x

4

}

{x

1

,x

3

}

∪

{x

2

, x

5

, x

6

}

{x

1

,x

3

}

∪

{x

2

, x

5

, x

6

}

∪

{x

4

}

Natomiast wszystkich podzbiorów zbioru obiektów systemu jest 2

6

= 64

Tak więc dokładność systemu wynosi:

Uwaga

Najdokładniejszy jest system selektywny jego dokładność wynosi

λ

S

= 1.

Efektywność języka charakteryzuje stopień jego wykorzystania do zadawania

pytań. Wynika to z faktu, że wiele termów prostych języka w danym systemie
jest pustych.

Efektywność języka w systemie S

gdzie:

k – liczba zbiorów elementarnych systemie S

oznacza stosunek liczby wszystkich termów prostych systemie S, do liczby termów

prostych niepustych.

0 <

η

S

≤

1

Efektywność języka systemu zupełnego wynosi 1.

Uwaga

Każdy selektywny język ma największą dokładność, dokładność każdy system

zupełny – największą efektywności.

2

3

λ

S

=

= 2

–3

2

6

k

η

S

=

∏

card

(V

a

)

a

∈A

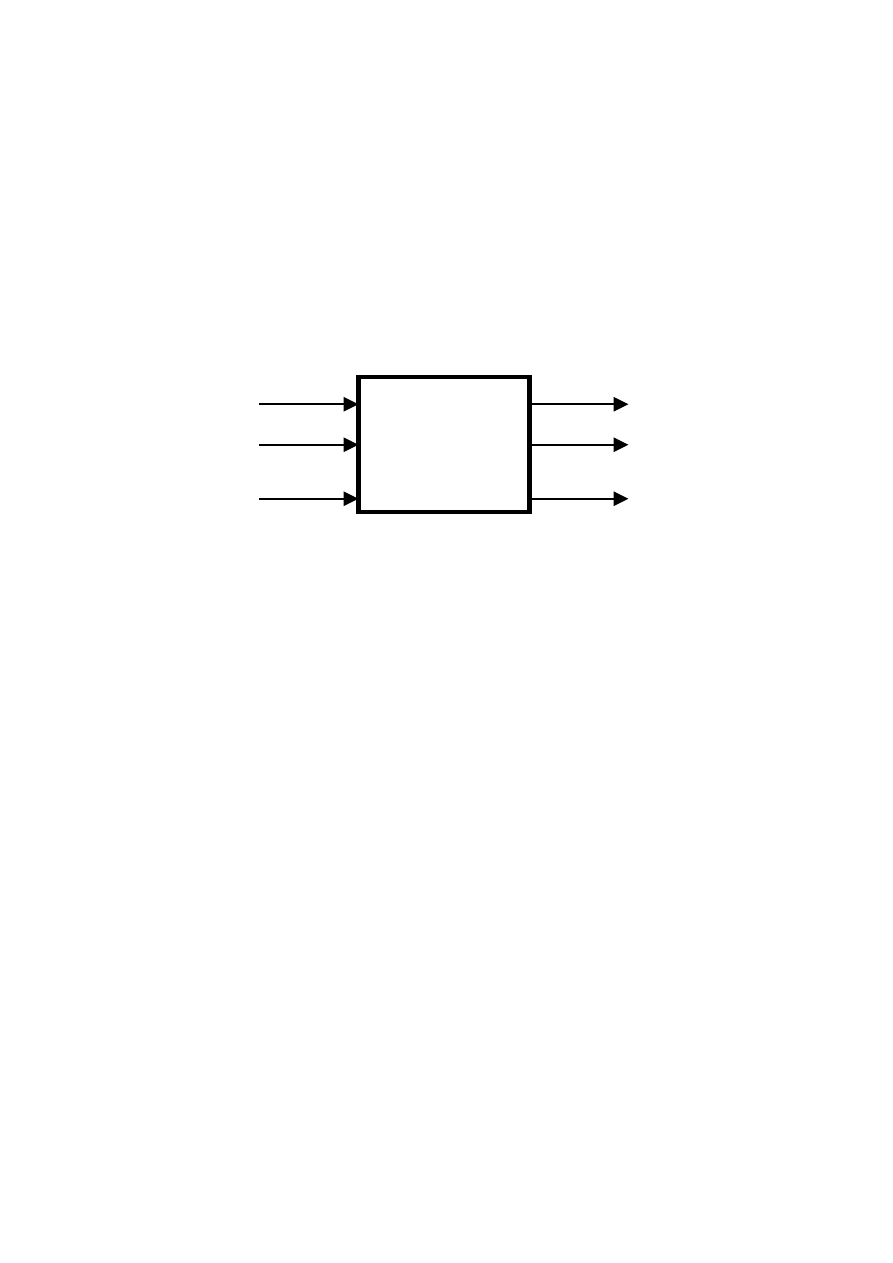
56

12. AUTOMATY.

• Układy sekwencyjne i kombinacyjne.

• Automaty

• Automaty Meale’go i Moore’a.

• Język wyrażeń regularnych.

Automat – urządzenie, którego istotna cecha jest samoczynne wykonywanie

czynności zgodnie z jakimś z góry zadanym algorytmem działania.

y

1

= f(x

1

,x

2

,...,x

k

)

y

2

= f(x

1

,x

2

,...,x

k

)

. . . .

y

k

= f(x

1

,x

2

,...,x

k

)

Y(t) = F(X(t))

Funkcja przełączająca – funkcja która jest określona na argumentach

przyjmujących wartości ze zbioru {0,1} i która sama
również przyjmuje tylko wartości z tego zbioru

.

y = f(x

1

,x

2

,...,x

n

)

Uwaga

Liczba k możliwych wartości funkcji f dla n zmiennych k =2

n

Liczba funkcji

F

określona na

k ciągach wynosi

2

k

Wyrażenia strukturalne – wyrażenia opisujące funkcje przełączające.

A

x

1

x

2

.

.

.

x

k

y

1

y

2

.

.

.

y

n

57

Rozkład wyrażeń strukturalnych

Rozkład jedności

x

∨ ¬x ⇔1

x

1

∨ ¬x

1

⇔1 ; x

2

∨ ¬x

2

⇔1

1

⇔1 ∧ 1

1

⇔ (x

1

∨ ¬x

1

)

∧ (x

2

∨ ¬x

2

)

1

⇔ x

2

∧ x

1

∨

x

2

∧ ¬x

1

∨

¬x

2

∧ x

1

∨

¬x

2

∧ ¬x

1

Uwaga

Jedność można przedstawić jako sumę składników, z których każdy jest

jedną ze wszystkich możliwych kombinacji wszystkich zmiennych lub
ich negacji. (suma elementarnych iloczynów zupełnych).

Rozkład zera

x

∧ ¬x ⇔0

x

1

∧ ¬x

1

⇔ 0

;

x

2

∧ ¬x

2

⇔ 0

0

⇔0 ∨ 0

0

⇔ (x

1

∧ ¬x

1

)

∨ (x

2

∧ ¬x

2

)

0

⇔ (¬x

2

∨ ¬x

1

)

∧

(

¬x

2

∨ x

1

)

∧

(x

2

∨ ¬x

1

)

∧

(x

2

∨ x

1

)

Uwaga

Zero

można przedstawić jako iloczyn czynników, z których każdy jest

jedną ze wszystkich możliwych kombinacji wszystkich zmiennych lub
ich negacji (iloczyn elementarnych sum zupełnych).

ROZKŁAD FUNKCJI WZGLĘDEM SKŁADNIKÓW JEDNOŚCI

Każda funkcja przełączająca może być przedstawiona w postaci sumy
wybranych iloczynów elementarnych zupełnych, przy czym postać taka dla
danej funkcji jest tylko jedna i nosi nazwę postaci normalnej zupełnej sumy.

58

Postać rozkładu dowolnej funkcji przełączającej

f(x

n

,x

n-1

,...,x

2

,x

1

) = f(1,1,...,1,1) x

n

∧x

n-1

∧,...,∧x

2

∧x

1

∨

∨

f(1,1,...,1,0) x

n

∧x

n-1

∧,...,∧x

2

,

∧¬x

1

∨

∨

f(1,1,...,0,1) x

n

∧x

n-1

∧,..., ∧¬x

2

∧x

1

∨

...

...

...

∨

f(0,0,...,0,1)

¬x

n

∧ ¬x

n-1

∧,..., ∧¬x

2

∧x

1

∨

∨

f(0,0,...,0,1)

¬x

n

∧¬x

n-1

∧,..., ∧¬x

2

∧ ¬x

1

Przykład

Dana jest funkcja trzech zmiennych

y = f(x

3

,x

2

,x

1

) = x

3

∧ (¬x

2

∨ ¬x

1

)

∨ ¬x

3

∧ x

1

należy podać postać normalną zupełną sumy tej funkcji.

Dla

x

3

= 0 , x

2

= 0 , x

1

= 0

y = x

3

(

¬x

2

∨ ¬x

1

)

∨ ¬x

3

∧ x

1

= 0

∧ (1 ∨ 1) ∨ 1 ∧ 0 = 0

zatem

y = x

3

∧ (¬x

2

∨ ¬x

1

)

∨ ¬x

3

∧ x

1

= 0

∧¬x

3

∧¬x

2

∧¬x

1

∨

∨ 1 ∧¬x

3

∧¬x

2

∧x

1

∨ 0 ∧¬x

3

∧x

2

∧¬x

1

∨ 1 ∧¬x

3

∧x

2

∧x

1

∨

∨ 1 ∧x

3

∧¬x

2

∧¬x

1

∨ 1 ∧x

3

∧¬x

2

∧x

1

∨ 1 ∧x

3

∧x

2

∧¬x

1

∨

∨ 0 ∧x

3

∧x

2

∧x

1

=

=

¬x

3

∧¬x

2

∧x

1

∨ ¬x

3

∧x

2

∧x

1

∨ x

3

∧¬x

2

∧¬x

1

∨ x

3

∧¬x

2

∧x

1

∨ x

3

∧x

2

∧¬x

1

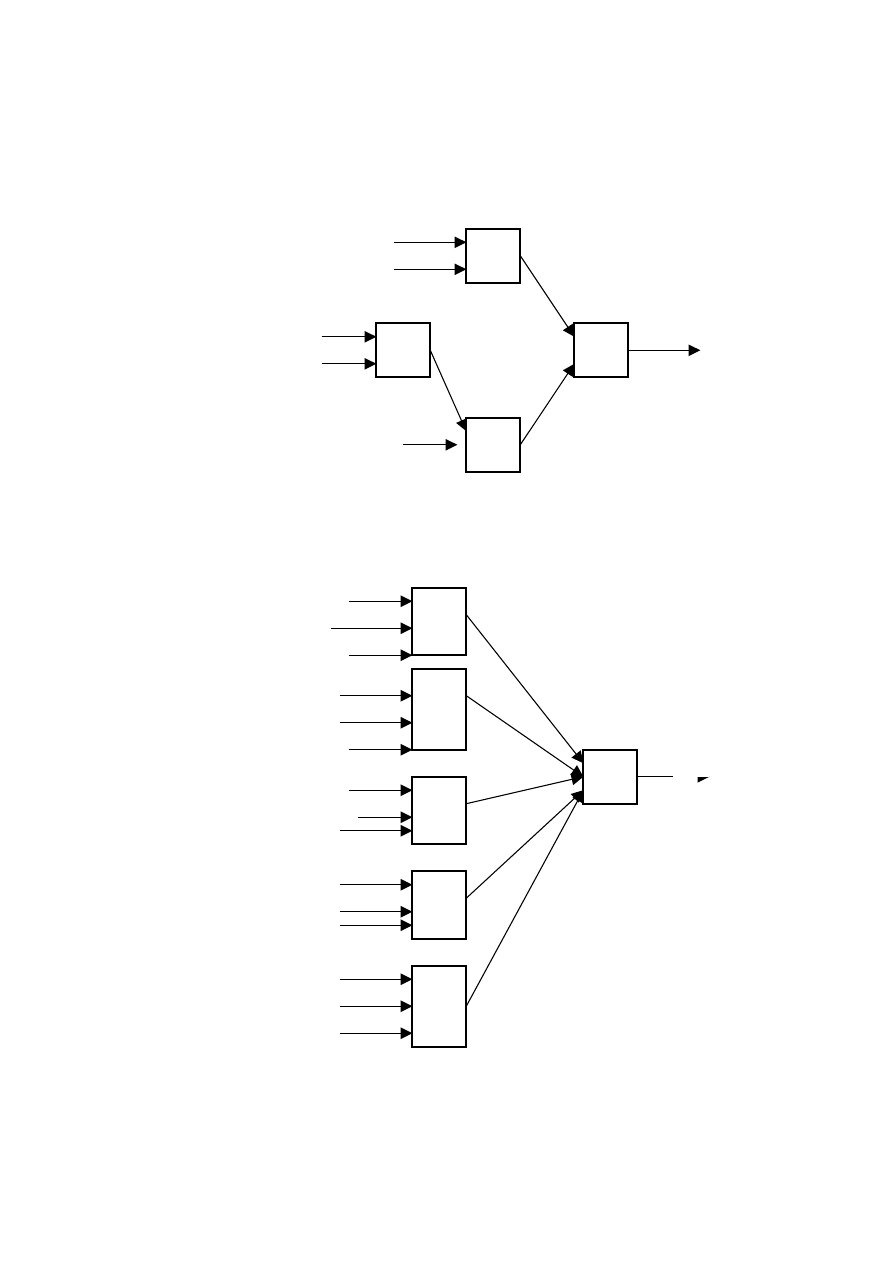
59

Schematy logiczne funkcji dla postaci uproszczonej a) i postaci normalnej zupełnej
sumy b)

a)














b)

∧

∧

∨

∨

¬

x

3

x

1

¬

X

2

¬

x

1

x

3

y

∧

∨

∧

∧

∧

∧

X

3

x

2

¬

X

2

x

3

¬

X

2

x

1

X

3

¬

x

2

¬

X

2

¬

x

3

X

2

x

1

¬

X

3

¬

x

2

x

1

y

60

ROZKŁAD FUNKCJI WZGLĘDEM CZYNNIKÓW ZERA

Każda funkcja przełączająca może być przedstawiona w postaci iloczynu
wybranych sum elementarnych zupełnych, przy czym postać taka dla danej
funkcji jest tylko jedna i nosi nazwę postaci normalnej zupełnej iloczynu.

Postać rozkładu dowolnej funkcji przełączającej

f(x

n

,x

n-1

,...,x

2

,x

1

) = [f(0,0,...,0,0)

∨( x

n

∨x

n-1

∨,...,∨x

2

∨x

1

)]

∧

∧

[f(0,0,...,0,1)

∨ (x

n

∨x

n-1

∨,...,∨x

2

,

∨¬x

1

)]

∧

∧

...

...

...

∧

[f(1,1,...,1,1)

∨ (¬x

n

∨ ¬x

n-1

∨,..., ∨¬x

2

∨¬x

1

)]

∧

∧

f(0,0,...,0,1)

¬x

n

∧¬x

n-1

∧,..., ∧¬x

2

∧ ¬x

1

Przykład

y = x

3

∧ (¬x

2

∨ ¬x

1

)

∨ ¬x

3

∧ x

1

= (0

∨x

3

∨x

2

∨x

1

)

∧

∧

(1

∨x

3

∨x

2

∨¬x

1

)

∧

( 0

∨x

3

∨¬x

2

∨x

1

)

∧

(1

∨x

3

∨¬x

2

∨¬x

1

)

∧

∧

(1

∨¬x

3

∨x

2

∨x

1

)

∧

(1

∨x

3

∨x

2

∨¬x

1

)

∧

(1

∨¬x

3

∨∧¬x

2

∨x

1

)

∧

∧

(0

∨¬x

3

∨¬x

2

∨¬x

1

) =

= (x

3

∨x

2

∨x

1

)

∧

(x

3

∨¬x

2

∨x

1

)

∧

(x

3

∨¬x

2

∨¬x

1

)

∧

(

¬x

3

∨¬x

2

∨¬x

1

)

Uwaga

Czy obie postacie sa sobie równoważne?

¬x

3

∧¬x

2

∧x

1

∨

¬x

3

∧x

2

∧x

1

∨

x

3

∧¬x

2

∧¬x

1

∨

x

3

∧¬x

2

∧x

1

∨

∨

x

3

∧x

2

∧¬x

1

= (x

3

∨x

2

∨x

1

)

∧

(x

3

∨¬x

2

∨x

1

)

∧

(x

3

∨¬x

2

∨¬x

1

)

∧

∧

(

¬x

3

∨¬x

2

∨¬x

1

)

Wniosek

Każda funkcję przełączająca można przedstawić za pomocą dwóch
postaci:

61

• Postaci normalnej zupełnej sumy, której elementami są elementarne

iloczyny zupełne. (sumę składników jedności) (iloczyn czynników
zera)

• Postaci normalnej zupełnej iloczynu, której czynnikami są

elementarne sumy zupełnej. (suma składników jedności)

Automaty bez pamięci – nie zachodzi potrzeba zapamiętywania informacji

wprowadzonej lub przekształconej.

Układy kombinacyjne – działanie których zależy od wzajemnej kombinacji wartości

zmiennych tworzących informacje.

Przykład

Dane są trzy zbiorniki wyposażone w trzy sygnalizatory dwupołożeniowe
podające informacje o poziomach cieczy.
Należy zasygnalizować dwa przypadki:

• Gdy wszystkie zbiorniki osiągną określony poziom

• Gdy co najmniej dwa zbiorniki osiągną ten poziom

Notując odpowiednie informacje przez a, b, c warunki te można zapisać:

• a∧b∧c
• a∧b ; a∧c ;

b

∧c

Odpowiednia funkcja przełączająca ma postać:

y = a

∧b∧c ∨ a∧b ∨ a∧c ∨ b∧c

Rozszerzając to wyrażenie do postaci elementarnych iloczynów zupełnych

y = a

∧b∧c

∨

a

∧b∧1

∨

a

∧1∧c

∨

1

∧b∧c =

= a

∧b∧c

∨

a

∧b∧(c∨¬c)

∨

a

∧(b∨¬b)

∧c

∨

(

a

∨¬a)

∧b∧c =

= a

∧b∧c

∨

a

∧b∧¬c

∨

a

∧¬b ∧c

∨

¬a ∧b∧c

i przeprowadzając jej minimalizacje

y = a

∧b

∨

a

∧c

∨

b

∧c = c∧(a ∨ b)

∨

a

∧b

Otrzymujemy schemat logiczny układu

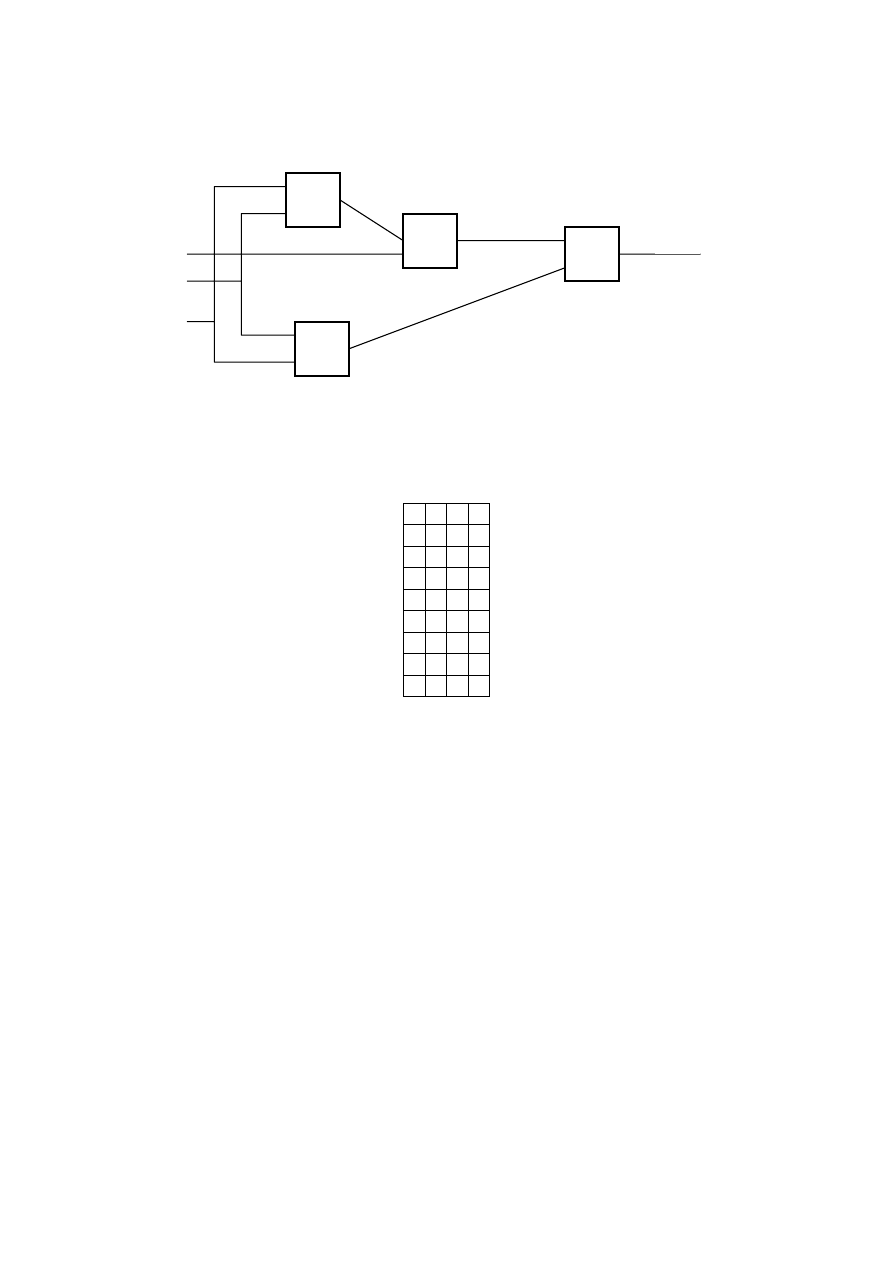
62

Przykład

Dane są informacje z trzech punktów:

a, b c. Sygnalizowane maja być

sytuacje gdy na wejściach

a lub c lub na dwóch dowolnych pojawi się 1.

a b c y
o o o o
o o 1 1
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 0

Zestawiając funkcję dla warunków działania otrzymujemy

y

0

=

=

¬

a

∧¬b∧c

∨

a

∧¬b∧¬c

∨

¬a∧b ∧c

∨

a

∧¬b∧c

∨

a

∧b ∧¬c

Przeprowadzając minimalizację otrzymujemy:

y

0

=

¬

b

∧c∧(a∨¬a)

∨

a

∧¬b∧(c∨¬c)

∨

a

∧¬ c∧(b∨¬b)

∨

¬a∧c∧(b∨¬b) =

=

¬

b

∧c

∨

a

∧¬b

∨

a

∧¬ c

∨

¬a∧c

co odpowiada zestawieniu funkcji dla warunków niedziałania

y

1

=

(a

∨

b

∨c)

∧

(a

∨¬b∨c)

∧

(

¬a∨b∨c) =

=

¬

b

∧c

∨

a

∧¬b

∨

a

∧¬ c

∨

¬a∧c = y

1

Co po doprowadzeniu do odpowiedniej postaci nawiasowej

c

b

a

∨

∧

∧

∨

y

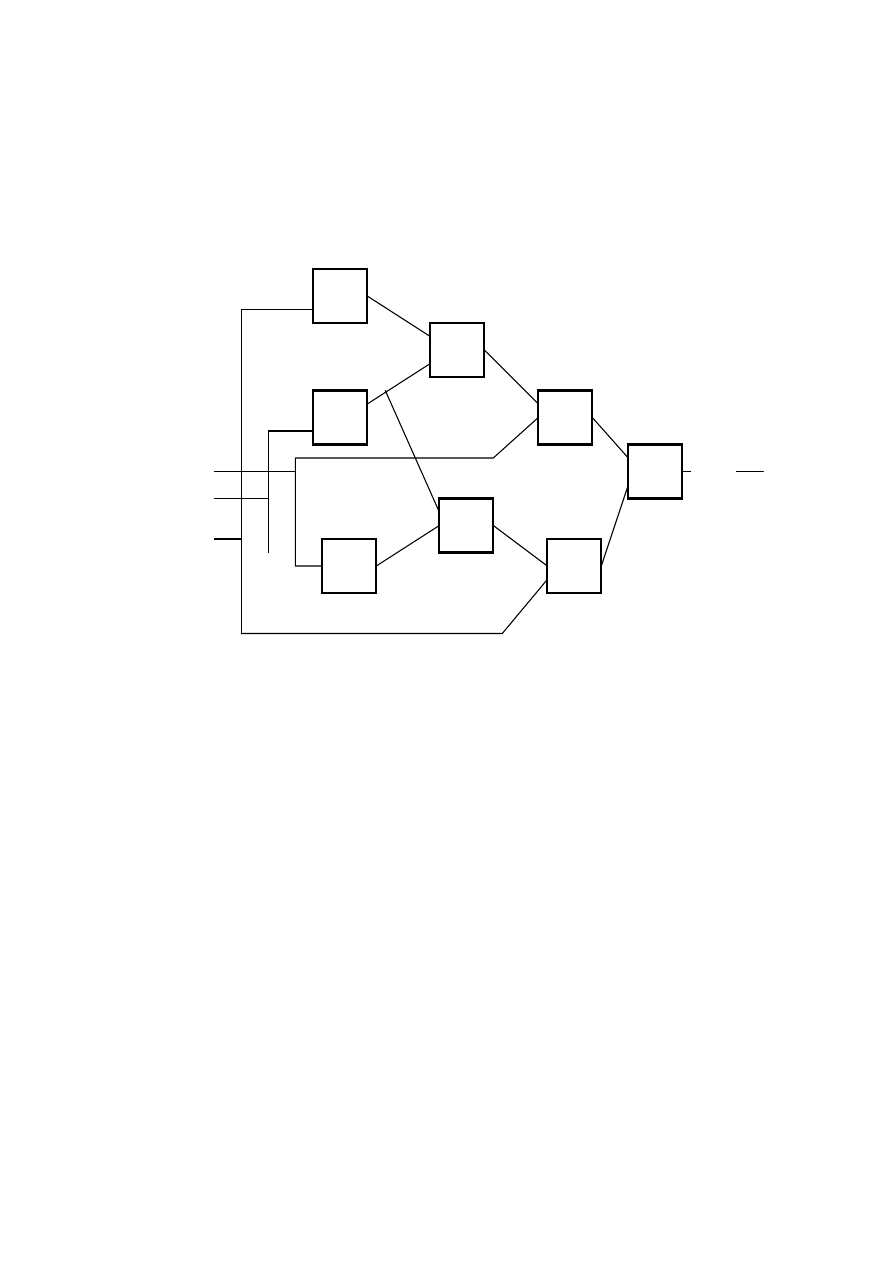
63

y = y

1

= y

0

= a

∧(¬b ∨¬c)

∨

c

∧(¬a ∨¬b)

prowadzi do schematu strukturalnego układu

Automat z pamięcią

Automat skończony

A = (X,Y,S,.s

0

,

α

(X,S),

λ

(X,S))

Gdzie

X – zbiór słów wejściowych
Y– zbiór słów wyjściowych
S– zbiór stanów
s

0

– stan początkowy

α

(X,S) – funkcja przejść określająca zmiany stanów automatu

λ

(X,S) – funkcja przejść określająca zmiany słów wyjściowych

Uwaga

Zarówno funkcja wyjść jak i funkcja przejść są funkcjami rekurencyjnymi
dla zmiennych dyskretnych

∨

c

b

a

¬

¬

y

∧

∧

∨

∨

¬

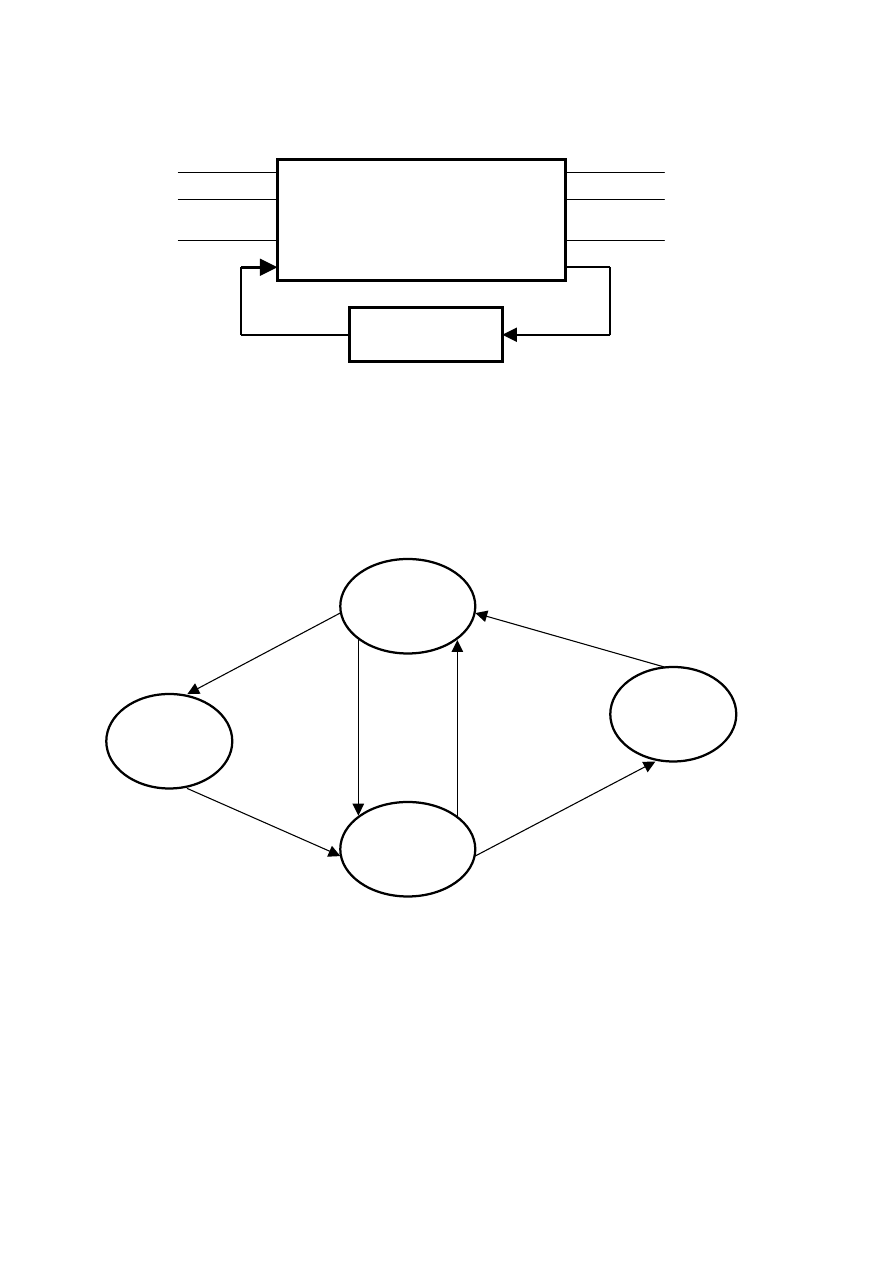
64

. . .

Układ kombinacyjny

Automat bez pamięci

. . .

X

Y

Pa

Zamykanie ukończone

Zamykanie

Otwieranie

Zamknięte

Opuszczanie

Otwarte

Podnosze
nie

Zamykanie

Otwieranie ukończone

Otwieranie

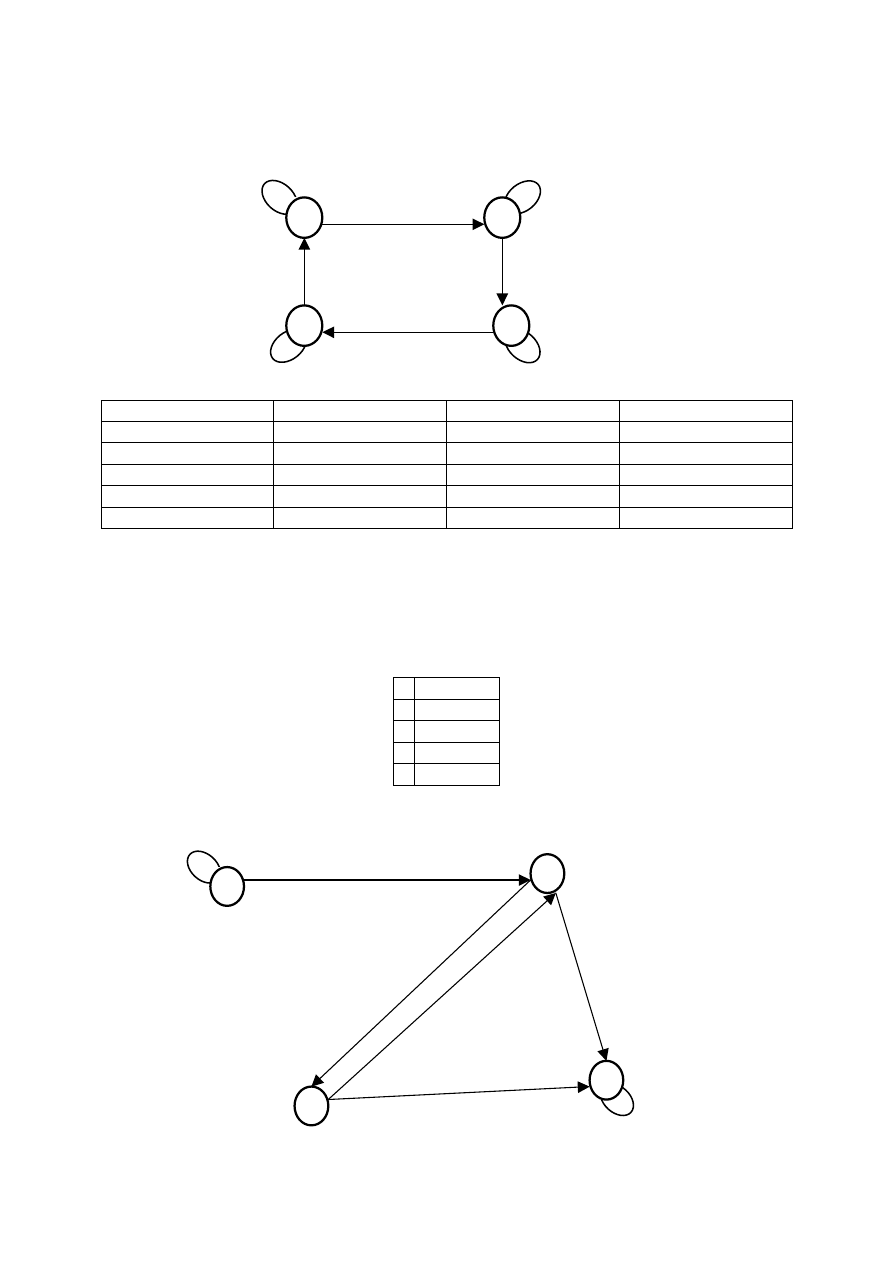
65

Przykład

Stan bieżący Symbol

bieżący Stan

kolejny

Pozostałe symbole

0 a 1 baa
1 b 1 aa
1 a 3 a
3 a 2
2

Język wyrażeń regularnych

Przykład

a b
0 1 0
1 3 2
2 1 3
3 3 3

S

0

= 0 , S

k

= {2}

b

0

2

3

1

a

a

a

a

b

b

b

b

2

1

a

a

a

b

3

b

0

b

66

Automat Meale’a

S(t+1) =

α

(X(t),S(t))

Y(t) =

λ

(X(t),S(t))

Automat Moore’a

S(t+1) =

α

(X(t),S(t))

Y(t+1) =

λ

(X(t+1))

13. AUTOMATY.

• Realizacje automatów.

• Synteza abstrakcyjna z wykorzystaniem charakterystyki wejście-

wyjście.

14. SIECI PETRIEGO.

• Definicja i klasyfikacje sieci Petriego.

• Reprezentacje teoriomnogościowa, graficzna i macierzowa.

• Modelowanie - przykłady zastosowań.

15. SIECI PETRIEGO

• Analiza właściwości – żywotność strukturalna i funkcjonalna.

• Zjawiska blokady i konfuzji.

• Niezmienniki.

• Rozszerzenia sieci – czasowe, kolorowane, stochastyczne