
Poj
Poj
ę
ę
cie
cie
ś
ś
redniej
redniej
mo
mo
ż
ż
na rozumie
na rozumie
ć
ć
dwojako
dwojako
:
:
ś
ś
redni
redni
a
a
wyznaczon
wyznaczon
a
a
dla wielu identycznych
dla wielu identycznych
ł
ł
a
a
ń
ń
cuch
cuch
ó
ó
w
w
lub
lub
ś
ś
redni
redni
a
a
warto
warto
ść
ść
odleg
odleg
ł
ł
o
o
ś
ś
ci pomi
ci pomi
ę
ę
dzy ko
dzy ko
ń
ń
cami
cami
ł
ł
a
a
ń
ń
cucha
cucha
pojedynczej cz
pojedynczej cz
ą
ą
steczki dla wszystkich konformacji, jakie
steczki dla wszystkich konformacji, jakie
cz
cz
ą
ą
steczka ta przyjmie w d
steczka ta przyjmie w d
ł
ł
ugim
ugim
czasie
czasie
.
.
Istnienie k
Istnienie k
ą
ą
t
t
ó
ó
w walencyjnych (a nie dowolnych jak w modelu
w walencyjnych (a nie dowolnych jak w modelu
ł
ł
a
a
ń
ń
cucha swobodnie zwi
cucha swobodnie zwi
ą
ą
zanego) i barier rotacji powoduje,
zanego) i barier rotacji powoduje,
ż
ż
e
e
odleg
odleg
ł
ł
o
o
ś
ś
ci ko
ci ko
ń
ń
c
c
ó
ó
w s
w s
ą
ą
wi
wi
ę
ę
ksze ni
ksze ni
ż
ż
wskazuje teoria. Jednak
wskazuje teoria. Jednak
rzeczywiste wymiary k
rzeczywiste wymiary k
łę
łę
bk
bk
ó
ó
w w stanie niezak
w w stanie niezak
ł
ł
ó
ó
conym s
conym s
ą
ą
proporcjonalne do pierwiastka stopnia polimeryzacji.
proporcjonalne do pierwiastka stopnia polimeryzacji.
Łańcuch polimeru w przestrzeni
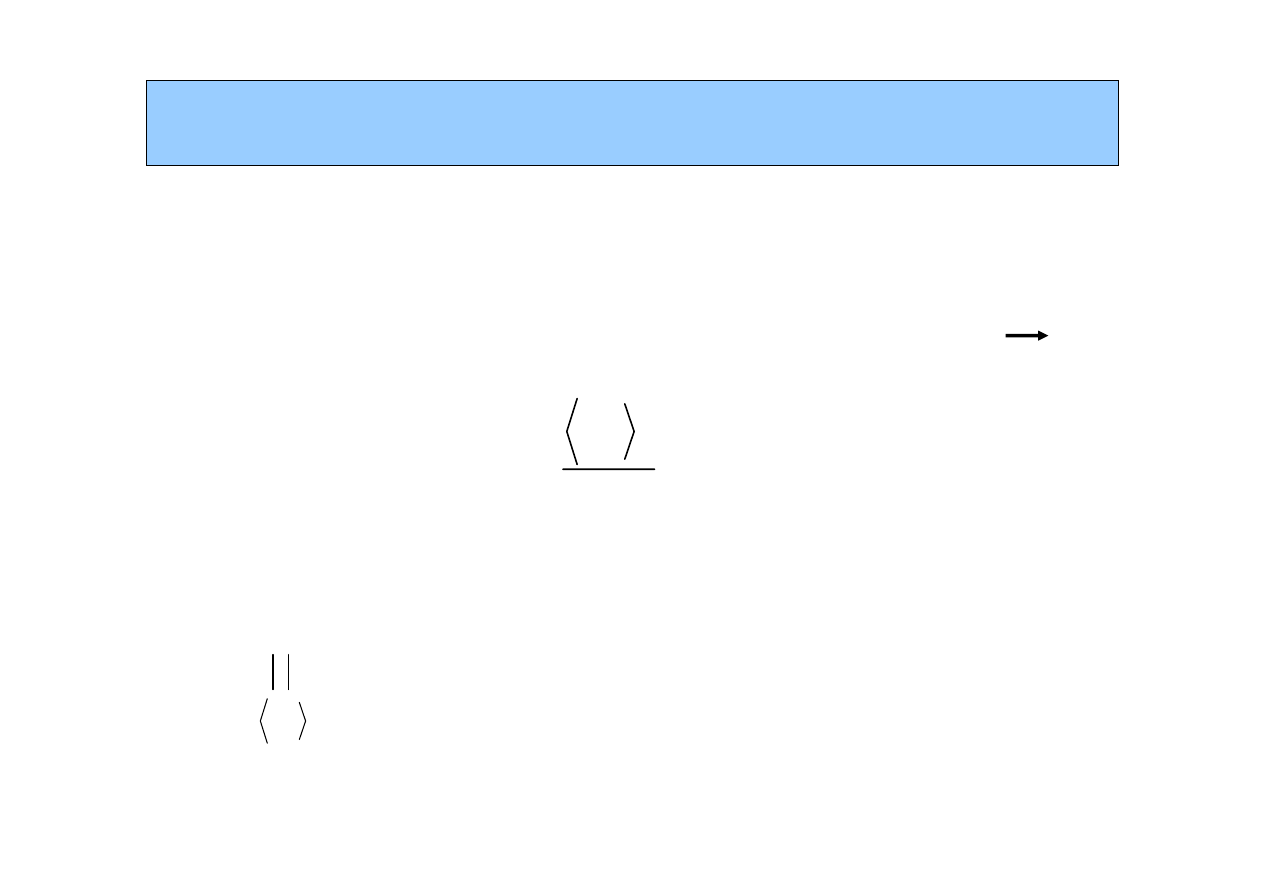
Miar
Miar
ą
ą
odst
odst
ę
ę
pstwa w zachowaniu si
pstwa w zachowaniu si
ę
ę
rzeczywistego
rzeczywistego
ł
ł
a
a
ń
ń
cucha polimeru
cucha polimeru
od warto
od warto
ś
ś
ci przewidzianej przez model
ci przewidzianej przez model
ł
ł
a
a
ń
ń
cucha swobodnie
cucha swobodnie
zwi
zwi
ą
ą
zanego jest tzw.
zanego jest tzw.
stosunek charakterystyczny
stosunek charakterystyczny
C
C
N
N
dla N
dla N
∞
∞
Łańcuch polimeru w przestrzeni
∞
→
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
N
N
Nb
R
C
2
0
2
b
=
r
gdzie:
N jest liczbą wiązań
0
2
R
„
doświadczalne” wylicza się np. z pomiarów lepkościowych

Łańcuch polimeru w przestrzeni
Łańcuch polimeru w przestrzeni
lub
P
P
ytanie
ytanie
:
:
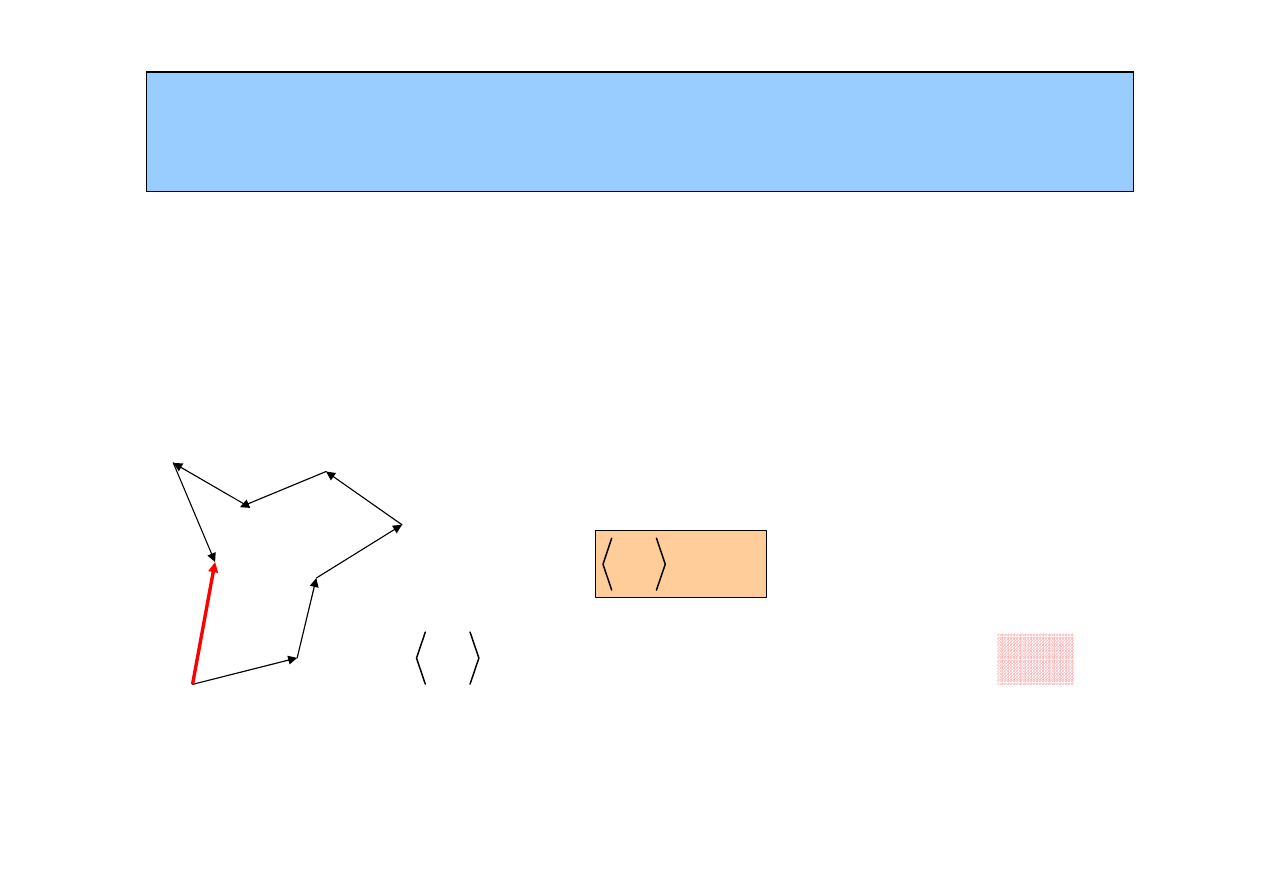
jak daleko zajdzie pijany poruszaj
jak daleko zajdzie pijany poruszaj
ą
ą
c si
c si
ę
ę
przypadkowo z punktu A do B, czyli
przypadkowo z punktu A do B, czyli
jaka jest odleg
jaka jest odleg
ł
ł
o
o
ść
ść
od punktu A do B. Zak
od punktu A do B. Zak
ł
ł
adamy,
adamy,
ż
ż
e kroki jego s
e kroki jego s
ą
ą
niezale
niezale
ż
ż
ne jeden
ne jeden
od drugiego oraz,
od drugiego oraz,
ż
ż
e wykonuje 1 krok
e wykonuje 1 krok
na
na
1 s w czasie 1 h, przy czym ka
1 s w czasie 1 h, przy czym ka
ż
ż
dy krok
dy krok
ma d
ma d
ł
ł
ugo
ugo
ść
ść
b = 1 m.
b = 1 m.
R
R
Rozwiązanie
Liczba kroków w czasie 1 h, N = 3600.
Przebyty dystans wynosi 3600 * 1m =3600 m.
Ś
Ś
redni
redni
kwadrat
kwadrat
odleg
odleg
ł
ł
o
o
ś
ś
ci
ci
ko
ko
ń
ń
c
c
ó
ó
w
w
ł
ł
a
a
ń
ń
cucha
cucha
<
<
R
R
2
2
>
>
A
B
2
2
Nb
R
=
( )
m
m
bN
Nb
R
R
60
3600
1
2
/
1
2
/
1
2
/
1
2
2
/
1
2
=
⋅
=
=
=
=
trasa pijanego
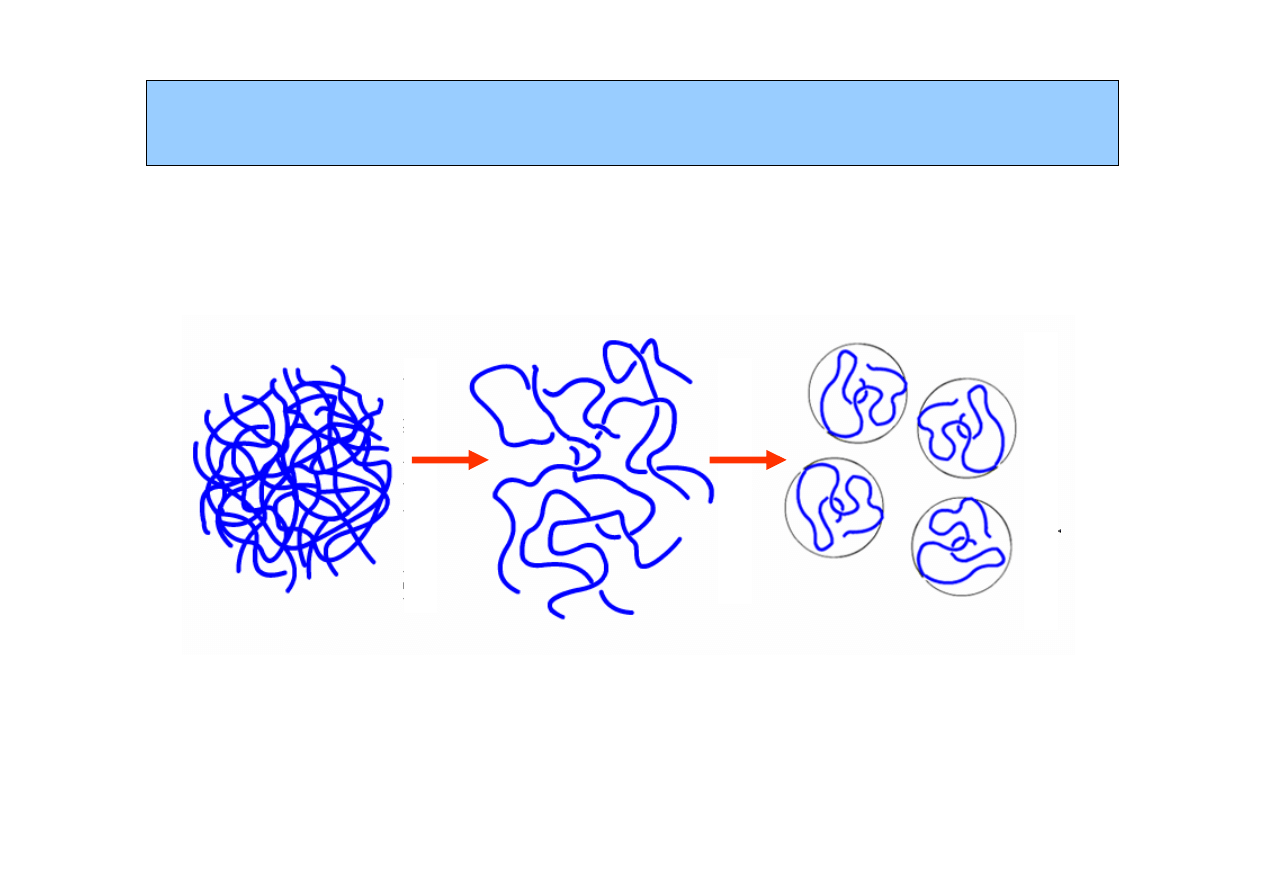
Łańcuch polimeru w roztworze
Rozpuszczanie polimeru
Rozpuszczanie polimeru
Sta
Sta
ł
ł
y polimer tu
y polimer tu
ż
ż
po
po
wprowadzeniu go
wprowadzeniu go
rozpuszczalnika
rozpuszczalnika
Pierwszy etap: sp
Pierwszy etap: sp
ę
ę
czniony
czniony
ż
ż
el w roztworze
el w roztworze
Drugi etap:
Drugi etap:
solwatowane
solwatowane
ł
ł
a
a
ń
ń
cuchy polimeru
cuchy polimeru
zdyspergowane w
zdyspergowane w
roztworze
roztworze

polimer-polimer > polimer-rozpuszczalnik
(kłębek zwinięty, zły rozpuszczalnik)
polimer-polimer = polimer-rozpuszczalnik
(kłębek swobodny, rozpuszczalnik
θ
lub temperatura
θ
)
polimer-polimer < polimer-rozpuszczalnik
(kłębek rozprostowany, dobry rozpuszczalnik)
Gi
Gi
ę
ę
tkie makrocz
tkie makrocz
ą
ą
steczki w roztworach mog
steczki w roztworach mog
ą
ą
znajdowa
znajdowa
ć
ć
si
si
ę
ę
w r
w r
ó
ó
ż
ż
nych
nych
stanach w zale
stanach w zale
ż
ż
no
no
ś
ś
ci od:
ci od:
•
•
st
st
ęż
ęż
enia
enia
•
•
temperatury
temperatury
•
•
rozpuszczalnika
rozpuszczalnika
Łańcuch polimeru w roztworze
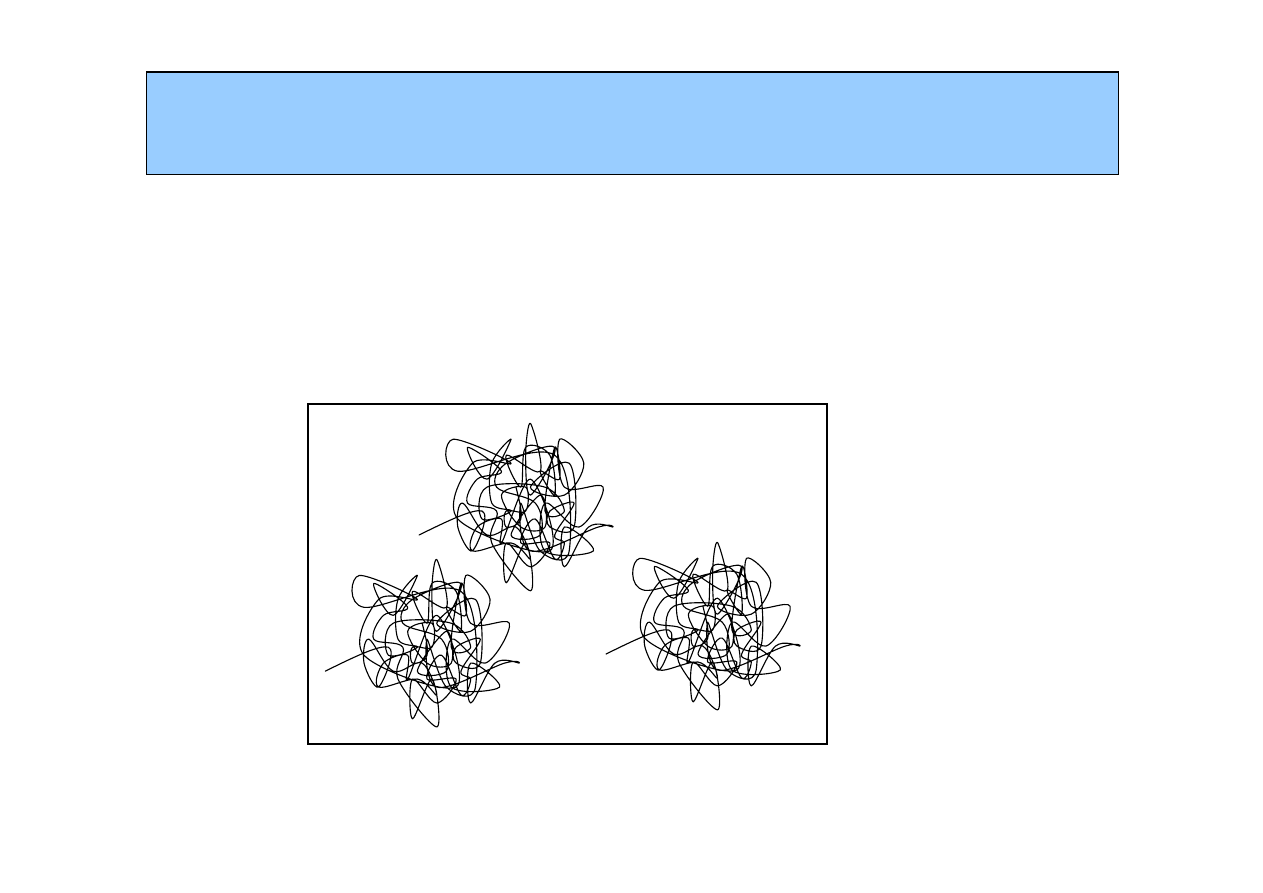
Łańcuch polimeru w roztworze
Rozcie
Rozcie
ń
ń
czony roztw
czony roztw
ó
ó
r
r
-
-
w obr
w obr
ę
ę
bie pojedynczego k
bie pojedynczego k
łę
łę
bka st
bka st
ęż
ęż
enie segment
enie segment
ó
ó
w jest sta
w jest sta
ł
ł
e
e
-
-
s
s
ą
ą
obszary w roztworze o zerowym st
obszary w roztworze o zerowym st
ęż
ęż
eniu segment
eniu segment
ó
ó
w polimeru
w polimeru
-
-
k
k
łę
łę
bki polimeru s
bki polimeru s
ą
ą
izolowane
izolowane

Łańcuch polimeru w roztworze
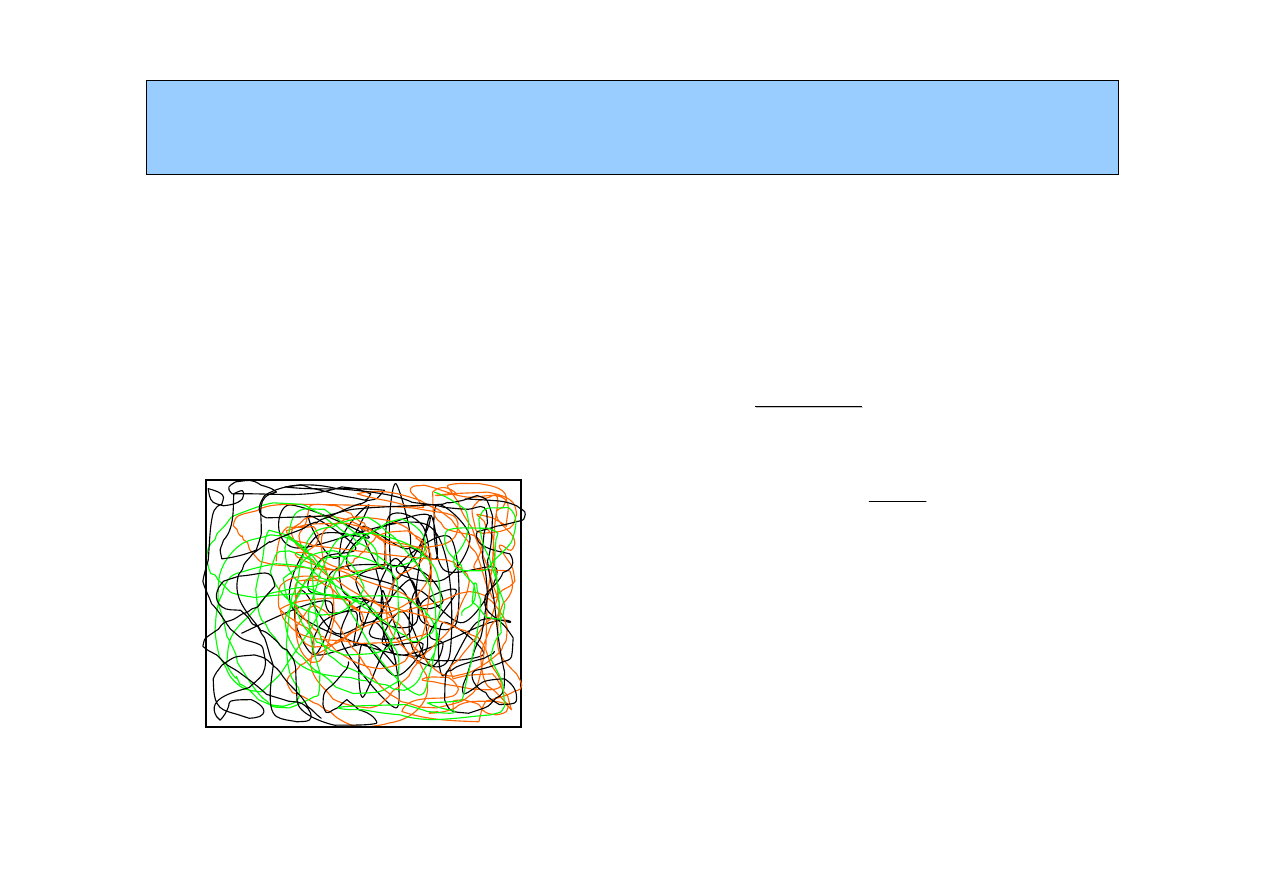
Semirozcie
Semirozcie
ń
ń
czony
czony
roztw
roztw
ó
ó
r
r
-
-
w obr
w obr
ę
ę
bie pojedynczego k
bie pojedynczego k
łę
łę
bka st
bka st
ęż
ęż
enie segment
enie segment
ó
ó
w jest sta
w jest sta
ł
ł
e
e
-
-
wyr
wyr
ó
ó
wnanie st
wnanie st
ęż
ęż
enia segment
enia segment
ó
ó
w w ca
w w ca
ł
ł
ym roztworze
ym roztworze
-
-
pocz
pocz
ą
ą
tek przenikania si
tek przenikania si
ę
ę
k
k
łę
łę
bk
bk
ó
ó
w polimeru
w polimeru
Łańcuch polimeru w roztworze
St
St
ęż
ęż
ony roztw
ony roztw
ó
ó
r
r
-
-
oddzia
oddzia
ł
ł
ywania mi
ywania mi
ę
ę
dzy segmentami pochodz
dzy segmentami pochodz
ą
ą
cymi od r
cymi od r
ó
ó
ż
ż
nych
nych
ł
ł
a
a
ń
ń
cuch
cuch
ó
ó
w
w
-
-
przenikanie si
przenikanie si
ę
ę
k
k
łę
łę
bk
bk
ó
ó
w polimeru
w polimeru
r
G
s
c
R
N
c
c
〉
≈
〉
∗
3
St
St
ęż
ęż
enie
enie
segment
segment
ó
ó
w
w
wewn
wewn
ą
ą
trz izolowanego
trz izolowanego
pojedynczego k
pojedynczego k
łę
łę
bka makrocz
bka makrocz
ą
ą
steczki
steczki
r
c
s
c
∗
c
-
-
roztw
roztw
ó
ó
r rozcie
r rozcie
ń
ń
czony
czony
-
-
roztw
roztw
ó
ó
r o st
r o st
ęż
ęż
eniu granicznym
eniu granicznym
-
-
roztw
roztw
ó
ó
r st
r st
ęż
ęż
ony
ony
G
R
-
-
promie
promie
ń
ń
bezw
bezw
ł
ł
adno
adno
ś
ś
ci
ci
N
-
-
liczba segment
liczba segment
ó
ó
w w przeci
w w przeci
ę
ę
tnej
tnej
cz
cz
ą
ą
steczce
steczce

Łańcuch polimeru w roztworze
Poj
Poj
ę
ę
cie obj
cie obj
ę
ę
to
to
ś
ś
ci wy
ci wy
łą
łą
czonej
czonej
Oddzia
Oddzia
ł
ł
ywanie rozpuszczalnika z segmentami
ywanie rozpuszczalnika z segmentami
ł
ł
a
a
ń
ń
cucha
cucha
polimerowego powoduje wyst
polimerowego powoduje wyst
ę
ę
powanie tzw.
powanie tzw.
efektu obj
efektu obj
ę
ę
to
to
ś
ś
ci wy
ci wy
łą
łą
czonej
czonej
W dobrym rozpuszczalniku k
W dobrym rozpuszczalniku k
łę
łę
bki nie przenikaj
bki nie przenikaj
ą
ą
si
si
ę
ę
–
–
powodem tego jest
powodem tego jest
zaniedbywana (w rozwa
zaniedbywana (w rozwa
ż
ż
aniach teoretycznych) realna obj
aniach teoretycznych) realna obj
ę
ę
to
to
ść
ść
segment
segment
ó
ó
w
w
W najprostszym opisie ilo
W najprostszym opisie ilo
ś
ś
ciowym efekt obj
ciowym efekt obj
ę
ę
to
to
ś
ś
ci wy
ci wy
łą
łą
czonej opisywany jest
czonej opisywany jest
parametrem
parametrem
χ
χ
(bezwymiarowy) okre
(bezwymiarowy) okre
ś
ś
laj
laj
ą
ą
cy charakter oddzia
cy charakter oddzia
ł
ł
ywa
ywa
ń
ń
polimer
polimer
-
-
rozpuszczalnik
rozpuszczalnik
χ
χ
≤
≤
0 d
0 d
obry rozpuszczalnik
obry rozpuszczalnik
χ
χ
≈
≈
1/2 s
1/2 s
ł
ł
aby rozpuszczalnik (r
aby rozpuszczalnik (r
ó
ó
wnowaga)
wnowaga)
χ
χ
>
>
½
½
„
„
z
z
ł
ł
y rozpuszczalnik
y rozpuszczalnik
”
”

Łańcuch polimeru w roztworze
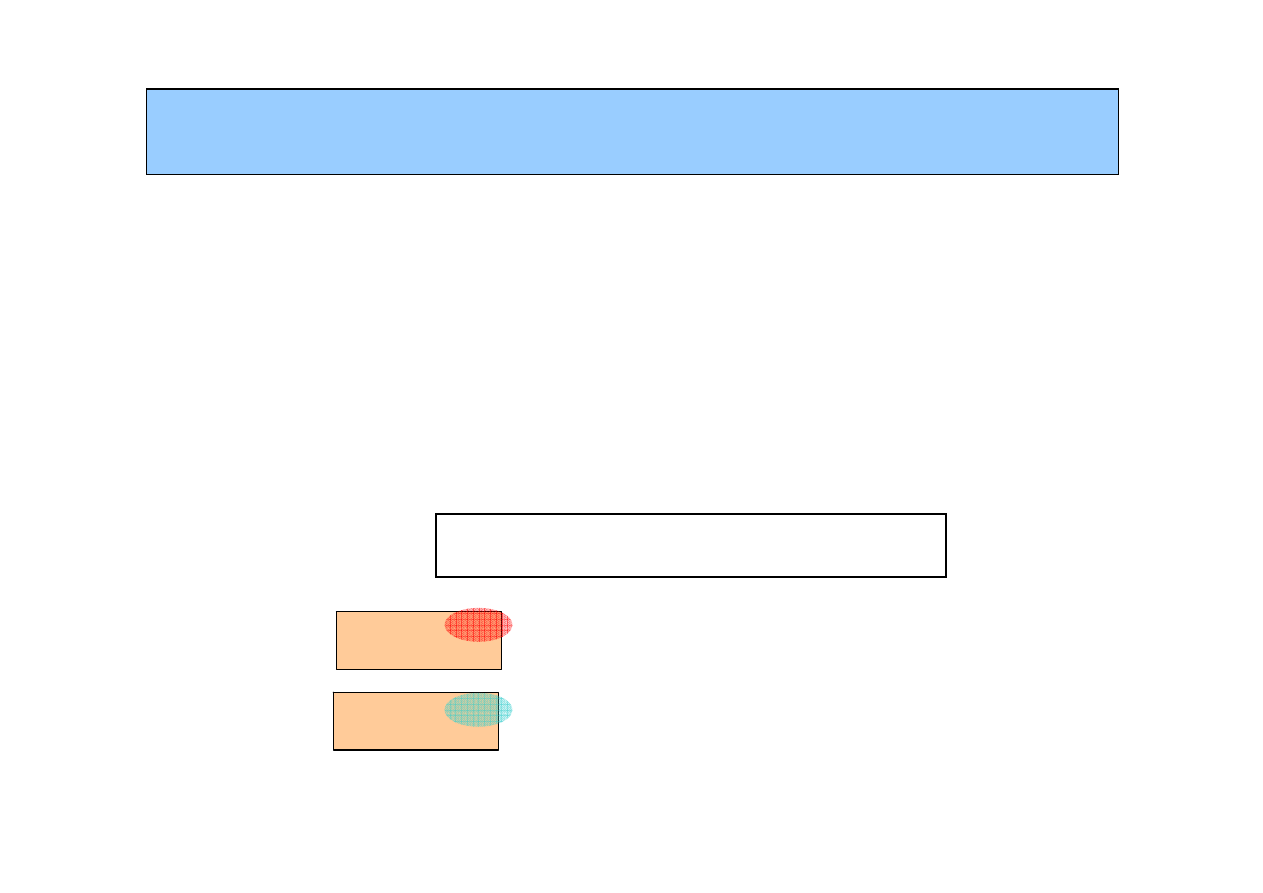
Parametr obj
Parametr obj
ę
ę
to
to
ś
ś
ci wy
ci wy
łą
łą
czonej
czonej
ν
ν
(i jego zwi
(i jego zwi
ą
ą
zek z
zek z
χ
χ
)
)
χ)
/
(
ν~b
−
2
1
3
charakteryzuje zmian
charakteryzuje zmian
ę
ę
obj
obj
ę
ę
to
to
ś
ś
ci pojedynczego
ci pojedynczego
segmentu wywo
segmentu wywo
ł
ł
ana obecno
ana obecno
ś
ś
ci
ci
ą
ą
rozpuszczalnika
rozpuszczalnika
b
b
–
–
d
d
ł
ł
ugo
ugo
ść
ść
elementarnego fragmentu
elementarnego fragmentu
makrocz
makrocz
ą
ą
steczki (segmentu)
steczki (segmentu)
Łańcuch polimeru w roztworze
Je
Je
ż
ż
eli w roztworze nie wyst
eli w roztworze nie wyst
ę
ę
puj
puj
ą
ą
netto
netto
ż
ż
adne oddzia
adne oddzia
ł
ł
ywania, np.
ywania, np.
przyci
przyci
ą
ą
ganie segment
ganie segment
-
-
segment r
segment r
ó
ó
wnowa
wnowa
ż
ż
one s
one s
ą
ą
oddzia
oddzia
ł
ł
ywaniem
ywaniem
segment
segment
–
–
rozpuszczalnik, w
rozpuszczalnik, w
ó
ó
wczas k
wczas k
łę
łę
bki maj
bki maj
ą
ą
takie wymiary
takie wymiary
jakie mia
jakie mia
ł
ł
yby
yby
ł
ł
a
a
ń
ń
cuchy w przestrzeni
cuchy w przestrzeni
Dla danej pary polimer – rozpuszczalnik istnieje
temperatura, w której spęczniający efekt rozpuszczalnika
(oddziaływania z rozpuszczalnikiem) równoważony jest
przez wzajemne przyciąganie segmentów
Jest to temperatura
Jest to temperatura
theta
theta
(
(
θ
θ
)
)
2
/
1
bN
R
G
≈
dla rozpuszczalnika
dla rozpuszczalnika
θ
θ
dla dobrego rozpuszczalnika
dla dobrego rozpuszczalnika
5
/
3
bN
R
G
≈
Wyszukiwarka
Podobne podstrony:
promien bezwladnosci i makrocza Nieznany
dlugosc persystentna promien bezwladnosci
3B Promieniowanie jonizujące
sem 2 promieniowanie rtg
Promieniowanie ultrafioletowe
Dozymetria Promieniowania Jonizującego cz 1
PROMIENIOWANIE JONIZUJĄCE2
Promieniowanie podczerwone(1)
Wpływ promieniowania jonizującego na materiał biologiczny
Promieniowanie słoneczne
Wpływ pyłów i promieniowania na uszkodzenie j ustenj(2)
Promieniowanie jonizujące(1)
07 04 Materialy promieniotworcze i radioaktywne
PROMIENIOWANIE
więcej podobnych podstron