PRZYKŁAD OBLICZENIOWY Z KONSTRUKCJI MUROWYCH

wg PN-EN 1996-1-1

ŚCIANA ZEWNĘTRZNA NA OSTATNIEJ

KONDYGNACJI

KONDYGNACJI

1

2

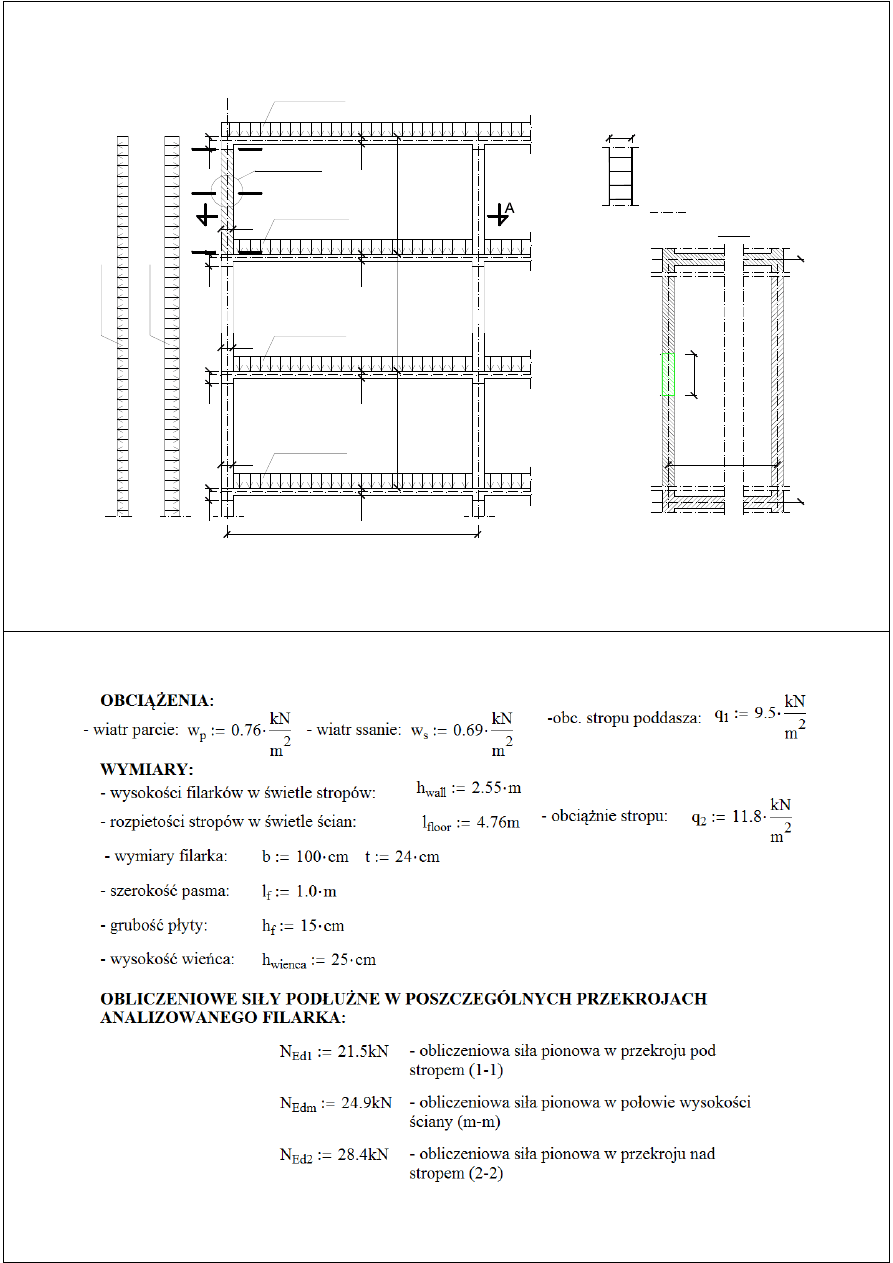
SZCZEGÓŁ A

24

25

25

2

1

28

0

III KONDYGNACJA

24

15

2

SZCZEGÓŁ A

1

28

0

15

IV KONDYGNACJA

q

2

=11.8kN/m2

q

1

=9.5kN/m2

m

m

w

p=

0,

76

kN

/m

2

pa

rci

e

w

ia

tr

u

w

s=

0,

69

kN

/m

2

ssa

ni

e

w

ia

tr

u

A

A - A

3

25

25

28

0

15

500

I KONDYGNACJA

24

q

2

=11.8kN/m2

15

II KONDYGNACJA

q

2

=11.8kN/m2

obc. stałe + zmienne

24

28

0

w

p=

0,

76

kN

/m

2

pa

rci

e

w

ia

tr

u

w

s=

0,

69

kN

/m

2

ssa

ni

e

w

ia

tr

u

10

0

500

70

0

4

5

6

7

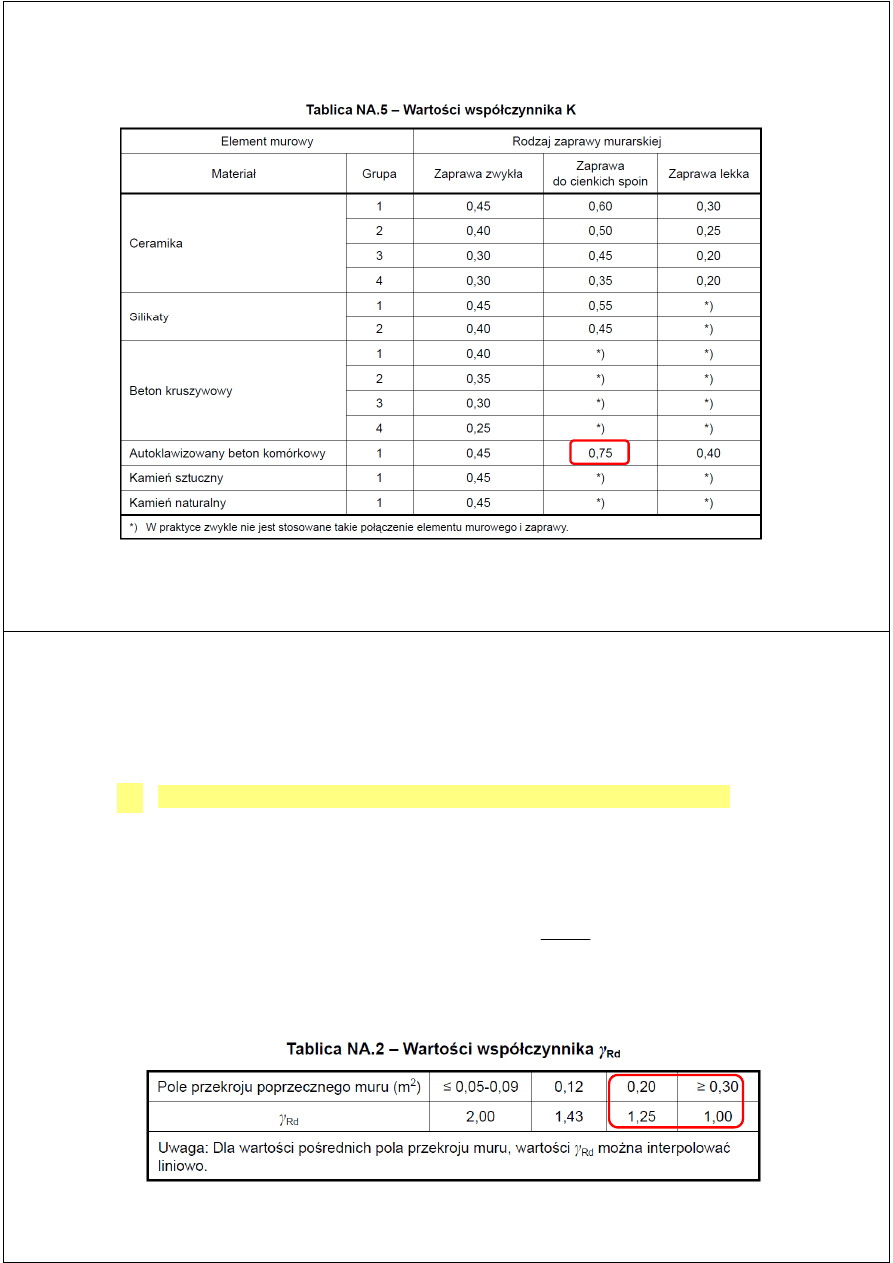
WYTRZYMAŁOŚĆ OBLICZENIOWA MURU (p. 2.4.3, p. 6.1.2.1):

γ

m

1.7

:=

- częściowy współczynnik bezpieczeństwa p. 2.4.3 tabl. NA.1

γ

Rd

- współczynnik z Tab. NA2(zał. krajowy), zależy od pola powierzchni filarka tu:

Powierzchnia filarka: A

f

b t

⋅

:=

A

f

0.24 m

2

=

γ

Rd

1.0

:=

A

f

0.3m

2

<

tu pasmo ściany więc

f

d

f

k

γ

γ

⋅

:=

f

d

2.02 MPa

=

8

f

d

γ

m

γ

Rd

⋅

:=

f

d

2.02 MPa

=

9

10

11

Charakterystyki poszczególnych prętów (EI):

Moduły sprężystości:
moduł sprężystości muru (p. 3.7.2 NA.6): K

E

600

:=

E

K

E

f

k

⋅

:=

E

2.06 GPa

=

moduł sprężystości betonu: E

cm

30 GPa

⋅

:=

12

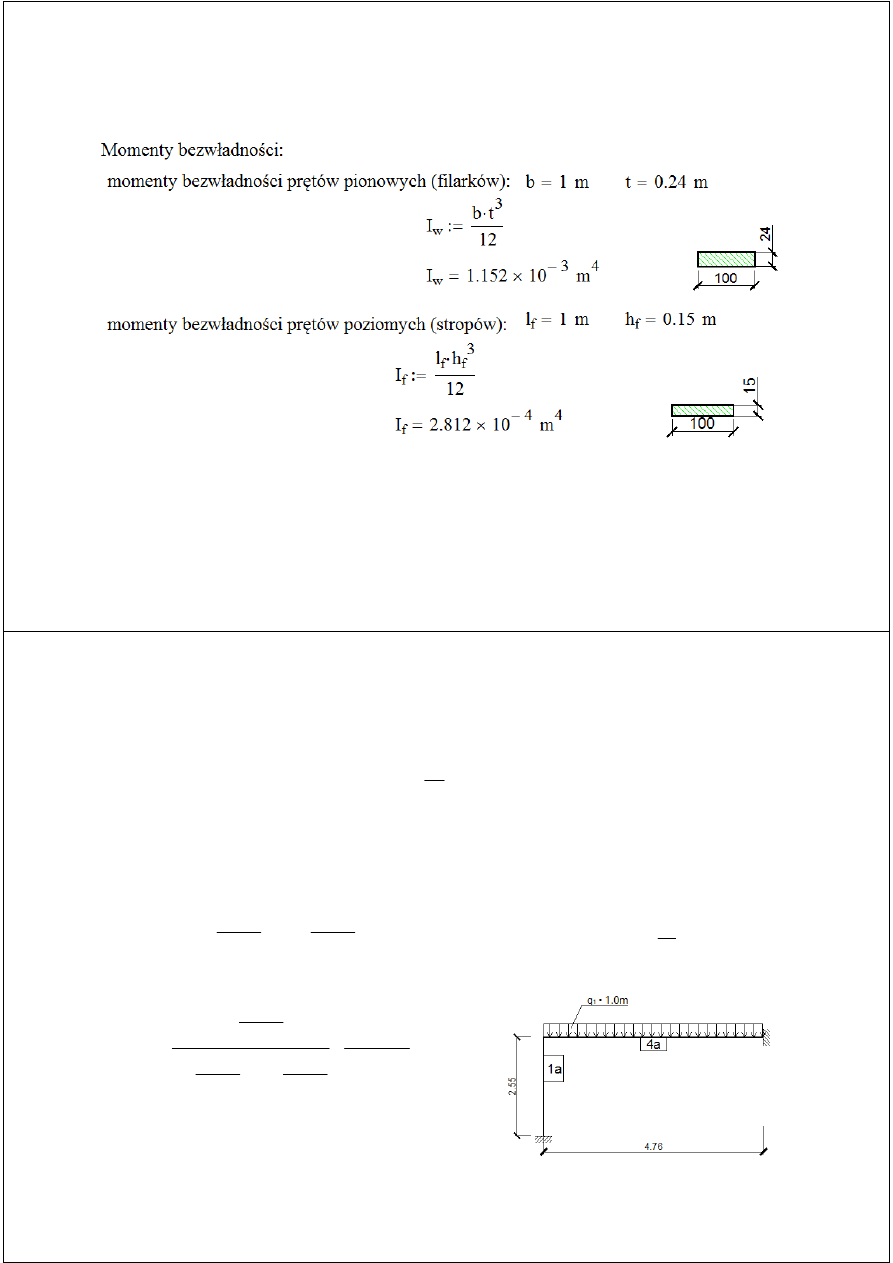
13

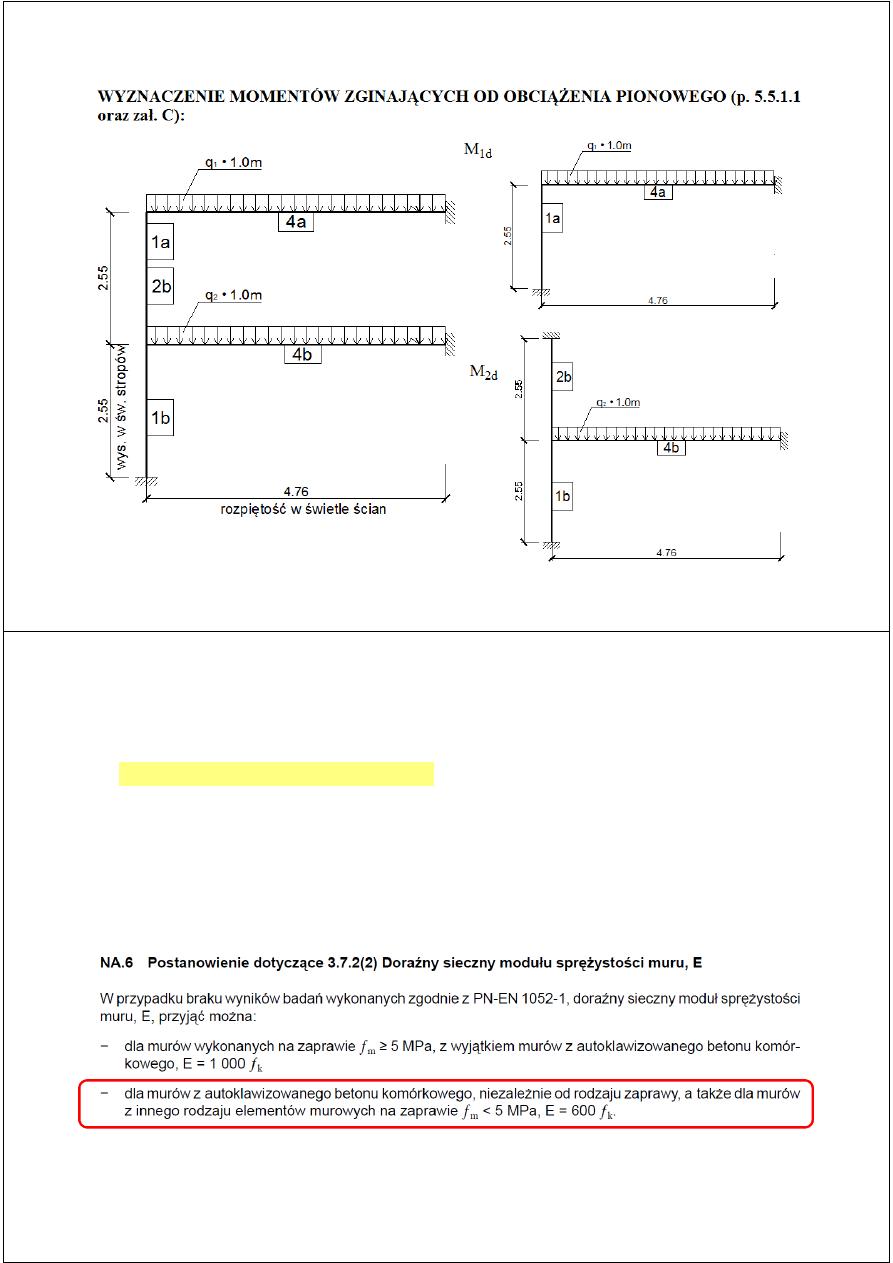
Momenty zginające w poszczególnych przekrojach filarka od obciążenia pionowego (zał. C):
Moment u góry ściany:

- obciążenie pasma stropu: w

4a

q

1

l

f

⋅

:=

w

4a

9.5

kN

m

=

- współczynnik redukujący moment w węźle ze względu na brak całkowitej sztywności węzła

-pręty utwierdzone => n

1a

4

:=

n

4a

4

:=

E

1a

E

:=

E

4a

E

cm

:=

h

1a

h

w all

:=

l

4a

l

floor

:=

I

1a

I

w

:=

I

4a

I

f

:=

k

m

min

n

4a

E

4a

I

4a

⋅

l

4a

⋅













n

1a

E

1a

I

1a

⋅

h

1a

⋅













1

−

⋅

2.0

,













:=

η

1

k

m

4

−













:=

(C.2)

η

0.52

=

l

4a





h

1a









4





(C.2)

η

0.52

=

k

m

1.9

=

M

1d

η

n

1a

E

1a

I

1a

⋅

h

1a

n

1a

E

1a

I

1a

⋅

h

1a

n

4a

E

4a

I

4a

⋅

l

4a

+

⋅

w

4a

l

4a

2

⋅

4 n

4a

1

−

(

)













⋅

:=

M

1d

3.24 kN m

⋅

=

(C.1)

14

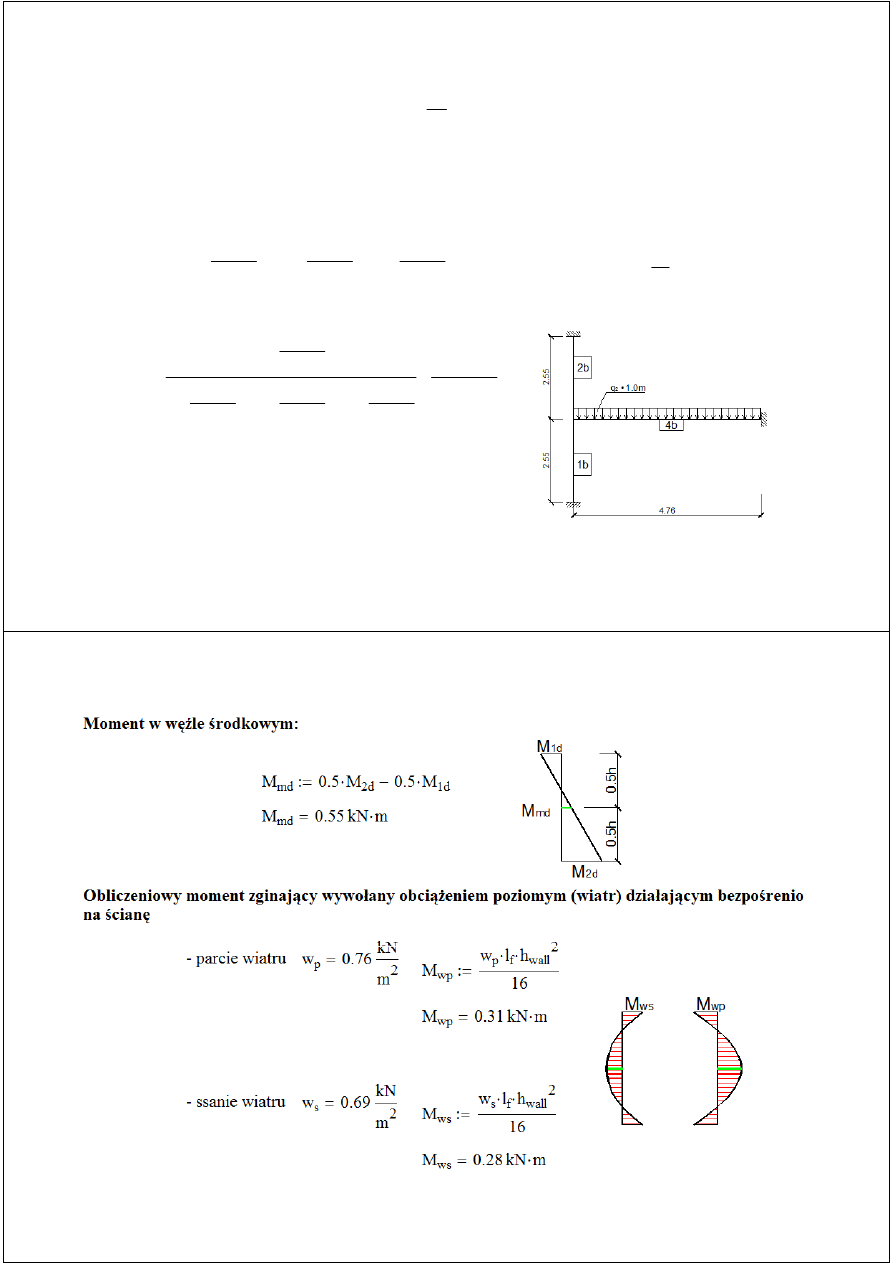
Moment u dołu ściany:

- obciążenie pasma stropu: w

4b

q

2

l

f

⋅

:=

w

4b

11.8

kN

m

=

- współczynnik redukujący moment w węźle ze względu na brak całkowitej sztywności węzła

-pręty utwierdzone => n

1b

4

:=

n

2b

4

:=

n

4b

4

:=

E

1b

E

:=

E

2b

E

:=

E

4b

E

cm

:=

h

1b

h

w all

:=

h

2b

h

w all

:=

l

4b

l

floor

:=

I

1b

I

w

:=

I

2b

I

w

:=

I

4b

I

f

:=

k

m

min

n

4b

E

4b

I

4b

⋅

l

4b

⋅













n

1b

E

1b

I

1b

⋅

h

1b

⋅

n

2b

E

2b

I

2b

⋅

h

2b

⋅

+













1

−

⋅

2.0

,













:=

(C.2)

η

1

k

m

4

−













:=

η

0.76

=

k

m

0.95

=

15

M

2d

η

n

2b

E

2b

I

2b

⋅

h

2b

n

1b

E

1b

I

1b

⋅

h

1b

n

2b

E

2b

I

2b

⋅

h

2b

+

n

4b

E

4b

I

4b

⋅

l

4b

+

⋅

w

4b

l

4b

2

⋅

4 n

4b

1

−

(

)













⋅

:=

M

2d

4.35 kN m

⋅

=

(C.1)

16

WYZNACZENIE MIMOŚRODÓW I SPRAWDZENIE NOŚNOŚCI W POSZCZEGÓLNYCH

PRZEKROJACH FILARKA:

Wysokość efektywna ściany (p. 5.5.1.2):

e

1

M

1d

N

Ed1

M

w p

N

Ed1

+

:=

e

1

16.52 cm

=

0.25 t

⋅

6 cm

=

- długość ściany pomiędzy ścianami prostopałdymi: l

1

7m

:=

30 t

⋅

7.2 m

=

l

1

30 t

⋅

≥

0

=

=> ścian usztywniona na
krawędziach pionowych

h

h

w all

:=

h

2.55 m

=

h

1.15l

1

≤

1

=

e

0.25t

≤

0

=

=>

ρ

1.0

:=

17

e

1

0.25t

≤

0

=

=>

ρ

2

1.0

:=

ρ

4

1

1

ρ

2

h

l

1

⋅













2

+

ρ

2

⋅

:=

ρ

4

0.88

=

ρ

n

ρ

4

:=

h

ef

ρ

n

h

⋅

:=

h

ef

2.25 m

=

Mimośród początkowy: (p. 5.5.1.1)

e

init

h

ef

450

:=

e

init

0.5 cm

=

18

19

20

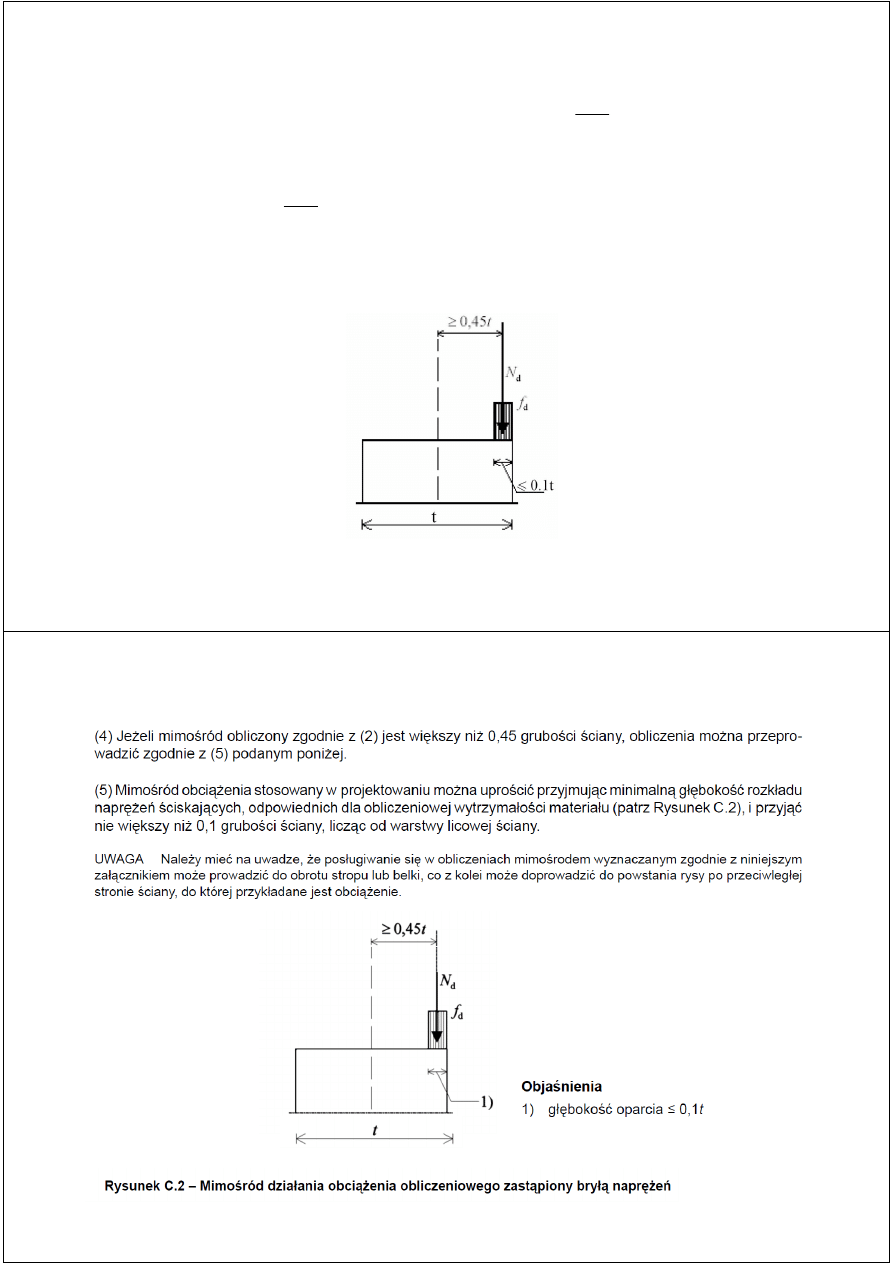
PRZEKRÓJ 1-1

Mimośród od obciążenia poziomego (wiatr-parcie):

e

h1

M

w p

N

Ed1

:=

e

h1

1.44 cm

=

Mimośród u góry ściany (p. 6.1.2.2):

e

1

M

1d

N

Ed1

e

h1

+

e

init

+

:=

> 0.05 t

⋅

1.2 cm

=

(6.5)

e

1

17.02 cm

=

0.45 t

⋅

10.8 cm

=

e

1

0.45 t

⋅

>

=> ZMIANA SPOSOBU WYZNACZANIA MIMOŚRODU
(zał. C p.4)

21

22

- wysokość strefy przekazywania naprężeń
ze stropu:

x

w

min

N

Ed1

f

d

b

⋅

0.1t

,













:=

N

Ed1

f

d

b

⋅

1.06 cm

=

x

w

1.06 cm

=

0.1t

2.4 cm

=

- moment w przekroju 1-1:

M

1d

N

Ed1

0.5 t

⋅

0.5 x

w

⋅

−

(

)

⋅

:=

M

1d

2.47 kN m

⋅

=

Mimośród u góry ściany (p. 6.1.2.2):

e

h1

0 cm

⋅

:=

e

1

M

1d

N

Ed1

:=

>

0.05 t

⋅

1.2 cm

=

(6.5)

23

N

Ed1

e

1

11.47 cm

=

Współczynnik redukcyjny (p. 6.1.2.2):

Φ

1

1

2 e

1

⋅

t

−

:=

Φ

1

0.04

=

(6.4)

Nośność obliczeniowa ściany w przekroju pod stropem górnej
kondygnacji (p. 6.1.2.1)

b

1 m

=

t

0.24 m

=

N

Rd1

Φ

1

t

⋅ f

d

⋅

b

⋅

:=

(6.1)

N

Rd1

21.5 kN

=

> N

Ed1

21.5 kN

=

nośność wystarczająca

PRZEKRÓJ 2-2

- wysokość strefy przekazywania
naprężeń ze stropu:

x

w

min

N

Ed2

f

d

b

⋅

0.1t

,













:=

N

Ed2

f

d

b

⋅

1.4 cm

=

x

w

1.4 cm

=

0.1t

2.4 cm

=

- moment w przekroju 2-2:

M

2d

N

Ed2

0.5 t

⋅

0.5 x

w

⋅

−

(

)

⋅

:=

M

2d

3.21 kN m

⋅

=

Mimośród u dołu ściany (p. 6.1.2.2):

e

2

M

2d

N

Ed2

:=

> 0.05t 1.2cm

=

(6.5)

e

2

max e

2

0.05t

,

(

)

:=

24

e

2

max e

2

0.05t

,

(

)

:=

e

2

11.3 cm

=

Współczynnik redukcyjny (p. 6.1.2.2):

Φ

2

1

2 e

2

⋅

t

−

:=

Φ

2

0.06

=

(6.4)

Nośność obliczeniowa ściany w przekroju pod stropem górnej
kondygnacji (p. 6.1.2.1)

N

Rd2

Φ

2

t

⋅ f

d

⋅

b

⋅

:=

(6.1)

N

Rd2

28.4 kN

=

> N

Ed2

28.4 kN

=

nośność wystarczająca

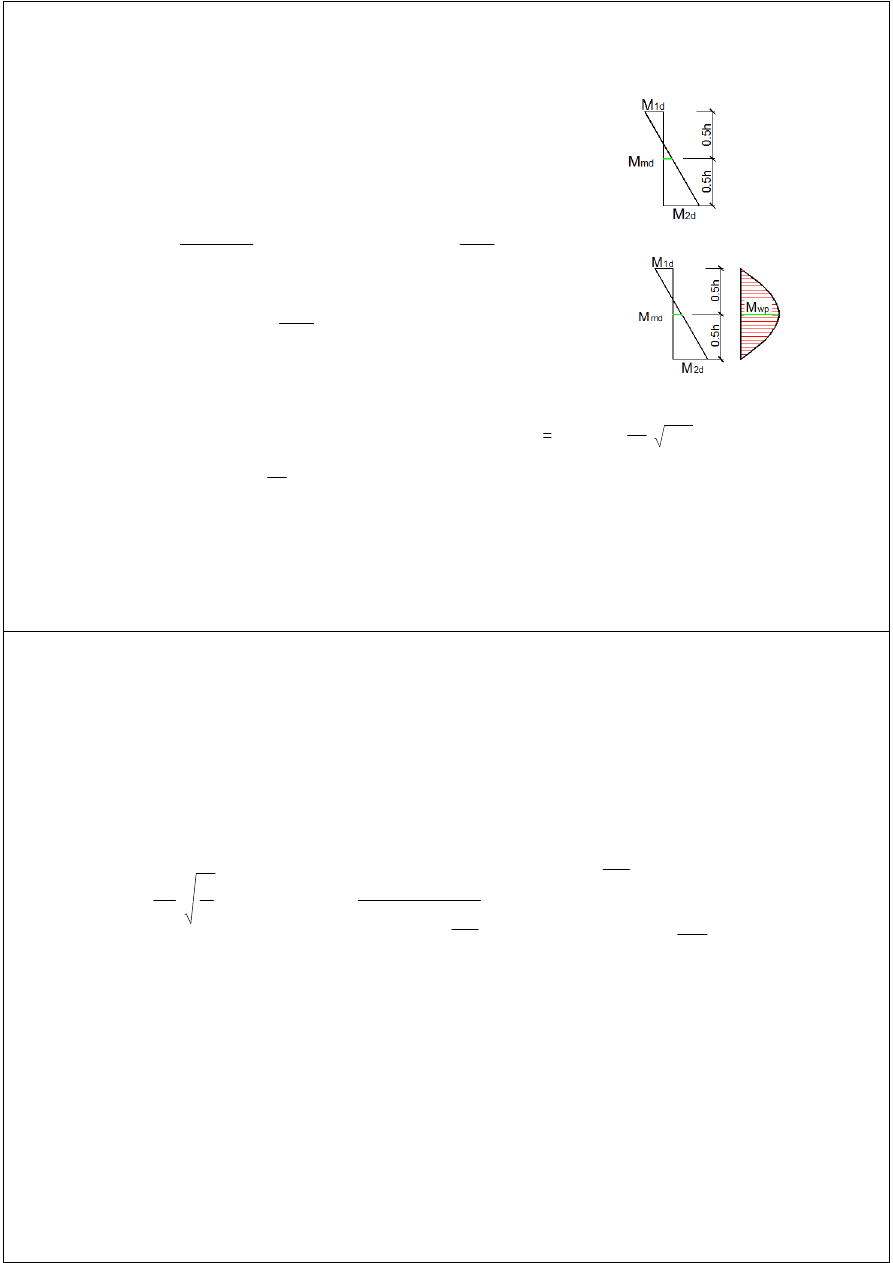
PRZEKRÓJ m-m

Moment od obciążenia pionowego w środku ściany:

M

md

0.5M

2d

0.5M

1d

−

:=

M

md

0.37 kN m

⋅

=

Mimośród od obciążenia poziomego (wiatr-parcie):

M

w p

w

p

l

f

h

w all

2

⋅

⋅

8

:=

M

w p

0.62 kN m

⋅

=

e

hm

M

w p

N

Edm

:=

e

hm

2.48 cm

=

Mimośród działania obciążenia (p. 6.1.2.2):

e

M

md

e

+

e

+

:=

25

e

m

M

md

N

Edm

e

hm

+

e

init

+

:=

>

0.05 t

⋅

1.2 cm

=

(6.7)

e

m

4.47 cm

=

e

m

max e

m

0.05t

,

(

)

:=

e

m

4.47 cm

=

Mimośród wywołany przez pełzanie: e

k

t

ef

t

:=

e

k

0.002

φ

oo

⋅

h

ef

t

ef

⋅

t e

m

⋅

⋅

λ

c

h

ef

t

:=

λ

c

9.38

=

λ

c

15

≤

=>

e

k

0 cm

⋅

:=

Mimośród w połowie wysokości ściany:

e

mk

e

m

e

k

+

:=

(6.6)

e

mk

4.47 cm

=

Współczynnik redukcyjny w połowie wysokości ściany (zał. G):

t

ef

t

:=

E

600 f

k

⋅

:=

E

2.06 GPa

=

A

1

1

2

e

mk

t

⋅

−

:=

A

1

0.63

=

(G.2)

λ

h

ef

t

ef

f

k

E

⋅

:=

u

λ

0.063

−

0.73

1.17

e

mk

t

⋅

−

:=

(G.4)

(G.3)

(G.1)

Φ

A e

u

2

−

2

⋅

:=

26

t

(G.1)

Φ

m

A

1

e

2

⋅

:=

λ

0.38

=

u

0.62

=

Φ

m

0.52

=

Nośność obliczeniowa w środku ściany (p. 6.1.2.1)

N

Rdm

Φ

m

t

⋅ f

d

⋅

b

⋅

:=

(6.1)

N

Rdm

250.54 kN

=

> N

Edm

24.9 kN

=

nośność wystarczająca