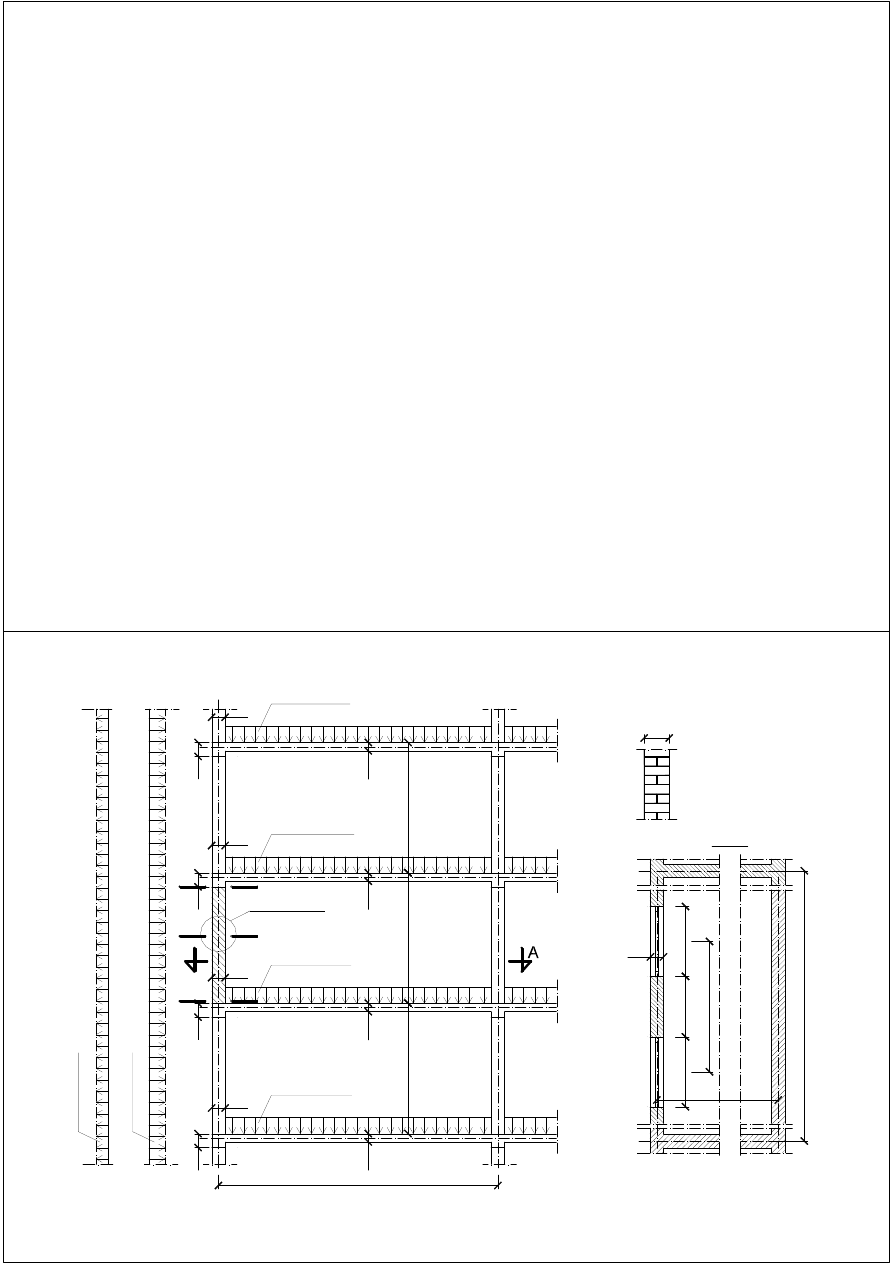
PRZYKŁAD OBLICZEIOWY Z KOSTRUKCJI MUROWYCH
FILAREK MIĘDZYOKIEY wg P-E 1996-1-1
Sprawdzić nośność filarka międzyokiennego ściany zewnętrznej na II kondygnacji w budynku
pokazanym na rysunku.
MATERIAŁY:
I, II, III KONDYGNACJA: ściany z elementów murowych ceramicznych grupy 1, f
b
=20MPa (np.
cegła pełna) , kategoria produkcji I, na zaprawie cem.-wap. M10, klasa wykonania robót B,
STROPY: płyta żelbetowa gr. 18cm z betonu C20/25, E
cm
=30GPa
OBCIĄŻEIA:
Całkowite obciążenie stropów: q=12.8kN/m
2
(wartość obliczeniowa uwzględniająca ciężar własny i
obciążenie zmienne stropów)
Obciążenie wiatrem (wartości obliczeniowe): parcie w
p
=0.76kN/m
2
; ssanie w
s
=0.69kN/m
2
Całkowite, obliczeniowe siły ściskające w przekrojach 1-1, m-m, 2-2, wynoszą odpowiednio:
N
1d
= 337.8kN; N
md
= 349.3kN; N
2d
= 360.7kN.
2
8
0
III KONDYGNACJA
25
1
8
1
8
II KONDYGNACJA
q=12,8kN/m2
obc. stałe + zmienne
25
2
SZCZEGÓŁ A
1
2
8
0
1
8
IV KONDYGNACJA
q=12,8kN/m2
q=12,8kN/m2
25
m
m
w
p
=
0
,7
6
k
N
/m
2
p
a
rc
ie
w
ia
tr
u
w
s
=
0
,6
9
k
N
/m
2
s
s
a
n
ie
w
ia
tr
u
A
7
0
0
2
5
2
5
2
5
2
5
2
1
2
8
0
1
8
600
I KONDYGNACJA
25
q=12,8kN/m2
SZCZEGÓŁ A
25
1
5
0
1
3
0
1
5
0
A - A
25
2
8
0
600
OBCIĄŻEIA:
- wiatr parcie:
w
p
0.76
kN
m
2
⋅
=
- wiatr ssanie: w
s
0.69
kN
m
2
⋅
=
- obciążnie stropu: q
12.8
kN
m
2
⋅
=
WYMIARY:
h
wall
2.55 m
⋅
=
- wysokości filarków w świetle stropów:
- rozpietości stropów w świetle ścian:
l
floor
5.75m
=
- wymiary filarka:
b
130 cm
⋅
=
t
25 cm
⋅
=
- szerokość pasmo:
l
f
2.80 m
⋅
=
- grubość płyty:
h
f
18 cm
⋅
=
- wysokość wieńca:
h
wienca
25 cm
⋅
=
OBLICZEIOWE SIŁY PODŁUŻE W POSZCZEGÓLYCH PRZEKROJACH
AALIZOWAEGO FILARKA:
N
Ed1
337.8kN
=
- obliczeniowa siła pionowa w przekroju pod
stropem (1-1)
N
Edm
349.3kN
=
- obliczeniowa siła pionowa w połowie wysokości
ściany (m-m)
N
Ed2
360.7kN
=
- obliczeniowa siła pionowa w przekroju nad
stropem (2-2)
WYTRZYMAŁOŚĆ CHARAKTERYSTYCZA MURU A ŚCISKAIE (p. 3.6.1.2):
η
0.8
=
- wyływ spoiny podłużnej
K
0.45
=
- współczynnik z Tabl. NA.5
f
b
20 MPa
⋅
=
- znormalizowana wytrzymałość elementu murowego na ściskanie
f
m
10 MPa
⋅
=
- wytrzymałość zaprawy na ściskanie
f
k
η K
⋅
f
b
0.7
⋅
f
m
0.3
⋅
=
f
k
5.85 MPa
=
(NA.1)
WYTRZYMAŁOŚĆ OBLICZEIOWA MURU (p. 2.4.3):
γ
m
2.2
=
- częściowy współczynnik bezpieczeństwa tabl. NA.1
γ
Rd
- współczynnik z Tab. NA2(zał. krajowy), zależy od pola powierzchni filarka tu:
Powierzchnia filarka: A
f
b t
⋅
=
A
f
0.325 m
2
=
A
f
0.3m
2
>
więc
γ
Rd
1
=
f
d
f
k
γ
m
γ
Rd
⋅
=
f
d
2.66 MPa
=
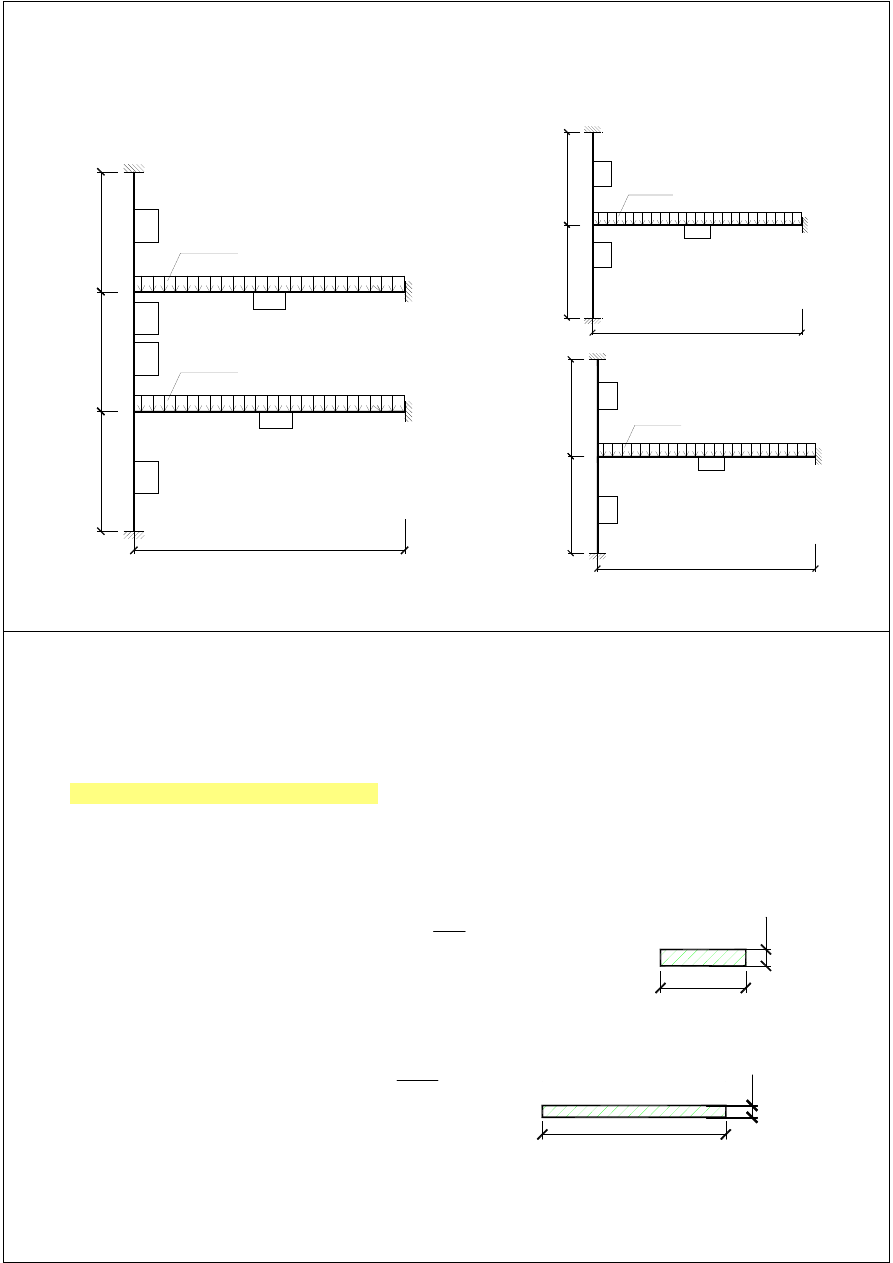
WYZACZEIE MOMETÓW ZGIAJĄCYCH OD OBCIĄŻEIA PIOOWEGO (p. 5.5.1.1
oraz zał. C):
4a
1a
5.75
2
.5
5
2
.5
5
q•
2 . 8 0 m
2a
4a
4b
1a
5.75
2
.5
5
2
.5
5
2
.5
5
q•
2 . 8 0 m
q•
2 . 8 0 m
2a
1b
rozpiętość w świetle ścian
w
y
s
.
w
ś
w
.
s
tr
o
p
ó
w
2b
M
1d
4b
5.75
2
.5
5
2
.5
5
q•
2 . 8 0 m
1b
2b
M
2d
Charakterystyki poszczególnych prętów (EI):
Moduły sprężystości:
moduł sprężystości muru (p. 3.7.2 NA.6): K
E
1000
=
E
K
E
f
k
⋅
=
E
5.85 GPa
=
moduł sprężystości betonu: E
cm
30 GPa
⋅
=
Momenty bezwładności:
momenty bezwładności prętów pionowych (filarków): b
1.3 m
=
t
0.25 m
=
130
2
5
I
w
b t
3
⋅
12
=
I
w
1.693
10
3
−
×
m
4
=
l
f
2.8 m
=
h
f
0.18 m
=
momenty bezwładności prętów poziomych (stropów):
280
1
8
I
f
l
f
h
f
3
⋅
12
=
I
f
1.361
10
3
−
×
m
4
=
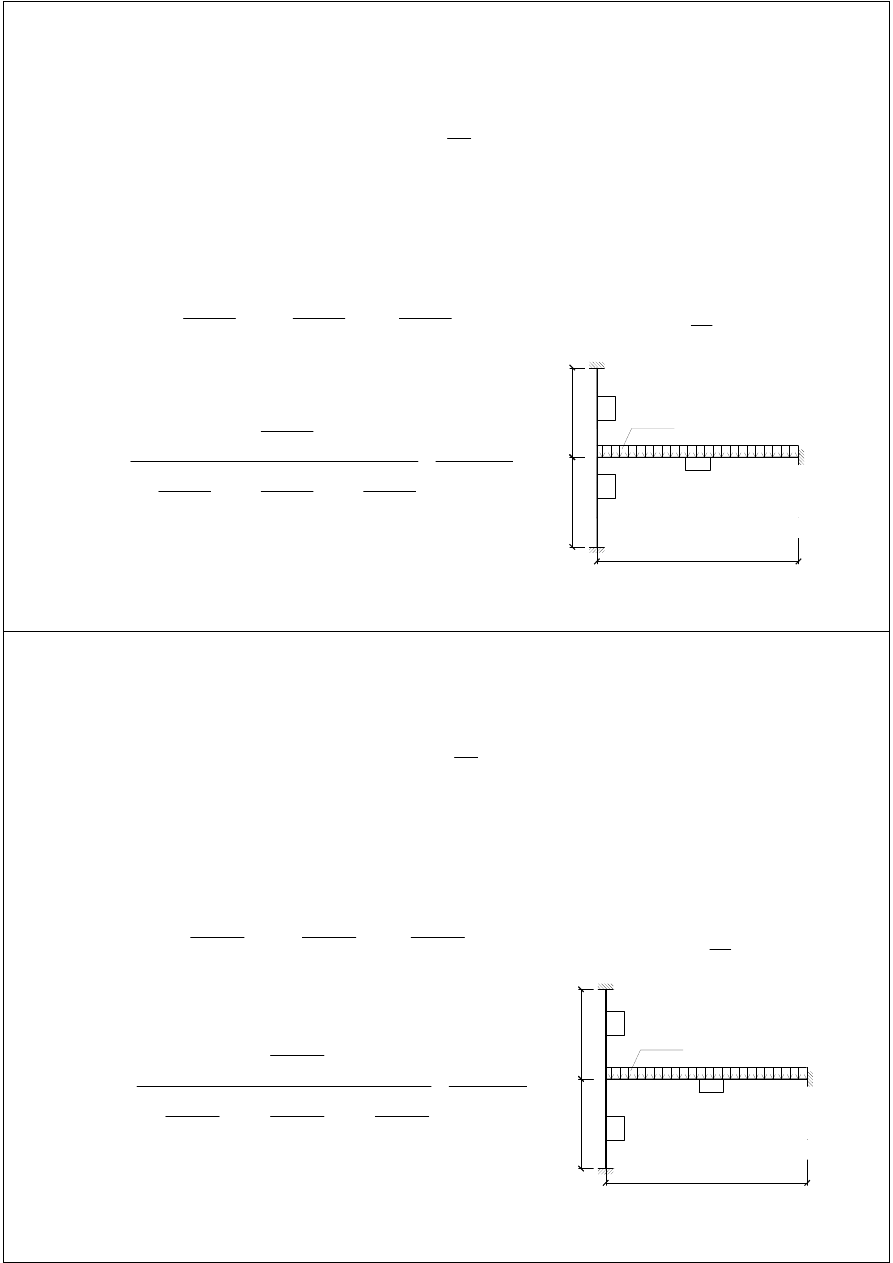
Momenty zginające w poszczególnych przekrojach filarka od obciążenia pionowego (zał. C):
Moment u góry ściany:
- obciążenie pasma stropu: w
4a
q l
f
⋅
=
w
4a
35.84
kN
m
=
- współczynnik redukujący moment w węźle ze względu na brak całkowitej sztywności węzła
-pręty utwierdzone => n
1a
4
=
n
2a
4
=
n
4a
4
=
E
1a
E
=
E
2a
E
=
E
4a
E
cm
=
h
1a
h
wall
=
h
2a
h
wall
=
l
4a
l
floor
=
I
1a
I
w
=
I
2a
I
w
=
I
4a
I
f
=
k
m
min n
4a
E
4a
I
4a
⋅
l
4a
⋅
n
1a
E
1a
I
1a
⋅
h
1a
⋅
n
2a
E
2a
I
2a
⋅
h
2a
⋅
+
1
−
⋅
2.0
,
=
(C.2)
η
1
k
m
4
−
=
η
0.77
=
4a
1a
5.75
2
.5
5
2
.5
5
q•
2 . 8 0 m
2a
k
m
0.91
=
M
1d
η
n
1a
E
1a
I
1a
⋅
h
1a
n
1a
E
1a
I
1a
⋅
h
1a
n
2a
E
2a
I
2a
⋅
h
2a
+
n
4a
E
4a
I
4a
⋅
l
4a
+
⋅
w
4a
l
4a
2
⋅
4 n
4a
1
−
(
)
⋅
=
M
1d
19.89 kN m
⋅
=
(C.1)
Moment u dołu ściany:
- obciążenie pasma stropu: w
4b
q l
f
⋅
=
w
4b
35.84
kN
m
=
- współczynnik redukujący moment w węźle ze względu na brak całkowitej sztywności węzła
-pręty utwierdzone => n
1b
4
=
n
2b
4
=
n
4b
4
=
E
1b
E
=
E
2b
E
=
E
4b
E
cm
=
h
1b
h
wall
=
h
2b
h
wall
=
l
4b
l
floor
=
I
1b
I
w
=
I
2b
I
w
=
I
4b
I
f
=
k
m
min n
4b
E
4b
I
4b
⋅
l
4b
⋅
n
1b
E
1b
I
1b
⋅
h
1b
⋅
n
2b
E
2b
I
2b
⋅
h
2b
⋅
+
1
−
⋅
2.0
,
=
(C.2)
η
1
k
m
4
−
=
η
0.77
=
4b
5.75
2
.5
5
2
.5
5
q•
2 . 8 0 m
1b
2b
k
m
0.91
=
M
2d
η
n
2b
E
2b
I
2b
⋅
h
2b
n
1b
E
1b
I
1b
⋅
h
1b
n
2b
E
2b
I
2b
⋅
h
2b
+
n
4b
E
4b
I
4b
⋅
l
4b
+
⋅
w
4b
l
4b
2
⋅
4 n
4b
1
−
(
)
⋅
=
M
2d
19.89 kN m
⋅
=
(C.1)
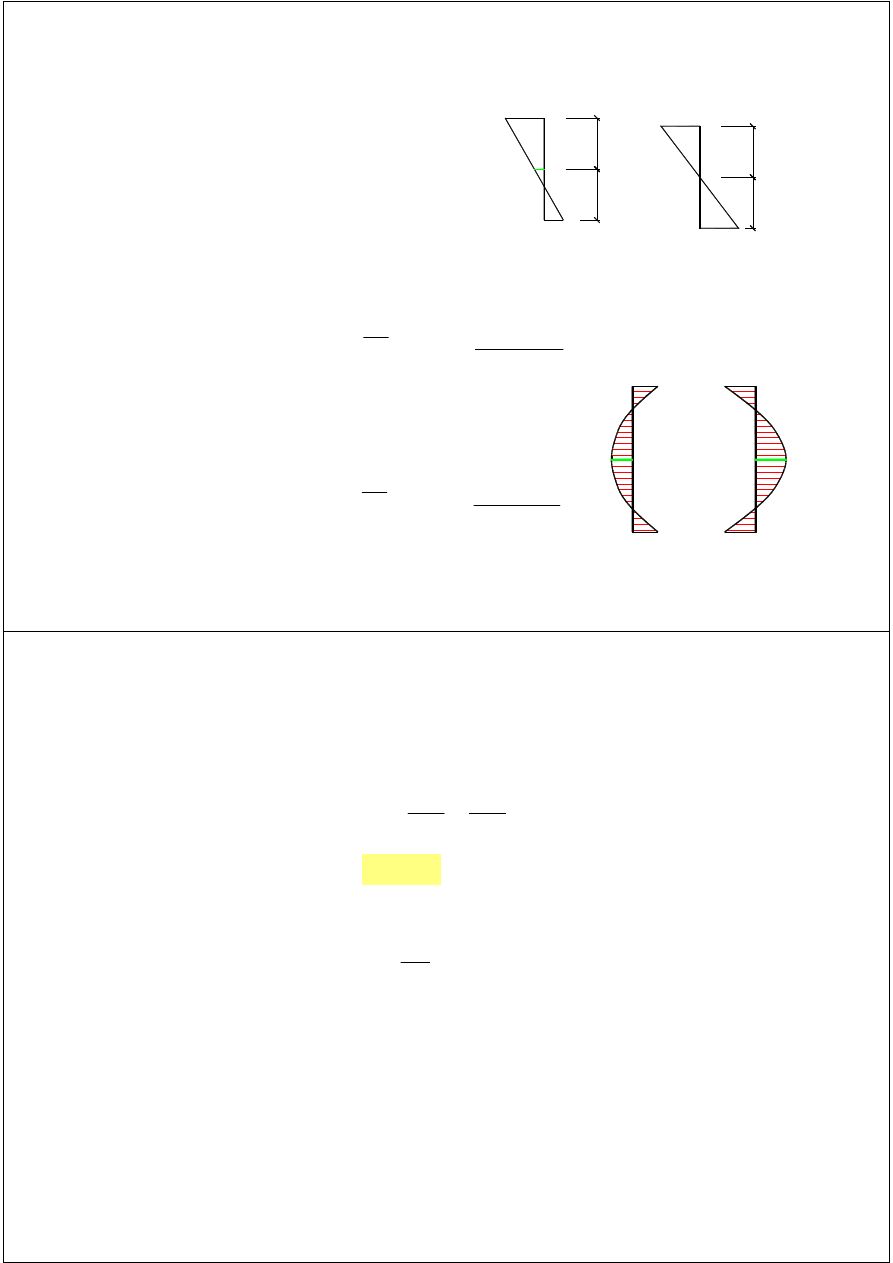
Moment w węźle środkowym:
M
1d
M
2d
0.
5h
0.
5h
M
1d
M
2d
M
md
0.
5h
0.
5h
M
md
0.5 M
1d
⋅
0.5 M
2d
⋅
−
=
M
md
0 kN m
⋅
=
Obliczeniowy moment zginający wywołany obciążeniem poziomym (wiatr) działającym bezpośrenio
na ścianę
- parcie wiatru w
p
0.76
kN
m
2
=
M
wp
w
p
l
f
⋅ h
wall
2
⋅
16
=
M
ws
M
wp
M
wp
0.86 kN m
⋅
=
- ssanie wiatru w
s
0.69
kN
m
2
=
M
ws
w
s
l
f
⋅ h
wall
2
⋅
16
=
M
ws
0.79 kN m
⋅
=
WYZACZEIE MIMOŚRODÓW I SPRAWDZEIE OŚOŚCI W POSZCZEGÓLYCH
PRZEKROJACH FILARKA:
Wysokość efektywna ściany (p. 5.5.1.2):
e
1
M
1d
N
Ed1
M
wp
N
Ed1
+
=
e
1
6.15 cm
=
0.25 t
⋅
6.25 cm
=
e
1
0.25t
≤
1
=
=>
ρ
n
0.75
=
h
h
wall
=
h
ef
ρ
n
h
⋅
=
h
ef
1.91 m
=
Mimośród początkowy: (p. 5.5.1.1)
e
init
h
ef
450
=
e
init
0.43 cm
=
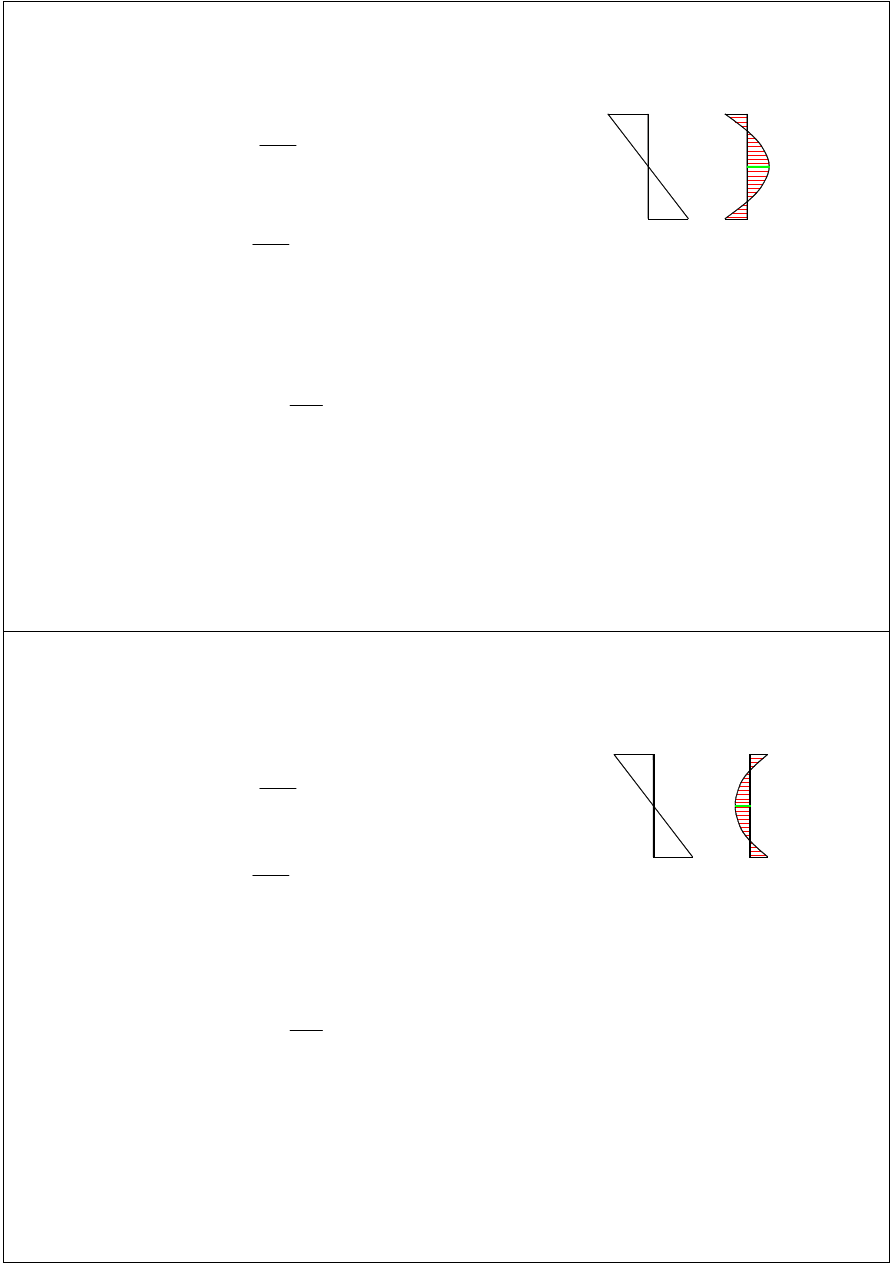
PRZEKRÓJ 1-1
M
1d
M
2d
M
wp
Mimośród od obciążenia poziomego (wiatr-parcie):
e
h1
M
wp
N
Ed1
=
e
h1
0.26 cm
=
Mimośród u góry ściany (p. 6.1.2.2):
e
1
M
1d
N
Ed1
e
h1
+
e
init
+
=
> 0.05 t
⋅
1.25 cm
=
(6.5)
e
1
6.57 cm
=
0.45 t
⋅
11.25 cm
=
e
1
0.45 t
⋅
<
=> SŁUSZNY MODEL (zał. C p.4)
Współczynnik redukcyjny (p. 6.1.2.2):
Φ
1
1
2 e
1
⋅
t
−
=
Φ
1
0.47
=
(6.4)
Nośność obliczeniowa ściany w przekroju pod stropem górnej
kondygnacji (p. 6.1.2.1)
b
1.3 m
=
t
0.25 m
=
N
Rd1
Φ
1
t
⋅ f
d
⋅
b
⋅
=
(6.1)
N
Rd1
409.83 kN
=
> N
Ed1
337.8 kN
=
nośność wystarczająca
PRZEKRÓJ 2-2
M
1d
M
2d
M
ws
Mimośród od obciążenia poziomego (wiatr-ssanie):
e
h2
M
ws
N
Ed2
=
e
h2
0.22 cm
=
Mimośród u dołu ściany (p. 6.1.2.2):
e
2
M
2d
N
Ed2
e
h2
+
e
init
+
=
> 0.05 t
⋅
1.25 cm
=
(6.5)
e
2
6.16 cm
=
0.45 t
⋅
11.25 cm
=
e
2
0.45 t
⋅
<
=> SŁUSZNY MODEL (zał. C p.4)
Współczynnik redukcyjny (p. 6.1.2.2):
Φ
2
1
2 e
2
⋅
t
−
=
Φ
2
0.51
=
(6.4)
Nośność obliczeniowa ściany w przekroju pod stropem górnej kondygnacji (p. 6.1.2.1)
N
Rd2
Φ
2
t
⋅ f
d
⋅
b
⋅
=
(6.1)
N
Rd2
438.32 kN
=
> N
Ed2
360.7 kN
=
nośność wystarczająca
M
1d
M
2d
M
ws
M
wp
0
.5
h
0
.5
h
PRZEKRÓJ m-m
Mimośród od obciążenia poziomego (wiatr-parcie):
e
hm
M
wp
N
Edm
=
e
hm
0.25 cm
=
Mimośród działania obciążenia (p. 6.1.2.2):
e
m
M
md
N
Edm
e
hm
+
e
init
+
=
>
0.05 t
⋅
1.25 cm
=
(6.7)
e
m
0.67 cm
=
e
m
max e
m
0.05t
,
(
)
=
e
m
1.25 cm
=
Mimośród wywołany przez pełzanie: e
k
t
ef
t
=
e
k
0.002 φ
oo
⋅
h
ef
t
ef
⋅
t e
m
⋅
⋅
=
λ
c
h
ef
t
=
λ
c
7.65
=
λ
c
15
≤
=>
e
k
0 cm
⋅
=
Mimośród w połowie wysokości ściany:
e
mk
e
m
e
k
+
=
(6.6)
e
mk
1.25 cm
=
Współczynnik redukcyjny w połowie wysokości ściany (zał. G):
t
ef
t
=
E
1000 f
k
⋅
=
E
5.85 GPa
=
A
1
1
2
e
mk
t
⋅
−
=
A
1
0.9
=
(G.2)
λ
h
ef
t
ef
f
k
E
⋅
=
u
λ
0.063
−
0.73
1.17
e
mk
t
⋅
−
=
(G.4)
(G.3)
(G.1)
Φ
m
A
1
e
u
2
−
2
⋅
=
λ
0.24
=
u
0.27
=
Φ
m
0.87
=
Nośność obliczeniowa w środku ściany (p. 6.1.2.1)
N
Rdm
Φ
m
t
⋅ f
d
⋅
b
⋅
=
(6.1)
N
Rdm
750.43 kN
=
> N
Edm
349.3 kN
=
nośność wystarczająca