Zadanie 1. Z platformą manipulatora równoległego związany jest układ π

1

, natomiast

układ π

0

związany jest z podstawą. W danej chwili usytułowanie układu π

1

względem π

0

opisuje

wektor r

(0)
01

i kąt obrotu względnego α. Na platformę działa siła F przechodząca przez początek

układu π

1

oraz moment M . Manipulator nie porusza się. Obciążenie zewnętrzne równoważone

jest przez siły napędowe, każda wynosi τ = 100 N. Obliczyć moment M .

x

0

y

0

x

1

y

1

α

B

C

M

F

r

C

r

B

s

P

P

r

(0)
01

= [4 2]

>

r

(0)
B

= [8 2]

>

r

(0)
C

= [4 4]

>

s

(1)
P

= [5 0]

>

sin α = 0.8

cos α = 0.6

Zadanie 2. Uwaga moment oznaczony J

(0)
P

wyznaczony został dla układu współrzędnych

o początku w punkcie P. Obliczyć energię kinetyczną członu wirującego z prędkością kątową ω

p

q

p

q

A

B

C

ω

x

0

y

0

ω = [−1 2 0]

>

p = 2
q = 1
m

A

= m

B

= 120

J

(0)
A

= J

(0)
B

= diag(40,4,40)

J

(0)
C

= diag(8,80,80)

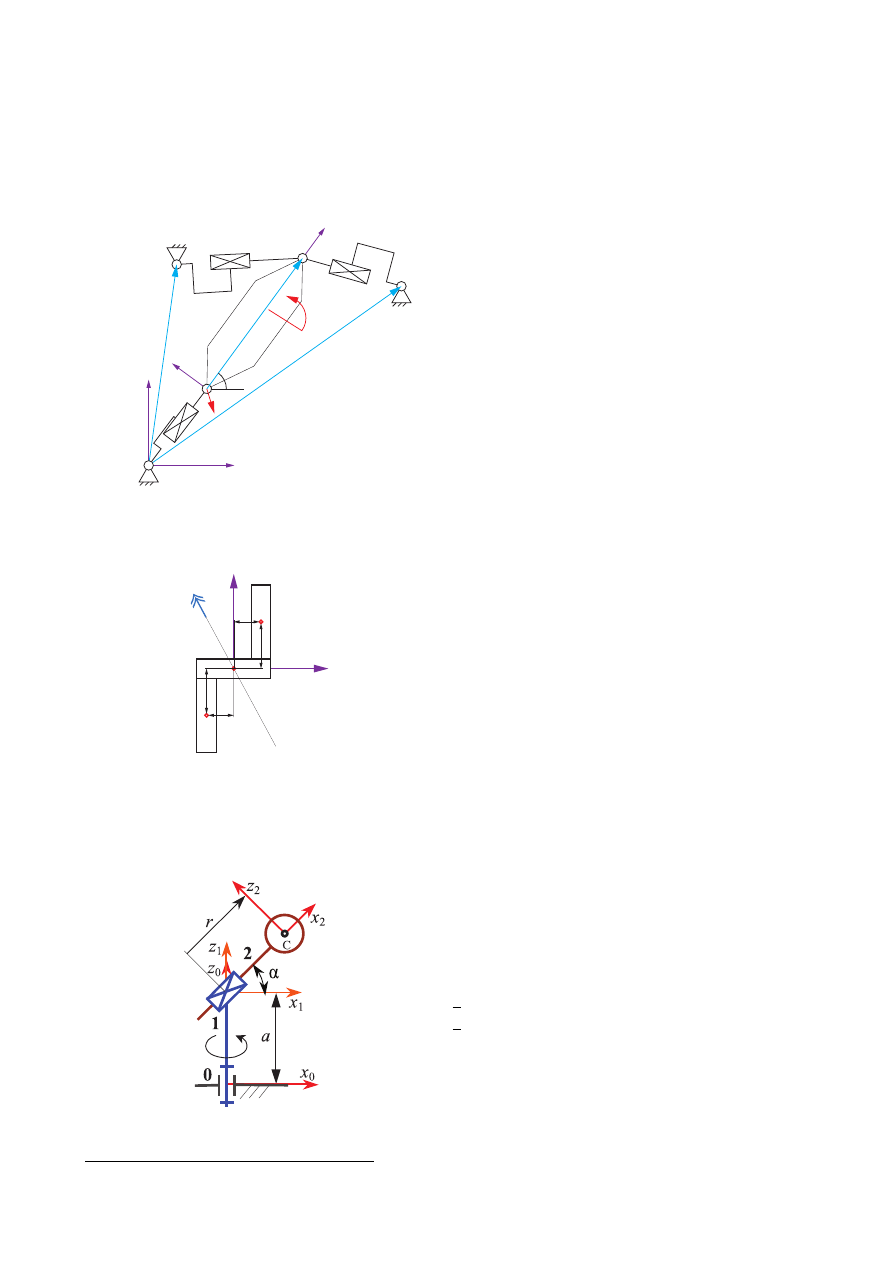
Zadanie 3. Manipulator przenosi jednorodną kulę o masie m i promieniowym momencie

bezwładności J . W rozpatrywanej chwili układy π

0

i π

1

mają jednakową orientację. Obliczyć

F

(0)

oraz moment M

(0)

jakimi człon 1 oddziałuje na podstawę 0. Do tabelki wpisać składową

momentu M

z

ω

J = 8
m = 4
α = π/4
a = 0.6
ω = 4

˙

ω = 8
r = 0.2

√

2

˙r = 0.8

√

2

¨

r = 0

Wszelkie zadania zastrzeżone. Rozwiązywanie surowo wzbronione.