
Lecture Notes: Introduction to Finite Element Method
Chapter 3. Two-Dimensional Problems
© 1998 Yijun Liu, University of Cincinnati
82
II. Finite Elements for 2-D Problems
A General Formula for the Stiffness Matrix
Displacements (u, v) in a plane element are interpolated
from nodal displacements (u
i
, v
i
) using shape functions N
i
as
follows,
u
v
N
N
N
N
u
v
u
v
=
=
1
2
1
2
1
1
2
2
0
0
0
0
L
L
M
or
u
Nd
(11)
where N is the shape function matrix, u the displacement vector
and d the nodal displacement vector. Here we have assumed
that u depends on the nodal values of u only, and v on nodal
values of v only.
From strain-displacement relation (Eq.(8)), the strain vector
is,
ε
ε
=
=
=
Du
DNd
Bd
,
or
(12)
where B = DN is the strain-displacement matrix.
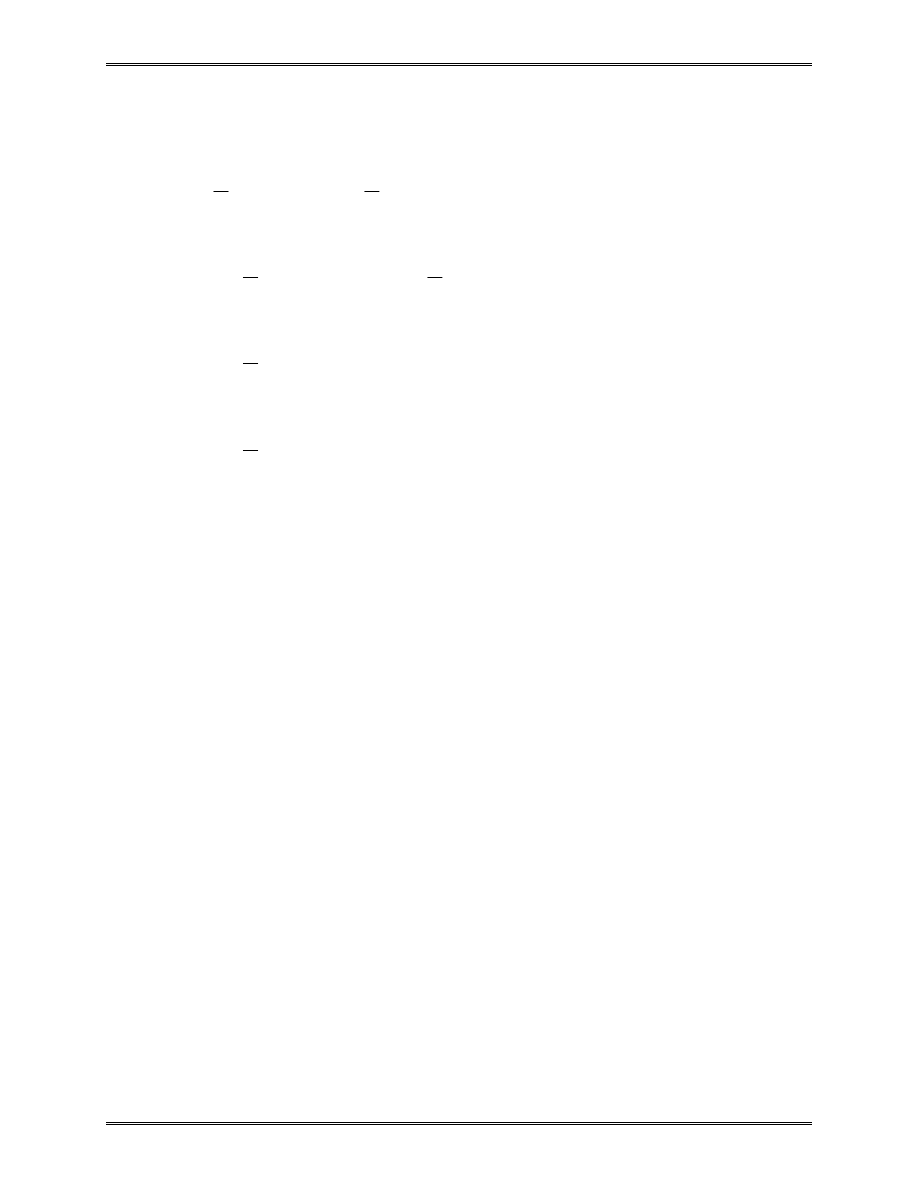
Lecture Notes: Introduction to Finite Element Method
Chapter 3. Two-Dimensional Problems
© 1998 Yijun Liu, University of Cincinnati
83
Consider the strain energy stored in an element,
(
)
( )
U
dV
dV
dV
dV
dV
T
V
x
x
y
y
xy
xy
V
T
V
T
V
T
T
V
T
=
=
+
+
=
=
=
=
∫
∫
∫
∫
∫
1
2
1
2
1
2
1
2
1
2
1
2
σ ε
σ ε σ ε
τ γ
ε ε
ε ε
E
E
d
B EB
d
d kd
From this, we obtain the general formula for the element
stiffness matrix,
k
B EB
=
∫
T
V
dV
(13)
Note that unlike the 1-D cases, E here is a matrix which is given
by the stress-strain relation (e.g., Eq.(5) for plane stress).
The stiffness matrix k defined by (13) is symmetric since E
is symmetric. Also note that given the material property, the
behavior of k depends on the B matrix only, which in turn on
the shape functions. Thus, the quality of finite elements in
representing the behavior of a structure is entirely determined by
the choice of shape functions.
Most commonly employed 2-D elements are linear or
quadratic triangles and quadrilaterals.
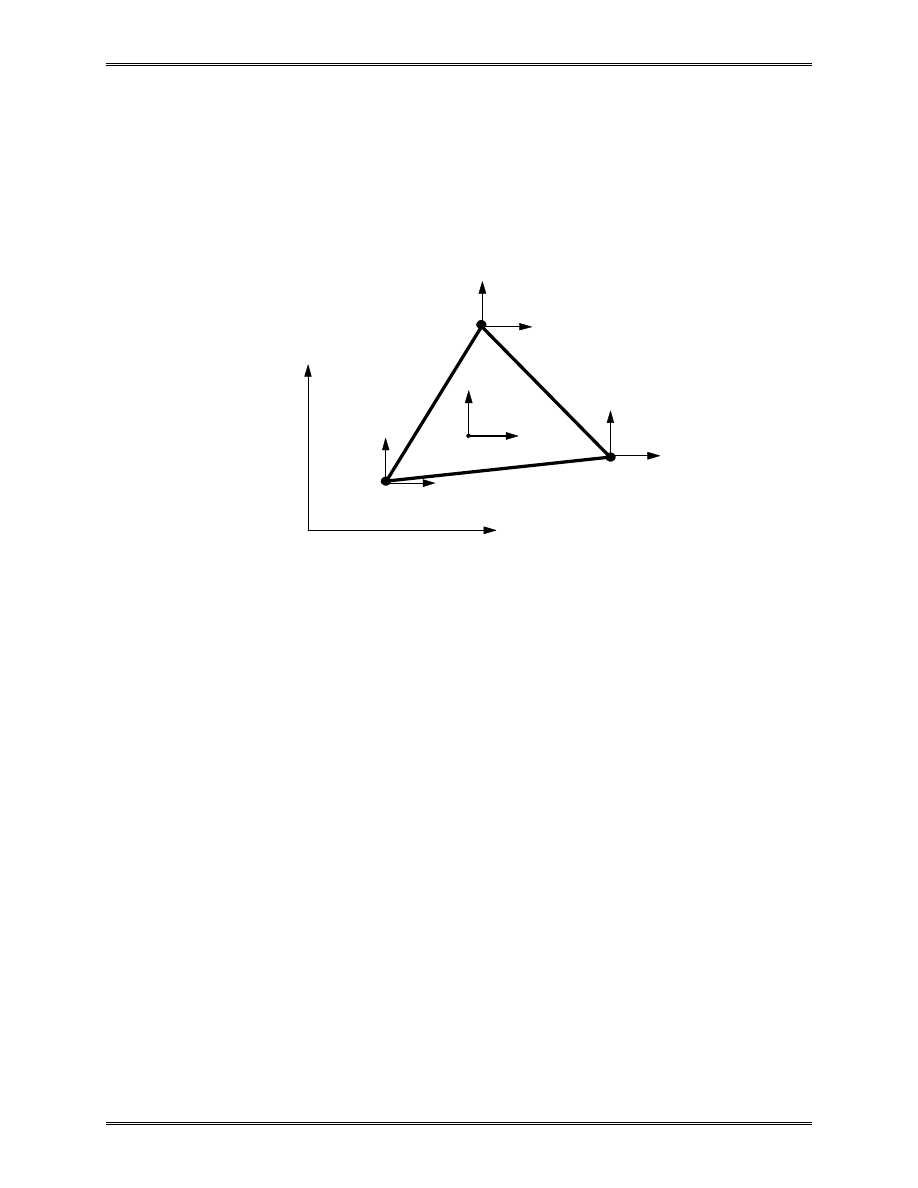
Lecture Notes: Introduction to Finite Element Method
Chapter 3. Two-Dimensional Problems
© 1998 Yijun Liu, University of Cincinnati
84
Constant Strain Triangle (CST or T3)
This is the simplest 2-D element, which is also called
linear triangular element.
For this element, we have three nodes at the vertices of the
triangle, which are numbered around the element in the
counterclockwise direction. Each node has two degrees of
freedom (can move in the x and y directions). The
displacements u and v are assumed to be linear functions within
the element, that is,
u
b
b x
b y
v
b
b x
b y
= +
+
=
+
+
1
2
3
4
5
6
,
(14)
where b
i
(i = 1, 2, ..., 6) are constants. From these, the strains
are found to be,
ε
ε
γ
x
y
xy
b
b
b
b
=
=
= +
2
6
3
5
,
,
(15)
which are constant throughout the element. Thus, we have the
name “constant strain triangle” (CST).
x
y
1
3
2
(x
1
, y
1
)
(x
3
, y
3
)
(x
2
, y
2
)
u
v
(x, y)
u
1
v
1
u
2
v
2
u
3
v
3
Linear Triangular Element

Lecture Notes: Introduction to Finite Element Method
Chapter 3. Two-Dimensional Problems
© 1998 Yijun Liu, University of Cincinnati
85
Displacements given by (14) should satisfy the following
six equations,
u
b
b x
b y
u
b
b x
b y
v
b
b x
b y
1
1
2
1
3
1
2
1
2
2
3
2
3
4
5
3
6
3
= +
+
= +
+
= +
+
M
Solving these equations, we can find the coefficients b
1
, b
2
, ...,
and b
6
in terms of nodal displacements and coordinates.
Substituting these coefficients into (14) and rearranging the
terms, we obtain,
u
v
N
N
N
N
N
N
u
v
u
v
u
v
=
1
2
3
1
2
3
1
1
2
2
3
3
0
0
0
0
0
0
(16)
where the shape functions (linear functions in x and y) are
{
}
{
}
{
}
N
A
x y
x y
y
y x
x
x
y
N
A
x y
x y
y
y x
x
x y
N
A
x y
x y
y
y x
x
x y
1
2
3
3
2
2
3
3
2
2
3
1
1
3
3
1
1
3
3
1
2
2
1
1
2
2
1
1
2
1
2
1
2
=
−
+
−
+
−
=
−
+
−
+
−
=
−
+
−
+
−
(
) (
)
(
)
(
) (
)
(
)
(
) (
)
(
)
(17)
and

Lecture Notes: Introduction to Finite Element Method
Chapter 3. Two-Dimensional Problems
© 1998 Yijun Liu, University of Cincinnati
86
A
x
y
x
y
x
y
=
1
2
1
1
1
1
1
2
2
3
3
det
(18)
is the area of the triangle (Prove this!).
Using the strain-displacement relation (8), results (16) and
(17), we have,
ε
ε
γ
x
y
xy
A
y
y
y
x
x
x
x
y
x
y
x
y
u
v
u
v
u
v
=
=
Bd
1
2
0
0
0
0
0
0
23
31
12
32
13
21
32
23
13
31
21
12
1
1
2
2
3
3
(19)
where x
ij
= x
i
- x
j
and y
ij
= y
i
- y
j
(i, j = 1, 2, 3). Again, we see
constant strains within the element. From stress-strain relation
(Eq.(5), for example), we see that stresses obtained using the
CST element are also constant.
Applying formula (13), we obtain the element stiffness
matrix for the CST element,
k
B EB
B EB
=
=
∫
T
V
T
dV
tA(
)
(20)
in which t is the thickness of the element. Notice that k for CST
is a 6 by 6 symmetric matrix. The matrix multiplication in (20)
can be carried out by a computer program.
Lecture Notes: Introduction to Finite Element Method
Chapter 3. Two-Dimensional Problems
© 1998 Yijun Liu, University of Cincinnati
87
Both the expressions of the shape functions in (17) and
their derivations are lengthy and offer little insight into the
behavior of the element.
We introduce the natural coordinates
( , )
ξ η on the
triangle, then the shape functions can be represented simply by,
N
N
N
1
2
3
1
=
=
= − −
ξ
η
ξ η
,
,
(21)
Notice that,
N
N
N
1
2
3
1
+
+
=
(22)
which ensures that the rigid body translation is represented by
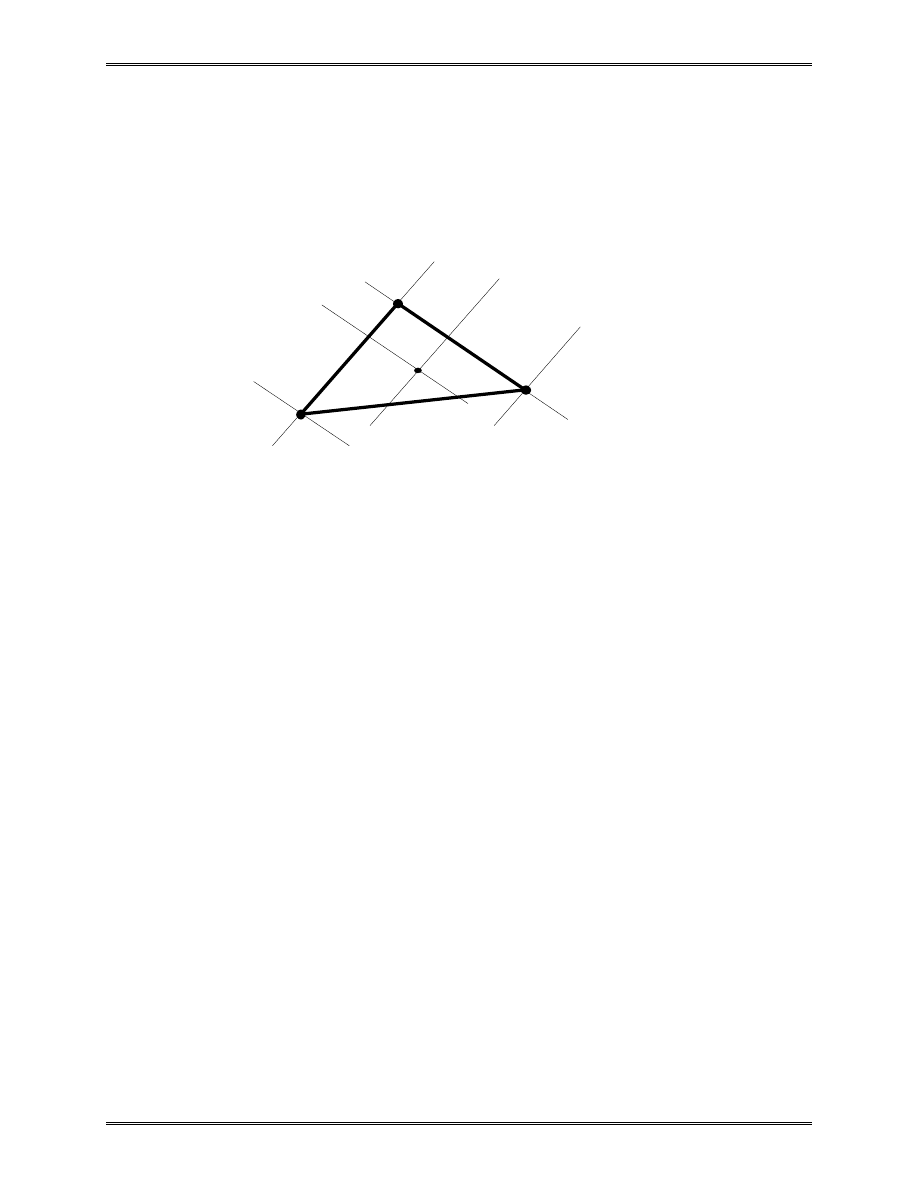
the chosen shape functions. Also, as in the 1-D case,
N
i
=
1
0
,
,
at node i;
at the other nodes
(23)
and varies linearly within the element. The plot for shape
function N
1
is shown in the following figure. N
2
and N
3
have
similar features.
1
3
2
ξ
=0
ξ
=1
ξ
=a
η
=0
η
=1
η
=b
The Natural Coordinates
(a, b)

Lecture Notes: Introduction to Finite Element Method
Chapter 3. Two-Dimensional Problems
© 1998 Yijun Liu, University of Cincinnati
88
We have two coordinate systems for the element: the global
coordinates (x, y) and the natural coordinates
( , )
ξ η . The
relation between the two is given by
x
N x
N x
N x
y
N y
N y
N y
=
+
+
=
+
+
1 1
2
2
3
3
1
1
2
2
3
3
(24)
or,
x
x
x
x
y
y
y
y
=
+
+
=
+
+
13
23
3
13
23
3
ξ
η
ξ
η
(25)
where x
ij
= x
i
- x
j
and y
ij
= y
i
- y
j
(i, j = 1, 2, 3) as defined earlier.
Displacement u or v on the element can be viewed as
functions of (x, y) or
( , )
ξ η . Using the chain rule for derivatives,
we have,
∂
∂ξ
∂
∂η
∂
∂ξ
∂
∂ξ
∂
∂η
∂
∂η
∂
∂
∂
∂
∂
∂
∂
∂
u
u
x
y
x
y
u
x
u
y
u
x
u
y
=
=
J
(26)
where J is called the Jacobian matrix of the transformation.
1
3
2
ξ
=0
ξ
=1
Shape Function N
1
for CST
N
1
1
Lecture Notes: Introduction to Finite Element Method
Chapter 3. Two-Dimensional Problems
© 1998 Yijun Liu, University of Cincinnati
89
From (25), we calculate,
J
J
=
=
−
−
−
x
y
x
y
A
y
y
x
x
13
13
23
23
1
23
13
23
13
1
2
,
(27)
where
det J
=
−
=
x y
x y
A
13
23
23
13
2 has been used (A is the area of
the triangular element. Prove this!).
From (26), (27), (16) and (21) we have,
∂
∂
∂
∂
∂
∂ξ
∂
∂η
u
x
u
y
A
y
y
x
x
u
u
A
y
y
x
x
u
u
u
u
=
−
−
=
−
−
−
−
1
2
1
2
23
13
23
13
23
13
23
13
1
3
2
3
(28)
Similarly,
∂
∂
∂
∂
v
x
v
y
A
y
y
x
x
v
v
v
v
=
−
−
−
−
1
2
23
13
23
13
1
3
2
3
(29)
Using the results in (28) and (29), and the relations
ε
=
=
=
Du
DNd
Bd , we obtain the strain-displacement matrix,
B
=
1
2
0
0
0
0
0
0
23
31
12
32
13
21
32
23
13
31
21
12
A
y
y
y
x
x
x
x
y
x
y
x
y
(30)
which is the same as we derived earlier in (19).

Lecture Notes: Introduction to Finite Element Method
Chapter 3. Two-Dimensional Problems
© 1998 Yijun Liu, University of Cincinnati
90
Applications of the CST Element:
•
Use in areas where the strain gradient is small.
•
Use in mesh transition areas (fine mesh to coarse mesh).
•
Avoid using CST in stress concentration or other crucial
areas in the structure, such as edges of holes and corners.
•
Recommended for quick and preliminary FE analysis of
2-D problems.
Wyszukiwarka
Podobne podstrony:
Chapt 02 Lect02
Chapt 06 Lect02
Chapt 03 Lect03
Chapt 03 Lect04
Chapt 03 Lect01
Chapt 01 Lect02
Chapt 07 Lect02
Chapt 05 Lect02
Chapt 04 Lect02
Chapt 02 Lect02
03 Sejsmika04 plytkieid 4624 ppt
03 Odświeżanie pamięci DRAMid 4244 ppt
podrecznik 2 18 03 05
od Elwiry, prawo gospodarcze 03
Probl inter i kard 06'03
TT Sem III 14 03
więcej podobnych podstron