Lecture Notes: Introduction to Finite Element Method Chapter 6. Solid Elements
© 1999 Yijun Liu, University of Cincinnati
144
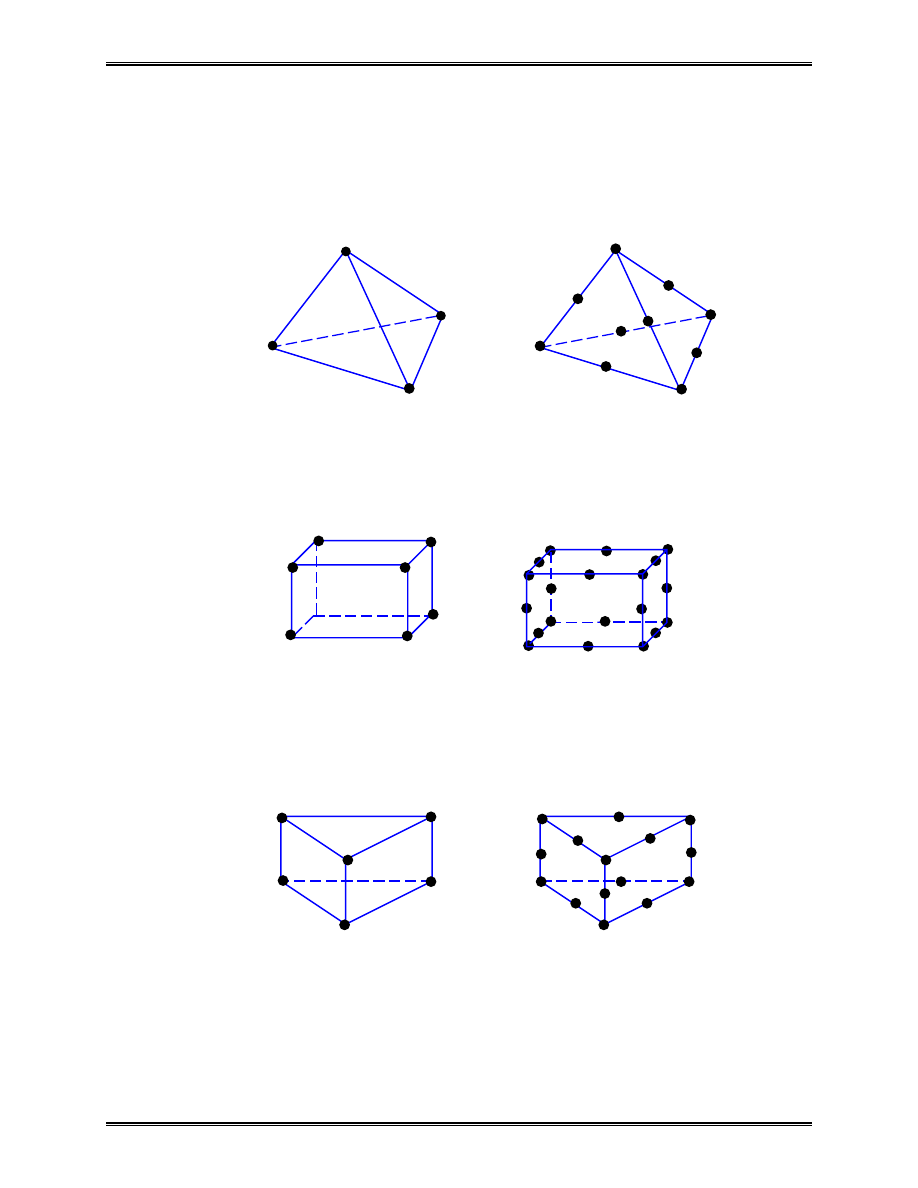
III Typical 3-D Solid Elements
Tetrahedron:
Hexahedron (brick):
Penta:
Avoid using the linear (4-node) tetrahedron element in 3-D
stress analysis (Inaccurate! But it is OK for dynamic analysis).
linear (4 nodes) quadratic (10 nodes)
linear (8 nodes) quadratic (20 nodes)
linear (6 nodes) quadratic (15 nodes)
Lecture Notes: Introduction to Finite Element Method Chapter 6. Solid Elements
© 1999 Yijun Liu, University of Cincinnati
145
Element Formulation:
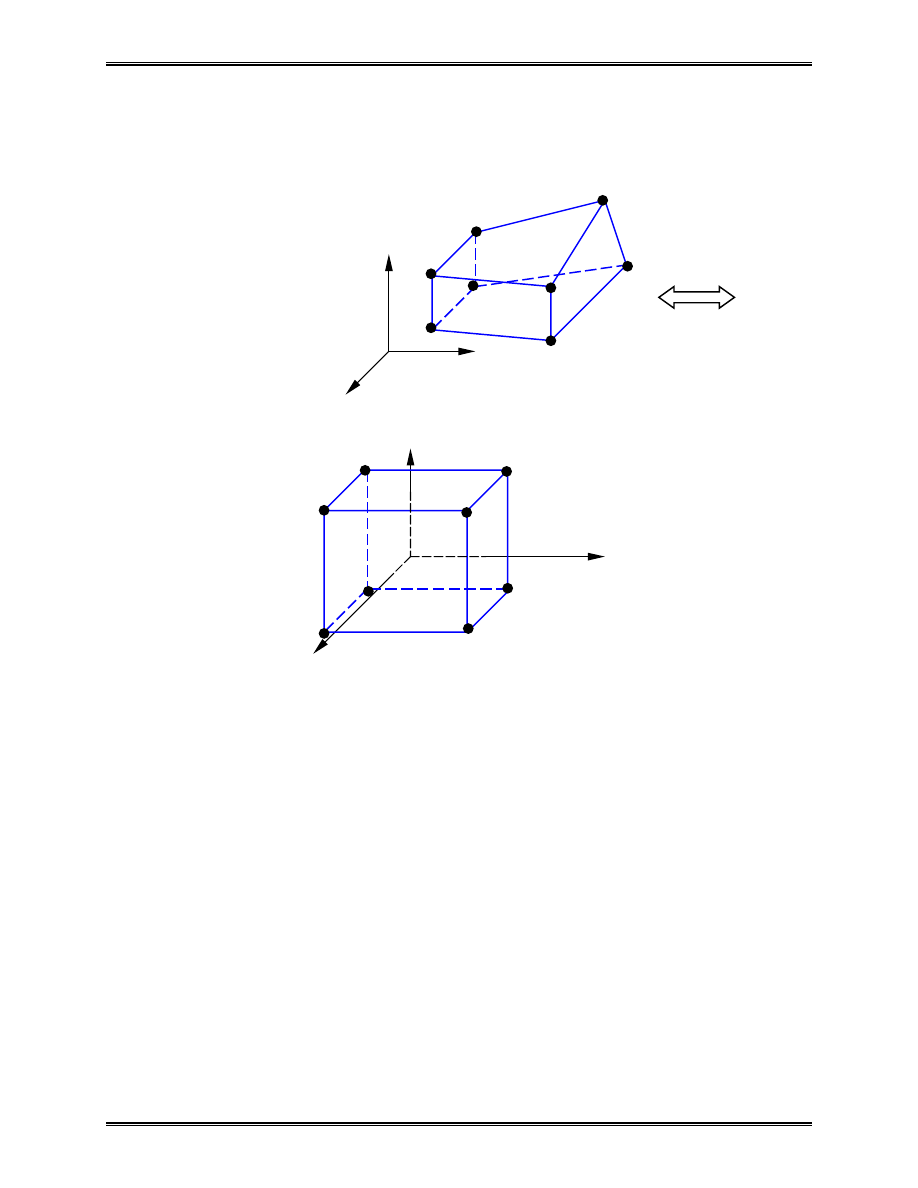
Linear Hexahedron Element
Displacement field in the element:
)
11
(
,
,
8
1
8
1
1
8
1
∑
∑
∑
=
=
=
=
=
=
i
i
i
i
i
i
i
i
i
w
N
w
v
N
v
u
N
u
6
5
y 8
7
2
1
4
3
mapping (x
↔ξ
)
x (-1
≤
ξ
,
η
,
ζ
≤
1)
z
η
(-1,1,-1) 4 3 (1,1,-1)
(-1,1,1) 8
7 (1,1,1)
o
ξ
(-1,-1,-1) 1
2 (1,-1,-1)
(-1,-1,1) 5
6 (1,-1,1)
ζ

Lecture Notes: Introduction to Finite Element Method Chapter 6. Solid Elements
© 1999 Yijun Liu, University of Cincinnati
146
Shape functions:
.
)
1
(
)
1
(
)
1
(
8
1
)
,
,
(
)
12
(
,
)
1
(
)
1
(
)
1
(
8
1
)
,
,
(
,
)
1
(
)
1
(
)
1
(
8
1
)
,
,
(
,
)
1
(
)
1
(
)
1
(
8
1
)
,
,
(
8
3
2
1
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
+
+
−
=
−
+
+
=
−
−
+
=
−
−
−
=
N
N
N
N
M
M
Note that we have the following relations for the shape
functions:
.
1
)
,
,
(
.
8
,
,
2
,
1
,
,
)
,
,
(
8
1
∑
=
=
=
=
i
i
ij
j
j
j
i
N
j
i
N
ζ
η
ξ
δ
ζ
η
ξ
L
Coordinate Transformation (Mapping):
)
13
(
.
,
,
8
1
8
1
8
1
∑
∑
∑
=
=
=
=
=
=
i
i
i
i
i
i
i
i
i
z
N
z
y
N
y
x
N
x
The same shape functions are used as for the displacement
field.
⇒
Isoparametric element.
Lecture Notes: Introduction to Finite Element Method Chapter 6. Solid Elements
© 1999 Yijun Liu, University of Cincinnati
147
Jacobian Matrix:
matrix
Jacobian
z
u
y
u
x
u
z
y
x
z
y
x
z
y
x
u
u
u
J
≡
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
∂
∂
∂
∂
)
14
(
ζ
ζ
ζ
η
η
η
ξ
ξ
ξ
ζ
η
ξ
⇒
∂
∂
=
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
∂
∂
∂
∂
∑
=
−
.
,
,
8
1
1
etc
u
N
u
u
u
u
z
u
y
u
x
u
i
i
i
ξ
ξ
ζ
η
ξ
J
and
)
15
(
,
1
∂
∂
∂
∂
∂
∂
=
∂
∂
∂
∂
∂
∂
−
ζ
η
ξ
v
v
v
z
v
y
v
x
v
J
also for w.
Lecture Notes: Introduction to Finite Element Method Chapter 6. Solid Elements
© 1999 Yijun Liu, University of Cincinnati
148
⇒
where d is the nodal displacement vector,
i.e.,
)
16
(
d
B
å
=
(6
×
1) (6
×
24)
×
(24
×
1)
d
B
å
=
=
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
∂
∂
∂
∂
=
=
)
15
(
use
zx
yz
xy
z
y
x
x
w
z
u
z
v
y
w
y
u
x
x
z
w
y
v
x
u
L
γ
γ
γ
ε
ε
ε
Lecture Notes: Introduction to Finite Element Method Chapter 6. Solid Elements
© 1999 Yijun Liu, University of Cincinnati
149
Strain energy,
)
17
(
2
1
2
1
)
(
2
1
2
1
d
B
E
B
d
å
E
å
å
E
å
å
ó
=
=
=
=
∫
∫
∫
∫
V
T
T
V
T
V
T
V
T
dV
dV
dV
dV
U
Element stiffness matrix,
)
18
(
∫
=
V
T
dV
B
E
B
k
(24
×
24) (24
×
6)
×
(6
×
6)
×
(6
×
24)
In
ξηζ
coordinates:
)
19
(
)
det
(
ζ
η
ξ
d
d
d
dV
J
=
⇒
)
20
(
)
(det
1
1
1
1
1
1
∫ ∫ ∫
− − −
=
ζ
η
ξ
d
d
d
T
J
B
E
B
k
( Numerical integration)
•
3-D elements usually do not use rotational DOFs.
Lecture Notes: Introduction to Finite Element Method Chapter 6. Solid Elements
© 1999 Yijun Liu, University of Cincinnati
150
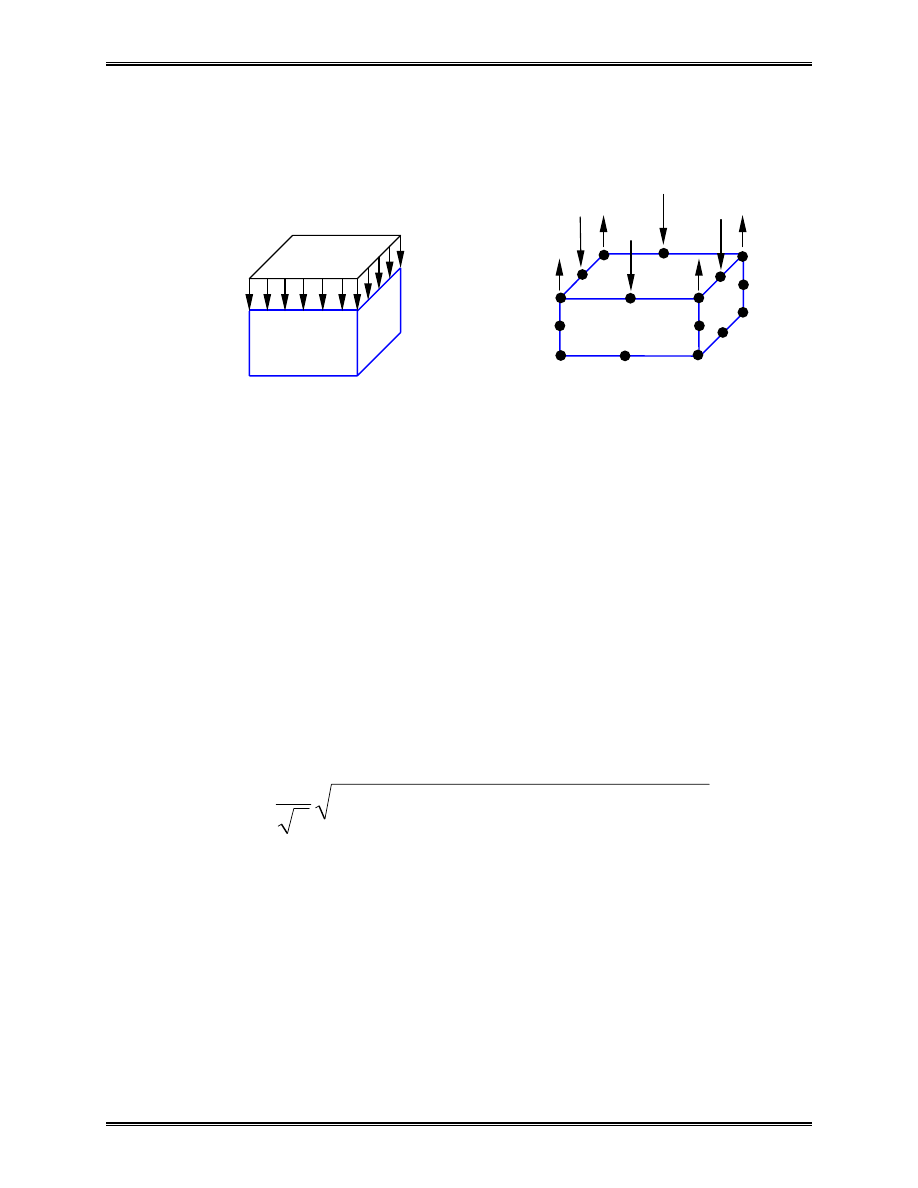
Loads:
Distributed loads
⇒
Nodal forces
Area =A Nodal forces for 20-node
Hexahedron
Stresses:
d
B
E
å
E
ó
=
=
Principal stresses:
.
,
,
3
2
1
σ
σ
σ
von Mises stress:
2
1
3
2
3
2
2
2
1
)
(
)
(
)
(
2
1
σ
σ
σ
σ
σ
σ
σ
σ
−
+
−
+
−
=
=
VM
e
.
Stresses are evaluated at selected points (including nodes)
on each element. Averaging (around a node, for example) may
be employed to smooth the field.
Examples: …
pA/3 pA/12
p
Wyszukiwarka
Podobne podstrony:
Chapt 02 Lect02
Chapt 06 Lect03
Chapt 06 Lect01
Chapt 01 Lect02
Chapt 07 Lect02
Chapt 05 Lect02
Chapt 04 Lect02
Chapt 03 Lect02
Chapt 02 Lect02
Chapt 06
MT st w 06
Kosci, kregoslup 28[1][1][1] 10 06 dla studentow
06 Kwestia potencjalności Aid 6191 ppt
06 Podstawy syntezy polimerówid 6357 ppt
06
06 Psych zaburz z somatoformiczne i dysocjacyjne
GbpUsd analysis for July 06 Part 1
więcej podobnych podstron