Politechnika Warszawska

Instytut Automatyki i Robotyki

Prof. dr hab. inż. Jan Maciej Kościelny

PODSTAWY AUTOMATYKI

część 1

Pojęcia podstawowe, klasyfikacja układów sterowania

2

Program

Podstawy Automatyki

Instytut Automatyki i Robotyki

Autorzy programu:

prof. dr hab. inż. Jan Maciej Kościelny, doc. dr inż. Marek Żelazny

Semestr IV-V

Liczba godzin zajęć według planu studiów:

Wykład 30

E

Ćwiczenia 15

Laboratorium 30

Liczba punktów kredytowych: 6

3

Program wykładu

Pojęcia podstawowe: sygnał, informacja, element automatyki, układ automatyki, obiekt,

regulator. Struktury przyrządowe i klasyfikacje układów automatyki.

Układy liniowe: opis matematyczny (równania różniczkowe, transmitancja operatorowa,

równania stanu i wyjść, podstawy opisu układów dyskretnych), linearyzacja,
przedstawianie właściwości statycznych i dynamicznych. Podstawowe człony
dynamiczne, charakterystyki częstotliwościowe. Schematy blokowe.

Obiekty regulacji i regulatory przemysłowe: obiekty statyczne i astatyczne, metody

identyfikacji. Regulatory PID - realizacja mikroprocesorowa, właściwości funkcjonalne.

Wymagania stawiane układom automatyki: stabilność (podstawowe kryteria),

dokładność statyczna, jakość dynamiczna i jej wskaźniki. Dobór nastaw regulatorów.

Struktury układów automatyki i przykładowe zastosowania: regulacja

jednoobwodowa, kaskadowa, z korekcją dynamiczną, regulacja stosunku prosta i
kaskadowa, układy zamknięto-otwarte. Zastosowania w energetyce, przemyśle
chemicznym, przemyśle spożywczym.

Układy nieliniowe: typowe nieliniowości, opis matematyczny, rodzaje stabilności, metody

Lapunowa. Płaszczyzna fazowa. Metoda funkcji opisującej.

Technika automatyzacji: Realizowane zadania. Struktury funkcjonalne układów

automatyki. Struktury sprzętowe: systemy zintegrowane - klasy DCS, sterowniki
programowalne, systemy monitorowania - SCADA, sieci w układach automatyki,
układy blokad i zabezpieczeń. Konfigurowanie układów automatyki.

4

Program ćwiczeń audytoryjnych

Ćwiczenia audytoryjne są ściśle skorelowane z materiałem wykładowym i

obejmują:

- formułowanie opisu matematycznego wybranych elementów automatyki
- wyznaczanie odpowiedzi na typowe wymuszenia przy użyciu rachunku

operatorowego (przekształcenia Laplace

- układanie i przekształcanie schematów blokowych
- analityczne i wykreślne metody wyznaczania charakterystyk

częstotliwościowych

- badanie stabilności układów automatyki (metody Hurwitza i Nyquista)
- badanie dokładności statycznej układów automatyki
- identyfikacja obiektów regulacji na podstawie zarejestrowanych

odpowiedzi skokowych obiektu lub charakterystyk częstotliwościowych

- dobór nastaw regulatora do przykładowych obiektów regulacji
- analiza nieliniowych układów automatyki metodą płaszczyzny fazowej
- badanie stabilności nieliniowych układów automatyki rozszerzoną metodą

Nyquista (wykorzystanie funkcji opisującej)

5

Literatura do wykładu

Żelazny M.: Materiały pomocnicze do wykładu: Podstawy Automatyki

Żelazny M.: Podstawy Automatyki. WNT, Warszawa 1976

Kościelny W.: Materiały pomocnicze do nauczania podstaw automatyki. Oficyna

Wydawnicza PW, Warszawa 1997

Gessing R.: Podstawy automatyki. Wydawnictwo Politechniki Śląskiej, 2001

Mazurek J., Vogt H., Zydanowicz W.: Podstawy automatyki. Oficyna Wydawnicza

PW, Warszawa 2002

Pułaczewski J, Szacka K. Manitius A.: Zasady automatyki. WNT, Warszwa, 1974

Węgrzyn S.: Podstawy automatyki. PWN, Warszawa, 1980

Kaczorek T.: Teoria układów regulacji automatycznej. WNT, Warszawa, 1974

Pełczewski W.: Teoria sterowania. Ciągłe stacjonarne układy liniowe. WNT,

Warszawa1980

Dorf R., Bishop R.: Modern Control Systems. Addison-Wesley Publishing

Company, 1995

Żelazny M.: Materiały pomocnicze do wykładu: Podstawy Automatyki

Żelazny M.: Podstawy Automatyki. WNT, Warszawa 1976

Kościelny W.: Materiały pomocnicze do nauczania podstaw automatyki. Oficyna

Wydawnicza PW, Warszawa 1997

Gessing R.: Podstawy automatyki. Wydawnictwo Politechniki Śląskiej, 2001

Mazurek J., Vogt H., Zydanowicz W.: Podstawy automatyki. Oficyna Wydawnicza

PW, Warszawa 2002

Pułaczewski J, Szacka K. Manitius A.: Zasady automatyki. WNT, Warszwa, 1974

Węgrzyn S.: Podstawy automatyki. PWN, Warszawa, 1980

Kaczorek T.: Teoria układów regulacji automatycznej. WNT, Warszawa, 1974

Pełczewski W.: Teoria sterowania. Ciągłe stacjonarne układy liniowe. WNT,

Warszawa1980

Dorf R., Bishop R.: Modern Control Systems. Addison-Wesley Publishing

Company, 1995

6

Literatura do ćwiczeń audytoryjnych

Holejko D., Kościelny W., Niewczas W.: Zbiór zadań z podstaw automatyki. Oficyna

Wydawnicza PW, Warszawa 1985

Amborski K., Marusak A.: Teoria sterowania w ćwiczeniach. PWN, Warszawa 1978

Holejko D., Kościelny W., Niewczas W.: Zbiór zadań z podstaw automatyki. Oficyna

Wydawnicza PW, Warszawa 1985

Amborski K., Marusak A.: Teoria sterowania w ćwiczeniach. PWN, Warszawa 1978

7

Pojęcia podstawowe

Sygnał - wielkość fizyczna występująca w procesie sterowania będąca

nośnikiem informacji

(sygnały ciągłe i dyskretne)

Sygnał - wielkość fizyczna występująca w procesie sterowania będąca

nośnikiem informacji

(sygnały ciągłe i dyskretne)

Informacja - wartość lub kształt przebiegu sygnału

Informacja - wartość lub kształt przebiegu sygnału

Sygnały:
• ciągłe - będące ciągłą funkcją czasu
• dyskretne (wielostanowe) – wartości należą do dyskretnego

(przeliczalnego) zbioru

Sygnały dyskretne można otrzymać z sygnału ciągłego w wyniku

kwantowania wartości

Szczególnym przypadkiem sygnałów dyskretnych są sygnały binarne

– {0,1})

Sygnały:
• ciągłe - będące ciągłą funkcją czasu
• dyskretne (wielostanowe) – wartości należą do dyskretnego

(przeliczalnego) zbioru

Sygnały dyskretne można otrzymać z sygnału ciągłego w wyniku

kwantowania wartości

Szczególnym przypadkiem sygnałów dyskretnych są sygnały binarne

– {0,1})

8

Pojęcia podstawowe

Układ automatyki - zespół wzajemnie powiązanych elementów biorących

udział w sterowaniu automatycznym danego procesu
(uporządkowany zgodnie z kierunkiem przekazywania sygnałów)

Układ automatyki - zespół wzajemnie powiązanych elementów biorących

udział w sterowaniu automatycznym danego procesu
(uporządkowany zgodnie z kierunkiem przekazywania sygnałów)

Sterowanie automatyczne - oddziaływanie na proces, którego

zamierzony przebieg chcemy uzyskać bez udziału człowieka, za
pomocą urządzeń nazywanych ogólnie aparaturą automatyki.

Sterowanie automatyczne - oddziaływanie na proces, którego

zamierzony przebieg chcemy uzyskać bez udziału człowieka, za
pomocą urządzeń nazywanych ogólnie aparaturą automatyki.

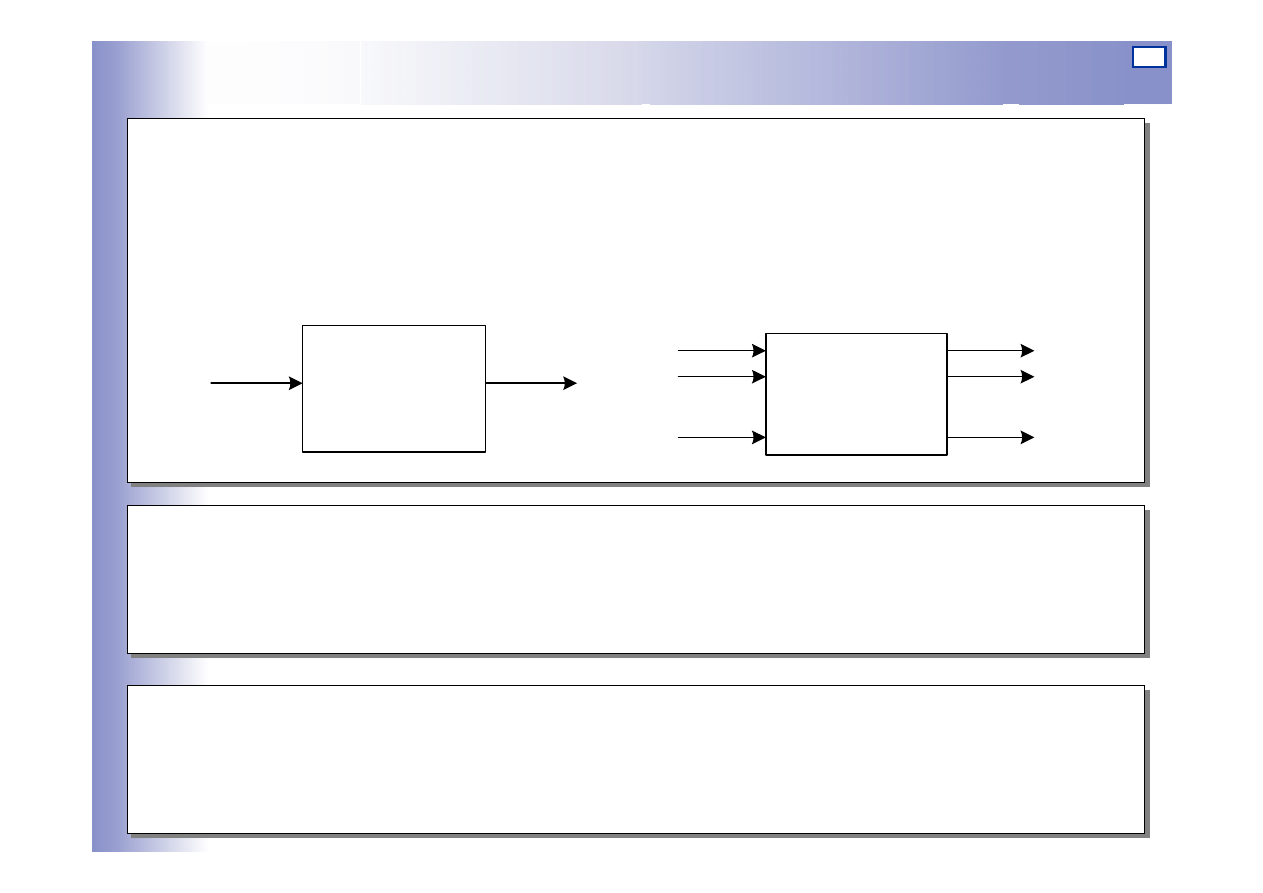
Element automatyki (człon) - podzespół, zespół, przyrząd lub

urządzenie, w którym można wyróżnić sygnał wejściowy i sygnał
wyjściowy - rys. a, lub sygnały wejściowe i wyjściowe - rys. b.

Element automatyki (człon) - podzespół, zespół, przyrząd lub

urządzenie, w którym można wyróżnić sygnał wejściowy i sygnał
wyjściowy - rys. a, lub sygnały wejściowe i wyjściowe - rys. b.

a)

b)

..

.

..

.

u

1

u

2

u

m

y

1

y

2

y

m

u

y

9

Pojęcia podstawowe

Układy sterowania procesami ciągłymi:
• otwarte
• zamknięte (ze sprzężeniem zwrotnym)
-------------------
• ciągłe
• dyskretne (kwantowane w czasie)

Układy sterowania procesami ciągłymi:
• otwarte
• zamknięte (ze sprzężeniem zwrotnym)
-------------------
• ciągłe
• dyskretne (kwantowane w czasie)

Procesy:
• ciągłe – ciągłe sygnały
• dyskretne (binarne) – dyskretne (binarne) wartości sygnałów

Procesy:
• ciągłe – ciągłe sygnały
• dyskretne (binarne) – dyskretne (binarne) wartości sygnałów

Układy sterowania :
• procesami ciągłymi
• procesami dyskretnymi (odrębny wykład)

Układy sterowania :
• procesami ciągłymi
• procesami dyskretnymi (odrębny wykład)

10

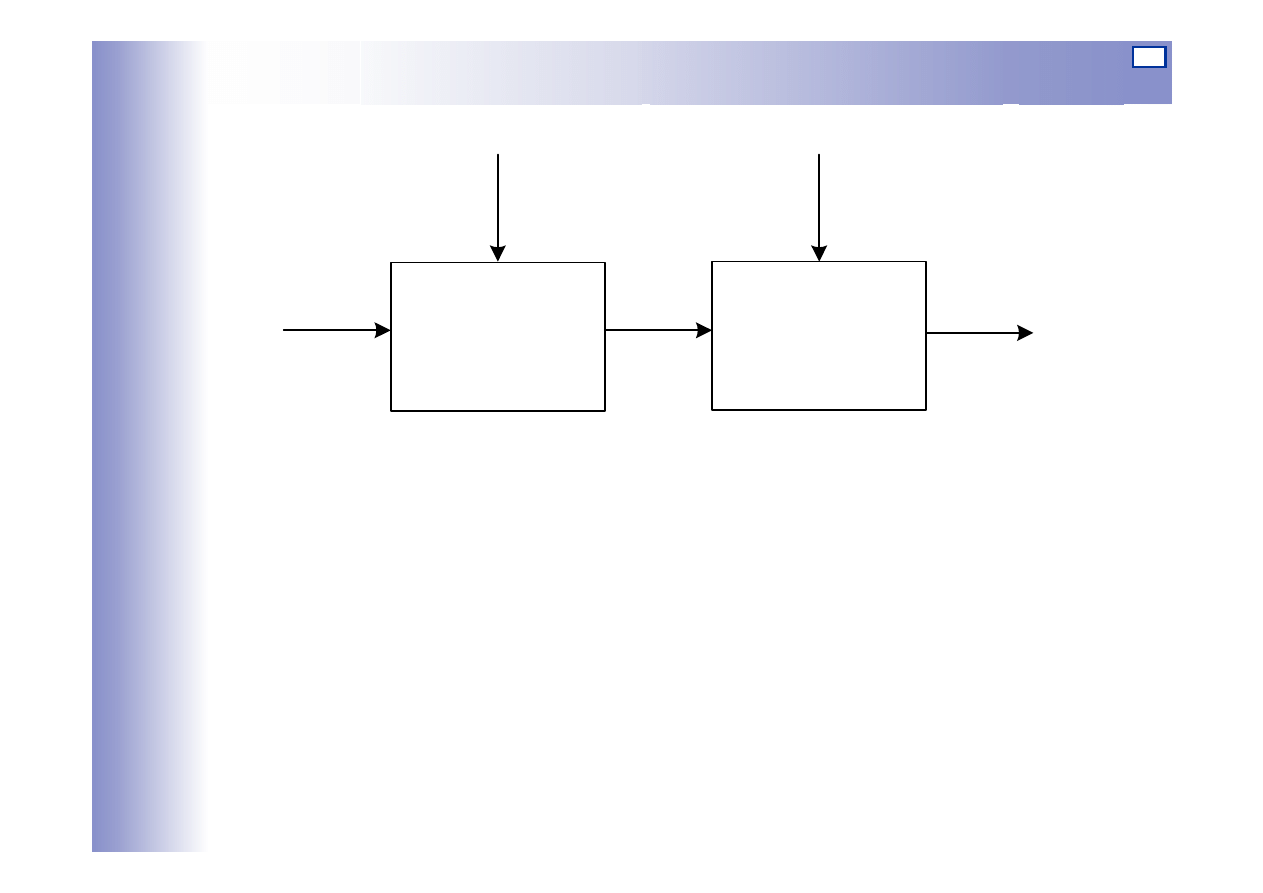
Sterowanie w układzie otwartym

w

u

z

z

y

U.S.

O

w - wartość zadana wielkości sterowanej
u - sygnał sterujący
y - wielkość sterowana
z - sygnał zakłócający

US - urządzenie sterujące
O – obiekt (proces) podlegający sterowaniu

11

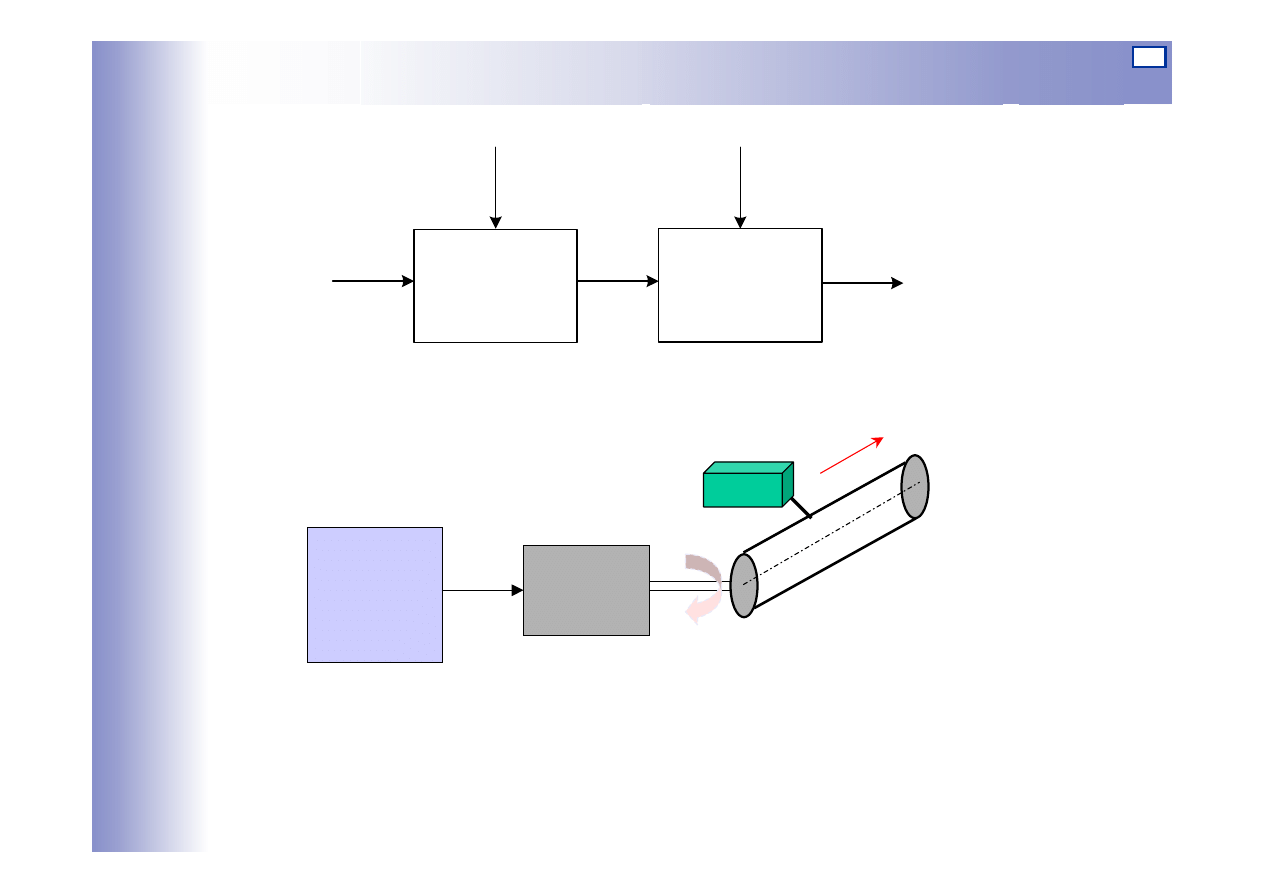
Sterowanie w układzie otwartym

w

u

z

z

y

U.S.

O

Układ

sterujący

Silnik

skokowy

u

y

12

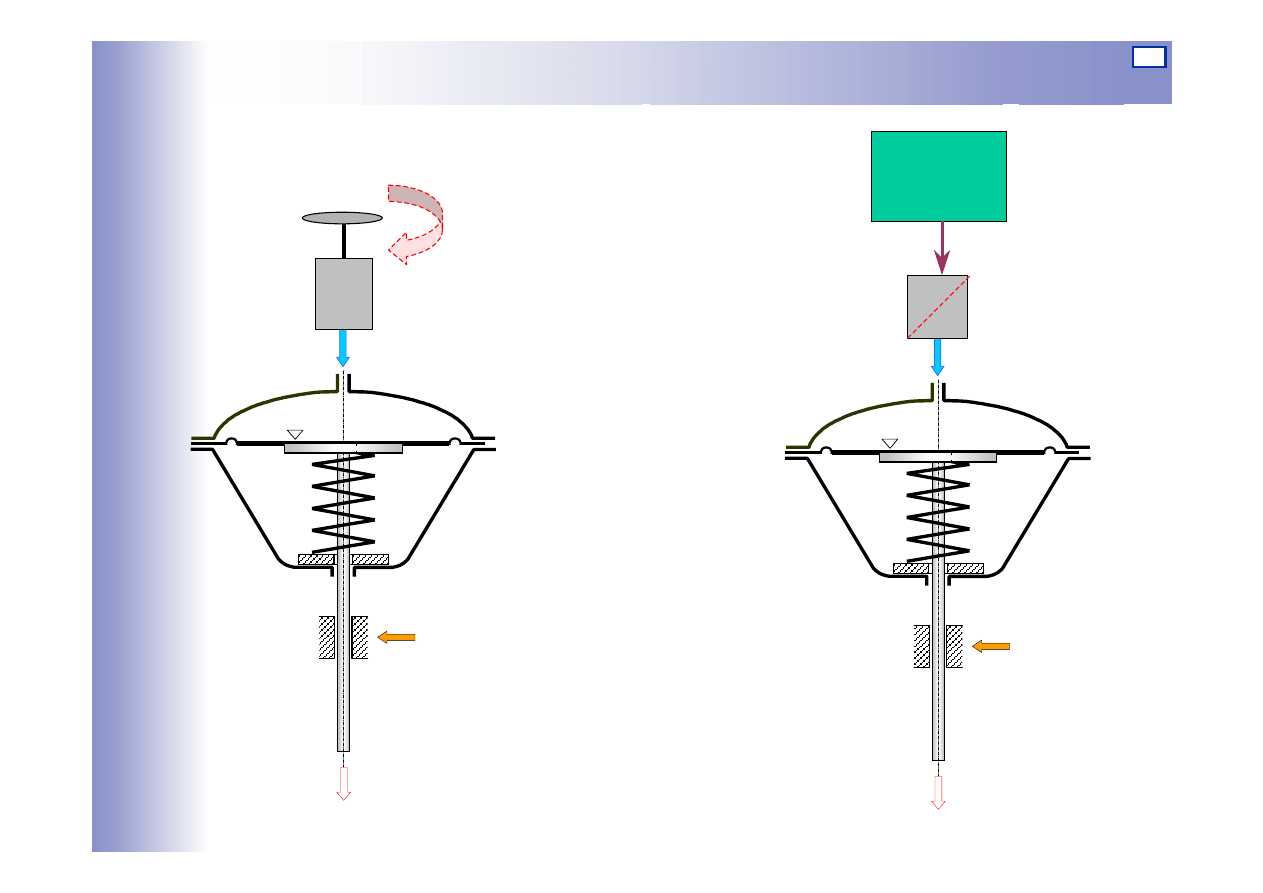
Sterowanie w układzie otwartym

p

s

k

s

A

e

k

d

z

y

Zadajnik

ciśnienia

ręczne

automatyczne

Sterownik

p

s

k

s

A

e

k

d

z

y

e

p

u

13

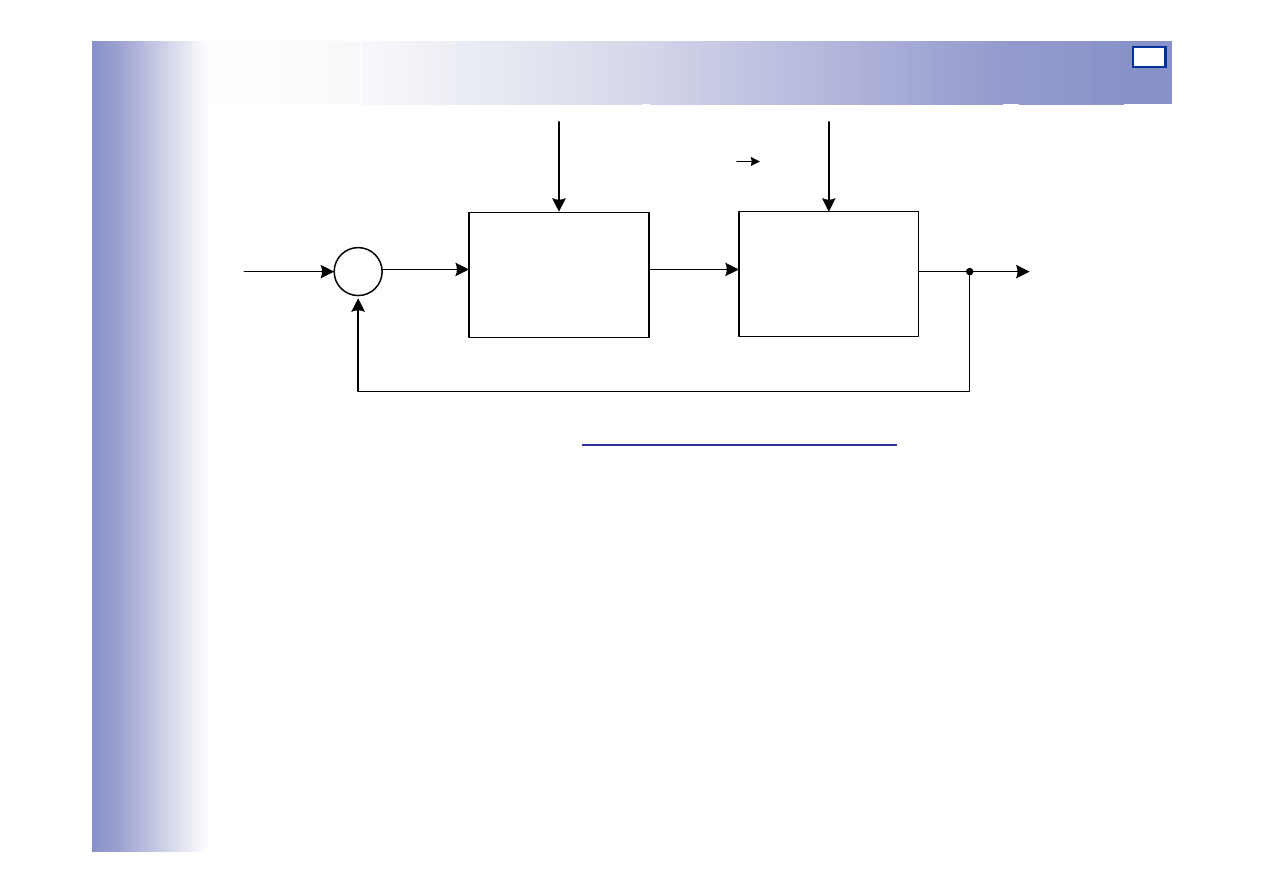
Sterowanie w układzie zamkniętym

e

u

z

z

y

U.S.

O

w

+

-

tor główny w y

sprzężenie zwrotne

e=w-y

y - wielkość regulowana
w - wartość zadana wielkości regulowanej
e – odchyłka regulacji
u - sygnał sterujący
z - sygnał zakłócający

US - regulator
O -obiekt regulacji (proces regulowany)

Układ ze sprzężeniem zwrotnym,

14

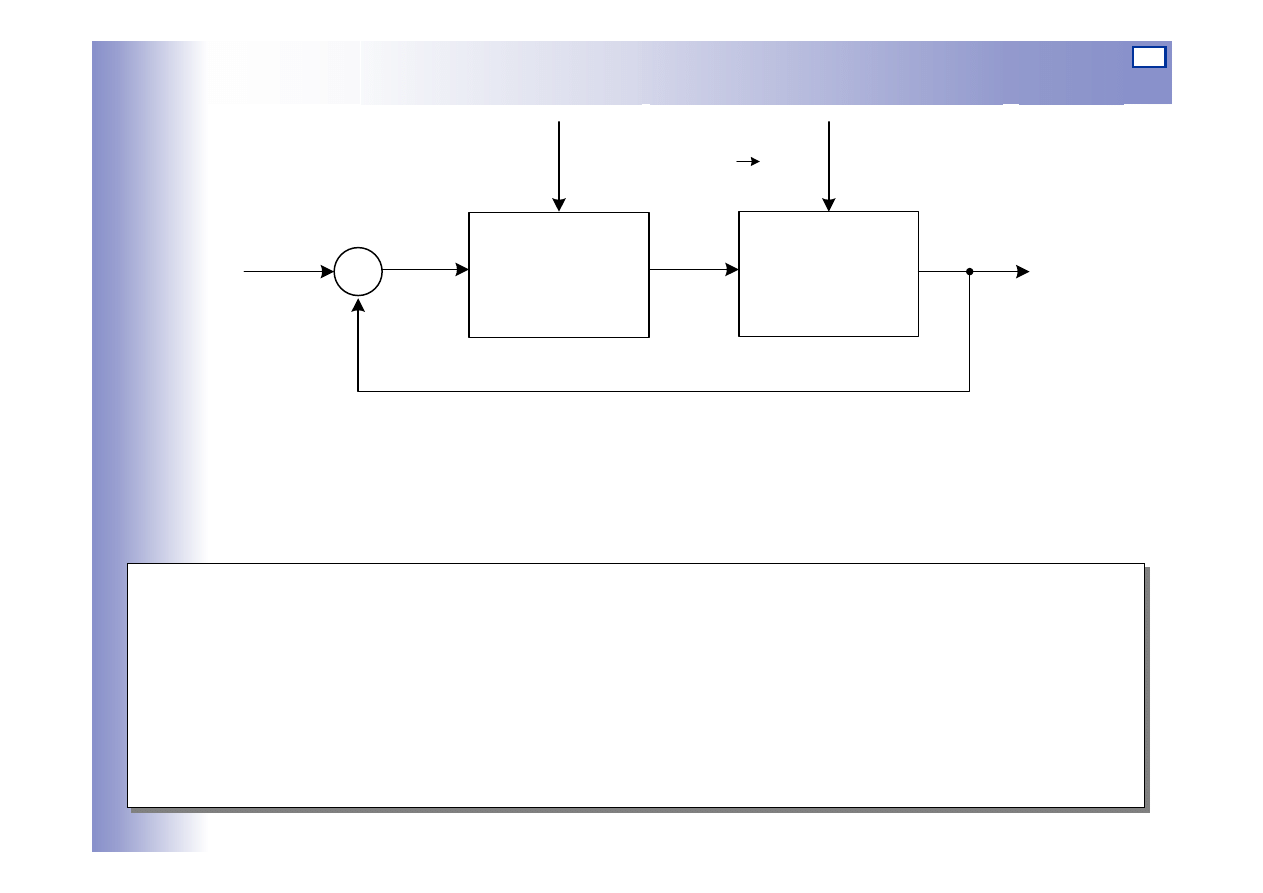
Sterowanie w układzie zamkniętym

Układ regulacji automatycznej

e

u

z

z

y

U.S.

O

w

+

-

tor główny w y

sprzężenie zwrotne

e=w-y

Tor główny wskazuje zawsze zasadniczą wielkość wejściową układu

(w tym przypadku w) i wielkość wyjściową y. Tor ten ilustruje zwykle
przepływ głównego strumienia materiału lub energii w układzie.

Tor sprzężenia zwrotnego służy do przekazywania informacji.

Zapotrzebowanie energetyczne tego toru jest zwykle pomijanie małe.

Tor główny wskazuje zawsze zasadniczą wielkość wejściową układu

(w tym przypadku w) i wielkość wyjściową y. Tor ten ilustruje zwykle
przepływ głównego strumienia materiału lub energii w układzie.

Tor sprzężenia zwrotnego służy do przekazywania informacji.

Zapotrzebowanie energetyczne tego toru jest zwykle pomijanie małe.

15

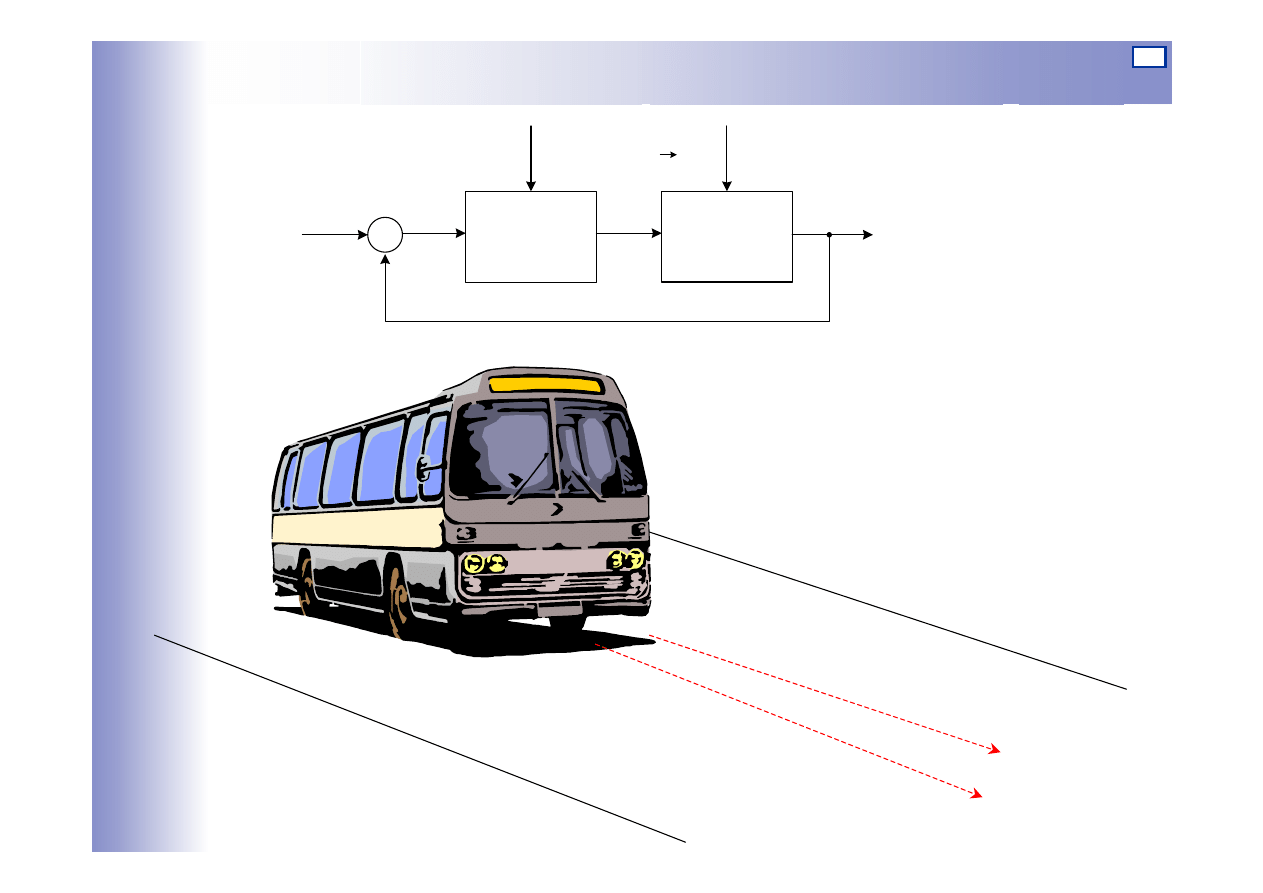
Sterowanie ręczne w układzie zamkniętym

e

u

z

z

y

U.S.

O

w

+

-

tor główny w y

sprzężenie zwrotne

e=w-y

Kierunek zadany

Kierunek aktualny

16

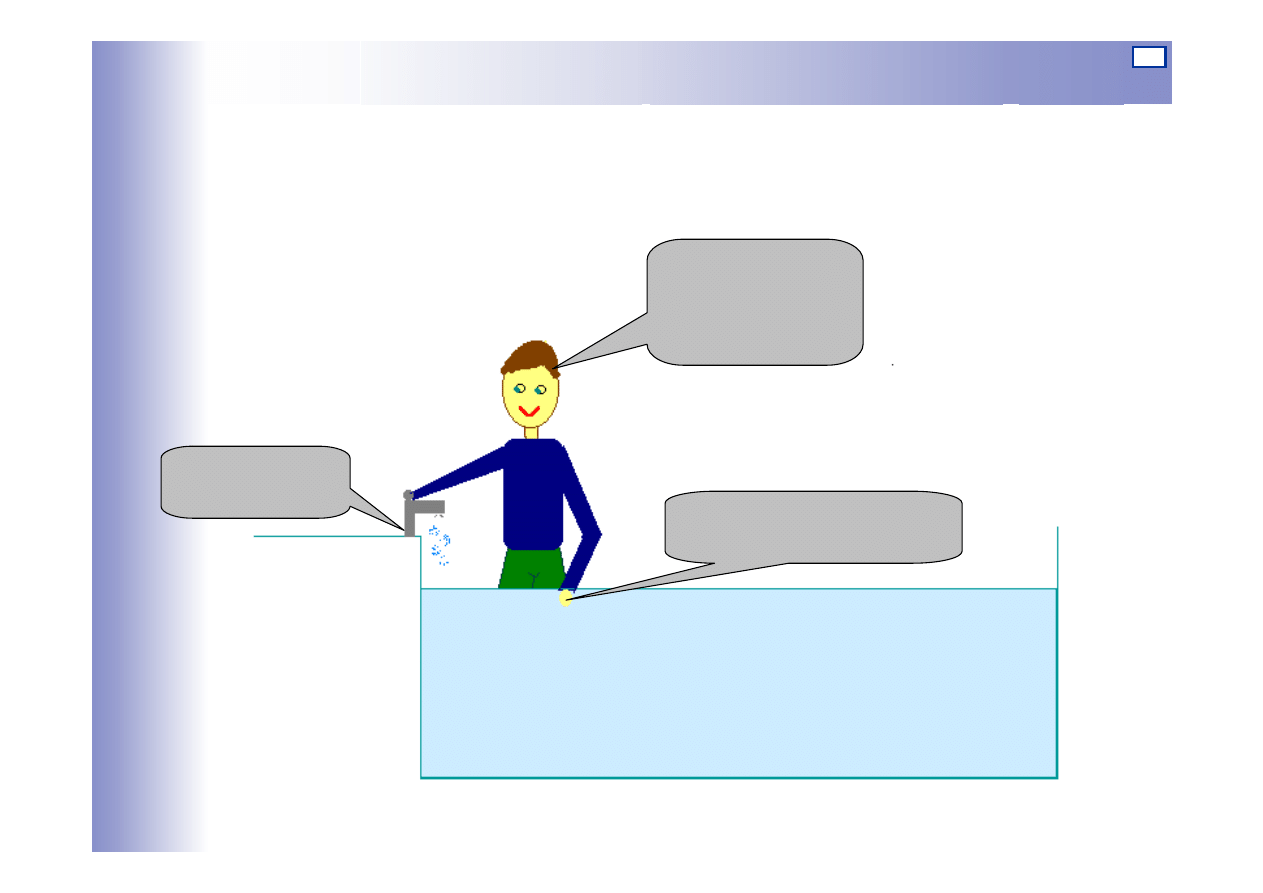
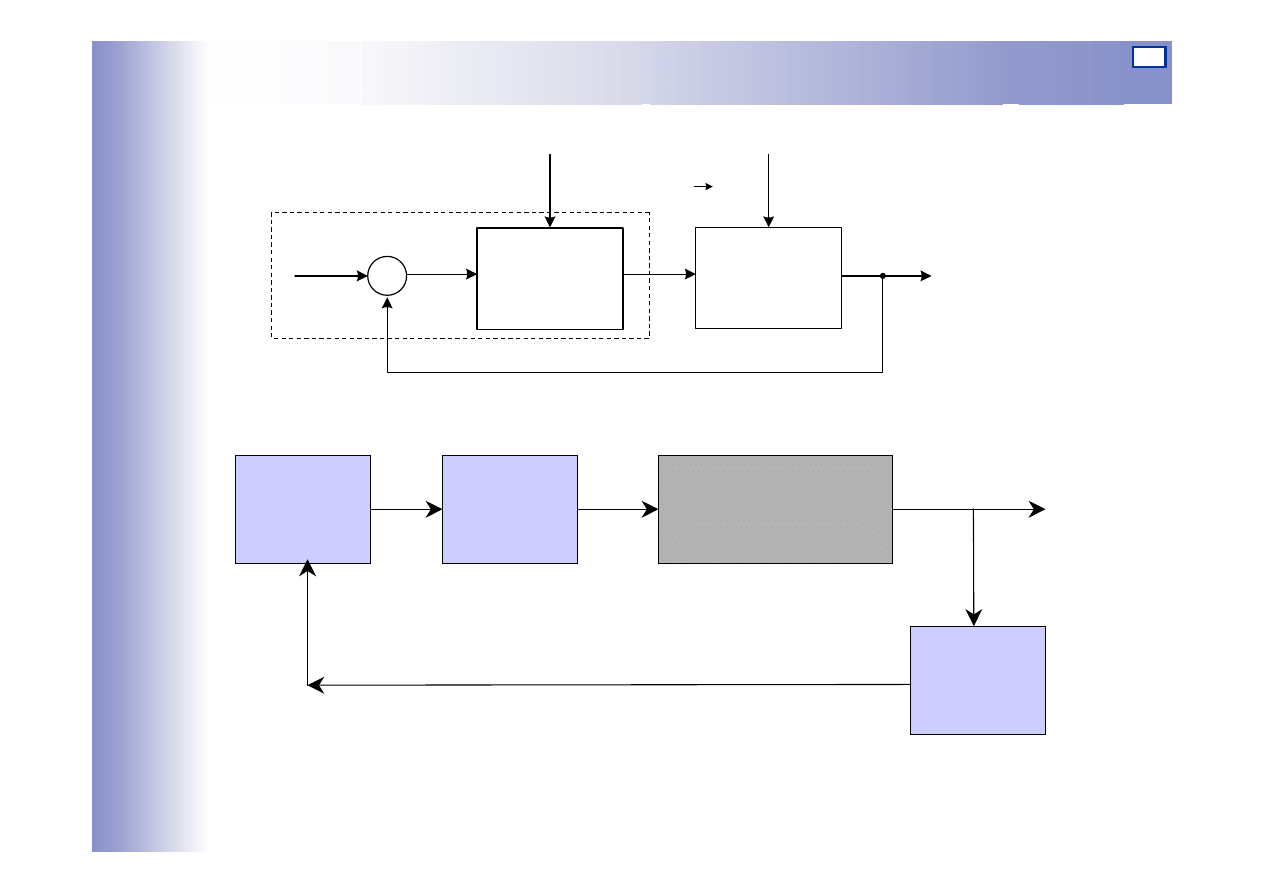
Sterowanie ręczne w układzie zamkniętym

Regulacja ręczna temperatury wody w układzie zamkniętym

Realizacja

algorytmu

sterowania

Oddziaływanie

Pomiar temperatury

17

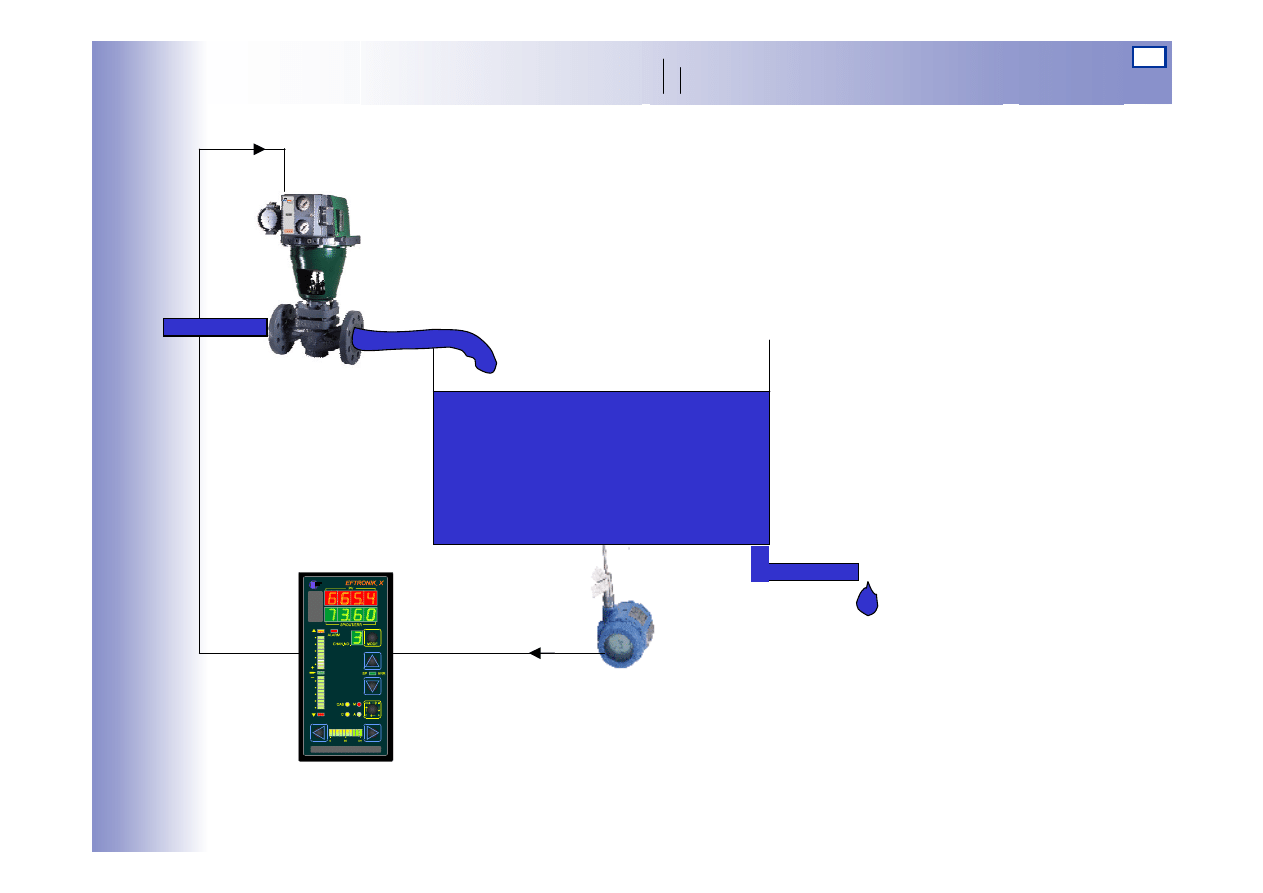
Regulacja automatyczna – struktura aparaturowa

e

u

z

z

y

U.S.

O

w

+

-

tor główny w y

sprzężenie zwrotne

e=w-y

Regulator

Obiekt

regulacji

Przetwornik

pomiarowy

Element

wykonawczy

u

y

y

m

w

18

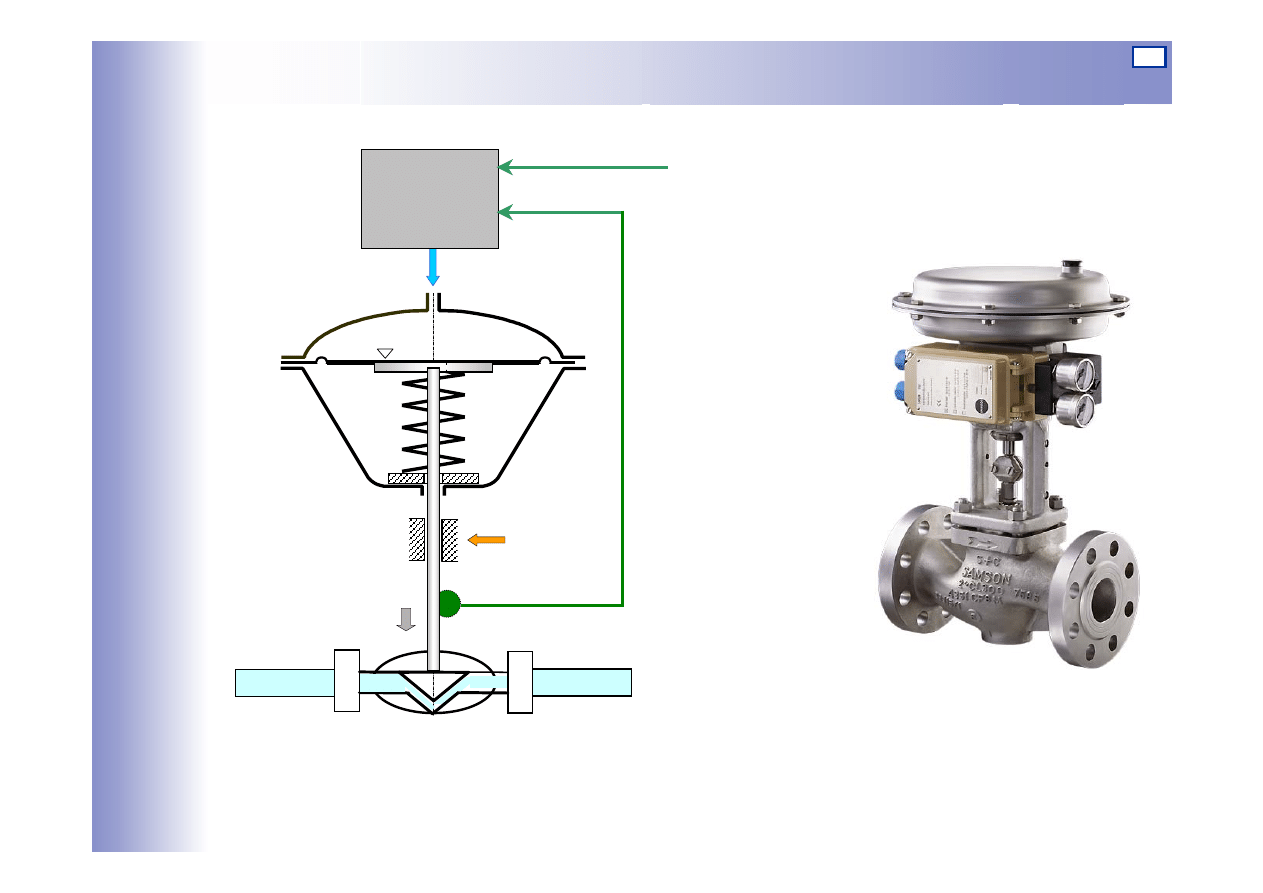
Regulacja automatyczna – struktura aparaturowa

Układ regulacji poziomu wody

Element wykonawczy

Przetwornik pomiarowy

Regulator

Obiekt regulacji:
proces zmian
poziomu w zbiorniku

y

m

u

19

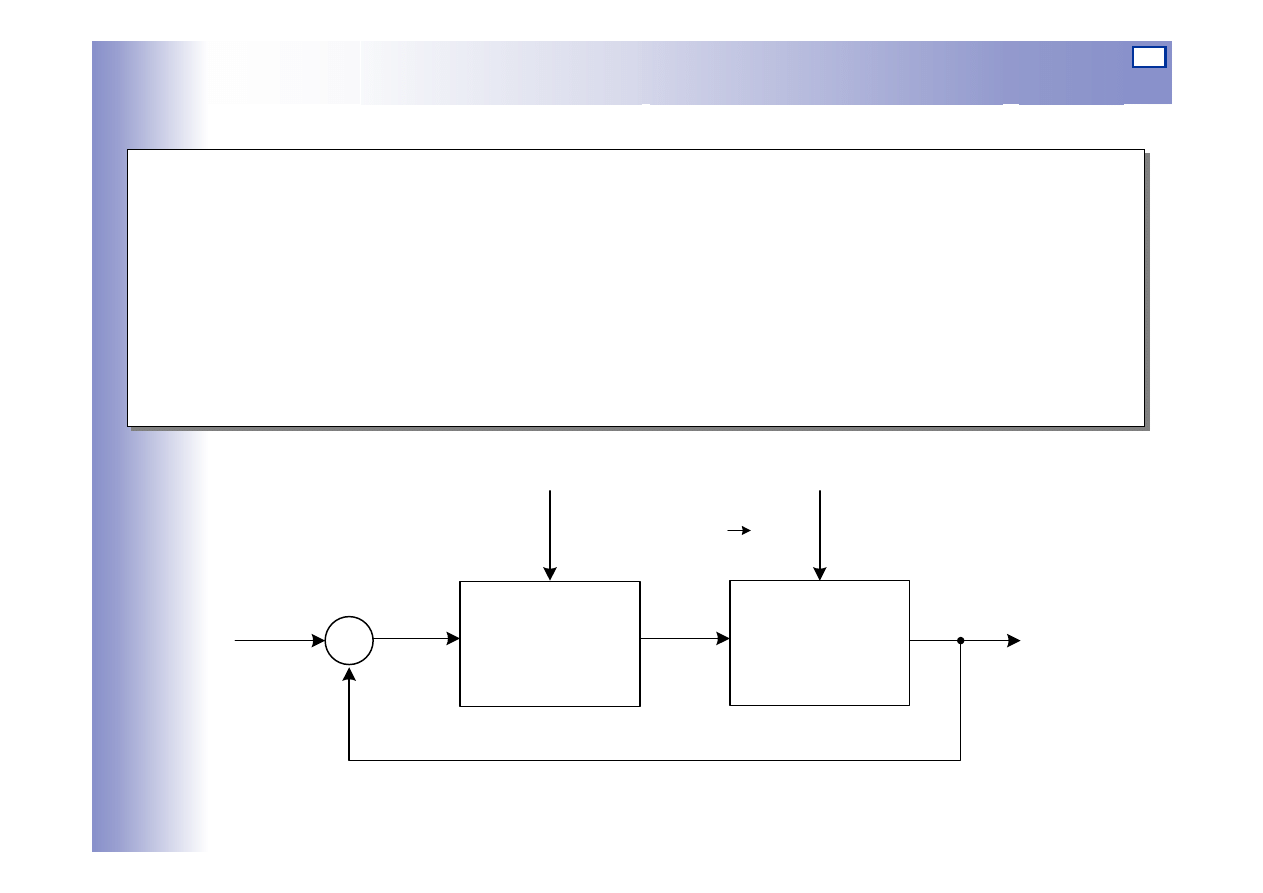
Regulacja automatyczna

p

s

k

s

A

e

k

d

F

n

Regulator

y

Wartość

zadana

y

m

w

20

Klasyfikacja układów regulacji automatycznej

Ze względu na zadanie realizowane przez układ wyróżnia się:

• układy stabilizujące (układy regulacji stało wartościowej), w=const

• układy programowe (regulacji programowej), w=w(t)

• układy nadążne (serwomechanizmy), w=w[

ϕ(t)]

• inne

Ze względu na zadanie realizowane przez układ wyróżnia się:

• układy stabilizujące (układy regulacji stało wartościowej), w=const

• układy programowe (regulacji programowej), w=w(t)

• układy nadążne (serwomechanizmy), w=w[

ϕ(t)]

• inne

e

u

z

z

y

U.S.

O

w

+

-

tor główny w y

sprzężenie zwrotne

e=w-y

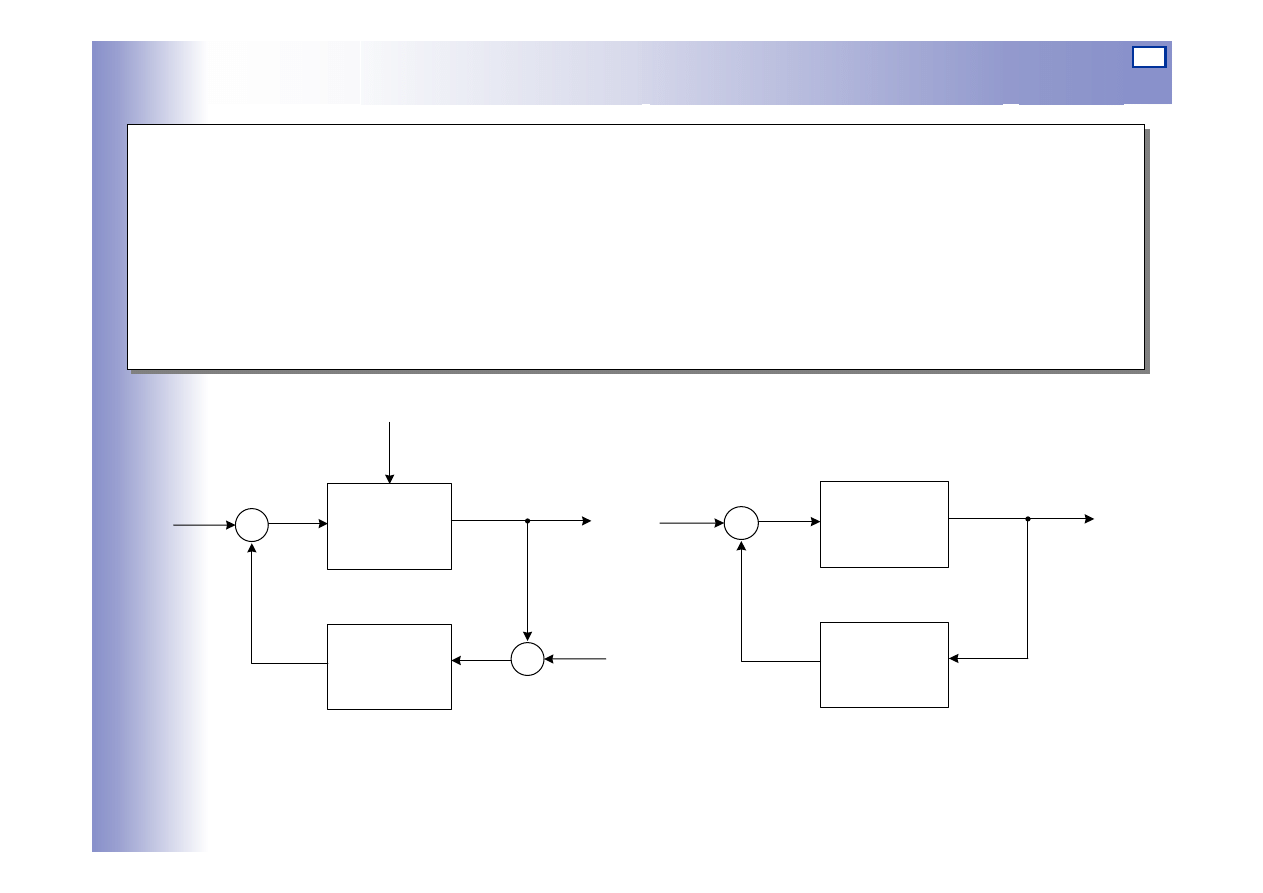
21

Układy stabilizujące

Zadaniem układu jest utrzymanie możliwie stałej, pożądanej wartości

wielkości wyjściowej oraz minimalizacja wpływu zakłóceń na tę
wielkość.

Często główne zakłócenia wchodzą wraz ze strumieniem materiału lub

energii na obiekt, tworząc tor główny od z

1

do y.

Zadaniem układu jest utrzymanie możliwie stałej, pożądanej wartości

wielkości wyjściowej oraz minimalizacja wpływu zakłóceń na tę
wielkość.

Często główne zakłócenia wchodzą wraz ze strumieniem materiału lub

energii na obiekt, tworząc tor główny od z

1

do y.

e

y

R

O

z

1

u

-

+

-

+

y

z

2

w

ebiegi

pracy

∆"

e=

∆y

R

O

∆z

1

∆u

-

+

∆y

∆z

2

Przykłady: regulacja ciśnienia, poziomu cieczy, natężenia przepływu, pH itd.

22

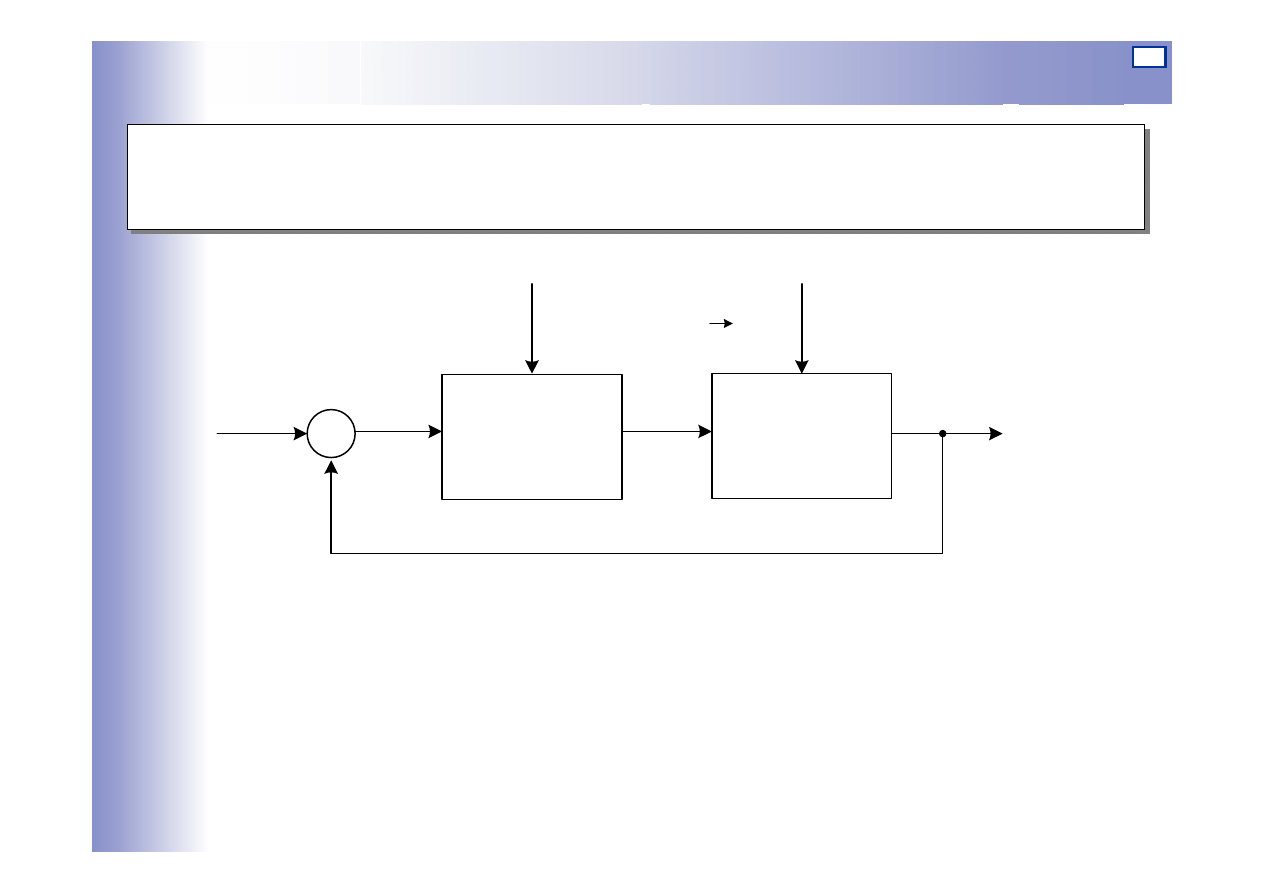
Układy regulacji programowej

Zadaniem układu jest uzyskanie przewidzianych określonym programem

czasowym zmian wielkości regulowanej (sterowanej)

Zadaniem układu jest uzyskanie przewidzianych określonym programem

czasowym zmian wielkości regulowanej (sterowanej)

e

u

z

z

y

U.S.

O

w

+

-

tor główny w y

sprzężenie zwrotne

e=w-y

Przykłady:
• programowa regulacja temperatury w budynku mieszkalnym
• programowa regulacja temperatury w piecu hartowniczym
• programowa regulacja jednej lub kilku wielkości w procesie rozruchu

(stopniowe dochodzenie do nominalnego stanu pracy)

23

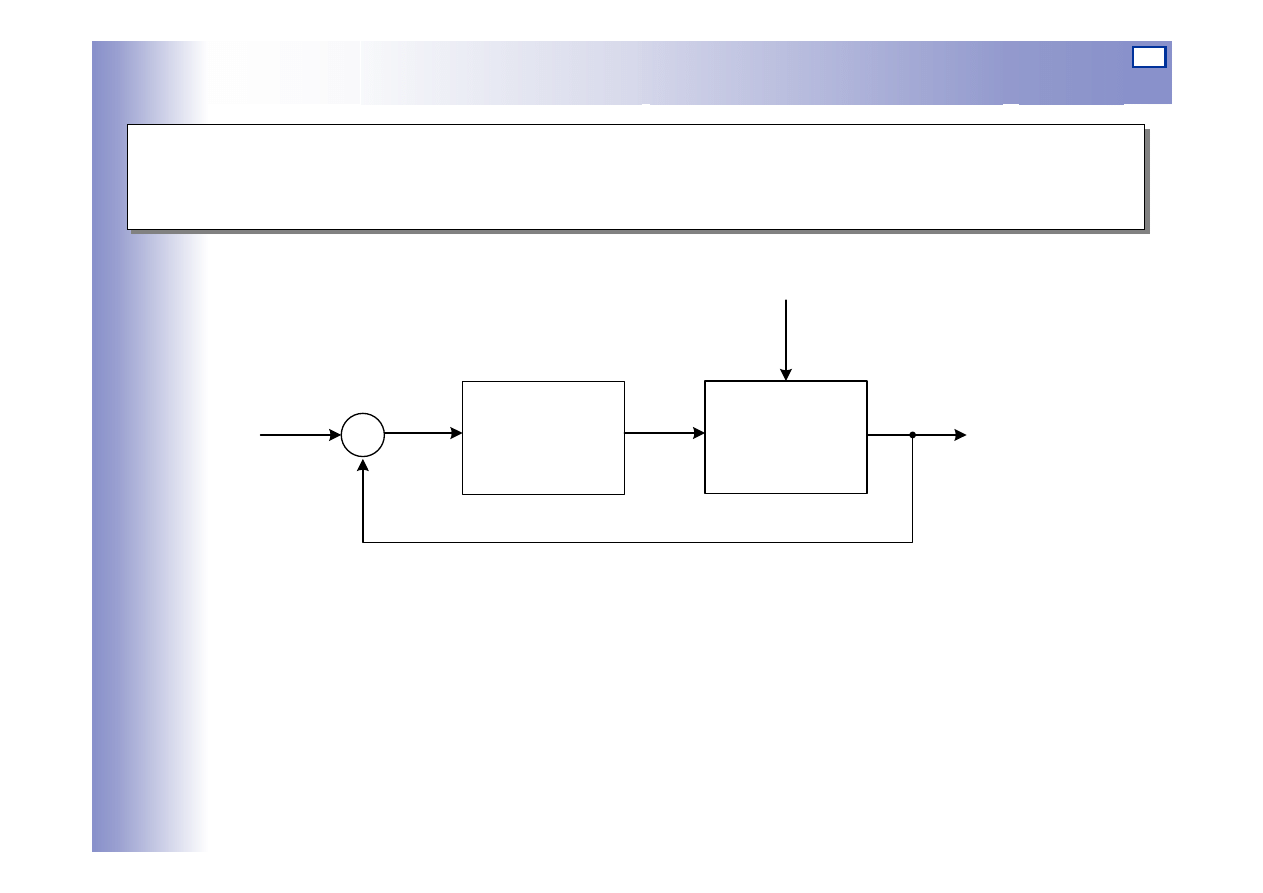
Układy nadążne

Zadaniem układu jest nadążanie wielkości wyjściowej y za zmieniającą się

w nieznany nam sposób wartością zadaną w

Zadaniem układu jest nadążanie wielkości wyjściowej y za zmieniającą się

w nieznany nam sposób wartością zadaną w

e

u

z

y

R

O

w

+

-

Przykłady:
• sterowanie położeniem y dział przeciwlotniczych wg wskazań radaru

określającego położenie w samolotu

• sterowanie położeniem y pisaka rejestratora wg aktualnej wartości w

mierzonej i rejestrowanej wielkości fizycznej

24

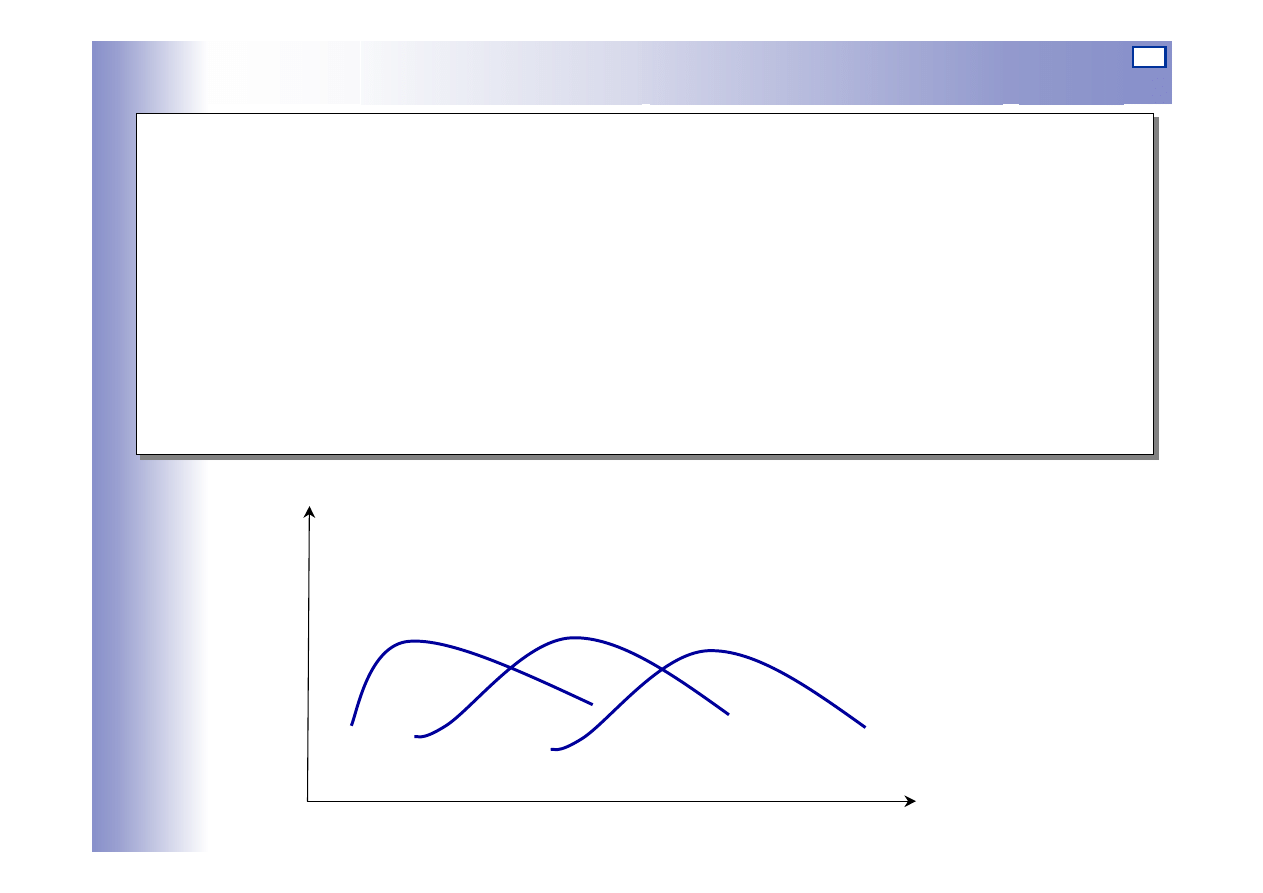
Układy sterowania optymalnego

Zadaniem układu jest utrzymywanie wielkości regulowanej na wartości

ekstremalnej.

Położenie ekstremum zazwyczaj nie jest stałe i zależy od wartości

sygnałów zakłócających

Optymalizacja przebiegu procesów - np. minimalizacja zużycia energii,

minimalizacja kosztów lub maksymalizacja zysku przy założonych
ograniczeniach

Zadaniem układu jest utrzymywanie wielkości regulowanej na wartości

ekstremalnej.

Położenie ekstremum zazwyczaj nie jest stałe i zależy od wartości

sygnałów zakłócających

Optymalizacja przebiegu procesów - np. minimalizacja zużycia energii,

minimalizacja kosztów lub maksymalizacja zysku przy założonych
ograniczeniach

z=a

z=b

z=v

y

u

25

Układy ciągłe i dyskretne w czasie

Układy ciągłe – zmiany wejścia obiektu oraz obserwacje (pomiary) wyjścia

mogą odbywać się w każdym momencie t .

W opisie układu występują wtedy funkcje czasu u(t), y(t), itp.

Układy ciągłe – zmiany wejścia obiektu oraz obserwacje (pomiary) wyjścia

mogą odbywać się w każdym momencie t .

W opisie układu występują wtedy funkcje czasu u(t), y(t), itp.

Układy dyskretne (w czasie) – zmiany wejścia obiektu oraz obserwacje

(pomiary) wyjścia mogą odbywać się w w ściśle określonych
chwilach, zwykle równoodległych -

∆t

W opisie układu występują wtedy dyskretne funkcje czasu, czyli ciągi: u(k),

y(k), itp., gdzie k oznacza numer kolejnego taktu

Sterowanie komputerowe ma charakter dyskretny.

Układy dyskretne (w czasie) – zmiany wejścia obiektu oraz obserwacje

(pomiary) wyjścia mogą odbywać się w w ściśle określonych
chwilach, zwykle równoodległych -

∆t

W opisie układu występują wtedy dyskretne funkcje czasu, czyli ciągi: u(k),

y(k), itp., gdzie k oznacza numer kolejnego taktu

Sterowanie komputerowe ma charakter dyskretny.

26

Układy liniowe i nieliniowe

Układy liniowe – układy, które zawierają wyłącznie elementy liniowe, tzn.

elementy o liniowych charakterystykach statycznych, opisywane
za pomocą liniowych równań różniczkowych lub różnicowych

Rzeczywiste układy są nieliniowe, ale w wielu przypadkach z

zadawalającym przybliżeniem można opisać działanie układu
nieliniowego, linearyzując jego charakterystyki w otoczeniu
nominalnego punktu pracy

Układy liniowe – układy, które zawierają wyłącznie elementy liniowe, tzn.

elementy o liniowych charakterystykach statycznych, opisywane
za pomocą liniowych równań różniczkowych lub różnicowych

Rzeczywiste układy są nieliniowe, ale w wielu przypadkach z

zadawalającym przybliżeniem można opisać działanie układu
nieliniowego, linearyzując jego charakterystyki w otoczeniu
nominalnego punktu pracy

Układy nieliniowe – układy, które zawierają chociaż jeden element

nieliniowy

Układy nieliniowe – układy, które zawierają chociaż jeden element

nieliniowy

27

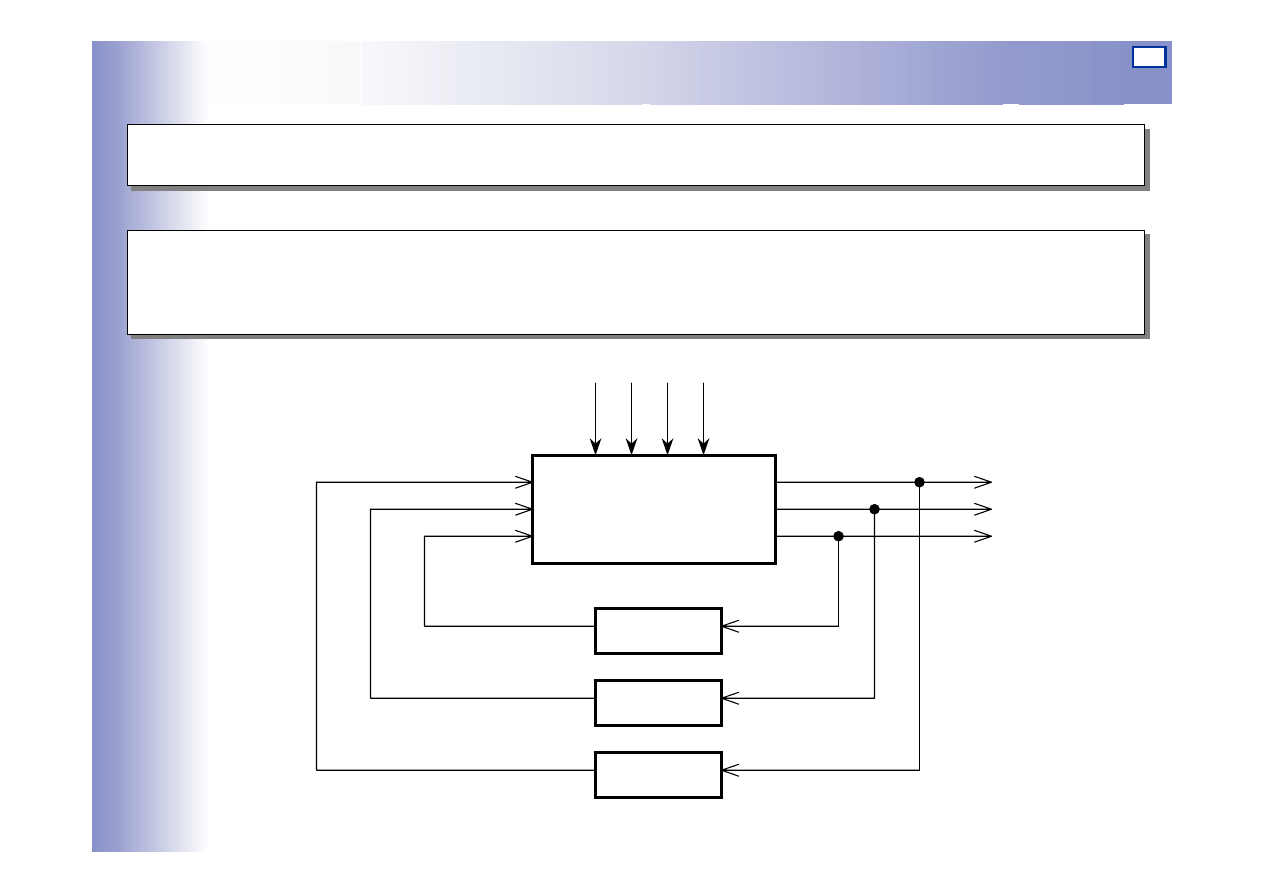
Układy jeno- i wielowymiarowe

Układy jednowymiarowe – układy o jednym wejściu i jednym wyjściu

Układy jednowymiarowe – układy o jednym wejściu i jednym wyjściu

Układy wielowymiarowe – wielkości u oraz y są wektorami (wiele wejść

i wiele wyjść)

Układy wielowymiarowe – wielkości u oraz y są wektorami (wiele wejść

i wiele wyjść)

Obiekt

Reg. 1

Reg. 2

Reg. 3

u

1

u

2

u

3

y

1

y

2

y

3