Automatyka i Robotyka

2011/12

Fizyka 1

Materiały do wykładu 3

21 10 2011

⃗

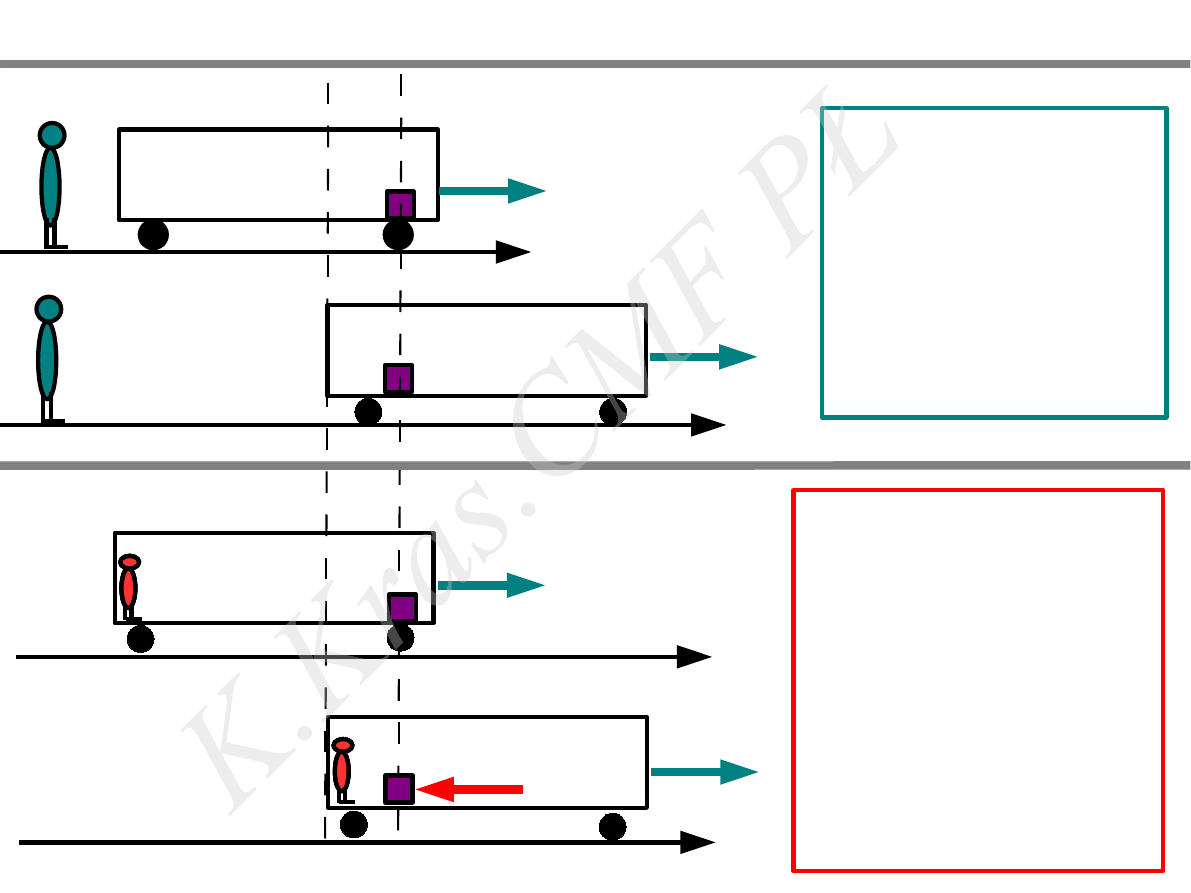
a

w

⃗

a

w

brak tarcia pomiędzy wózkiem i klockiem (m)

inercjalny

⃗

a

w

⃗

a

w

nieinercjalny

F

kx

=

0

a

kx

=

0

x

x

x

x

przyspieszenie klocka
względem ziemi

⃗

a

w

⃗

B

a

kx

≠

0

a

kx

= −

a

w

m a

kx

=

0

przyspieszenie klocka
względem wagonu

m a

kx

=

m(−a

w

)

⃗

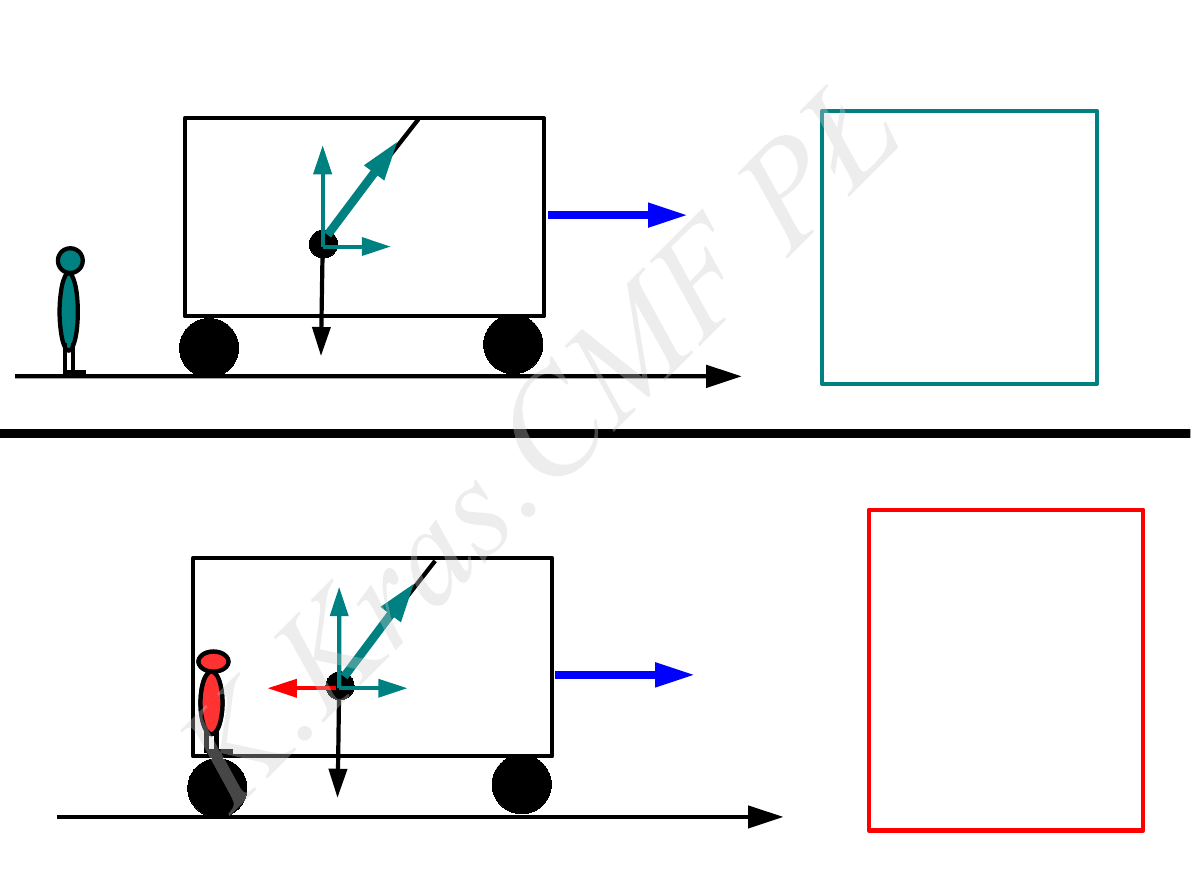
a

w

inercjalny

nieinercjalny

⃗

N

x

=

m ⃗

a

w

x

⃗

N

x

− ⃗

B =0

⃗

a

x

=

0

⃗

a

w

x

⃗

mg

⃗

N

⃗

N

x

⃗

mg

⃗

N

⃗

N

x

⃗

B

⃗

a

x

= ⃗

a

w

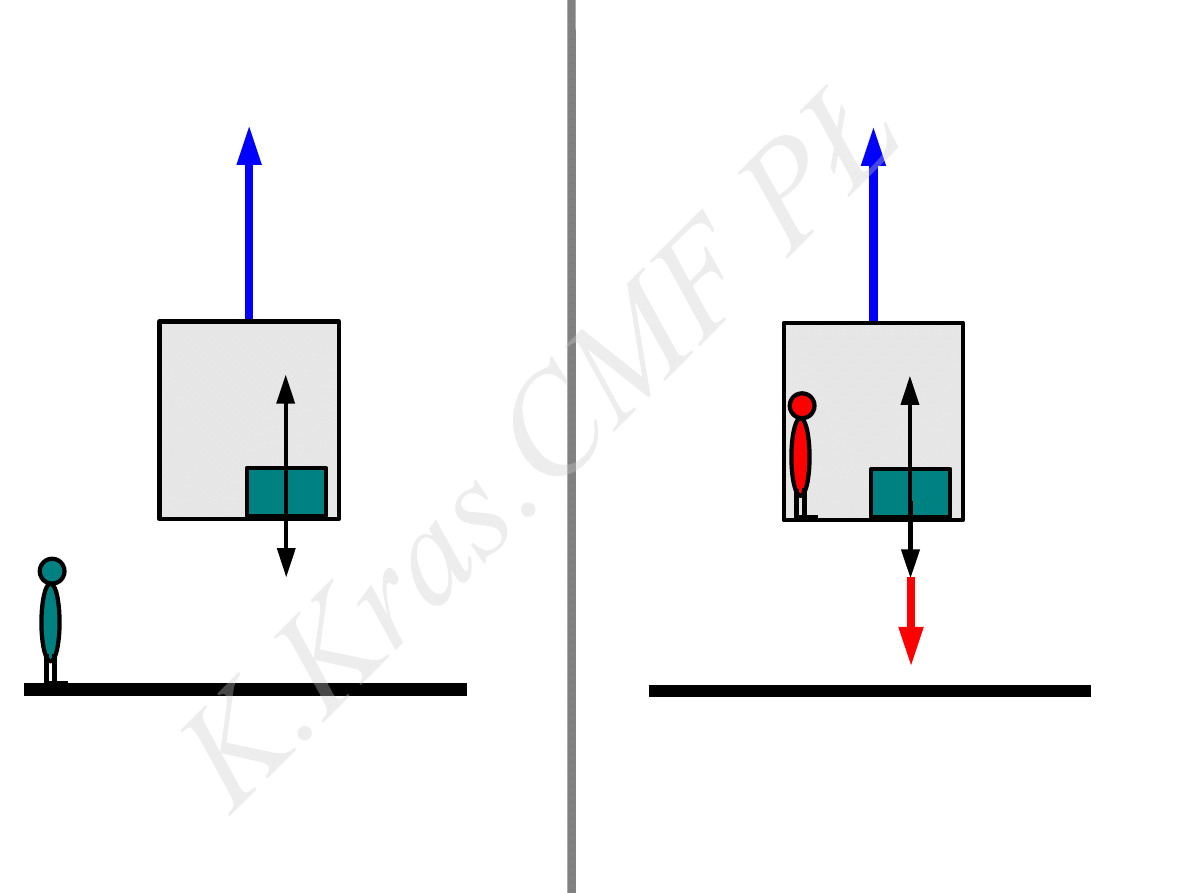
m

⃗

a

w

m ⃗g

R

⃗

a

m

= ⃗

a

w

m

⃗

a

w

m ⃗g

R

⃗

a

m

=

0

⃗

B=m ⃗

a

w

inercjalny

nieinercjalny

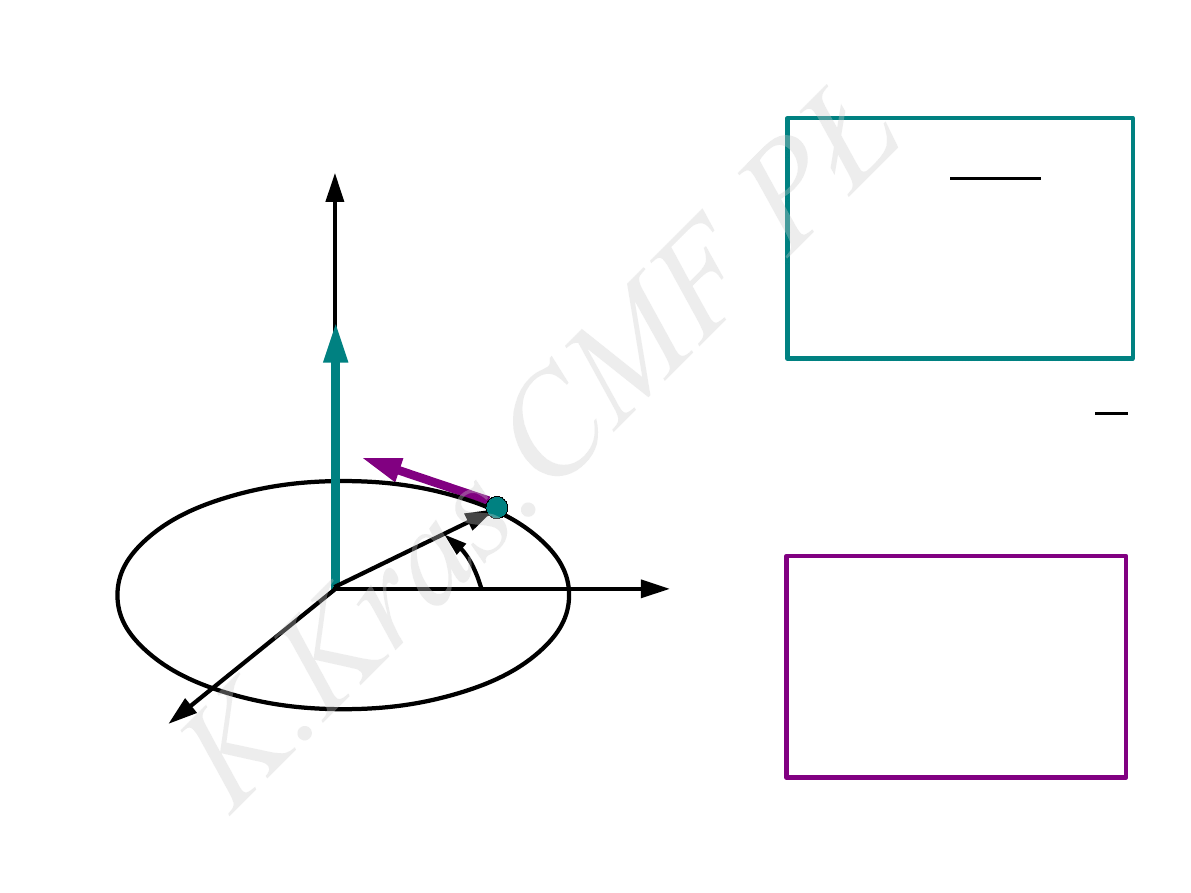
⃗r

⃗

V

⃗

ω

x

z

y

⃗

V = ⃗

ω×⃗r

α

ω =

d α

dt

prędkość kątowa

prędkość liniowa

ω=

const ⇒ ω=α

t

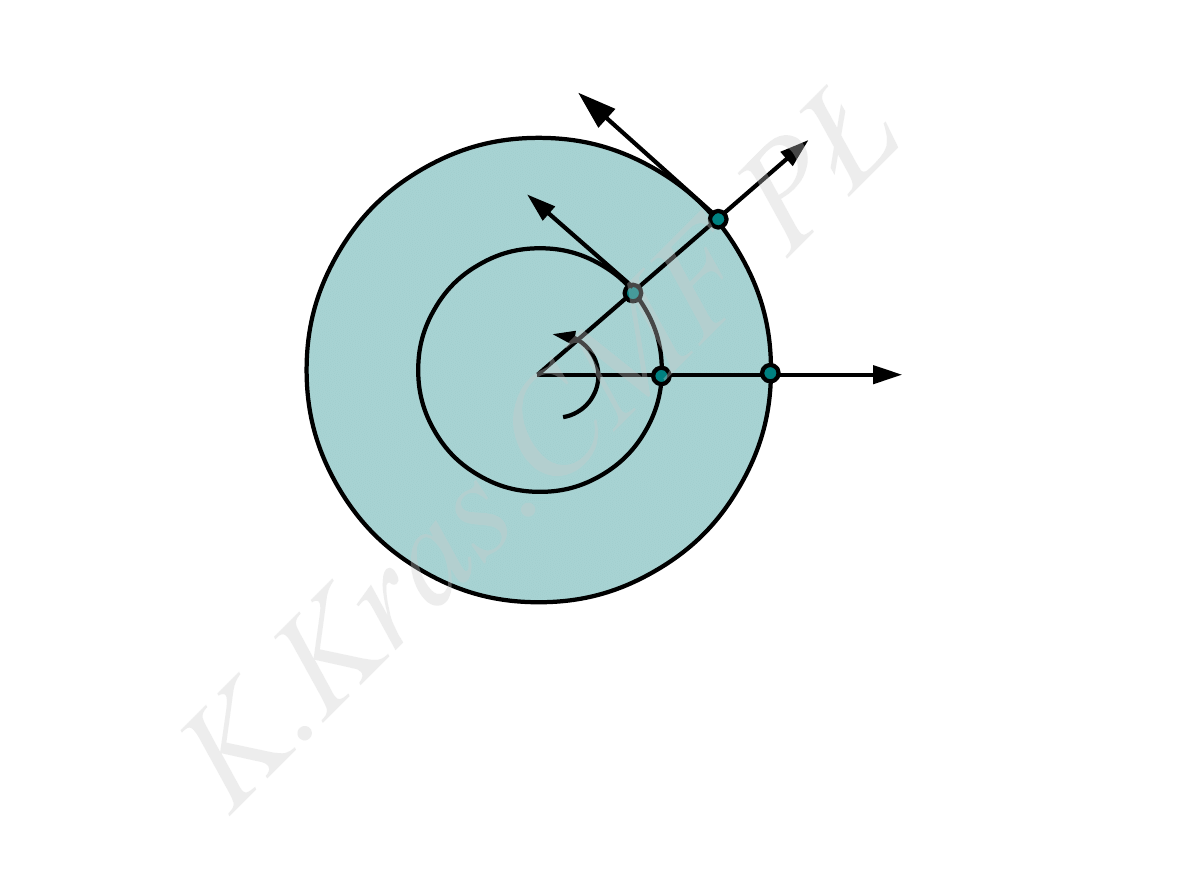
V

1

V

2

V

2

>

V

1

s

1

s

2

s

2

>

s

1

⃗

V = ⃗

ω×⃗r

ω

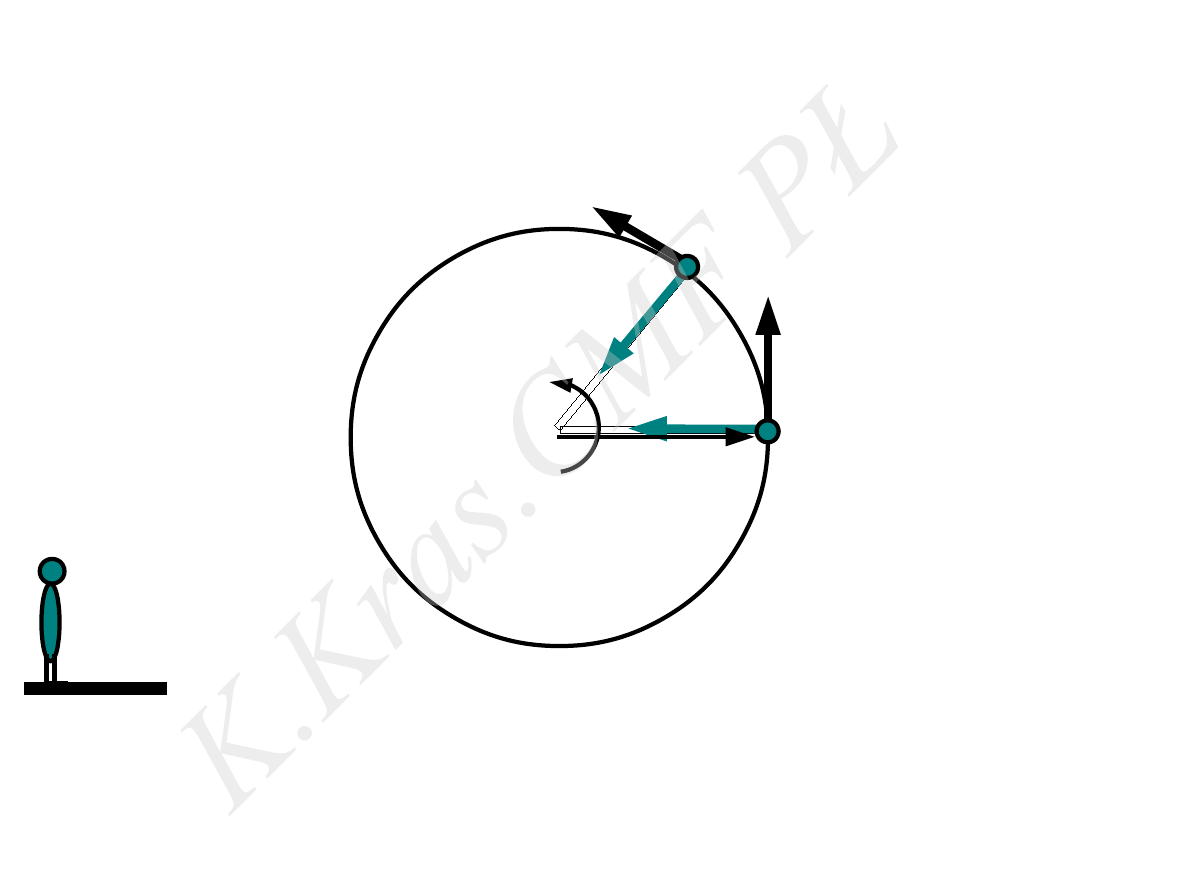
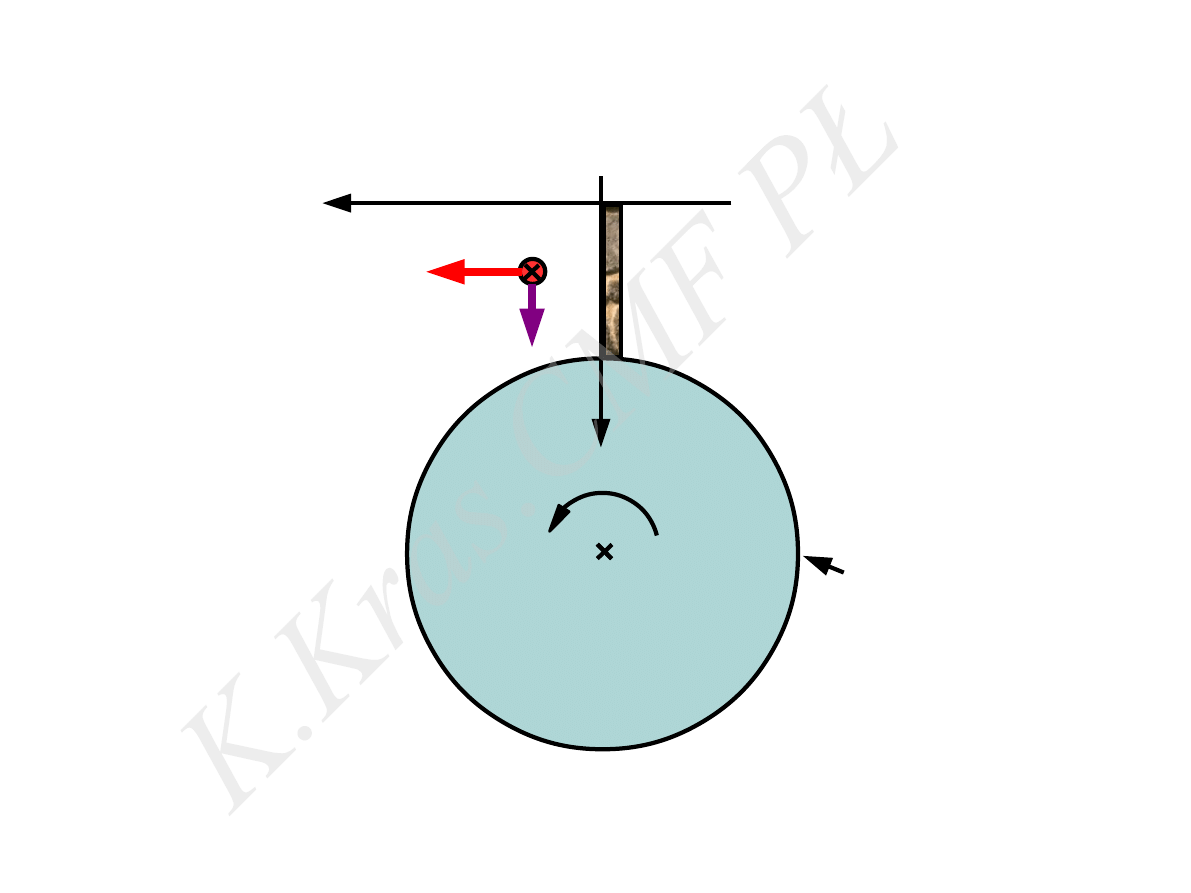
siła dośrodkowa

układ inercjalny

⃗

F

d

⃗

F

d

⃗

V

⃗

V

F

d

=

m ω

2

r

m

m

ω

⃗r

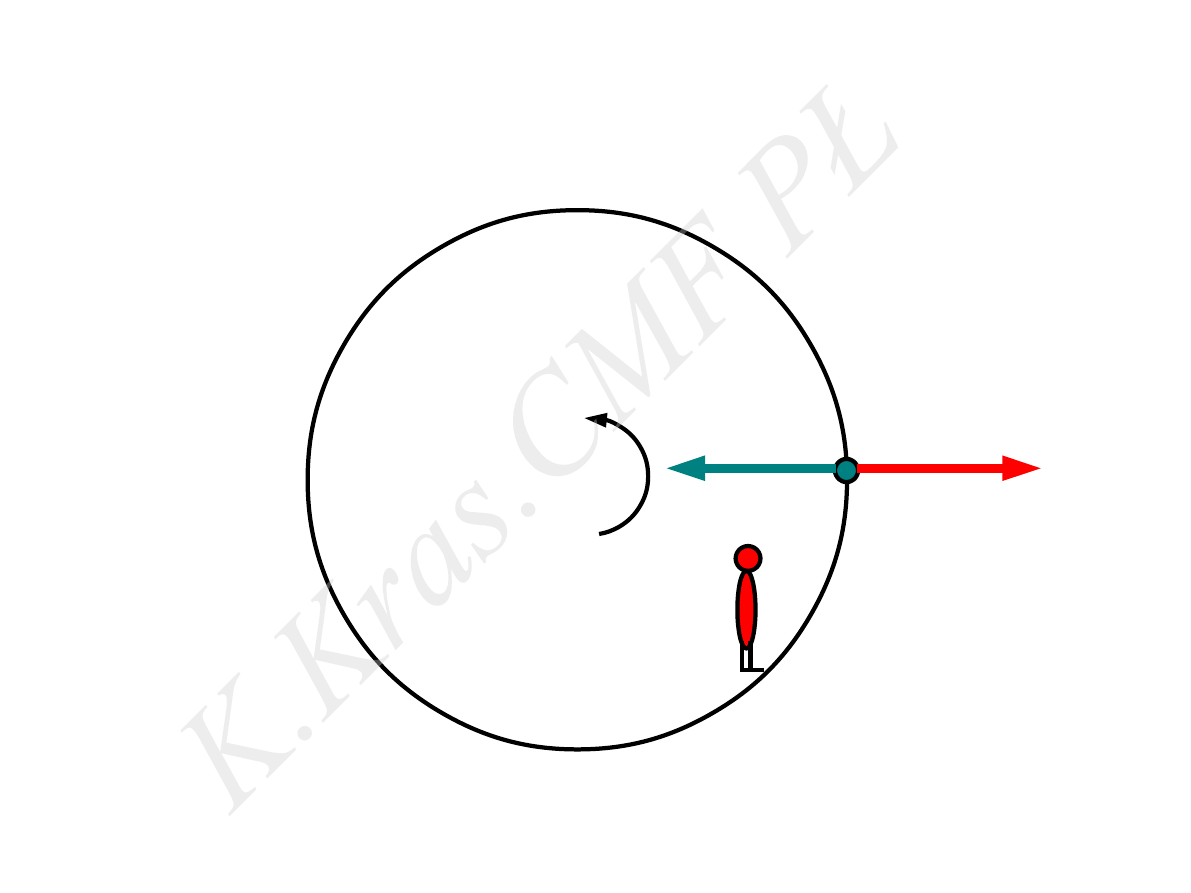
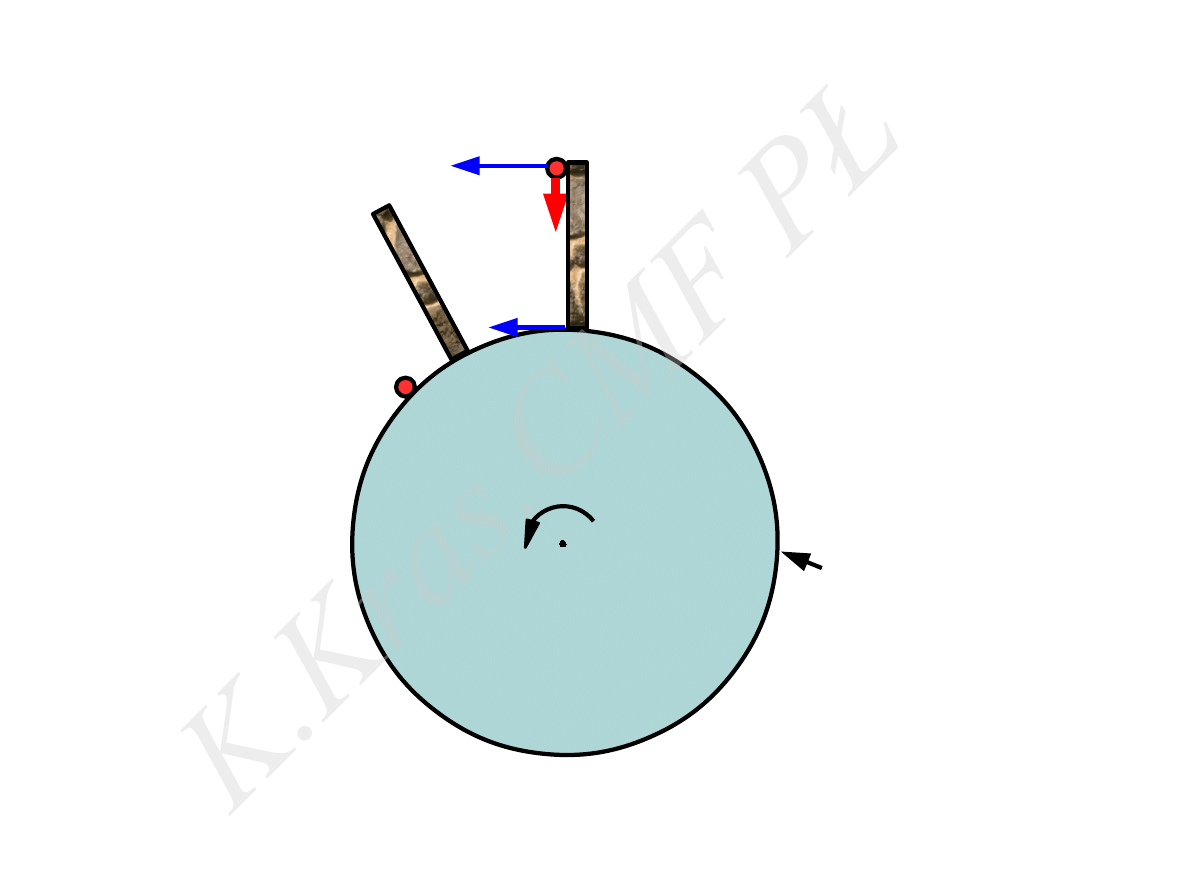
siła dośrodkowa i odśrodkowa

układ nieinercjalny

⃗

F

d

⃗

F

o

ω

⃗

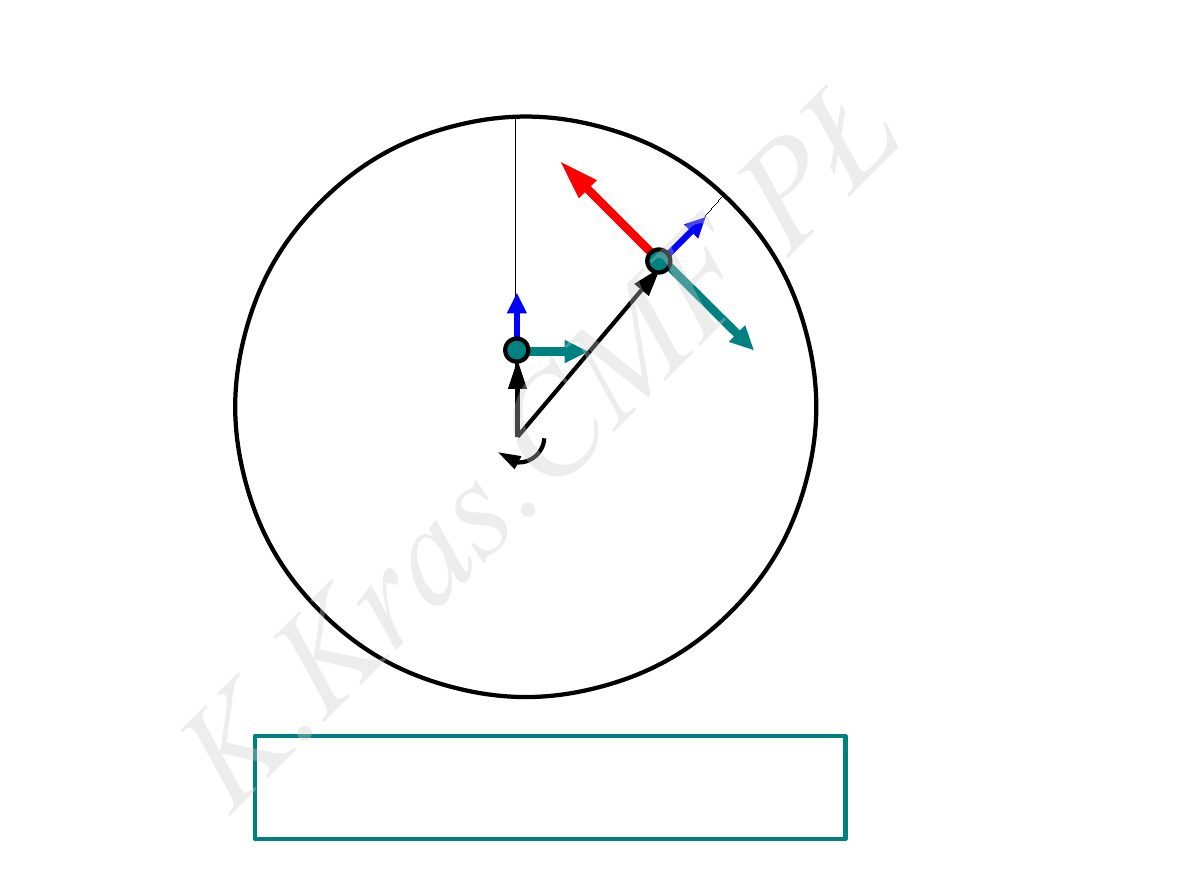
V

⃗

V

⃗

r

1

a

C

= −

2 ⃗

ω× ⃗

V

⃗

r

2

przyspieszenie Coriolisa

–

układ nieinecjalny

ω

r

1

ω

r

2

⃗

a

C

ω

⃗

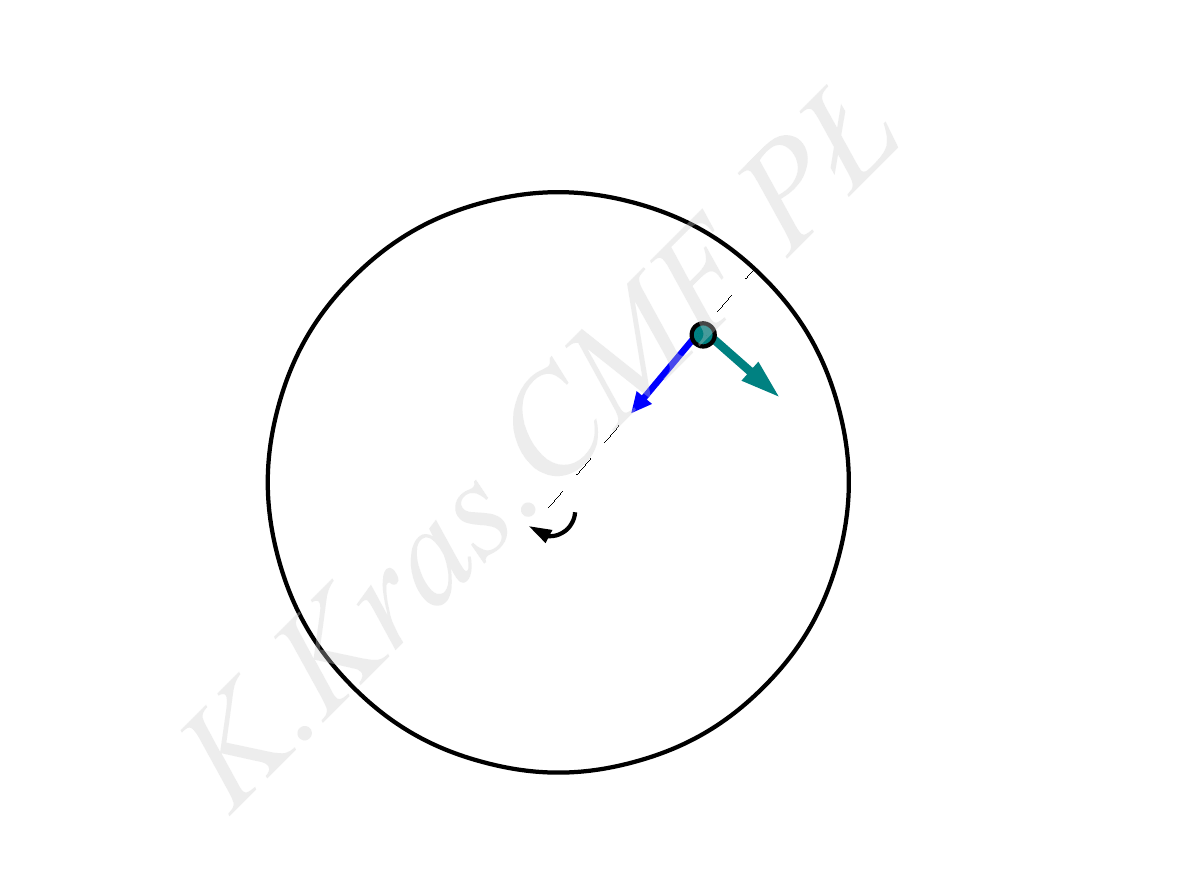
V

⃗

a

C

ω

przyspieszenie Coriolisa –

układ nieinecjalny

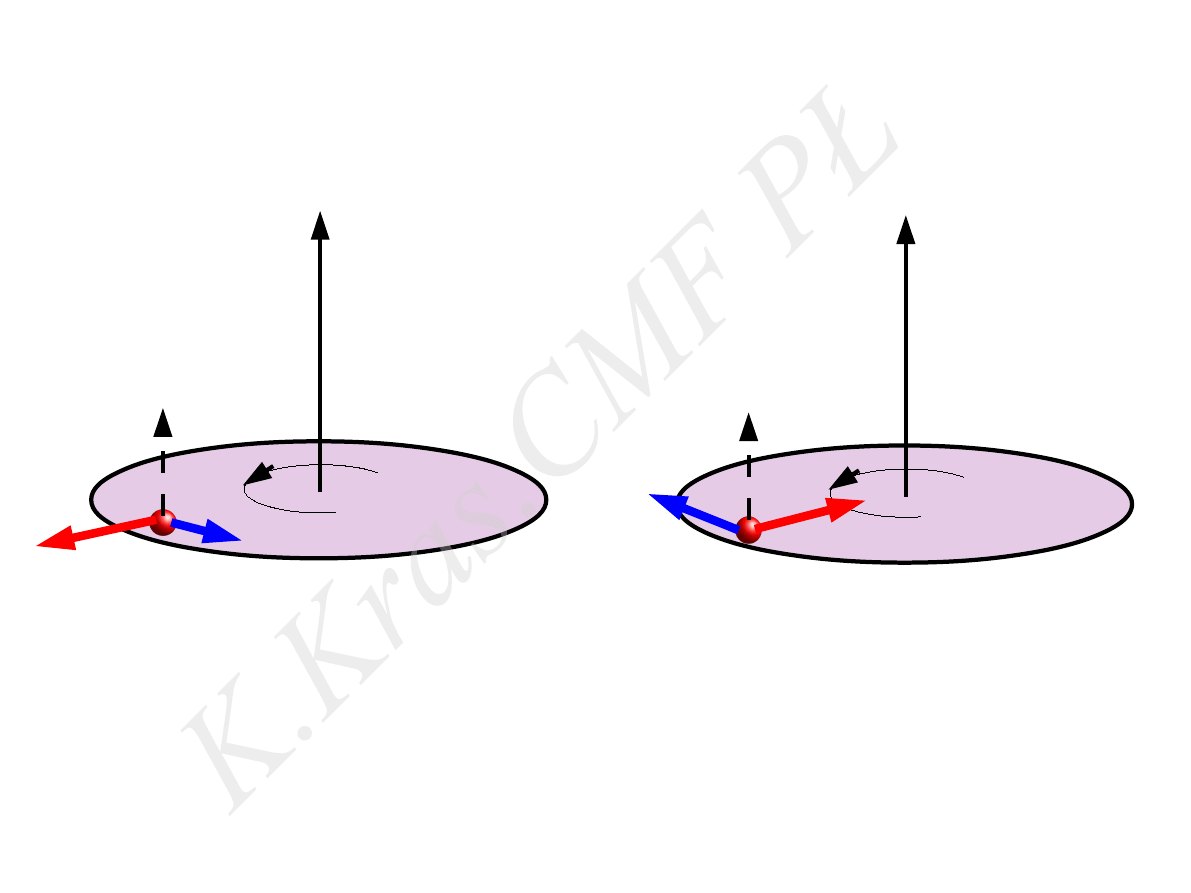
ω

ω

⃗

V

⃗

F

c

ω

ω

⃗

V

⃗

F

c

przyspieszenie Coriolisa

–

układ nieinecjalny

⃗

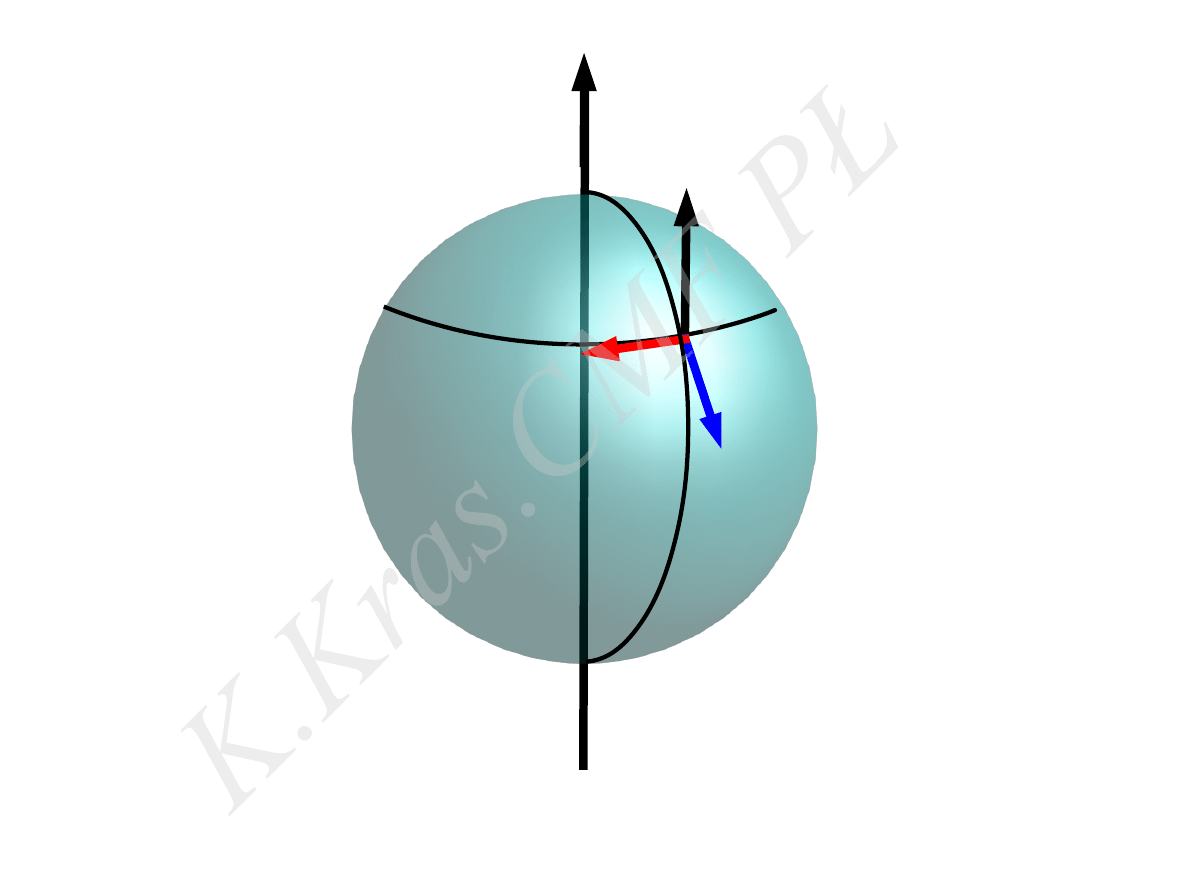
V

ω

ω

⃗

F

c

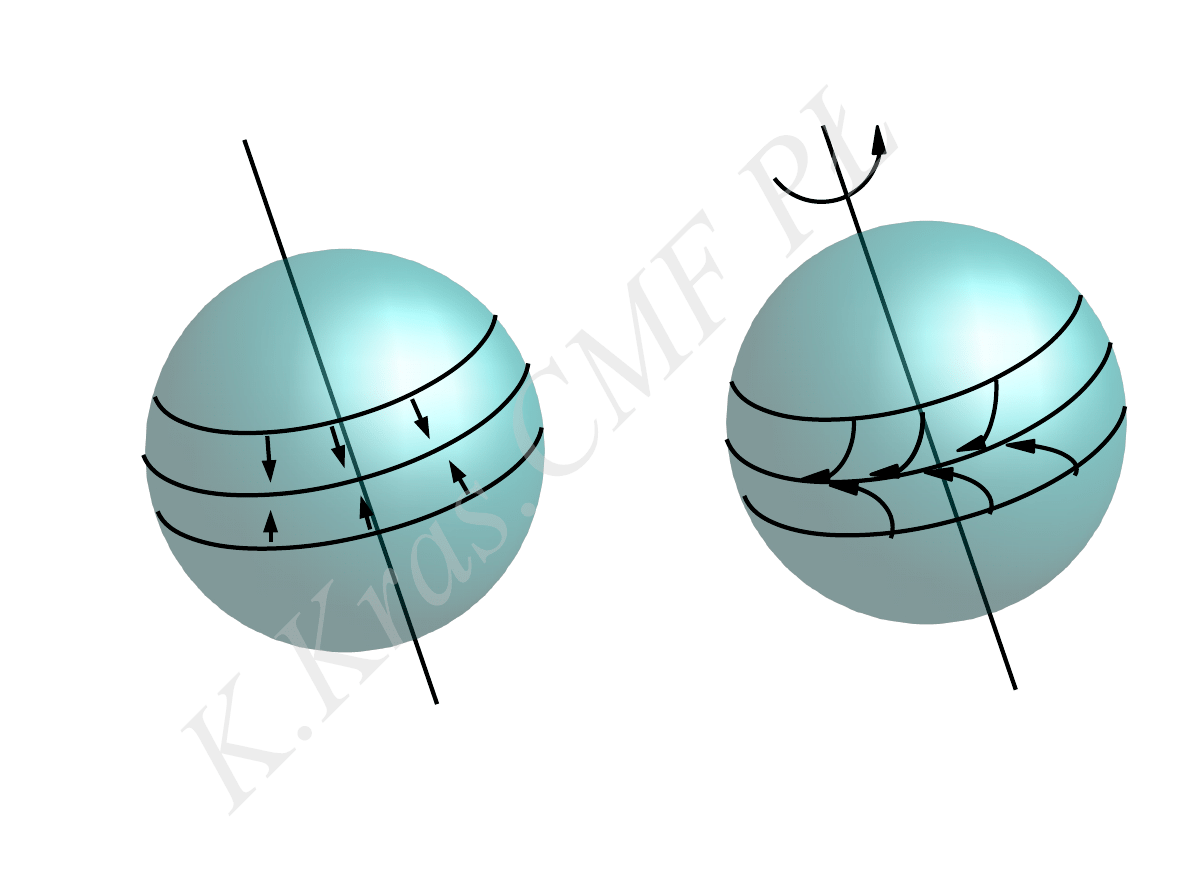
bez obrotu

obrót

⃗

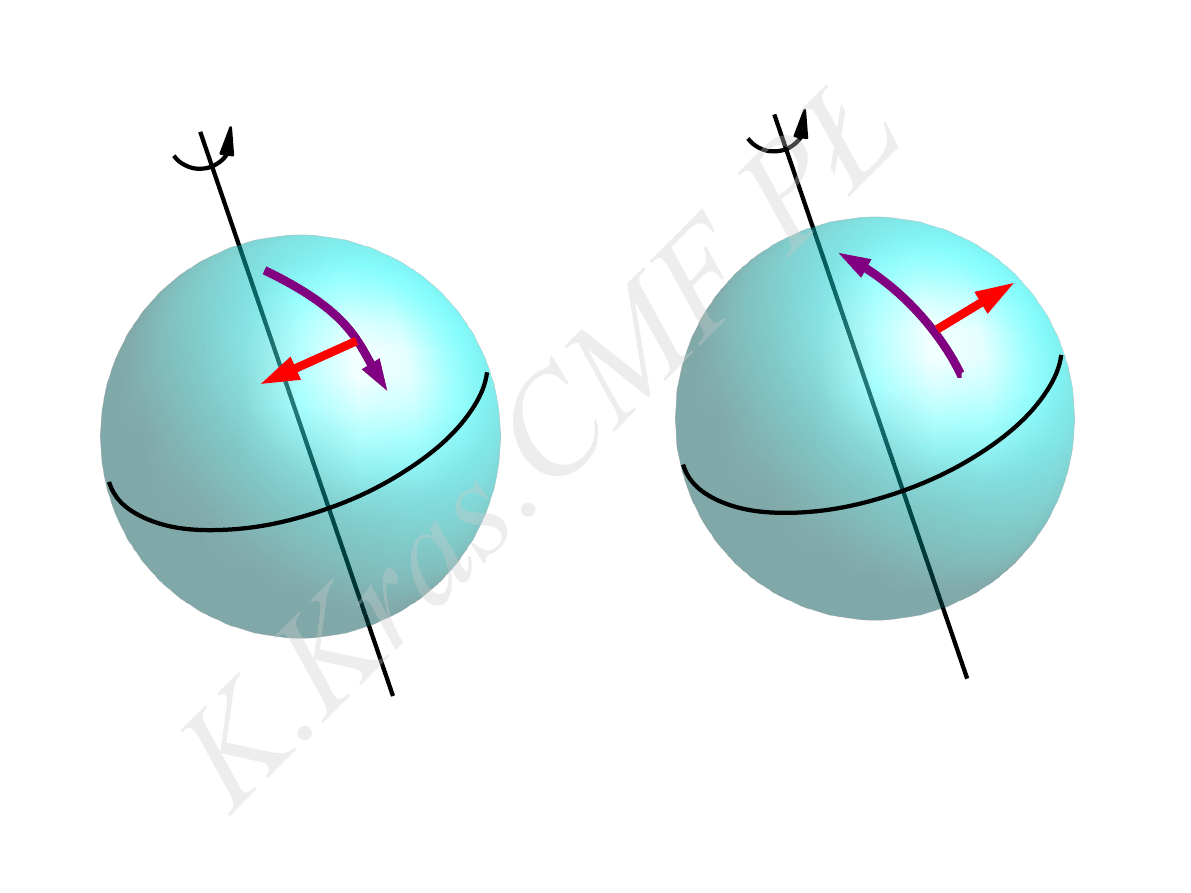
F

c

⃗

F

c

⃗

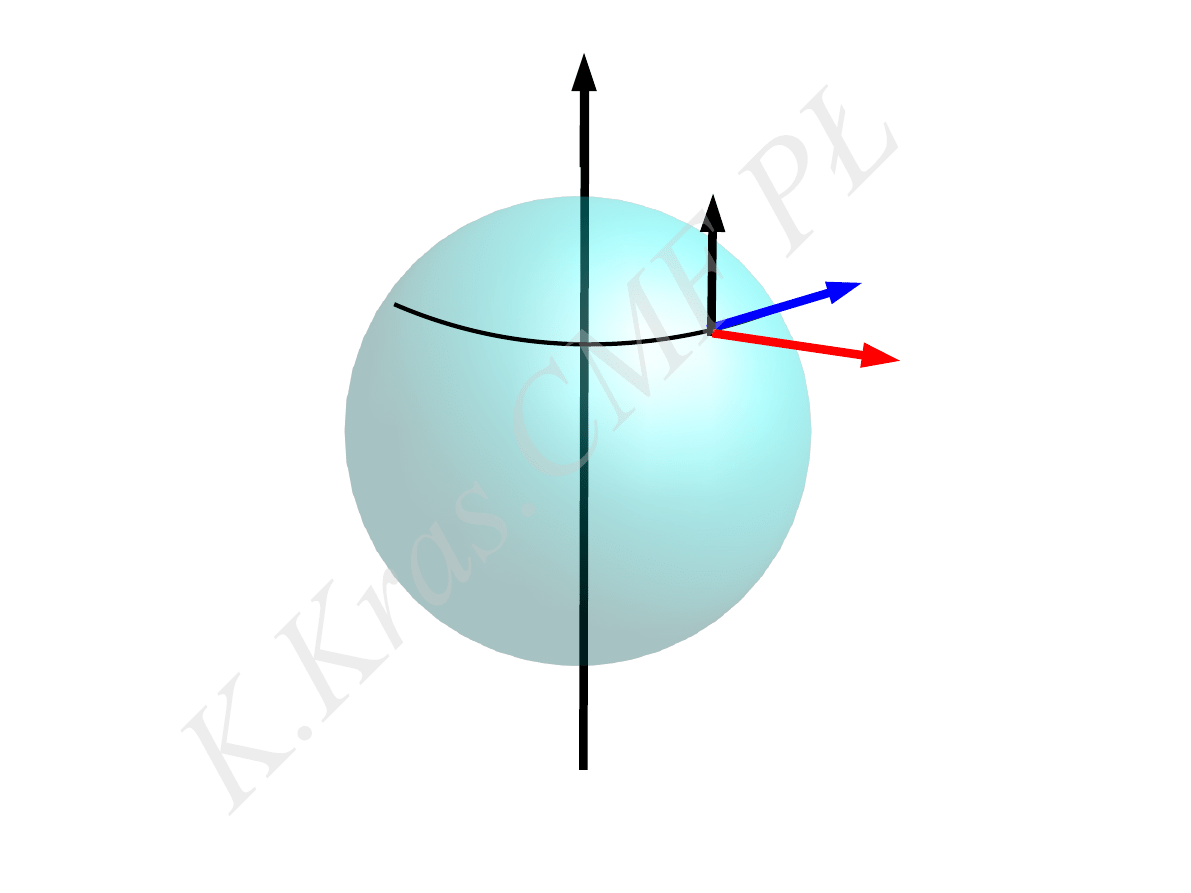
V

ω

ω

⃗

F

c

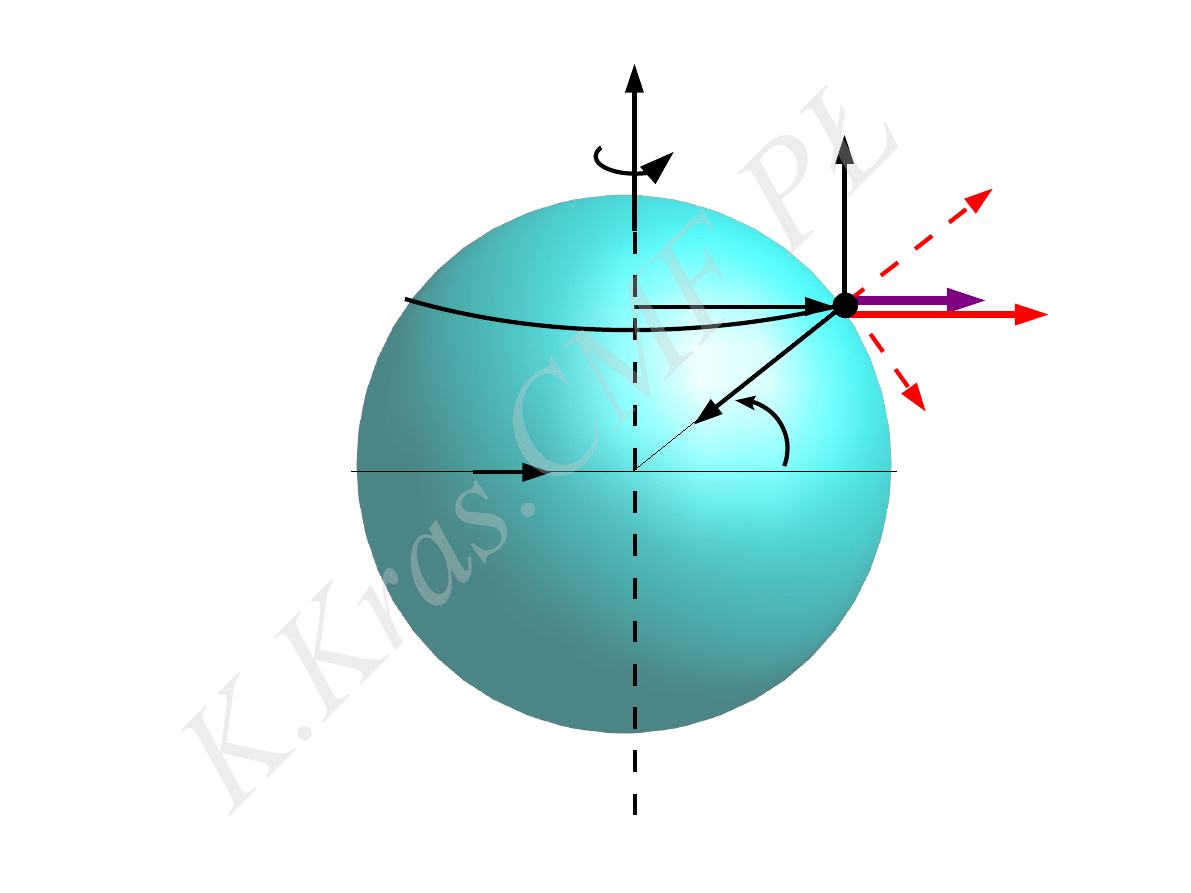
ϕ

⃗

ω

⃗

F

O

⃗

V

R

Z

⃗

F

C

⃗

ω

⃗r

⃗

V −za ekran

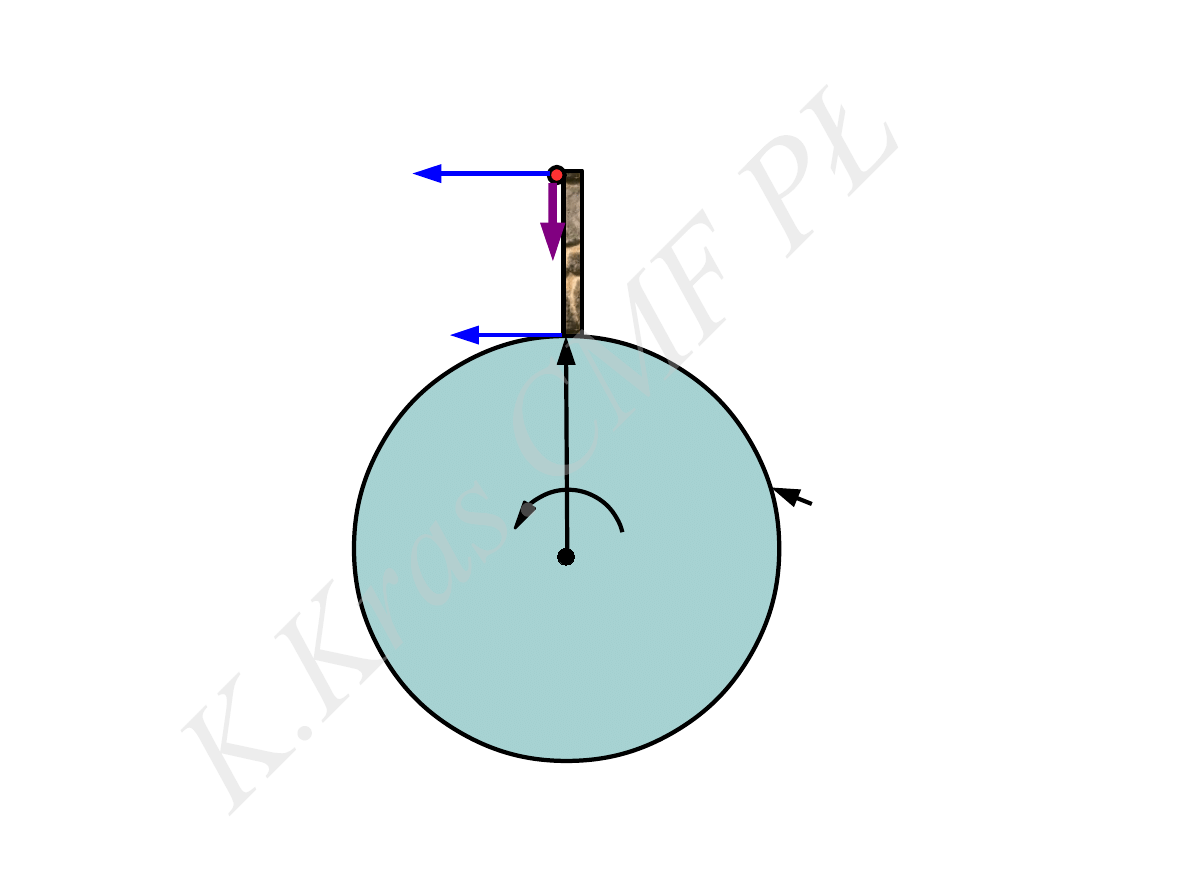
N

R

h

⃗

V (R)

⃗

V (R+h)

równik

⃗

U

x

Y

U

biegun
N

ω

ω

a

Cx

równik

N

równik