XII. Zmienna losowa typu skokowego (dyskretnego)
Zmienna losowa X jest typu skokowego (dyskretnego), jeśli przyjmuje ona tylko skończoną (lub przeliczalną)
liczbę wartości {x
1
, x
2
, x
3
,..., x
n
} (tzw. punkty skokowe), tak, że dla każdego i=1,2,...,n.) (i=1,2,....)
P(X= x
i
)= p
i
>0,
gdzie
1
1
=
∑
=
n
i
i
p
(
1
1
=
∑
∞
=
i
i
p
).
Oznacza to, że zmienna losowa X przyjmuje wartość
i
x
z prawdopodobieństwem
i
p
.
Funkcją rozkładu prawdopodobieństwa (funkcją prawdopodobieństwa, rozkładem prawdopodobieństwa)
zmiennej losowej X nazywamy funkcję p określoną wzorem
p(x
i
)=P(X= x
i
)
i
.
Funkcję prawdopodobieństwa P określoną na wartości x
i
oznaczamy przez p
i
, czyli p
i
=p(x
i
).
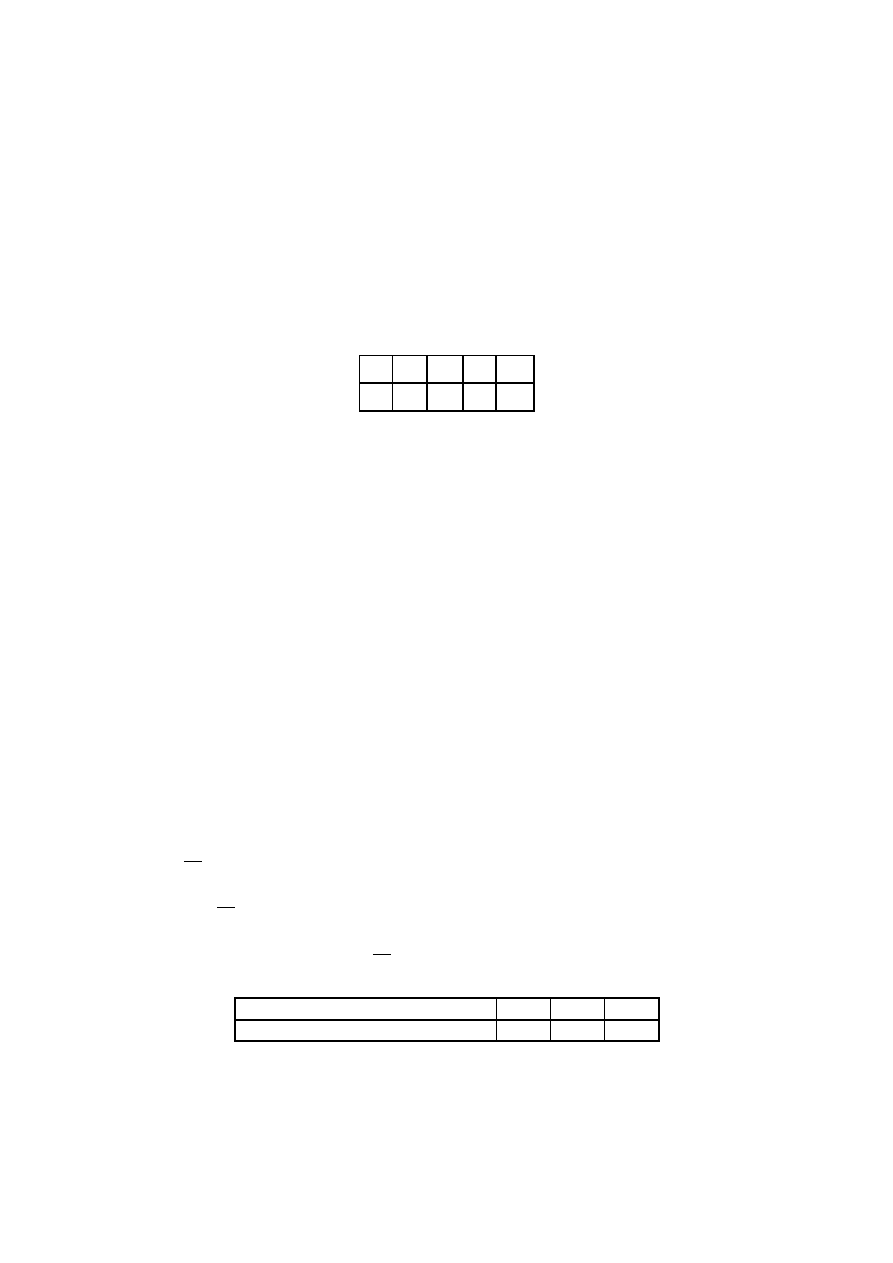
Innym sposobem określania funkcji prawdopodobieństwa zmiennej losowej X jest metoda tabelkowa:
i
x
1
x
2
x
n
x
i
p
1
p
2
p
n
p
Dystrybuantą zmiennej losowej skokowej X jest funkcja F określona wzorem
( )
(
)
∑
<
<
∞
−
=
<
=
x
x
i
i
p
x
X
P
x
F
,
gdzie sumowanie odbywa się po tych
i
x
, które spełniają nierówności
x
x
i
<
<
∞
−
.
UWAGA!!!
Mając dany rozkład prawdopodobieństwa możemy wyznaczyć jej dystrybuantę i odwrotnie, mając daną
dystrybuantę zmiennej losowej X możemy podać rozkład prawdopodobieństwa.
Przykład
(1)
W pudełku jest 10 losów ponumerowanych od 1 do 10. Na los z numerem 1 pada główna wygrana 10,
na losy z numerami 2 i 3 wygrana pocieszenia 1, a za wyciągnięcie pozostałych płacimy 2(wygrywamy
– 2). Załóżmy, że wyciągnięcie każdego z losów jest jednakowo prawdopodobne. Doświadczenie
polega na wyciągnięciu jednego losu.
Przestrzeń zdarzeń elementarnych
Ω
={1,2,...,10} i jest skończona. Określmy funkcję
R
A
X
⊂
→
Ω
:
X będzie zmienną losową skokową oznaczającą wygraną. gdzie A={-2,1,10}. Zauważmy, że
X(1)=10, X(2)=X(3)=1, X(4)=X(5)=...=X(10)=-2.
Określmy rozkład prawdopodobieństwa zmiennej losowej X
P(X=10)=p
1
=
10
1
P(X=1)= p
2
+ p
3
=
10
2
P(X=-2)= p
4
+ p
5
+ p
6
+ p
7
+ p
8
+ p
9
+ p
10
=
10
7
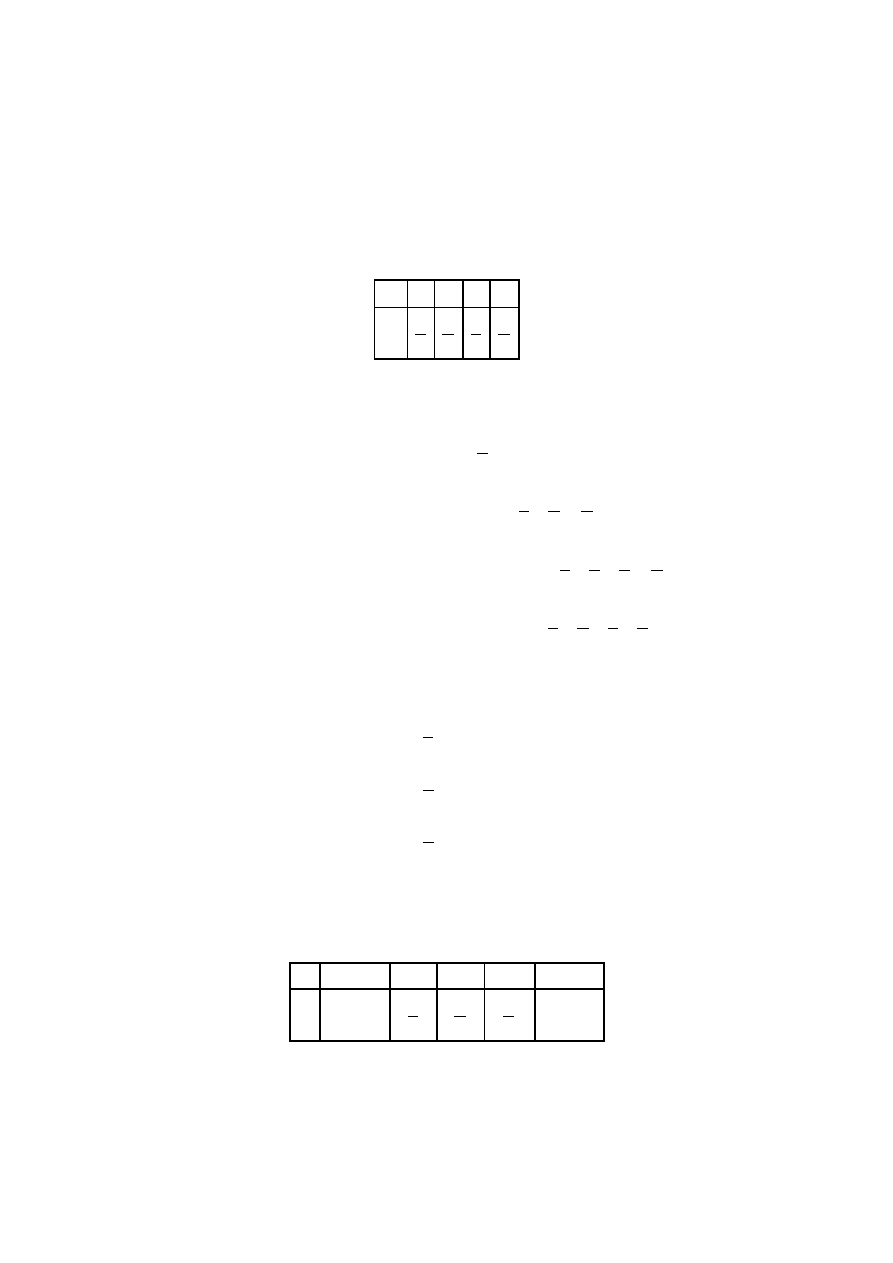
Zapis tabelkowy
wartość zmiennej losowejł
-2
1
10
prawdopodobieństwo
0,7
0,2
0,1
Wyznaczmy dystrybuantę zmiennej losowej
Dla
x
≤
-2
F(x)=P(X<x)=
∑
<
x
x
i
i
p =0
Dla
–2<x
≤
1
F(x)=
∑
<
x
x
i
i
p =p
1
=0,7
1
Dla
1<x
≤
10
F(x)=
∑
<
x
x
i
i
p =p
1
+ p
2
=0,7+0,2=0,9
Dla
x>10 F(x)=
∑
<
x
x
i
i
p =p
1
+ p
2
+ p
3
=0,7+0,2+0,1=1
Tak więc
10
10
1
1
2
2
1
9
,
0
7
,
0
0
)
(
>
≤
<
≤
<
−
−
≤
=
x
x
x
x
dla
dla
dla
dla
x
F
(2)
Niech zmienna losowa X ma rozkład prawdopodobieństwa
i
x
0 1 3 6
i
p
3
1
6
1
3
1
6
1
Wówczas dystrybuantę wyliczamy w następujący sposób
dla
0
≤
x
( )
(
)
0
=
=
<
=
∑
<
x
x
i
i
p
x
X
P
x
F
dla
1
0
≤
<
x
( )
3
1
1
=
=
=
∑
<
p
p
x
F
x
x
i
i
dla
3
1
≤
<
x
( )
2
1
6
1
3
1
2
1
=
+
=
+
=
=
∑
<
p
p
p
x
F
x
x
i
i
dla
6
3
≤
<
x
( )
6
5
3
1
6
1
3
1
3
2
1
=
+
+
=
+
+
=
=
∑
<
p
p
p
p
x
F
x
x
i
i
dla
6
>
x
( )
1
6
1
3
1
6
1
3
1
4
3
2
1
=
+
+
+
=
+
+
+
=
=
∑
<
p
p
p
p
p
x
F
x
x
i
i
Zatem możemy teraz zapisać dystrybuantę w uproszczony sposób
( )
>
≤
<
≤
<
≤
<
≤
=
6
,
1
6
3
,
6
5
3
1
,
2
1
1
0
,
3
1
0
,
0
x
x
x
x
x
x
F
lub za pomocą tabelki
x
(
]
0
,
∞
−
(
]
1
,
0
(
]
3
,
1
(
]
6
,
3
(
)
+ ∞
,
6
F
0
3
1
2
1
6
5
1
Problem ten możemy teraz odwrócić, tzn. mamy zadaną dystrybuantę zmiennej losowej X określoną przy
pomocy powyższej tabelki. Szukamy rozkładu prawdopodobieństwa tej zmiennej losowej. Zauważamy, że
punktami skokowymi są punkty 0, 1, 3, i 6 (jako punkty nieciągłości dystrybuanty), których
prawdopodobieństwa wyznaczamy za pomocą następujących zależności
2
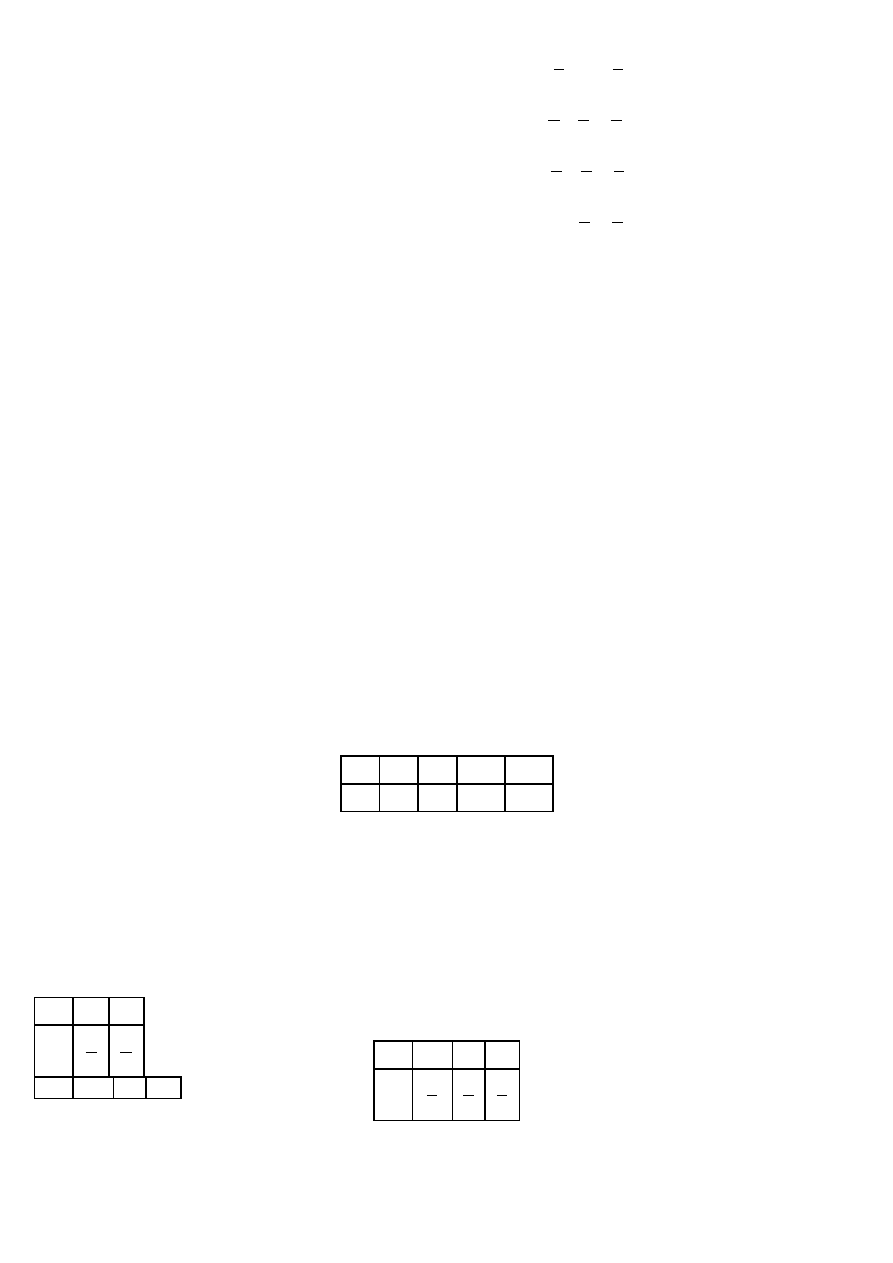
(
)
( )
( )
3
1
0
3
1
0
lim
0
0
1
=
−
=
−
=
=
=
+
→
F
x
F
X
P
p
x
(
)
( )
( )
6
1
3
1
2
1
1
lim
1
1
2
=
−
=
−
=
=
=
+
→
F
x
F
X
P
p
x
(
)
( )
( )
3
1
2
1
6
5
3
lim
3
3
3
=
−
=
−
=
=
=
+
→
F
x
F
X
P
p
x
(
)
( )
( )
6
1
6
5
1
6
lim
6
6
4
=
−
=
−
=
=
=
+
→
F
x
F
X
P
p
x
Stąd rozkład prawdopodobieństwa przedstawia się jak w tabelce na początku tego przykładu.
Możemy teraz, mając daną jedną zmienną losową, tworzyć na jej podstawie inne zmienne losowe.
XIII.
Charakterystyki liczbowe zmiennej losowej skokowej
Zmienna losowa X typu skokowego przyjmuje wartości ze zbioru {x
1
, x
2
, x
3
,..., x
n
}, zaś jego funkcją rozkładu
prawdopodobieństwa jest p.
Wartością oczekiwaną (wartością przeciętną, wartością średnią, nadzieją matematyczną) zmiennej losowej
skokowej X nazywamy liczbę
∑
=
+
+
=
=
n
i
n
n
i
i
p
x
p
x
p
x
EX
1
1
1
.
Wartość oczekiwana jest to więc pewna średnia ważona wartości zmiennej losowej.
UWAGA
Własności wartości oczekiwanej:
1.
( )
c
c
E
=
2.
( )
aEX
aX
E
=
3.
b
EX
b
X
E
+
=
+
)
(
4.
(
)
EY
EX
Y
X
E
+
=
+
5.
(
)
0
=
−
EX
X
E
6.
(
)
bEY
aEX
bY
aX
E
+
=
+
.
Przykład
(1)
Zmienna losowa X ma rozkład zadany za pomocą tabelki
i
x
-5
-1
0
3
i
p
0,2 0,1 0,45 0,25
Policzmy wartość oczekiwaną tej zmiennej losowej:
( )
35
,
0
75
,
0
1
,
0
1
25
,
0
3
45
,
0
0
1
,
0
1
2
,
0
5
1
−
=
+
−
−
=
⋅
+
⋅
+
⋅
−
+
⋅
−
=
=
∑
=
n
i
i
i
p
x
EX
Wartość oczekiwana zmiennej losowej X wynosi
–0,35.
(2)
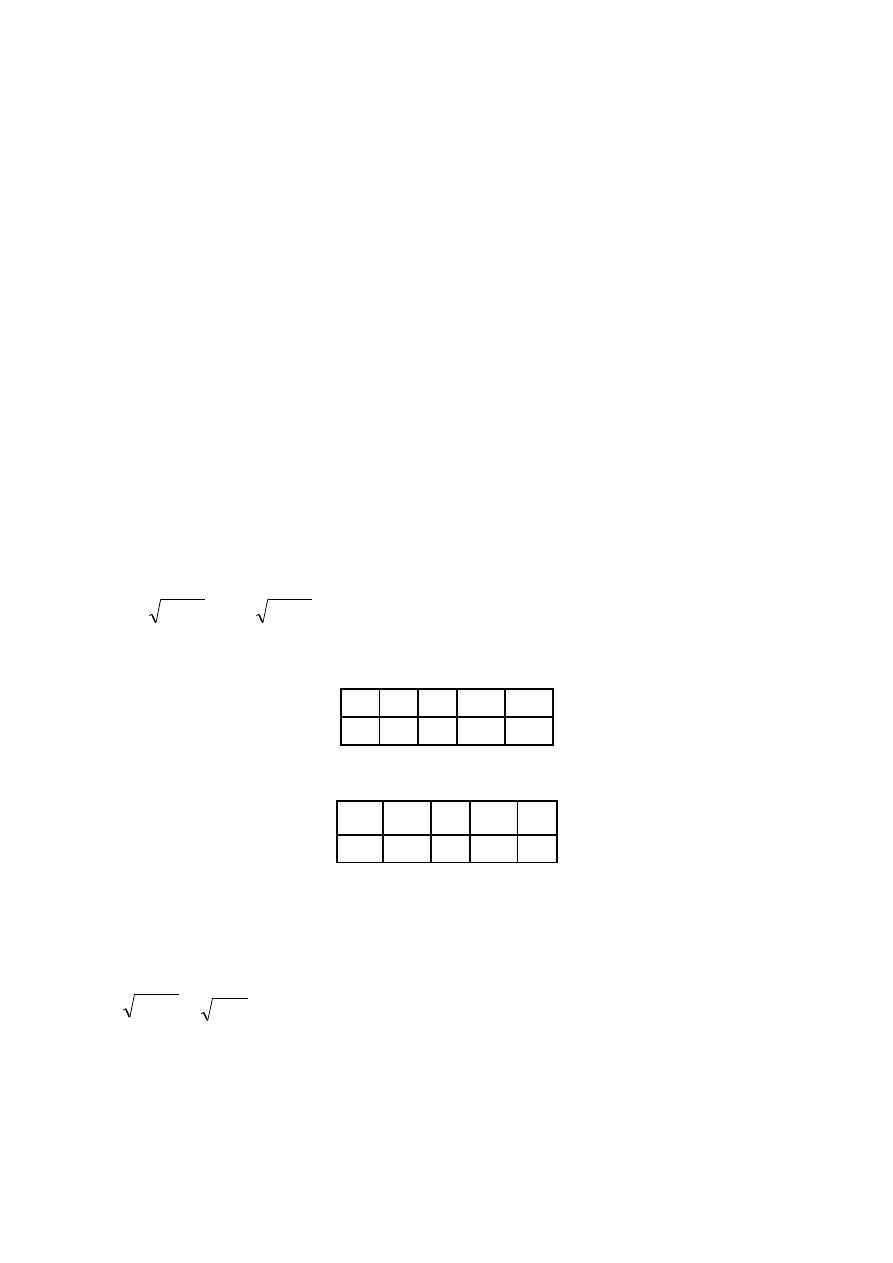
Czasem dwie różne zmienne losowe mogą mieć takie same wartości oczekiwane, np. dla zmiennych
losowych X i Y o rozkładach prawdopodobieństwa
i
x
2
6
i
p
2
1
2
1
W obu przypadkach wartości oczekiwane wynoszą 4 (EX=4, EY=4,), jednak zmienna losowa X ma
znacznie mniejszy rozrzut wartości (6-2=4) od zmiennej losowej Y (30-(-21)=51). W celu
i
y
-21
3
30
i
p
3
1
3
1
3
1
3
dokładniejszego opisania zmiennej losowej wprowadza się nowy charakteryzujący ją parametr – jest to
wariancja.
Zmienną losową
d
X
−
nazywamy odchyleniem zmiennej losowej X od jej wartości oczekiwanej
d
EX
=
.
Wariancją zmiennej losowej X nazywamy wartość oczekiwaną kwadratu odchylenia zmiennej losowej
X od jej wartości oczekiwanej -EX, tzn.
D
2
X=E(X-EX)
2
.
Inaczej
(
)
(
)
(
)
n
n
n
i
i
i
p
EX
x
p
EX
x
p
EX
x
X
D
2
1
2
1
1
2
2
−
+
+
−
=
−
=
∑
=
.
Czasem wariancję zmiennej losowej X oznacza się przez
VarX
. Wariancja jest to więc miara rozrzutu
zmiennej losowej X.
Uwaga
Własności wariancji:
1.
( )
0
2
=
c
D
2.
( )
X
D
a
aX
D
2
2
2
=
3.
(
)
X
D
b
X
D
2
2
=
+
4.
(
)
Y
D
X
D
Y
X
D
2
2
2
+
=
+
5.
( )
( )
2
2
2
EX
X
E
X
D
−
=
Odchyleniem standardowym (odchyleniem średnim) zmiennej losowej skokowej X nazywamy liczbę
X
D
DX
2
=
(
X
D
2
=
σ
).
Przykład
(1)
Policzmy wariancję i odchylenie standardowe zmiennej losowej X o rozkładzie prawdopodobieństwa
i
x
-5
-1
0
3
i
p
0,2 0,1 0,45 0,25
W tym celu musimy najpierw obliczyć
( )
2
X
E
. Zapiszmy rozkład prawdopodobieństwa nowej
zmiennej losowej
2
X
2
i
x
0
1
9
25
i
p
0,45 0,1 0,25 0,2
Wówczas
( )
35
,
7
5
25
,
2
1
,
0
2
,
0
25
25
,
0
9
1
,
0
1
45
,
0
0
2
=
+
+
=
⋅
+
⋅
+
⋅
+
⋅
=
X
E
35
,
0
−
=
EX
możemy obliczyć wariancję
( )
( )
(
)
7,23
12
,
0
35
,
7
35
,
0
35
,
7
2
2
2
2
=
−
=
−
−
=
−
=
EX
X
E
X
D
Wariancja zmiennej losowej X jest zatem równa 7,23. Stąd odchylenie standardowe wynosi
68
,
2
23
,
7
2
=
=
=
X
D
DX
.
XIV.
Rozkłady zmiennych losowych skokowych.
Zmienna losowa X typu skokowego przyjmuje wartości ze zbioru {x
1
, x
2
, x
3
,..., x
n
}, zaś jego funkcją rozkładu
prawdopodobieństwa jest p
1.
Rozkład równomierny
Zmienna losowa X ma rozkład skokowy równomierny, jeśli jej funkcja prawdopodobieństwa jest postaci
4
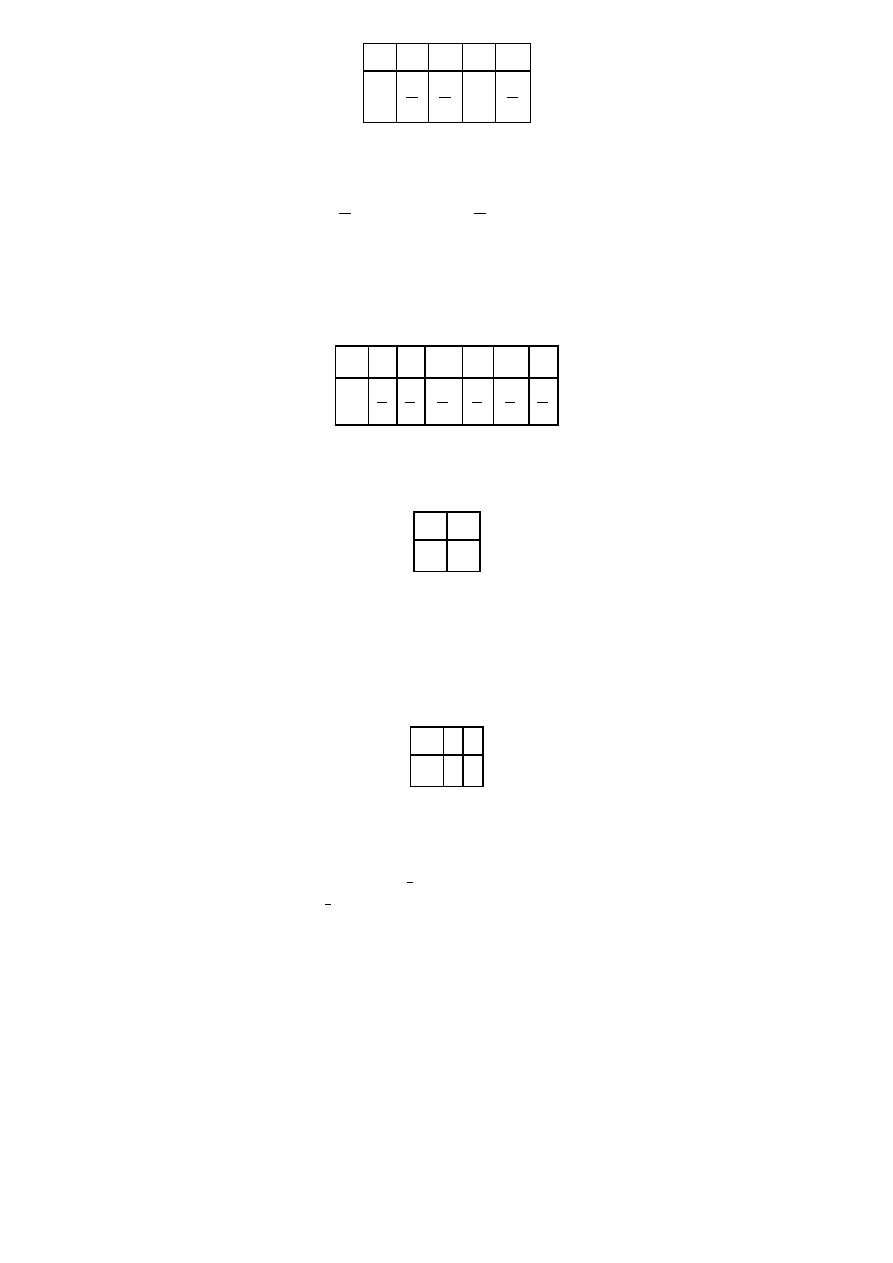
i
x
1
x
2
x
n
x
i
p
n
1
n
1
n
1
tzn. każda wartość zmiennej losowej jest przyjmowana z jednakowym prawdopodobieństwem.
Wówczas wartość oczekiwana i wariancja wyrażają się wzorami
∑
=
=
n
i
i
x
n
EX
1
1
,
(
)
∑
=
−
=
n
i
i
EX
x
n
X
D
1
2
2
1
,
zatem wartość oczekiwana zmiennej losowej skokowej o rozkładzie równomiernym jest średnią arytmetyczną
wartości tej zmiennej losowej.
Przykład.
Rzucamy raz sześcienną kostką .Niech zmienna losowa X oznacza ilość wyrzuconych oczek. Wówczas X jest
zmienna losową skokową ponieważ zbiór wartości jest skończony oraz jest to rozkład równomierny postaci
i
x
1 2
3
4
5
6
i
p
6
1
6
1
6
1
6
1
6
1
6
1
EX=11/6
D
2
X=91/6-11/6=40/3
2
. Rozkład jednopunktowy
Zmienna losowa X ma rozkład skokowy jednopunktowy, jeśli jej funkcja prawdopodobieństwa jest postaci
i
x
1
x
i
p
1
Jest to szczególny przypadek zmiennej losowej o rozkładzie równomiernym
Wówczas wartość oczekiwana i wariancja wyrażają się wzorami
1
x
EX
=
,
0
2
=
X
D
.
3
. Rozkład zero-jedynkowy
Zmienna losowa X ma rozkład skokowy zero-jedynkowy, jeśli jej funkcja prawdopodobieństwa jest postaci
i
x
0 1
i
p
q p
gdzie
p
q
−
=
1
.
Wówczas wartość oczekiwana i wariancja wyrażają się wzorami
p
EX
=
,
pq
X
D
=
2
.
4.
Rozkład Bernoulliego (rozkład dwumianowy)
Schemat Bernoulliego (dwumianowy)
Schematem n prób Bernoulliego nazywamy n niezależnych doświadczeń losowych, w którym
prawdopodobieństwo sukcesu (zajścia określonego zdarzenia) w każdym doświadczeniu jest stałe, niezależne
od wyników poprzednich i równe p.
Prawdopodobieństwo, że na n przeprowadzonych doświadczeń według schematu Bernoulliego uzyska się k
)
0
(
n
k
≤
≤
sukcesów w dowolnej kolejności, wyraża się wzorem
k
n
k
k
n
q
p
k
n
P
−
⋅
⋅
=
,
, gdzie
p
q
p
−
=
<
<
1
,
1
0
.
Przykład
Mamy trzy pojemniki typu
1
A , dwa pojemniki typu
2
A i pięć pojemników typu
3
A . Pojemniki typu
1
A
zawierają 12 białych kul, 3 zielone, 4 czarne i 1 niebieską. Pojemniki typu
2
A zawierają 3 białe kule, 12
zielonych, 4 czarne i 1 niebieską. Pojemniki typu
3
A zawierają 4 białe kule, 3 zielone, 12 czarnych i 1
5
niebieską. Losujemy ze zwrotem (zwracamy wylosowaną kulę do pojemnika z którego została wyjęta) 5
kul. Obliczyć prawdopodobieństwo wylosowania 2 kul zielonych.
Losowanie odbywa się ze zwrotem, więc mamy do czynienia z doświadczeniami niezależnymi. Łatwo
ustalamy, że
5
=
n
,
2
=
k
i prawdopodobieństwo pojedynczego sukcesu (wylosowania kuli zielonej)
obliczymy stosując wzór na prawdopodobieństwo całkowite
24
,
0
20
3
10
5
20
12
10
2
20
3
10
3
=
⋅
+
⋅
+
⋅
=
p
, więc
76
,
0
1
=
−
=
p
q
. Stosujemy wzór Bernoulliego
253
,
0
439
,
0
0576
,
0
10
)
76
,
0
(
)
24
,
0
(
2
5
3
2
2
,
5
=
⋅
⋅
=
⋅
⋅
=
P
.
Zmienna losowa X ma rozkład skokowy Bernoulliego (rozkład dwumianowy) z parametrami
(
)
p
n,
, gdzie
N
n
∈
,
1
0
<
<
p
, jeśli jej funkcja prawdopodobieństwa jest postaci
(
)
(
)
k
n
k
q
p
k
n
p
n
k
P
k
X
P
−
=
=
=
,
,
gdzie
p
q
−
=
1
,
n
k
≤
≤
0
.
Wówczas wartość oczekiwana i wariancja wyrażają się wzorami
np
EX
=
,
npq
X
D
=
2
.
Przykład (rozkład Bernoulliego).
Koszykarz oddaje 4 rzuty do kosza. Piłka wpada do kosza z prawdopodobieństwem 0,8. Znajdźmy
rozkład zmiennej losowej X przyjmującej wartości celnych rzutów do kosza.
Koszykarz może trafić 4 razy, 3 razy, itd., lub może nie trafić wcale. Wykorzystując schemat
Bernoulliego obliczmy prawdopodobieństwa poszczególnej liczby sukcesów (trafionych rzutów) w
pięciu próbach
(
)
625
256
5
4
5
1
5
4
4
4
4
4
0
4
4
=
=
⋅
⋅
=
=
k
P
,
(
)
625
256
5
1
5
4
4
5
1
5
4
3
4
3
3
1
3
4
=
⋅
⋅
=
⋅
⋅
=
=
k
P
,
(
)
625
96
5
1
5
4
6
5
1
5
4
2
4
2
2
2
2
2
4
=
⋅
⋅
=
⋅
⋅
=
=
k
P
,
(
)
625
16
5
1
5
4
4
5
1
5
4
1
4
1
3
3
1
4
=
⋅
⋅
=
⋅
⋅
=
=
k
P
,
(
)
625
1
5
1
5
1
5
4
0
4
0
4
4
0
4
=
=
⋅
⋅
=
=
k
P
.
Rozkład prawdopodobieństwa szukanej zmiennej losowej wygląda następująco
i
x
0
1
2
3
4
i
p
625
1
625
16
625
96
625
256
625
256
Możemy teraz także obliczyć wartość oczekiwaną
2
,
3
625
2000
625
1024
625
768
625
192
625
16
625
256
4
625
256
3
625
96
2
625
16
1
625
1
0
=
=
+
+
+
=
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
EX
zatem
koszykarz średnio odda 3,2 (3 w zaokrągleniu do liczby całkowitej) rzuty celne do kosza. Obliczenie
wariancji, pozostawiamy czytelnikowi .
4.Rozkład Poissona.
Zmienna losowa X ma rozkład skokowy Poissona z parametrem
0
>
λ
, jeśli jej funkcja prawdopodobieństwa
jest postaci
6

(
)
!
,
k
e
k
P
k
λ
λ
λ
−
=
,
gdzie
{ }
0
∪
∈
N
k
. Parametr
λ
ma interpretację wartości oczekiwanej i jest on równy prawdopodobieństwu p
uzyskania sukcesu w pojedynczej próbie pomnożony przez ilość tych prób n, natomiast k oznacza liczbę
sukcesów w n próbach.
Rozkład Poissona wiąże się z rozkładem Bernoulliego zależnością:
Dla dużych n następuje zbieżność rozkładu Bernoulliego do rozkładu Poissona z parametrem
λ
!
k
e
q
p
k
n
k
k
n
k
λ
λ
−
−
≈
,
gdzie
np
=
λ
. Przybliżenie to jest w miarę dokładne, gdy
50
≥
n
(czasem przyjmuje się, że
100
≥
n
) i
1
,
0
≤
p
,
10
≤
=
np
λ
(czasem przyjmuje się, że
[
]
10
,
1
.
0
∈
λ
, czyli gdy liczba prób jest większa lub równa
50, zaś prawdopodobieństwo sukcesu w jednej próbie nie przekracza
10
1
oraz
10
≤
np
.
Wówczas wartość oczekiwana i wariancja wyrażają się wzorami
λ
=
EX
,
λ
=
X
D
2
.
Przykład
(1)
Mamy trzy pojemniki typu
1
A , dwa pojemniki typu
2
A i pięć pojemników typu
3
A . Pojemniki typu
1
A
zawierają 12 białych kul, 3 zielone, 4 czarne i 1 niebieską. Pojemniki typu
2
A zawierają 3 białe kule, 12
zielonych, 4 czarne i 1 niebieską. Pojemniki typu
3
A zawierają 4 białe kule, 3 zielone, 12 czarnych i 1
niebieską. Losujemy 120 kul ze zwrotem. Obliczyć prawdopodobieństwo wylosowania co najwyżej 1
kuli niebieskiej.
Obliczamy prawdopodobieństwo wylosowania kuli niebieskiej
05
,
0
20
1
10
5
20
1
10
2
20
1
10
3
=
⋅
+
⋅
+
⋅
=
p
.
Zastosujemy wzór Poissona dla
05
,
0
,
1
lub
0
,
120
=
=
=
p
k
n
, więc
6
05
,
0
120
=
⋅
=
λ
. Mamy
0025
,
0
1
!
0
6
)
6
,
0
(
6
0
6
≈
=
=
−
e
e
P
,
015
,
0
6
!
1
6
)
6
,
1
(
6
1
6
≈
=
=
−
e
e
P
. Ostatecznie szukane
prawdopodobieństwo wynosi
0175
,
0
015
,
0
0025
,
0
)
6
,
1
(
)
6
,
0
(
≈
+
=
+
P
P
.
(2)
Obliczyć prawdopodobieństwo wylosowania co najwyżej trzech osób leworęcznych w 200 losowaniach,
jeśli wiadomo, że prawdopodobieństwo spotkania osoby leworęcznej w pewnej populacji ludzi wynosi
0,05.
Ponieważ spełnione są warunki:
1
,
0
05
,
0
≤
=
p
oraz
50
200
≥
=
n
, zatem mamy do czynienia z
rozkładem Poissona. Wówczas
10
200
05
,
0
=
⋅
=
λ
oraz
(
)
(
) (
) (
) (
)
3
2
1
0
3
0
=
+
=
+
=
+
=
=
≤
≤
k
P
k
P
k
P
k
P
k
P
Ale
(
)
!
,
k
e
k
P
k
λ
λ
λ
−
=
, zatem
(
)
!
10
10
,
10
k
e
k
P
k
−
=
, czyli (uwaga:
1
!
0
=
)
(
)
=
+
+
+
=
≤
≤
−
−
−
−
!
3
10
!
2
10
!
1
10
!
0
10
3
0
3
10
2
10
1
10
0
10
e
e
e
e
k
P
=
+
+
+
=
+
+
+
=
−
−
−
−
−
−
−
−
10
10
10
10
10
10
10
10
3
500
50
10
6
1000
2
100
10
e
e
e
e
e
e
e
e
011
,
0
61767
683
20589
3
683
3
683
3
683
10
10
≈
=
⋅
≈
⋅
=
=
−
e
e
Ostatecznie szukane prawdopodobieństwo wylosowania co najwyżej trzech osób leworęcznych wynosi
0,011.
7
Zadania
Zad. 1 Rzucamy raz sześcienną kostką .Niech zmienna losowa X oznacza ilość wyrzuconych oczek. Wyznacz
funkcję rozkładu prawdopodobieństwa zmiennej losowej X.
Zad. 2 W pudełku jest 10 losów ponumerowanych od 1 do 10. Na los z numerem 1 pada główna wygrana 10,
na losy z numerami 2 i 3 wygrana pocieszenia 1, a za wyciągnięcie pozostałych płacimy 2(wygrywamy – 2).
Załóżmy, że wyciągnięcie każdego z losów jest jednakowo prawdopodobne. Niech zmienna losowa X oznacza
wartość wygranej. Wyznacz funkcję rozkładu prawdopodobieństwa.
Zad. 3 Rzucamy dwiema kostkami do gry. Podać rozkład zmiennej losowej, która przyjmuje wartości równe
sumie oczek na dwóch kostkach. Wyznaczyć dystrybuantę tej zmiennej. Obliczyć P(5
≤
X<8), wartość
oczekiwaną, wariancję i odchylenie standardowe tej zmiennej.
Zad. 4 Rzucamy dwiema kostkami do gry. Podać rozkład zmiennej losowej, która przyjmuje wartości równe
bezwzględnej różnicy liczby oczek na dwóch kostkach. Wyznaczyć dystrybuantę tej zmiennej i narysować jej
wykres
Zad. 5 W urnie mamy 6 kul białych i 4 czarne. Ciągniemy z urny kule ze zwrotem aż do otrzymania kuli białej
ale co najwyżej 3 razy. Oblicz w tych warunkach wartość przeciętną, wariancję i odchylenie standardowe.
Zad. 6 Z bieżącej produkcji pobrano losowo 5 sztuk towaru. Niech X oznacza liczbę sztuk wadliwych wśród
pobranych. Znaleźć rozkład zmiennej losowej X, jeśli wiadomo, że prawdopodobieństwo wystąpienia sztuki
wadliwej wynosi 0,1.
Zad. 7. Zmienna losowa X ma rozkład prawdopodobieństwa
x
i
-5
-2
0
1
3 8
pi
0,1 0,2 0,1 0,2 C 0,1
Wyznaczyć stałą C oraz dystrybuantę F zmiennej losowej X. Oblicz P(X=1), P(X=2), P(X<3), P(-2
≤
X<3),
F(1), F(2), EX, D
2
X.Wyznacz funkcję prawdopodobieństwa zmiennej losowej U=2X+3 i W=X
2
-1 .
Zad. 8 Zmienna losowa X ma rozkład prawdopodobieństwa
i
x
-5 -3 -1
4
7
i
p
0,2 c 0,2 0,2 0,2
Wyznaczyć stałą c oraz dystrybuantę zmiennej losowej X.
Obliczyć
(
)
4
4
≤
<
−
X
P
,
EX
i
X
D
2
.
Zad. 9.Zmienna losowa Y ma rozkład prawdopodobieństwa
x
k
0
1
2
3
4
p
k
0,2
0,3 c
0,3
0,1
Wyznacz stała c. Wyznaczyć dystrybuantę zmiennej losowej Y .Oblicz EY, D
2
Y, DY
Zad. 10 Zmienna losowa X ma rozkład podany w tabelce
x
i
-2
-1
0
1
2
p
i
8/20
2/20
6/20
1/20
3/20
Obliczyć wartość oczekiwaną i wariancje zmiennej losowej X oraz Y=X
2
Zad. 11 Niech zmienna losowa X ma rozkład prawdopodobieństwa
i
x
0
1
i
p
1/3 2/3
Wyznacz dystrybuantę F. Oblicz P(X=0), P(X=1), F(0), F(1)b
Zad. 12 Zmienna losowa X przyjmuje wartości x
1
=1, x
2
=3,x
3
=4 z prawdopodobieństwami równymi
odpowiednio 1/3,1/4,5/12. Wyznaczyć wartość dystrybuanty F(1), F(2,5), F(6).
Zad. 13 Dystrybuanta zmiennej losowej X dana jest wzorem
∞
<
<
≤
<
≤
<
≤
<
≤
=
x
dla
x
dla
x
dla
x
dla
x
dla
x
F
10
1
10
5
7
6
5
2
7
3
2
1
7
1
1
0
)
(
.
Oblicz P(5
≤
X<8).Wyznacz funkcję prawdopodobieństwa tej zmiennej. Oblicz EX, DX.
8

Zad. 14. Zmienna losowa Z przyjmuje wartości 0,1,2. Wiemy, że EX=1 oraz E
2
X=1,5. Wyznacz rozkład
zmiennej losowej X
Zad. 15 Siła kiełkowania na partii pewnych ziaren została oceniona na 80%. Jakie jest prawdopodobieństwo ,
że spośród 5 ziaren wykiełkuje:
(a)
dokładnie 4 ziarna
(b)
mniej niż 4 ziarna
Zad. 16 Oblicz prawdopodobieństwo, że na 7 rzutów kostką do gry co najwyżej 2 razy wypadnie liczba oczek
mniejsza niż 3.
Zad. 17 Podać rozkład Bernoulliego zmiennej losowej X dla n=5 i p=0,1.
Zad. 18 Rzucamy 10 razy symetryczną monetą. Jakie jest prawdopodobieństwo zdarzenia, że wyrzucimy co
najmniej raz reszkę. Oblicz wartość oczekiwaną i wariancję wyrzuconych reszek.
Zad. 19 Koszykarz oddaje 4 rzuty do kosza. Piłka wpada do kosza z prawdopodobieństwem 0,8. Znajdźmy
rozkład zmiennej losowej X przyjmującej wartości celnych rzutów do kosza. Oblicz przeciętną liczbę celnych
rzutów
Zad. 20. Mamy trzy pojemniki typu
1
A , dwa pojemniki typu
2
A i pięć pojemników typu
3
A . Pojemniki typu
1
A zawierają 12 białych kul, 3 zielone, 4 czarne i 1 niebieską. Pojemniki typu
2
A zawierają 3 białe kule, 12
zielonych, 4 czarne i 1 niebieską. Pojemniki typu
3
A zawierają 4 białe kule, 3 zielone, 12 czarnych i 1
niebieską. Losujemy 120 kul ze zwrotem. Obliczyć prawdopodobieństwo wylosowania co najwyżej 1 kuli
niebieskiej.
Zad. 21 Obliczyć prawdopodobieństwo wylosowania co najwyżej trzech osób leworęcznych w 200
losowaniach, jeśli wiadomo, że prawdopodobieństwo spotkania osoby leworęcznej w pewnej populacji ludzi
wynosi 0,05.
Zad. 22 Prawdopodobieństwo wyprodukowaniu sztuki wadliwej wynosi 2%. Oblicz prawdopodobieństwo, że
w partii towaru liczącej 100 sztuk znajduje się:
(a) zero sztuk wadliwych
(b) jedna sztuka wadliwa
(c) dwie sztuka wadliwa
(d) co najmniej trzy sztuki wadliwe
Zad. 23 Prawdopodobieństwo zdania egzaminu z rachunku prawdopodobieństwa na ocenę bardzo dobrą
wynosi 0,1. Jakie jest prawdopodobieństwo, że spośród 50 studentów informatyki zdających egzamin co
najmniej jeden uzyska ocenę bardzo dobrą. Oblicz wartość oczekiwaną studentów z oceną bardzo dobrą.
9
Document Outline
Wyszukiwarka
Podobne podstrony:
(3924) 5zmienna losowa typu skokowego, Matematyka ▬▬▬▬▬▬▬▬▬▬
6 3 Zmienna losowa typu skokowego
Zmienna losowa typu ciaglego, ZUT, III Semestr, Metody probabilistyczne i statystyka
jurlewicz,probabilistyka, rozkład typu skokowego
6 4 Zmienna losowa typu ciągłego
DOBÓR NASTAW REGULATORÓW TYPU PID METODĄ CHARAKTERYSTYK SKOKOWYCH
Statystyka zmienna losowa skokowa
rozw zmienna losowa skokowa
Cukrzyca typu 1
3 Cukrzyca typu LADA i MODY
Urazy kolana i stawu skokowego
Charakterystyka odpowiedzi immunologicznej typu GALT faza indukcji
AKCJA Z UŻYCIEM PASA RATOWNICZEGO TYPU WĘGORZ
więcej podobnych podstron