
6.4. Zmienna losowa typu ciągłego
Definicja
Funkcją gęstości prawdopodobieństwa zmiennej losowej ciągłej X nazywamy funkcję
f określoną na zbiorze liczb rzeczywistych i spełniającą warunki:
a) f(x)
≥
0 dla każdej liczby rzeczywistej x,
b)
∫
b
a
dx
x
f
)
(
= P(a < X
≤
b), dla dowolnych a < b, czyli prawdopodobieństwo, że
zmienna losowa X przyjmuje wartości między a i b jest
∫
b
a
dx
x
f
)
(
.
Z tej definicji wynika, że
∫
∞
∞
−
dx
x
f
)
(
= 1.
Definicja
Rozkładem zmiennej losowej X:
Ω
Ω
Ω
Ω
→
R typu ciągłego o funkcji gęstości f nazywamy
funkcję przyporządkowującą każdemu przedziałowi (x
1
, x
2
) prawdopodobieństwo, że
wartości zmiennej losowej z przedziału [x
1
, x
2
] spełniają warunek:
[x
1
, x
2
]
→
P( {
ω
ω
ω
ω
: x
1
≤
X(
ω
ω
ω
ω
)
≤
x
2
} ) =
∫
2
1
)
(
x
x
dx
x
f
.
Przykład 1.
Czujnik sterujący oświetleniem jest nastawiony na godzinę h. Stosownie do wielkości
zachmurzenia może włączyć się nie wcześniej niż godzinę przed ale nie później niż pół
godziny po czasie h. Przyjmujemy, że zdarzeniem elementarnym jest moment włączenia
oświetlenia. Niech zmienną losową X będzie czas włączenia oświetlenia.
Zmienna X może przyjąć każdą wartość z przedziału [ h – 1 , h + ½ ] ; jest to zatem
zmienna losowa ciągła.
Załóżmy, że każdy moment włączenia oświetlenia jest tak samo prawdopodobny oraz
h = 18. Zatem wartości X należą do przedziału [17 ; 18,5].
Założenie jednakowego prawdopodobieństwa implikuje, że funkcja f gęstości
prawdopodobieństwa w przedziale [17 ; 18,5] jest stała (przyjmijmy, że np. f(x) = k), zaś poza

tym przedziałem f(x) = 0.
Obliczymy wartość k wykorzystując warunek
∫
∞
∞
−
dx
x
f
)
(
= 1.
Mamy 1 =
∫
∞
∞
−
dx
x
f
)
(
=
∫
∞
−
17
)
(
dx
x
f
+
∫
5
,
18
17
)
( dx
x
f
+
∫
∞
5
,
18
)
( dx
x
f
=
=
∫
∞
−
17
0dx +
∫
5
,
18
17
kdx
+
∫
∞
5
,
18
0dx = 0 +
5
,
18
17
|
kx
+ 0 = 1,5k.
Zatem k =
15
10
=
3
2
.
Funkcja gęstości ma postać:
f(x) =
>
≤
≤
<
5
,
18
0
5
,
18
17
3
2
17
0
x
dla
x
dla
x
dla
.
Definicja
Dystrybuantą zmiennej losowej X o funkcji gęstości f nazywamy funkcję F określoną
dla wszystkich liczb rzeczywistych w następujący sposób:
x
→
F(x) = P(X
≤
x) dla każdego x
∈
R.
Czyli dystrybuanta zmiennej losowej X każdej liczbie rzeczywistej x przyporządkowuje
prawdopodobieństwo tego, że zmienna losowa przyjmuje wartości nie większe od x.
Twierdzenie
•
Dystrybuanta F zmiennej losowej spełnia warunek 0
≤
F(x)
≤
1 dla każdego x.
•
−∞
→
x
lim
F(x) = 0,
∞
→
x
lim
F(x) = 1.
•
Dystrybuanta F zmiennej losowej jest funkcją niemalejącą
Przykład 2.
Czujnik sterujący oświetleniem jest nastawiony na godzinę 0. Stosownie do wielkości
zachmurzenia może włączyć się nie wcześniej niż godzinę przed a nie później niż pół
godziny po godzinie 0. Przyjmujemy, że zdarzeniem elementarnym jest moment
włączenia oświetlenia. Niech zmienną losową X będzie czas włączenia oświetlenia.

Zmienna X może przyjąć każdą wartość z przedziału [ – 1 , ½ ] ; jest to zmienna losowa
ciągła.
Załóżmy, że prawdopodobieństwo włączenia oświetlenia w chwili x opisuje funkcja
f(x) =
9
8
(1 - x
2
) dla x z przedziału [-1, ½ ] oraz f(x) = 0 dla pozostałych x.
Zatem wartości X należą do przedziału [-1; ½ ].
Mamy P(X = x) =
9
8
(1 - x
2
) .
Sprawdzamy, czy f jest funkcją gęstości zmiennej X; w tym celu wystarczy zbadać, czy
f(x)
≥
0 dla x z przedziału [-1; ½ ] oraz
∫
∞
∞
−
dx
x
f
)
(
= 1.
•
Z własności funkcji kwadratowej wynika, że 1- x
2
≥
0 dla x
∈
[-1, 1]. Tym samym
9
8
(1 - x
2
)
≥
0. Czyli f(x)
≥
0 dla x
∈
[-1; ½ ].
•
Mamy
∫
∞
∞
−
dx
x
f
)
(
=
∫
−
∞
−
1
)
(
dx
x
f
+
∫
−
5
,
0
1
)
( dx
x
f
+
∫
∞
5
,
0
)
( dx
x
f
=
=
∫
−
∞
−
1
0dx
+
∫
−
−
5
,
0
1
2
)
1
(
9
8
dx
x
+
∫
∞
5
,
0
0dx
= 0 +
9
8
[x -
3
3
1
x
5
,
0
1
|
]
−
+ 0 =
=
9
8
⋅
24
27
= 1.
•
Zatem funkcja gęstości ma postać:
f(x) =
>
≤
≤
−
−
−
<
5
,
0
0
5
,
0
1
)
1
(
9
8
1
0
2
x
dla
x
dla
x
x
dla
.
•
Dystrybuanta tej zmiennej losowej ma postać:
F(x) = P(X
≤
x) =
∫
∞
−
x
dt
t
f
)
(
dla każdego x
∈
R.
Zgodnie z określeniem funkcji f mamy
F(x) =
∫
∞
−
x
dt
t
f
)
(
=
>
+
−
+
−
∈
−
+
−
<
∫
∫
∫
∫
∫
∫
−
∞
−
−
−
∞
−
−
∞
−
1
5
,
0
1
5
,
0
2
1
1
2
5
,
0
0
)
1
(
9
8
0
]
5
,
0
;
1
[
)
1
(
9
8
0
1
0
x
x
x
x
dla
dt
dt
t
dt
x
dla
dt
t
dt
x
dla
dt
Stąd
F(x) =
∫
∞
−
x
dt
t
f
)
(
=
>
−
∈
+
−
−
<
5
,
0
0
]
5
,
0
;
1
[
)
3
2
3
1
(
9
8
1
0
3
x
dla
x
dla
x
x
x
dla
.
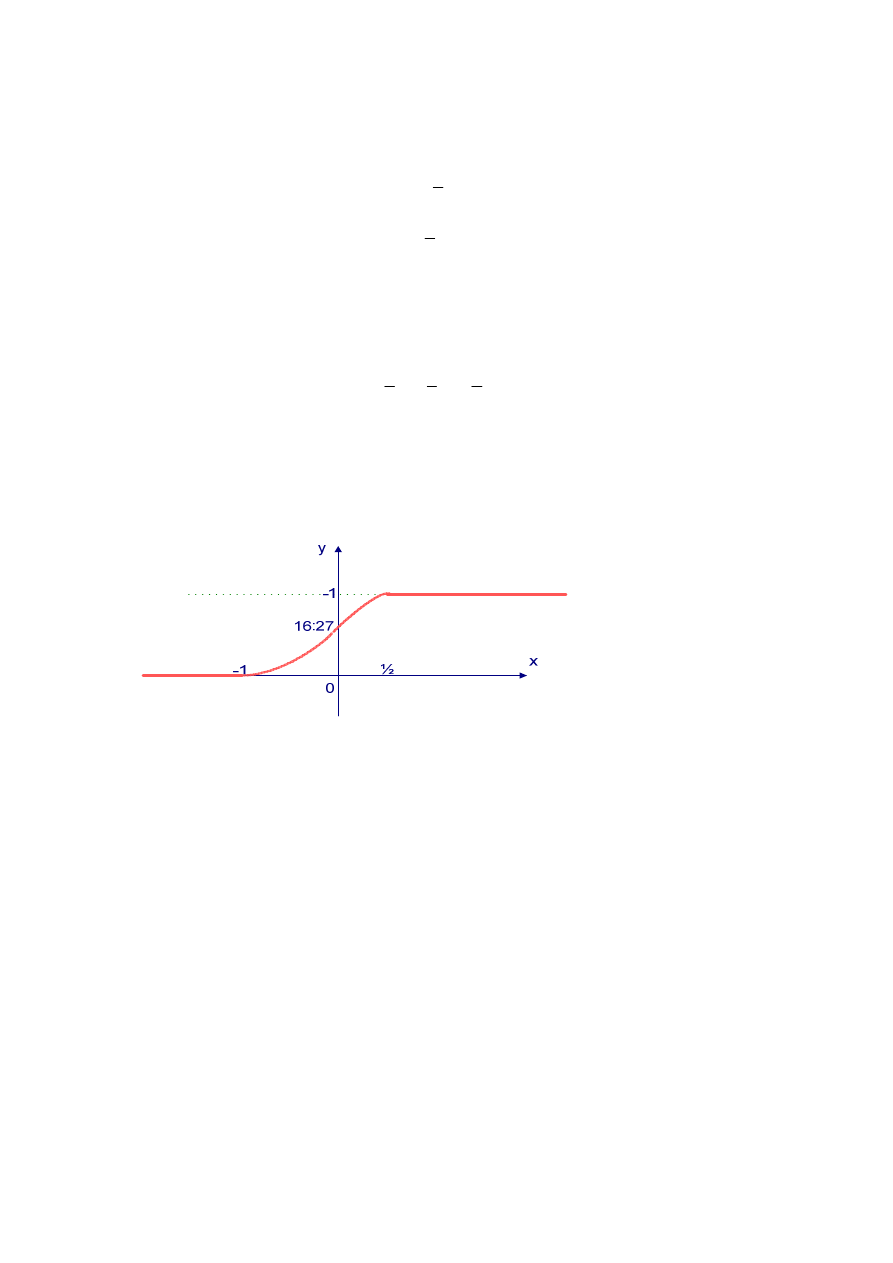
Wykres dystrybuanty przedstawia poniższy rysunek.
Wyszukiwarka
Podobne podstrony:
Zmienna losowa typu ciaglego, ZUT, III Semestr, Metody probabilistyczne i statystyka
6 3 Zmienna losowa typu skokowego
02 Statystyka Matematyczna Zmienna Losowa Ciągłaid 3789
6 czerwca Zmienna losowa
zmienna losowa ciągła, statystyka matematyczna(1)
3 zmienna losowa odp
36 ?finicja zmiennej losowej Zmienna losowa i jej rozkład
5. Zmienna losowa, licencjat(1)
zmienna losowa przykład
29 30 Zmienna losowa jednowymiarowa
2 zmienna losowa zadania
zmienna losowa i jej rozklad
Zmienna losowa ciągła wykresy
zmienna losowa, przykład
Zmienna losowa i rozklad prawdopodobienstwa - zadania, Pliki, Studia PK (Mechaniczny & WIL)
więcej podobnych podstron