6.3. Zmienna losowa typu skokowego

Rozkład

zmiennej losowej typu skokowego

Definicja

Zmienną losową X nazywamy skokową (typu skokowego, dyskretną), jeżeli zbiór war-

tości X jest zbiorem skończonym lub przeliczalnym (tzn. wartości zmiennej można przed-

stawić jako ciąg liczbowy).

Każda wartość zmiennej losowej jest związana z pewnym prawdopodobieństwem jej

wystąpienia. Często osiągnięcie przez zmienną niektórych wartości jest znacznie bardziej

prawdopodobne niż osiągnięcie innych i znajomość tych prawdopodobieństw ma spore zna-

czenie praktyczne. Dlatego dla zmiennych losowych określa się rozkład prawdopodobień-

stwa. W przypadku zmiennych losowych skokowych definiuje się funkcję prawdopodobień-

stwa, przypisując wartości prawdopodobieństwa konkretnym - wszystkim - wartościom

zmiennej losowej.

Definicja

Jeżeli zmienna losowa X typu skokowego przyjmuje wartości x

1

, x

2

... odpowiednio z

prawdopodobieństwami p

1,

p

2

, ..., to rozkładem

zmiennej losowej (funkcją prawdo-

podobieństwa zmiennej losowej) X typu skokowego nazywamy funkcję przypisującą

każdej przyjmowanej przez X wartości x, prawdopodobieństwo osiągnięcia tej wartości.

Inaczej x

i

→

P(x

i

) = p

i

, dla i = 1, 2, …, gdzie P(x

i

) = p

i

jest prawdopodobień-

stwem wystąpienia wartości x

i

.

Uwaga

Fakt, że zmienna losowa X przyjmuje wartość x

i

z prawdopodobieństwem p

i

piszemy krótko:

P(X = x

i

) = p

i

.

Twierdzenie

Gdy zmienna losowa ma n wartości, to zachodzi związek

∑

=

n

i

i

p

1

= 1.

Gdy zmienna przyjmuje przeliczalną liczbę wartości, to zachodzi związek

∑

∞

=

1

i

i

p

= 1.

Przykład 1.

Rozważamy doświadczenie losowe polegające na jednokrotnym rzucie trzema monetami i

obserwowania górnej strony monet. Przyjmijmy oznaczenia: o – wypadł orzeł, r – wypa-

dła reszka. Rozpatrujemy dwie sytuacje:

R) monety są rozróżnialne i można jednoznacznie ustalić, co wypadło na danej monecie,

N) monety są nierozróżnialne.

Szczegółowo opiszemy sytuację R.

Sytuacja R

Zbiór zdarzeń elementarnych

Ω

Ω

Ω

Ω

R

jest zbiorem trójek postaci (x, y, z), gdzie x strona górna

pierwszej monety, y – strona górna drugiej monety, z - strona górna trzeciej monety; x, y,

z jest o lub r.

Zatem

Ω

Ω

Ω

Ω

R

= {(x, y, z) : x = o lub x = r , y = o lub y = r, z = o lub z = r }.

Mamy osiem zdarzeń

ω

ω

ω

ω

1

= (o, o, o),

ω

ω

ω

ω

2

= (r, o, o),

ω

ω

ω

ω

3

= (o, r, o),

ω

ω

ω

ω

4

= (o, o, r),

ω

ω

ω

ω

5

= (r, r, o),

ω

ω

ω

ω

6

= (o, r, r),

ω

ω

ω

ω

7

= (r, o, r),

ω

ω

ω

ω

8

= (r, r, r).

Przykładowo definiujemy dwie zmienne losowe.

Zmienna losowa X

1

: przyporządkowujemy zdarzeniu elementarnemu liczbę wylosowa-

nych reszek. Zmienna ta przyjmuje cztery wartości 0, 1, 2, 3.

W tym przypadku mamy:

P(X

1

= 0) =

8

1

= 0,125 czyli prawdopodobieństwo tego, że zmienna X

1

przyjmuje

wartość 0 wynosi

8

1

; P(X

1

= 1) =

8

3

; P(X

1

= 2) =

8

3

; P(X

1

= 3) =

8

1

.

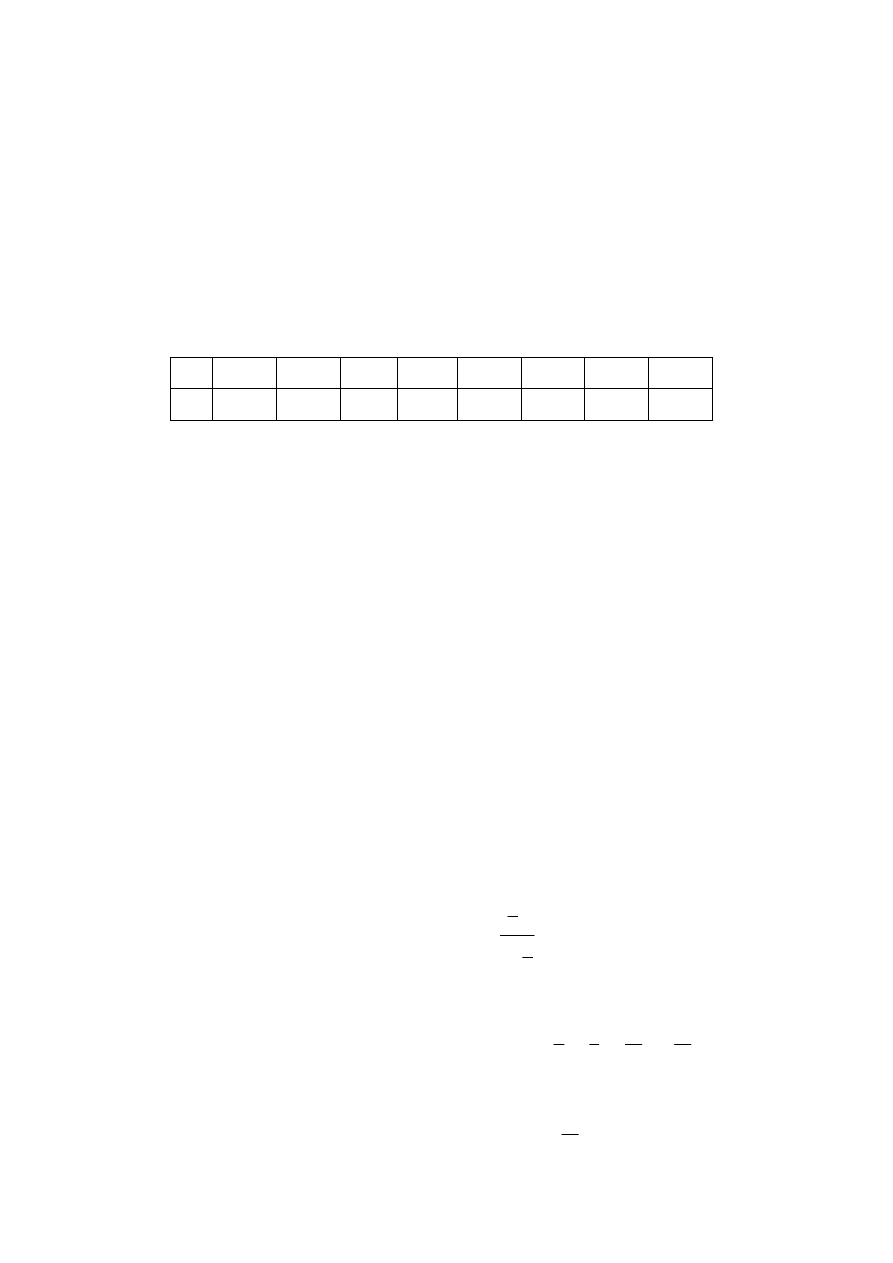
Rozkład zmiennej X

1

(funkcje prawdopodobieństwa) można zapisać w tabelce:

x

i

0

1

2

3

p

i

0,125

0,375

0,375

0,125

Jej wykres przedstawia rysunek.

X-Axis

Y

-A

x

is

0,125

0,375

Zmienna losowa X

2

: przyporządkowujemy zdarzeniom elementarnym kolejno liczby

będące wskaźnikami w określeniu zdarzenia:

ω

ω

ω

ω

1

= (o, o, o) liczbę 1,

ω

ω

ω

ω

2

= (r, o, o)

liczbę 2 itd . Zmienna ta przyjmuje osiem wartości 1, 2, 3, 4, 5, 6, 7, 8.

W tym przypadku mamy:

P(X

2

= 1) = P(X

2

= 2) = P(X

2

= 3) = P(X

2

= 4) = P(X

2

= 5) = P(X

2

= 6) =

= P(X

2

= 7) = P(X

2

= 8) = 0,125.

Rozkład zmiennej X

2

:

x

i

1

2

3

4

5

6

7

8

p

i

0,125

0,125

0,125 0,125 0,125

0,125

0,125

0,125

Przykład 2.

Zmienna losowa przyjmuje wartości będące liczbami naturalnymi.

Wiadomo, że P(X = k) = c

⋅

2

-k

, gdzie c jest dana konkretnie liczbą rzeczywistą.

Wyznacz c oraz oblicz P(X

≥

5).

Rozwiązanie

Warunek P(X = k) = c

⋅

2

-k

( słownie: prawdopodobieństwo, że zmienna X przyjmuje

wartość k jest równe c

⋅

2

-k

) określa rozkład zmiennej losowej skokowej wtedy, gdy

∑

∞

=

−

⋅

1

2

k

k

c

= 1.

Suma szeregu

∑

∞

=

−

⋅

1

2

k

k

c

jest sumą ciągu geometrycznego o wyrazie pierwszym równym

½ c oraz ilorazie q = ½ . Jest ona równa

∑

∞

=

−

⋅

1

2

k

k

c

=

2

1

1

2

1

−

c

= c.

Zatem c = 1. Szukanym rozkładem zmiennej jest P(X = k) = 2

-k

.

Obliczamy P(X

≥

5) = 1 - P(X

≤

4) = 1 -

∑

=

−

4

1

2

k

k

= 1 – ( ½ +

4

1

+

8

1

+

16

1

) =

16

1

.

Odpowiedź:

Warunek P(X = k) = 2

-k

określa rozkład zmiennej. P(X

≥

5) =

16

1

.

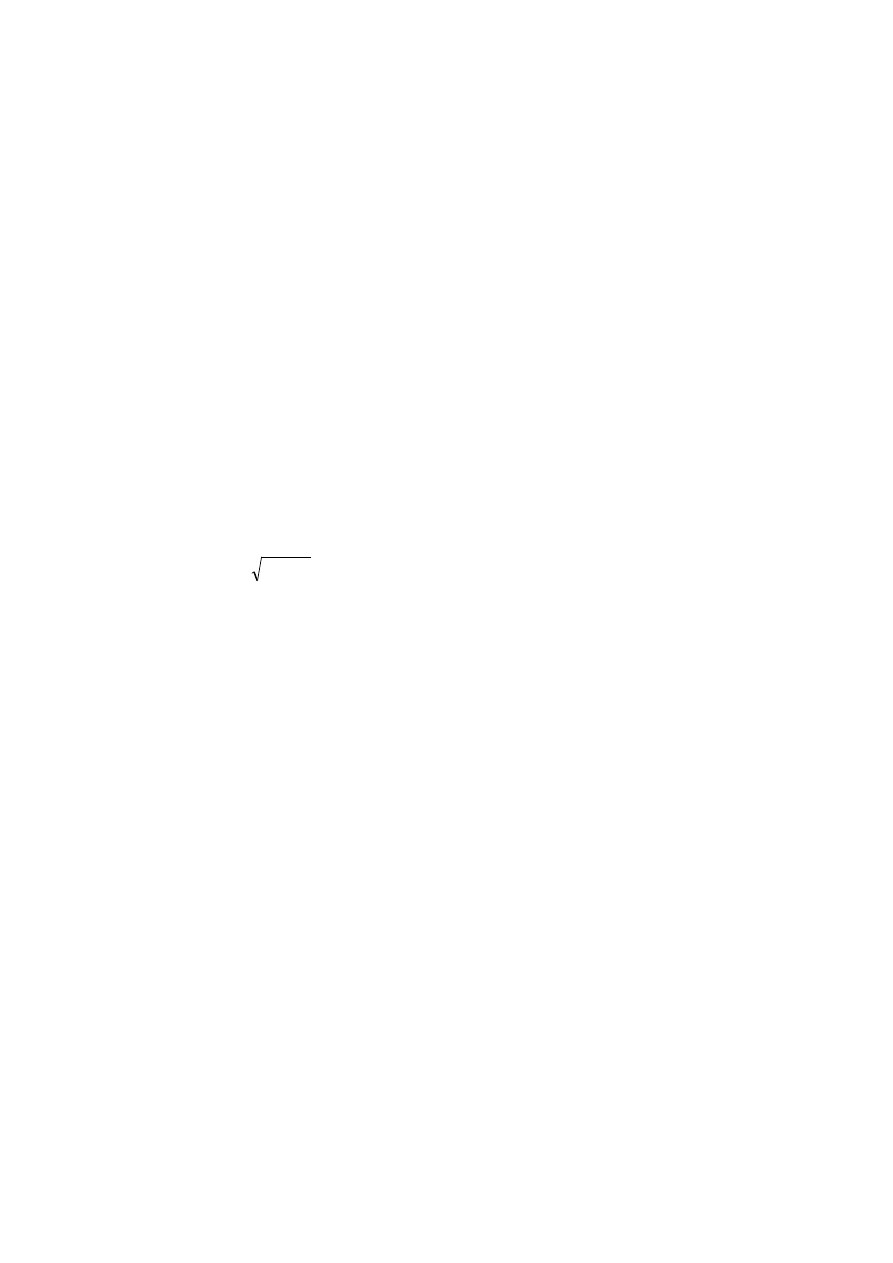
Wartość oczekiwana, wariancja, odchylenie standardowe

zmiennej losowej typu skokowego.

Definicja

Niech (

Ω

Ω

Ω

Ω

, p ) będzie przestrzenią probabilistyczną która ma przeliczalną liczbę zdarzeń

elementarnych; czyli

Ω

Ω

Ω

Ω

= {

ω

ω

ω

ω

1

,

ω

ω

ω

ω

2

, … ,

ω

ω

ω

ω

n

, …}.

Niech X będzie zmienną losową typu skokowego (dyskretną), przy czym X = {x

1

, x

2

…)

oraz P(x

i

) = p

i

.

a) Wartością oczekiwaną zmiennej losowej typu skokowego (dyskretnej) nazywamy

liczbę E(X) =

∑

i

i

i

p

x

dla i = 1, 2, …

b) Wariancją zmiennej losowej typu skokowego nazywamy liczbę

D

2

(X) = E(X – E(X) )

2

=

∑

−

i

i

i

p

X

E

x

2

))

(

(

dla i = 1, 2, …

c) Odchyleniem standardowym zmiennej losowej typu skokowego nazywamy liczbę

D(X) =

)

(

2

X

D

.

Przykład 3.

Breloczki z aplikacją złotą lub srebrną są pakowane tak, że nie da się bezpośrednio usta-

lić rodzaju aplikacji. Wiadomo, że breloczków z aplikacją złotą jest trzy razy więcej niż

z aplikacją srebrną. Sprzedawca wyjął 4 breloczki z szuflady, w której ich było 16.

a) Określ prawdopodobieństwo, że wyjęte breloczki mają złotą aplikację.

b). Oblicz wartość oczekiwaną, wariancję i odchylenie standardowe zmiennej losowej

określającej liczbę breloczków z aplikacją złotą.

Rozwiązanie

Rozważamy, jako model teoretyczny tej sytuacji, doświadczenie losowe polegające na

losowaniu czterech breloczków spośród szesnastu. Zdarzenie elementarne, to czwórka

wylosowanych breloczków. Zakładamy, że każde z nich jest tak samo prawdopodobne.

a) Z treści zadania wiadomo, że mamy 4 breloczki z aplikacją srebrną, a 12 z apli-

kacją złotą. Mamy zatem













4

16

= 1820 zdarzeń elementarnych.

Interesuje nas zdarzenie A polegające na tym, że wszystkie 4 breloczki mają złotą

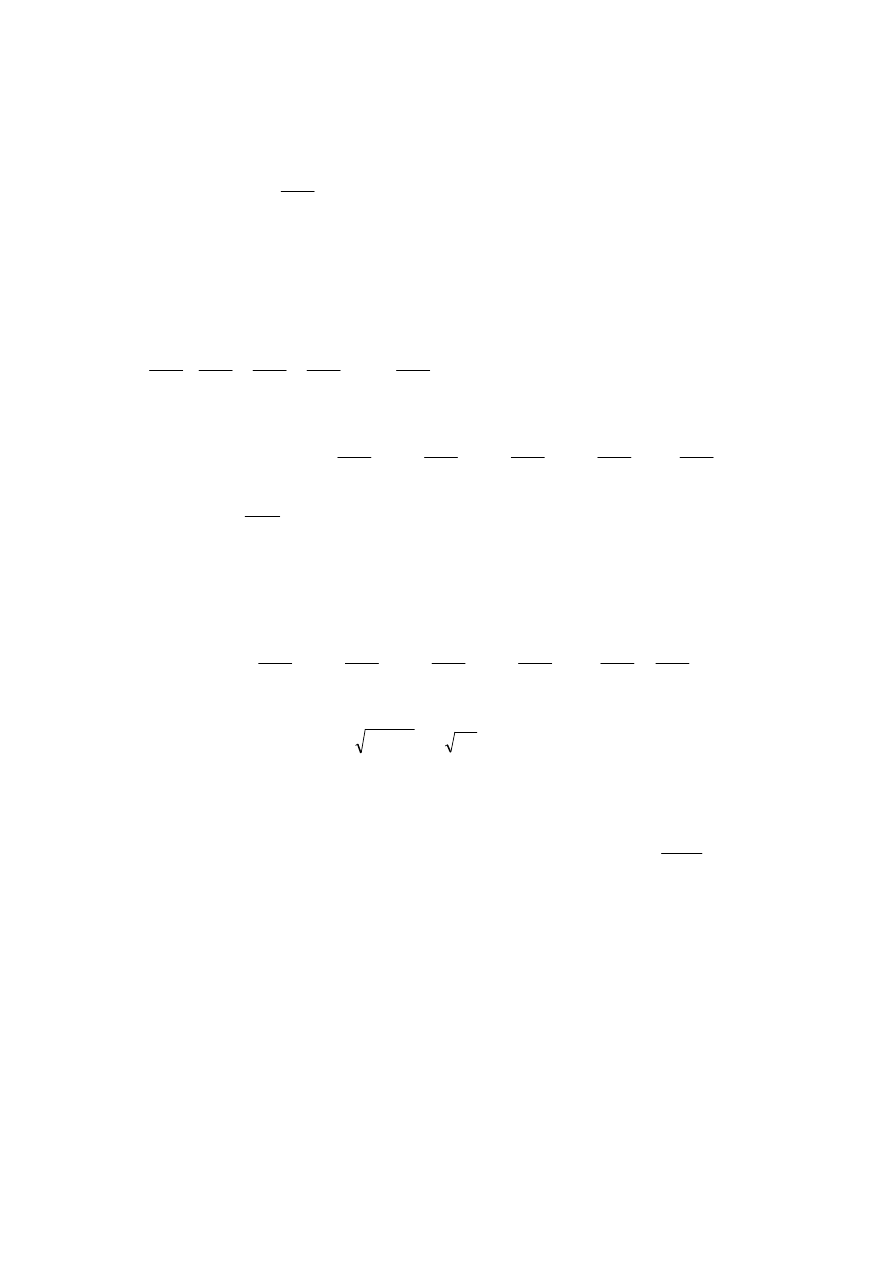
aplikację. Zdarzeń sprzyjających temu zdarzeniu jest













4

12

⋅













4

4

= 495.

Zatem P(A) =

1820

495

≈

0,27.

b) Definiujemy zmienną losową tego doświadczenia; niech X będzie funkcją przy-

porządkowującą czwórce wybranych losowo breloczków liczbę breloczków z aplikacją

złotą.

Zmienna X przyjmuje wartość 0, 1, 2, 3, 4 odpowiednio z prawdopodobieństwami

1820

1

,

1820

48

,

1820

396

,

1820

880

oraz

1820

495

.

Wartość oczekiwana liczby breloczków z aplikacją złotą wynosi więc:

E(X) =

∑

=

5

1

i

i

i

p

x

= 0

⋅

1820

1

+ 1

⋅

1820

48

+ 2

⋅

1820

396

+ 3

⋅

1820

880

+ 4

⋅

1820

495

=

=

1820

5460

= 3.

Wariancja liczby breloczków z aplikacją złotą wynosi:

D

2

(X) = E( X – E(X) )

2

=

∑

=

−

5

1

2

))

(

(

i

i

i

p

X

E

x

=

∑

=

−

5

1

2

)

3

(

i

i

i

p

x

=

= 9

⋅

1820

1

+ 4

⋅

1820

48

+ 1

⋅

1820

396

+ 0

⋅

1820

880

+ 1

⋅

1820

495

=

1820

1092

= 0,6.

Odchylenie standardowe jest równe:

D(X) =

)

(

2

X

D

=

6

,

0

≈

0,7746.

Można powiedzieć, że liczba wyłożonych breloczków z aplikacją złotą różni się od 3

przeciętnie o około 1 breloczek.

Odchylenie standardowe w stosunku do wartości oczekiwanej stanowi

)

(

)

(

X

E

X

D

≈

26%.

Odpowiedź

a)

Prawdopodobieństwo, że wyjęte breloczki mają złotą aplikację jest równe około

0,27; jest zatem niewielkie.

b)

Wartość oczekiwana liczby breloczków z aplikacją złotą wynosi 3; interpretując tę

liczbę można powiedzieć, że gdyby powtarzać to doświadczenie wielokrotnie, to

wśród czterech breloczków byłyby średnio 3 ze aplikacją złotą.

c)

Wariancja liczby breloczków z aplikacją złotą wynosi 0,6. Można powiedzieć, że

liczba wyłożonych breloczków z aplikacją złotą różni się od 3 przeciętnie o około 1

breloczek.

d)

Odchylenie standardowe liczby breloczków z aplikacją złotą jest równe około

0,7746.

e)

Odchylenie standardowe w stosunku do wartości oczekiwanej stanowi

)

(

)

(

X

E

X

D

≈

26%.

To znaczy, że wartości odległe od 3 są stosunkowo mało prawdopodobne.

Rozkład dwumianowy (rozkład Bernoulliego)

Rozważmy doświadczenie losowe, które kończy się jednym z dwóch wyników: „sukce-

sem" z prawdopodobieństwem p lub „porażką" z prawdopodobieństwem 1- p. Powtarzamy to

doświadczenie n razy – otrzymujemy eksperyment losowy o wielkości serii n; zakładamy, że

wyniki kolejnych doświadczeń nie zależą od wyników poprzednich.

Definicja

Zmienną losową Bernoulliego dla danego p oraz wielkości serii n nazywamy zmienną X

o wartościach określających liczbę sukcesów w tej serii w opisanym eksperymencie losowym.

Ta zmienna przyjmuje wartości ze zbioru {0, 1, ..., n}.

Funkcja prawdopodobieństwa w rozkładzie Bernoulliego jest określona wzorem:

P(X = k) =

k

n

k

p

p

k

n

k

n

−

−

−

)

1

(

)!

(

!

!

dla k = 0, 1, 2, …

Rozkład Bernoulliego jest symetryczny dla p = ½ . Im p jest bliższe 0 lub 1 tym większa

jest asymetria rozkładu.

Poniższy rysunek przedstawia wykres funkcji prawdopodobieństwa zmiennej o roz-

kładzie Bernoulliego dla n = 10 i p = 0,2.

Przykład 4.

Oświetlenie sali wykładowej zapewnia 5 niezależnych punktów oświetleniowych. Ich

awarie występują niezależnie od siebie, przy czym prawdopodobieństwo awarii każdego

z nich wynosi 0,1.

Oblicz prawdopodobieństwo awarii: a) jednego z nich, b) co najwyżej czterech z nich.

Rozwiązanie

Liczbę awarii można opisać rozkładem Bernoulliego dla n = 5, p = 0,1.

Mamy P(X = 1) =

4

1

)

9

,

0

(

1

,

0

)!

4

(

!

1

!

5

= 5

⋅

0,1

⋅

0,9

4

= 0,5

⋅

0,6561 = 0,32805

≈

0,33.

P(X

≤

4) = 1 – P(5) = 1 -

0

5

)

9

,

0

(

1

,

0

)!

0

(

!

5

!

5

= 1 – 0,00001= 0,99999.

Odpowiedź: Prawdopodobieństwo awarii jednego z nich wynosi ok. 33% ;

prawdopodobieństwo awarii co najwyżej czterech z nich wynosi ok. 0,999999.

Twierdzenie

Wartość oczekiwana i wariancja w rozkładzie dwumianowanym - w rozkładzie Bernoullie-

go danego p oraz wielkości serii n - są równe:

a) E(X) = n

⋅

p,

b) D

2

(X) = n

⋅

p

⋅

(1 – p).

Zadania do samodzielnego rozwiązywania

Zadanie 1.

Rozważamy doświadczenie losowe polegające na jednokrotnym rzucie trzema monetami i

obserwowania górnej strony monet. Przyjmijmy oznaczenia: o – wypadł orzeł, r – wypadła

reszka. Przyjmujemy, że monety są nierozróżnialne.

a) Zdefiniuj zmienną losową.

b)

Wyznacz rozkład tej zmiennej losowej, podaj jego wykres.

c)

Oblicz wartość oczekiwaną, wariancję i odchylenie standardowe tej zmiennej.

Zadanie 2.

Obliczono – na postawie statystyki z wielu zawodów sportowych – że pewien biatlonista w

postawie stojącej średnio trafia do tarczy 9 razy na 10 strzałów. Jakie jest prawdopodobień-

stwo, że w pewnych zawodach spudłuje on raz, dwa razy, trzy lub cztery razy?

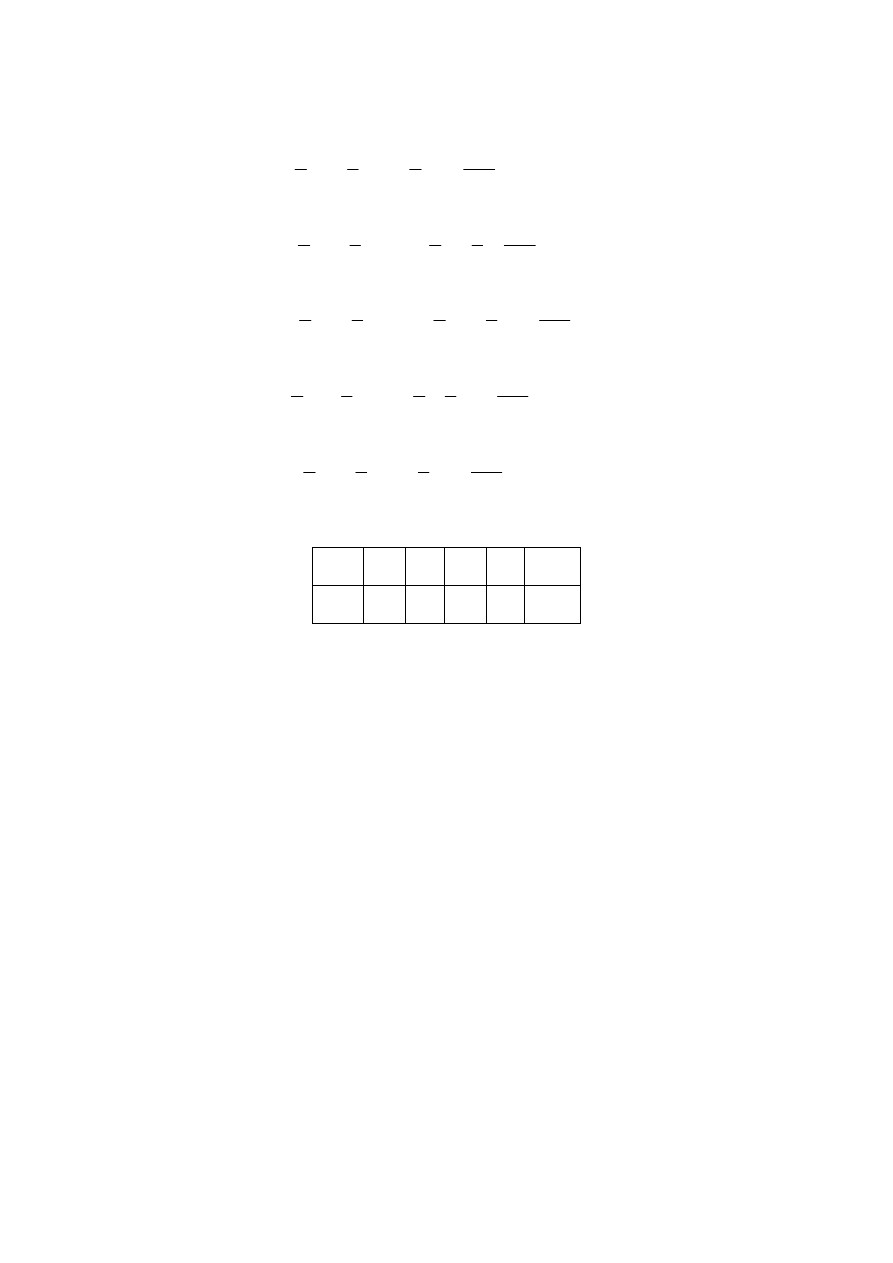
Wykorzystując schemat Bernoulliego obliczmy:

(

)

625

256

5

4

5

1

5

4

4

4

4

4

0

4

4

=













=













⋅













⋅













=

=

k

P

,

(

)

625

256

5

1

5

4

4

5

1

5

4

3

4

3

3

1

3

4

=

⋅













⋅

=













⋅













⋅













=

=

k

P

,

(

)

625

96

5

1

5

4

6

5

1

5

4

2

4

2

2

2

2

2

4

=













⋅













⋅

=













⋅













⋅













=

=

k

P

,

(

)

625

16

5

1

5

4

4

5

1

5

4

1

4

1

3

3

1

4

=













⋅

⋅

=













⋅













⋅













=

=

k

P

,

(

)

625

1

5

1

5

1

5

4

0

4

0

4

4

0

4

=













=













⋅













⋅













=

=

k

P

.

Rozkład prawdopodobieństwa szukanej zmiennej losowej:

i

x

0

1

2

3

4

i

p

Możemy teraz także obliczyć wartość oczekiwaną;

E(X) = …………………………….. = 3,2.

D

2

(X) = ……………. D(X) = …………………..

Zadanie 3.

Futerały do okularów sprzedaje się w kolorach zielonym i brązowym, przy czym tych w kolo-

rze zielonym jest trzy razy więcej niż w kolorze brązowym.. Są one pakowane w folię tak, że

nie da się bezpośrednio ustalić koloru futerału. Sprzedawca wyłożył na ladę 4 opakowania,

które wyjął z szuflady zawierającej 16 futerałów.

a) Określ rozkład prawdopodobieństwa zmiennej losowej, której wartościami to liczby opa-

kowań futerałów w kolorze zielonym.

b) Oblicz wartość oczekiwaną, wariancję i odchylenie standardowe tej zmiennej losowej.

Zadanie 4.

Doświadczenie losowe polega na rzucie dwiema rozróżnialnymi kostkami do gry. Definiuje-

my zmienną losową X przyjmującą wartości równe sumie oczek na tych kostkach.

a)

Podaj rozkład prawdopodobieństwa tej zmiennej.

b)

Oblicz wartość oczekiwaną, wariancję i odchylenie standardowe tej zmiennej losowej.

Zadanie 5.

W loterii finansowej obowiązują następujące reguły:

•

rzucamy dwiema kostkami do gry,

•

wygrywamy 12 złotych, jeżeli wylosujemy sumę oczek równą 12,

•

wygrywamy 6 złotych, jeżeli wylosujemy sumę oczek równą 3,

•

we wszystkich pozostałych przypadkach przegrywamy 1 zł.

a)

Zdefiniuj zmienną losową związaną z tą loterią. Podaj rozkład tej zmiennej losowej.

b)

Oblicz wartość oczekiwaną, wariancję i odchylenie standardowe tej zmiennej losowej.