P O D S T A W Y O C E A N O L O G I I
ĆWICZENIE LABORATORYJNE
OBLICZANIE
PRĘDKOŚCI DŹWIĘKU W WODZIE
Grupa
Imię i nazwisko uczestników ćwiczenia
1.
Data
ćwiczenia
Ocena
wykonania
ćwiczenia
Podpis
prowadzącego
ćwiczenia
Data złożenia
sprawozdania
Ocena
opracowania
Podpis
oceniającego
opracowanie
ćwiczenia
2.
3.
4.
5.
6.

1. C
EL ĆWICZENIA
Celem ćwiczenia jest zapoznanie studentów z problematyką teoretycznego wyznaczania
prędkości dźwięku w wodzie, co wiąże się bezpośrednio z podstawowymi zagadnieniami
propagacji fali sprężystej w wodzie. Ponadto studenci wykonując ćwiczenia będą doskonalić
umiejętność posługiwania się środowiskami programistycznymi, przeznaczonymi do
prowadzenia obliczeń inżynierskich.
2. W
STĘP TEORETYCZNY
Prędkość rozchodzenia się dźwięku w wodzie morskiej uzależniona jest głównie od trzech
czynników: temperatury wody, zasolenia i ciśnienia hydrostatycznego lub głębokości morza,
co można wyrazić następującym równaniem:
)
,
,
(
p
S
T
f
c
(1)
Zmiana temperatury o 1
C wywołuje zmianę prędkości dźwięku od 4.7[m/s] przy
temperaturze początkowej 0°C, do 2.2 [m/s] przy temperaturze początkowej około 30
C.
Zmiana zasolenia wody o 1‰ wywołuje zmianę prędkości dźwięku o 1.4[m/s] przy zasoleniu
początkowym 0‰, natomiast przy zasoleniu początkowym 40‰ tylko o 1.0[m/s].
Zwiększenia głębokości morza o 10[m] lub ciśnienia o 1[atm] (atmosfera) wywołuje zmianę
prędkości dźwięku o 0,175 [m/s].
W związku z tym, że temperatura, zasolenie i ciśnienie hydrostatyczne zmieniają się w
czasie i przestrzeni, to również i prędkość dźwięku ulega takim zmianom. Prędkość dźwięku
we „wszechoceanie” zmienia się w granicach od 1440 [m/s] do 1550 [m/s]. Do obliczeń
przybliżonych przyjmuje się prędkość średnią 1500 [m/s].
Opracowany jest szereg wzorów do obliczania prędkości, jak np. wzór Wilsona, wzór
Wooda czy wzór Del-Grosso. Jednakże najnowszy i najdokładniejszy jest wzór opracowany
przez Chen-Tung Chen i Franka J. Millero.
Znajomość prędkości rozchodzenia się dźwięku w środowisku wodnym jest niezwykle
istotna z punktu widzenia hydroakustyki. Po pierwsze, prędkość dźwięku określa czas
niezbędny dla pokonania przez sygnał odległości między dwoma obiektami. W zależności od
prędkości dźwięku czas służy do wyznaczenia odległości do celu. Zmiany prędkości dźwięku
w warunkach rzeczywistych wykazują znaczący wpływ na dokładność określenia
współrzędnych celu, szczególnie na określenie głębokości jego zanurzenia.
Refrakcja dźwięku powodowana przez zmianę prędkości dźwięku jest przyczyną
odchylania promienia dźwiękowego (droga promienia przestaje być linią prostą) i w efekcie
zwiększenia błędów określenia współrzędnych celu. Determinuje to konieczność
precyzyjnego określania wielkości prędkości dźwięku i jej zależności od charakterystyk wody
morskiej.
Charakter zależności wielkości
K
(współczynnik odbicia) i
(gęstość) od temperatury
T
, zasolenia
S
i ciśnienia hydrostatycznego
p
jest bardzo skomplikowany i
niewystarczająco zbadany. Określenie wielkości i zależności
)
,
,
(
p
S
T
c
odbywa się, więc
drogą doświadczalną. Wyniki doświadczeń przedstawia się w postaci wzorów empirycznych
lub tablic.

Do najbardziej popularnych należy wzór Wilsona, który w postaci ogólnej można zapisać
następująco:
TSp
p
S
T
c
c
c
c
c
14
.
1449
(2)
gdzie:
T
c
- poprawka na temperaturę wody,
S
c
- poprawka na zasolenie,
p
c
-
poprawka na ciśnienie statyczne,
TSp
c
- poprawka na współzależność ciśnienia, zasolenia i
temperatury.
Powyższe poprawki są wyrażone następującymi wzorami:
4
6
3
4
2
2
10
9851
.
7
10
604
.
2
10
4532
.
4
5721
.
4
T
T
T
T
c
T
(3)
2
3
)
35
(
10
69202
.
1
)
35
(
39799
.
1
S
S
c
S
(4)
4
12
3
9
2
5
1
10
3603
.
3
10
5216
.
3
10
0268
.
1
10
60272
.
1
p
p
p
p
c
p
(5)
)
10
9646
.
1
(
)
10
8563
.
1
10
5294
.
2
(
)
10
5283
.
4
10
4812
.
7
10
8607
.
1
(
)
10
5790
.
1
10
1580
.
3
10
2943
.
1
10
7016
.
7
10
7711
.
7
10
1244
.
1
)(
35
(
10
3
2
9
7
2
3
8
2
6
4
2
9
8
2
7
5
2
7
2
T
p
T
T
p
T
T
T
p
pT
pT
p
p
T
T
S
c
TSp
(6)
W 1969 roku Leroy zaproponował inny dokładny i prosty wzór:
h
S
T
S
T
T
T
c
0164
.
0
)
35
)(
18
(
01
.
0
)
35
(
2
.
1
)
18
(
04
.
0
)
10
(
006
.
0
)
10
(
3
9
.
1492
2
2
(7)
We wzorze
T
wyrażono w [°C],
S
- w [‰],
h
- głębokość w [m],
c - prędkość w [m/s].
Znajduje on zastosowanie przy głębokościach do 1000 [m], zasoleniu od 30‰ do 42‰ i
temperaturze od -2
C do 24.5°C. Zakres zastosowania tego wzoru jednoznacznie wskazuje na
to, że nie może on być wykorzystywany do obliczania prędkości dla warunków panujących w
Południowym Bałtyku.
Wartości prędkości dźwięku obliczone wg wzoru Leroy'a różnią się od wartości
otrzymanych przez Wilsona (przy spełnionych wymaganiach dla obydwu wzorów) zaledwie o
0.2 [m/s].
Wzór Wilsona uważany jest za jeden z najbardziej dokładnych, bowiem pozwala obliczyć
prędkość dźwięku z dokładnością do 0.39 [m/s] w porównaniu z rzeczywistą prędkością
dźwięku, pod warunkiem, że: – 2°C < T < 32°C, 0‰ < S < 40‰, 1 < p < 100000 [kPa].

Kolejnym popularnym wzorem na wyznaczanie prędkości dźwięku jest wzór Wooda:
h
S
T
T
c
0175
.
0
)
35
(
137
.
1
036
.
0
206
.
4
1450
2
(8)
gdzie:
c
- prędkość dźwięku [m/s],
T
- temperatura wody [°C],
S
- zasolenie [‰],
h
-
głębokość [m]
Błąd wyniku uzyskany przy pomocy tego wzoru jest najmniejszy przy temperaturach
około 10°C, dla różnych wartości zasolenia. Dla tych warunków różnica pomiędzy prędkością
dźwięku otrzymaną z pomiarów a prędkością wyznaczoną z obliczeń nie przekracza 1.5
[m/s]. Największy błąd (6 [m/s]) powstaje przy obliczeniach dla wody słodkiej o temperaturze
30°C.
W 1981 Coppens zaproponował również dość prosty wzór do obliczenia prędkości
dźwięku w wodzie, który miał następującą postać:
tD
S -
S-
.
+
.
+
D
t
.
-
.
D +
t
.
+
.
t
S
c
c
)
35
)](
35
(
0002
0
016
0
[
)
1
0
213
0
(
)
253
0
23
16
(
)
,
,
0
(
2
(9)
)
35
)(
009
0
126
0
333
1
(
23
0
21
5
7
45
05
449
1
2
3
2
S -
t
.
t +
.
-
.
+
t
.
+
t
.
t -
.
+
.
c
(10)
gdzie:
c
- prędkość dźwięku [m/s],
T
T
t
,
10
/
- temperatura wody [°C],
S
- zasolenie
[‰],
D
- głębokość [km]
Zakres stosowalności tego wzoru to: temperatura od 0 do 35 °C, zasolenie od 0 do 45‰,
głębokość 0 do 4000 m.
Innym najczęściej stosowanym wzorem jest wzór Del-Grosso który można przedstawić w
postaci:
h
T
T
S
T
S
T
S
S
T
T
T
c
0175
.
0
)
0072
.
0
577
.
0
1
(
)
35
(
10
2
)
35
(
10
0027
.
0
)
35
(
011
.
0
)
35
(
25
.
1
00023
.
0
0523
.
0
618
.
4
6
.
1448
2
4
7
4
5
3
2
(11)
Wzór ten zapewnia jedną z większych dokładności. Przy odpowiedniej temperaturze i
zasoleniu ponad 15‰ błąd wyniku nie przekracza 0,5 [m/s]. Przy zasoleniu poniżej 15‰ i
temperaturze ponad 10°C błąd jest zawsze mniejszy od 0,8 [m/s].
Z powyższych wzorów jednoznacznie wynika, że wraz ze wzrostem temperatury,
zasolenia oraz ciśnienia statycznego prędkość dźwięku wzrasta, przy czym ze wzrostem
zasolenia i ciśnienia statycznego - w sposób liniowy.
W zasadzie do wyznaczenia prędkości dźwięku w zadanym akwenie (Bałtyk Południowy)
wykorzystywać można wszystkie powyższe wzory za wyjątkiem wzoru Leroy
a. Praktycznie
największą dokładność dla tego akwenu zapewniają wzory Wilsona i Del-Grosso, wzór
Wooda jakkolwiek możliwy do wykorzystania zapewnia jednak w warunkach małego
zasolenia, z jakim mamy do czynienia na Bałtyku zdecydowanie mniejszą dokładność
obliczeń.

W 1977 roku Chen i Millero podali następujący wzór na obliczenie prędkości dźwięku w
wodzie:
2
2
3
)
,
(
)
,
(
)
,
(
)
,
(
S
P
T
D
S
P
T
B
S
P
T
A
P
T
C
c
w
(12)
Gdzie:
3
2
12
10
9
2
4
12
3
10
2
8
6
5
4
10
3
7
2
6
4
5
9
4
6
3
4
2
2
)
10
3643
.
2
10
8504
.
3
10
7729
.
9
(
)
10
0405
.
1
10
5335
.
2
10
5974
.
2
10
7107
.
1
10
1260
.
3
(
)
10
1185
.
6
10
3621
.
1
10
1788
.
8
10
8982
.
6
153563
.
0
(
10
1464
.
3
10
478
.
1
10
3420
.
3
10
80852
.
5
03711
.
5
388
.
1402
)
,
(
p
T
T
p
T
T
T
T
p
T
T
T
T
T
T
T
T
T
P
T
C
w
3
2
13
12
10
2
3
12
2
10
9
7
4
10
3
8
2
8
5
5
4
8
3
6
2
5
2
)
10
389
.
3
10
649
.
6
10
1
.
1
(
)
10
988
.
7
10
6002
.
1
10
1041
.
9
10
9064
.
3
(
)
10
0122
.
2
10
0507
.
1
10
4885
.
6
10
2580
.
1
10
4742
.
9
(
10
21
.
3
10
006
.
2
10
164
.
7
10
262
.
1
389
.
1
)
,
(
p
T
T
p
T
T
T
p
T
T
T
T
T
T
T
T
P
T
A
p
T
T
P
T
B
)
10
7945
.
1
10
3637
.
7
(
10
42
.
4
10
922
.
1
)
,
(
7
5
5
2
p
P
T
D
6
3
10
9836
.
7
10
727
.
1
)
,
(
We wzorze tym temperaturę
T
wyrażono w [°C], zasolenie
S
- w [‰], ciśnienie
p
- w
[dbar],
c
- prędkość w [m/s]. Znajduje on zastosowanie przy zasoleniu od 0‰ do 40‰,
temperaturze od 0
C do 40°C oraz ciśnieniu od 0 [dbar] do 10000 [dbar]. Błąd obliczeniowy
jest mniejszy od 0.19 [m/s] co powoduje że wzór ten jest bardzo dokładny.
Chcąc ocenić wartość zmian prędkości dźwięku najczęściej posługujemy się pojęciem
gradientu. Przy czy największe znaczenie ma pionowy gradient prędkości dźwięku
p
c
G
,
;
horyzontalny gradient prędkości dźwięku
h
c
G
,
przeciętnie osiąga wartości rzędu dwu,
trzykrotnie (100 – 1000 - krotnie) mniejszego niż pionowy. W związku z tym, na
interesujących nas odległościach poziomych (zasięgi stacji hydrolokacyjnych) możemy
przyjąć, że gradient poziomy
0
,
h
c
G
jest równy zeru i pomijać go w dalszych rozważaniach.
Oznaczając pionowy gradient prędkości dźwięku jako
c
G otrzymamy:
dh
h
S
t
dc
G
c
)
,
,
(
(13)
gdzie:
)
,
,
(
h
S
t
c
- funkcja zależności prędkości dźwięku od temperatury, zasolenia i
głębokości.
Posługując się wzorem Wooda otrzymamy wzór na wartość gradientu prędkości w danym
punkcie:

0175
.
0
14
.
1
)
073
.
0
21
.
4
(
dh
dS
dh
dT
T
dh
dc
G
c
(14)
Oznaczając:
S
T
G
dh
dS
G
dh
dT
;
, gdzie:
T
G i
S
G - gradienty temperatury i zasolenia.
Z powyższego otrzymamy:
0175
.
0
14
.
1
)
073
.
0
21
.
4
(
S
T
c
G
G
t
G
(15)
gdzie:
c
G - wyrażona w [Hz],
T
G
- wyrażona w [
C/m],
S
G - wyrażona w [‰/m]
Ostatnia składowa we wzorze wyraża wpływ ciśnienia statycznego. Wartość zmiany
prędkości dźwięku dla każdej składowej wynosi:
p
c
S
c
T
c
G
p
G
G
S
G
G
T
T
G
175
.
0
)
(
14
.
1
)
(
)
073
.
0
21
.
4
(
)
(
(16)
gdzie:
p
G
- gradient ciśnienia statycznego,
p
G
= 100 [hPa/m].
W przytoczonych wzorach na prędkość dźwięku jednym z parametrów jest głębokość
akwenu, jednakże część wzorów wymaga podania głębokości w metrach zaś część w
jednostkach ciśnienia. Aby móc dokonać konwersji jednych jednostek na drugie należy
posłużyć się odpowiednimi wzorami które zostały zdefiniowane przez Leroya i Parthiota w
1998 roku. Podane zależności zostały wyznaczone dla wody o temperaturze 0°C i zasoleniu
35‰.
Aby przeliczyć głębokość wyrażoną w jednostkach ciśnienia na jednostki długości
(metry) należy zastosować następujący wzór:
P
.
+
g
P
.
-
P
.
+
P
.
P -
.
=
P,
Z
-
-
-
-
S
4
4
7
3
4
2
1
2
10
092
1
)
(
10
82
1
10
279
2
10
2512
2
10
72659
9
)
(
(17)
gdzie:
Z
– głębokość w metrach,
P
- ciśnienie w MPa (relatywnie do ciśnienia
atmosferycznego),
- szerokość geograficzna, zaś
)
(
g
to grawitacja określona
następującym wzorem:
)
sin
10
2.36
+
sin
10
5.2788
+
(1
9.780318
=
)
(
4
-5
2
-3
g
(18)
Przy przeliczaniu głębokości wyrażonej w metrach na jednostki ciśnienia należy posłużyć
się następującym wzorem:

Z
.
+
Z+
Z/
=
Z
h
.
+
.
=
g
Z
-
.
Z
-
g
=
Z,
k
Z
.
+
Z
.
-
Z
.
Z +
.
=
Z,
h
Z
h
Z,
k
Z,
=h
Z,
P
-
-
-
-
-
-
-
-
-
6
2
0
2
3
5
5
4
19
3
13
2
8
2
0
10
2
6
)
100
(
10
)
(
)
sin
10
3
5
1
(
7803
9
)
(
)
10
2
80612
9
/(
)
10
2
)
(
(
)
(
10
8
2
10
25
1
10
465
2
10
00818
1
)
45
(
)
(
)
(
)
45
(
)
(
(19)
gdzie:
Z
– głębokość w metrach,
P
- ciśnienie w MPa (relatywnie do ciśnienia
atmosferycznego),
- szerokość geograficzna.
Leroy i Parthiot podali także tabele poprawek których zastosowanie pozwala uzyskać
bardzo dużą dokładność przeliczania głębokości wyrażonej w metrach na jednostki ciśnienia i
odwrotnie.
3. P
RZEPROWADZENIE ĆWICZENIA
Należy zdefiniować:
– dane z pomiarów dla wskazanych przez prowadzącego 3 miesięcy, korzystając z
poniższych tabel przedstawiających wyniki pomiaru prędkości dźwięku dla Głębi
Gdańskiej;
– dla wskazanych przez prowadzącego trzech wzorów na prędkość dźwięku w
wodzie zdefiniować ich parametry;
– zapisać wskazane przez prowadzącego wzory pozwalające na obliczenie prędkości
dźwięku w wodzie.
Następnie należy przeprowadzić badania pozwalające porównać dokładność
wyznaczonych empirycznie prędkości dźwięku z uzyskanymi w trakcie pomiarów. W tym
celu należy dla parametrów: temperatura, głębokość, zasolenie uzyskanych z pomiarów,
wyznaczyć prędkość dźwięku. Wyniki uzyskanych obliczeń należy przedstawić w postaci
wykresów:
wykres prędkości dźwięku w funkcji głębokości dla zadanych miesięcy, zgodnie z
wynikami pomiaru,
trzy wykresy prędkości dźwięku od głębokości wyznaczone na podstawie trzech
różnych wzorów dla wybranego miesiąca;
trzy wykresy różnic pomiędzy prędkością pomierzoną a obliczoną na podstawie
trzech różnych wzorów dla wybranego miesiąca.
Należy pamiętać o właściwym opisie osi wykresów oraz nałożeniu siatki ułatwiającej
analizę uzyskanych wyników.
Następnie korzystając z poniższych tabel przedstawiających wyniki pomiaru prędkości
dźwięku dla Głębi Bałtyckiej, dla wskazanych przez prowadzącego miesięcy policzyć
prędkość dźwięku korzystając ze wskazanego przez prowadzącego wzoru. Wykreślić
obliczone teoretycznie prędkości oraz faktycznie pomierzone. Wykreślić różnicę pomiędzy
wartościami teoretycznie obliczonymi oraz uzyskanymi w trakcie pomiaru.
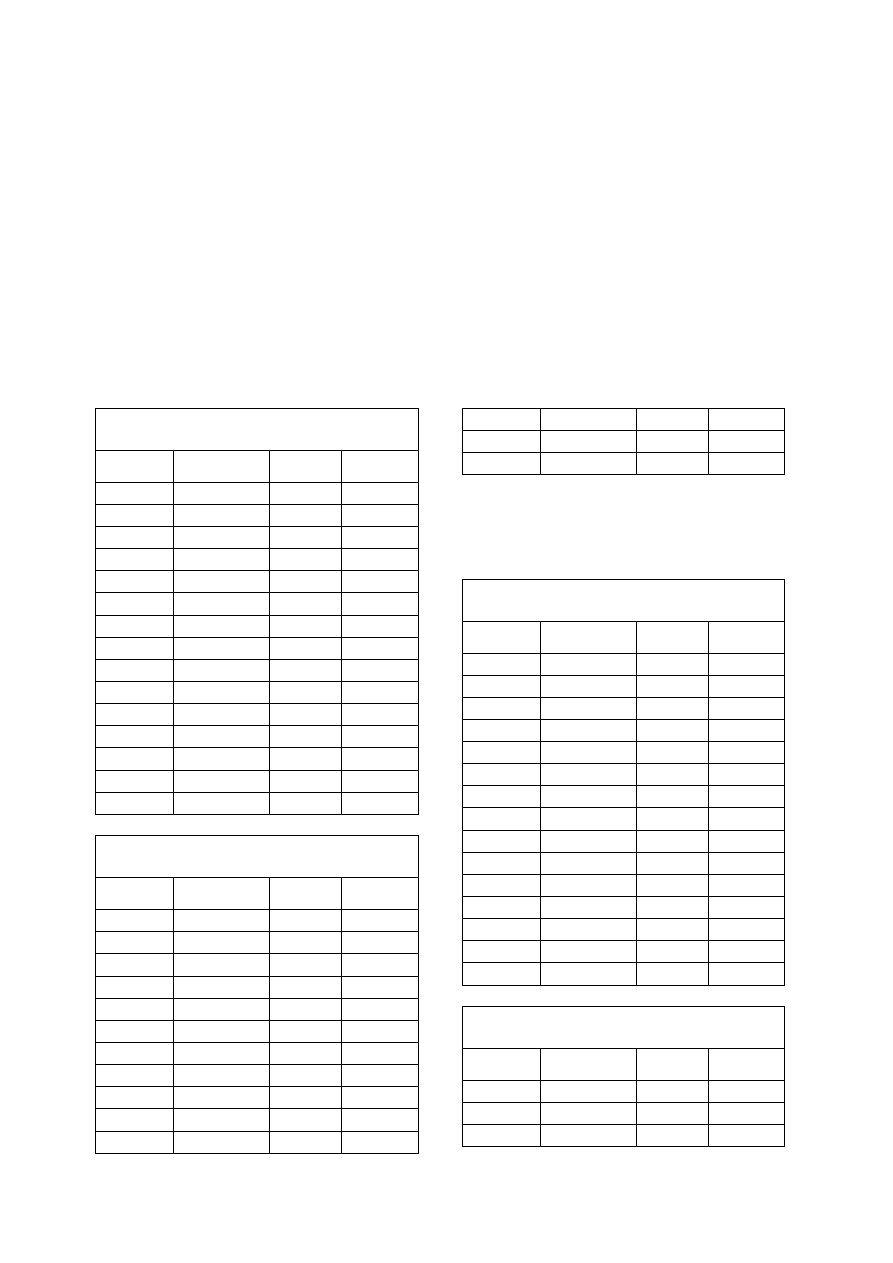
4. O
PRACOWANIE WYNIKÓW ĆWICZENIA
W ramach sprawozdania z przeprowadzonego ćwiczenia laboratoryjnego należy
przedstawić:
– Wykresy prędkości dźwięku w funkcji głębokości wykonanego zgodnie z
wynikami pomiarów oraz obliczonych teoretycznie na podstawie pomiarów
– Wykresy różnicy prędkości dźwięku obliczonego teoretycznie oraz wyznaczonego
w trakcie pomiarów
– Dyskusję na temat istnienia lub braku różnic pomiędzy rozkładami prędkości
obliczonymi teoretycznie a wynikającymi z pomiarów.
– Własne wnioski wynikające z przeprowadzonego ćwiczenia laboratoryjnego.
Tabela. 1. Wyniki pomiaru prędkości dźwięku dla Głębi Gdańskiej.
Kwiecień
Głębokość
(m)
Temperatura
(
o
C)
Zasolenie
(PSU)
Prędkość
(m/s)
0
2.85
7.48
1426.106
3
2.85
7.47
1426.14
5
2.85
7.47
1426.171
10
2.85
7.47
1426.25
15
2.85
7.47
1426.328
20
2.85
7.48
1426.42
30
2.85
7.48
1426.577
40
2.85
7.47
1426.721
50
2.85
7.45
1426.852
60
2.76
7.52
1426.683
70
2.91
7.84
1427.95
80
3.87
9.23
1434.278
90
4.7
10.54
1439.802
100
4.97
10.91
1441.613
105
5.04
11.04
1442.163
Czerwiec
Głębokość
(m)
Temperatura
(
o
C)
Zasolenie
(PSU)
Prędkość
(m/s)
0
12.19
7.27
1464.515
5
12.2
7.27
1464.633
10
12.13
7.28
1464.467
15
7.78
7.39
1447.731
20
4.2
7.46
1432.537
30
3.35
7.51
1428.914
40
3.23
7.52
1428.535
50
3.16
7.54
1428.397
60
3.11
7.54
1428.325
70
3.01
7.86
1428.437
80
3.75
9.48
1434.06
90
4.06
10.27
1436.624
100
4.38
10.69
1438.742
106
4.5
10.74
1439.431
lipiec
Głębokość
(m)
Temperatura
(
o
C)
Zasolenie
(PSU)
Prędkość
(m/s)
0
18.35
7.65
1485.947
3
18.35
7.67
1486.019
5
18.26
7.67
1485.769
10
17.24
7.67
1482.597
15
16.94
7.67
1481.705
20
16.79
7.67
1481.297
30
15.02
7.67
1475.533
40
5.87
7.74
1440.538
50
2.51
7.74
1425.651
60
1.9
7.78
1422.998
70
1.7
7.83
1422.272
80
2.81
8.89
1429.011
90
3.95
10.09
1435.901
100
4.38
10.84
1438.934
106
4.38
10.85
1439.042
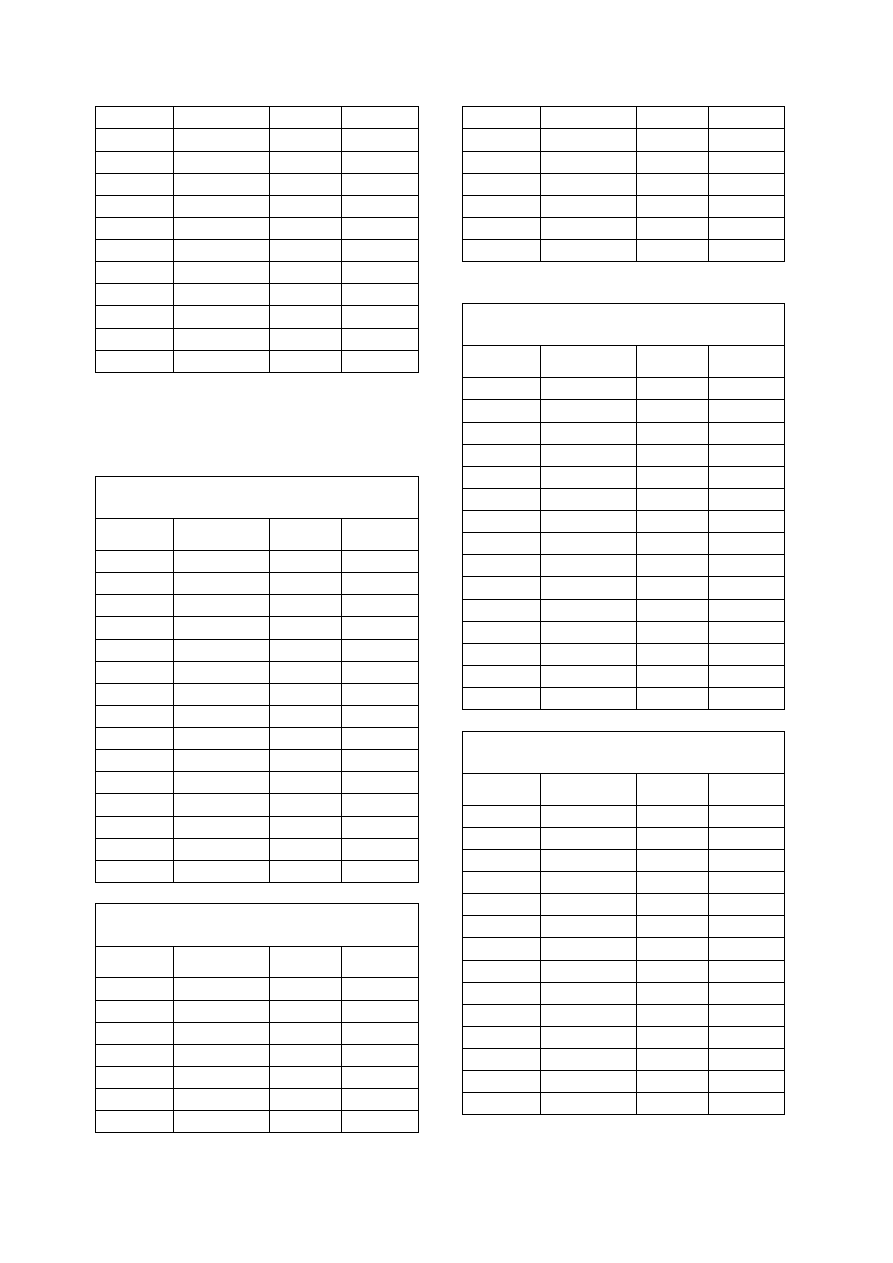
sierpień
Głębokość
(m)
Temperatura
(
o
C)
Zasolenie
(PSU)
Prędkość
(m/s)
0
13.45
7.55
1469.415
3
13.45
7.55
1469.464
5
13.45
7.54
1469.484
10
13.44
7.54
1469.53
15
13.44
7.55
1469.623
20
13.42
7.55
1469.633
30
12.23
7.61
1465.553
40
6.73
7.65
1444.085
50
3.92
7.68
1432.035
60
2.31
7.7
1424.822
70
1.19
7.77
1419.757
80
1.82
8.34
1423.668
90
2.91
9.6
1430.552
100
5.27
11.47
1443.626
106
5.53
11.65
1445.069
wrzesień
Głębokość
(m)
Temperatura
(
o
C)
Zasolenie
(PSU)
Prędkość
(m/s)
0
15.51
6.98
1475.91
3
15.51
7.49
1476.551
5
15.51
7.49
1476.584
10
15.51
7.48
1476.654
15
15.5
7.5
1476.725
20
15.48
7.5
1476.739
30
6.27
7.65
1441.978
40
3.06
7.71
1428.001
50
2.66
7.74
1426.349
60
2.28
7.8
1424.812
70
2.1
7.95
1424.32
80
3.5
9.59
1433.073
90
4.24
10.61
1437.861
100
4.32
10.73
1438.528
105
4.37
10.78
1438.892
październik
Głębokość
(m)
Temperatura
(
o
C)
Zasolenie
(PSU)
Prędkość
(m/s)
0
12.36
7.43
1465.331
5
12.35
7.43
1465.375
10
12.36
7.44
1465.504
15
12.35
7.44
1465.549
20
12.35
7.44
1465.629
30
12.33
7.44
1465.718
40
12.25
7.53
1465.693
50
12.18
7.55
1465.621
60
2.9
7.95
1427.89
70
2.69
9.42
1428.989
80
3.12
10.46
1432.47
90
3.08
10.59
1432.614
100
3.65
10.85
1435.691
105
4.62
11.17
1440.492
listopad
Głębokość
(m)
Temperatura
(
o
C)
Zasolenie
(PSU)
Prędkość
(m/s)
0
7.1
7.58
1444.91
3
7.1
7.58
1444.96
5
7.11
7.58
1445.03
10
7.1
7.58
1445.07
15
7.1
7.58
1445.15
20
6.9
7.67
1444.51
30
4
8.36
1432.95
40
3.33
8.91
1430.79
50
3.34
9.2
1431.37
60
3.28
9.57
1431.73
70
3.4
9.95
1432.93
80
3.42
10.2
1433.50
90
3.49
10.45
1434.30
100
3.91
10.79
1436.78
105
4.14
10.97
1438.12
grudzień
Głębokość
(m)
Temperatura
(
o
C)
Zasolenie
(PSU)
Prędkość
(m/s)
0
5.29
7.55
1437.15
5
5.29
7.55
1437.23
10
5.3
7.56
1437.37
15
5.29
7.55
1437.39
20
5.29
7.55
1437.47
30
5.31
7.56
1437.73
40
5.31
7.56
1437.89
50
5.3
7.58
1438.03
60
5.25
7.6
1437.99
70
2.84
8.45
1428.42
80
3.8
9.26
1434.00
90
4.04
9.6
1435.67
100
3.56
10.51
1434.85
105
4.2
11.17
1438.64
Wyszukiwarka
Podobne podstrony:
Cwiczenia obliczenia 2014 id 12 Nieznany
cwiczenia3 skrypty petle id 124 Nieznany
PPG cwiczenia skrypt id 381324
praktyka skrypt mikrobiologia id 384986
Patrologia Ćwiczenia Skrypt
Cwiczenie nr 8 Teksty id 99954
Cwiczenia nr 2 RPiS id 124688 Nieznany
Harmonogram ćwiczeń s5 2014 TABL 03 (08 10 14 )
cwiczenie 3 leki przeciwdepresyjne id 12532
HPP skrypt WZ 2 id 206452
projekt sr tr 2014 id 398557 Nieznany
cwiczenie 1b inkscape id 125205 Nieznany
Cwiczenie 8 Komponent Radiobutton id 99753
cyw1 skrypt zobowiazania id 126 Nieznany
BIOCHEMIA skrypt 2010 id 86508 Nieznany
Kropki cwiczenie na kreatywnosc id 250
Cwiczenie 1, Skrypty, UR - materiały ze studiów, studia, studia, 3 STASZEK, Woiągi
prawo materialne ue skrypt prawo id 387355
więcej podobnych podstron