1

ALEKSANDER WARCHAŁOWSKI

OCHRONA POWIETRZA

- OCENA ODDZIAŁYWANIA INSTALACJI NA STAN POWIETRZA – ASPEKTY

PRAKTYCZNE ZWIĄZANE Z PRZYGOTOWANIEM I SPRAWDZANIEM

WNIOSKÓW O WYDANIE POZWOLENIA I RAPORTÓW O ODDZIAŁYWANIU

INSTALACJI NA ŚRODOWISKO

Podczas przygotowywania bądź uzgadniania wniosków (dokumentacji) o wydanie

pozwolenia, poza znajomością zagadnień formalno-prawnych, bardzo ważna jest umiejętność

wyznaczania (obliczania) emisji z instalacji do celów porównania z normami emisji,

umiejętność wyznaczania emisji w sposób maksymalnie odwzorowujący proces

technologiczny (w przekroju rocznym, tygodniowym i dobowym) oraz umiejętność oceny

wyboru modelu rozprzestrzeniania się zanieczyszczeń i oceny uzyskanych wyników obliczeń

rozprzestrzeniania się zanieczyszczeń w powietrzu.

1. KRYTERIA ZAGROŻENIA ŚRODOWISKA WYWOŁANEGO

ZANIECZYSZCZENIEM POWIETRZA

Emisja zanieczyszczeń powietrza tym głównie tlenków siarki i azotu stanowi jedno z

głównych źródeł zagrożenia środowiska w Polsce jak również w całej Europie. Przenoszenie

zanieczyszczeń na dalekie odległości oraz zachodzące podczas tego transportu przemiany

fizyczne i chemiczne powodują, że ich niekorzystny wpływ przejawia się zarówno w postaci

wysokich stężeń zanieczyszczeń oraz w depozycji kwaśnej. Głośne w całej Europie opady

kwaśnych deszczy to właśnie skutek m.in. emisji zanieczyszczeń ze źródeł antropogennych.

Rozwiązanie tego problemu zarówno w skali lokalnej (zakładu, miasta) mezo (województwo,

region} oraz makro (kraj, kontynent) wymaga podjęcia działań nad ograniczeniem emisji tych

zanieczyszczeń. Procedura postępowania w tym zakresie wynika z jednej strony z

dotrzymywania norm emisji, w tym wynikających również z zobowiązań międzynarodowych

oraz z oceny stanu imisji w rozpatrywanej skali.

Dokonanie oceny stanu jakości powietrza zarówno dla stanu istniejącego jak i

perspektywy wymaga odpowiednich narzędzi takiej oceny. Brak w pełni reprezentatywnej

2

sieci monitoringu jakości powietrza nie pozwala na obiektywne wnioskowanie o rozkładzie

stężeń. Dlatego też do takich analiz zarówno w kraju jak i na świecie stosowane są

odpowiednie modele dyfuzji zanieczyszczeń zwane modelami rozprzestrzeniania się

zanieczyszczeń. Można zatem stwierdzić, że modele rozprzestrzenia się zanieczyszczeń w

atmosferze są jednym z podstawowych narzędzi w ocenie istniejącego stanu zanieczyszczenia

powietrza i prognozowania mogących wystąpić stężeń zanieczyszczeń i ich depozycji

W ochronie atmosfery stosowane są obecnie następujące kryteria zagrożenia

środowiska:

1. Emisja zanieczyszczeń - wyrażona w jednostkach masy określonego zanieczyszczenia na

jednostkę czasu, jednostkę emitowanych gazów, jednostkę zużywanych surowców lub

jednostkę produktu finalnego, np. g/h, g/m

3

, g/GJ, g/kWh

2. Stężenie zanieczyszczeń powietrza - wyrażone w masie danego zanieczyszczenia na

jednostkę objętości powietrza np. mg/m

3

, czy

µ

g/m

3

3. Kwaśny strumień (Acid deposition) - suma związków zakwaszających (acid substances)

głownie związków siarki i azotu, osiadających na powierzchni ziemi na skutek suchego

pochłania (dry deposition) i wymywania przez opady (wet deposition), wyrażone w

jednostkach masy poszczególnych związków na jednostkę powierzchni ziemi i jednostkę

czasu. Sumaryczny kwaśny strumień jest wyrażony w jednostkach molowych i następnie

przeliczany na tzw. równoważnik kwasowości (Acid equivalent - eq).

Równoważnik kwasowości odpowiada molowemu stężeniu jonów wodorowych /H

+

/.

Ponieważ jeden mol związków siarki generuje 2 mole /H

+

/, natomiast jeden mol związków

azotu generuje jeden mol /H

+

/, można napisać, że 1 acid eq odpowiada 16 g S i

odpowiednio 14 g N. Zwyczajowo równoważnik kwasowości podawany jest w jednostce

eq/ha/rok, natomiast strumienie całkowite związków siarki i azotu podawane są w

g/m

2

/rok.

Z podanych wartości wynikają więc następujące zależności

g S/m

2

/rok = 625 eq/ha/rok

g N/m

2

/rok = 714 eq/ha/rok

3

4. Kwaśny opad (Acid precipitation). Kwaśny opad jest wynikiem wydzielania z atmosfery

związków zakwaszających (siarki i azotu) przez opady deszczu i śniegu, w czasie

transportu zanieczyszczeń w atmosferze.

5. Kwaśny deszcz (Acid rain). Kwaśny deszcz jest wynikiem wydzielania z atmosfery

związków zakwaszających (siarki i azotu) przez opady deszczu w czasie transportu

zanieczyszczeń w atmosferze.

Deszcz jest z reguły naturalnie kwasowy (pH = 5.0

÷

6.0). Deszcz o większej kwasowości

(pH < 5.0) uważany jest za deszcz kwaśny.

Podane kryteria służą do bezpośredniej oceny zagrożenia środowiska wywoływanego

zanieczyszczeniami powietrza. Emisja zanieczyszczeń odniesiona do powierzchni kraju,

liczby mieszkańców, czy np. dochodu narodowego, jest pierwszym generalnym wskaźnikiem

zagrożenia.

Dopuszczalna emisja zanieczyszczeń powietrza jest najczęściej normowaną wartością,

że względu na łatwość jej kontrolowania. Powszechnie normowane są również najwyższe

dopuszczalne stężenia zanieczyszczeń powietrza, przy czym przyjmowanym kryterium jest tu

z zasady oddziaływanie poszczególnych zanieczyszczeń na środowisko i zdrowie ludności.

Dla innych z podanych kryteriów zagrożenia środowiska nie opracowano jeszcze

wartości dopuszczalnych. Dla wykorzystywanego w świecie coraz powszechniej kryterium

kwaśnych strumieni i opadów wprowadza się pojęcie ładunku krytycznego (critical load).

Według definicji ładunek krytyczny jest równy granicznej depozycji związków

zakwaszających, poniżej której, według obecnej wiedzy, nie występują szkodliwe skutki dla

danego elementu środowiska. Najbardziej rozpowszechnione są obecnie analizy krytycznych

ładunków dla gleb. Dla gleb wrażliwych ten krytyczny ładunek określono na 200 eq/ha/rok.

Omówiony sposób określania szkodliwego oddziaływania na środowisko posiada tę istotną

zaletę, że nie wiąże strat w środowisku z jednym określonym zanieczyszczeniem, ale

obejmuje łącznie wszystkie zanieczyszczenia powodujące "zakwaszenie" środowiska.

Wykorzystywane w niektórych ośrodkach naukowych w Polsce modele obliczeniowe

rozprzestrzeniania się zanieczyszczeń pozwalają na określenie stężeń i strumieni związków

siarki i azotu. Ponieważ jak na razie obowiązują w Polsce tylko normy dopuszczalnych stężeń

zanieczyszczeń powietrza, będą one wykorzystywane jako kryterium określania stopnia

zagrożenia środowiska podczas szkolenia.

4

2. PRZYKŁADY OBLICZEŃ INŻYNIERSKICH EMISJI I JEJ PARAMETRÓW

2.1. Zadanie A
2.1.1. Cel projektu

Celem projektu jest:

- policzenie aktualnej emisji pyłu SO

2

, CO i NO

2

w kg/h

- obliczenie stężenia zanieczyszczeń w spalinach wprowadzanych do powietrza, a następnie

porównanie z normami,

- w przypadku przekroczenia dopuszczalnych emisji określenie stopnia redukcji emisji

zanieczyszczenia i wyznaczenie rocznej wartości opłat i kar za wprowadzanie

wymienionych zanieczyszczeń do powietrza

2.1.2. Dane projektowe

Charakterystyka kotłów:

- liczba kotłów - 5
- wydajność kotła -110 t pary/h
- sprawność kotła : 82 %
- unos popiołu z paleniska - 80 %
- współczynnik nadmiaru powietrza - l,23
- parametry pary świeżej:
---- ciśnienie -13,5 MPa
---- temperatura - 540oC
- temperatura wody zasilającej - 200oC

Sprawność urządzenia odpylającego - 60 %
Charakterystyka węgla:
- wartość opałowa - 22 000 kJ/kg
- zawartość siarki - 0,9 %
- zawartość popiołu - 15 %

Zawartość wilgoci w spalinach - 10 %

Stężenie tlenków azotu w spalinach w przeliczeniu na NO

2

- 240 ppm spalin

5

Stężenie CO w spalinach - 140 ppm spalin

Charakterystyka pracy kotłów w ciągu roku:
- 10 dni - maksymalne obciążenie 5 kotłów
- 70 dni - pracują 5 kotły z obciążeniem 80 %
-100 dni - pracują 4 kotły z obciążeniem 80 %


2.1.3. Wzory wykorzystane w projekcie

E

i

= V

sp

C

i

B n [kg/h]

gdzie:
E

i

- emisja zanieczyszczenia [kg/h]

V

sp

- objętość spalin suchych [Nm

3

/kg paliwa]

C

i

- stężenie i-tego zanieczyszczenia [kg/Nm

3

spalin suchych]

B - godzinowe zużycie paliwa [kg/h]
n - ilość kotłów

[kg/h]

Q

W

B

⋅

=

ηηηη

gdzie:
W - wydajność cieplna kotła [kJ/h]
Q - wartość opałowa paliwa [kJ/kg]

W = D (h

D

- h

W

) [kJ/h]

gdzie:
D - wydajność kotła [ton pary/ h]
h

P

- entalpia pary pierwotnie przegrzanej [kJ / kg]

h

w

- entalpia wody zasilającej [kJ / kg]

V

sp

=

w

sp

V (1 - X

w

) [ Nm

3

/kg paliwa]

gdzie:
V

sp

- objętość spalin suchych [Nm

3

/kg paliwa]

V

sp

w

- objętość spalin wilgotnych [Nm

3

/kg paliwa]

X

w

- zawartość wilgoci w spalinach [%]

(

)

w

t

pow

w

sp

w

sp

y

V

V

V

⋅

⋅

⋅

+

−

+

=

602

,

1

1

,

,

λλλλ

λλλλ

[ Nm

3

/kg paliwa]

6

gdzie:

w

sp

V

,

- jednostkowa objętość spalin [Nm

3

/kg paliwa]

λ

- współczynnik nadmiaru powietrza

y

w

- zawartość wilgoci w powietrzu

[kg/kg powietrza suchego]

V

pow,t

- teoretyczna objętość powietrza do procesu spalania (teoretyczne zapotrzebowanie

powietrza do spalenia 1 kg paliwa) [Nm

3

/kg paliwa]

]

paliwa

/kg

[Nm

65

,

1

1000

212

,

0

]

paliwa

/kg

[Nm

5

,

0

1000

241

,

0

3

,

3

,

+

=

+

=

Q

V

Q

V

w

sp

t

pow

sp

SO

V

s

C

⋅

=

2

2

gdzie:
s - zawartość siarki [%]
V

sp

- objętość spalin suchych [Nm

3

/kg paliwa]

[ ]

[

]

suchych

spalin

kg/Nm

10

3

6

−

⋅

⋅

=

m

CO

CO

CO

V

M

ppm

C

C

gdzie:
M

CO

- masa molowa CO - 28,01 kg / kmol

V

m

- objętość molowa - 22,41 Nm

3

/kmol

[

]

[

]

suchych

spalin

kg/Nm

10

3

6

2

2

2

−

⋅

⋅

=

m

NO

NO

NO

V

M

ppm

C

C

gdzie:
M

NO2

- masa molowa NO

2

- 46,01 kg/ kmol

V

m

- objętość molowa - 22,41 Nm

3

/kmol

suchych]

spalin

[kg/Nm

3

pylu

sp

V

u

a

C

⋅

=

gdzie:
a - zawartość popiołu [%]
u - unos popiołu z paleniska [%]

7

]

[MW

10

3600

t

3

⋅

=

W

M

gdzie:
M - moc cieplna źródła w MW

t

)]

(6%O

[mg/Nm

21

,

0

21

,

0

2

3

1

2

2

x

x

C

C

i

x

i

−

−

⋅

=

(

)

%

100

100

1

1

21

,

0

,

1

⋅













−

⋅

⋅

−

⋅

=

w

w

sp

t

pow

X

V

V

x

λ

gdzie:
C

i

x2

- stężenie i-tego zanieczyszczenia przy x

2

zawartości O

2

x

2

- 6 %

%

100

%

6

%

6

⋅

−

=

i

i

i

i

C

D

C

ηηηη

gdzie:

η

i

- minimalny stopień redukcji przekroczonych emisji zanieczyszczeń

D

i

- dopuszczalna ilość substancji zanieczyszczającej

2.1.4. Część obliczeniowa

Obliczamy V

pow,t

V

pow t

,

,

,

,

=

⋅

+

=

0 241

1000

22000 0 5 5 8 [Nm / kg paliwa]

3

Obliczamy

w

sp

V

,

paliwa]

/kg

[Nm

31

,

6

65

,

1

22000

1000

212

,

0

3

,

=

+

⋅

=

w

sp

V

Obliczamy V

sp

w

V

sp

w

= 6,31 + (1,23 - 1)

⋅

5,8 + 1,602

⋅

1.23

⋅

5.8

⋅

0,1 = 8,79 [Nm

3

/kg paliwa]

Obliczamy V

sp

8

V

sp

= 8,79

⋅

(1 - 0,1) = 7,91 [Nm

3

/kg paliwa]

Obliczamy W

(odczytana wartość z tablic h

D

dla p = 13,5 MPa i temperatury 540oC wynosi 3350 [kJ/kg])

(odczytana z tablic wartość h

w

dla temperatury 200oC wynosi 852,45 [kJ/kg]

W =110 *1000 *(3350 - 852,45) = 274 730 500 [kJ/h]

Obliczamy B

B

=

⋅

=

274730500

0 82 22000

15228 96

,

, [kJ / h]

Obliczamy C

SO2

6

2

10

2276

91

,

7

009

,

0

2

−

⋅

=

⋅

=

SO

C

[kg/Nm

3

spalin ]

Obliczamy E

SO2

E

SO2

= 7.91

⋅

2276

⋅

10

-6

⋅

15228,96

⋅

5 = 1370,85 [kg/h]

Obliczamy C

NO2

spalin]

[kg/Nm

10

493

10

41

,

22

01

,

46

240

3

6

6

2

−

−

⋅

=

⋅

⋅

=

NO

C

Obliczamy E

NO2

E

NO2

= 7.91

⋅

493

⋅

10

-6

⋅

15228,96

⋅

5 = 296,94 [kg/h]

Obliczamy C

CO

spalin]

[kg/Nm

10

175

10

41

,

22

01

,

28

140

3

6

6

−

−

⋅

=

⋅

⋅

=

CO

C

Obliczamy E

CO

E

CO

= 7.91

⋅

175

⋅

10

-6

⋅

15228,96

⋅

5 = 105,4 [kg/h]

Obliczamy C

pyłu

spalin]

[kg/Nm

10

15171

91

,

7

8

,

0

15

,

0

3

6

−

⋅

=

⋅

=

pyl

C

Obliczamy E

pyłu

9

E

pyłu

= 7.91

⋅

15171

⋅

10

-6

⋅

15228,96

⋅

5

⋅

(1-0,6) = 3655,03 [kg/h]

Obliczamy moc cieplną źródła

]

[MW

31

,

76

10

3600

274730500

t

3

=

⋅

=

M

Zbiorcze zestawienie wyliczonej emisji:
SO

2

- 1 370,85 [kg/h]

NO

2

- 296,94 [kg/h]

CO

- 105,4 [kg/h]

Pył

- 3 655,03 [kg/h]

Przeliczamy stężenie na zawartość 6 % Q

2

(

)

(

)

[ ]

%

54

,

3

%

100

1

,

0

1

79

,

8

8

,

5

1

23

,

1

21

,

0

1

=

⋅

−

⋅

−

⋅

=

x

)]

O

%

(6

/Nm

SO

[mg

1955

0354

,

0

21

,

0

06

,

0

21

,

0

2276

2

3

2

%

6

2

=

−

−

⋅

=

SO

C

)]

O

%

(6

/Nm

NO

[mg

424

0354

,

0

21

,

0

06

,

0

21

,

0

493

2

3

2

%

6

2

=

−

−

⋅

=

NO

C

)]

O

%

(6

/Nm

CO

[mg

150

0354

,

0

21

,

0

06

,

0

21

,

0

175

2

3

%

6

=

−

−

⋅

=

CO

C

)]

O

%

(6

pylu /Nm

[mg

13034

0354

,

0

21

,

0

06

,

0

21

,

0

15000

2

3

6%

pylu

=

−

−

⋅

=

C

2.1.5. Porównanie emisji z normami

Moc cieplna źródła w naszym przypadku wynosi 76,3 MW

t

.

Odczytaliśmy z rozporządzenia MŚ dopuszczalne ilości substancji zanieczyszczających ze

spalania paliw w źródłach.

Dopuszczalne ilości tych substancji wynoszą:

D

SO2

= 850 mg/m

3

D

NO2

= 460 mg/m

3

D

CO

= 200 mg/m

3

D

pyłu

= 350 mg/m

3

Poniżej w tabeli przedstawiamy porównanie naszych wyników z normami Liczby tłustym
drukiem oznaczają przekroczenie normy.

10

Ilość substancji zanieczyszczającej

[mg/Nm

3

(6 % O

2

)]

Norma

[mg/Nm

3

]

C

SO2

6%

1 955

850

C

NO2

6%

424

460

C

CO

6%

150

200

C

pyłu

6%

13 034

350

Następnie obliczamy minimalny stopień redukcji SO

2

i pyłu

%

31

,

97

%

100

887

12

350

887

12

%

52

,

56

%

100

1955

850

1955

pylu

2

=

⋅

−

=

=

⋅

−

=

η

η

SO

11

2.2. Zadanie B
2.2.1. Cel projektu.

Elektrociepłownia wyposażona jest w kotły parowe. Spaliny przed odprowadzeniem do

komina są odpylane w multicyklonach. Do użytkowania urządzeń przystąpiono w 1994 roku.
Obliczyć aktualną emisję pyłu lotnego, SO

2

, CO, NO

2

w kg / h. Wyznaczyć roczną wartość

opłat i kar za wprowadzanie wymienionych zanieczyszczeń do powietrza.

Wyznaczyć stężenie wymienionych zanieczyszczeń w spalinach, sprawdzić czy

dotrzymane są ilości substancji zanieczyszczających wprowadzanych do powietrza określone
w rozporządzeniu MŚ. W przypadku przekroczenia dopuszczalnych ilości określić minimalny
stopień redukcji zanieczyszczeń.

2.2.2. Dane projektowe.
I.iczba kotłów: 2
Charakterystyka kotłów·

•

Wydajność kotła: 80 t pary / h,

•

Sprawność kotła: 82 %,

•

Unos popiołu z paleniska: 76 %,

•

Współczynnik nadmiaru powietrza:1,25,

•

Parametry pary świeżej : ciśnienie 13 MPa, temperatura 540oC,

•

Temperatura wody zasilającej 200oC.

Sprawność urządzenia odpylającego: 60 %

Charakterystyka węgla:

•

Wartość opałowa: 21 000 kJ / kg

•

Zawartość siarki:1,0 %,

•

Zawartość popiołu: l5 %

Zawartość wilgoci w spalinach: 9 o/o,
Stężenie tlenków azotu w spaIinach w przeliczeniu na NO

2

: 190 ppm spalin,

Stężenie CO w spalinach: 90 ppm spalin.

Charakterystyka pracy kotłów w ciągu roku:
17 dni - maksymalne obciążenie 2 kotłów, ·
60 dni - pracują 2 kot z obciążeniem 85 %, ·
90 dni - pracują 2 kotły z obciążeniem 75 %,

2.2.3. Część obliczeniowa

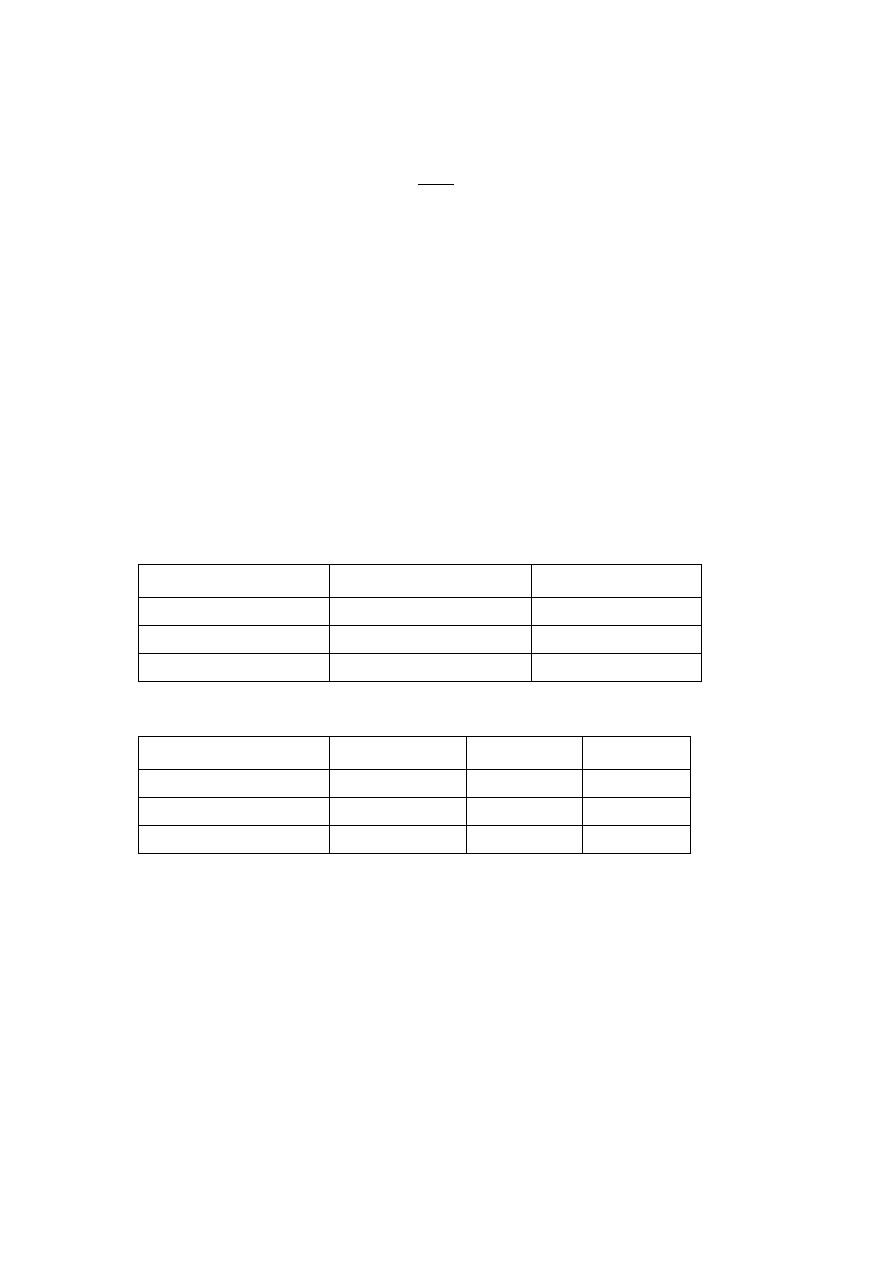
12

OBLICZENIE ZUŻYCIA PAI.IWA

[

]

h

kg

Q

W

B

h

/

η

=

(1)

gdzie:
W – wydajność cieplna kotła [kJ / h]

η

- sprawność kotła [%]

Q - wartość opałowa paliwa [kJ/kg].

W = D (h

D

– h

W

)

(2)

gdzie:
D - wydajność pary (strumień) [kg / s],
H

D

- entalpia pary [kJ / kg] dla 13 MPa i 540oC,

H

W

- entalpia wody zasilającej [ kJ / kg] dla 200oC.

Z tablic odczytano wartości h

p

oraz h

wz

- są to wartości interpolowane.

Temperatura [oC] h

wz

(entalpia wody)

h

p

(entalpia pary)

198.3 844.84

2792.20

200 852.55

2793.08

212.4 908.79

2799.50

Temperatura [oC]

12 MPa

13 MPa

14 MPa

520 3401.8

-

33777.8

540 3454

3458.5

3431.9

560 3506

-

3486

Korzystając ze wzoru (2) obliczono wydajność cieplną kotła:
D

= 80 t pary/h = 80 000 kg/h

h

D

= 3459,5 [kJ / kg] dla 13 MPa i 540

o

C,

h

W

= 852,45 [kJ / kg] dla 200

o

C

W = 80 000*(3459,5 - 852,55) = 208 556 000 kJ/h

η

= 82 %

Q = 21 000 kJ/kg
Ze wzoru (1) obliczono godzinowe zużycie paliwa:

13

B

kg h

h

=

∗

=

208556000

0 82 21000

12111 27

,

,

/

Zużycie paliwa

wynosi B

h

=12 111,27 kg / h.

OBLICZENIE AKTUALNEJ EMISJI PYŁU SO

2

, CO, NO

2

Emisja SO

2

Emisję SO

2

wyznacza się ze wzoru:

E

SO2

= V

sp

* C

SO2

* B * n [kg/h]

(3)

gdzie :
V

sp

- objętość spalin suchych [Nm

3

/ kg paliwa],

C

SO2

- stężenie SO

2

w spalinach [kg / Nm

3

spalin],

B

- zużycie paIiwa [kg / h],

n

- ilość kotłów

(

)

V

V

X

sp

sp

w

w

=

−

1

(4.)

gdzie:

V

sp

w

-

objętość spalin wilgotnych [Nm

3

/ kg paliwa],

X

w

-

zawartość wilgoci w spalinach

V

sp

w

= V

sp,w

+ (

λ

- 1) V

pow,.t

+ 1,602

λ

V

pow,.t

y

w

(5)

gdzie:
V

sp,w

- jednostkowy strumień spalin [Nm

3

/ kg]

y

w

- zawartość wilgoci w powietrzu - kg/kg powietrza suchego

λ

- współczynnik nadmiaru powietrza

V

pow,t

- teoretyczne zapotrzebowanie powietrza dla spalenia 1 kg paliwa.

[

]

kg

Nm

Q

V

t

pow

/

5

,

0

1000

241

,

0

3

.

+

=

]

/

[

65

,

1

1000

212

,

0

3

,

kg

Nm

Q

V

w

sp

+

=

(6)

(7)

ze wzoru (6) obliczono

w

sp

V

,

14

w

sp

V

,

= (0,212*21 000) / 1000 + 1,65 = 6,102 Nm

3

/ kg

w

sp

V

,

= 6.102 Nm3/kg

ze wzoru (7) obliczono V

pow.t

V

pow.t

= (0,241 * 21000) / 1000 + 0,5 = 5,561 Nm

3

/ kg

V

pow.t

= 5.561 Nm

3

/ kg

λ

= 1,25

y

w

= 0.09 kg/kg powietrza suchego

ze wzoru (5) obliczono V

sp

w

V

sp

w

= 6,102 + (1,25 - l ) * 5,561 + l,602 * 1,25 * 5,561 * 0,09 = 8,494 Nm

3

/kg

V

sp

w

= 8,494 Nm

3

/ k

ze wzoru (4) obliczono V

sp

V

sp

= 8,494 * (1 - 0,09) = 7,730 Nm

3

/ kg

V

sp

= 7,730 Nm

3

/kg

Stężenie SO

2

w spalinach suchych obliczono ze wzoru:

C

s

V

SO

so

2

2

=

(8)

gdzie:
s - zawartość siarki w węglu
s = 1 % = 0,0l
C

SO2

= (2*0,01) / 7,726 = 2587 * 10

-6

kg / Nm

3

C

SO2

= 2587 * 10

-6

kg/Nm

3

Emisję SO

2

obliczono ze wzoru (3)

E

SO2

= 7,730 * 2587 * l0

-6

* 12111,27 * 2 = 484,39 kg / h

E

SO2

= 484,39 kg / h

EMISJA CO
Emisję CO wyznaczono ze wzoru

E

CO

= V

sp.

* C

CO

* B * n [kg/h]

Stężenie CO wyznaczono ze wzoru:

15

(

)

[

]

3

6

/

10

Nm

kg

V

M

C

C

m

i

ppm

CO

CO

−

=

(9)

C

CO(ppm)

= 90 ppm

M

i

= 28 kg / mol

V

m

= 22,41 Nm

3

/ mol

C

CO

= (90 * 28 * 10

-6

) / 22,41= 1,12 * 10

-4

kg / Nm

3

C

CO

= 112 * 10

-6

kg/ Nm

3

E

CO

= 7,726 * 1l2 * l0

-6

* 12111,27 * 2 = 20,97 kg / h

E

CO

= 20,97 kg/h

EMISJA NO

2

Emisję NO

2

wyznaczono ze wzoru:

E

NO2

= V

sp

* C

NO2

* B * n [kg/h]

Stężenie NO

2

wyznaczono ze wzoru:

(

)

[

]

C

C

M

V

NO

NO ppm

i

m

2

2

6

10

=

−

kg / Nm

3

(10)

C

NO2

= 190 ppm

M

i

= 46 kg/kmol

V

m

= 22,41 Nm

3

/kmol

C

NO2

= (190 * 46 * 10

-6

) / 22,41 = 0, 39 * 10

-3

kg /Nm

3

C

NO2

= 390 * 10

-6

kg/Nm

3

E

NO2

= 7,726 * 390 * 10

-6

* 12111,27 * 2 = 73,02 kg / h

E

NO2

= 73,02 kg / h

EMISJA PYŁU
Emisję pyłu wyznaczono ze wzoru:

E

p

= V

sp

* C

p

* B * n [kg / h]

Stężenie pyłu wyznaczono ze wzoru:

[

]

C

a u

V

p

sp

= ∗

10

6

mg / Nm

3

(11)

16

gdzie:
a - zawartość popiołu
u - unos pyłu z paleniska
a =15 % = 0,15
u = 80 % = 0,80

C

p

= (0,15 * 0,8) / 7,726 = 14748* 10

-6

kg / Nm

3

C

p

= 14748* 10

-6

kg/Nm

3

E

p

= 7,726 * 14748* 10

-6

* 12111,27 * 2 (1 -

η

odp

) = 1104,57 kg / h

E

p

= 1104,57 kg / h

AKTUALNE EMISJE:

Emisja SO

2

wynosi

484,39 kg / h

Emisja CO wynosi 20,97 kg / h
Emisja NO

2

wynosi 73,02 kg / h

Emisja pyłu po przejściu przez multicyklony wynosi 1104,57 kg/ h


2.2.4. OKREŚLENIE STĘŻENIA PYŁU SO

2

, CO, NO

2

I PORÓWNANIE Z NORMAMI

•

Określenie mocy cieplnej źródła

[

]

M

Q

MW

t

=

∗

3600 10

3

(13)

[

]

M

MW

t

=

∗

=

208556000

3600 10

57,93

3

Zgodnie z rozporządzeniem MŚ wyznaczono dopuszczalne do wprowadzenia do

powietrza ilości substancji zanieczyszczających ze spalania paliw w źródłach, do których
użytkowania przystąpiono po dniu 18.03.1990 r. dla mocy cieplnej źródła wynoszącej 57,93
MW

t

.

W naszym projekcie do użytkowania urządzeń przystąpiono w 1994 r.
Dopuszczalne wartości emisji są następujące:
- D

SO2

= 850 mg / m

3

,

17

- D

CO

= 200 mg / m

3

,

- D

NO2

= 460 mg / m

3

,

- D

pyłu

= 350 mg / m

3

.

•

Przeliczenie stęźeń zanieczyszczeń na zawartość 6% O

2

SO

2

[

]

)

O

%

(6

m

/N

SO

mg

21

,

0

21

,

0

2

3

2

1

2

2

2

2

X

X

C

C

SO

X

SO

−

−

=

(14)

(

)

%

100

1

21

,

0

.

1

sp

t

pow

V

V

x

−

=

λ

(15)

(

)

%

78

,

3

%

100

726

,

7

561

,

5

1

25

,

1

21

,

0

1

=

∗

∗

−

∗

=

x

x

1

= 3,78 %,

x

2

= 6 %,

3

3

6

mg/Nm

87

25

kg/Nm

10

2587

2

=

∗

=

−

SO

C

3

2

mg/Nm

2253

0378

,

0

21

,

0

06

,

0

21

,

0

2587

2

=

−

−

=

X

SO

C

C

SO2

6%

= 2253 mg/Nm

3

Norma 850 mg/ Nm

3

CO

[

]

)

O

%

(6

m

CO/N

mg

21

,

0

21

,

0

2

3

1

2

2

X

X

C

C

CO

X

CO

−

−

=

3

3

6

mg/Nm

112

kg/Nm

10

112

=

∗

=

−

CO

C

3

2

mg/Nm

98

0378

,

0

21

,

0

06

,

0

21

,

0

112

=

−

−

=

X

CO

C

C

CO

6%

= 98 mg/Nm

3

Norma 200 mg/ Nm

3

NO

2

[

]

)

O

%

(6

m

/N

O

mg

21

,

0

21

,

0

2

3

2

1

2

1

2

2

2

N

X

X

C

C

NO

X

NO

−

−

=

18

3

3

6

mg/Nm

390

kg/Nm

10

390

2

=

∗

=

−

NO

C

3

2

mg/Nm

340

0378

,

0

21

,

0

06

,

0

21

,

0

390

2

=

−

−

=

X

NO

C

C

NO2

6%

= 340mg/Nm

3

Norma 460 mg/ Nm

3

Pył

[

]

)

O

%

(6

m

/N

CO

mg

21

,

0

21

,

0

2

3

2

1

2

2

X

X

C

C

pyl

X

pyl

−

−

=

C

pyłu

= 14748* 10

-6

kg/Nm

3

= 14748 mg/ Nm

3

3

2

pyµu

mg/Nm

12847

0378

,

0

21

,

0

06

,

0

21

,

0

14748

=

−

−

=

X

C

C

pyłu

6%

= 12847 mg/Nm

3

Norma 350 mg/ Nm

3

Ilość wprowadzanego do atmosfery SO

2

jest prawie trzykrotnie większa od wartości

dopuszczalnych, również ilość wprowadzanego pyłu jest znacznie przekroczona, aż 41 razy
większa od wartości dopuszczalnej. Ilości CO oraz NO

2

nie są przekroczone. W związku z

przekroczeniami należy wyznaczyć minimalny stopień redukcji emisji tych zanieczyszczeń.

SO

2

%

100

2

2

2

2

2

2

X

SO

SO

X

SO

SO

C

D

C

−

=

η

(16)

C

SO2

X2

= 2253 mg/Nm

3

D

SO2

= 850 mg/Nm

3

%

27

,

62

%

100

2253

850

2253

2

=

∗

−

=

SO

η

Minimalny stopień redukcji SO

2

wynosi 62,27%.

Pył

C

pyłu

X2

= 12847 mg/Nm

3

D

pyłu

= 350 mg/Nm

3

19

%

28

,

97

%

100

12847

350

12847

pyµu

=

∗

−

=

η

Minimalny stopień redukcji pyłu wynosi 97,28 %.

3. ZAGADNIANIA MODELOWANIA ROZPRZESTRZENIANIA
ZANIECZYSZCZEŃ

3.1. CHARAKTERYSTYKA „IDEALNEGO” MODELU

Model idealny powinien umożliwiać:

•

stosowanie dla różnych:

−

skal czasowych i przestrzennych

−

warunków meteorologicznych i topograficznych

−

źródeł emisji (punktowe, liniowe, powierzchniowe)

−

rodzajów zanieczyszczeń

•

łatwe uzyskiwanie danych wejściowych

ponadto powinien być:

−

łatwy do implementacji

−

łatwy do zrozumienia i eksploatacji

−

szybko działający

−

pracujący w systemie interakcyjnym

−

dobrze udokumentowany

−

całkowicie zweryfikowany

Należy zawsze pamiętać że:

•

idealny model nie istnieje, gdyż pewne cechy wykluczają się

•

dokładność wyników modelowania jest mniejsza od dokładności danych

wejściowych

3.2. KLASYFIKACJA MODELI
Ze względu na podstawową strukturę:

−

deterministyczne - niedeterministyczne

−

stacjonarne – niestacjonarne

Ze względu na system odniesienia:

−

Eulerowskie

−

Lagrange’owskie

Ze względu na wymiarowość:

−

1 - wymiarowe (1D)

−

2 - wymiarowe (2D)

−

3 - wymiarowe (3D)

−

wielopoziomowe

Ze względu na metody rozwiązywania równań:

−

analityczne

−

numeryczne

20

KLASYFIKACJA MODELI WG ICH CHARAKTERYSTYKI
Ze względu na skalę przestrzenną:

−

lokalne

−

regionalne

−

skala kraju

−

skala kontynentu

−

modele globalne

Ze względu na: skalę czasową:

−

dzień

−

godzina

−

miesiąc

−

rok

−

dekada

Ze względu na: rodzaj zanieczyszczenia:

−

SO2,

−

NOx,

−

CO,

−

węglowodory,

−

Pył,

−

itd.

KLASYFIKACJA MODELI WG ICH STRUKTURY

•

modele analityczne

•

modele numeryczne

−

domknięcie 1 - go rzędu

−

siatka eulerowska

−

trajektorie Lagrange’a

−

hybrydowy eulerowsko-lagrange’owski

−

(pic) particle in cell

−

pudełkowy (box model)

•

modele statystyczne

•

modele fizyczne

Wszystkie matematyczne modele rozprzestrzeniania zanieczyszczeń w powietrzu

atmosferycznym, bazują na równaniu adwekcji-dyfuzji. Równanie to, przy założeniu równania
ciągłości w postaci (2), zastosowaniu prawa Fick'a do opisu członów dyfuzji turbulencyjnej
(proporcjonalność strumienia do gradientu stężenia) oraz założeniu diagonalnej postaci
tensora współczynników dyfuzji Kx, Ky i Kz przyjmuje następującą formę matematyczną (1):

∂

∂

∂

∂

∂

∂

∂
∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂
∂

c

t

u

c

x

v

c

y

w

c
z

x

K

c

x

y

K

c

y

z

K

c
z

Q R

x

y

z

+

+

+

=

+

+

+ +

(1)

przy równaniu ciągłości w postaci:

21

∂

∂

∂

∂

∂

∂

u

x

v

y

w

z

+

+

=

0

(2)

gdzie:

c stężenie zanieczyszczeń,
u, v, w

składowe x, y i z prędkości wiatru

K

x

,K

y

K

z

współczynniki dyfuzji turbulencyjnej,

Q

emisja zanieczyszczeń,

R człon opisujący procesy usuwania zanieczyszczeń z powietrza

(osiadanie suche + wymywanie przez opady) oraz transformację

chemiczną zanieczyszczeń.

Rozwiązanie układu równań (1) i (2) jest możliwe, gdy wielkości meteorologiczne:
pole wiatru, współczynniki dyfuzji turbulencyjnej, pole temperatury, pole opadu, wielkość
pokrywy chmur są znanymi funkcjami zmiennych przestrzennych x, y i z oraz czasu t. Ponadto
wymagana jest znajomość emisji zanieczyszczeń, parametrów związanych z opisem procesów
osiadania suchego zanieczyszczeń, wymywania przez opad, szybkość reakcji chemicznych
opisujących przemiany danego zanieczyszczenia i aerodynamiczna szorstkość terenu. Bez
wprowadzania określonych założeń upraszczających rozwiązanie jest możliwe jedynie
metodami numerycznymi. W wyniku takiego rozwiązania możemy otrzymać czasowo-
przestrzenne rozkłady stężenia i depozycji zanieczyszczeń.

Posługiwanie się rozwiązaniami numerycznymi równania adwekcji - dyfuzji związane

jest z dużym nakładem czasu obliczeniowego oraz skomplikowanym przygotowaniem danych
wejściowych. W związku z tym w zastosowaniach inżynierskich często (również w Polsce)
stosowane są rozwiązania analityczne równania adwekcji – dyfuzji możliwe do uzyskania
przy następujących założeniach upraszczających:

! Stacjonarność rozwiązania (

)

0

=

∂

∂

t

c

,

! Zaniedbanie pionowej składowej pola wiatru (w=0),

! Oś x jest zgodna ze składową kierunku wiatru u (v = 0),

! Zaniedbuje się proces dyfuzji turbulencyjnej w kierunku osi x (

x

= 0),

! Zakłada się, że prędkość wiatru u ma wartość stałą (wartość średnia w warstwie od

powierzchni ziemi do wysokości H),

! Zakłada się ustalone warunki meteorologiczne na trasie od źródła do receptora,

! Zakłada się stałość współczynników dyfuzji y i

z

z wysokością (wartości średnie

tych współczynników w warstwie od powierzchni ziemi do wysokości H).

! Przyjmuje się stałą wartość parametru aerodynamicznej szorstkości terenu zo.

! Zakłada się, że teren można z dobrym przybliżeniem uznać za płaski

! Zakłada się, że wielkość emisji jest ustalona w czasie oraz, że zanieczyszczenie jest

tzw. zanieczyszczeniem pasywnym, a więc nie wpływającym na dynamikę i stan

ośrodka w którym podlega transportowi.

! Pomija się przemiany chemiczne zanieczyszczeń.

22

! Pomija się wymywanie zanieczyszczeń przez opady.

! Pomija się suche osiadanie zanieczyszczeń.

! Rozwiązanie musi spełniać dwa warunki brzegowe:

gdy z = 0,

∂

c/

∂

z = 0 czyli idealne odbicie od podłoża;

gdy z

⇒∞, c ⇒0. Zaniedbuje się błąd zależny od wzajemnej relacji

wysokości źródła emisji i położenia górnej inwersji temperatury.

Jednym z analitycznych rozwiązań równania adwekcji - dyfuzji jest model Pasquill'a
(stosowany w Polsce jako obowiązujący w obliczeniach inżynierskich). Model ten bazuje na
podanych wyżej założeniach upraszczających, w istotny sposób ograniczających zakres
czasowy i przestrzenny jego stosowalności. Podstawowa formuła modelu Pasquill’a opisująca
stężenie zanieczyszczenia gazowego w punkcie o współrzędnych x, y, z jest następująca:

c(x,y,z) =

E

2 u

e

e

+ e

y

z

y

2

( z H )

2

(z+ H )

2

2

2

y

2

2

z

2

2

z

π σ σ

σ

σ

σ

−

−

−

−









(3)

przy czym :

c - stężenie zanieczyszczenia,
u - średnia prędkość wiatru,
E - emisja,

σ

y

- współczynnik dyfuzji turbulencyjnej w kierunku osi y,

σ

z

- współczynnik dyfuzji turbulencyjnej w kierunku osi z,

H - wysokość efektywna źródła,
x, y, z -

współrzędne prostokątnego układu kartezjańskiego.

Istnieje możliwość uwzględnienia w ww. rozwiązaniu analitycznym przemian chemicznych
pierwszego rzędu, wymywania przez opady oraz suchego osiadania przez wprowadzenie
parametrów opisujących te zjawiska w następującej postaci:

(

)

3

2

1

2

)

(

2

)

(

2

)

(

2

,

,

2

2

2

2

2

2

R

R

R

e

e

e

u

E

z

y

x

S

z

z

y

H

z

H

z

y

z

y

⋅

⋅

⋅

+

⋅

⋅

⋅

⋅

⋅

⋅

=

⋅

+

−

⋅

−

−

⋅

−

σ

σ

σ

σ

σ

π

(4)

gdzie poza oznaczeniami jak we wzorze ():

R1 przemiana chemiczna zanieczyszczeń,

R2 wymywanie

zanieczyszczeń przez opady,

R3 suche osiadanie zanieczyszczeń.

Człony R1, R2, i R3 występujące w równaniu (4) wyrażone są następująco:

Przemiana chemiczna zanieczyszczeń.

2

1

693

,

0

1

τ

τ

⋅

−

=

e

R

(5)

τ

= x/u - czas transportu zanieczyszczenia,

τ

1/2

- okres połowicznego zaniku zanieczyszczenia,

ln 2 = 0,693.
Wymywanie zanieczyszczeń przez opady.

R

e

2

=

− ⋅

λ τ

(6)

τ

= x/u - czas transportu zanieczyszczenia,

λ

-

współczynnik wymywania.

Suche osiadanie (pochłanianie przez podłoże).

23

∫

⋅

−

⋅

⋅

⋅

−

=

z

z

H

z

d

dx

e

u

e

R

0

2

2

2

1

2

3

σ

ν

σ

π

(7)

vd -

prędkość suchego osiadania,

u,

σ

z i H

- jak w powyższych wzorach.

Prostota rozwiązania analitycznego w porównaniu z rozwiązaniami numerycznymi okupiona
jest jednak istotnymi ograniczeniami jego stosowania, wynikającymi z przyjętych założeń
upraszczających. Głównymi ograniczeniami są:

! prędkość wiatru > 1 m/s (0.5 m/s ?),

! czas transportu < 3 godz.

! skala przestrzenna 10 (30) km,

! teren płaski,

! zanieczyszczenia pasywne.

Niezależnie od podanych ograniczeń stosowania, rozwiązanie analityczne umożliwia

uzyskiwanie ograniczonych informacji o rozkładach stężeń. Z modelu analitycznego można
uzyskać jedynie:

−

stężenie maksymalne (chwilowe) nie wymaga danych meteorologicznych,

−

częstość przekraczania określonych poziomów stężeń chwilowych,

−

stężenie średnioroczne,

−

opad pyłu.

Informacje te nie spełniają wymagań Rozporządzenia MŚ z dnia 06.06.2002 zgodnie z

którym model powinien umożliwiać uzyskanie informacji o przestrzennych rozkładach
następujących charakterystyk imisji

! maksymalnych stężeń 1-godzinnych w dowolnym okresie,
! częstości przekraczania dowolnie zadanego poziomu przez stężenia 1-godzinne w

dowolnym okresie,

! maksymalnych stężeń 8-godzinnych w dowolnym okresie,
! maksymalnych stężeń średniodobowych w dowolnym okresie,
! częstości przekraczania dowolnie zadanego poziomu przez stężenia średniodobowe w

dowolnym okresie,

! stężeń średnich dla dowolnego okresu (średnioroczne).

W związku z tym przed modelem stawiane są następujące wymagania:

! uwzględnienie przestrzennej i czasowej zmienności warunków meteorologicznych,

! uwzględnienie zmienności warunków emisji,

! możliwość wykorzystania dla dowolnej skali czasowej i przestrzennej,

! możliwość łatwego uzyskania danych wejściowych (meteorologicznych),

! możliwość zaimplementowania kodu modelu na komputerze osobistym klasy PC,

! stosunkowo krótki czas obliczeń.

Dodatkowym, bardzo istotnym warunkiem jest, aby w swoich podstawowych założeniach
model był spójny z aktualnie obowiązującymi wytycznymi.

24

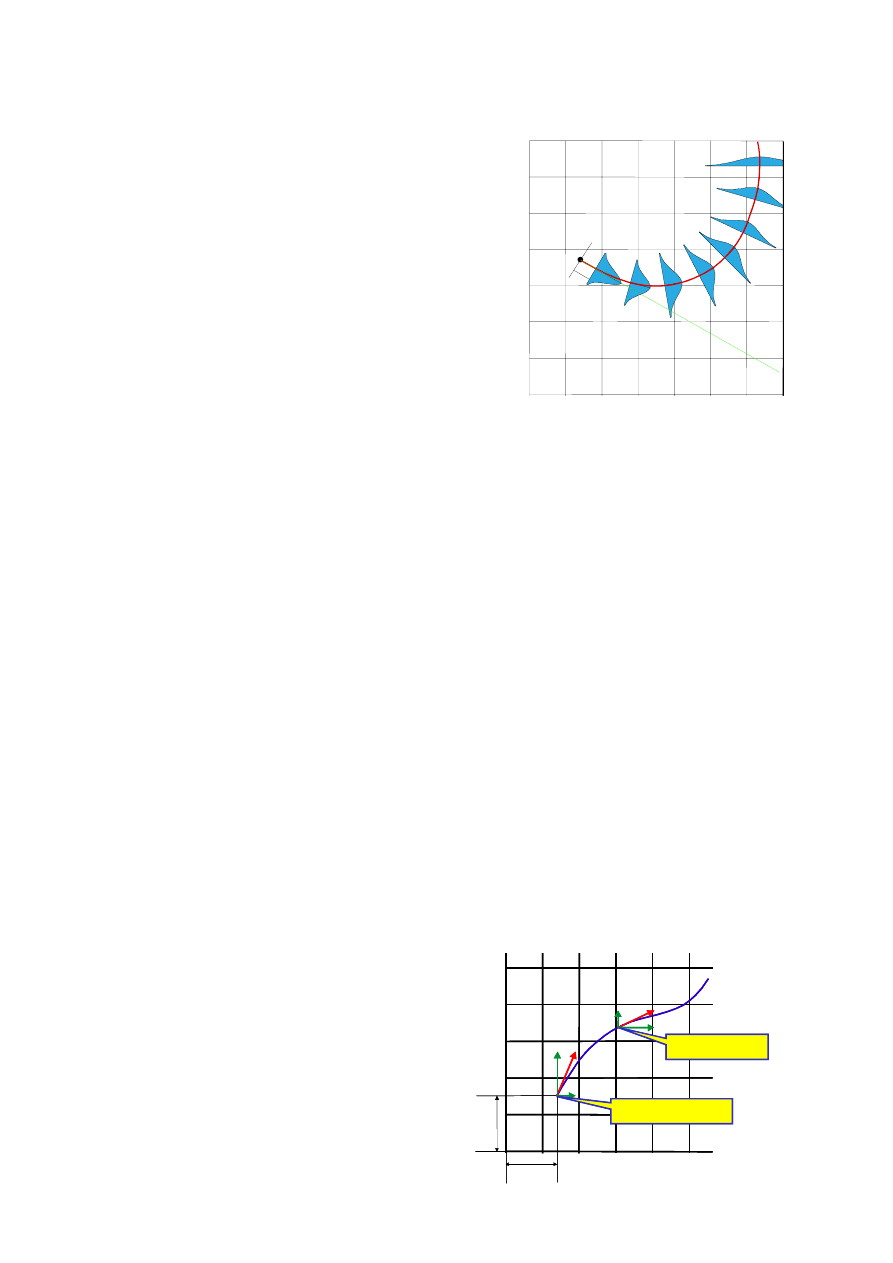
3.3. ANALITYCZNY MODEL TRAJEKTORII „AMOT”
Podane wyżej wymagania spełnia model „AMOT”,
którego idea polega na połączeniu modelu trajektorii z
analitycznym rozwiązaniem równania dyfuzji. Idea ta
jest przedstawiona na rysunku obok. Model trajektorii
umożliwia uwzględnienie zmienności w czasie i
przestrzeni warunków meteorologicznych (prędkość i
kierunek wiatru, stan równowagi), natomiast analityczny
model dyfuzji zapewnia zachowanie spójności
uzyskiwanych wyników z wynikami modelu
stosowanego zgodnie z rozporządzeniem Ministra
Środowiska z dnia 5 grudnia 2002 r. - Dz.U. z 2003 r.
Nr 1, poz. 12 (wzory na wyniesienie, wykładnik
meteorologiczny, współczynniki dyfuzji).

W pierwszej fazie obliczeń wyznaczane są kolejne punkty trajektorii (dla kolejnych

kroków czasowych

∆

t). Trajektoria jest prowadzona bądź do czasu wyjścia poza granicę

modelowanego obszaru, bądź też jest śledzona przez okres 48 h. Jeżeli po czasie 48 h nie
opuści ona obszaru modelowania, to wówczas przyjmuje wartości prędkości i kierunku wiatru
takie jak w ostatnim punkcie trajektorii 48 godzinnej, kreślona jest trajektoria prostoliniowa
aż do momentu przecięcia z granicą obszaru. Ta metoda postępowania w odniesieniu do
trajektorii 48 h nie jest istotnym źródłem błędów z uwagi na to, że po czasie 48 h wartości
stężeń i strumieni zanieczyszczeń osiadających na podłożu są bardzo małe. Sytuacje takie dla
niedużych obszarów przestrzennych występują sporadycznie, natomiast plusem takiego
podejścia jest całkowite zbilansowanie masy zanieczyszczeń na modelowanym obszarze. Dla
każdego źródła emisji tak opisana trajektoria jest wykreślana z częstotliwością co 1 h.
Oczywiście wykreślenie każdej z trajektorii wymaga interpolacji zarówno czasowej jak i
przestrzennej pola wiatru (zdefiniowanego uprzednio na podstawie danych meteorologicznych
w węzłach regularnej siatki przestrzennej). Interpolacja po czasie, jest interpolacją liniową
dokonywaną na każdym kroku czasowym

∆

t w węzłach regularnej siatki przestrzennej.

Interpolacja przestrzenna z węzłów siatki do danego punktu na trajektorii dokonywana jest
metodą funkcji wagowych odwrotnie proporcjonalnych do kwadratu odległości. Pole wiatru
zdefiniowane w węzłach regularnej siatki przestrzennej na podstawie danych
meteorologicznych jest polem średnim wiatru w warstwie powietrza od powierzchni ziemi do
wysokości warstwy dobrze wymieszanej, stanowiącej górną granicę do której mogą
rozprzestrzeniać się zanieczyszczenia. Intensywność opadu atmosferycznego przyjęta została
na podstawie pomiarów z najbliższej stacji synoptycznej, przy czym opad podzielony jest na
opad deszczu i opad śniegu. Rozróżnienie to jest istotne ze względu na różną efektywność
procesu wymywania zanieczyszczeń przez każdy rodzaj opadu.
W kolejnych punktach trajektorii interpolowane
są też: współczynniki dyfuzji, wykładnik
meteorologiczny opisujący wzrost prędkości
wiatru z wysokością, oraz wysokość warstwy
dobrze wymieszanej. W wyniku tej procedury,
otrzymuje się współrzędne punktów danej
trajektorii wraz z obliczonymi dla nich wyżej
wymienionymi wielkościami.
Następnie obliczane są stężenia i
strumienie zanieczyszczeń na powierzchni ziemi,

i+1

x

i

xE

yE

y

j

j+1

X(t0), y(t0), u(t0), v(t0), hm(t0),

σx(0t), σy(t0), op(t0), .........

X(t), y(t), u(t), v(t), hm(t),

σx(t), σy(t), op(t), .........

i+1

x

i

xE

yE

y

j

j+1

X(t0), y(t0), u(t0), v(t0), hm(t0),

σx(0t), σy(t0), op(t0), .........

X(t), y(t), u(t), v(t), hm(t),

σx(t), σy(t), op(t), .........

25

ich wartości zliczane i uśredniane przestrzennie w oczkach siatki obliczeniowej. Siatka ta
może być wprowadzona niezależnie od siatki w której zadane były pola meteorologiczne. Pola
stężeń i strumieni są obliczane modelem analitycznym rozszerzonego Pasquill'a z
zastosowaniem metodyki opisanej w rozporządzeniu Ministra Środowiska z dnia 5 grudnia
2002 r. w sprawie wartości odniesienia dla niektórych substancji w powietrzu (Dz.U. z 2003 r.
Nr 1, poz. 12). Uwzględnienie zmiennych warunków meteorologicznych w sąsiednich
punktach trajektorii jest możliwe, dzięki dopasowaniu profilu stężenia do zmieniających się
warunków. Matematycznie odpowiada to założeniu ciągłości przy przejściu profilu stężenia
od jednej sytuacji meteorologicznej do następnej na kolejnych krokach czasowych

∆

t.

Procedura opisana powyżej jest powtarzana co 1 h dla kolejno prowadzonych trajektorii dla
każdego źródła emisji.
Przygotowanie danych meteorologicznych

Dane meteorologiczne zostały przygotowane na podstawie pomiarów ze wszystkich

stacji meteorologicznych sieci IMGW.

Dane o prędkości i kierunku wiatru zostały zinterpolowane do siatki obliczeniowej o

kroku dx = dy = 30 km. Interpolacji dokonano przy użyciu funkcji wagowych odwrotnie
proporcjonalnych do kwadratu odległości. Następnie przy uwzględnieniu klasy równowagi
atmosfery (obliczonej dla każdego terminu meteorologicznego przy pomocy metodyki
identycznej jak przy tworzeniu „Katalogu danych .......”) oraz odpowiadającej danej klasie
równowagi atmosfery wysokości warstwy mieszania - obliczone zostały średnie prędkości
wiatru w tej warstwie. Uzyskane w ten sposób pole, poddane zostało dodatkowemu
przetworzeniu metodą analizy wariacyjnej. Metoda ta polega na uzgodnieniu pola wiatru z
równaniem ciągłości masy przy założeniu przepływu nieściśliwego ośrodka ciągłego.
Wynikowe pole wiatru stanowi pole wejściowe do lagrange’owskiego modelu trajektorii.

Dane źródłowe dotyczące opadu atmosferycznego (niezbędnego w modelu dyspersji

do parametryzacji procesu wymywania zanieczyszczeń) wyrażone są w jednostkach [mm/6h].
Dane te zostały dla modelowanego obszaru przyjęte jako wartości zmierzone na najbliższej
stacji synoptycznej, będąc miarą średniej intensywności opadu dla każdego sześciogodzinnego
odcinka czasu.

Oprócz w/w pól meteorologicznych przygotowany został dla każdego trzygodzinnego

terminu zbiór z wartościami następujących wielkości meteorologicznych:
H -

wysokość warstwy mieszania (średnia dla modelowanego obszaru)

Kl

- klasa równowagi atmosfery wg klasyfikacji Pasquill'a (średnia dla

modelowanego obszaru)

T

- temperatura powietrza (średnia dla modelowanego obszaru)

Klasa

równowagi

atmosfery

została wyliczona oddzielnym programem

(zgodnym z metodyką tworzenia „Katalogu danych .......”), na podstawie zmierzonych na
stacjach synoptycznych: prędkości wiatru i zachmurzenia, przy uwzględnieniu wielkości
promieniowania słonecznego determinowanego terminem dokonanego pomiaru (miesiąc,
dzień, godzina). Na podstawie klasy równowagi wyliczonej dla każdej ze stacji, zostały
określone wysokości warstwy mieszania. Podstawą przypisania klasom równowagi atmosfery
tych wysokości, były prace eksperymentalne wykonane w ramach programu PR-8 przez
Zakład Aerologii w Legionowie. Wysokości warstwy mieszania jak również wyliczone klasy
równowagi atmosfery, zostały uśrednione dla obszaru siatki obliczeniowej. Podobne
uśrednienia dokonano dla temperatury powietrza.

Przygotowane w opisany wyżej sposób pola meteorologiczne zostały umieszczone w

plikach oddzielnie dla kolejnych lat.

26

Przygotowanie danych o emisji

Ponieważ program umożliwia uwzględnienie zmienności parametrów emisji w czasie,

konieczne jest podanie odpowiednich informacji w pliku z danymi emisji. (nazwa pliku emisji
dowolna).

3.4. MOŻLIWOŚCI ZASTOSOWANIA MODLEU „AMOT”

Model AMOT może być stosowany we wszystkich przypadkach praktycznych, kiedy

nie jest możliwe korzystnie z klasycznego rozwiązania analitycznego ze względu na
ograniczenia jego stosowania, z których podstawowym jest ograniczenie skali czasowej i
przestrzennej, oraz ograniczony zakres uzyskiwania informacji, wynikających z rodzaju
wykorzystywanych danych meteorologicznych (trójwymiarowe klimatologiczne statystyki
kierunku i prędkości wiatru oraz stanu równowagi atmosfery).

Z uwagi na fakt, że model AMOT wykorzystuje chronologiczne ciągi pól parametrów

meteorologicznych, możliwe jest obliczanie wartości stężeń dla dowolnych czasów
uśredniania, m.inn. dla czasów uśredniania zgodnych z wymaganiami rozporządzenia MŚ z
dnia 06.06.2002, tzn.

•

maksymalnych stężeń 1-godzinnych w dowolnym okresie,

•

częstości przekraczania dowolnie zadanego poziomu przez stężenia 1-godzinne

w dowolnym okresie.,

•

maksymalnych stężeń 8-godzinnych w dowolnym okresie,

•

maksymalnych stężeń średniodobowych w dowolnym okresie,

•

częstości przekraczania dowolnie zadanego poziomu przez stężenia

średniodobowe w dowolnym okresie.

bez ograniczenia skali czasowej i przestrzennej.

Model był wielokrotnie wykorzystywany do wykonywania obliczeń rozprzestrzeniania

zanieczyszczeń z wysokich kominów (elektrowni) niezbędnych przy wykonywaniu operatów
ochrony powietrza i ocen oddziaływania na środowisko w skali kilku powiatów(skala
programów ochrony atmosfery). Wyniki takich obliczeń mogą być również przestawiane
graficznie na odpowiednich podkładach mapowych.

Ponadto model AMOT może być wykorzystany również do określania eksportu

zanieczyszczeń poza granice Polski, do określania międzywojewódzkich przepływów
zanieczyszczeń powietrza, oraz do opracowywania programów ochrony powietrza w strefach.

Model istnieje w wersji operacyjnej i pracuje w środowisku Windows co w

porównaniu z większością stosowanych w Polsce programów pracujących w środowisku
DOS, znacznie ułatwia posługiwanie się programem.