
1
Wykład XI Mechanika
Przekształcenia kanoniczne
W formalizmie Lagrange’a możemy dowolnie zmieniać współrzędne uogólnione, a postać
równań ruch nie ulega zmianie tzn. jeśli wprowadzimy współrzędne
)
,
,
,
(
2
1
n
i
q
q
q
Q
K
, to
spełniają one równania
0
=
∂
∂
−
∂
∂
i
i
Q
L
Q
L
dt
d
&
, jeśli
i
q spełniają
0
=
∂
∂
−
∂
∂
i
i
q
L
q
L
dt
d
&
.
W formalizmie Hamiltona tak nie jest, bo
i
q i
i
p musza spełniać jeszcze związek
i
i
q
L
p
∂
∂
=
&
.
Definicja
Transformacja
n
i
p
p
p
q
q
q
P
p
p
p
p
q
q
q
Q
q
n
n
i
i
n
n
i
i
,
,
2
,
1
)
,
,
,
;
,
,
,
(
)
,
,
,
;
,
,
,
(
2
1
2
1
2
1
2
1
K
K
K
K
K
=
→
→
nazywa się kanoniczną jeśli
i
Q i
i
P spełniają równania kanoniczne. Tzn. jeśli
i
q i
i
p spełniają
i
i
i
i
q
t
q
p
H
p
p
t
q
p
H
q
∂
∂
−
=
∂
∂
=
)
,
,
(
,
)
,
,
(
&
&
(1)
to
i
Q i
i
P maj
ą
spełnia
ć
i
i
i
i
Q
t
Q
P
H'
P
P
t
Q
P
H'
Q
∂
∂
−
=
∂
∂
=
)
,
,
(
,
)
,
,
(
&
&
(2)
gdzie
H'
jest now
ą
funkcja Hamiltona
(
)
t
p
Q
q
p
Q
p
H
t
Q
P
H'
),
,
(
),
,
(
)
,
,
(
≡
.
Warunki, które musi spełnia
ć
transformacja,
ż
eby była kanoniczn
ą
mo
ż
na otrzyma
ć
z zasady wariacyjnej Hamiltona. Równania (1) bowiem wynikaj
ą
ze znikania wariacji
∫
∑
=
−
=
2
1
0
)
,
,
(
1
t
t
N
i
i
i
t
q
p
H
p
q
dt
&
δ
natomiast równania (2) z
∫
∑
=
−
=
2
1
0
)
,
,
(
'
1
t
t
N
i
i
i
t
Q
P
H
P
Q
dt
&
δ
.
Ponieważ
0
)
(
)
(
2
1
=
=
t
q
t
q
δ
δ
oraz
0
)
(
)
(
2
1
=
=
t
Q
t
Q
δ
δ
, więc do każdej funkcji podcałkowej
można dodać zupełną pochodną dowolnej funkcji współrzędnych i czasu, odpowiednio
dt
t
q
dg
)
,
(
lub
dt
t
Q
dG
)
,
(
, gdyż
[
]
∫
=
−
=
2
1
0
)
),
(
(
)
),
(
(
)
,
(
1
1
2
2
t
t
t
t
q
g
t
t
q
g
dt
t
q
dg
dt
δ
δ
.
A zatem różnicą funkcji podcałkowych może być
dt
t
Q
q
dF
)
,
,
(
, tzn.

2
Wykład XI cd. Mechanika
dt
t
Q
q
dF
t
Q
P
H'
P
Q
t
q
p
H
p
q
N
i
i
i
N
i
i
i
)
,
,
(
)
,
,
(
)
,
,
(
1
1
=
+
−
−
∑
∑
=
=
&
&
co daje
dt
t
F
dQ
Q
F
dq
q
F
t
Q
q
dF
dt
t
Q
P
H'
dQ
P
dt
t
q
p
H
dq
p
N
i
i
i
i
i
N
i
i
i
N
i
i
i
∂
∂
−
∂
∂
+
∂
∂
=
=
+
−
−
∑
∑
∑
=
=
=
1
1
1
)
,
,
(
)
,
,
(
)
,
,
(
Przy dowolnych q
δ
oraz Q
δ
dostajemy
t
t
Q
q
F
t
Q
P
H
t
q
p
H
Q
t
Q
q
F
P
q
t
Q
q
F
p
i
i
i
i
∂
∂
=
−
∂
∂
−
=
∂
∂
=
)
,
,
(
)
,
,
(
'
)
,
,
(
,
)
,
,
(
,
)
,
,
(
co prowadzi do związku
i
j
j
i
j
i
q
P
Q
q
t
Q
q
F
Q
p
∂
∂
−
=
∂
∂
∂
=
∂
∂
)
,
,
(
2
)
,
,
(
t
Q
q
F
nazywa się funkcja tworząca transformacji kanonicznej.
Definiujemy nową funkcję tworzącą
∑
+
≡
Φ
i
i
i
P
Q
t
P
q
Q
q
F
t
P
q
)
),
,
(
,
(
)
,
,
(
,
(
)
∑
+
+
=
Φ
i
i
i
i
i
dP
Q
dQ
P
dF
d
Jak poprzednio, żądamy
(
)
∑
∑
∑
+
−
Φ
=
=
+
−
−
=
=
i
i
i
i
i
N
i
i
i
N
i
i
i
dP
Q
dQ
P
t
P
q
d
dF
dt
t
Q
P
H'
dQ
P
dt
t
q
p
H
dq
p
)
,
,
(
)
,
,
(
)
,
,
(
1
1
Uwzględniając, że
dt
t
dP
P
dq
q
t
P
q
d
N
i
i
i
i
i
∂
Φ
∂
−
∂
Φ
∂
+
∂
Φ
∂
=
Φ
∑
=1
)
,
,
(
,
dostajemy
t
t
P
q
t
Q
P
H
t
q
p
H
P
t
P
q
Q
q
t
P
q
p
i
i
i
i
∂
Φ
∂
−
=
−
∂
Φ
∂
=
∂
Φ
∂
=
)
,
,
(
)
,
,
(
'
)
,
,
(
,
)
,
,
(
,
)
,
,
(
co daje
i
j
j
i
j
i
q
Q
P
q
t
P
q
P
p
∂
∂
=
∂
∂
Φ
∂
=
∂
∂
)
,
,
(
2
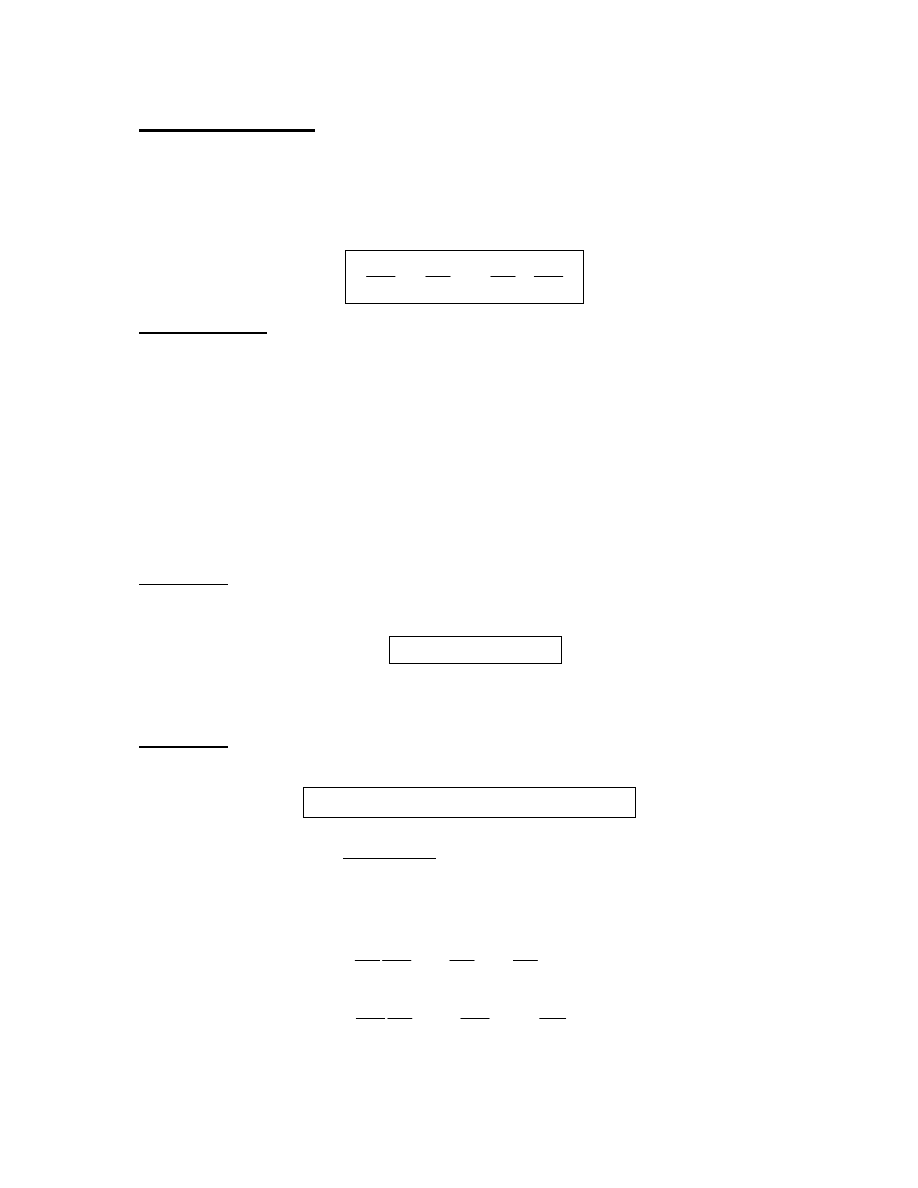
3
Wykład XI cd. Mechanika
Jeśli transformacja
n
i
p
p
p
q
q
q
P
p
p
p
p
q
q
q
Q
q
n
n
i
i
n
n
i
i
,
,
2
,
1
)
,
,
,
;
,
,
,
(
)
,
,
,
;
,
,
,
(
2
1
2
1
2
1
2
1
K
K
K
K
K
=
→
→
jest kanoniczna to
(3)
Nawiasy Poissona
Bezpośrednio z definicji nawiasów Poissona mamy
{
}
{
}
{
}
ij
pq
j
i
pq
j
i
pq
j
i
q
p
p
p
q
q
δ
=
=
=
,
,
,
0
,
{
}
pq
K
K,
- nawias Poissona obliczany przy użyciu współrzędnych i pędów p i q.
Równanie (3) zaś daje
{
}
{
}
{
}
ij
pq
j
i
pq
j
i
pq
j
i
Q
P
P
P
Q
Q
δ
=
=
=
,
,
,
0
,
co dowodzi się prostym przeliczeniem.
Twierdzenie
Nawias Poissona dwóch dowolnych wielkości f i g jest niezmiennikiem transformacji
kanonicznej tzn.
Dowodzi się dosyć żmudnym przeliczeniem.
Twierdzenie
Zachodzenie związków
jest warunkiem koniecznym i dostatecznym, że transformacja
)
,
,
(
)
,
,
(
H'
P
Q
H
p
q
→
jest
kanoniczna.
Konieczność została wykazana powyżej. Dostateczność łatwo wykazać dla transformacji
niezależnych od czasu. Wtedy
{
}
{
}
i
j
ij
j
j
j
i
j
PQ
i
pq
i
i
P
H
P
H
Q
Q
P
H
Q
H
Q
H
Q
∂
∂
=
∂
∂
=
∂
∂
∂
∂
=
=
=
∑
∑
δ
,
,
&
{
}
{
}
i
j
ij
j
j
j
i
j
PQ
i
pq
i
i
Q
H
Q
H
P
P
Q
H
P
H
P
H
P
∂
∂
−
=
∂
∂
−
=
∂
∂
∂
∂
−
=
=
=
∑
∑
δ
,
,
&
Ogólny dowód pomijam.
i
j
j
i
i
j
j
i
q
Q
P
p
q
P
Q
p
∂
∂
=
∂
∂
∂
∂
−
=
∂
∂
,
{
}
{
}
PQ
pq
g
f
g
f
,
,
=
{
}
{
}
{
}
ij
pq
j
i
pq
j
i
pq
j
i
Q
P
P
P
Q
Q
δ
=
=
=
,
,
,
0
,
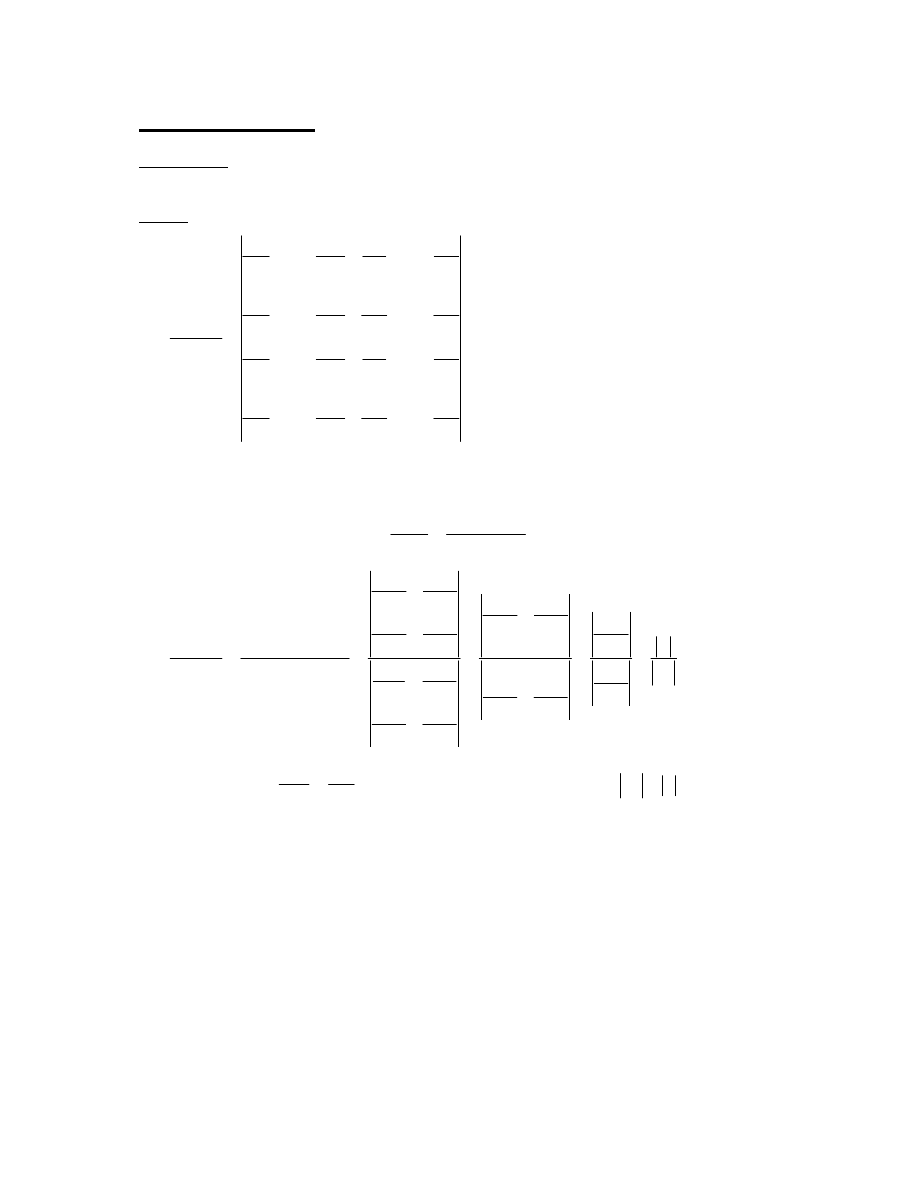
4
Wykład XI cd. Mechanika
Twierdzenie
Jakobian transformacji kanonicznej jest równy jedności.
Dowód
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
p
P
p
P
p
Q
p
Q
p
P
p
P
p
Q
p
Q
q
P
q
P
q
Q
q
Q
q
P
q
P
q
Q
q
Q
p
q
P
Q
J
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
≡
L
L
M
M
M
M
M
M
L
L
L
L
M
M
M
M
M
M
L
L
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
)
,
(
)
,
(
Korzystamy z własności jakobianów dotyczącej złożenia transformacji
)
(
)
(
)
(
Z
Y
X
→
→
:
)
(
/
)
(
)
(
/
)
(
)
(
)
(
Z
Y
Z
X
Y
X
∂
∂
∂
∂
=
∂
∂
1
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
0
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
,
(
/
)
,
(
)
,
(
/
)
,
(
)
,
(
)
,
(
=
=
∂
∂
∂
∂
=
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
∂
∂
=
∂
∂
≡
T
A
A
P
p
q
Q
P
p
P
q
q
P
q
Q
P
p
P
q
q
p
q
q
P
P
P
Q
q
P
q
Q
P
q
p
q
P
q
P
Q
p
q
P
Q
J
1
1
gdzie macierz
j
i
i
j
ij
P
p
q
Q
A
∂
∂
=
∂
∂
≡
,
T
A oznacza macierz transponowaną
(
)
A
A
T
=
.
Wyszukiwarka
Podobne podstrony:
Mechanika-XI
WYKŁAD Mechanika Ogólna Część Xi XI
mechanika czesc XI
Mechanika techniczna(12)
Mechanika Semest I pytania egz
wykl 8 Mechanizmy
mechanizm mycia i prania
MECHANIKA II DYN
METODY KOMPUTEROWE W MECHANICE 2
08 BIOCHEMIA mechanizmy adaptac mikroor ANG 2id 7389 ppt
Mechanizm obrzęków
Mechanizmy swoistej immunoterapii alergii 3
Wykład XI Metody opisu układów cyfrowych
więcej podobnych podstron