1

ANALIZA PRZEŻYCIA

- (wikipedia) zbiór metod statystycznych badających procesy, w których interesujący jest

czas, jaki upłynie do (pierwszego) wystąpienia pewnego zdarzenia. Główną interesującą nas
zmienną będzie liczba dni, którą przeżyją pacjenci.

- (z ,,wykładu”) służy do oceny szansy przeżycia dla pacjentów po trudnych operacjach. W I

okresie zaczynamy badać parametry co jakiś czas, przez pewien okres czasu. Może nastąpić wtedy
zdarzenie, lub nie.

Za zdarzenia uznajemy:



śmierć pacjenta (stąd nazwa metody)



awaria urządzenia



zaprzestanie płacenia rachunków przez klienta



odejście pracownika z firmy

W zbiorze danych do analizy przeżycia wyróżnia się tzw. obserwacje ucięte albo cenzorowane, o
których wiadomo, że proces stochastyczny trwał dalej, jednak o jego dalszym czasie nie ma dalszych
danych (np. pacjenci wypisani ze szpitala). W naszym przypadku także tacy, którzy przeżyli dany
okres, czyli nie wystąpiło w ich przypadku zdarzenie. Terminu censoring (ucinanie) użył po raz
pierwszy Hald, 1949.

Czas przeżycia T – stan między stanem wyjścia a wystąpieniem zdarzenia.

Funkcja przeżycia:

S(t) = P (T >t)

Funkcja hazardu -chwilowy potencjał wystąpienia zdarzenia, o ile pacjent dożyje czasu t:

2

Dokładność zależy od wybranego modeli (wykładniczy < Gompertza < Weilbulla)

Do estymacji:

Rokład wykładniczy:

f(x) = λe

λx

λ- wpółczynnik, λ>0, x ϵ (0, +∞)

Typowe metody analizy przeżycia obejmują:



tworzenie tablic trwania życia



estymację funkcji przeżycia (np. estymator Kaplana-Meiera, prawo umieralności Weibulla)



modele regresyjne (np. model proporcjonalnego hazardu Coksa)

Tablica trwania życia - Technika oparta na tablicach trwania życia jest jedną z najstarszych

metod analizy danych dotyczących przeżycia (czasu bezawaryjności); np. patrz Berkson i Gage,
1950; Cutler i Ederer, 1958; Gehan, 1969. Tablicę taką można traktować jako rozbudowaną tablicę
rozkładu liczności. Rozkład czasów przeżycia dzieli się na pewną liczbę przedziałów. Dla każdego
przedziału możemy obliczyć liczbę i proporcję przypadków lub obiektów, które weszły do danego
przedziału "żywe", liczbę i proporcję przypadków, które uległy awarii w danym przedziale (tzn.
liczbę ostatecznych zdarzeń lub liczbę przypadków, które "wymarły") oraz liczbę przypadków
utraconych lub uciętych w danym przedziale.

Liczba przypadków zagrożonych. Jest to liczba przypadków, które weszły do danego przedziału

żywe minus połowa liczby przypadków utraconych lub

uciętych

w danym przedziale.

Proporcja przypadków ulegających awarii. Proporcję tę oblicza się jako stosunek liczby

przypadków wymierających w danym przedziale do liczby przypadków zagrożonych w tym
przedziale.

Proporcja przypadków przeżywających. Proporcję tę oblicza się jako 1 minus proporcja

przypadków wymierających.

Skumulowana proporcja przeżywających (Funkcja przeżycia). Jest to skumulowana proporcja

przypadków przeżywających aż do danego przedziału. Ponieważ zakłada się, że
prawdopodobieństwa przeżycia są niezależne w kolejnych przedziałach, prawdopodobieństwo to
oblicza się przez wymnożenie prawdopodobieństw przeżycia ze wszystkich poprzednich
przedziałów. Wynikową funkcję nazywa się także przeżyciem lub funkcją przeżycia.

Gęstość prawdopodobieństwa. Jest to oszacowane prawdopodobieństwo defektu w danym

przedziale obliczone w jednostce czasu, to jest:

F

i

= (P

i

-P

i+1

) /h

i

W powyższym wzorze,

F

i

oznacza odpowiednią gęstość prawdopodobieństwa w i-tym przedziale,

P

i

to oszacowana skumulowana proporcja przeżywających na początku i-tego przedziału (na końcu

3

przedziału i-1 ),

P

i+1

to skumulowana proporcja przeżywających przy końcu przedziału i, a

h

i

to

szerokość danego przedziału.

Stopa hazardu. Stopę hazardu (terminu użył po raz pierwszy Barlow, w roku 1963) definiuje

się jako prawdopodobieństwo na jednostkę czasu, że przypadek, który przeżył do początku danego
przedziału ulegnie w tym przedziale awarii. W szczególności oblicza się ją jako liczbę przypadków
awarii w jednostkach czasu w danym przedziale, podzieloną przez przeciętną liczbę przypadków
przeżywających w środku przedziału.

Mediana czasu przeżycia. Jest to czas przeżycia, w którym skumulowana funkcja przeżycia

jest równa 0.5. Odpowiednio można policzyć inne percentyle (percentyl 25 i 75) skumulowanej
funkcji przeżycia. Zauważmy, że 50 percentyl (mediana) skumulowanej funkcji przeżycia zazwyczaj
nie jest tym samym punktem w czasie, do którego przeżyło 50% próby. (Byłoby tak tylko wtedy,
gdyby w czasie poprzedzającym nie było żadnych obserwacji uciętych ).

Wymagane wielkości prób. Aby otrzymać rzetelne oszacowania trzech głównych funkcji

(przeżycia, gęstości prawdopodobieństwa i hazardu) oraz ich błędy standardowe, w każdym
przedziale czasowym minimalna zalecana wielkość próby powinna wynosić 30.

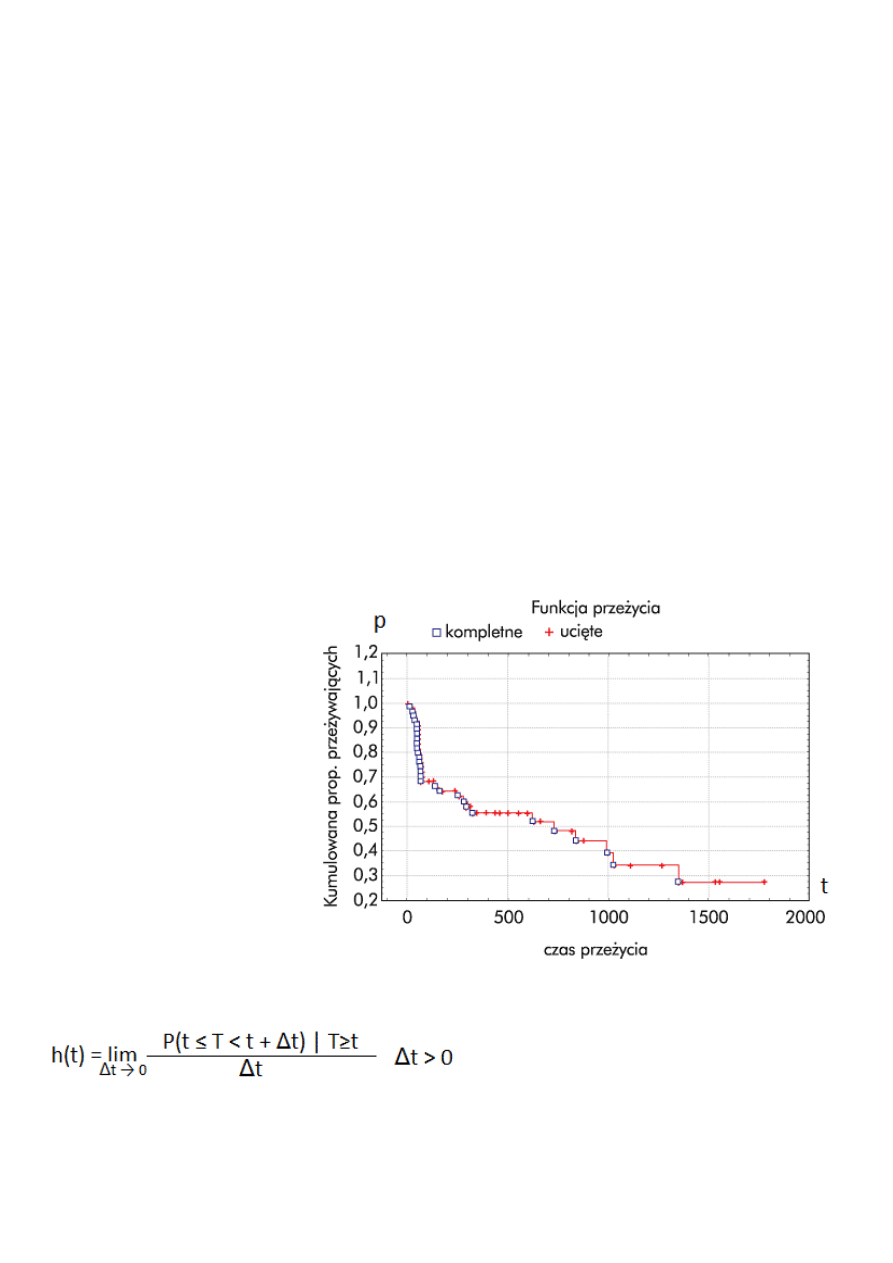
Estymator Kaplana-Meiera – używany w statystycznej analizie przeżycia estymator

prognozujący funkcję przeżycia. W badaniach medycznych może być użyty np. do przewidywania
frakcji pacjentów, którzy przeżyją określony czas po operacji. Ekonomista może szacować czas jaki
ludzie pozostają bezrobotni po utracie pracy. Inżynier może mierzyć czas do awarii urządzenia.

Wykres estymaty Kaplana-Meiera funkcji przeżycia składa się z szeregu poziomych odcinków,

schodzących coraz niżej (funkcja schodkowa). Coraz większa próba statystyczna powoduje
powstanie coraz większej liczby coraz krótszych odcinków, w granicy dążąc do prawdziwej funkcji
przeżycia.

Ważną zaletą estymatora Kaplana-Meiera jest branie pod uwagę obserwacji cenzorowanych

– braków danych od pewnego momentu czasu, różnego dla każdego obserwowanego obiektu (np.
w przypadku odejścia pacjenta ze szpitala, utraty kontaktu z badanym, itp.).

W statystyce medycznej typowe zastosowanie może obejmować podział pacjentów na grupy

różniące się tylko jedną cechą, np. występowaniem określonego genu, albo podawaniem innego
leku. Na wykresie pacjenci z grupy B umierają znacznie szybciej niż z grupy A. Po dwóch latach 80%
pacjentów z grupy A ciągle żyje, a z grupy B mniej niż połowa.

Wartość charakterystyczna przeżycia – w statystycznej analizie przeżycia czas do momentu

w którym

populacji zginęło (uległo awarii). Wielkość ta jest równa parametrowi skali

w dopasowanym do danych rozkładzie Weibulla.

ANALIZA DYSKRYMINACYJNA

- (wikipedia) zespół metod wielowymiarowej analizy danych. Zalicza się do grupy prognoz

ilościowych. Zawiera metody, które czynią z tej techniki niezwykle efektywne narzędzie do
zagadnień klasyfikacyjnych i technik eksploracja danych. Jej zadaniem jest rozstrzyganie, które
zmienne w najlepszy sposób dzielą dany zbiór przypadków na występujące w naturalny sposób
grupy. Pozwala rozstrzygnąć, czy grupy różnią się ze względu na średnią pewnej zmiennej, oraz
wykorzystanie tej zmiennej do przewidywania przynależności do danej grupy.

- (z ,,wykładu”) podział dużego zbioru danych na grupy wg jakiejś cechy (czynnika

dyskryminacyjnego), pozwala wyróżnić tą cechę, jaką powodującą różnice między tymi grupami

4

Założenia:

1) Wielowymiarowa normalność (dane wylosowane z populacji musza reprezentować próbę z

wielowymiarowego rozkładu normalnego).

2) Macierze wariancji i kowariancji muszą być jednorodne
3) Średnie zmiennych w grupach nie mogą (nie powinny) być skorelowane z wariancjami
4) Minimalna liczebność najmniejszej grupy wynosi p-2 (p – liczba zmiennych

dyskryminacyjnych)

5) Wartości odstające należy zidentyfikować i usunąć

Funkcja dyskryminacyjna

D

jk

= β

0

+ β

1

x

1jk

+ … + β

p

x

ijk

ANALIZA SKUPIEŃ

- (wikipedia

) pojęcie z zakresu eksploracji danych oraz uczenia maszynowego, wywodzące się

z szerszego pojęcia, jakim jest klasyfikacja bezwzorcowa.

p – liczba zmiennych dyskryminacyjnych
g – liczba grup
n – liczebność grupy
β – współczynniki kanonicznej funkcji dyskryminacyjnej
D

jk

– wartości kanonicznej funkcji dyskryminacyjnej dla

k-tego przypadku w j-tej grupie
x

ijk

– i-ta zmienna dyskryminacyjna kanonicznej funkcji

dyskryminacyjnej dla k-tego przypadku w j-tej grupie

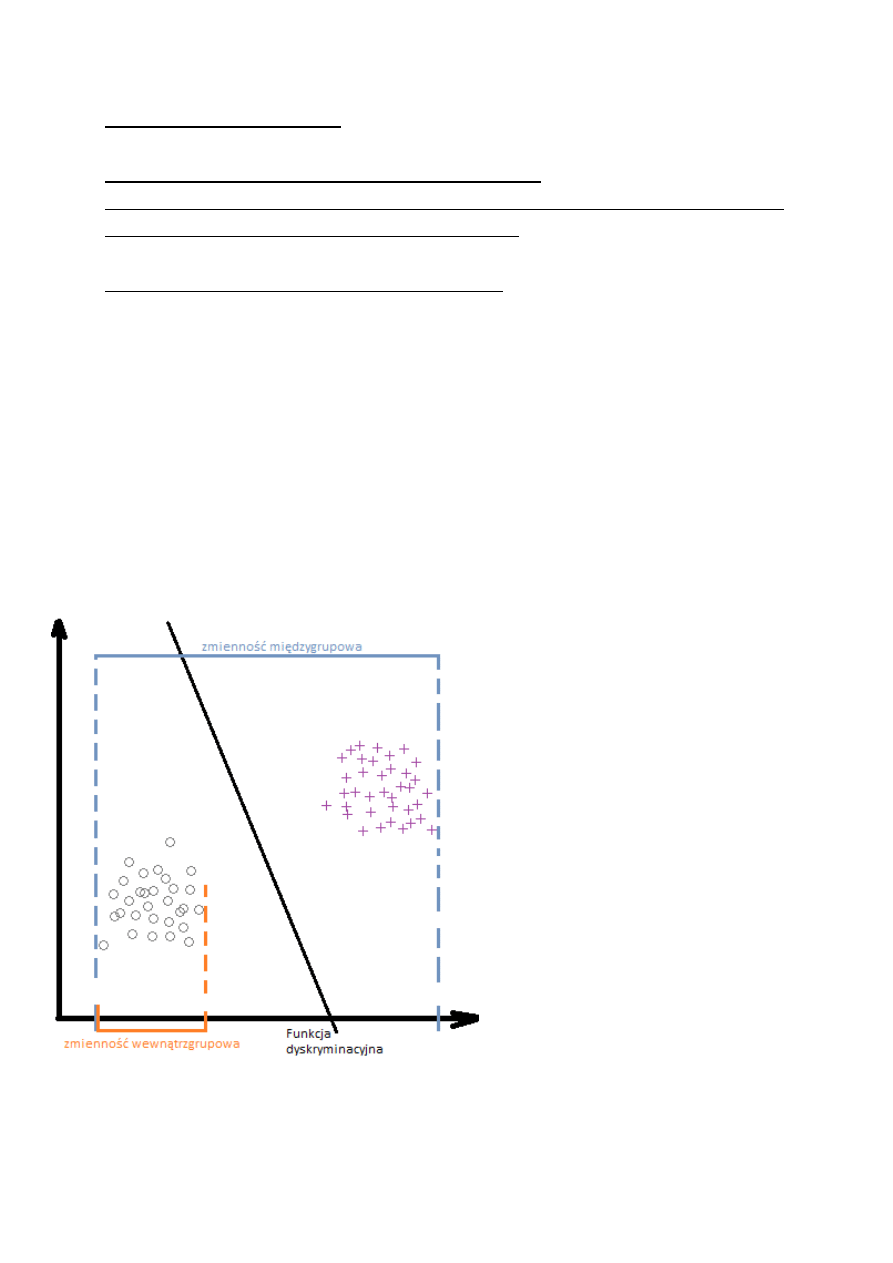
Średnia dla obiektu z 1 grupy

musi być bardziej zbliżona do
wartości swojej grupy niż grupy 2.

Ceintroidy – punkty, wokół

których koncentrują się wartości
grup.

k ϵ <1,n>
j ϵ <1,g>
i ϵ <1,p>

5

Analiza skupień jest metodą tzw. klasyfikacji bez nadzoru. Jest to metoda dokonująca

grupowania elementów we względnie jednorodne klasy. Podstawą grupowania w większości
algorytmów jest podobieństwo pomiędzy elementami – wyrażone przy pomocy funkcji (metryki)
podobieństwa.

Poprzez grupowanie można również rozwiązać problemy z gatunku odkrywania struktury w

danych oraz dokonywanie uogólniania. Grupowanie polega na wyodrębnianiu grup (klas,
podzbiorów).

Wybrane cele dokonywania grupowania są następujące:



uzyskanie jednorodnych przedmiotów badania, ułatwiających wyodrębnienie ich
zasadniczych cech,



zredukowanie dużej liczby danych pierwotnych do kilku podstawowych kategorii, które
mogą być traktowane jako przedmioty dalszej analizy,



zmniejszenie nakładu pracy i czasu analiz, których przedmiotem będzie uzyskanie klasyfikacji
obiektów typowych,



odkrycie nieznanej struktury analizowanych danych,



porównywanie obiektów wielocechowych.

- (z ,,wykładu”) podział na grupy, dokonanie redukcji dużego zbioru danych na skupienia

- (podręcznik statsoftu) Pojęcie analizy skupień (termin wprowadzony w pracy Tryon, 1939)
obejmuje faktycznie kilka różnych algorytmów klasyfikacji. Ogólny problem badaczy wielu
dyscyplin polega na organizowaniu obserwowanych danych w sensowne struktury lub
grupowaniu danych. Innymi słowy, analiza skupień jest narzędziem do eksploaracyjnej analizy
danych, której celem jest ułożenie obiektów w grupy w taki sposób, aby stopień powiązania
obiektów z obiektami należącymi do tej samej grupy był jak największy, a z obiektami z
pozostałych grup jak najmniejszy. Analiza skupień może być wykorzystywana do wykrywania
struktur w danych bez wyprowadzania interpretacji/wyjaśnienia. Mówiąc krótko: analiza
skupień jedynie wykrywa struktury w danych bez wyjaśniania dlaczego one występują.

Populacja generalna Ω: n obiektów ϵ (

O

1

, …, O

n

)

Podzbiory: k zbiorów ϵ (

S

1

, …, S

k

)

Obiekty podobne mają być w tym samym skupieniu.

a) S

i

ᴖ S

j

= ∅

b) S

i

ᴗ S

j =

Ω

Odległość d(

O

i

, O

j

)

– miara niepodobieństwa obiektów

Macierz odległości d:

|0 … … d

n1

|

D=|d

21

0 … d

n2

|

|… … … … |
|d

n1

d

n2

… 0 |

i, j ϵ <1,k>

6

Metoda analizy skupień hierarchicznych (aglomeracyjne (każdy w osobnych skupieniu) i
podziałowe(jedno skupienie))

Gdy znamy problem i znamy liczbę skupień – metoda k średnich 1975

Analiza głównych składowych pca – redukcja wymiarowości (przekształcenie zmiennych
obserwowalnych w nowy zbiór nieskorelowanych zmiennych). 1936



zakładamy, że nie nastąpiła zmiana informacji



powstają zmienne nieobserwowalne

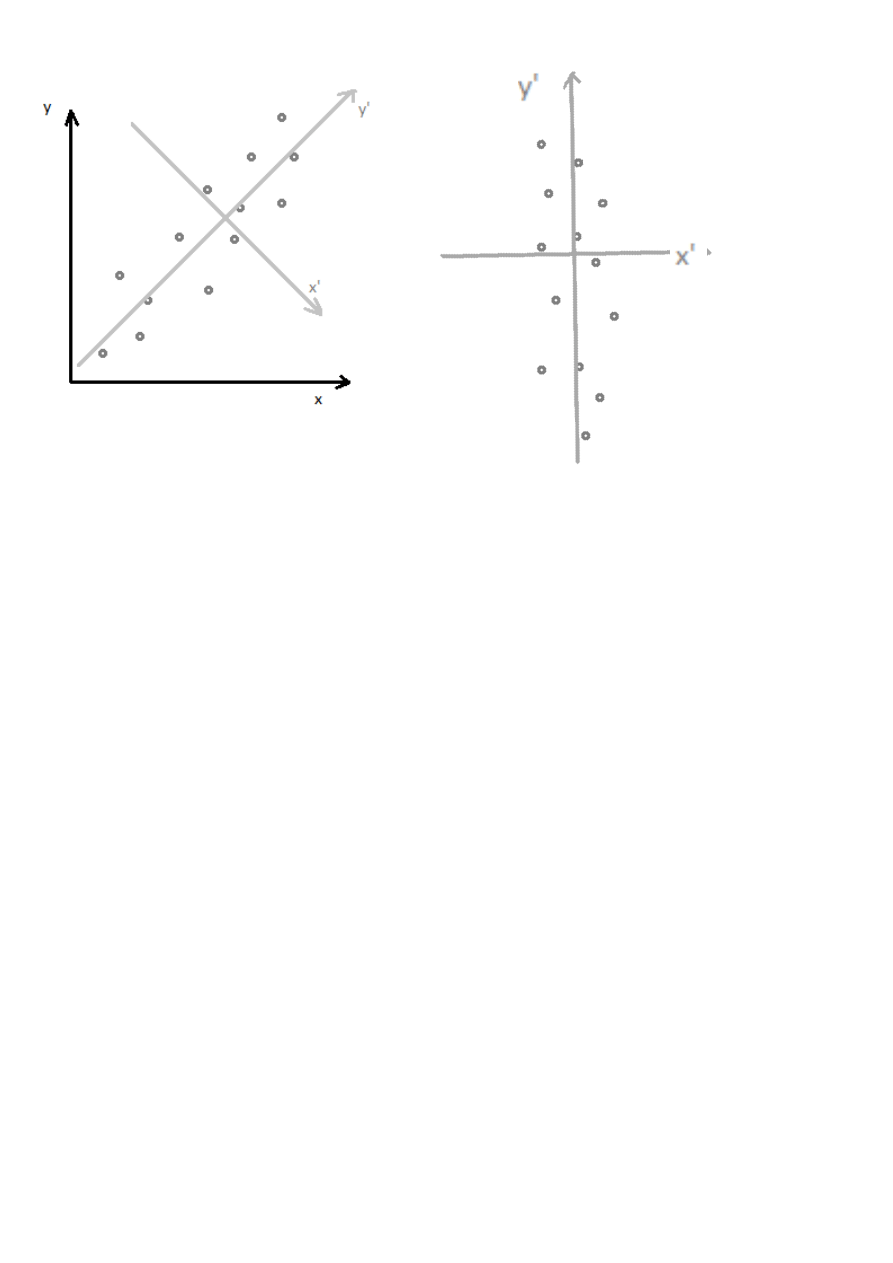
7

Uznajemy y za mało istotne, przekształcamy układ współrzędnych z XY na X’Y’
Y’=0 – zostają nam tylko wartości dla x’.
Dane:
p – zespół zmiennych początkowych (obserwowalne)
Z

1

– pierwsza składowa główna (nieobserwowalne)

Z

1

= a

11

x

1

+ a

12

x

2

+ … + a

1p

xp

a – współczynniki szukane, dobrane tak, by wariancja Z

1

była jak największa. (

a

11

…

a

1p

)

∑ a

1i

= 1

(S – λI) a

1

= 0

<- p równań w formie macierzy

S – macierz kowariancji dla zmiennych

x

1

… x

p

I

– macierz jednostkowa

a

1

–

wektor zawierający współrzędne (

a

11

…

a

1p

)

λ –

wartości własne macierzy S

I

a

1

= 0

(S – λI)=

0 -> wyliczenie wyznacznika -> wyliczenie λ

Mając wynik (

a

11

…

a

1p

)

należy ,,zrobić jak najmniej zmiennych”.

8

Metoda EM

Kryteria analizy wartości:

1) Procent wariancji wyjaśnianej przez daną zmienną – odrzucamy np. te wyjaśniające poniżej

5% lub 2%

2) Kryterium Kaisera – zakłada, że skoro standaryzowane zmienne mają wariancję równą 1, to

nowe zmienne też powinny mieć wariancję równą 1. 1960

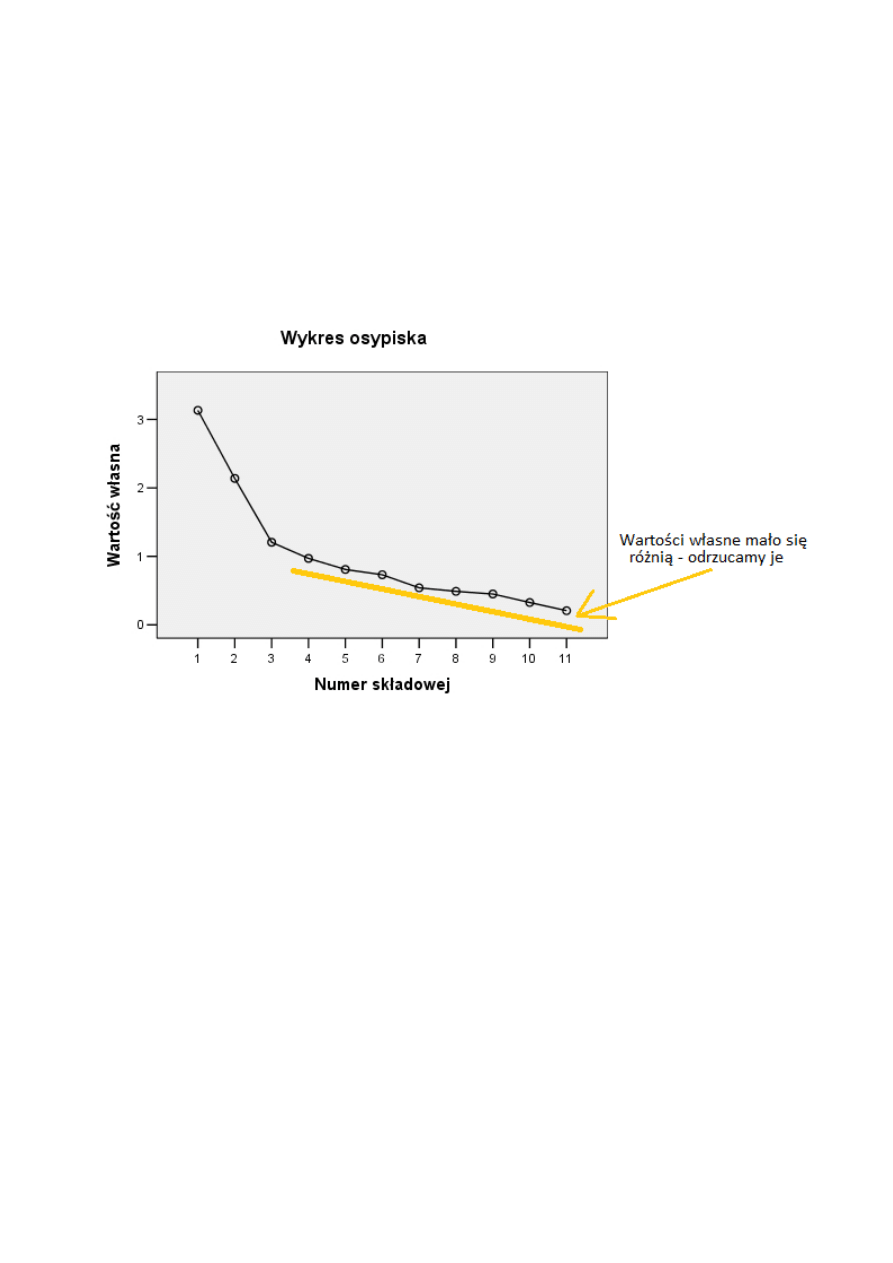
3) Oparty na kryterium Kaisera wykres osypiska (liniowy wykres kolejnych wartości własnych)