1
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
In
fo
rm
ac
je
o
g
ó
ln
e
K
A
T
E
D
R
A
T
E
O
R
I
I
K
O
N
S
T
R
U
K
C
J
I
B
U
D
O
W
L
A
N
Y
C
H
h
tt
p
:/
/k
a
te
k
o
.r
b
.p
o
ls
l.p
l/
~
sd
m
b
3
h
tt
p
:/
/k
a
te
k
o
.r
b
.p
o
ls
l.p
l/
~
b
w
ie
/s
tu
d
e
n
ci
P
ro
w
a
d
z
ą
c
y
:
d
r i
n
ż
. B
a
rb
a
ra
W
IE
C
Z
O
R
E
K
2
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
W
y
m
ia
ro
w
an
ie
k
o
n
st
ru
k
cj
i
W
a
ru
n
k
i b
e
z
p
ie
c
z
n
e
j p
ra
c
y
k
o
n
s
tr
u
k
c
ji:
-
w
a
ru
n
e
k
w
y
tr
z
y
m
a
ło
ś
c
i
-
w
a
ru
n
e
k
s
z
ty
w
n
o
ś
c
i
-
w
a
ru
n
e
k
s
ta
te
c
z
n
o
ś
c
i
w
a
ru
n
e
k
w
y
trz
y
m
a
ło
ś
c
i
–
z
a
ło
ż
o
n
e
o
d
d
z
ia
ły
w
a
n
ia
n
a
k
o
n
s
tr
u
k
c
j
ę
n
ie
p
o
w
o
d
u
j
ą
je
j z
n
is
z
c
z
e
n
ia
P
3
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
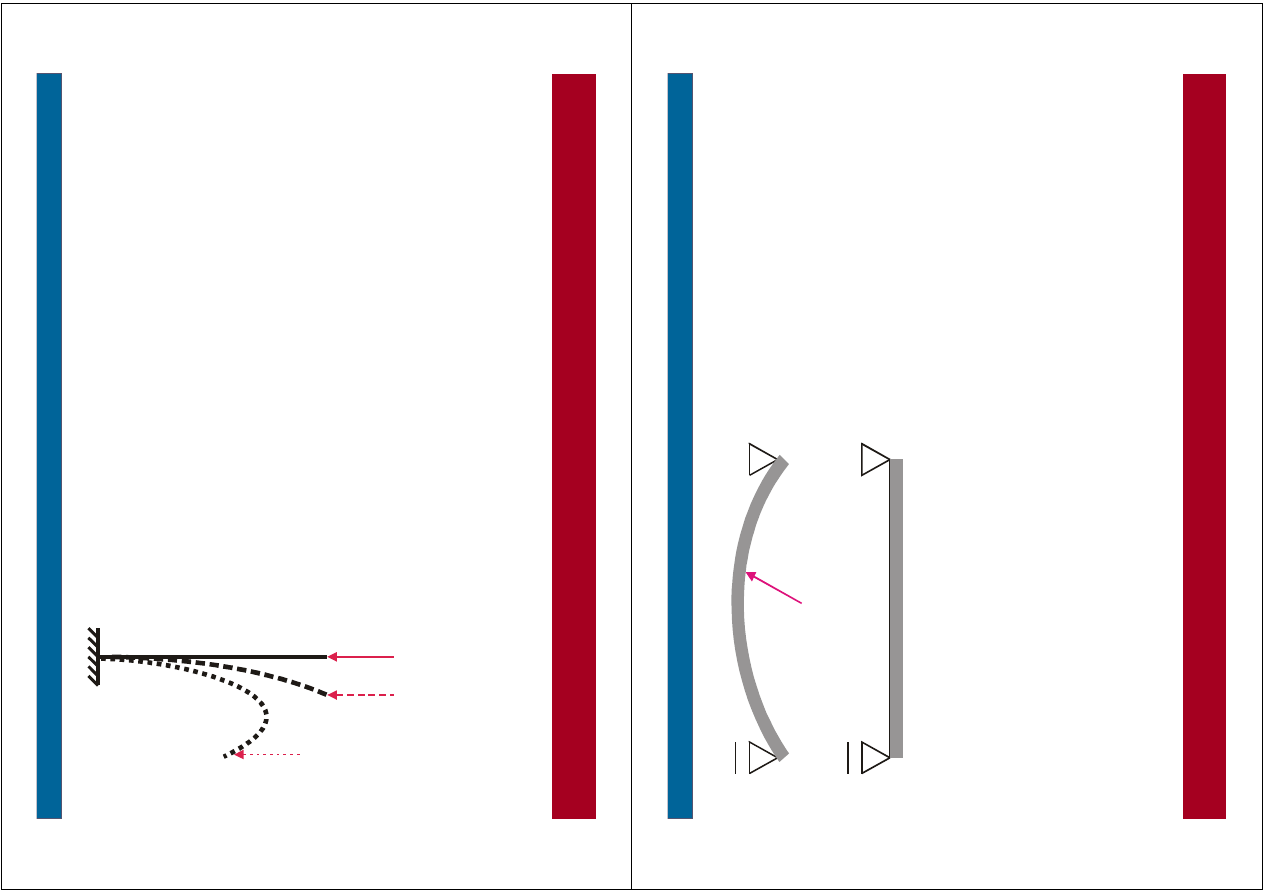
W
y
m
ia
ro
w
an
ie
k
o
n
st
ru
k
cj
i
w
a
ru
n
e
k
s
z
ty
w
n
o
ś
c
i
–
p
o
d
w
p
ły
w
e
m
o
d
d
z
ia
ły
w
a
ń
d
e
fo
rm
a
c
je
w
k
o
n
s
tr
u
k
c
ji
n
ie
p
rz
e
k
ra
c
z
a
j
ą
w
a
rto
ś
c
i
d
o
p
u
s
z
c
z
a
ln
y
c
h
P
W
a
ru
n
k
i b
e
z
p
ie
c
z
n
e
j p
ra
c
y
k
o
n
s
tr
u
k
c
ji:
-
w
a
ru
n
e
k
w
y
tr
z
y
m
a
ło
ś
c
i
-
w
a
ru
n
e
k
s
z
ty
w
n
o
ś
c
i
-
w
a
ru
n
e
k
s
ta
te
c
z
n
o
ś
c
i
4
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
W
y
m
ia
ro
w
an
ie
k
o
n
st
ru
k
cj
i
w
a
ru
n
e
k
s
ta
te
c
z
n
o
ś
c
i
–
m
a
łe
z
m
ia
n
y
o
d
d
z
ia
ły
w
a
ń
n
ie
m
o
g
ą
p
o
w
o
d
o
w
a
ć
d
u
ż
y
c
h
z
m
ia
n
k
o
n
s
tr
u
k
c
ji
W
a
ru
n
k
i b
e
z
p
ie
c
z
n
e
j p
ra
c
y
k
o
n
s
tr
u
k
c
ji:
-
w
a
ru
n
e
k
w
y
tr
z
y
m
a
ło
ś
c
i
-
w
a
ru
n
e
k
s
z
ty
w
n
o
ś
c
i
-
w
a
ru
n
e
k
s
ta
te
c
z
n
o
ś
c
i
5
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
S
ta
n
g
ra
n
ic
zn
y
n
o
ś
n
o
ś
ci
-
w
p
ro
w
ad
ze
n
ie
w
a
ru
n
ek
w
y
tr
zy
m
a
ło
śc
i
n
R
d
o
p
=
≤
σ
σ
R
–
g
ra
n
ic
a
p
la
s
ty
c
z
n
o
ś
c
i l
u
b
w
y
tr
z
y
m
a
ło
ś
c
i
n
–
w
s
p
ó
łc
z
y
n
n
ik
b
e
z
p
ie
c
z
e
ń
s
tw
a
M
E
T
O
D
A
N
A
P
R
Ę
ś
E
Ń
N
I
E
P
R
Z
E
K
R
A
C
Z
A
L
N
Y
C
H
n
P
P
n
≤
P
–
o
b
c
i
ą
ż
e
n
ie
o
b
lic
z
e
n
io
w
e
P
n
–
n
o
ś
n
o
ś
ć
k
o
n
s
tr
u
k
c
ji
n
–
w
s
p
ó
łc
z
y
n
n
ik
b
e
z
p
ie
c
z
e
ń
s
tw
a
M
E
T
O
D
A
N
O
Ś
N
O
Ś
C
I
G
R
A
N
I
C
Z
N
E
J
n
o
ś
n
o
ś
ć
k
o
n
s
tru
k
c
ji
-
w
a
rto
ś
ć
o
b
c
i
ą
ż
e
n
ia
, p
rz
y
k
tó
re
j n
a
s
t
ę
p
u
je
z
n
is
z
c
z
e
n
ie
k
o
n
s
tr
u
k
c
ji
lu
b
je
j c
z
ę
ś
c
i
lu
b
o
d
k
s
z
ta
łc
e
n
ia
m
o
g
ą
w
z
ra
s
ta
ć
b
e
z
p
rz
y
ro
s
tu
o
b
c
i
ą
ż
e
n
ia
6
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
S
ta
n
g
ra
n
ic
zn
y
n
o
ś
n
o
ś
ci
-
w
p
ro
w
ad
ze
n
ie
M
et
o
d
y
p
ro
je
k
to
w
a
n
ia
k
o
n
st
ru
k
cj
i:
•
st
a
n
g
ra
n
ic
zn
y
n
o
śn
o
śc
i (
w
a
ru
n
ek
S
GN
)
•
st
a
n
u
g
ra
n
ic
zn
y
u
ż
y
tk
o
w
a
n
ia
(
w
a
ru
n
ek
S
GU
)
•
st
a
n
g
ra
n
ic
zn
y
p
o
w
st
a
w
a
n
ia
lu
b
r
o
zw
a
rc
ia
r
y
s
7
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
W
y
k
re
s z
al
e
ż
n
o
ś
ci
σ −
ε
rz
ec
zy
w
is
ty
w
y
k
re
s
m
o
d
el
s
p
rę
ż
y
st
o
-p
la
st
y
cz
n
y
m
o
d
el
s
zt
y
w
n
o
-p
la
st
y
cz
n
y
8
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t o
si
o
w
o
r
o
zc
ią
g
an
y
lu
b
ś
ci
sk
an
y
F
N
d
o
p
d
o
p
=
σ
M
E
T
O
D
A
N
A
P
R
Ę
ś
E
Ń
N
I
E
P
R
Z
E
K
R
A
C
Z
A
L
N
Y
C
H
M
E
T
O
D
A
N
O
Ś
N
O
Ś
C
I
G
R
A
N
I
C
Z
N
E
J
n
R
F
F
N
p
l
d
o
p
d
o
p
n
p
l
R
d
o
p
⋅
=
⋅
=
⇒
=
σ
σ
F
N
n
n
=
σ
p
l
R
n
n
R
F
F
N
p
l
n
⋅
=
⋅
=
⇒
=
σ
σ
n
N
N
n
d
o
p
=
d
o
p
p
l
F
n
R
F
n
p
l
R
d
o
p
σ
σ
⋅
=
⋅
=
=
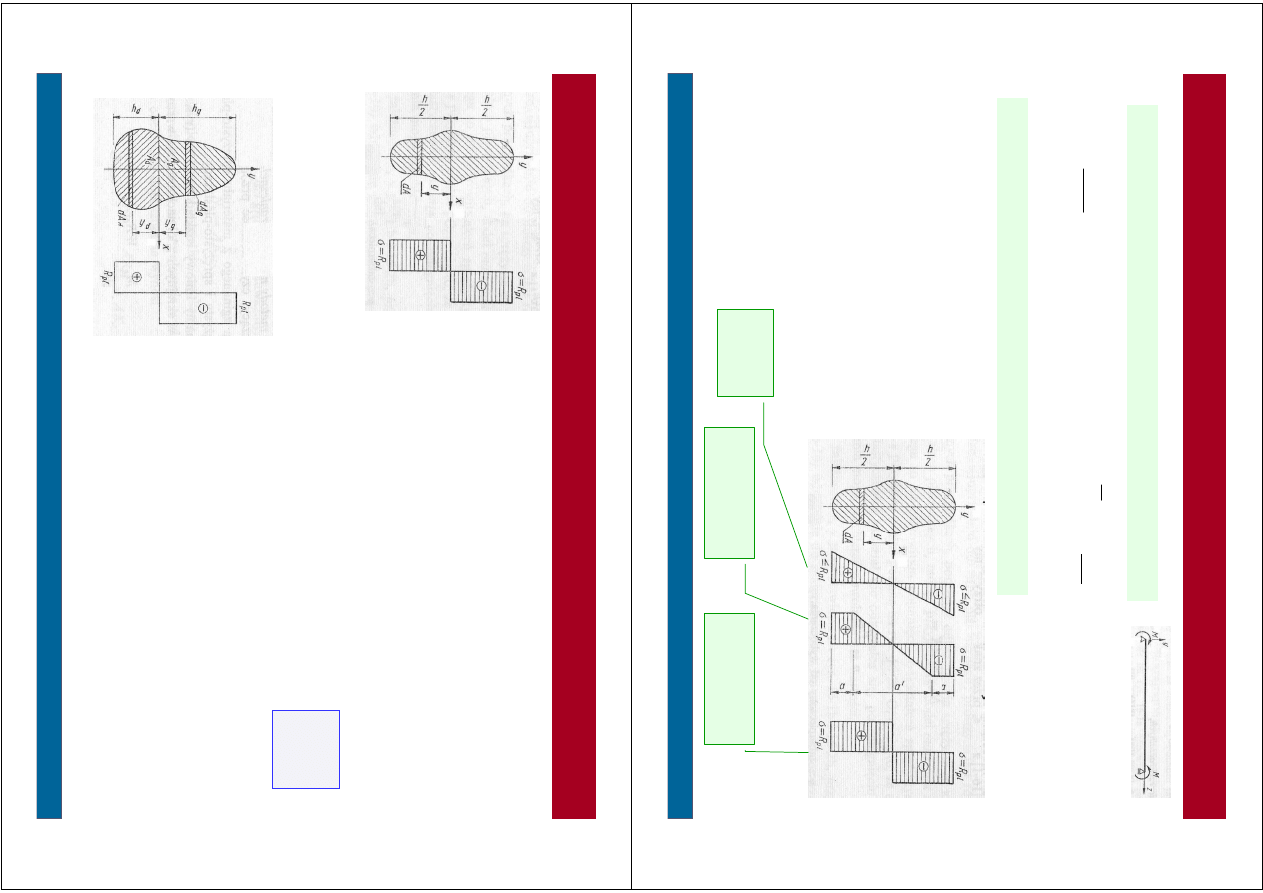
W
y
m
ia
ro
w
a
n
ie
p
r
ę
ta
r
o
z
c
i
ą
g
a
n
e
g
o
(
lu
b
ś
c
is
k
a
n
e
g
o
)
d
a
je
w
e
d
łu
g
o
b
u
m
e
to
d
te
s
a
m
e
w
y
n
ik
i.
d
o
p
d
o
p
N
N
=
9
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t z
g
in
an
y
W
M
d
o
p
d
o
p
=
σ
M
E
T
O
D
A
N
A
P
R
Ę
ś
E
Ń
N
I
E
P
R
Z
E
K
R
A
C
Z
A
L
N
Y
C
H
M
E
T
O
D
A
N
O
Ś
N
O
Ś
C
I
G
R
A
N
I
C
Z
N
E
J
n
R
W
W
M
p
l
d
o
p
d
o
p
n
p
l
R
d
o
p
⋅
=
⋅
=
⇒
=
σ
σ
p
l
s
R
W
M
⋅
=
∫
=
⋅
=
2
h
0
y
n
d
A
y
2
M
/
σ
o
k
re
s
sp
rę
ż
y
sty
cz
ę
ś
cio
w
e
u
p
la
sty
cz
n
ie
n
ie
ca
łk
o
w
it
e
u
p
la
sty
cz
n
ie
n
ie
∫
=
⋅
=
2
h
0
y
p
l
d
A
y
2
R
/
p
l
p
l
S
2
:
W
d
y
p
l
W
R
S
2
R
d
y
p
l
⋅
=
⋅
⋅
=
=
W
p
l
–
p
la
s
ty
c
z
n
y
w
s
k
a
ź
n
ik
W
–
s
p
r
ę
ż
y
s
ty
w
s
k
a
ź
n
ik
1
0
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
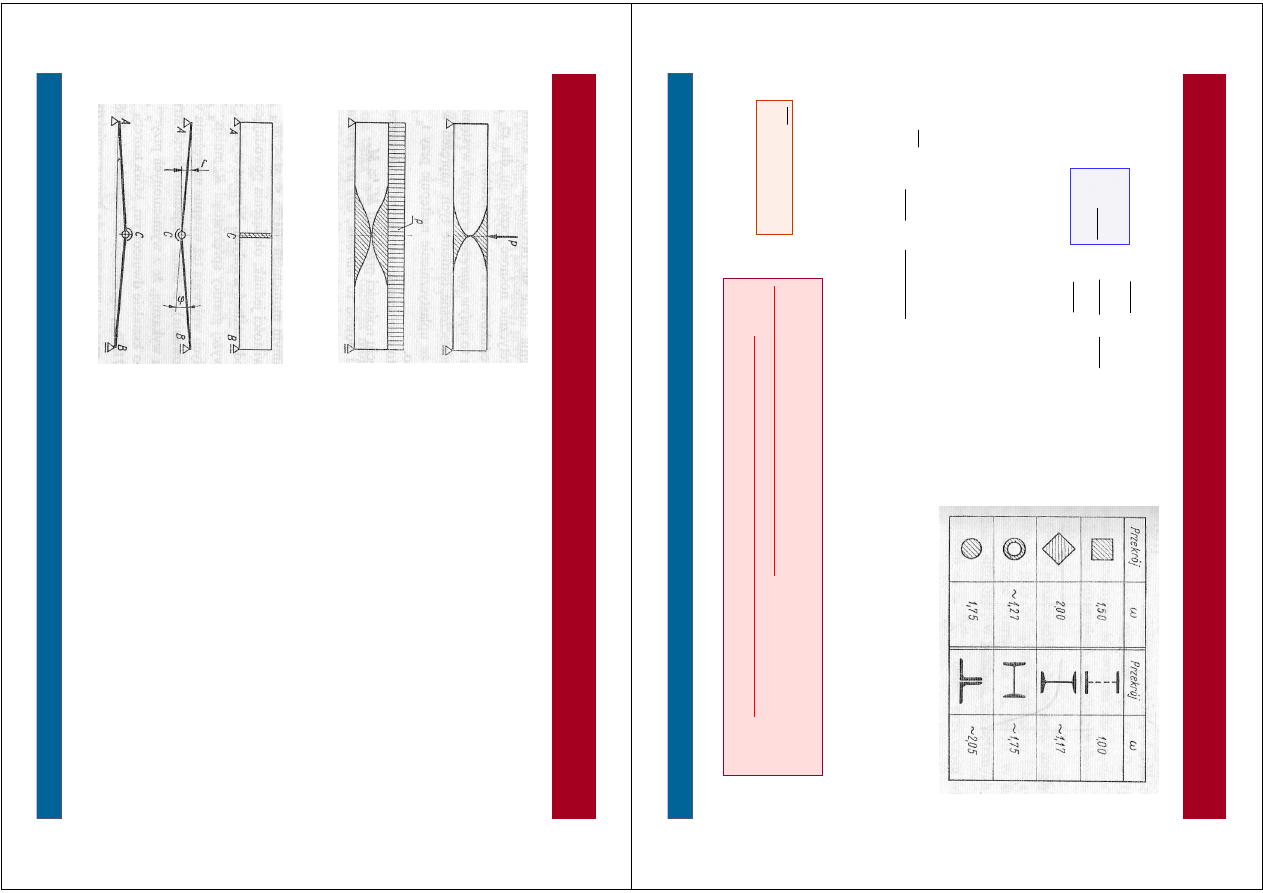
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t z
g
in
an
y
=
⋅
=
⋅
=
∫
∫
=
=
2
h
0
y
p
l
2
h
0
y
n
d
A
y
2
R
d
A
y
2
M
/
/
σ
p
l
p
l
S
2
:
W
d
y
p
l
W
R
S
2
R
d
y
p
l
⋅
=
⋅
⋅
=
=
∫
∫
=
=
⋅
+
⋅
=
g
g
d
d
h
0
y
g
g
h
0
y
d
d
n
d
A
y
d
A
y
M
σ
σ
+
⋅
=
∫
∫
=
=
g
g
d
d
h
0
y
g
g
h
0
y
d
d
p
l
d
A
y
d
A
y
R
(
)
p
l
p
l
S
S
W
g
y
d
y
p
l
W
R
S
S
R
g
y
d
y
p
l
⋅
=
+
⋅
=
+
=
:
0
d
A
d
A
g
d
A
g
A
d
=
+
∫
∫
σ
σ
(
)
g
d
p
l
g
p
l
d
p
l
A
A
R
A
R
A
R
0
−
⋅
=
⋅
−
⋅
=
⇒
g
d
A
A
=
⇓
1
1
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t z
g
in
an
y
w
s
p
ó
łc
z
y
n
n
ik
W
W
p
l
=
ω
s
n
p
l
s
p
l
n
M
M
R
M
R
M
=
=
n
M
M
n
d
o
p
=
d
o
p
d
o
p
W
W
p
l
p
l
M
W
n
R
W
p
l
⋅
=
⋅
⋅
=
⋅
=
⋅
=
ω
σ
ω
ω
d
o
p
d
o
p
M
M
⋅
=
ω
W
y
m
ia
ro
w
a
n
ie
p
r
ę
ta
z
g
in
a
n
e
g
o
w
e
d
łu
g
k
a
ż
d
e
j z
m
e
to
d
d
a
je
r
ó
ż
n
e
w
y
n
ik
i.
1
2
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
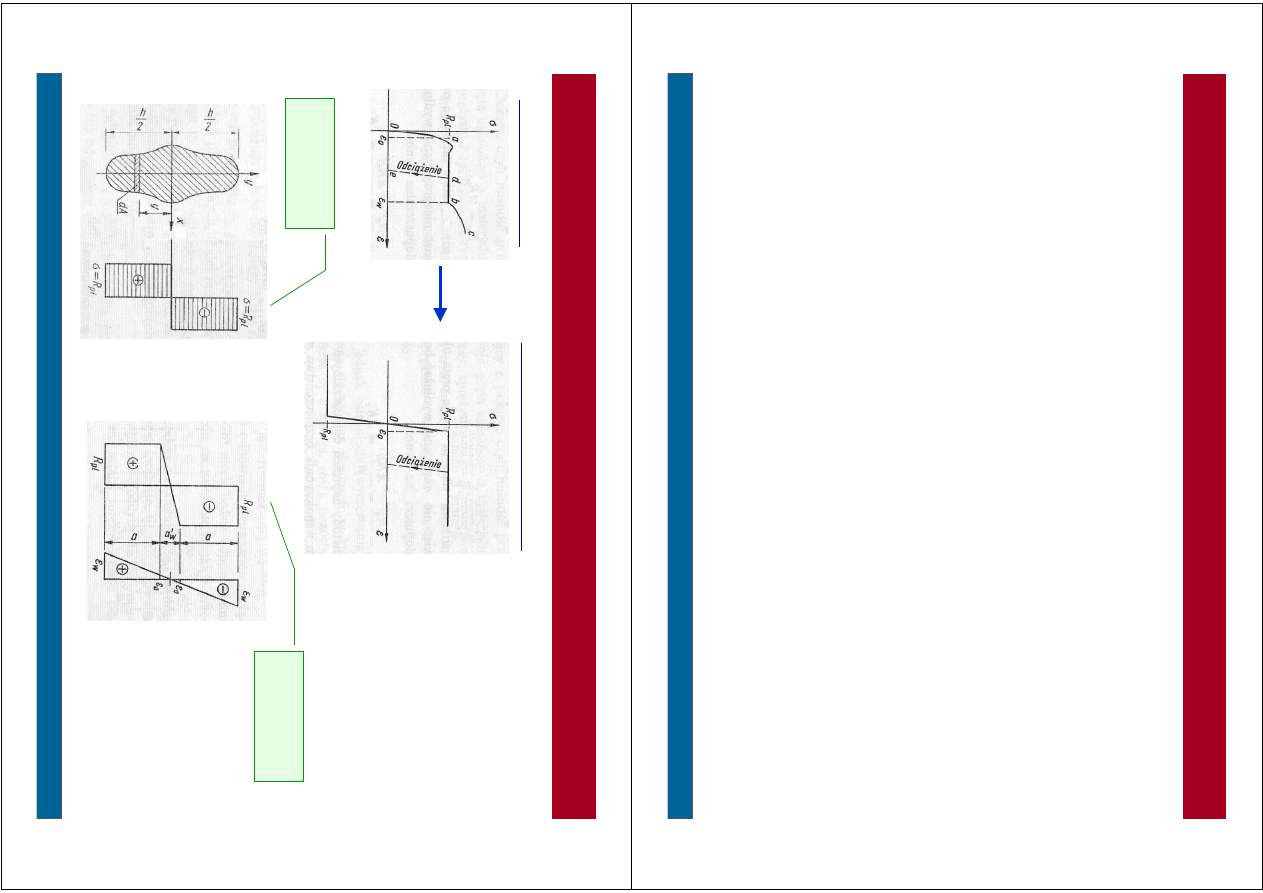
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t z
g
in
an
y
p
rz
e
g
u
b
p
la
s
ty
c
z
n
y
-
m
ie
js
c
e
, w
k
tó
ry
m
n
a
s
t
ę
p
u
je
u
p
la
s
ty
c
z
n
ie
n
ie
m
a
te
ria
łu
w
c
a
ły
m
p
rz
e
k
ro
ju
p
o
p
rz
e
c
z
n
y
m
p
rz
eg
u
b
p
la
st
y
cz
n
y
p
rz
eg
u
b
z
w
y
k
ły
co
n
st
M
M
n
=
=
0
M
=
1
3
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t z
g
in
an
y
R
ed
u
k
cj
a
n
o
śn
o
śc
i p
rz
ek
ro
ju
d
la
c
zy
st
eg
o
z
g
in
a
n
ia
ze
w
zg
lę
d
u
n
a
k
o
n
ie
cz
n
o
ść
:
•
u
w
zg
lę
d
n
ie
n
ia
w
p
ły
w
u
n
a
p
r
ę
ż
e
ń
st
y
cz
n
y
ch
•
o
g
ra
n
ic
ze
n
ia
o
d
k
sz
ta
łc
e
ń
t
rw
a
ły
ch
•
sp
eł
n
ie
n
ie
w
a
ru
n
k
u
, a
b
y
p
rz
y
p
o
w
ta
rz
a
n
y
ch
o
b
ci
ą
ż
en
ia
ch
n
ie
n
a
ra
st
a
ły
o
d
k
sz
ta
łc
en
ia
1
4
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t z
g
in
an
y
rz
ec
zy
w
is
ty
w
y
k
re
s
m
o
d
el
s
p
rę
ż
y
st
o
-p
la
st
y
cz
n
y
cz
ę
ś
cio
w
e
u
p
la
sty
cz
n
ie
n
ie
ca
łk
o
w
it
e
u
p
la
sty
cz
n
ie
n
ie
1
5
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t z
g
in
an
y
cz
ę
ś
cio
w
e
u
p
la
sty
cz
n
ie
n
ie
ca
łk
o
w
it
e
u
p
la
sty
cz
n
ie
n
ie
o
w
w
ε
ε
a
5.
0
h
5.
0
=
'
w
o
w
ε
ε
h
a
=
⇓
'
h
1
0
a
0
1
5
0
ε
0
0
1
3
0
ε
b
u
d
o
w
la
n
ej
st
a
li
d
la
w
w
o
.
.
.
'
=
⇒
≈
≈
p
l
p
l
n
W
R
M
⋅
=
∫
∫
=
=
⋅
+
⋅
=
h
5
0
h
0
5
0
y
p
l
h
0
5
0
0
y
n
d
A
y
R
d
A
y
2
M
.
.
.
'
σ
'
.
w
p
l
a
5
0
y
R
g
d
zi
e
=
σ
d
la
p
ro
st
o
k
ą
ta
2
p
l
n
h
b
2
5
0
R
M
.
⋅
=
(
)
2
p
l
3
p
l
h
5
0
h
0
5
0
y
p
l
h
0
5
0
0
y
2
p
l
n
b
h
2
4
7
7
0
R
h
4
5
0
5
0
h
0
5
0
h
4
5
0
b
2
1
2
h
0
5
0
b
h
0
5
0
1
R
d
A
y
R
2
d
A
y
R
2
M
.
.
.
.
.
)
.
(
.
.
.
.
'
⋅
=
⋅
+
⋅
+
=
=
+
=
∫
∫
=
=
1
6
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
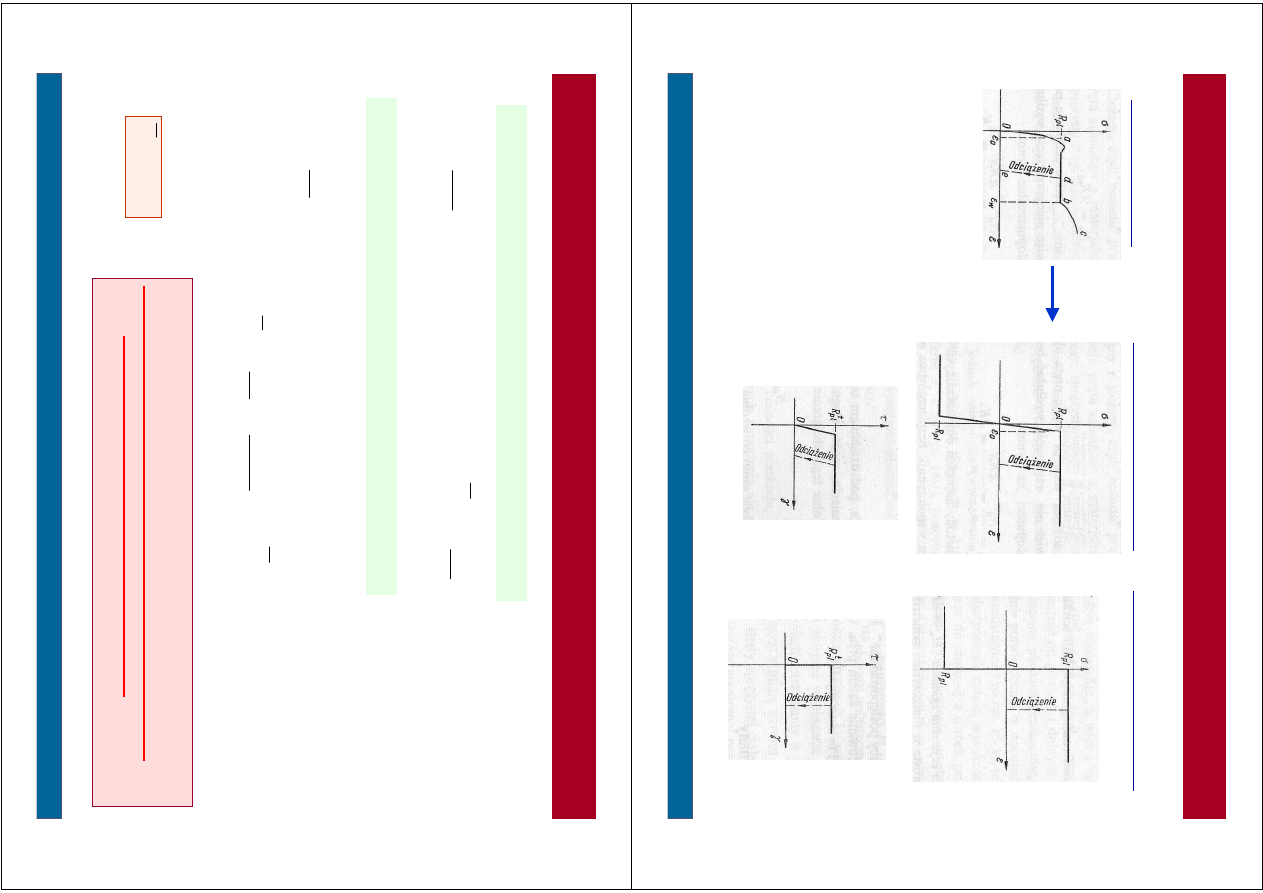
zn
ac
zn
e
cz
ę
ś
ci
o
w
e
u
p
la
st
y
cz
n
ie
n
ie
o
d
c
i
ą
ż
e
n
ie
o
d
c
i
ą
ż
e
n
ie
zn
ac
zn
e
cz
ę
ś
ci
o
w
e
u
p
la
st
y
cz
n
ie
n
ie
ca
łk
o
w
ite
u
p
la
st
y
cz
n
ie
n
ie
n
ap
rę
ż
en
ia
w
st
ę
p
n
e
n
ap
rę
ż
en
ia
w
st
ę
p
n
e
S
ta
n
g
ra
n
ic
zn
y
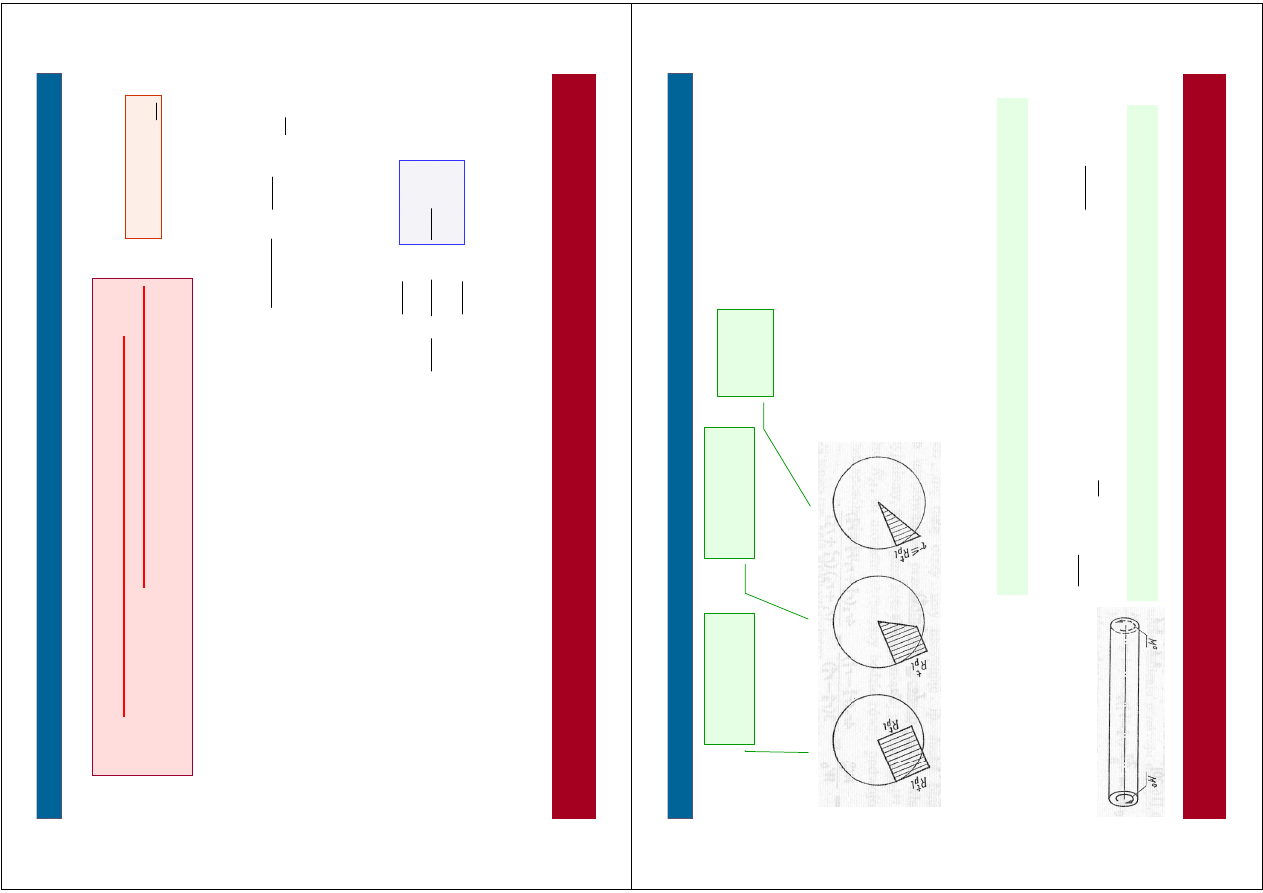
–
p
rę
t z
g
in
an
y
1
7
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t sk
rę
ca
n
y
o
o
d
o
p
d
o
p
W
M
=
τ
M
E
T
O
D
A
N
A
P
R
Ę
ś
E
Ń
N
I
E
P
R
Z
E
K
R
A
C
Z
A
L
N
Y
C
H
M
E
T
O
D
A
N
O
Ś
N
O
Ś
C
I
G
R
A
N
I
C
Z
N
E
J
n
R
W
W
M
t
p
l
o
d
o
p
o
o
d
o
p
n
t
p
l
R
d
o
p
⋅
=
⋅
=
⇒
=
τ
τ
t
p
l
o
s
R
W
M
⋅
=
∫
⋅
=
A
o
n
d
A
M
τ
ρ
o
k
re
s
sp
rę
ż
y
sty
cz
ę
ś
cio
w
e
u
p
la
sty
cz
n
ie
n
ie
ca
łk
o
w
it
e
u
p
la
sty
cz
n
ie
n
ie
o
p
l
t
p
l
A
t
p
l
W
R
d
A
R
⋅
=
=
∫
ρ
W
o
p
l
–
p
la
s
ty
c
z
n
y
w
s
k
a
ź
n
ik
W
o
–
s
p
r
ę
ż
y
s
ty
w
s
k
a
ź
n
ik
1
8
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
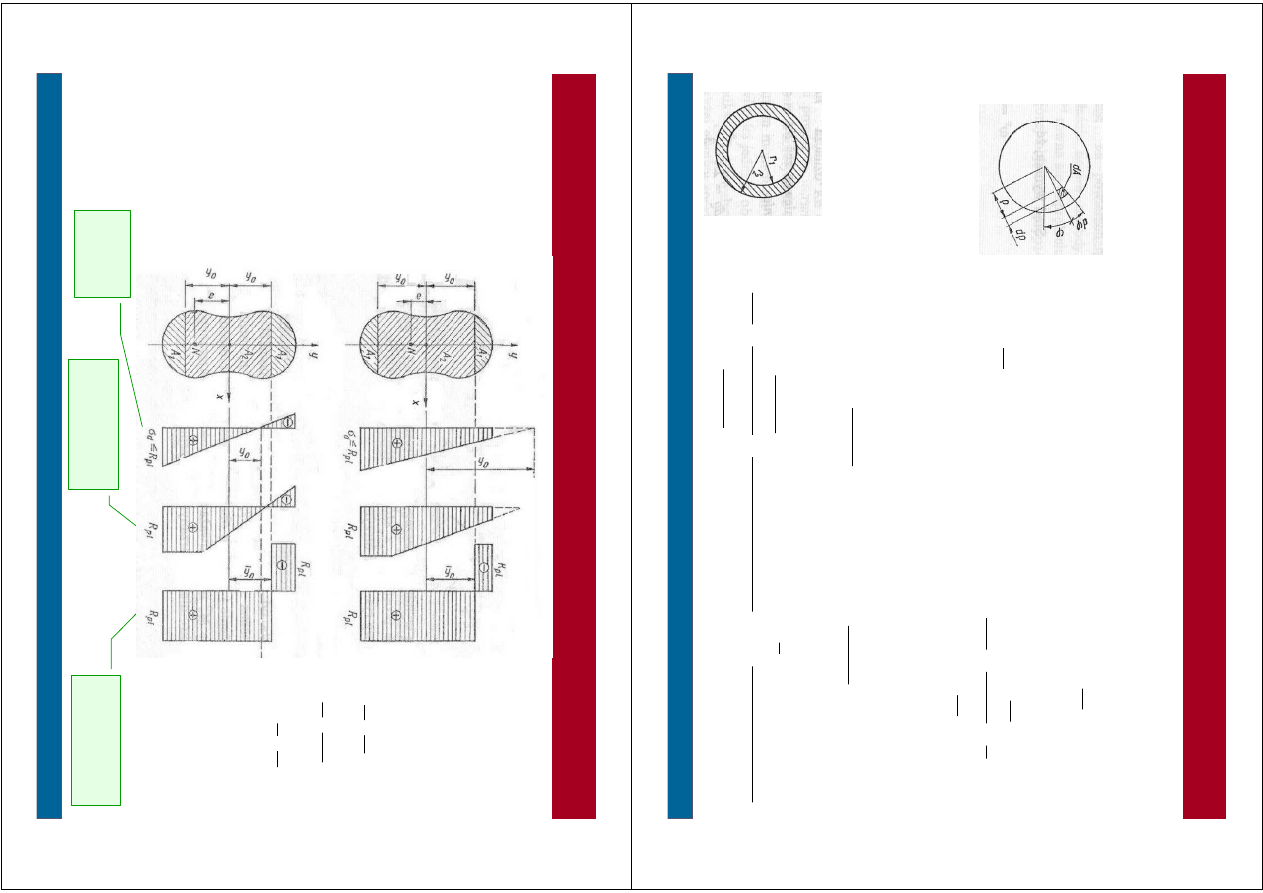
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t sk
rę
ca
n
y
w
s
p
ó
łc
z
y
n
n
ik
o
o
p
l
o
W
W
=
ω
o
s
o
n
t
p
l
o
s
t
p
l
o
n
M
M
R
M
R
M
=
=
n
M
M
o
n
o
d
o
p
=
o
d
o
p
o
d
o
p
o
o
W
W
p
l
o
p
l
M
W
n
R
W
o
o
o
p
l
⋅
=
⋅
⋅
=
⋅
=
⋅
=
ω
τ
ω
ω
o
d
o
p
o
o
d
o
p
M
M
⋅
=
ω
W
y
m
ia
ro
w
a
n
ie
p
r
ę
ta
s
k
r
ę
c
a
n
e
g
o
w
e
d
łu
g
k
a
ż
d
e
j z
m
e
to
d
d
a
je
r
ó
ż
n
e
w
y
n
ik
i.
1
9
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t sk
rę
ca
n
y
d
la
p
rz
ek
ro
ju
k
o
ło
w
eg
o
3
r
2
d
A
d
d
A
S
W
3
2
0
r
0
2
d
d
d
A
A
o
o
p
l
π
ρ
ρ
ρ
π
ϕ
ρ
ϕ
ρ
ρ
=
=
=
=
∫
∫
∫
=
=
=
2
r
W
3
o
π
=
d
la
p
rz
ek
ro
ju
p
ie
rś
ci
en
io
w
eg
o
3
r
r
2
d
A
S
W
3
1
3
2
A
o
o
p
l
−
=
=
=
∫
π
ρ
2
4
1
4
2
o
r
2
r
r
W
−
=
π
3
4
2
r
3
r
2
W
W
3
3
o
o
p
l
o
=
=
=
π
π
ω
(
)
(
)(
)
(
)
(
)
(
)
1
1
3
1
4
r
r
r
r
3
r
r
r
r
r
4
r
2
r
r
3
r
r
2
W
W
2
2
r
r
2
2
2
1
2
1
2
2
2
1
2
1
2
2
4
1
4
2
3
1
3
2
o
o
p
l
o
2
1
+
+
+
+
=
+
+
+
+
=
−
−
=
=
=
α
α
α
α
π
π
ω
α
:
2
0
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
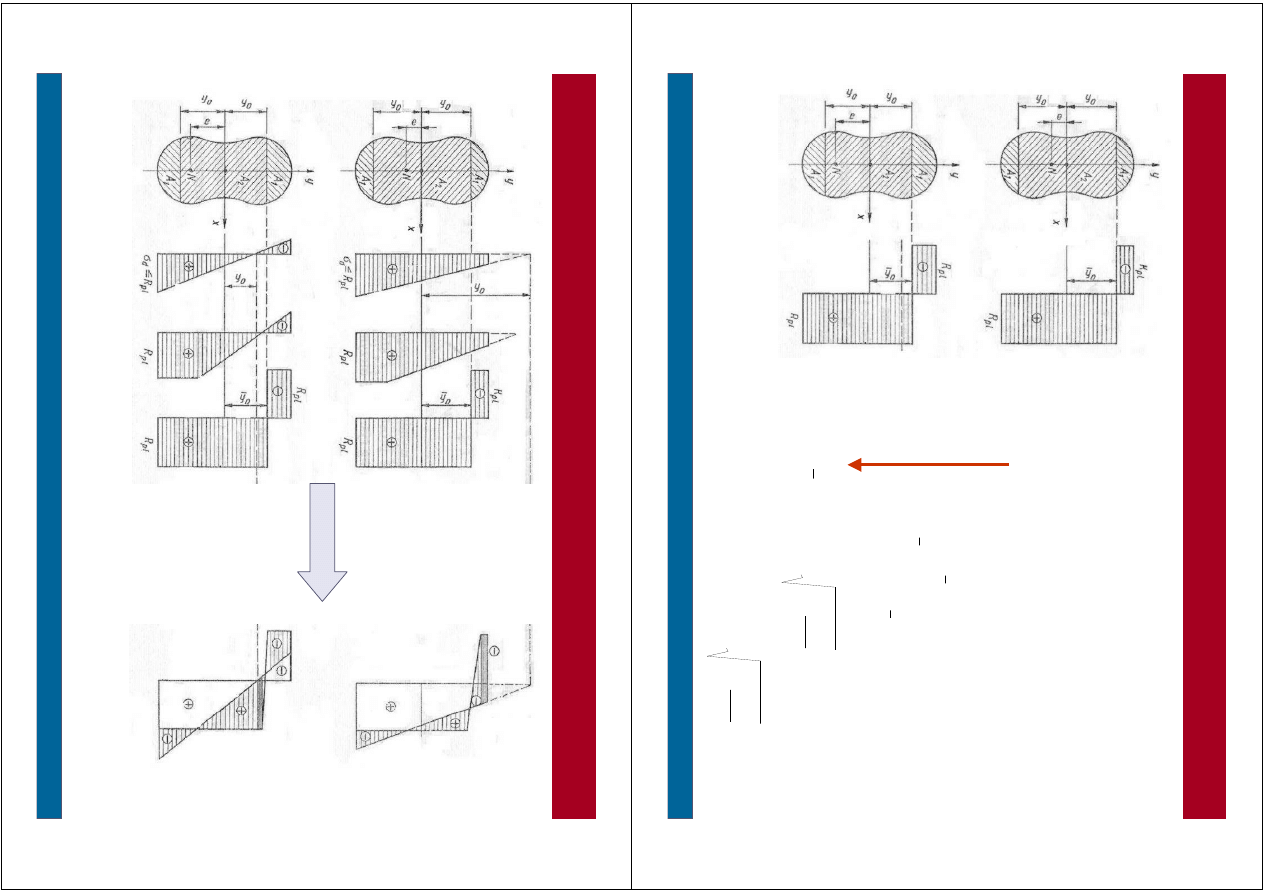
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t m
im
o
ś
ro
d
o
w
o
ś
ci
sk
an
y
cz
ę
ś
cio
w
e
u
p
la
sty
cz
n
ie
n
ie
ca
łk
o
w
it
e
u
p
la
sty
cz
n
ie
n
ie
d
la
si
ły
N
w
g
ra
n
ic
ac
h
rd
ze
n
ia
d
la
si
ły
N
p
o
za
r
d
ze
n
ie
m
o
k
re
s
sp
rę
ż
y
sty
p
l
d
R
W
e
A
1
N
W
e
N
A
N
W
M
A
N
=
+
=
=
⋅
+
=
=
+
=
σ
2
1
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
∫
⋅
=
⋅
=
A
n
n
d
A
y
e
N
M
σ
∫
⋅
=
1
A
p
l
d
A
y
2
R
1
p
l
S
2
R
⋅
⋅
=
∫
=
A
n
d
A
N
σ
2
p
l
A
R
⋅
=
ró
w
n
an
ia
r
ó
w
n
o
w
ag
i
(
)
(
)
2
o
2
1
o
2
o
1
y
h
2
5
0
b
5
0
S
y
b
2
A
y
h
5
0
b
A
ta
p
ro
st
o
k
ą
d
la
−
=
⋅
=
−
=
.
.
.
+
+
−
=
2
2
o
e
4
h
1
1
e
y
+
+
−
⋅
⋅
=
2
2
p
l
n
e
4
h
1
1
e
b
2
R
N
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t m
im
o
ś
ro
d
o
w
o
ś
ci
sk
an
y
2
2
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
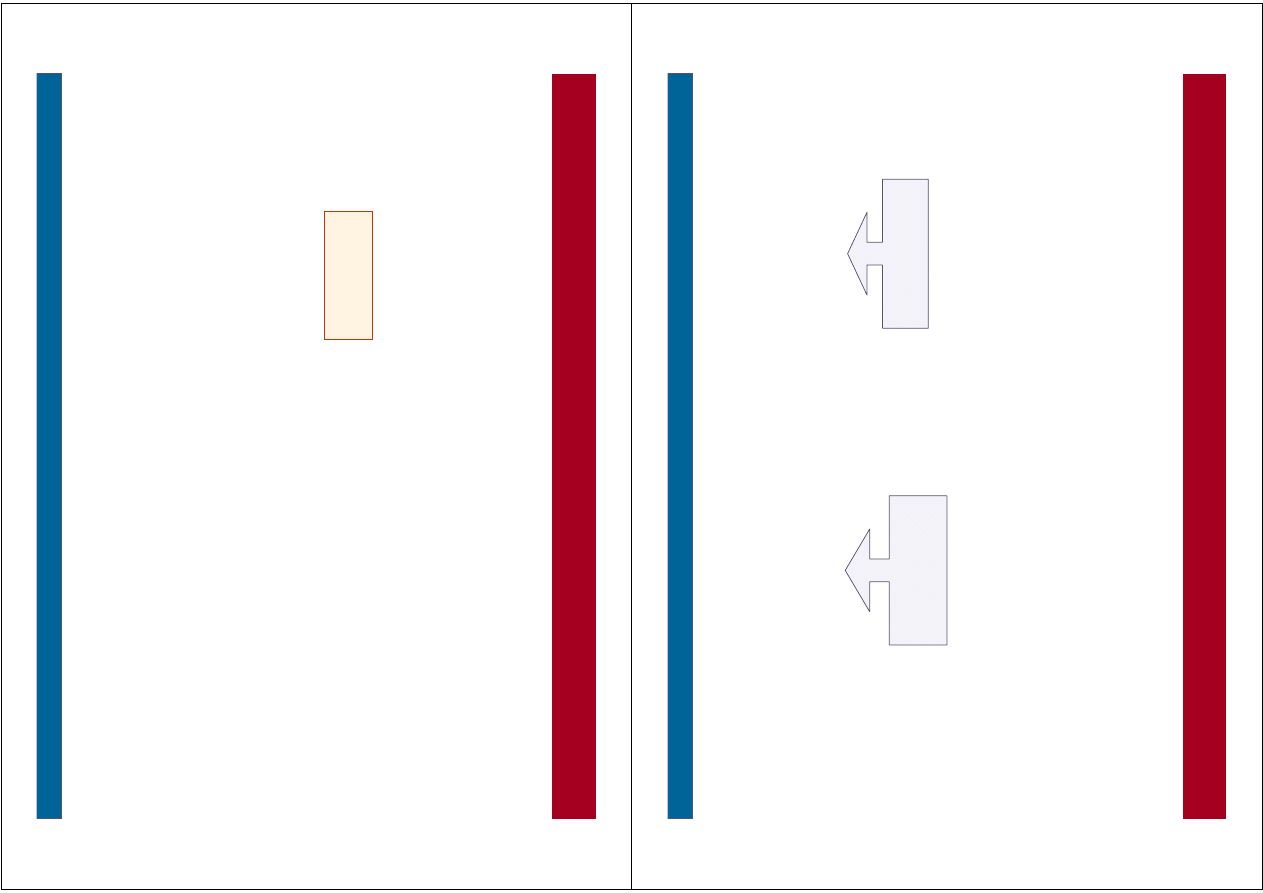
S
ta
n
g
ra
n
ic
zn
y
–
p
rę
t m
im
o
ś
ro
d
o
w
o
ś
ci
sk
an
y
o
d
c
i
ą
ż
e
n
ie
zn
ac
zn
e
cz
ę
ś
ci
o
w
e
u
p
la
st
y
cz
n
ie
n
ie
ca
łk
o
w
ite
u
p
la
st
y
cz
n
ie
n
ie
n
ap
rę
ż
en
ia
w
st
ę
p
n
e
st
an
sp
rę
ż
y
st
y
2
3
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
S
p
o
so
b
y
o
b
lic
za
n
ia
n
o
ś
n
o
ś
ci
g
ra
n
ic
zn
ej
u
p
la
s
ty
c
z
n
ie
n
ie
-
w
y
s
t
ą
p
ie
n
ie
o
d
k
s
z
ta
łc
e
ń
tr
w
a
ły
c
h
,k
tó
re
m
o
g
ą
z
w
i
ę
k
s
z
a
ć
s
i
ę
b
e
z
w
z
ro
s
tu
o
b
c
i
ą
ż
e
n
ia
p
rz
e
g
u
b
p
la
s
ty
c
z
n
y
-
m
ie
js
c
e
, w
k
tó
ry
m
n
a
s
t
ą
p
iło
u
p
la
s
ty
c
z
n
ie
n
ie
m
a
te
ria
łu
w
c
a
ły
m
p
rz
e
k
ro
ju
z
g
in
a
n
ie
p
rz
e
g
u
b
p
la
s
ty
c
z
n
y
d
o
p
u
s
z
c
z
a
o
b
ro
ty
i p
rz
e
n
o
s
i m
o
m
e
n
t
o
s
ta
łe
j w
a
rto
ś
c
i
ro
z
c
i
ą
g
a
n
ie
o
s
io
w
e
p
rz
e
g
u
b
p
la
s
ty
c
z
n
y
d
o
p
u
s
z
c
z
a
w
y
d
łu
ż
e
n
ia
i p
rz
e
n
o
s
i s
ił
ę
p
o
d
łu
ż
n
ą
o
s
ta
łe
j w
a
rto
ś
c
i
p
l
p
l
n
R
W
M
⋅
=
p
l
n
R
A
N
⋅
=
2
4
W
y
k
ła
d
:
M
e
c
h
a
n
ik
a
B
u
d
o
w
li
–
c
z
. I
I
d
r i
n
ż
. B
a
rb
a
ra
W
ie
c
z
o
re
k
S
p
o
so
b
y
o
b
lic
za
n
ia
n
o
ś
n
o
ś
ci
g
ra
n
ic
zn
ej
Ob
lic
z
a
n
ie
n
o
ś
n
o
ś
c
i g
ra
n
ic
z
n
e
j u
s
tr
o
ju
p
o
le
g
a
n
a
a
n
a
liz
ie
je
g
o
p
ra
c
y
p
o
c
z
ą
w
s
z
y
o
d
s
ta
n
u
s
p
r
ę
ż
y
s
te
g
o
,
p
o
p
rz
e
z
k
o
le
jn
e
fa
z
y
s
ta
n
u
s
p
r
ę
ż
y
s
to
-p
la
s
ty
c
z
n
e
g
o
,
a
ż
d
o
u
p
la
s
ty
c
z
n
ie
n
ia
s
i
ę
ta
k
ie
j l
ic
z
b
y
p
rz
e
k
ro
jó
w
,
ż
e
u
s
tr
ó
j z
a
m
ie
n
ia
s
i
ę
w
g
e
o
m
e
tr
y
c
z
n
ie
z
m
ie
n
n
y
.
1
n
k
s
+
=
n
s
–
s
to
p
ie
ń
s
ta
ty
c
z
n
e
j n
ie
w
y
z
n
a
c
z
a
ln
o
ś
c
i u
k
ła
d
u
k
–
lic
z
b
a
p
rz
e
g
u
b
ó
w
p
la
s
ty
c
z
n
y
c
h
n
ie
z
b
ę
d
n
a
d
o
u
z
y
s
k
a
n
ia
p
ra
w
id
ło
w
e
g
o
m
e
c
h
a
n
iz
m
u
z
n
is
z
c
z
e
n
ia
a
zn
is
zc
ze
n
i
m
ec
h
a
n
iz
m
ś
ci
p
la
st
yc
zn
o
w
a
ru
n
ek
ró
w
n
o
w
a
g
i
ró
w
n
a
n
ia
n
e
zu
p
e
ł
za
n
ie
ro
zw
ią
st
a
ty
cz
n
e
za
n
ie
ro
zw
ią
n
e
ki
n
em
a
ty
cz
za
n
ie
ro
zw
ią
M
e
to
d
y
ro
z
w
i
ą
z
a
n
ia
: s
ta
ty
c
z
n
a
i
k
in
e
m
a
ty
c
z
n
a
ki
n
n
n
st
n
P
P
P
m
in
m
ax
≤
≤
n
ki
n
n
st
n
P
P
P
=
=
m
in
m
ax
Wyszukiwarka
Podobne podstrony:
MB w2 mini
MB SIZ w2
Psycholgia wychowawcza W2
SP dzienni w2
w2 klasy(1)
W2 Chemiczne skladniki komorki
OK W2 System informacyjny i informatyczny
W2 6
Algebra w2
W2 Uproszczone formy rachunkowości
W2 i W3
MB 7 2014
ulog w2
UC W2
w2 podsumowanie
więcej podobnych podstron