Wyznaczenie współczynnika załamania światła przy

użyciu mikroskopu optycznego.

Ćw.20

Cel ćwiczenia

Zapoznanie się z zasadą działania, budową i obsługą mikroskopu optycznego oraz poznanie metody

pomiaru współczynnika załamania światła przy użyciu mikroskopu optycznego.

Zakres obowiązującego materiału teoretycznego

Budowa i działanie mikroskopu. Falowo-korpuskularna natura światła. Odbicie i załamanie światła.

Współczynnik załamania światła względny i bezwzględny. Dyspersja światła, wyprowadzenie równania (8).

Wyznaczanie współczynnika załamania światła metodą mikroskopową.

Przyrządy i materiały używane w doświadczeniu

Mikroskop optyczny z mikrometrem, płytki płasko-równoległe z badanych materiałów oraz śruba

mikrometryczna.

Wprowadzenie

Jeśli światło odbija się od gładkiej powierzchni rozdzielającej ośrodki, to odbicie zachodzi tylko w

określonym kierunku. Załamanie światła zachodzi przy jego przejściu z jednego ośrodka do drugiego.

Prawo odbicia formułuje się następująco:

Kąt padania jest równy kątowi odbicia a promień padający, odbity i prosta prostopadła do powierzchni w

punkcie padania leżą w jednej płaszczyźnie.

Prawo załamania formułuje się następująco:

Stosunek sinusa kąta padania do sinusa kąta załamania dla danych dwóch ośrodków jest wielkością stałą a

promień padający, załamany i prosta do powierzchni rozgraniczającej ośrodki w punkcie padania leżą w

jednej płaszczyźnie.

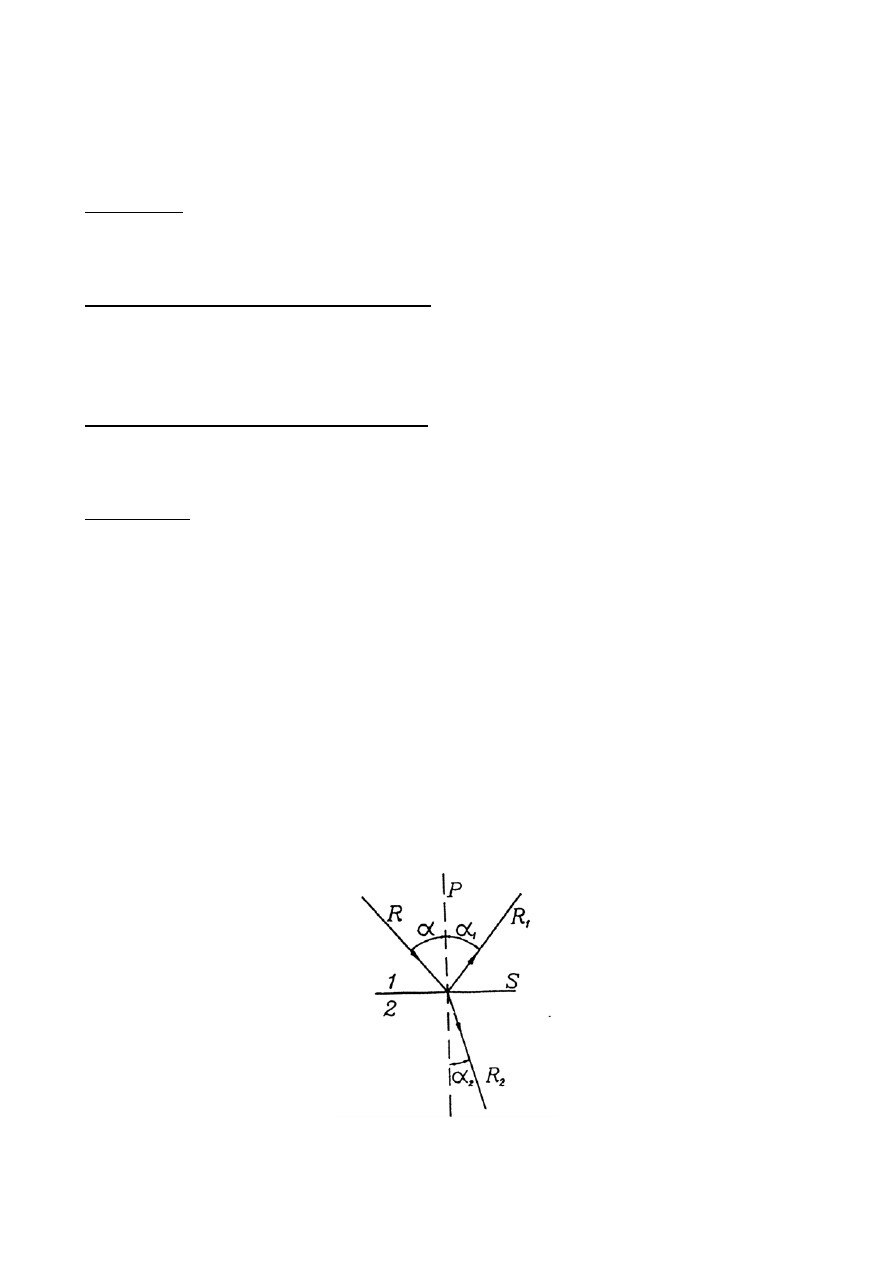
Powyższe prawa ilustruje rysunek rys.1. na którym symbole

α, α

1

oraz

α

2

oznaczają odpowiednio kąt

padania, kąt odbicia oraz kąt załamania względem prostej prostopadłej P do powierzchni S w punkcie

odbicia czy załamania. Oznaczenia R, R

1

oraz R

2

określają odpowiednio promień padający, odbity i

załamany.

Rys.1. Ilustracja do prawa odbicia i załamania (wyjaśnienie w tekście powyżej).

1

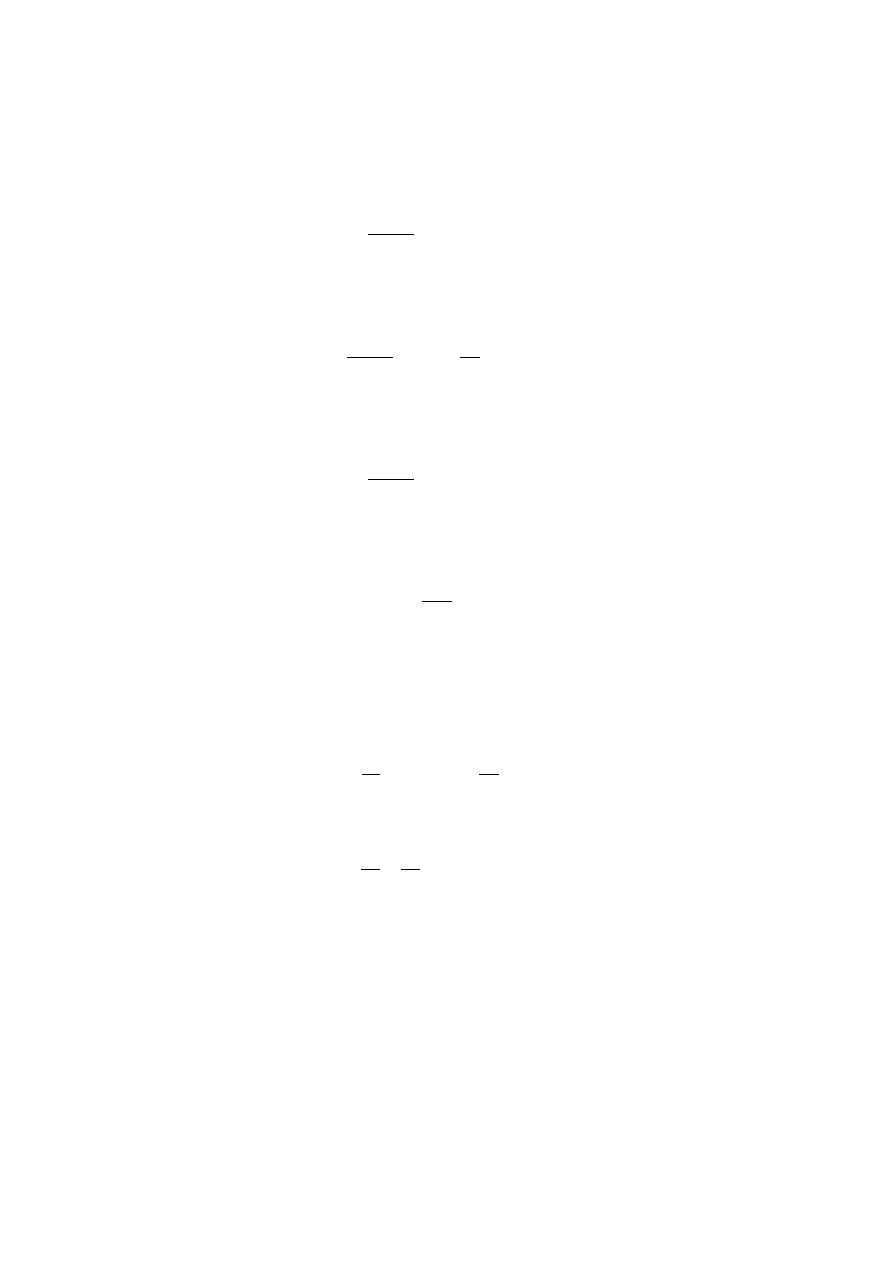
Zgodnie z prawem odbicia można zatem napisać:

1

α

=

α

(1)

Stały stosunek sinusa kąta padania do sinusa kąta załamania oznacza się symbolem n

2/1

i nazywa się

współczynnikiem załamania światła ośrodka drugiego względem pierwszego:

1

/

2

2

n

sin

sin

=

α

α

(2)

Z falowej teorii światła wynika, że stosunek sinusa kąta padania do sinusa kąta załamania równy jest

stosunkowi prędkości światła w ośrodku 1 (v

1

) do prędkości w ośrodku 2 (v

2

):

2

1

1

/

2

2

v

v

n

sin

sin

=

=

α

α

(3)

W sytuacji odwrotnej, gdy promień biegnie z ośrodka 2 do ośrodka 1 i pada na granicę ośrodków pod kątem

α

2

, kąt załamania wyniesie

α, co możemy zapisać:

2

/

1

2

n

sin

sin

=

α

α

W tym przypadku n

1/2

jest współczynnikiem załamania światła ośrodka 1 względem ośrodka 2. Porównując

powyższe z równaniem (2) można zauważyć, że:

2

/

1

1

/

2

n

1

n

=

(4)

Gdy jednym z ośrodków będzie próżnia (odniesienie do warunków próżni) wtedy współczynnik załamania

światła danego ośrodka względem próżni nazywa się bezwzględnym współczynnikiem załamania światła

danego ośrodka. Oznaczając bezwzględne współczynniki załamania światła ośrodków 1 i 2 odpowiednio

poprzez n

1

oraz n

2

zgodnie z równaniem (3) można napisać:

1

1

v

c

n

=

oraz

2

1

v

c

n

=

(5)

2

gdzie C jest prędkością światła w próżni. Dzieląc stronami równania (5) otrzymujemy:

1

/

2

2

1

1

2

n

v

v

n

n

=

=

Widać stąd, że względny współczynnik załamania światła 2 względem ośrodka 1 równy jest stosunkowi ich

współczynników bezwzględnych.

Należy również nadmienić, że wartość współczynnika załamania światła danego ośrodka zależy również od

długości fali.

2

Wyznaczanie współczynnika załamania światła metodą mikroskopową

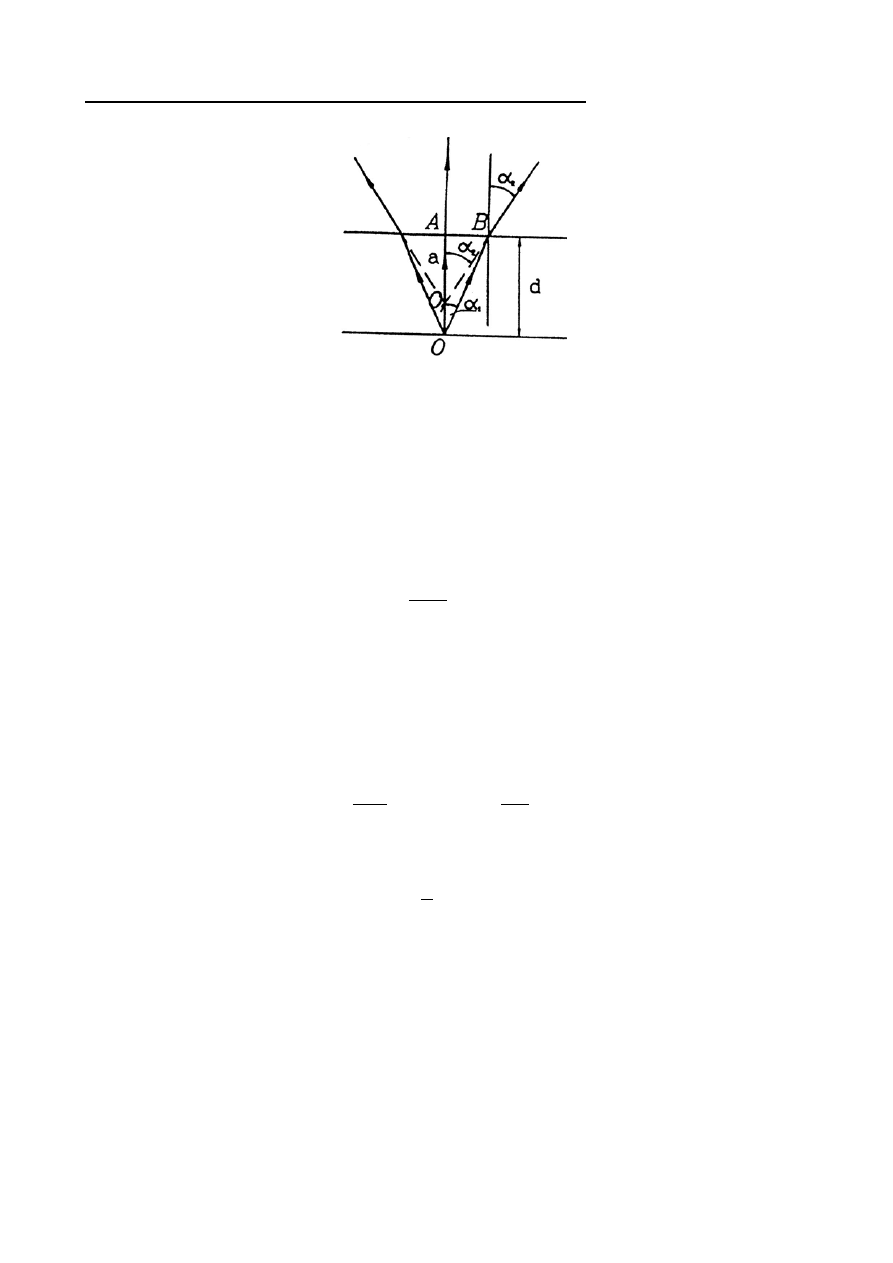
Zasadę pomiaru współczynnika załamania światła zilustrowano na rys.2.

Rys.2. Powstawanie obrazu pozornego (wyjaśnienie w tekście poniżej).

Rozważmy bieg wiązki promieni rozbieżnych wychodzących z punktu O, leżącego na dolnej powierzchni

płytki płasko-równoległej. Wybrany na rysunku promień pada na górną powierzchnię płytki w punkcie B pod

kątem

α

1

i przechodząc do ośrodka zewnętrznego (powietrza) załamuje się pod kątem

α

2

. Współczynnik n

załamania światła materiału płytki względem powietrza, zgodnie z równaniami definicyjnym (2) oraz z

wzorem (4) będzie równy ilorazowi sin

α

2

/sin

α

1

. Dla dostatecznie małych kątów iloraz sinusów kątów można

zastąpić ilorazem ich tangensów. Stąd:

1

2

tg

tg

n

α

α

=

(7)

W przypadku wiązki promieni rozbieżnych, przedłużenia promieni załamanych pod kątem

α

2

przecinają się

w punkcie O

1

(dla dostatecznie małych kątów). Punkt O

1

jest więc pozornym obrazem punktu O. Obserwator

patrzący na płytkę z góry będzie zatem widział zamiast punktu O punkt O

1

, leżący w odległości a od górnej

płaszczyzny płytki.

Z trójkątów ABO

1

i ABO widać, że

1

2

AO

AB

tg

=

α

oraz

AO

AB

tg

1

=

α

Po podstawieniu tych związków do równania (7) i po oznaczeniu AO

1

=a oraz AO=d otrzymamy:

a

d

n

=

(8)

Z ostatniego wzoru widać, że w celu wyznaczenia współczynnika załamania światła dla materiału, z którego

wykonana jest płytka należy zmierzyć jej grubość d oraz wyznaczyć odległość a. Grubość płytki można

między innymi zmierzyć za pomocą śruby mikrometrycznej lub mikromierza (grubościomierza

mikrometrycznego). Praktycznego pomiaru odległości a dokonuje się umieszczając badaną płytkę pod

mikroskopem i ustawiając go tak, aby było ostro widać dolną powierzchnię płytki (zwykle obserwuje się

przypadkowe zadrapania lub celowo naniesione barwne plamki). Następnie przesuwa się tubus mikroskopu

o odcinek a ku górze (lub stolik mikroskopu ku dołowi) tak, aby było ostro widać górną powierzchnię płytki

(punkt A na rys.2). Większość mikroskopów ma wzorcowane obroty pokrętła precyzyjnego przesuwu stolika

3

lub tubusu mikroskopu. Jeden obrót tego pokrętła odpowiada przesunięciu 0.1mm. Na pokrętle znajduje się

podziałka pozwalająca odczytać położenie stolika (tubusu) z dokładnością od 0.001mm do 0.01mm. Gdy

brak jest takiej podziałki wielkość przesunięcia możemy zmierzyć za pomocą grubościomierza

przymocowanego do mikroskopu.

W podobny sposób można wyznaczyć współczynnik załamania światła dla dowolnej cieczy. Wówczas

mikroskop ustawia się tak, aby było możliwym ostre widzenie plamki zrobionej na wewnętrznej stronie dna

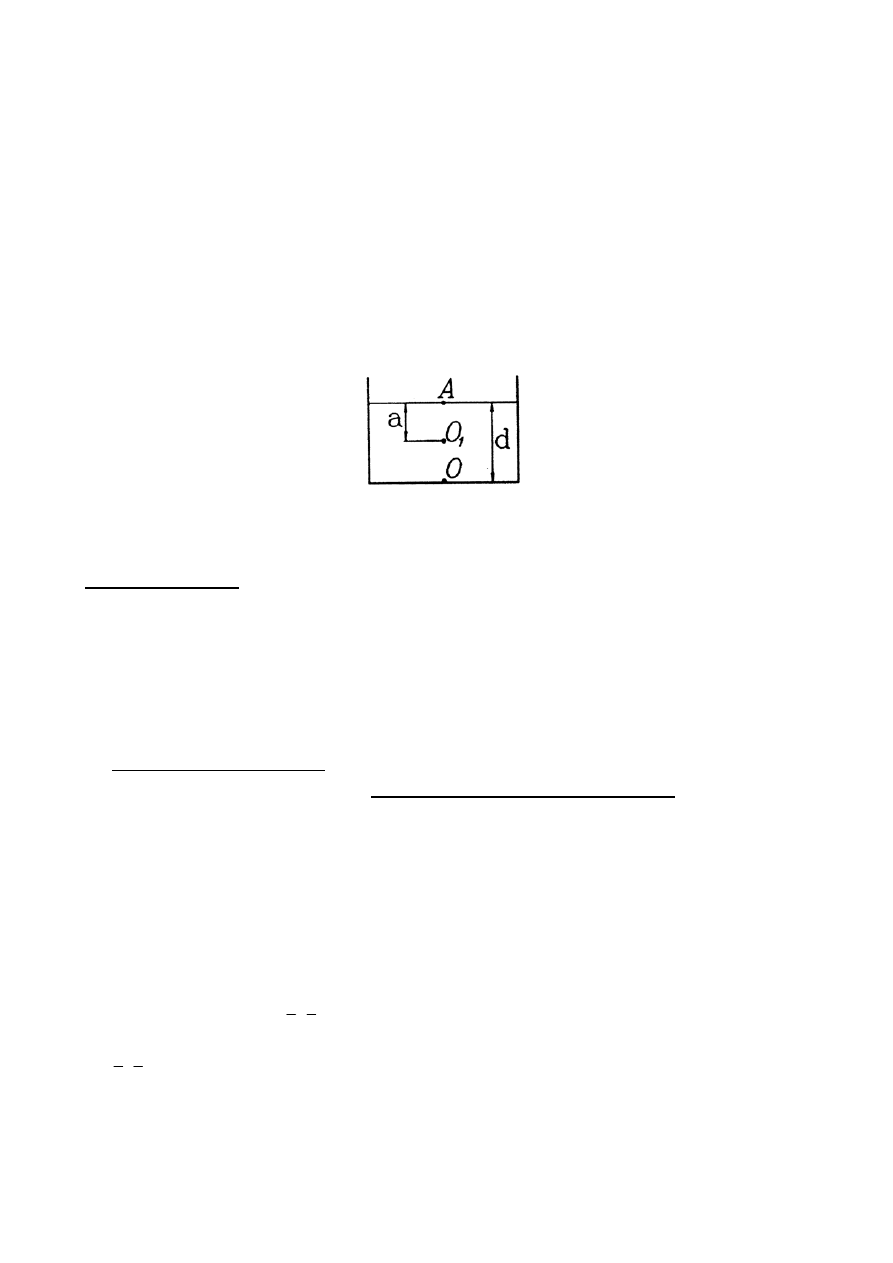
naczynia (punkt O na rys.3). Po nalaniu do naczynia badanej cieczy obserwacja obrazu pozornego (punktu

O

1

) staje się możliwa po przesunięciu stolika (tubusu) mikroskopu o odcinek (d-a) ku górze. Przesuwając

dalej stolik (tubus) mikroskopu, tak aby było ostro widać jakiś drobny przedmiot, np. włos, umieszczony na

powierzchni cieczy (punkt A na rys.3) można zmierzyć grubość warstwy cieczy d.

Rys.3. Wyznaczanie współczynnika załamania w cieczach (wyjaśnienie w tekście powyżej).

Wykonanie ćwiczenia

Pomiary współczynnika załamania światła przeprowadzamy kolejno dla płytek ze szkła (szkło

mikroskopowe), szkła organicznego (pleksi) oraz kwarcu.

1. Za

pomocą śruby mikrometrycznej dokonać 10 pomiarów grubości d płytki.

2. Unieść tubus ku górze lub opuścić stolik mikroskopu.

3. Naznaczyć różnymi kolorami lub znakami każdą ze stron badanej płytki i umieścić ją na stoliku

mikroskopu.

4. Obserwując obiektyw z boku opuścić tubus (unieść stolik) tak, aby obiektyw znajdował się tuż nad

powierzchnią badanej płytki uważając, aby obiektyw nie uderzył w badaną próbkę.

5. Unosząc tubus ku górze (lub opuszczając stolik) ustawić mikroskop na ostre pole widzenia dolnej

powierzchni płytki. Odczytać wskazanie a

1

grubościomierza.

6. Unosząc wyżej tubus (opuszczając dalej stolik) ustawić mikroskop na ostre widzenie górnej powierzchni

płytki i odczytać wskazania a

2

miernika.

7. Obliczyć wartość a = (a

1

- a

2

).

8. Czynności wymienione w punkcie 5, 6 i 7 powtórzyć sześciokrotnie.

9. Dokonać analogicznych pomiarów dla pozostałych płytek. Wartości d, a

1

i a

2

oraz a zapisać w

odpowiednich tabelach.

10. Wyliczyć średnie wartości d i a.

11. Współczynniki załamania światła poszczególnych płytek obliczyć według wzoru (8) dla średnich wartości

d i a.

4

12. Obliczyć średni błąd kwadratowy ze wzoru:

2

2
a

2

2
d

a

S

d

S

n

n

+

=

∆

(9)

gdzie:

(

)

(

)

1

k

k

d

d

S

k

1

i

2

i

2
d

−

−

=

∑

=

(10)

(

)

(

)

1

k

k

a

a

S

k

1

i

2

i

2
a

−

−

=

∑

=

(11)

We wzorach (9), (10) i (11) zmienne d

i

i a

i

oznaczają odpowiednie wartości zmierzone; d i a. – ich wartości

średnie, natomiast k - liczbę serii pomiarowych.

Opracowanie sprawozdania

Sprawozdanie powinno zawierać:

-

wstęp teoretyczny z podkreśleniem celu i zakresu wykonanych pomiarów;

-

tabele pomiarowe

podpisane przez prowadzącego bezpośrednio po wykonaniu ćwiczenia;

-

wyniki obliczeń zestawione w tabeli;

-

obliczenia błędu i oszacowanie granic wyników;

-

wyniki końcowe podane w postaci: n =n

obl

± ∆n;

-

porównanie uzyskanych wartości z wartościami tabelarycznymi;

-

wnioski.

5