1

Przykładowe zadania z „Fundamentowania”

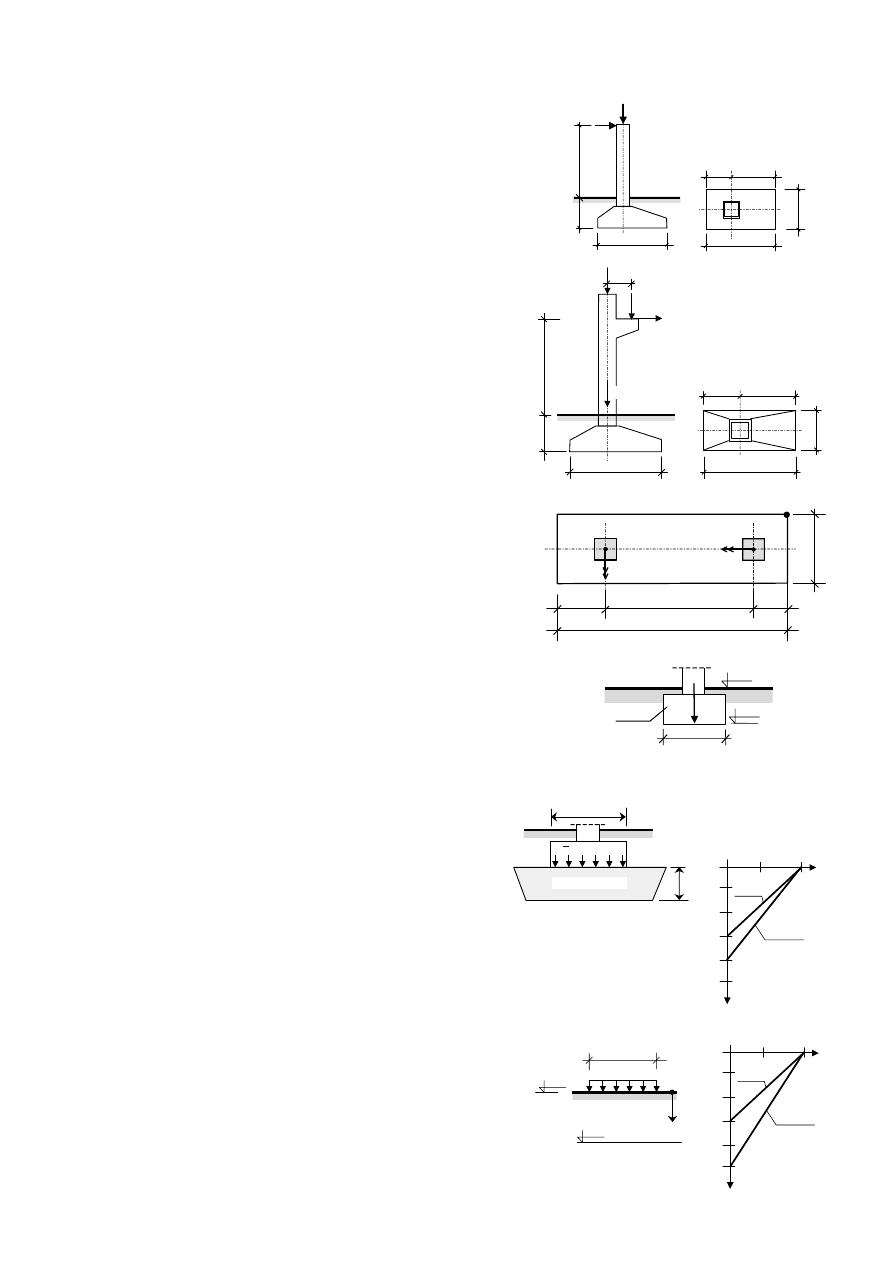
1. Policzyć maksymalne naciski pionowe przekazywane na grunt
przez fundament słupa obciążonego siłami pionowymi i poziomymi.
Uwzględnić ciężar fundamentu i gruntu znajdującego się nad nim
(

γ

śr

= 22.0 kN/m

3

). W sile pionowej V uwzgledniono już ciężar słupa.

Dane: V = 1200 kN,

H = 300 kN,

2. Sprawdzić czy wypadkowa obciążeń znajduje się w

rdzeniu podstawy fundamentu i policzyć wartości
nacisków na grunt. Uwzględnić ciężar fundamentu i
gruntu znajdującego się nad nim, przyjmując
γ

śr

=22kN/m

3

.

Dane: G

s

= 80 kN,

V

1

= 300 kN, V

2

= 600 kN, H = 180 kN

3. Policzyć wartość nacisków na grunt w punkcie A pod fundamentem
przedstawionym na rysunku, obciążonym dwoma słupami.
Uwzględnić ciężar fundamentu, którego grubość wynosi 1.20 m.
Ciężar objętościowy betonu przyjąć

γ

b

= 25 kN/m

3

.

Pytania dodatkowe: czy wypadkowa obciążeń jest w rdzeniu
podstawy fundamentu, jaka jest wartość maksymalnych nacisków na
grunt?

Dane: P

1

=1500 kN, M

1

=1000 kNm,P

2

= 2000 kN, M

2

= 1400 kNm

4. Dla jakiej głębokości posadowienia D=? fundamentu
przedstawionego na rysunku obok, spełniony będzie warunek
nośności pionowej podłoża gruntowego?

Dane: Q = 300 kN/m

5. Do jakiej głębokości należy zastosować poduszkę
piaskową pod stopą fundamentową, aby osiadania stopy
zmniejszyły się o połowę w stosunku do podłoża bez
poduszki piaskowej. Zastosować metodę odkształceń
jednoosiowych z liniowym rozkładem

η – jak na rysunku.

Obliczenia można wykonać metodą kolejnych przybliżeń.
Ze względu na liniowy rozkład

η można zaniechać podziału

warstw podłoża gruntowego na pod-warstwy obliczeniowe.

6. Obliczyć wartość osiadań podłoża gruntowego pod ławą
fundamentową przedstawioną na rysunku obok. Rozkład

η przyjąć

liniowy, jak pokazano na rysunku.

P

1

P

2

M

1

M

2

2.

5

2.0 1.5

9.0

5.5

A

Q

B= 1.50 m

P

g

,

φ

(n)

= 20

°

γ

(n)

=20 kN/m

3

c = 15 kPa

ława

B

× L

(L =

∞)

- D= ?

± 0.00

V

L = 4.00

B=2.

0

L = 4.0 m

h=

4.

5

0 m

D=

1.

5

m

H

Widok z góry

1.5

2.5

η

z/B

q = 150 kPa

B = 2.0m

± 0.00

ława fundamentowa

M

0

= 20 MPa

M

0

= 10 MPa

- 4.00

0

1

2

5

1

0.5

3

4

L/B =1

L/B =

∞

z

L = 4.0

h=5.

0m

D=1.

5m

V

2

G

s

H

1.2

B=2.0

Widok z góry na fundament

1.5

2.5

L = 4.0

V

1

z/B

q = 200 kPa

M

0

= 20 MPa

B

s

= 3.0 m

stopa fundamentowa

η

0

1

2

5

1

0.5

3

4

L/B =1

L/B =

∞

G

π

P

s

, M

0

= 60 MPa

h=?

2

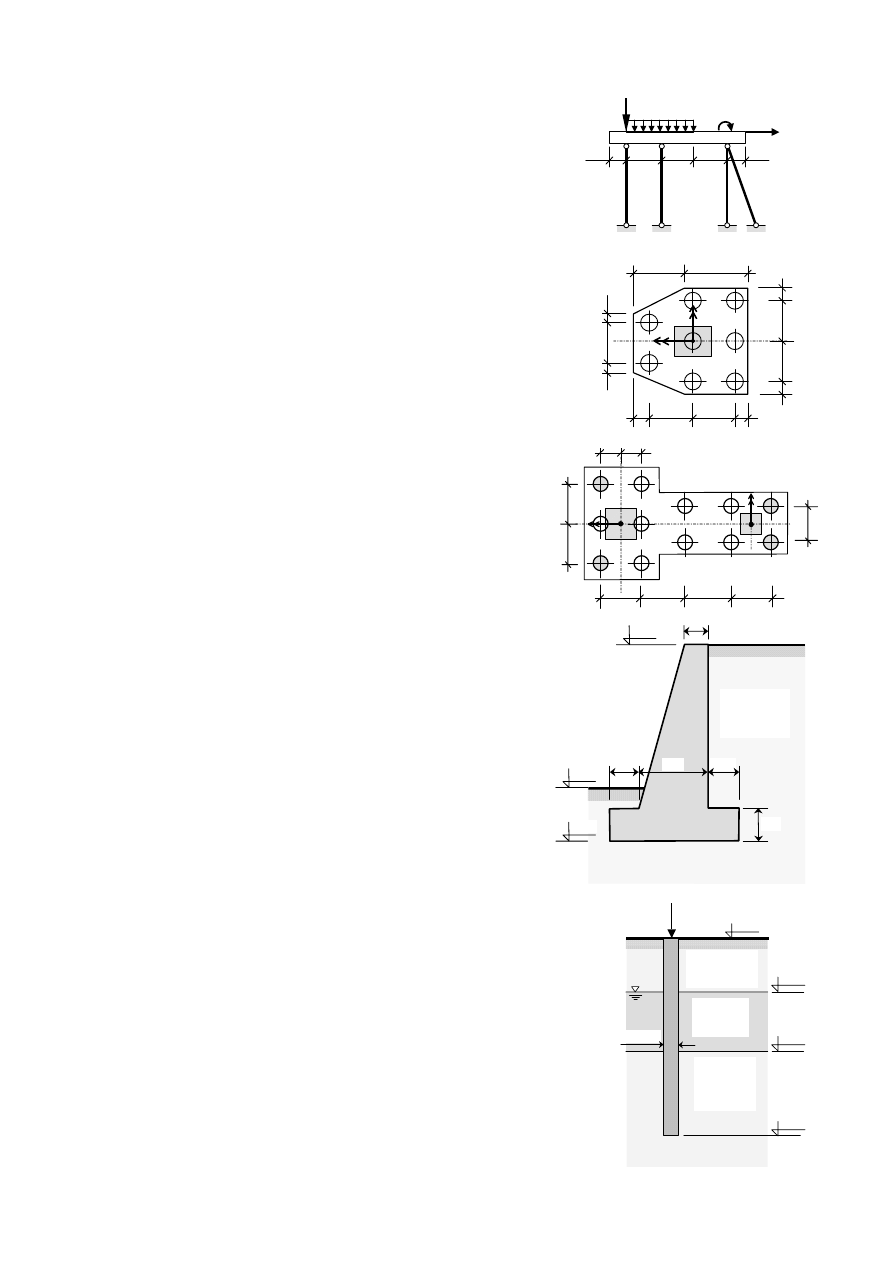
7. Metodą sztywnego oczepu wyznaczyć siłę w palu nr (4) od
obciążeń zewnętrznych. Pominąć ciężar oczepu. Pale przyjąć jako
pręty obustronnie przegubowe.

Zadanie dodatkowe: wyznaczyć siły we wszystkich palach układu.

8. Policzyć siłę w najbardziej obciążonym palu fundamentu słupa
konstrukcji inżynierskiej (rysunek obok). Obliczenia wykonać metodą
sztywnego oczepu. Pominąć ciężar oczepu.

Pytanie dodatkowe: czy jest jakiś pal wyciągany w fundamencie ?

Dane: P = 10000 kN, M

x

= 6000 kNm, M

y

= 3000 kNm

9. Policzyć siłę w najbardziej obciążonym palu fundamentu pod
dwa słupy, przedstawionego na rysunku obok. Zastosować
metodę sztywnego oczepu. Pominąć ciężar oczepu.

Zadanie nadliczbowe: policzyć siły we wszystkich

narożnych palach fundamentu (zaznaczonych na szaro)

Dane:

V

1

= 10000 kN, M

1

= 12000 kNm

V

2

= 6000 kN, M

2

= 7000 kNm

10. Sprawdzić czy wypadkowa obciążeń charakterystycznych
przekazywanych na grunt przez podstawę fundamentową
ściany oporowej znajduje się w rdzeniu tej podstawy oraz
policzyć wartości nacisków na grunt.

Przyjąć parcie graniczne gruntu zasypowego

o poziomym kierunku działania. Ciężar objętościowy betonu
przyjąć

γ

b

= 25 kN/m

3

.

11.

Oszacować według polskiej normy nośność na

wciskanie pala wbijanego, zagłębionego w

gruncie

przedstawionym obok.

Dane:

- współczynniki technologiczne: S

p

= 1.2, S

s

= 1.1

- opory dla P

d

:

I

D

= 0.33

→ q

(n)

= 1650 kPa, t

(n)

= 31 kPa

I

D

= 0.67

→ q

(n)

= 2700 kPa, t

(n)

= 62 kPa

P=1000 kN

q=150 kN/m M=450 kNm

T=200 kN

2.0

1.0 2.0

2.0 1.0

4:1

(1) (2) (3)

(4)

P

M

y

M

x

1 3.0

3.0 1

4.

0

4.0

1

1

4.0

0.

5

0.5

3.5 4.5

M

1

M

2

V

1

V

2

2.0

2.0 2.0 2.0

2.

0

2.

0

2.

0

1.0

1.0

P

d

,

φ = 30°

γ=18kN/m

3

0.8

1.4

0.8

0.8

0.00

- 1.0

+ 4.0

0.5

Q

Torf

γ=12kN/m

3

γ’=5kN/m

3

D=0.5 m

0.00

- 2.00

- 12.00

P

d

,

I

D

=0.60

γ=18kN/m

3

γ’=10kN/m

3

- 8.00

świeży nasyp

P

d

, I

D

=0.40

γ=17kN/m

3

zwg

3

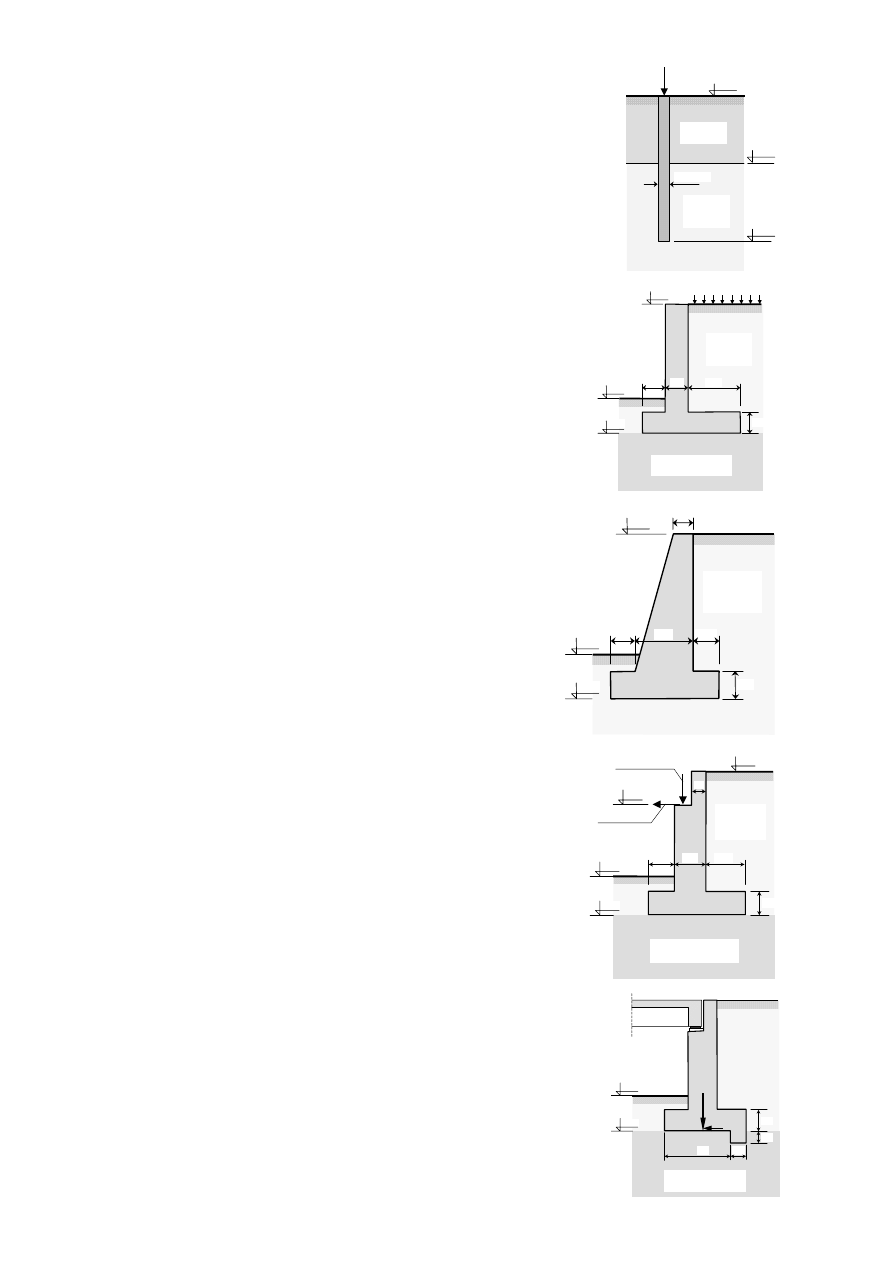
12. Obliczyć nośność na wciskanie i wyciąganie pala wierconego w
gruncie według polskiej normy.

Dane: współczynniki technologiczne: S

p

= 0.9, S

s

= 0.9

opory dla Pd: I

D

= 0.33

→ q

(n)

= 1650 kPa, t

(n)

= 31 kPa

I

D

= 0.67

→ q

(n)

= 2700 kPa, t

(n)

= 62 kPa

13. Sprawdzić warunek równowagi sił poziomych dla ściany
oporowej przedstawionej na rysunku obok. Przyjąć parcie graniczne
gruntu zasypowego o poziomym kierunku działania. Sprawdzenia
dokonać na wartościach obliczeniowych obciążeń i parametrów,
przyjmując dla wszystkich obciążeń

γ

f

= 1.1 lub 0.9, a dla parametrów

geotechnicznych podłoża gruntowego

γ

m

= 0.9. Ciężar objętościowy

betonu przyjąć 25 kN/m

3

.

Pytania dodatkowe:

- sprawdzić położenie wypadkowej obciążeń względem

podstawy fundamentu

- obliczyć wartości nacisków na grunt pod fundamentem.

14. Sprawdzić czy wypadkowa obciążeń charakterystycznych
przekazywanych na grunt przez podstawę fundamentową
ściany oporowej znajduje się w rdzeniu tej podstawy oraz
policzyć wartości nacisków na grunt.

Przyjąć parcie graniczne gruntu zasypowego

o poziomym kierunku działania. Ciężar objętościowy betonu
przyjąć

γ

b

= 25 kN/m

3

.

15. Sprawdzić warunek równowagi sił poziomych dla ściany przyczółka
przedstawionego na rysunku obok. Przyjąć parcie graniczne gruntu
zasypowego o poziomym kierunku działania. Sprawdzenia dokonać na
wartościach obliczeniowych obciążeń i parametrów, przyjmując dla
wszystkich obciążeń

γ

f

= 1.1 lub 0.9, a dla parametrów geotechnicznych

podłoża gruntowego

γ

m

= 0.9. Ciężar objętościowy betonu przyjąć 25

kN/m

3

. Obliczenia wykonać dla 1mb przyczółka.

Polecenia dodatkowe:

- sprawdzić położenie wypadkowej obciążeń względem środka

podstawy fundamentu

- obliczyć wartości nacisków na grunt pod fundamentem.
- sprawdzić warunek nośności pionowej podłoża gruntowego
- sprawdzić stateczność na obrót

16. Sprawdzić nośność poziomą podłoża gruntowego pod fundamentem przy-

czółka przedstawionego na rysunku poniżej. Długość przyczółka (w kie-
runku prostopadłym do mostu) wynosi L = 10 m.

Dla

obciążeń przyjąć współczynniki

γ

f

= 1

±0.1, a dla parametrów geo-

technicznych

γ

m

= 1

±0.1.

Przyjąć m

t

= 0.9.

P

d

,

φ = 30°

γ=18kN/m

3

p = 10 kN/m

2

G

p

,

φ = 15°, c = 20 kPa

0.8

0.8

2.0

0.8

± 0.00

- 1.2

+ 4.5

Q

Torf

γ=12kN/m

3

D=0.5 m

± 0.00

- 4.00

- 10.00

P

d

,

I

D

=0.60

γ=18kN/m

3

P

d

,

φ = 30°

γ=18kN/m

3

0.8

1.4

0.8

0.8

0.00

- 1.0

+ 4.0

0.5

P

s

,

φ = 33°

γ=18kN/m

3

G

p

,

φ = 15°, c = 20 kPa

1.2

1.2

2.0

1.0

± 0.00

- 1.2

+ 6.0

+ 4.5

R

v

= 150 kN/m

H = 35 kN/m

0.4

G

p

,

φ = 15°, c = 20 kPa

1.0

± 0.00

- 1.2

0.6

0.6

3.0

N

k

T

k

4

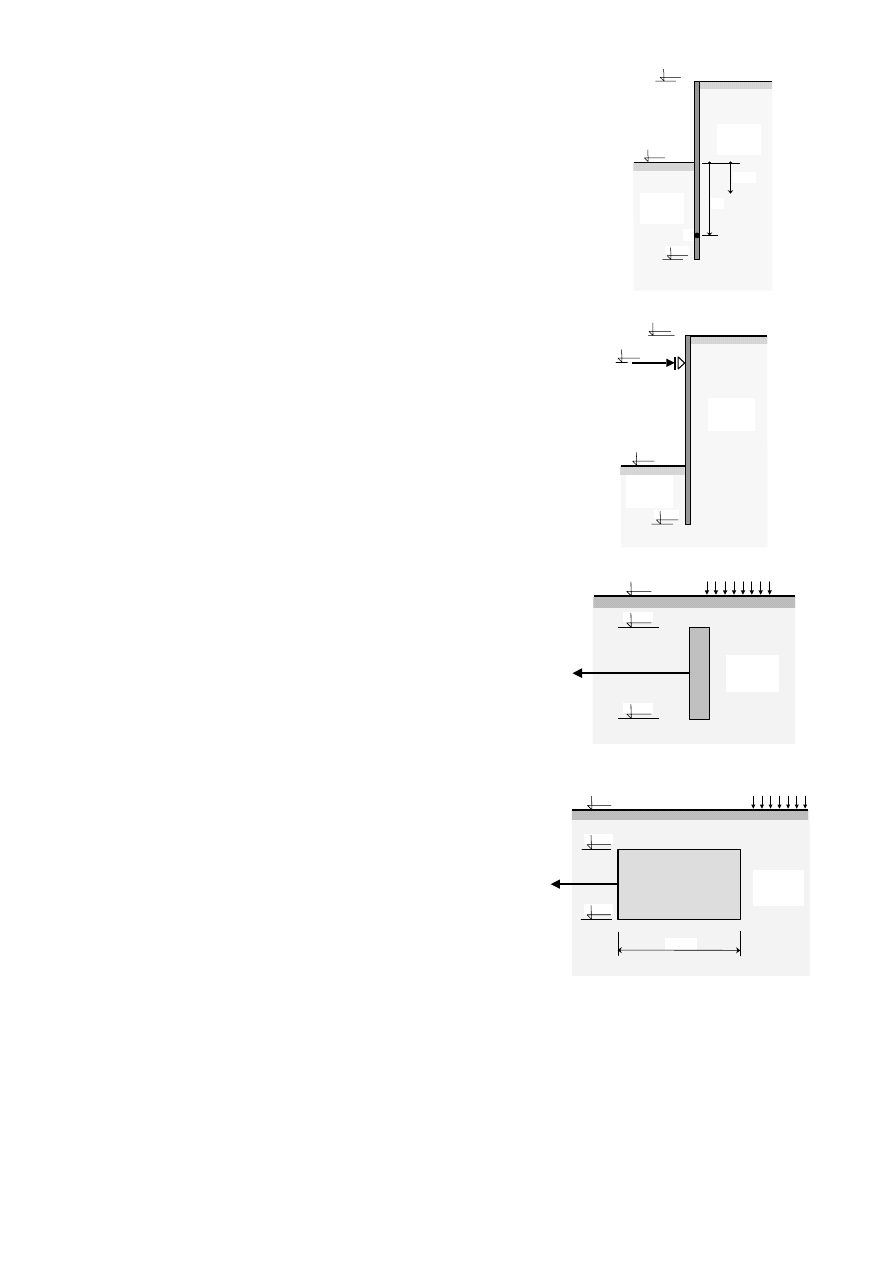
17. Obliczyć maksymalną charakterystyczną wartość momentu
zginającego w ściance szczelnej przedstawionej na rysunku obok.
Parcie i odpór gruntu przyjąć graniczne i poziome.

Pytania dodatkowe:

- wyznaczyć głębokość występowania maksymalnego momentu

zginającego (y

Mmax

)

- wyznaczyć głębokość położenia punktu F, w którym występuje

zerowy moment w ściance szczelnej (M = 0).

18. Obliczyć wartość charakterystyczną siły w ściągu S ścianki
szczelnej przedstawionej na rysunku obok, dołem swobodnie
podpartej w gruncie. Przyjąć graniczne i poziome parcie oraz odpór
gruntu.

Pytania dodatkowe:

- sprawdzić czy wystarczająca jest głębokość wbicia ścianki szczelnej

- obliczyć wartość charakterystyczną maksymalnego momentu

zginającego w ściance szczelnej

- wyznaczyć głębokość zerowania się wykresów parcia i odporu

gruntu działających na ściankę szczelną

19. Sprawdzić nośność zakotwienia ścianki szczelnej z płyty
kwadratowej, przedstawionej na rysunku obok. Przyjąć graniczne
i poziome parcie oraz odpór gruntu. Analizy dokonać na wartościach
charakterystycznych obciążeń i parametrów. Współczynnik
wyrażający przestrzenność działania odporu gruntu przyjąć

β = 2.

Rozstaw ściągów wynosi a = 2.4 m. Siła w pojedynczym ściągu
wynosi S = 80 kN, obciążenie naziomu – p = 10 kN/m

2

.

20. Sprawdzić nośność zakotwienia blokowego ścianki szczelnej,
przedstawionego na rysunku obok. Parcie i odpór gruntu na ściany
czołową i tylną przyjąć graniczne i poziome. Kąt tarcia gruntu o
powierzchnie boczne, dolną i górną bloku przyjąć równy

δ = φ/2.

Przekrój poprzeczny bloku jest kwadratowy. Współczynnik
przestrzenności działania odporu gruntu przyjąć

β = 2. Ciężar

objętościowy betonu przyjąć 24 kN/m

3

. Rozstaw ściągów wynosi a =

2.4 m. Siła w pojedynczym ściągu wynosi S = 120 kN, obciążenie
naziomu – p = 10 kN/m

2

Przygotowanie:

Dr inż. Adam Krasiński

Katedra

Geotechniki,

Geologii

i

Bud.

Morskiego

P

d

,

φ = 30°

γ=18kN/m

3

- 6.5

± 0.0

– 3.0

P

d

,

φ = 30°

γ=18kN/m

3

F

y

F

y

Mmax

P

d

,

φ = 30°

γ=18kN/m

3

- 7.0

± 0.0

– 5.0

P

d

,

φ = 30°

γ=18kN/m

3

– 1.0

S

S

p

- 1.5

- 0.5

± 0.0

P

s

,

φ = 33°

γ=18 kN/m

3

S

p

1.5 m

P

s

,

φ = 33°

γ=18 kN/m

3

- 1.5

- 0.5

± 0.0