1

Wstęp do fizyki kwantowej

Promieniowanie wysyłane przez ogrzane ciała nazywamy

promieniowaniem termicznym.

1) Promieniowanie (i absorpcja) ciała doskonale czarnego

KWANTOWA TEORIA ŚWIATŁA

Modelowe ciało

doskonale czarne

charakteryzuje

si

ę

tym,

ż

e pochłania całkowicie padaj

ą

ce na

ń

promieniowanie i posiada maksymaln

ą

zdolno

ść

emisyjn

ą

promieniowania.

Dla ciała tego wyst

ę

puje

stan równowagi

, tzn. ciało

w jednostce czasu pochłania tyle energii, ile
wypromieniowuje

Model ciała doskonale czarnego

lawa

sło

ń

ce

rozgrzane żelazo

kaloryfer

żarówka

2

1) Całkowita zdolno

ść

emisyjna zmienia si

ę

wraz z temperatur

ą

według

prawa Stefana-

Boltzmanna.

4

T

R

σ

=

σ

jest uniwersalną stałą (stała Stefana-Boltzmanna) równą 5.67·10

-8

W/(m

2

K

4

).

fakty do

ś

wiadczalne:

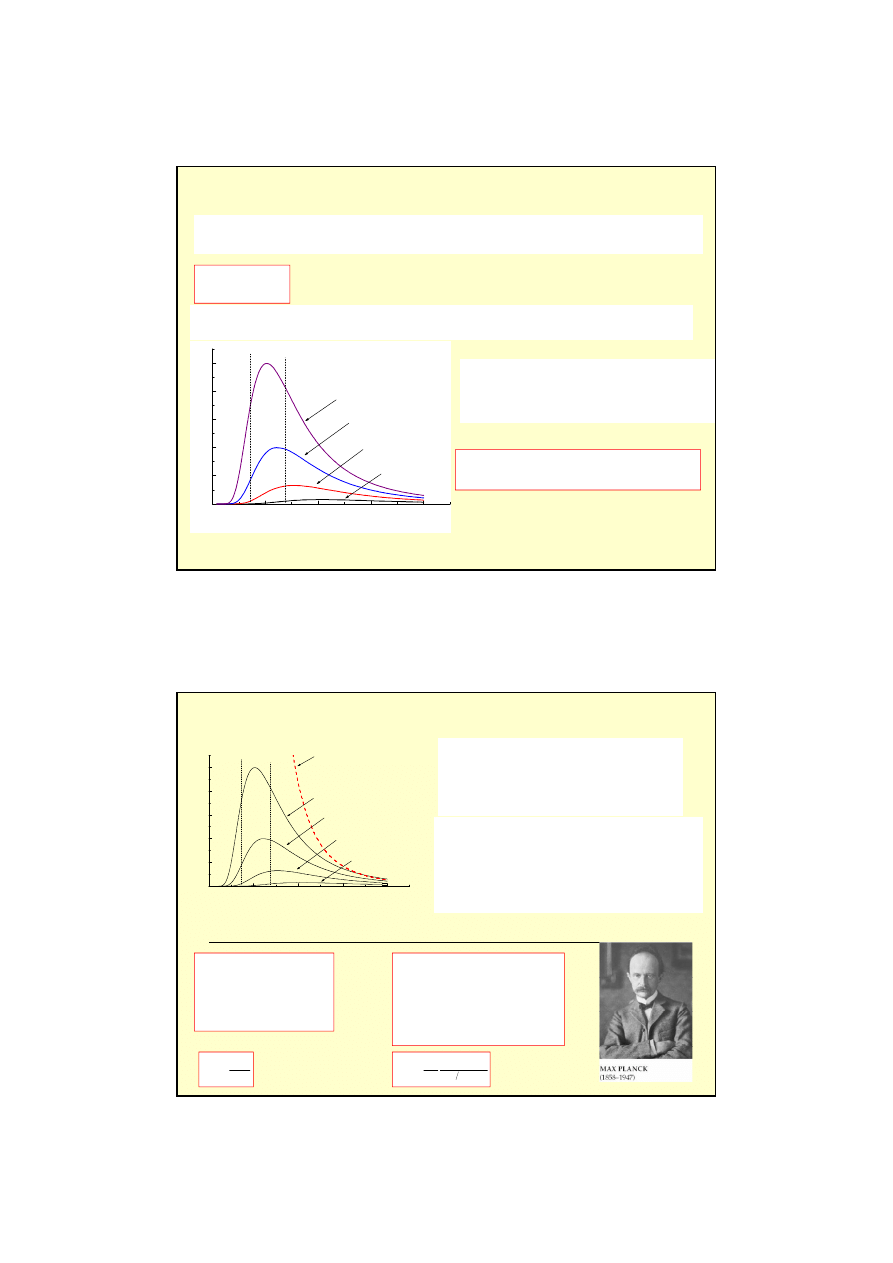
2) Widmowa zdolno

ść

emisyjna zale

ż

y tylko od temperatury i jest całkiem niezale

ż

ne od

materiału oraz kształtu i wielko

ś

ci ciała doskonale czarnego.

0.0

0.5

1.0

1.5

2.0

T = 3000 K

T = 4000 K

T = 5000 K

T = 6000 K

obszar widzialny

R

λ

λ

(

µ

m)

widmo ciała doskonale
czarnego

K

m

T

⋅

⋅

=

⋅

−

3

max

10

898

.

2

λ

3) Długo

ść

fali dla której przypada maksimum

emisji jest zgodnie z

prawem Wiena

odwrotnie proporcjonalna do temperatury
ciała.

0.0

0.5

1.0

1.5

2.0

T = 3000 K

T = 4000 K

T = 5000 K

T = 6000 K

obszar widzialny

klasyczna teoria

katastrofa w nadfiolecie

R

λ

λ

(

µ

m)

Rayleigh i Jeans

klasyczne obliczenia

energii promieniowania we wn

ę

ce (teoria

pola elektromagnetycznego, fale stoj

ą

ce)

widmowa zdolno

ść

emisyjna

katastrofa

w nadfiolecie.

Teoria promieniowania we wn

ę

ce, prawo Plancka (1900 rok, Nagroda

Nobla 1918)

Podstawowa ró

ż

nica mi

ę

dzy zdolno

ś

ci

ą

emisyjn

ą

wyliczon

ą

z powy

ż

szych teorii:

Stoj

ą

ce fale

elektromagnetyczne
według Rayleigha i
Jeansa mog

ą

mie

ć

dowolne energie

4

0

λ

λ

T

c

R

=

Fizyka

klasyczna

1

1

2

5

1

−

=

T

c

e

c

R

λ

λ

λ

Oscylatory (oraz fale stoj

ą

ce)

według Plancka, nie mog

ą

mie

ć

dowolnej energii, ale

tylko

ś

ci

ś

le okre

ś

lone warto

ś

ci

dane wzorem E= nh

ν

(n=1,2,.....)

Fizyka

kwantowa

Planck

nowa teoria promieniowania ciała

doskonale czarnego: Ka

ż

dy atom zachowuje si

ę

jak oscylator elektromagnetyczny posiadaj

ą

cy

charakterystyczn

ą

cz

ę

stotliwo

ść

ν

drga

ń

i

energi

ę

E= nh

νννν

(n=1,2,.....). Drgaj

ą

ce atomy

wytwarzaj

ą

stoj

ą

ce fale elektromagnetyczne.

3

ν

h

n

E

=

ν

częstość drgań oscylatora, h jest stałą (zwaną obecnie stałą Plancka)

h = 6.63·10

-34

Js = 4,136 ·10

-15

eV·s (1eV=1.6·10

-19

J)

n

pewną liczbę całkowitą (zwaną obecnie

liczbą kwantową

)

Oscylatory nie wypromieniowuj

ą

energii w sposób ci

ą

gły, lecz porcjami czyli kwantami,

gdy oscylator przechodzi ze stanu (kwantowego ) o danej energii do drugiego o innej,
mniejszej energii.

ν

h

E

=

∆

zmiana liczby kwantowej n o jedno

ść

Energia oscylatora mo

ż

e przyjmowa

ć

tylko

ś

ci

ś

le okre

ś

lone warto

ś

ci, jest skwantowana;

Dopóki oscylator pozostaje w jednym ze swoich stanów kwantowych dopóty ani nie emituje ani
nie absorbuje energii. Mówimy,

ż

e znajduje si

ę

w

stanie stacjonarny

.

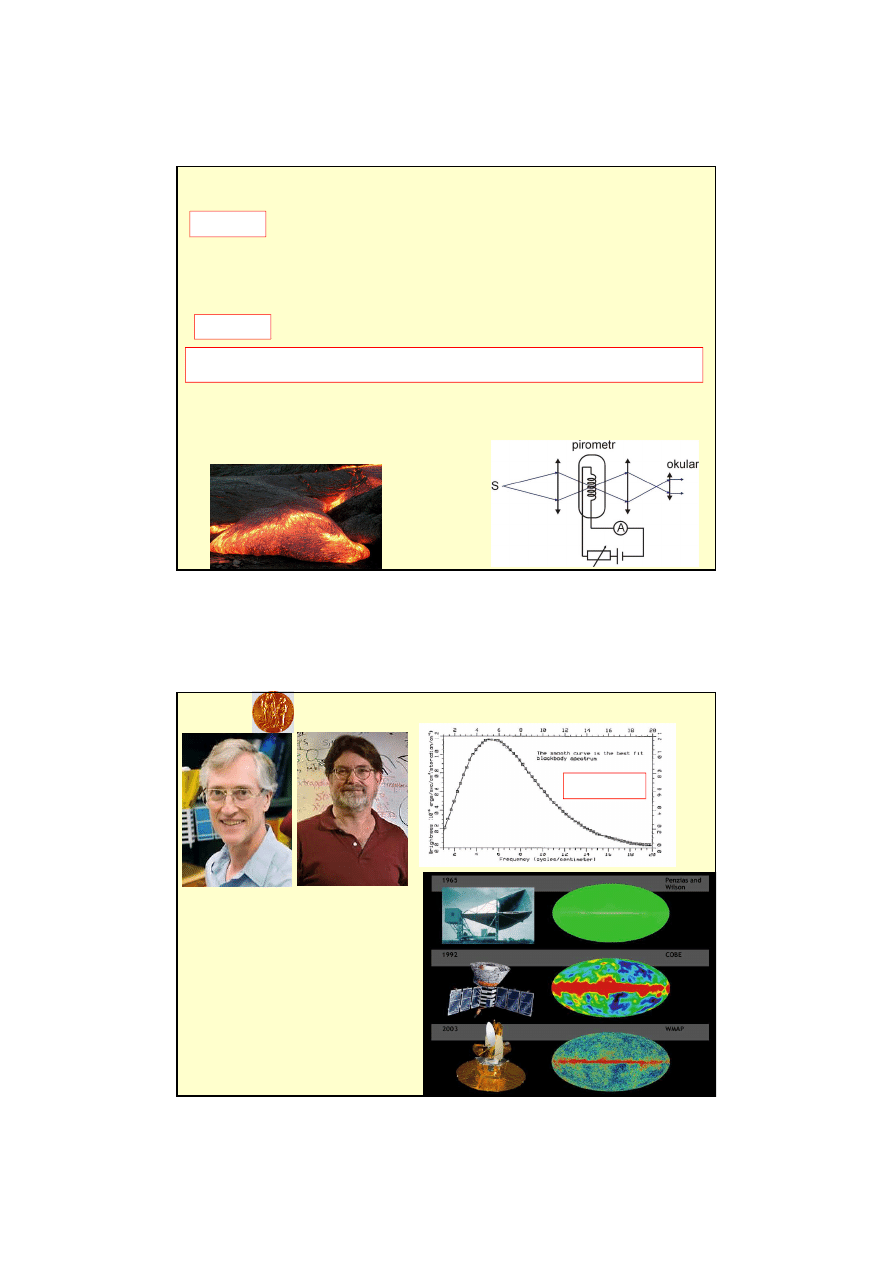
Zastosowanie prawa promieniowania

Pomiar tempetatury:

porównanie promieniowania jasno

ś

ci (i barwy) włókna lampy z

promieniuj

ą

cym ciałem

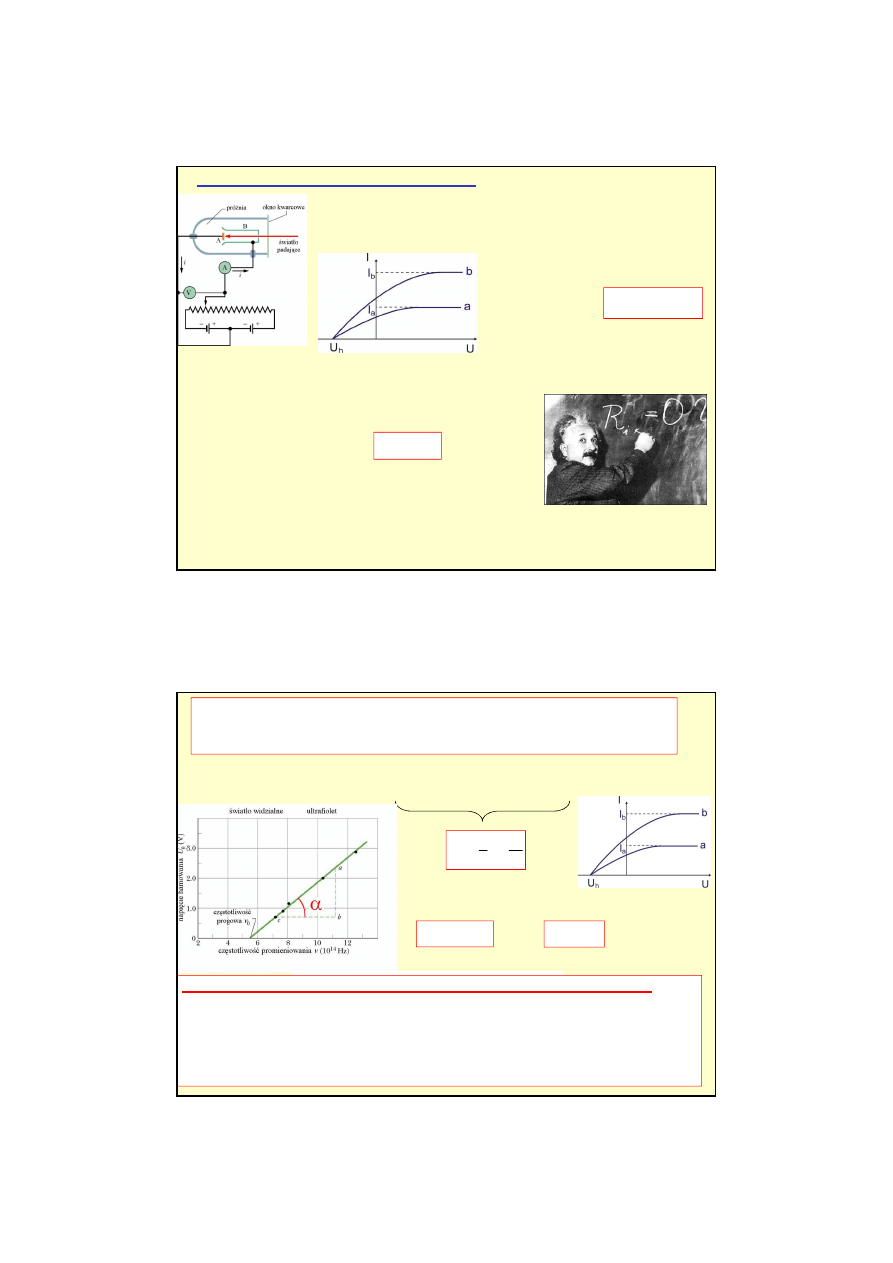
University of California
Berkeley, CA, USA

"for their discovery
of the blackbody form and
anisotropy of the cosmic
microwave background
radiation"

John C. Mather

George F. Smoot

NASA
Goddard Space Flight Center
Greenbelt, MD, USA

The Nobel Prize in Physics 2006

K

T

7

.

2

=

λ

max

=

1,1 mm

4

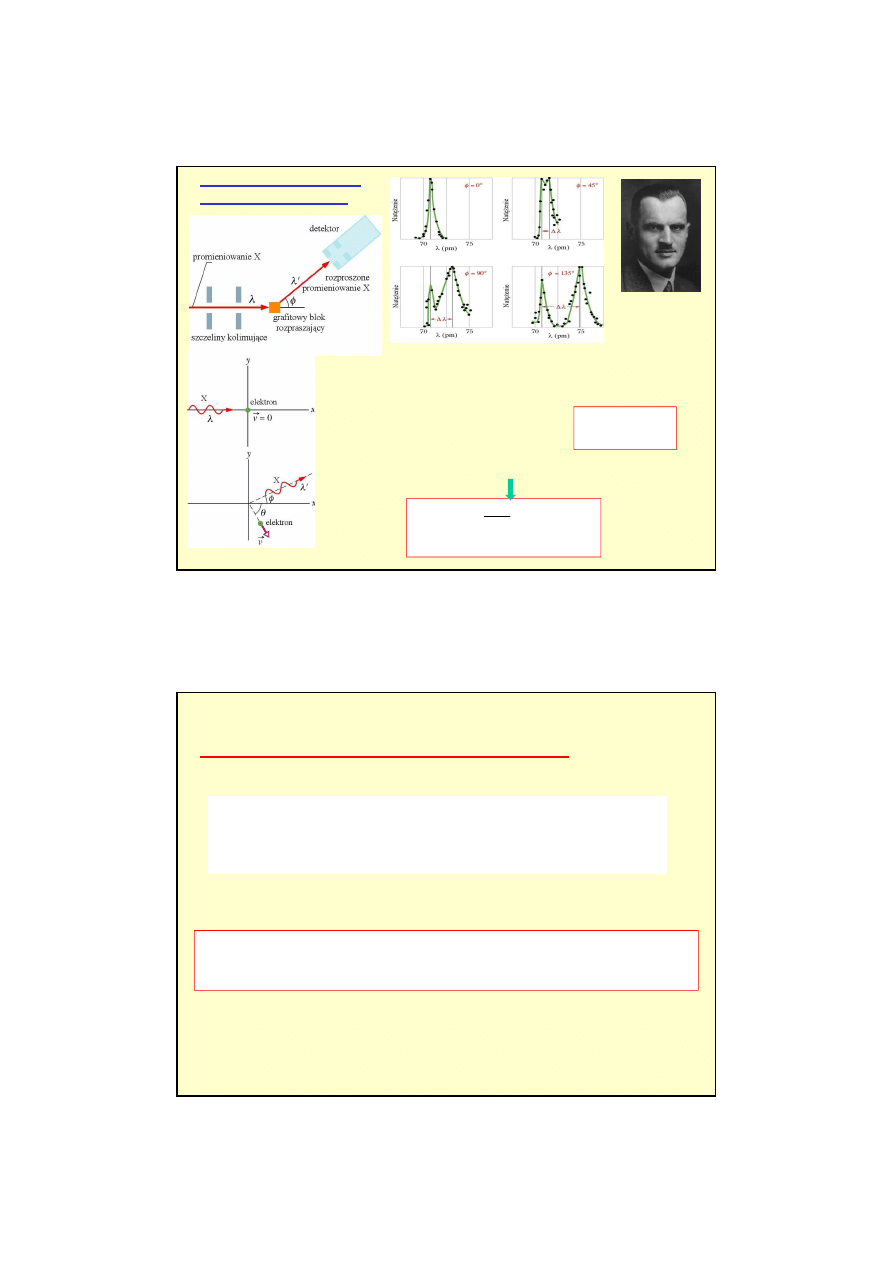
Zjawisko fotoelektryczne zewn

ę

trzne polega na wyrzucaniu elektronów

(zwanych fotoelektronami) z powierzchni ciała stałego pod wpływem
padaj

ą

cego promieniowania.

2) Zjawisko fotoelektryczne zewn

ę

trzne

Dwie krzywe dla tej
samej cz

ę

stotliwo

ś

ci

i ró

ż

nych nat

ęż

e

ń

padaj

ą

cego

ś

wiatła.

h

eU

E

=

kmax

Einstein:

energia wi

ą

zki

ś

wietlnej rozchodzi si

ę

w przestrzeni w

postaci sko

ń

czonych porcji (kwantów) energii zwanych fotonami

hv

E

=

energia fotonu:

Einstein:

•

Kwanty

ś

wiatła rozchodz

ą

si

ę

w przestrzeni jak cz

ą

stki materii.

•

Gdy foton zderzy si

ę

z elektronem w metalu to mo

ż

e zosta

ć

przez elektron

pochłoni

ę

ty. Wówczas energia fotonu zostanie przekazana elektronowi.

Kwantowa teoria Einsteina zjawiska fotoelektrycznego ( Nagroda
Nobla 1921)

kmax

E

W

hv

+

=

h

eU

E

=

kmax

e

W

v

e

h

U

h

−

=

Je

ż

eli do wyrwania elektronu z metalu potrzebna jest energia

W

to wówczas:

kmax

E

W

hv

+

=

Praca wyj

ś

cia

W

to energia potrzebna do wyrwania elektronu z metalu - jest ona charakterystyczna dla

danego metalu.

np. Cez W = h

ν

0

= 2.14 eV (

λ

0

~ 0. 581

µ

m =>

ν

0

=c/

λ

0

~ 5.16*10

14

Hz)

Z regresji liniowej mo

ż

na wyznaczy

ć

:

α

tg

e

h

=

0

hv

W

=

oraz

Zjawisko fotoelektryczne zachodzi
dla promieniowania ultrafioletowego i widzialnego

Teoria Einsteina: wyja

ś

nienie osobliwych wła

ś

ciwo

ś

ci zjawiska fotoelektrycznego:

1.

Dla cz

ę

stotliwo

ś

ci

ν

<

ν

0

niezale

ż

nie od nat

ęż

enia

ś

wiatła fotony nie maj

ą

dosy

ć

energii do

wywołania fotoemisji.

2.

Wi

ę

ksze nat

ęż

enie

ś

wiatła

wi

ę

cej fotonów (wi

ę

kszy fotopr

ą

d), ale nie zmieniona energia

E

kmax

,

nie zale

ż

y od nat

ęż

enia

ś

wiatła ale od cz

ę

stotliwo

ś

ci

ν

i pracy wyj

ś

cia W.

3.

Energia jest dostarczana w postaci skupionej (kwant, porcja) a nie rozło

ż

onej (fala);

elektron pochłania

natychmiast

cały kwant

brak opó

ź

nienia czasowego emisji elektronu.

5

Wi

ą

zka promieni X

strumie

ń

fotonów o energii

h

ν

.

Fotony (

jak cz

ą

stki

) zderzaj

ą

si

ę

z elektronami

swobodnymi w bloku grafitu.

Efekt Comptona (1922,
Nagroda Nobla 1927)

Arthur Holly Compton

(1892 – 1962)

/

/

/

f

f

f

E

h

hc

p

E

c

h

ν

λ

λ

=

=

=

=

Z zasady zachowania p

ę

du i energii wynika przesuni

ę

cie Comptona

∆λ

.

0

0

(1 cos )

e

e

h

m c

m

masa spoczynkowa elektronu

λ λ λ

ϕ

′

∆ = − =

−

−

Promieniowanie rentgenowskie
lub

γ

keV-MeV

2

2

2

2

4

0

0(

)

(

) :

:

0

fotonu

dla fotonu TW

E

p c

m c

gdzie m

−

=

=

Teoria promieniowanie ciała doskonale czarnego,zjawisko fotoelektryczne, efekt
Comptona

teoria fotonowa

Zjawiska dyfrakcji, interferencji, polaryzacji

teoria falowa.

Natura

ś

wiatła jest zło

ż

ona (dualizm korpuskularno-falowy) :

w pewnych warunkach zachowuje si

ę

jak fala, w innych jak cz

ą

stka,

czyli foton.

WNIOSKI WYNIKAJ

Ą

CE Z OMAWIANYCH ZJAWISK:

6

Model Thomsona:

ujemnie naładowane elektrony s

ą

równomiernie rozło

ż

one wewn

ą

trz

obszaru wypełnionego w sposób ci

ą

gły ładunkiem dodatnim. Ładunek dodatni tworzył kul

ę

o

promieniu rz

ę

du 10

-10

m.

Model Rutherforda:

ładunek dodatni nie jest rozło

ż

ony równomiernie wewn

ą

trz atomu, ale

skupiony w małym obszarze zwanym j

ą

drem (o rozmiarze 10

-15

- 10

-14

m) le

żą

cym

w

ś

rodku atomu.

Do

ś

wiadczenie

:

rozpraszania cz

ą

stek alfa

na atomach złota

MODEL BOHRA ATOMU WODORU

Model atomu

Zgodnie z modelem j

ą

drowym Rutherforda:

•

Masa jądra jest w przybliżeniu równej masie całego atomu,

•

Ładunek jądra jest równy iloczynowi liczby atomowej Z i ładunku
elektronu e,

•

Wokół jądra znajduje się Z elektronów, tak że cały atom jest
obojętny. Elektrony krążą po orbitach.

1) Problem

Zgodnie elektrodynamik

ą

klasyczn

ą

ka

ż

de

naładowane ciało poruszaj

ą

ce si

ę

ruchem przyspieszonym

wysyła promieniowanie elektromagnetyczne

elektron

kr

ążą

cy po orbicie traci energi

ę

mechaniczn

ą

„spada” na

j

ą

dro

Problemy z planetarnym modelem atomu atomu

2) Przełomowe do

ś

wiadczenie

:

pomiar

promieniowania emitowanego

przez gazy

pobudzone do

ś

wiecenia metod

ą

wyładowania elektrycznego.

widmo ciągłe

(np. ciała ogrzane do

wysokich temperatur ,)

emisyjne widmo
liniowe

atomu wodoru

absorpcyjne widmo
liniowe

atomu wodoru

Pojedyncze atomy (cz

ą

steczki) emituj

ą

i

absorbuj

ą

promieniowanie

o

ś

ci

ś

le

okre

ś

lonych długo

ś

ciach fal

.

7

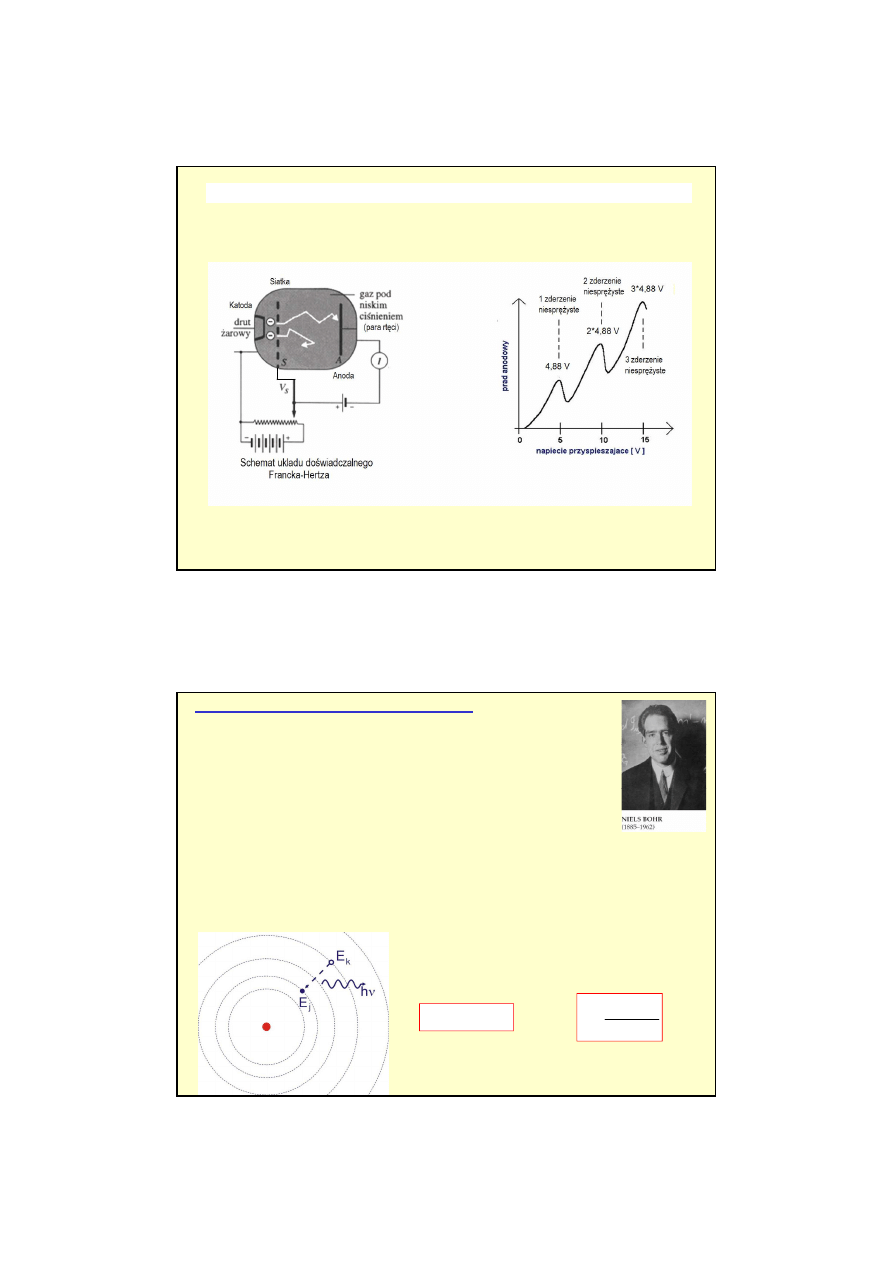
Drugie przełomowe do

ś

wiadczenie

:

DO

Ś

WIADCZENIE FRANCKA-HERTZA (1914)

Atomy rt

ę

ci absorbuj

ą

ś

ci

ś

le okre

ś

lone porcje

energii elektronów podczas

zderze

ń

niespr

ęż

ystych.

Kwantowy model Bohra atomu wodoru

Emisja fotonu przy zmianie orbity elektronu

h

E

E

v

j

k

−

=

h

ν

jest energi

ą

fotonu, który zostaje w trakcie

przej

ś

cia wypromieniowany przez atom.

j

k

E

E

h

−

=

ν

Kwantowe postulaty Bohra:
1. Elektron mo

ż

e porusza

ć

si

ę

tylko po pewnych

dozwolonych orbitach

.

2. Atom wodoru mo

ż

e znajdowa

ć

si

ę

tylko

ś

ci

ś

le

okre

ś

lonych stacjonarnych

stanach energetycznych

(całkowita energia pozostaje stała). Elektron

mimo,

ż

e doznaje przyspieszenia do

ś

rodkowego nie wypromieniowuje

energii.

3. Promieniowanie elektromagnetyczne zostaje wysłane tylko wtedy gdy

elektron poruszaj

ą

cy si

ę

po orbicie o całkowitej energii E

k

zmienia swój ruch

skokowo

, tak

ż

e porusza si

ę

nast

ę

pnie po orbicie o ni

ż

szej energii E

j

.

8

r

e

E

0

2

p

4

πε

−

=

r

e

m

E

0

2

2

8

2

1

πε

=

=

v

k

Hipoteza Bohra dotycz

ą

ca kwantyzacji parametrów orbity

moment p

ę

du elektronu

musi by

ć

całkowit

ą

wielokrotno

ś

ci

ą

stałej Plancka podzielonej przez 2

π

(elektron mo

ż

e

porusza

ć

si

ę

tylko po takich orbitach).

r

m

r

e

2

2

2

0

v

4

1

=

πε

,.....

2

,

1

,

2

v

=

=

=

n

h

n

r

m

L

π

energia
całkowita < 0

r

e

E

E

E

p

k

0

2

8

πε

−

=

+

=

Elektron porusza si

ę

po orbitach kołowych o promieniu

r pod wpływem siły Coulomba.

mr

e

0

2

4

v

πε

=

mr

h

n

π

2

v

=

1

2

2

0

2

2

r

n

me

h

n

r

n

=

=

π

ε

,....

2

,

1

=

n

n = 1 tzw. stan podstawowy, E

1

= −13.6 eV; n

∞

E = 0, elektron usuni

ę

ty poza atom

kwantowanie orbitalnego momentu p

ę

du elektronu

kwantowanie energii całkowitej

(warto

ś

ci

r, E

k

, E

p

, E, L

s

ą

równie

ż

skwantowane).

2

1

2

2

2

0

4

1

8

n

E

n

h

me

E

n

=

−

=

ε

,....

2

,

1

=

n

E

1

= −13.6 eV

wartości energii dozwolonych stanów stacjonarnych

Stany energetyczne i widmo atomowe wodoru

,.....

2

,

1

8

2

1

2

2

2

0

4

=

=

−

=

n

n

E

n

h

me

E

n

ε













−

=













−

=

−

=

=

2

2

2

2

1

1

1

*

[eV]

13.6

1

1

k

j

j

k

E

E

E

c

h

h

j

k

λ

ν

Kwantowy model Bohra budowy atomu
pozwala zrozumie

ć

własno

ś

ci widm

emisyjnych i absorpcyjnych atomu wodoru i
jonów jednoelektronowych.

Model Bohra nie wyja

ś

nia dlaczego poj

ęć

mechaniki klasycznej nie mo

ż

na

stosowa

ć

w

ś

wiecie atomów (cz

ą

stek elementarnych).

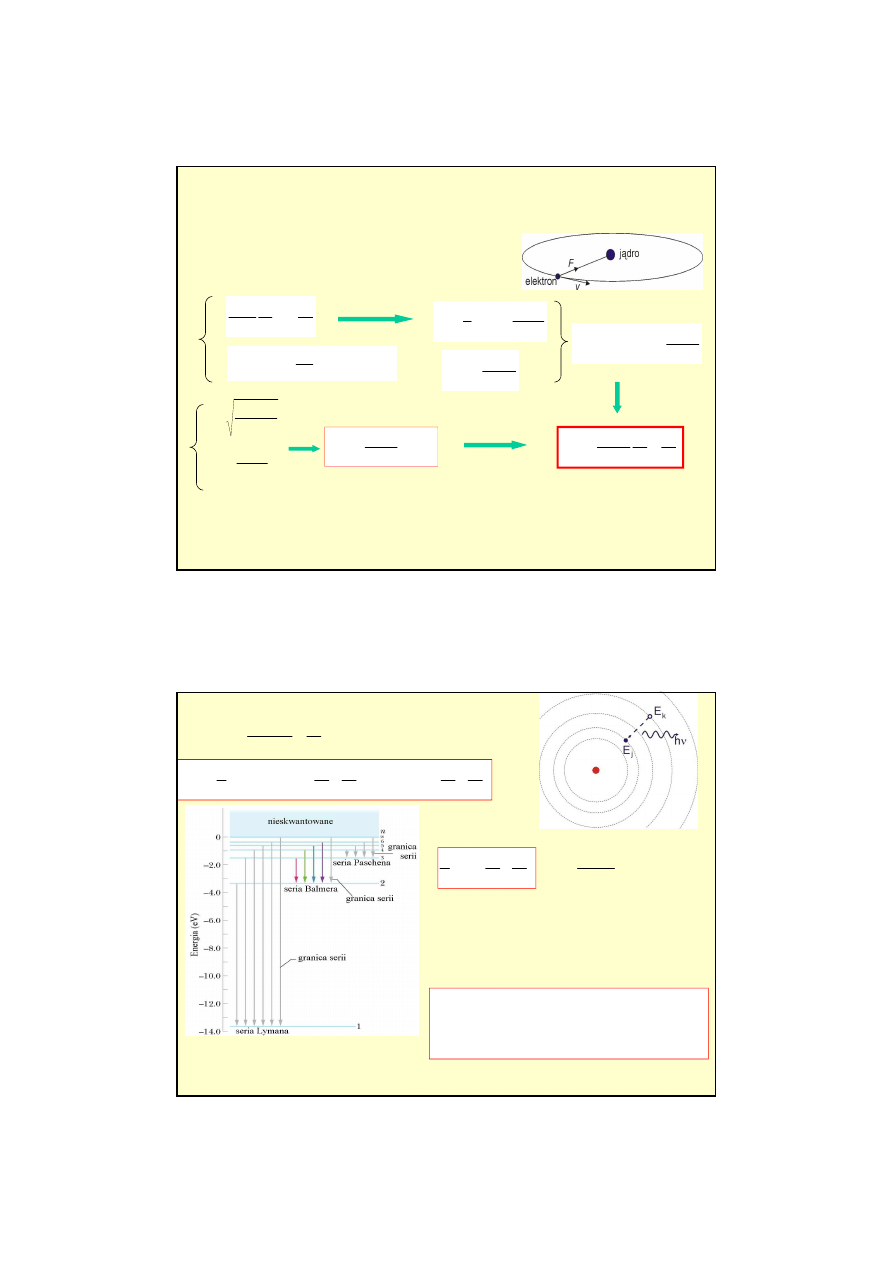
Przej

ś

cia pomi

ę

dzy stanami stacjonarnymi

i odpowiadaj

ą

ce im linie widmowe tworz

ą

serie widmowe.

91-122 nm

nadfiolet

365-656 nm

nadfiolet
i światło

widzialne

820-1875 nm

podczerwień

4

7

1

2

3

0

1.1*10

8

me

R

m

h c

ε

−

=

=

stała Rydberga

2

2

1

1

1

R

j

k

λ





=

−







