MO

Z4/19. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 19

1

Z4/19. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH –

ZADANIE 19

Z4/19.1. Zadanie 19

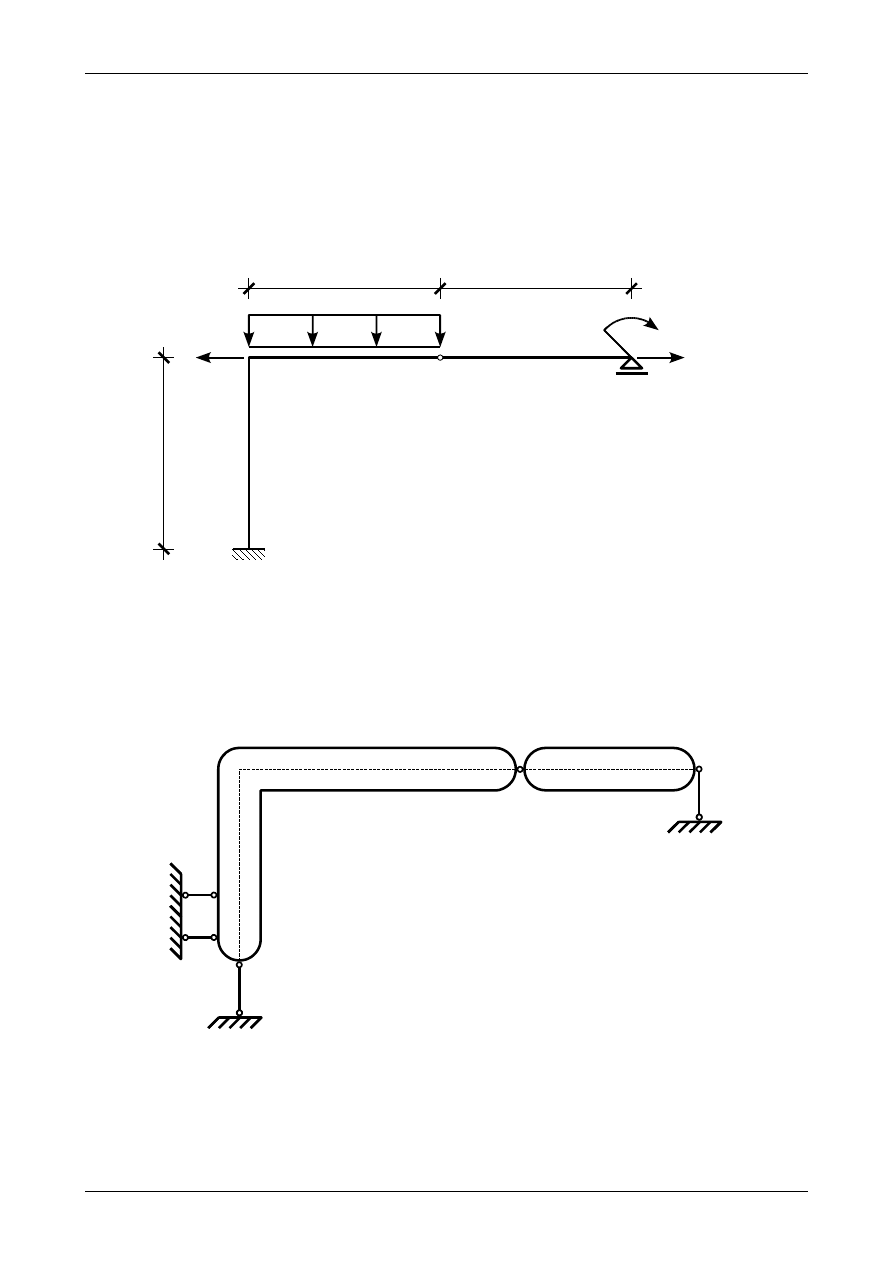
Narysować metodą ogólną wykresy sił przekrojowych dla ramy płaskiej przedstawionej na rysunku

Z4/19.1. Wymiary ramy podane są w metrach.

30,0 kNm

20,0 kN

15,0 kN/m

40,0 kN

A

B

C

D

3,0

3,0

3,0

[m]

Z4/19.1. Rama płaska

Z4/19.2. Analiza kinematyczna belki

Rysunek Z4/19.2. przedstawia ramę płaską traktowaną w analizie kinematycznej jako płaski układ

tarcz sztywnych.

1

4

2

3

C

I

II

Rys. Z4/19.2. Rama jako płaska tarcza sztywna

Układ tarcz sztywnych na rysunku Z4/19.2 posiada sześć stopni swobody. Jest on podparty czterema

prętami podporowymi 1, 2, 3 i 4 oraz przegubem rzeczywistym C. Wszystkie te więzy odbierają razem także
sześć stopni swobody. Został więc spełniony warunek konieczny geometrycznej niezmienności (1.4). Rama
może więc być układem geometrycznie niezmiennym i statycznie wyznaczalnym.

Dr inż. Janusz Dębiński

Zaoczni

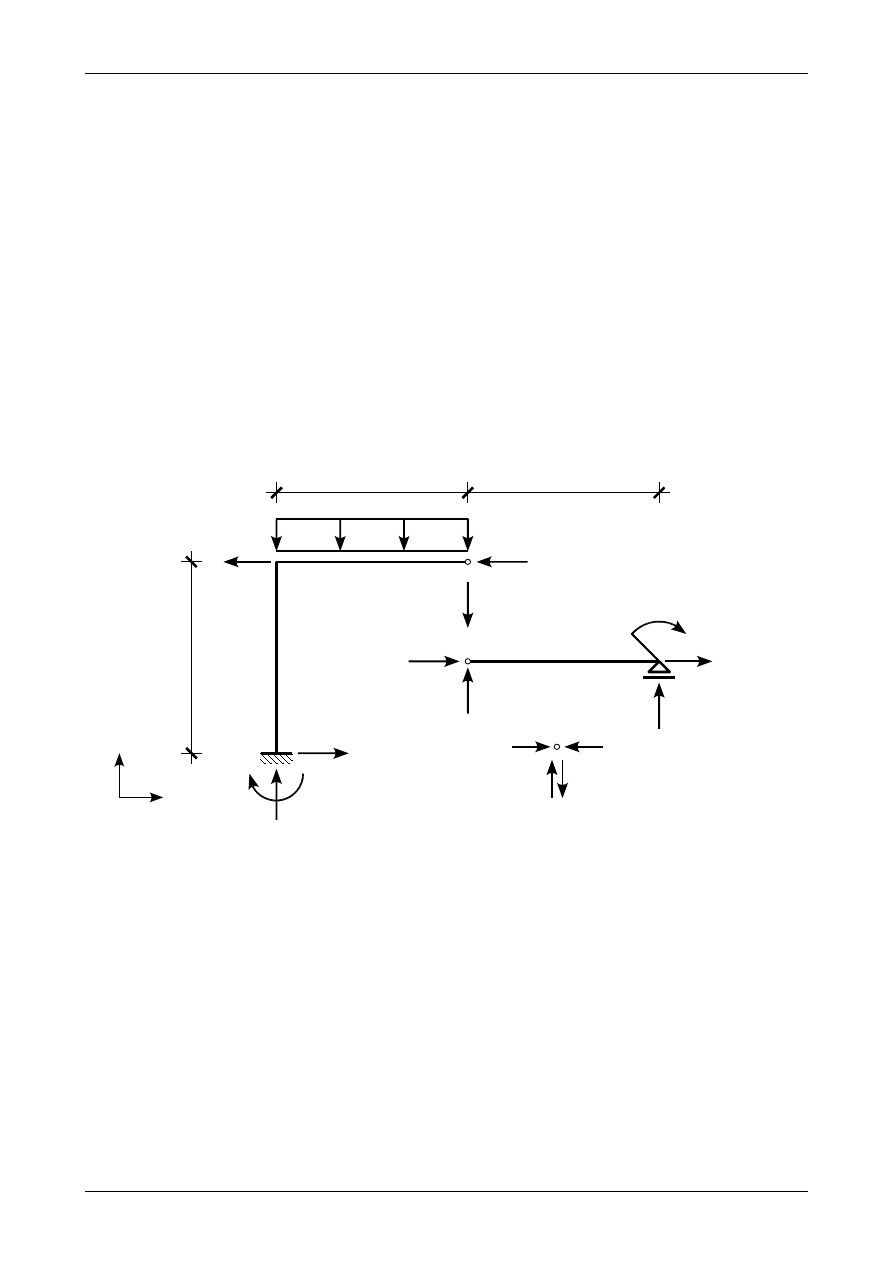
MO

Z4/19. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 19

2

Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie

przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
dla tej tarczy sztywnej. Jest więc ona geometrycznie niezmienna i statycznie wyznaczalana. Stanowi ona
podłoże dla tarczy sztywnej numer II.

Tarcza sztywna numer II jest podparta przegubem rzeczywistym C oraz prętem podporowym numer 4.

Przegub rzeczywisty C nie leży na kierunku pręta podporowego numer 4. Został więc spełniony warunek
dostateczny geometrycznej niezmienności dla tej tarczy sztywnej. Jest więc ona geometrycznie niezmienna i
statycznie wyznaczalana.

Ponieważ obie tarcze sztywne są geometrycznie niezmienne i statycznie wyznaczalne możemy więc

stwierdzić, że cały płaski układ tarcz sztywnych jest geometrycznie niezmienny i statycznie wyznaczalny.
Możemy więc przystąpić do dalszych obliczeń.

Z4/19.3. Wyznaczenie reakcji podporowych

Aby wyznaczyć wartości i zwroty reakcji podporowych w ramie płaskiej musimy najpierw przyjąć ich

dodatnie zwroty. Rysunek Z4/19.3 przedstawia założone zwroty reakcji we wszystkich podporach ramy.

15,0 kN/m

40,0 kN

A

B

C

3,0

3,0

3,0

[m]

30,0 kNm

20,0 kN

C

D

C

V

C

(CD)

H

C

(CD)

H

C

(AC)

V

C

(AC)

H

C

(CD)

V

C

(CD)

V

C

(AC)

V

C

(AC)

V

D

V

A

H

A

M

A

H

C

(AC)

X

Y

Rys. Z4/19.3. Założone zwroty reakcji podporowych

Zgodnie z rysunkiem Z4/19.3 wartości reakcji działających w przegubie rzeczywistym C spełniają

warunki.

H

C



AC



=

H

C



CD



,

(Z4/19.1)

V

C



AC



=

V

C



CD



.

(Z4/19.2)

Poziomą reakcję w przegubie rzeczywistym C wyznaczymy z równania sumy rzutów wszystkich sił

działających na pręt CD na oś poziomą X

Dr inż. Janusz Dębiński

Zaoczni

MO

Z4/19. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 19

3



X



CD



=

H

C



CD





20,0=0

H

C



CD



=−

20,0 kN

.

(Z4/19.3)

Reakcja ma zwrot przeciwny do założonego. Uwzględniając (Z4/19.1) otrzymamy

H

C



AC



=−

20,0 kN

.

(Z4/19.4)

Reakcja ma zwrot przeciwny do założonego.

Poziomą reakcję w utwierdzeniu A wyznaczymy z równania sumy rzutów wszystkich sił działających

na pręt AC na oś poziomą X



X



AC



=

H

A

−

H

C



AC



−

40,0=0

H

A

−



−

20,0



−

40,0=0

H

A

=

20,0 kN

.

(Z4/19.5)

Reakcja ma zwrot zgodny z założonym.

Wyznaczania reakcji pionowych zaczniemy od pręta CD, ponieważ na niego działają tylko dwie takie

reakcje, a my dysponujemy dwoma równaniami równowagi.

Pionową reakcję na podporze przegubowo-przesuwnej D otrzymamy z równania sumy momentów

wszystkich sił działających na pręt CD względem punktu C.



M

C



CD



=−

V

D

⋅

3,030,0=0

V

D

=

10,0 kN

.

(Z4/19.6)

Reakcja ma więc zwrot zgodny z założonym.

Pionową reakcję przegubie rzeczywistym C otrzymamy z równania sumy momentów wszystkich sił

działających na pręt CD względem punktu D.



M

D



CD



=

V

C



CD



⋅

3,030,0=0

V

C



CD



=−

10,0 kN

.

(Z4/19.7)

Reakcja ma więc zwrot przeciwny do założonego.

W celu sprawdzenia obliczeń reakcji pionowych zastosujemy równanie sumy rzutów wszystkich sił

działających na pręt CD na oś pionową Y.



Y



CD



=

V

C



CD





V

D

=−

10,010,0=0

.

(Z4/19.8)

Możemy więc stwierdzić, że pionowe reakcje działające na pręt CD zostały obliczone poprawnie i znajdują
się w równowadze.

Uwzględniając (Z4/19.2) otrzymamy

Dr inż. Janusz Dębiński

Zaoczni

MO

Z4/19. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 19

4

V

C



AC



=−

10,0 kN

.

(Z4/19.9)

Moment w utwierdzeniu A wyznaczymy z równania sumy momentów wszystkich sił działających na

pręt AC względem punktu A.



M

A



AC 

=

M

A

−

H

C



AC 

⋅

3,0



V

C



AC 

⋅

3,0

−

40,0

⋅

3,0



15,0

⋅

3,0

⋅

1
2

⋅

3,0

=

0

M

A

−



−

20,0



⋅

3,0

−

10,0

⋅

3,0

−

40,0

⋅

3,0



15,0

⋅

3,0

⋅

1
2

⋅

3,0

=

0

M

A

=

22,5 kNm

(Z4/19.10)

Reakcja ma więc zwrot zgodny z założonym.

Pionową reakcję w utwierdzeniu A wyznaczymy z równania sumy momentów wszystkich sił

działających na pręt AC względem punktu C.



M

C



AC



=

V

A

⋅

3,0M

A

−

H

A

⋅

3,0−15,0⋅3,0⋅

1
2

⋅

3,0=0

V

A

⋅

3,022,5−20,0⋅3,0−15,0⋅3,0⋅

1
2

⋅

3,0=0

V

A

=

35,0kNm

(Z4/19.11)

Reakcja ma więc zwrot zgodny z założonym.

W celu sprawdzenia obliczeń reakcji pionowych zastosujemy równanie sumy rzutów wszystkich sił

działających na pręt AC na oś pionową Y.



Y



AC



=

V

A

−

V

C



AC



−

15,0⋅3,0=35,0−



−

10,0



−

45,0=0

.

(Z4/19.12)

Możemy więc stwierdzić, że pionowe reakcje działające na pręt AC zostały obliczone poprawnie i znajdują
się w równowadze.

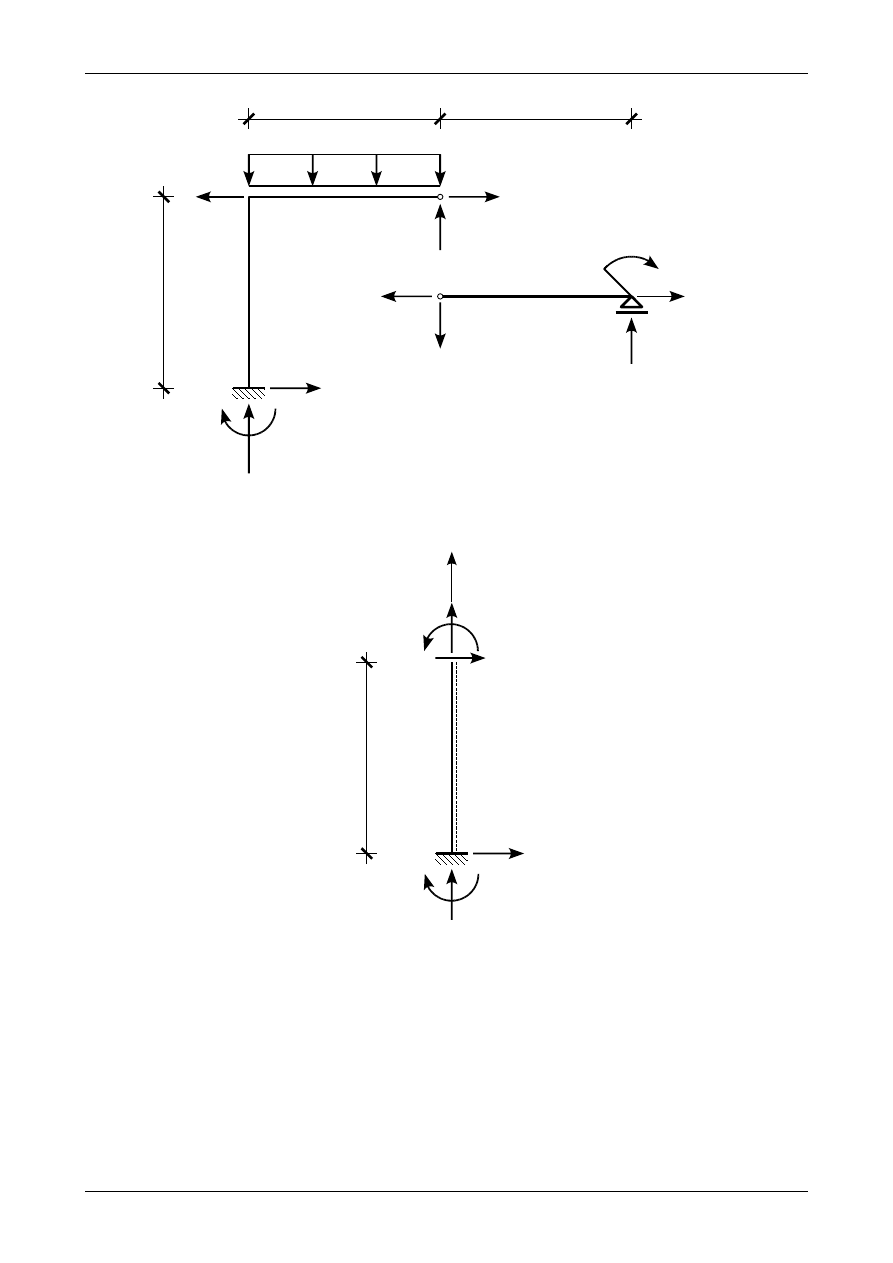
Rysunek Z4/19.4 przedstawia prawidłowe wartości i zwroty reakcji we wszystkich podporach danej

ramy płaskiej.

Z4/19.4. Funkcje sił przekrojowych w przedziale AB

Rysunek Z4/19.5 przedstawia siły działające na odciętą część ramy płaskiej w przedziale AB. Na

rysunku tym są zaznaczone dodatnie siły przekrojowe. Jako dolną część pręta AB przyjmiemy jego prawą
część zaznaczoną na rysunku Z4/19.5 linią przerywaną.

W dalszej części niniejszego opracowania przy wyznaczaniu postaci funkcji siły normalnej lub

poprzecznej oraz momentu zginającego w poszczególnych prętach ramy naszej płaskiej będziemy korzystali
z następujących zasad:

•

siły, które działają zgodnie z dodatnim zwrotem siły normalnej lub poprzecznej będziemy zapisywać
z minusem

•

siły, które działają przeciwnie do dodatniego zwrotu siły normalnej lub poprzecznej będziemy
zapisywać z plusem

Dr inż. Janusz Dębiński

Zaoczni

MO

Z4/19. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 19

5

15,0 kN/m

40,0 kN

A

B

C

3,0

3,0

3,0

[m]

30,0 kNm

20,0 kN

C

D

20,0 kN

20,0 kN

10,0 kN

10,0 kN

10,0 kN

20,0 kN

35,0 kN

22,5 kNm

Rys. Z4/19.4. Prawidłowe wartości i zwroty reakcji we wszystkich podporach ramy płaskiej

A

x

20,0 kN

35,0 kN

22,5 kNm

N(x)

T(x)

M(x)

X

Rys. Z4/19.5. Siły działające w przedziale AB

•

siły i momenty skupione, które kręcą zgodnie z dodatnim zwrotem momentu zginającego będziemy
zapisywać z minusem

•

siły i momenty skupione, które kręcą przeciwnie do dodatniego zwrotu momentu zginającego
będziemy zapisywać z plusem.

Funkcja obciążenia ciągłego równomiernie rozłożonego prostopadłego do osi pręta AB będzie

zerowa. Siła normalna ma postać

Dr inż. Janusz Dębiński

Zaoczni

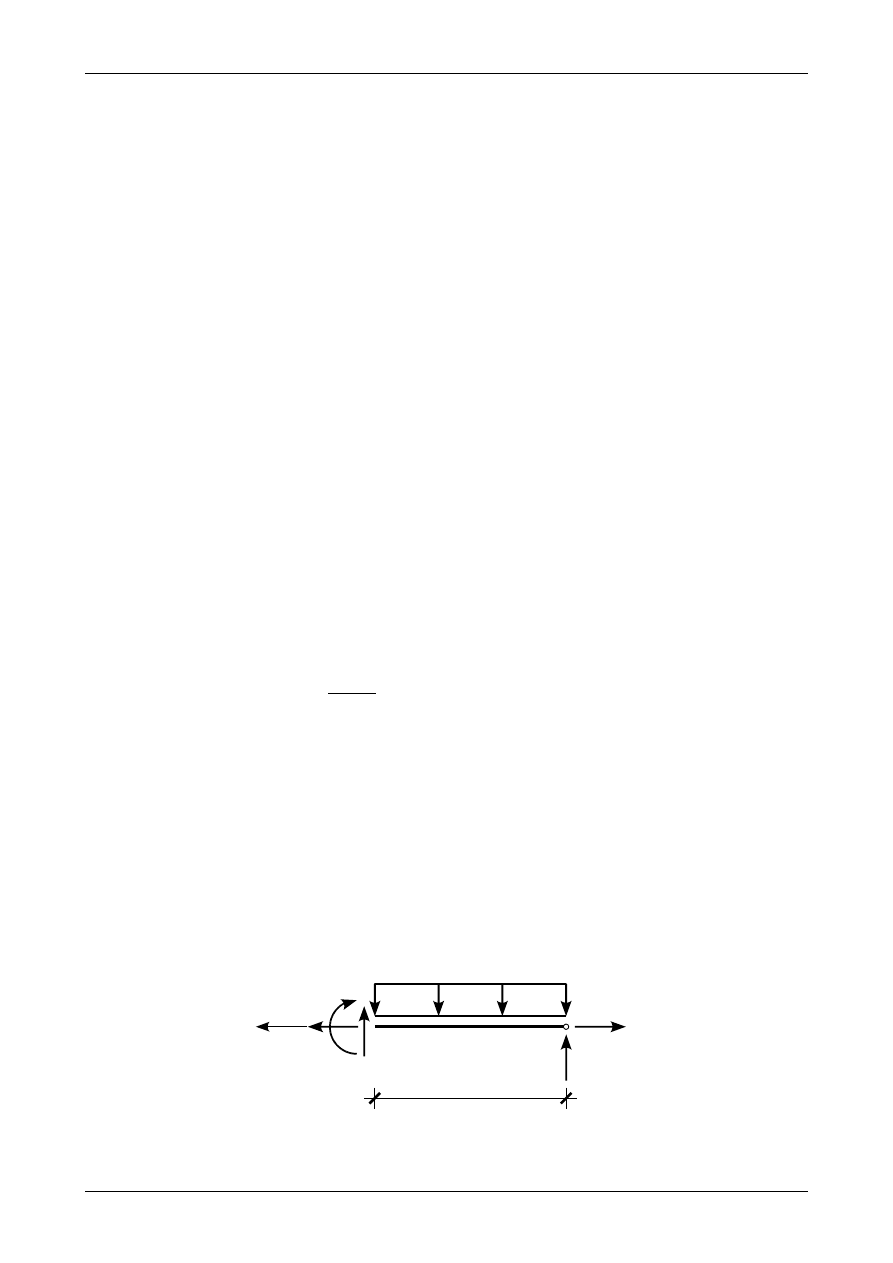
MO

Z4/19. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 19

6

N



x



=−

35,0 kN

.

(Z4/19.13)

Siła poprzeczna ma postać

T



x



=−

20,0 kN

.

(Z4/19.14)

Moment zginający w przedziale AB będzie miał postać

M



x



=

22,5−20,0⋅x

.

(Z4/19.15)

Funkcja momentu zginającego jest funkcją liniową i aby ją jednoznacznie narysować musimy wyznaczyć jej
wartości w dwóch punktach. Wynoszą one

M



0,0



=

22,5 kNm

M



3,0



=

22,5−20,0⋅3,0=−37,5 kNm

.

(Z4/19.16)

Jak wiadomo dodatnie momenty zginające rozciągają prawą część przekroju pręta i będziemy je odkładać z
prawej strony natomiast ujemne momenty zginające rozciągają lewą część przekroju pręta i będziemy je
odkładać z lewej strony.

Oś X układu współrzędnych jest skierowana w prawo, zastosujemy więc różniczkowe równania

równowagi (4.19), (4.20) i (4.21). Zastosujemy tylko równanie trzecie. Ma ono postać

dM



x



dx

=−

20,0=T



x



.

(Z4/19.17)

Jak więc widać różniczkowe równanie równowagi zostało spełnione.

Wykresy funkcji siły normalnej i poprzecznej oraz momentu zginającego w przedziale AB

przedstawiają rysunki Z4/19.8, Z4/19.9 i Z4/19.10.

Z4/19.5. Funkcje sił przekrojowych w przedziale BC

Rysunek Z4/19.6 przedstawia siły działające na odciętą część ramy płaskiej w przedziale BC. Na

rysunku tym są zaznaczone dodatnie siły przekrojowe.

15,0 kN/m

C

x

20,0 kN

10,0 kN

N(x)

T(x)

M(x)

X

Rys. Z4/19.6. Siły działające w przedziale BC

Dr inż. Janusz Dębiński

Zaoczni

MO

Z4/19. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 19

7

Funkcja obciążenia ciągłego równomiernie rozłożonego prostopadłego do osi belki będzie miała

postać

q



x



=

15,0

kN

m

.

(Z4/19.18)

Siła normalna w przedziale CD ma postać

N



x



=

20,0kN

.

(Z4/19.19)

Siła poprzeczna ma postać

T



x



=−

10,015,0⋅x

.

(Z4/19.20)

Siła poprzeczna jest funkcją liniową i aby ją jednoznacznie narysować należy wyznaczyć jej wartości na obu
końcach przedziału. Wartości te wynoszą

T



0,0



=−

10,0 kN

T



3,0



=−

10,015,0⋅3,0=35,0 kN

.

(Z4/19.21)

Siła poprzeczna ma na obu końcach przedziału BC wartości różnych znaków. Będzie ona więc miała
miejsce zerowe w tym przedziale. Znajduje się ono

−

10,015,0⋅x

0

=

0

x

0

=

0,6667 m

(Z4/19.22)

od początku przedziału BC czyli od punktu C.

Moment zginający w przedziale BC będzie miał postać

M



x



=

10,0⋅x−15,0⋅x⋅

x

2

=−

7,5⋅x

2



10,0⋅x

.

(Z4/19.23)

Funkcja momentu zginającego jest funkcją kwadratową i aby ją jednoznacznie narysować musimy
wyznaczyć jej wartości w trzech punktach. Wynoszą one

M



0,0



=

0,0 kNm

M



0,6667



=−

7,5⋅0,6667

2



10,0⋅0,6667=3,333 kNm

M



3,0



=−

7,5⋅3,0

2



10,0⋅3,0=−37,5 kNm

.

(Z4/19.24)

Jak wiadomo dodatnie momenty zginające w pręcie poziomym ramy płaskiej rozciągają dolną część
przekroju pręta i będziemy je odkładać na dole natomiast ujemne momenty zginające rozciągają górną część
przekroju pręta i będziemy je odkładać na górze.

Dr inż. Janusz Dębiński

Zaoczni

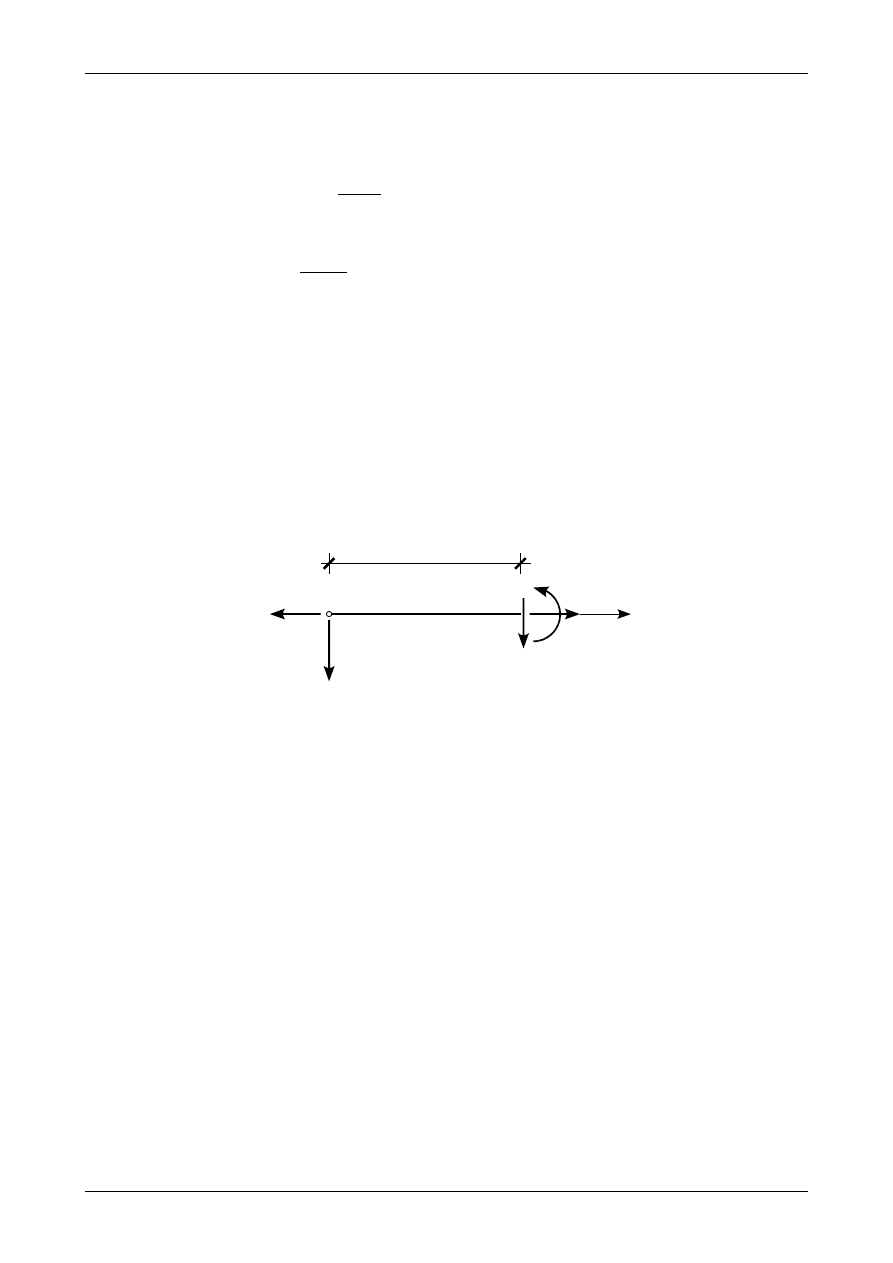
MO

Z4/19. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 19

8

Oś X układu współrzędnych jest skierowana w lewo, zastosujemy więc różniczkowe równania

równowagi (4.28), (4.29) i (4.30). Równania drugie i trzecie mają postać

dT



x



dx

=

15,0=q



x



,

(Z4/19.25)

dM



x



dx

=

10,0−15,0⋅x=−T



x



.

(Z4/19.26)

Jak więc widać oba różniczkowe równania równowagi zostały spełnione.

Wykresy funkcji siły normalnej i poprzecznej oraz momentu zginającego w przedziale BC

przedstawiają rysunki Z4/19.8, Z4/19.9 i Z4/19.10.

Z4/19.6. Funkcje sił przekrojowych w przedziale CD

Rysunek Z4/19.7 przedstawia siły działające na odciętą część ramy płaskiej w przedziale CD. Na

rysunku tym są zaznaczone dodatnie siły przekrojowe.

x

C

20,0 kN

10,0 kN

N(x)

T(x)

X

M(x)

Rys. Z4/19.7. Siły działające w przedziale CD

Funkcja obciążenia ciągłego równomiernie rozłożonego prostopadłego do osi pręta CD będzie

zerowa. Siła normalna ma postać

N



x



=

20,0kN

.

(Z4/19.27)

Siła poprzeczna ma postać

T



x



=−

10,0 kN

.

(Z4/19.28)

Moment zginający w przedziale CD będzie miał postać

M



x



=−

10,0⋅x

.

(Z4/19.29)

Funkcja momentu zginającego jest funkcją liniową i aby ją jednoznacznie narysować musimy wyznaczyć jej
wartości w dwóch punktach. Wynoszą one

Dr inż. Janusz Dębiński

Zaoczni

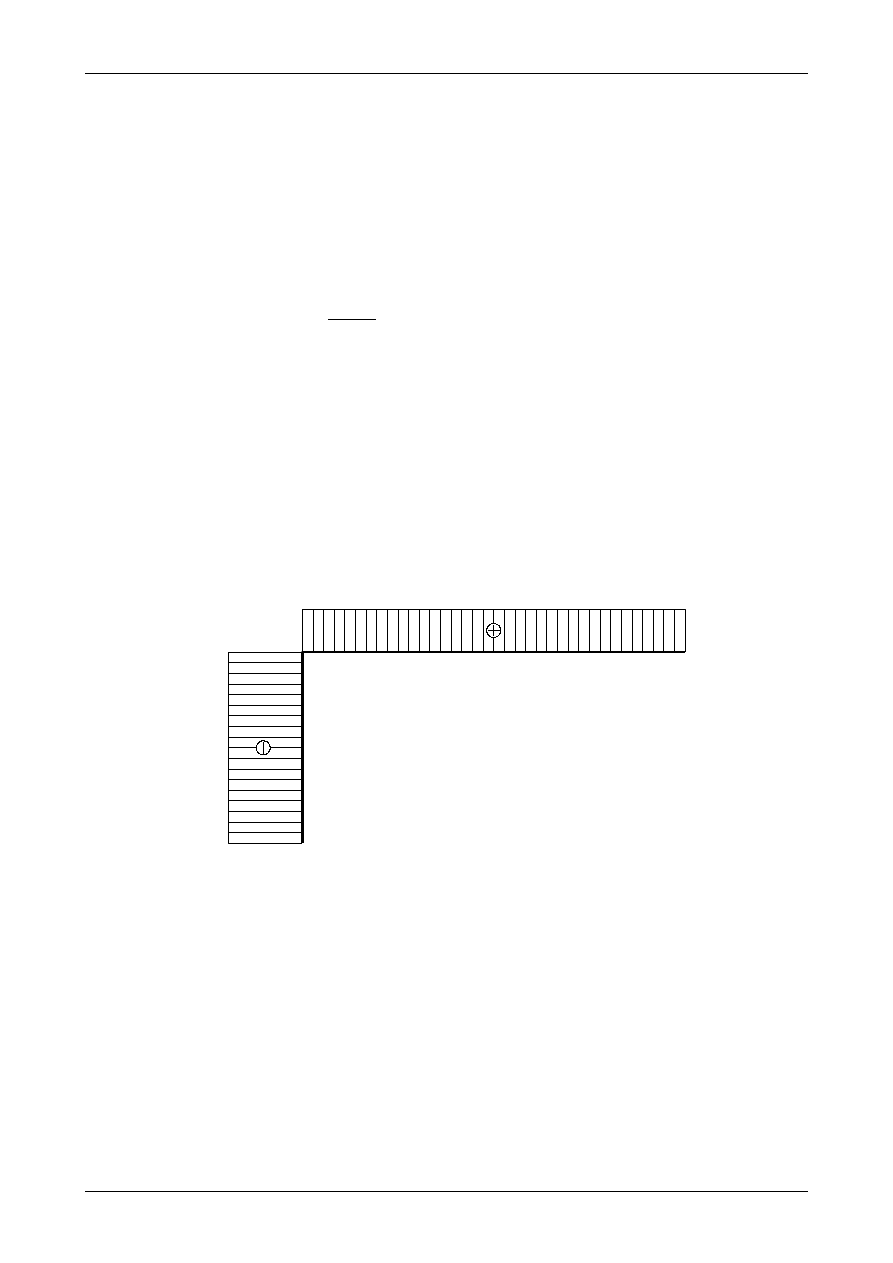
MO

Z4/19. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 19

9

M



0,0



=

0,0 kNm

M



3,0



=−

10,0⋅3,0=−30,0 kNm

.

(Z4/19.30)

Jak wiadomo ujemne momenty zginające rozciągają górną część przekroju pręta i będziemy je odkładać na
górze.

Oś X układu współrzędnych jest skierowana w prawo, zastosujemy więc różniczkowe równania

równowagi (4.19), (4.20) i (4.21). Zastosujemy tylko równanie trzecie. Ma ono postać

dM



x



dx

=−

10,0=T



x



.

(Z4/19.31)

Jak więc widać różniczkowe równanie równowagi zostało spełnione.

Wykresy funkcji siły normalnej i poprzecznej oraz momentu zginającego w przedziale CD

przedstawiają rysunki Z4/19.8, Z4/19.9 i Z4/19.10.

Z4/19.7. Wykresy sił przekrojowych

Rysunki Z4/19.8, Z4/19.9 i Z4/19.10 przedstawiają ostateczne wykresy funkcji siły normalnej i

poprzecznej oraz momentu zginającego w ramie płaskiej wyznaczone metodą ogólną.

N [kN]

20,0

35

,0

Rys. Z4/19.8. Wykres siły normalnej w ramie płaskiej

Z4/19.8. Sprawdzenie wykresów sił przekrojowych

W celu sprawdzenia poprawności wykonania wykresów siły normalnej i poprzecznej oraz momentu

zginającego przedstawionych na rysunkach Z4/19.8, Z4/19.9 i Z4/19.10 wykonamy sprawdzenie równowagi
sił oraz momentów w węźle B ramy płaskiej.

Rysunek Z4/19.11 a) przedstawia równowagę siły normalnej i poprzecznej w węźle B. Jak widać na

tym rysunku spełnione są równania sumy rzutów na oś poziomą X i pionową Y. Oznacza to, że siły te
znajdują się w równowadze.

Rysunek Z4/19.11 b) przedstawia równowagę momentów skupionego oraz zginających w węźle B.

Jak widać na tym rysunku spełnione jest równanie sumy momentów względem punktu B. Oznacza to, że
momenty te znajdują się w równowadze.

Dr inż. Janusz Dębiński

Zaoczni

MO

Z4/19. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 19

10

T [kN]

10,0

35

,0

20

,0

[m]

2,333

3,0

3,0

0,6667

Rys. Z4/19.9. Wykres siły poprzecznej w ramie płaskiej

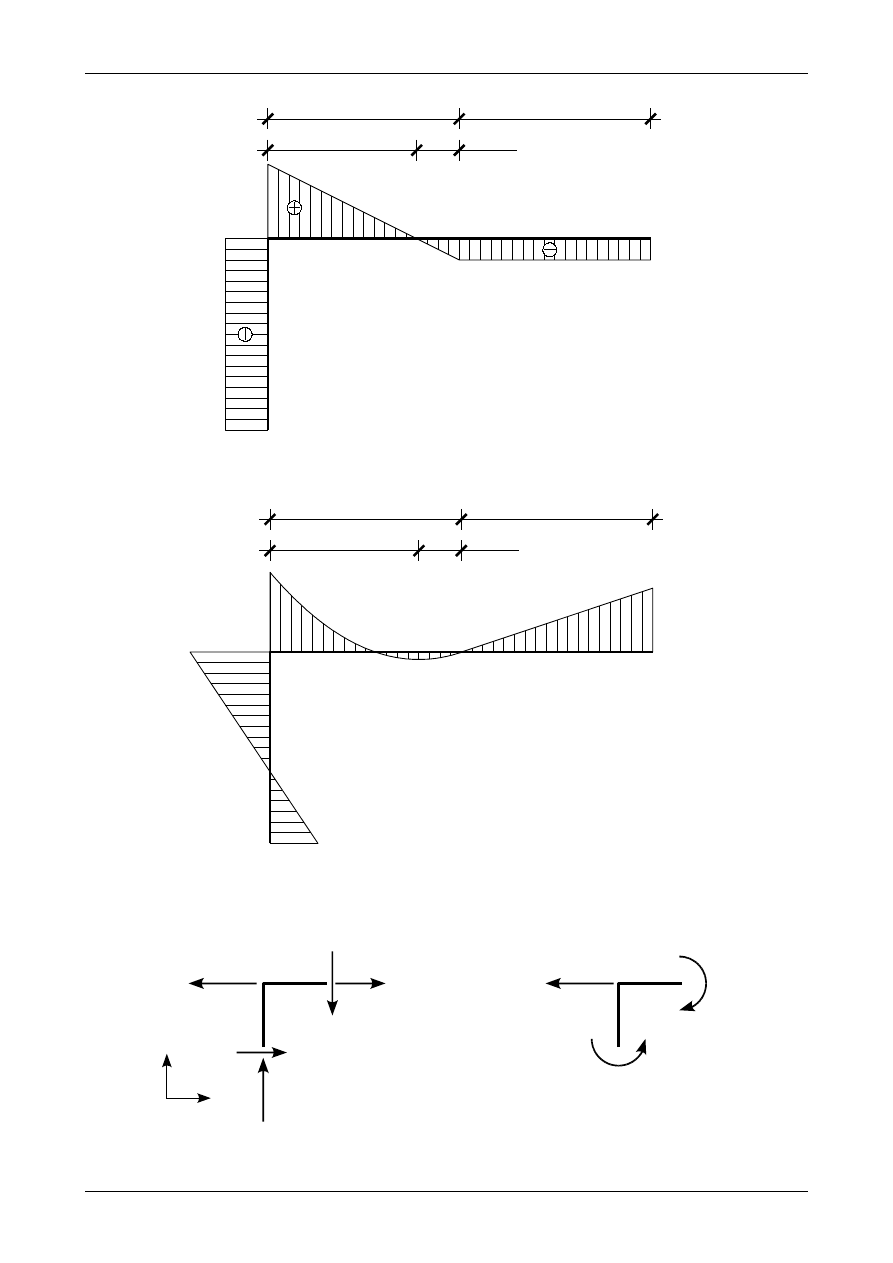
M [kNm]

2,333

[m]

3,0

3,0

0,6667

22,5

37

,5

37,5

3,

33

3

0,0

30

,0

Rys. Z4/19.10. Wykres momentu zginającego w ramie płaskiej

20,0 kN

20,0 kN

35,0 kN

B

B

37,5 kNm

X

Y

a)

b)

35,0 kN

40,0 kN

37,5 kNm

40,0 kN

Rys. Z4/19.11. Równowaga węzła B

Dr inż. Janusz Dębiński

Zaoczni