1

Podstawy elektrotechniki

2

Obwód magnetyczny (magnetowód)

n

rdz

eń

z m

ater

ia

łu

mag

ne

ty

czn

eg

o

(f

errom

agne

ty

k)

lity

lu

b sk

ład

an

y

uz

woje

ni

e

wz

budz

aj

ące

(n z

w

ojów)

szczelin

a

powie

tr

zn

a

3

Prawo przep

ływu

H

S

l

J

∫

∫

=
⋅

S

)

S(

d

d

S
J

H

l

l

c

I

=

l

1

l

2

l

3

l

4

n

I

I

n

I

c

⋅
=

Θ

=

H

1

H

2

H

3

H

4

za

ło

żen

ie:

(

)

.

const

H

H

1

1
1

=

=

l

(

)

.

const

H

H

2

2
2

=

=
l

(

)

.

const

H

H

3

3
3

=

=
l

(

)

.

const

H

H

4

4
4

=

=
l

k

4

1

k

k

)

S(

k

d
H

d

l

l

l

l

∑

∫

∫

=

=
⋅

H

∑

∫

=

















=

4

1

k

k

k

k

d

H

l

l

∑

=

=

4

1

k

k

k

H

l

Θ

=

∑

=

4

1

k

k

k

H

l

og

ól

nie

:

Θ

=

∑

=

N

1

k

k
k

l
H

S

-

pr

zep

ływ

(

am

pe

ro

zw

oj

e)

4

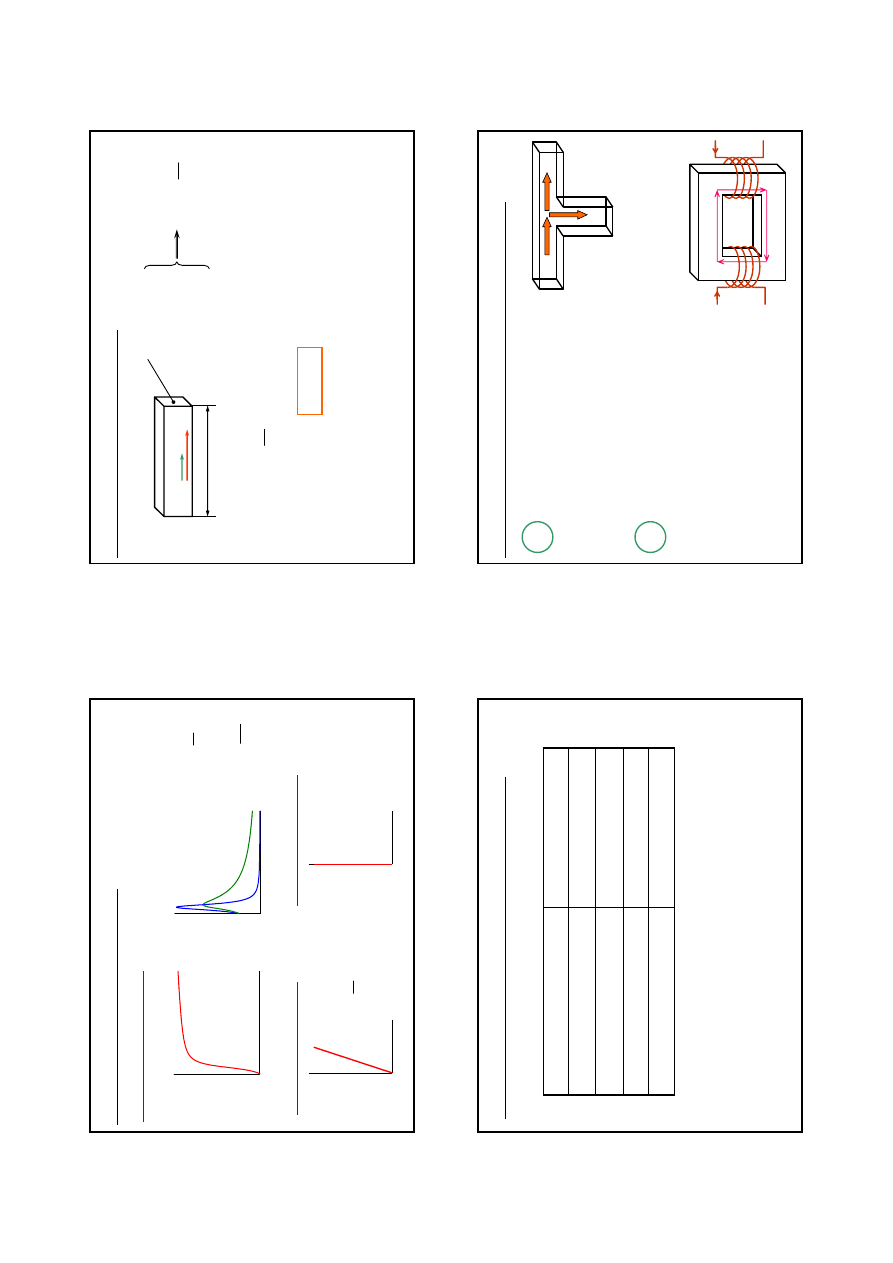
Wykorzystanie prawa przep

ływu

l

1

l

2

l

3

l

4

l

5

l

0

S

1

S

2

S

4

S

3

S

0

S

5

odc

in

ki

m

agne

to

wodu

o

sta

ły

m

p

rzek

ro

ju

:

l

0

, l

1

, l

2

, l

3

, l

4

, l

5

za

ło

żen

ie:

da

na

in

du

kc

ja

B

1

w odc

ink

u

l

1

1
1

S

B

=

Φ

5,

4,

3,

2,

0
k
,

S

B

k

k

=

Φ

=

w r

dzen

iu:

(

)

5,

4,

3,

2,1
k
,
B
H

H

k

k

k

=

=

w szczelinie

:

0

0

0

B

H

µ

=

Θ

=

∑

=

5

0
k

k

k

H

l

2

5

Charakterystyka rdzenia

fe

rro

m

agne

ty

k nie

lin

iow

y

H

B

chara

kt

erys

ty

ka m

ag

nes

ow

an

ia

chara

kt

erys

ty

ka

prze

ni

ka

ln

oś

ci

H

µ

µ

s

µ

d

H

B

s

=

µ

dH

dB

d

=
µ

fe

rro

m

agne

ty

k li

ni

ow

y

B

H

.

const

H

B

=

=

µ

fe

rro

m

agne

ty

k ide

al

ny

B

H

∞

→

µ

0

H

=

7

Oporno

ść

magnetyczna

-

re

lu

kta

nc

ja

(o

por

no

ść

m

agne

ty

cz

na

)

S

B

⋅
=

Φ

S

l

µ

B

H

H

B

⋅

µ

=

µ

=

⋅

U

H

l

µS

U

l

Φ

=

µ

µ

=

R

µS

l

Φ

=

µ

µ

R

U

-

prawo Oh

m

a

dla obwodów

m

agne

ty

cz

ny

ch

U

µ

–

spa

de

k na

pi

ęcia mag

nety

czn

eg

o

8

Analogie magnetyczno-elektryczne

Rez

ystancja R

Reluktancja R

µ

Napi

ęcie

źród

łowe

Przep

ły

w

(a

m

perozwoje)

Napi

ęcie U

Napi

ęcie m

agnety

czne

U

µ

Pr

ąd I

Strum

ie

ń

m

agnet

yczn

y

Φ

Obwody elektryc

zn

e

Obwody magnetycz

n

e

9

Prawa Kirchoffa

dla magnetowodów

I

S

uma

s

tr

umi

en

i w

w

ęź

le

obwodu

mag

ne

ty

czn

eg

o jest r

ówn

a zer

u

0

N

1

k

k

=
Φ

∑

=

Φ

1

Φ

2

Φ

3

II

Sum

a spa

dków na

pi

ęcia m

ag

ne

ty

czn

ego

w o

czk

u ob

wo

du

mag

ne

ty

czn

eg

o jest r

ówn

a su

mie p

rzep

ły

w

ów w ty

m

oc

zk

u

∑

∑

=

=

µ

=

N

1

k

k
k

M

1

k

k

I

n

U

U

µ1

I

1

n

1

n

2

I

2

U

µ3

U

µ2

U

µ4

3

10

Schema

t zast

ępczy

1
1

1

1

S

R

µ

=

µ

l

I

1

n

1

n

2

I

2

Θ

1

Θ

2

R

µ1

R

µ6

R

µ3

R

µ4

R

µ5

R

µ2

µ

1

µ

2

2
0

2

2

S

R

µ

=

µ

l

3
2

3

3

S

R

µ

=

µ

l

4
2

4

4

S

R

µ

=

µ

l

5
2

5

5

S

R

µ

=

µ

l

6
0

6

6

S

R

µ

=

µ

l

1

1

1

I

n

=
Θ

2
2

2

I

n

=
Θ

Φ

∑

=

µ

Θ

−

=

Φ

6

1

k

k

2

1

R

Θ