J:\2011 - 2012\energoelektronika sem IV wyklady\obwod RLE2.doc
J.Piłaciński: Materiały pomocnicze do wykładu z energoelektroniki
1
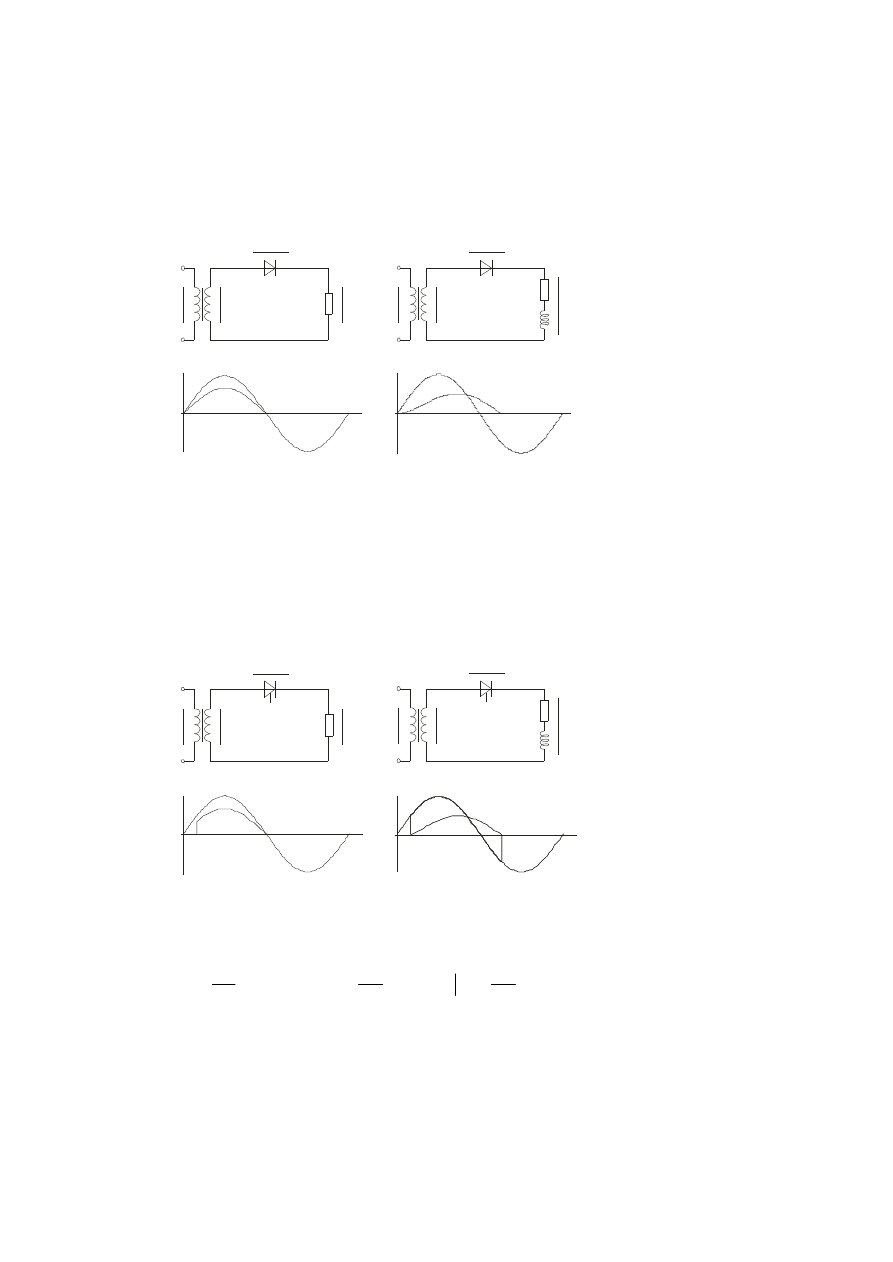
i
o
= i
s
u
o
u
s
0
ω
t
u
i
u
o
i
o
= i
s
u
s
0
ω
t
u
i
u
s
u
u
o
u
D
i
s
i
o
R
u
D
u
s
u
u
o
i
o
i
s
R
L
........................................................................................................................
u
s
u
u
o
u
Ty
i
s
i
o
R
u
Ty
u
s
u
u
o
i
o
i
s
R
L
i
o
= i
s
u
o
u
s
ω
t
0
u
i
i
o
= i
s
u
o
u
s
0
ω
t
u
i
t
U
u
m
ω
sin
=
w
z
t
α
ω
α
<
<
)
cos
(cos
2
)
cos
(
2
sin
2
1
w
z
m
m
m
d
U
t
U
t
td
U
U
w
z
w
z
α
α
π
ω
π
ω
ω
π
α
α
α
α
−
=
−
=
=
∫
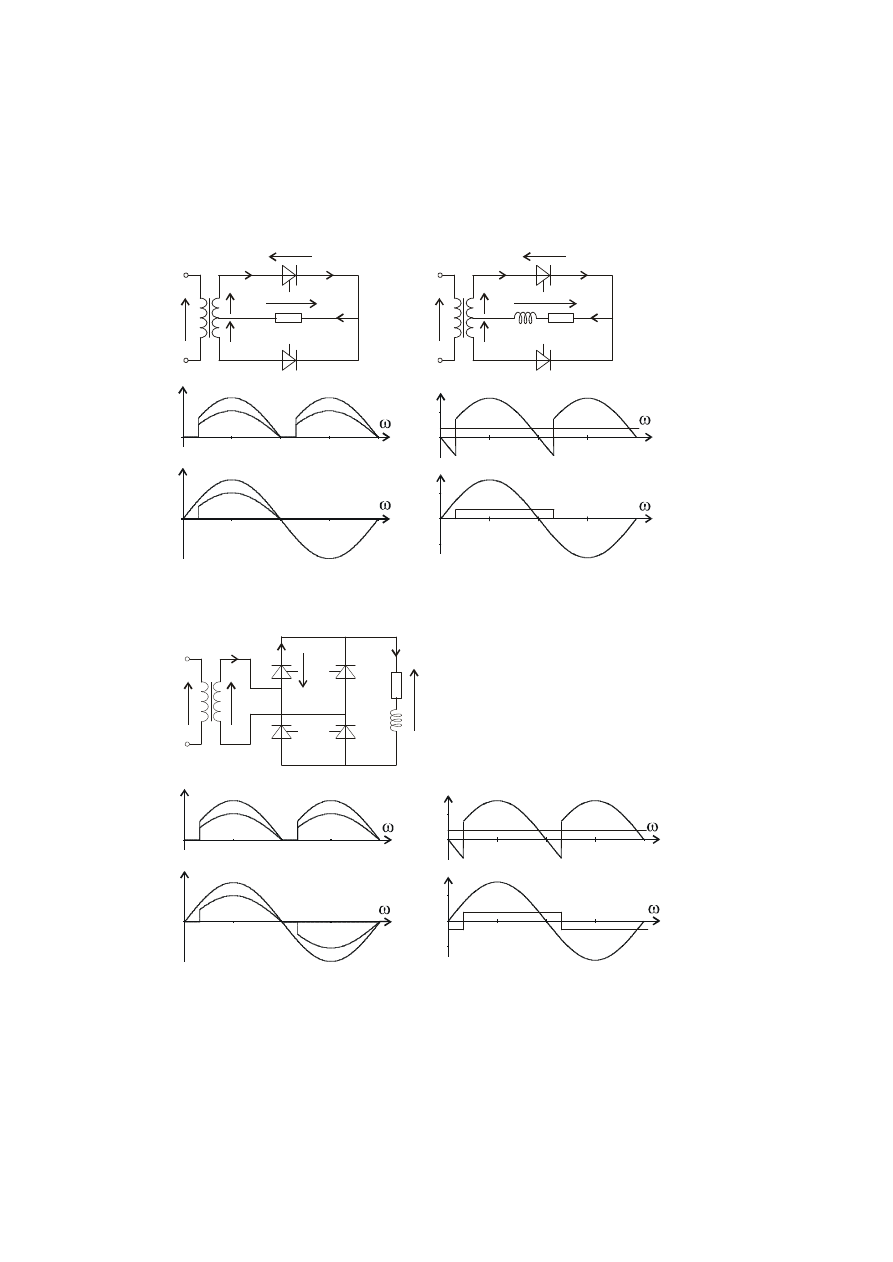
J:\2011 - 2012\energoelektronika sem IV wyklady\obwod RLE2.doc
J.Piłaciński: Materiały pomocnicze do wykładu z energoelektroniki
2
i
o
u
o
u
s
i
s
t
t
0
0
u
i
u
i
i
o
u
o
i
s
u
s
t
t
0
0
u
i
u
i
u
s
u
u
o
u
s
i
o
u
Ty
i
s
i
Ty
R
u
s
u
u
o
u
s
i
o
u
Ty
i
s
i
Ty
R
L
i
o
u
Ty
i
s
u
u
s
u
o
i
Ty
R
L
u
o
i
o
i
s
u
s
t
t
0
0
u
i
u
i
i
o
i
s
u
s
u
o
t
t
0
0
u
i
u
i
J:\2011 - 2012\energoelektronika sem IV wyklady\obwod RLE2.doc
J.Piłaciński: Materiały pomocnicze do wykładu z energoelektroniki
3
Obwód RLE z zaworem
Równanie różniczkowe dla obwodu RLE wynikające z II Prawa Kirchhoffa
ma następującą postać:
)
sin(
z
m
t
U
E
Ri
t
d
di
L
α
ω
ω
ω
+
=
+
+
w
z
t
α
ω
α
<
<
W zapisie operatorowym:
)
0
(
cos
sin
1
)
(
)
(
2
2
LI
s
s
U
E
s
s
RI
s
LI
s
z
z
m
ω
ω
α
ω
α
ω
+
+
+
=
+
+
Rozwiązanie ogólne:
(
) (
)
t
t
t
z
z
m
e
I
e
R
E
e
t
Z
U
i
ρω
ρω
ρω
ϕ
α
ϕ
α
ω
−
−
−
⋅
+
−
−
⋅
−
−
−
+
=
)
0
(
1
)
sin(
)
sin(
2
2
)
( L
R
Z
ω
+
=
,
R
L
arctg
ω
ϕ
=
,
L
R
ω
ρ
=
Obliczanie wartości średniej prądu
Całkując równanie różniczkowe w granicach kąta przewodzenia
z
w
α
α
λ
−
=
a następnie dzieląc stronami przez okres przebiegu,
otrzymamy:
∫
∫
∫
∫
+
=
+
+
λ
λ
λ
ω
α
ω
π
ω
π
ω
π
ω
π
0
0
0
)
0
(
)
(
)
sin(
2
1
)
(
2
1
)
(
2
1
2
1
t
d
t
U
t
Ed
t
Rid
Ldi
z
m
I
I
k
J:\2011 - 2012\energoelektronika sem IV wyklady\obwod RLE2.doc
J.Piłaciński: Materiały pomocnicze do wykładu z energoelektroniki
4
Wartość pierwszej całki w stanie ustalonym wynosi zero. Zarówno przy
przewodzeniu ciągłym jak i przy przewodzeniu przerywanym wartość prądu
na końcach przedziału całkowania jest taka sama. Pozostałe całki
wyznaczają wartości średnie odpowiednich napięć w obwodzie. Wartość
średnia prądu wynosi:
∫
∫
−
−
=
−
+
=
λ
λ
ελ
α
α
π
ω
π
ω
α
ω
π
0
)
cos
(cos
2
)
(
2
1
)
sin(
2
1
w
z
m
z
m
d
R
U
t
Ed
R
t
d
t
U
R
I
gdzie:
m
U
E
=
ε
.
Wartość średnią można obliczyć także całkując prąd i w okresie
przewodzenia.
∫
−
−
−
−
−
−
=
=
−
λ
ρλ
ϕ
ελ
ϕ
α
ϕ
ε
ρ
ϕ
α
π
ω
π
0
cos
)
1
(
)
sin(
cos
1
)
cos(
2
)
(
2
1
e
Z
U
t
id
I
z
z
m
d
Wartość kąta wyłączania niezbędną do obliczenia całki należy odczytać z
charakterystyki
)
,
,
(
ε
ϕ
α
α
tg
f
z
w
=
.