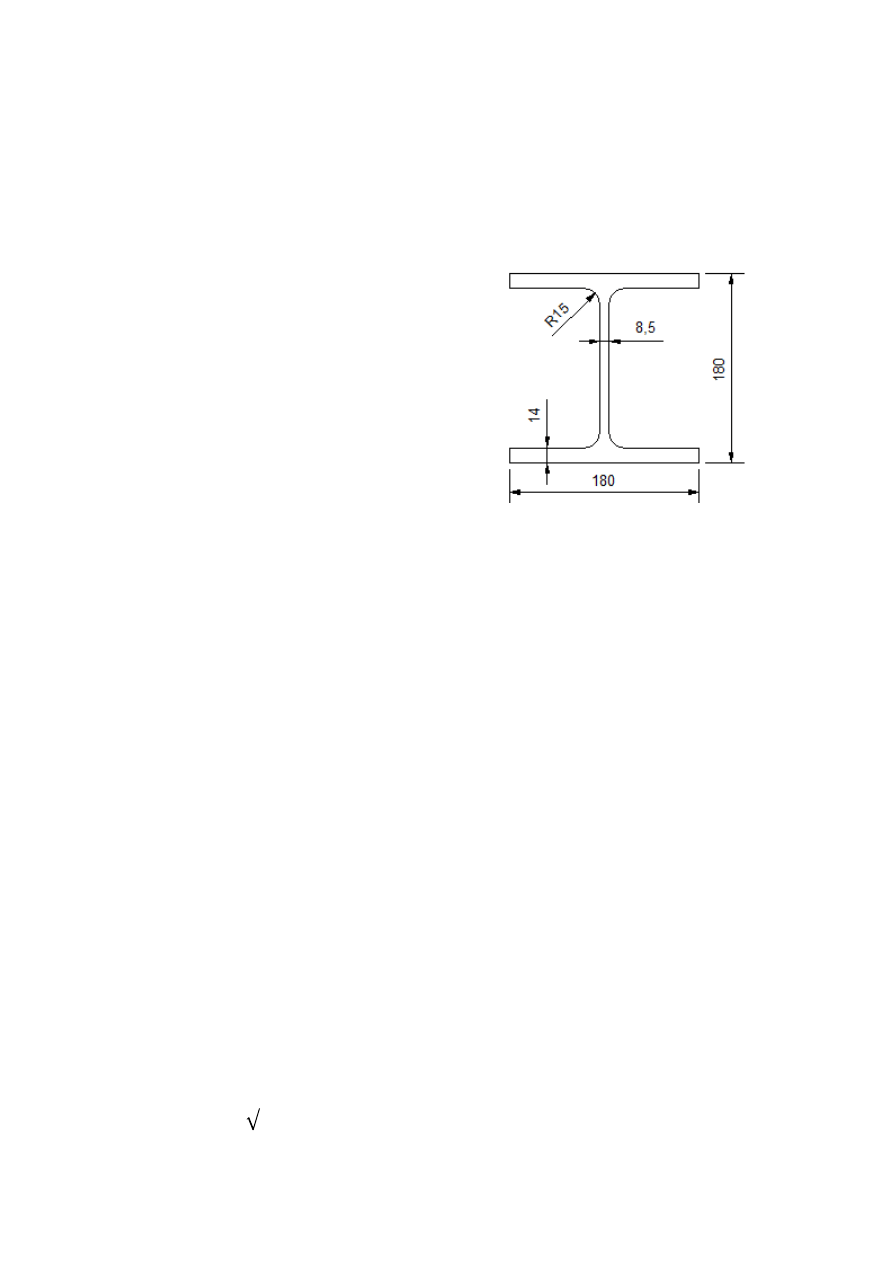
STYK UNIWERSALNY

DANE DO PROJEKTU:




Dwuteownik HEB 180
Gatunek stali : S 235

WYMIARY:

 Wysokość dwuteownika :

≔

h

180 mm

 Szerokość półek teownika :

≔

b

f

180 mm

 Szerokość środnika :

≔

t

w

8.5 mm

 Grubość półek :

≔

t

f

14 mm

 Promień zakrzywienia :

≔

R

15 mm

 Pole przekroju dwuteownika :

≔

A

65.3 cm

2

 Wskaźnik wytrzymałości

względem osi Z :

≔

W

plz

151 cm

3

 Moment bezwładności względem

osi Z :

≔

I

z

1360 cm

4

 Promień bezwładności względem

osi Z :

≔

i

z

4.57 cm

 Wskaźnik wytrzymałości

względem osi Y :

≔

W

ply

426 cm

3

 Moment bezwładności względem

osi Y :

≔

I

y

3830 cm

4

 Promień bezwładności względem

osi Y :

≔

i

y

7.66 cm

 Wytzrymałość na rozciąganie stali :

≔

f

u

360 MPa

wg PN-EN 1993-1-1 2006

str. 25 Tab. 3.1

 Granica plastyczności stali :

≔

f

y

235 MPa

≤

t

40 mm

1. Siły obciążeniowe

1.1. Moment obliczeniowy

≔

M

Ed

=

⋅

⋅

0.7 W

ply

f

y

70.08 kN·m

wg wytycznych projektu

1.2. Siła poprzeczna

 Pole przekroju czynnego przy ścinaniu :

≔

η

1

- współczynnik konwersji

wg PN-EN 1993-1-1 2006

str. 51 - 6.2.6 pkt. 3a

≔

A

v

=

max ⎛⎝

,

+

−

A

⋅

⋅

2 b

f

t

f

⋅

⎛⎝ +

t

w

⋅

2 R⎞⎠ t

f

⋅

⋅

η t

w

h⎞⎠ 20.29 cm

2

 Obliczeniowa siła poprzeczna :

≔

V

Ed

=

⋅

⋅

0.5 A

v

――

f

y

‾‾

2

3

137.64 kN

wg wytycznych projektu

1

2. Przyjęcie wymiaru nakładek i przykładek

2.1. Nakładki

 Grubość nakładek

≔

t

N

20 mm

 Szerokość nakładek

≔

b

N

=

b

f

180 mm

2.2. Przykładki

 Grubość przykładek

≔

t

p

10 mm

 Wysokość przykładek

≔

h

p

110 mm

 Sprawdzenie prawidłowości przyjętej wysokości przykładek

≔

h

0

=

−

−

h

⋅

2 t

f

⋅

2 R

122 mm

=

≤

h

p

h

0

1

2.3. Pola powierzchni przekroju

 Nakładki

≔

A

N

=

⋅

t

N

b

N

36 cm

2

 Przykładki

≔

A

P

=

⋅

h

p

t

p

11 cm

2

3. Momenty bezwładności nakładek i przykładek

 Moment bezwładności przykładki

≔

I

Py

=

⋅

⋅

2 t

p

――

h

p

3

12

221.83 cm

4

 Moment bezwładności nakładki

≔

I

Ny

=

⋅

2

⎛
⎜
⎜⎝

+

⋅

⋅

b

N

t

N

⎛
⎜

⎝

+

―

t

N

2

―

h

2

⎞
⎟

⎠

2

⋅

b

N

――

t

N

3

12

⎞
⎟
⎟⎠

7224 cm

4

 Suma momentów bezwładności nakładki i przykładki

≔

I

Cy

=

+

I

Py

I

Ny

7445.833 cm

4

4. Siły przejmowane przez nakładki i przykładki

4.1. Momenty

 Moment nakładek

≔

M

N

=

⋅

M

Ed

――

I

Ny

I

Cy

67.99 kN·m

 Moment przykładek

≔

M

P

=

⋅

M

Ed

――

I

Py

I

Cy

2.09 kN·m

2

4.2. Siły tnące

 Siły tnące nakładek

≔

V

N

0 kN

 Siły tnące przykładek

≔

V

P

=

V

Ed

137.64 kN

4.3. Siły rozciągające

 Siły rozciągające nakładek

≔

N

N

0 kN

 Siły rozciągające przykładek

≔

N

P

0 kN

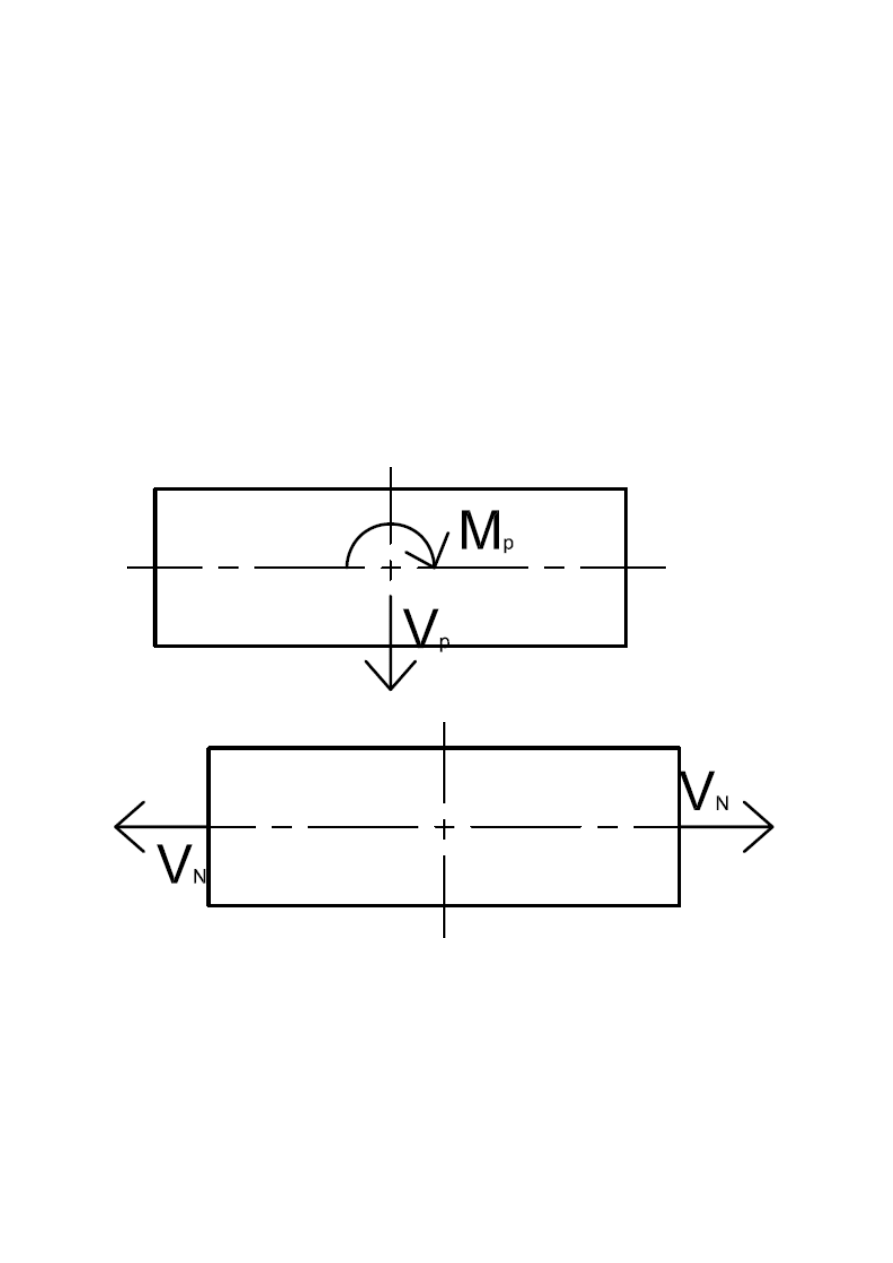
 Schemat działania sił w przykładce

 Schemat działania sił w nakładce

3

Połączenie na śruby wg EC3 Cz.1-8
Połączenie przykładek ze środnikiem

1. Założenia wstępne, dobór śrub oraz rozplanowanie śrub na środniku

 Kategoria styku : C

wg PN-EN 1993-1-8 2005

str. 21 - 3.4.1 pkt.a

 Typ śruby: ZGRUBNA z sześciokątnym łbem, trzpień gwintowany w całości

1.1. Klasa śrub

 Klasa śruby : 10.9

 Granica plastyczności śruby :

≔

f

ub

1000 MPa

wg PN-EN 1993-1-8 2005

str. 20 - tab. 3. 1

 Wytrzymałość na rozciąganie śruby :

≔

f

yb

900 MPa

1.2. Średnica śrub

≔

t

min

=

→

min ⎛⎝ ,

t

w

⋅

2 t

p

⎞⎠

min ((

,

⋅

8.5 mm

⋅

20 mm))

8.5 mm

→

≤

≤

⋅

1.5 t

min

d

⋅

2.5 t

min

≤

≤

⋅

12.75 mm

d

⋅

21.25 mm

 Przyjmuję śruby M16

≔

d

16 mm

 Pole przekroju czynnego rdzenia śruby :

≔

A

s

1.61 cm

2

 Średnica nominalna otworu :

≔

Δ

2 mm

- luz montażowy dla śrub o średnicy trzpienia 16 mm. oraz klasy wykonania C

≔

d

0

=

+

d

Δ

18 mm

1.3. Wstępne rozplanowanie śrub na środniku

 Przyjmuję wstępną ilość śrub :

≔

n

sprow

6

 Przyjmuję rozkład śrub :

NIEPRZESTAWIONY

 Odległość e

1

:

≔

e

1min

=

⋅

1.2 d

0

21.6 mm

≔

e

1max

=

+

⋅

4 t

min

40 mm

74 mm

Przyjmuję

:

≔

e

1

30 mm

 Rozstaw p

1

:

≔

p

1min

=

⋅

2.4 d

0

43.2 mm

≔

p

1max

=

min ⎛⎝

,

⋅

14 t

min

200 mm⎞⎠ 119 mm

Przyjmuję

:

≔

p

1

50 mm

 Odległość e

2

:

≔

e

2min

=

⋅

1.2 d

0

21.6 mm

≔

e

2max

=

+

⋅

4 t

min

40 mm

74 mm

4

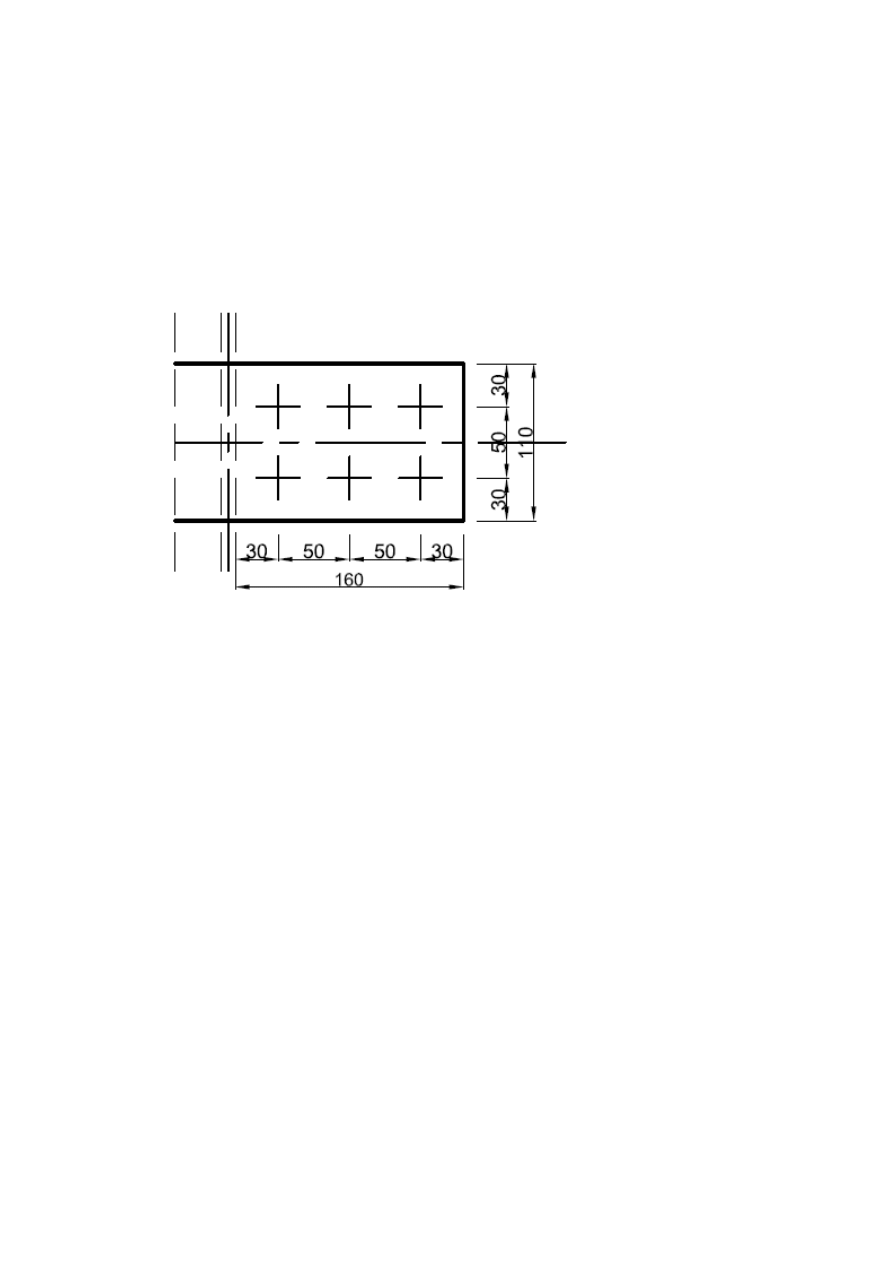
Przyjmuję

:

≔

e

2

30 mm

 Rozstaw p

2

:

≔

p

2min

=

⋅

2.2 d

0

39.6 mm

≔

p

2max

=

min ⎛⎝

,

⋅

14 t

min

200 mm⎞⎠ 119 mm

Przyjmuję

:

≔

p

2

50 mm

wg PN-EN 1993-1-8 2005

str. 23 - tab. 3. 3

2. Nośność obliczeniowa pojedynczej śruby na ścinanie

≔

α

v

0.5

wg PN-EN 1993-1-8 2005 str. 27 tab. 3.4

≔

γ

M2

1.25

- współczynnik bezpieczeństwa

wg PN-EN 1993-1-8 2005 str. 18

≔

n

2

- liczba styków ciernych

 Nośność na ścinanie dla pojedynczej śruby dwuciętej

≔

F

vRd

=

⋅

⋅

⋅

n α

v

f

ub

――

A

s

γ

M2

128.8 kN

wg PN-EN 1993-1-8 2005 str. 27 tab. 3.4

2.1. Złącze długie - współczynnik redukcyjny

βLf

≔

L

j

=

⋅

3 p

2

15 cm

=

⋅

15 d

24 cm

=

>

⋅

15 d

L

j

1

wg PN-EN 1993-1-8 2005

str. 29 - tab. 3.4

Nie uwzględniamy współczynnika redukcyjnego

3. Wyznaczenie nośności na poślizg

 Siła sprężania

≔

F

pC

=

⋅

⋅

0.7 f

ub

A

s

112.7 kN

 Współczynnik tarcia dla

klasy powierzchni ciernej B

≔

μ

0.4

wg PN-EN 1090-2 tab. 8

5

 Współczynnik kształtu otworów na śruby

≔

k

s

1

wg PN-EN 1993-1-8 2005

str. 30 - tab. 3.6

 Współczynnik częściowy

≔

γ

M3

1.25

 Obliczeniowa nośność na poślizg

≔

F

sRd

=

⋅

⋅

⋅

k

s

n μ ――

F

pC

γ

M3

72.128 kN

4. Nośność obliczeniowa na docisk dla najbardziej wytężonej śruby

4.1. Nośność obliczeniowa na docisk dla śrub skrajnych w kierunkach poziomym oraz pionowym

4.1.1. Kierunek poziomy

≔

α

d

=

――

e

1

⋅

3 d

0

0.556

≔

k

1

=

min

⎛
⎜
⎝

,

−

⋅

2.8 ―

e

2

d

0

1.7 2.5

⎞
⎟
⎠

2.5

≔

α

b

=

min

⎛
⎜
⎝

,

,

α

d

――

f

ub

f

u

1.0

⎞
⎟
⎠

0.556

 Obliczeniowa nośność na docisk w kierunku poziomym

wg PN-EN 1993-1-8 2005

str. 27 - tab. 3.4

≔

F

b.Rd_H

=

⋅

⋅

⋅

⋅

k

1

α

b

f

u

d ――

t

min

γ

M2

54.4 kN

4.1.2. Kierunek pionowy

≔

α

d

=

――

e

1

⋅

3 d

0

0.556

≔

k

1

=

min

⎛
⎜
⎝

,

−

⋅

2.8 ―

e

2

d

0

1.7 2.5

⎞
⎟
⎠

2.5

≔

α

b

=

min

⎛
⎜
⎝

,

,

α

d

――

f

ub

f

u

1.0

⎞
⎟
⎠

0.556

 Obliczeniowa nośność na docisk w kierunku pionowym

≔

F

b.Rd_V

=

⋅

⋅

⋅

⋅

k

1

α

b

f

u

d ――

t

p

γ

M2

64 kN

wg PN-EN 1993-1-8 2005

str. 27 - tab. 3.4

5. Wyznaczenie obliczeniowej siły przypadającej na najbardziej wytężoną śrubę

 Siła pochodząca od ścinania

≔

V

s

=

――

V

P

n

sprow

22.94 kN

 Mimośród siły

≔

e

v

=

+

+

p

1

e

2

5 mm

85 mm

 Moment przenoszony przez śrubę

≔

M

P0

=

+

M

P

⋅

V

Ed

e

v

13.788 kN·m

6

 Odległości śrub od środka ciężkości

≔

r

1

=

‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾

2

+

⎛⎝

+

5 mm

e

2

⎞⎠

2

⎛⎝

⋅

0.5 p

1

⎞⎠

2

43.012 mm

≔

r

2

=

‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾

2

+

⎛⎝

+

+

5 mm

e

2

p

2

⎞⎠

2

⎛⎝

⋅

0.5 p

1

⎞⎠

2

88.6 mm

≔

r

3

=

‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾

2

+

⎛⎝

+

+

5 mm

e

2

⋅

2 p

2

⎞⎠

2

⎛⎝

⋅

0.5 p

1

⎞⎠

2

137.295 mm

≔

Σr

i

=

+

+

⋅

2 r

1

2

⋅

2 r

2

2

⋅

2 r

3

2

57100 mm

2

 Maksymalna siła ścinająca pochodząca od momentu

Maksymalna siła ścinająca pochodząca od momentu wystąpi dla śruby najdalej oddalonej od środka ciężkości układu śrub

≔

F

M

=

⋅

M

P0

――

r

2

Σr

i

21.394 kN

 Odległości od środka ciężkości

≔

z

=

⋅

0.5 p

1

25 mm

≔

y

=

+

+

⋅

2 p

2

e

2

5 mm

135 mm

 Funkcje trygonometryczne

≔

sinα

=

―

z

r

3

0.182

≔

cosα

=

―

y

r

3

0.983

 Składowa pionowa

≔

F

MV

=

+

⋅

cosα F

M

V

s

43.977 kN

 Składowa pozioma

≔

F

MH

=

⋅

sinα F

M

3.896 kN

 Obliczeniowa siła w śrubie

≔

F

MAX

=

‾‾‾‾‾‾‾‾‾‾‾

2

+

F

MV

2

F

MH

2

44.149 kN

6. Sprawdzenie warunków nośności w stanie granicznym

 Nośność na poślizg

=

≤

F

MAX

F

sRd

1

=

――

F

MAX

F

sRd

%

61.21

 Nośność na docisk

 W kierunku pionowym

=

≤

F

MV

F

b.Rd_V

1

=

―――

F

MV

F

b.Rd_V

%

68.71

 W kierunku poziomym

=

≤

F

MH

F

b.Rd_H

1

=

―――

F

MH

F

b.Rd_H

%

7.16

7

Połączenie na śruby wg EC3 Cz.1-8
Połączenie nakładek z półkami

1. Założenia wstępne, dobór śrub oraz rozplanowanie śrub na półkach

 Kategoria styku : C

wg PN-EN 1993-1-8 2005

str. 21 - 3.4.1 pkt.a

 Typ śruby: ZGRUBNA z sześciokątnym łbem, trzpień gwintowany w całości

1.1. Klasa śrub

 Klasa śruby : 10.9

 Granica plastyczności śruby :

≔

f

ub

1000 MPa

wg PN-EN 1993-1-8 2005

str. 20 - tab. 3. 1

 Wytrzymałość na rozciąganie śruby :

≔

f

yb

900 MPa

1.2. Średnica śrub

≔

t

min

=

→

min ⎛⎝ ,

t

f

t

N

⎞⎠

min ((

,

⋅

14 mm

⋅

20 mm))

14 mm

→

≤

≤

⋅

1.5 t

min

d

⋅

2.5 t

min

≤

≤

⋅

21.0 mm

⋅

16 mm

⋅

35.0 mm

 Przyjmuję śruby M27

≔

d

27 mm

 Pole przekroju czynnego rdzenia śruby :

≔

A

s

4.60 cm

2

 Średnica nominalna otworu :

≔

Δ

3 mm

- luz montażowy dla śrub o średnicy trzpienia 30 mm. oraz klasy wykonania C

≔

d

0

=

+

d

Δ

30 mm

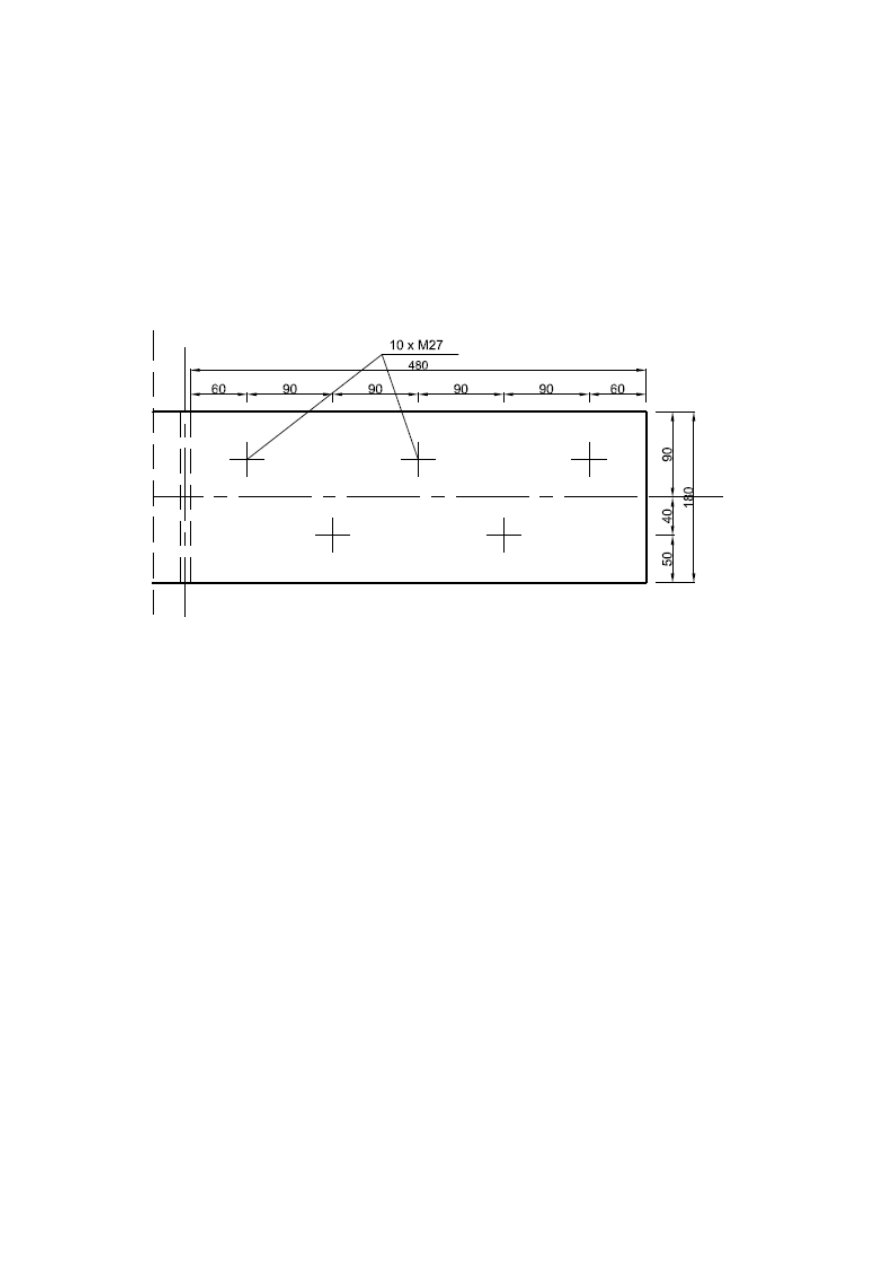
1.3. Wstępne rozplanowanie śrub na półce

 Przyjmuję wstępną ilość śrub :

≔

n

sprow

5

 Przyjmuję rozkład śrub :

PRZESTAWIONY

 Odległość e

1

:

≔

e

1min

=

⋅

1.2 d

0

36 mm

≔

e

1max

=

+

⋅

4 t

min

40 mm

96 mm

Przyjmuję

:

≔

e

1

60 mm

 Rozstaw p

1

:

≔

p

1min

=

⋅

2.2 d

0

66 mm

≔

p

1max

=

min ⎛⎝

,

⋅

14 t

min

200 mm⎞⎠ 196 mm

Przyjmuję

:

≔

p

1

190 mm

 Odległość e

2

:

≔

e

2min

=

⋅

1.2 d

0

36 mm

≔

e

2max

=

+

⋅

4 t

min

40 mm

96 mm

8

Przyjmuję

:

≔

e

2

50 mm

 Rozstaw p

2

:

≔

p

2min

=

⋅

2.4 d

0

72 mm

≔

p

2max

=

min ⎛⎝

,

⋅

14 t

min

200 mm⎞⎠ 196 mm

Przyjmuję

:

≔

p

2

80 mm

wg PN-EN 1993-1-8 2005

str. 23 - tab. 3. 3

 Graficzne przedstawienie rozplanowania śrub na półce :

2. Nośność obliczeniowa pojedynczej śruby na ścinanie

≔

α

v

0.5

wg PN-EN 1993-1-8 2005 str. 27 tab. 3.4

≔

γ

M2

1.25

- współczynnik bezpieczeństwa

wg PN-EN 1993-1-8 2005 str. 18

≔

n

1

- liczba styków ciernych

 Nośność na ścinanie dla pojedynczej śruby dwuciętej

wg PN-EN 1993-1-8 2005 str. 27 tab. 3.4

≔

F

vRd

=

⋅

⋅

⋅

n α

v

f

ub

――

A

s

γ

M2

184 kN

2.1. Złącze długie - współczynnik redukcyjny

βLf

≔

L

j

=

p

2

8 cm

=

⋅

15 d

40.5 cm

=

>

⋅

15 d

L

j

1

wg PN-EN 1993-1-8 2005

str. 29 - pkt. 3.8

Nie uwzględniamy współczynnika redukcyjnego

3. Wyznaczenie nośności na poślizg

 Siła sprężania

≔

F

pC

=

⋅

⋅

0.7 f

ub

A

s

322 kN

 Współczynnik tarcia dla

klasy powierzchni ciernej B

≔

μ

0.4

wg PN-EN 1090-2 tab. 8

9

 Współczynnik kształtu otworów na śruby

≔

k

s

1

wg PN-EN 1993-1-8 2005

str. 30 - tab. 3.6

 Współczynnik częściowy

≔

γ

M3

1.25

 Obliczeniowa nośność na poślizg

≔

F

sRd

=

⋅

⋅

⋅

k

s

n μ ――

F

pC

γ

M3

103.04 kN

 Obliczeniowa nośność na poślizg 5 śrub

≔

F

sRd5

=

⋅

5 F

sRd

515.2 kN

4. Wyznaczenie nośności śruby na docisk

4.1. Nośność obliczeniowa na docisk dla śrub skrajnych i pośrednich

4.1.1. Śruba skrajna - szereg skrajny

≔

α

d

=

――

e

1

⋅

3 d

0

0.667

≔

k

1

=

min

⎛
⎜
⎝

,

−

⋅

2.8 ―

e

2

d

0

1.7 2.5

⎞
⎟
⎠

2.5

≔

α

b

=

min

⎛
⎜
⎝

,

,

α

d

――

f

ub

f

u

1.0

⎞
⎟
⎠

0.667

 Obliczeniowa nośność na docisk - śruba skrajna, szereg skrajny

wg PN-EN 1993-1-8 2005

str. 27 - tab. 3.4

≔

F

b.Rd_s

=

⋅

⋅

⋅

⋅

k

1

α

b

f

u

d ――

t

min

γ

M2

181.44 kN

4.1.2. Śruba skrajna - szereg pośredni

≔

α

d

=

−

――

p

1

⋅

3 d

0

―

1

4

1.861

≔

k

1

=

min

⎛
⎜
⎝

,

−

⋅

1.4 ―

p

2

d

0

1.7 2.5

⎞
⎟
⎠

2.033

≔

α

b

=

min

⎛
⎜
⎝

,

,

α

d

――

f

ub

f

u

1.0

⎞
⎟
⎠

1

 Obliczeniowa nośność na docisk - śruba skrajna, szereg pośredni

≔

F

b.Rd_p

=

⋅

⋅

⋅

⋅

k

1

α

b

f

u

d ――

t

min

γ

M2

221.357 kN

wg PN-EN 1993-1-8 2005

str. 27 - tab. 3.4

 Nośność na docisk

≔

F

b.Rd

=

min ⎛⎝

,

F

b.Rd_s

F

b.Rd_p

⎞⎠ 181.44 kN

4.2. Wyznaczenie nośności grupy łączników

 Nośność na ścinanie :

=

F

vRd

184 kN

 Nośność na docisk - śruba skrajna :

=

F

b.Rd_s

181.44 kN

10

 Nośność na docisk - śruba pośrednia :

=

F

b.Rd_p

221.357 kN

 Warunek normowy :

=

∧

⎛⎝

≥

F

vRd

F

b.Rd_s

⎞⎠ ⎛⎝

≥

F

vRd

F

b.Rd_p

⎞⎠ 0

wg PN-EN 1993-1-8 2005

str. 29 - pkt. 3.7

 Nośność obliczeniowa grupy łączników:

≔

F

Rd

=

⋅

5 F

b.Rd_s

907.2 kN

5. Wyznaczenie obliczeniowej siły przypadającej na jedną śrubę

 Siła podłużna w jednej nakładce :

≔

N

Ed

=

――

M

N

+

t

N

h

339.946 kN

 Siła w pojedynczej śrubie :

≔

F

Ed

=

――

N

Ed

n

sprow

67.989 kN

6. Wyznaczenie nośności nakładki osłabionej otworami

 Pole przekroju netto nakładki :

≔

s

N

=

max

⎛
⎜
⎜

⎝

,

⋅

d

0

t

N

⋅

t

N

⎛
⎜
⎜

⎝

−

⋅

2 d

0

――――

⎛⎝

⋅

0.5 p

1

⎞⎠

2

⋅

4 p

2

⎞
⎟
⎟

⎠

⎞
⎟
⎟

⎠

635.94 mm

2

≔

A

netN

=

−

⋅

b

N

t

N

s

N

2964.063 mm

2

wg PN-EN 1993-1-1 2006

str. 47 - pkt. 6.2.2 (4)

 Współczynnik bezpieczeństwa :

≔

γ

M0

1

 Nośność nakładki osłabionej otworami:

≔

N

netN

=

⋅

A

netN

――

f

y

γ

M0

696.555 kN

7. Wyznaczenie nośności półki osłabionej otworami

 Pole przekroju netto nakładki :

≔

s

P

=

max

⎛
⎜
⎜

⎝

,

⋅

d

0

t

f

⋅

t

f

⎛
⎜
⎜

⎝

−

⋅

2 d

0

――――

⎛⎝

⋅

0.5 p

1

⎞⎠

2

⋅

4 p

2

⎞
⎟
⎟

⎠

⎞
⎟
⎟

⎠

445.16 mm

2

≔

A

netP

=

−

⋅

b

f

t

f

s

P

2074.844 mm

2

wg PN-EN 1993-1-1 2006

str. 47 - pkt. 6.2.2 (4)

 Współczynnik bezpieczeństwa :

≔

γ

M0

1

 Nośność nakładki osłabionej otworami:

≔

N

netP

=

⋅

A

netP

――

f

y

γ

M0

487.588 kN

8. Sprawdzenie warunków nośności w stanie granicznym

 Nośność na poślizg :

=

≤

N

Ed

F

sRd5

1

=

――

N

Ed

F

sRd5

%

65.98

 Nośność grupy łączników :

=

≤

N

Ed

F

Rd

1

=

――

N

Ed

F

Rd

%

37.47

 Nośność nakładki osłabionej otworami :

=

≤

N

Ed

N

netN

1

=

――

N

Ed

N

netN

%

48.8

 Nośność półki osłabionej otworami :

=

≤

N

Ed

N

netP

1

=

――

N

Ed

N

netP

%

69.72

11

Połączenie spawane wg EC3 Cz.1-8
Nośność spoiny między nakładką a półką obliczana metodą uproszczoną

1. Przyjęcie wymiaru nakładek i przykładek oraz obliczenie sił i momentów

1.1. Nakładki

 Grubość nakładek

≔

t

N

20 mm

 Wysokość nakładek

≔

h

N

140 mm

 Szerokość nakładek

≔

b

N

140 mm

1.2. Przykładki

 Grubość przykładek

≔

t

P

10 mm

 Wysokość przykładek

≔

h

P

80 mm

 Szerokość przykładek

≔

b

P

80 mm

 Sprawdzenie prawidłowości przyjętej wysokości przykładek

≔

h

0

=

−

−

h

⋅

2 t

f

⋅

2 R

122 mm

=

≤

h

P

h

0

1

1.3. Momenty bezwładności przykładek i nakładek

 Moment bezwładności przykładki

≔

I

Py

=

⋅

⋅

2 t

P

――

h

P

3

12

85.33 cm

4

 Moment bezwładności nakładki

≔

I

Ny

=

⋅

2

⎛
⎜
⎜⎝

+

⋅

⋅

h

N

t

N

⎛
⎜

⎝

+

―

t

N

2

―

h

2

⎞
⎟

⎠

2

⋅

t

N

――

h

N

3

12

⎞
⎟
⎟⎠

6514.6667 cm

4

 Suma momentów bezwładności nakładki i przykładki

≔

I

Cy

=

+

I

Py

I

Ny

6600 cm

4

1.4. Momenty

 Moment nakładek

≔

M

N

=

⋅

M

Ed

――

I

Ny

I

Cy

69.17 kN·m

 Moment przykładek

≔

M

P

=

⋅

M

Ed

――

I

Py

I

Cy

⎛⎝

⋅

906.05 10

−3

⎞⎠ kN·m

2. Ustalenie grubości i długości spoiny

≔

t

max

=

max ⎛⎝ ,

t

f

t

N

⎞⎠ 20 mm

≔

t

min

=

min ⎛⎝ ,

t

f

t

N

⎞⎠ 14 mm

≔

a

snmin

=

max ⎛⎝

,

⋅

0.2 t

max

3 mm⎞⎠ 4 mm

≔

a

snmax

=

⋅

0.7 t

min

9.8 mm

12

 Grubość spoiny :

≔

a

sn

8 mm

 Sprawdzenie warunku :

=

≥

≥

a

snmax

a

sn

a

snmin

1

≔

l

min

=

max ⎛⎝

,

30 mm

⋅

6 a

sn

⎞⎠ 48 mm

≔

l

max

=

⋅

150 a

sn

1200 mm

 Długość spoiny :

≔

l

sn

140 mm

 Sprawdzenie warunku :

=

≥

≥

l

max

l

sn

l

min

1

2. Ustalenie nośności spoin pachwinowych:

 Współczynnik korelacji dla spoin pachwinowych

≔

β

w

0.8

wg PN-EN 1993-1-8 2005

str. 42 - tab.4.1 dla S235

 Współczynnik częściowy

≔

γ

M2

1.25

wg PN-EN 1993-1-1 2006

str. 45 - UWAGA 2B

 Siła podłużna w jednej nakładce :

≔

N

Ed

=

――

M

N

+

t

N

h

345.855 kN

 Naprężenia w przekroju spoiny

≔

τ

∥

=

―――

N

Ed

⋅

⋅

2 a

sn

l

sn

154.4 MPa

≔

σ

p

0 MPa

≔

τ

p

0 MPa

 Warunek nośności obliczeniowej spoiny

wg PN-EN 1993-1-1 2006

str. 45 - UWAGA 2B

=

‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾

2

⎛

⎝

+

σ

p

2

⋅

3 ⎛⎝

+

τ

p

2

τ

∥

2

⎞

⎠

⎞

⎠

267.43 MPa

=

―――

f

u

⋅

β

w

γ

M2

360 MPa

=

≤

267.43 MPa

360 MPa

1

≔

f

vw.d

=

―――

――

f

u

‾‾

2

3

⋅

β

w

γ

M2

207.85 MPa

=

≤

σ

p

―――

⋅

0.9 f

u

γ

M2

1

=

――

τ

∥

f

vw.d

%

74.29

Warunek został spełniony

Nośność spoiny między przykładką a środnikiem obliczana metodą kierunkową

1. Ustalenie grubości i długości spoiny

≔

t

max

=

max ⎛⎝ ,

t

f

t

P

⎞⎠ 14 mm

≔

t

min

=

min ⎛⎝ ,

t

f

t

P

⎞⎠ 10 mm

≔

a

spmin

=

max ⎛⎝

,

⋅

0.2 t

max

3 mm⎞⎠ 3 mm

≔

a

spmax

=

⋅

0.7 t

min

7 mm

 Grubość spoiny :

≔

a

sp

6 mm

=

≥

≥

a

spmax

a

sp

a

spmin

1

13

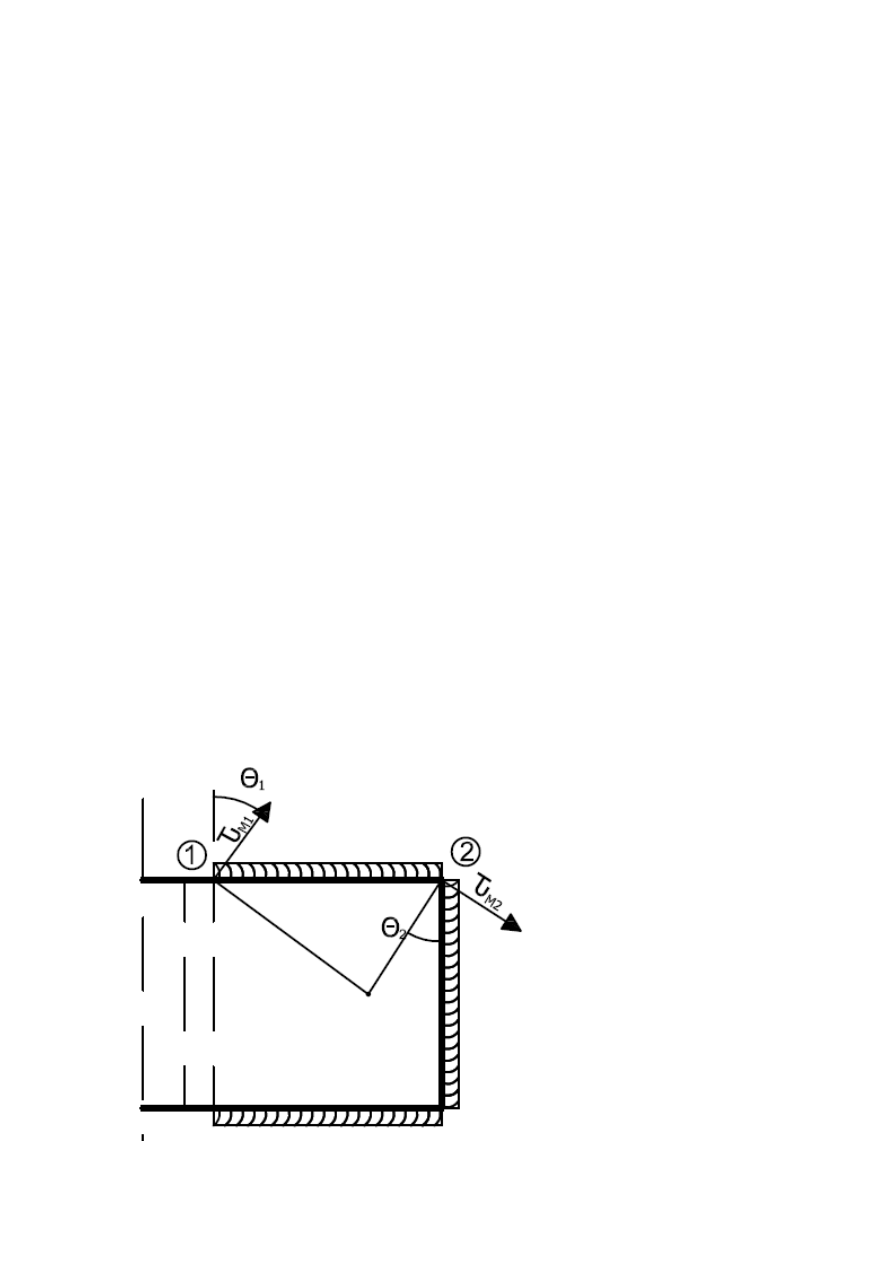
2. Środek ciężkości układu spoin

≔

S

z

=

+

⋅

⋅

⋅

2 b

P

a

sp

⎛
⎜

⎝

+

―

b

P

2

5 mm

⎞
⎟

⎠

⋅

⋅

h

P

a

sp

⎛
⎜

⎝

+

+

b

P

――

a

sp

2

5 mm

⎞
⎟

⎠

85.44 cm

3

≔

A

s

=

+

⋅

⋅

2 a

sp

b

P

⋅

a

sp

h

P

14.4 cm

2

≔

x

0

=

―

S

z

A

s

5.93 cm

3. Biegunowy moment bezwladności układu spoin

≔

I

x

=

+

⋅

2

⎛
⎜
⎜⎝

+

―――

⋅

b

P

a

sp

3

12

⋅

⋅

a

sp

b

P

⎛
⎜

⎝

―――

+

h

P

a

sp

2

⎞
⎟

⎠

2

⎞
⎟
⎟⎠

―――

⋅

a

sp

b

P

3

12

203.39 cm

4

≔

I

z

+

+

⋅

2

⎛
⎜
⎜⎝

+

―――

⋅

a

sp

b

P

3

12

⋅

⋅

a

sp

b

P

⎛
⎜

⎝

−

x

0

―

b

P

2

⎞
⎟

⎠

2

⎞
⎟
⎟⎠

―――

⋅

h

P

a

sp

3

12

⋅

⋅

h

P

a

sp

⎛⎝

−

+

b

P

⋅

0.5 a

sp

x

0

⎞⎠

2

=

I

z

114.11 cm

4

≔

I

0

=

⋅

2 ⎛⎝ +

I

x

I

z

⎞⎠ 635.01 cm

4

4. Mimośród

≔

e

=

+

x

0

5 mm

6.43 cm

5. Siły przekrojowe

 Siła tnąca :

≔

V

1

=

V

P

137.64 kN

 Siła rozciągająca :

≔

N

1

=

N

P

0 kN

 Moment :

≔

M

1

=

+

M

P

⋅

V

P

e

9.76 kN·m

14



Promień pierwszego najbardziej wytężonego punktu

≔

x

1max

=

−

x

0

5 mm

54.33 mm

≔

z

1max

=

―

h

P

2

40 mm

≔

r

1max

=

‾‾‾‾‾‾‾‾‾‾‾‾

2

+

x

1max

2

z

1max

2

67.47 mm



Naprężenia

 Kąt θ

1

pomiędzy składową pionową a

składową prostopadłą do r

1

:

≔

θ

1

=

atan

⎛
⎜
⎝

――

z

1max

x

1max

⎞
⎟
⎠

36.36 °

≔

τ

M1

=

――――

⋅

M

1

r

1max

I

0

103.71 MPa

 Składowe naprężeń:

≔

σ

M1

=

⋅

τ

M1

cos ⎛⎝θ

1

⎞⎠ 83.52 MPa

≔

τ

∥

=

⋅

τ

M1

sin ⎛⎝θ

1

⎞⎠ 61.49 MPa

≔

σ

TM

=

―――

⋅

σ

M1

‾‾

2

2

2

59.06 MPa

≔

τ

TM

=

―――

⋅

σ

M1

‾‾

2

2

2

59.06 MPa



Normowa wytrzymałość spoiny w punkcie 1

=

≤

‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾

2

⎛

⎝

+

σ

TM

2

⋅

3 ⎛⎝

+

τ

TM

2

τ

∥

2

⎞

⎠

⎞

⎠

―――

f

u

⋅

β

w

γ

M2

1

=

―――――――――

‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾

2

⎛

⎝

+

σ

TM

2

⋅

3 ⎛⎝

+

τ

TM

2

τ

∥

2

⎞

⎠

⎞

⎠

―――

f

u

⋅

β

w

γ

M2

%

44.18

=

≤

σ

TM

―――

⋅

0.9 f

u

γ

M2

1

=

―――

σ

TM

―――

⋅

0.9 f

u

γ

M2

%

22.78

Warunek został spełniony



Promień drugiego najbardziej wytężonego punktu

≔

x

2max

=

−

+

b

P

5 mm

x

0

25.67 mm

≔

z

2max

=

―

h

P

2

40 mm

≔

r

2max

=

‾‾‾‾‾‾‾‾‾‾‾‾

2

+

x

2max

2

z

2max

2

47.53 mm

15



Naprężenia

 Kąt θ

2

pomiędzy składową pionową a

składową prostopadłą do r

2

:

≔

θ

2

=

atan

⎛
⎜
⎝

――

z

2max

x

2max

⎞
⎟
⎠

57.31 °

≔

τ

M2

=

――――

⋅

M

1

r

2max

I

0

73.06 MPa

 Składowe naprężeń:

≔

σ

M2

=

⋅

τ

M2

cos ⎛⎝θ

2

⎞⎠ 39.45 MPa

≔

τ

∥

=

⋅

τ

M2

sin ⎛⎝θ

2

⎞⎠ 61.49 MPa

≔

σ

TM

=

―――

⋅

σ

M2

‾‾

2

2

2

27.9 MPa

≔

τ

TM

=

―――

⋅

σ

M2

‾‾

2

2

2

27.9 MPa

≔

V

2

=

V

P

137.64 kN

 Naprężenie pochodzące od siły

działającej na przykładkę:

≔

τ

V2

=

――

V

2

⋅

2 A

s

47.79 MPa



Normowa wytrzymałość spoiny w punkcie 2

=

≤

‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾

2

⎛
⎝

+

σ

TM

2

⋅

3

⎛
⎝

+

τ

TM

2

⎛⎝ +

τ

∥

τ

V2

⎞⎠

2

⎞
⎠

⎞
⎠

―――

f

u

⋅

β

w

γ

M2

1

=

―――――――――――

‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾

2

⎛
⎝

+

σ

TM

2

⋅

3

⎛
⎝

+

τ

TM

2

⎛⎝ +

τ

∥

τ

V2

⎞⎠

2

⎞
⎠

⎞
⎠

―――

f

u

⋅

β

w

γ

M2

%

54.81

=

≤

σ

TM

―――

⋅

0.9 f

u

γ

M2

1

=

―――

σ

TM

―――

⋅

0.9 f

u

γ

M2

%

10.76

Warunek został spełniony - styk
zaprojektowany poprawnie

16