drogi i cykle w grafach

1

Drogi i cykle w grafach

Graf – zbiór wierzchołków V i krawędzi E.

Krawędź - para wierzchołków.

Krawędź może mieć wagę (graf z wagami).

Graf nieskierowany - gdy pary wierzchołków krawędzi są
nieuporządkowane.
Kolejność wierzchołków krawędzi istotna - graf skierowany

(digraf).

Stopień wierzchołka v - liczba krawędzi wychodzących z tego

wierzchołka. Oznaczać przez d(v).

Ponadto

|E| - liczba krawędzi grafu

|V| - liczba wierzchołków grafu.

Własność: Suma stopni wierzchołków w grafie jest równa
podwojonej liczbie krawędzi grafu.

|

|

2

)

(

E

v

d

V

v

=

∑

∈

Wniosek: liczba wierzchołków o nieparzystych stopniach jest
parzysta.

Drogi i cykle

Droga (ścieżka) – ciąg wierzchołków v

0

, v

1

, ..., v

k

taki, ze każde

dwa kolejne v

i

, v

i+1

są połączone krawędzią.

Długością drogi dla grafów bez wag jest liczba tych krawędzi, a

dla grafów z wagami suma wag tych krawędzi.

Droga jest zamknięta, gdy v

0

= v

k

.

drogi i cykle w grafach

2

Droga prosta – gdy wszystkie jej krawędzie są różne.

Cykl – droga zamknięta, w której wszystkie wierzchołki oprócz

pierwszego i ostatniego są różne.

Graf nie zawierający cykli nazywamy acyklicznym.
Graf jest spójny gdy między każdą parę wierzchołków można
poprowadzić drogę. Składowa spójności – maksymalny spójny
podgraf.
Własność:
Każda droga zamknięta o różnych wierzchołkach v

0

, v

1

, ..., v

k-1

i

co najmniej trzech krawędziach jest cyklem.
Własność:
Droga ma wszystkie wierzchołki różne wtedy i tylko wtedy, gdy
jest prosta i acykliczna.
Własność:
Jeżeli w grafie istnieje droga od wierzchołka u do v
(u ≠ v) , to istnieje także droga prosta acykliczna od u do v.

Drogi i cykle Eulera

Droga Eulera - droga która przechodzi dokładnie jeden raz
przez każdą krawędź grafu.
Cykl Eulera – droga zamknięta w której każda krawędź grafu
występuje dokładnie jeden raz.
Cykl Eulera jest związany z mostami w Królewcu (XVIII w) –
czy można przejść dokładnie raz przez mosty i wrócić do punktu
wyjścia?

Rys. Mosty królewieckie i odpowiadający im graf

rzeka

ląd

wyspa

wyspa

ląd

graf

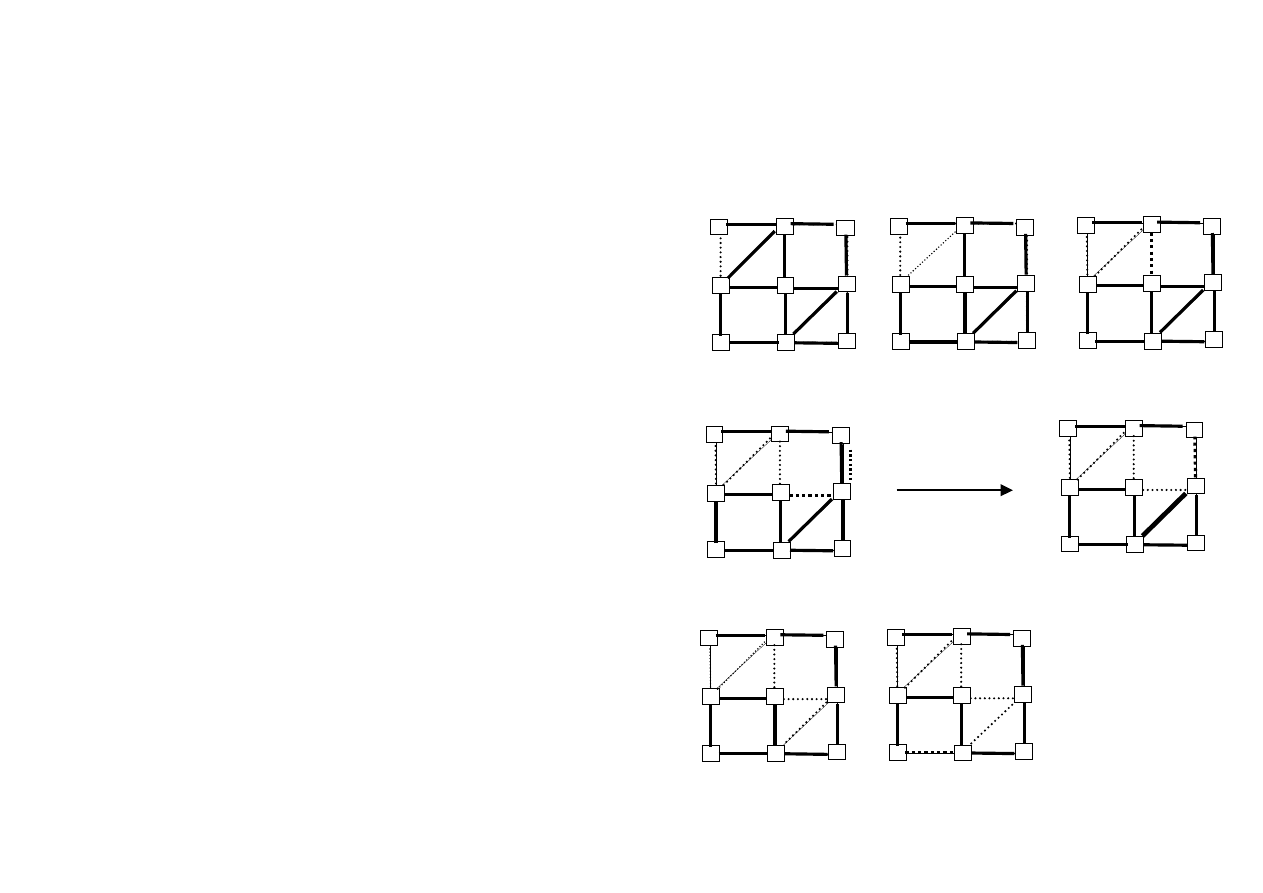
drogi i cykle w grafach

3

Jak wykazał Euler (1736), dla mostów królewieckich
rozwiązanie takie nie istnieje.

Twierdzenie:
Graf spójny posiada:

- cykl Eulera wtedy i tylko wtedy, gdy każdy jego

wierzchołek jest parzystego stopnia

- drogę Eulera – jeżeli co najwyżej dwa jego wierzchołki są

stopnia nieparzystego

Uzasadnienie: Droga Eulera przechodzi dokładnie raz przez
każdą krawędź. Przechodząc przez wierzchołek możemy usunąć
krawędź którą przyszliśmy i krawędź którą wyszliśmy. Dlatego z
każdego wierzchołka musi wychodzić parzysta liczba krawędzi,
z wyjątkiem co najwyżej początku i końca drogi. Jeżeli jednak
początek drogi pokrywa się z jej końcem, to także i ten
wierzchołek musi być stopnia parzystego (wychodzimy i
wchodzimy).

Algorytm wyszukiwania cyklu Eulera:

1. Wybieramy wierzchołek początkowy v

0

(dowolnie)

2. Powtarzamy aż do wyczerpania krawędzi

a) jeżeli z bieżącego wierzchołka nie odchodzi żadna

krawędź, to koniec

b) jeżeli z bieżącego wierzchołka v odchodzi tylko jedna

krawędź, to przechodzimy wzdłuż tej krawędzi do
następnego wierzchołka, usuwamy tę krawędź i
wierzchołek v z grafu

c) jeżeli z v odchodzi więcej niż jedna krawędź, wtedy

wybieramy taką, by po jej usunięciu graf pozostał spójny;
wzdłuż tej krawędzi przechodzimy do następnego
wierzchołka i usuwamy tę krawędź z grafu.

drogi i cykle w grafach

4

Powyższy algorytm jest niezbyt wygodny , ponieważ na każdym
kroku wymaga sprawdzania czy graf pozostaje spójny.


Cykl Eulera – algorytm I (z badaniem spójności grafu}

1

4

7

2

3

9

8

6

5

1

4

7

2

3

9

8

6

5

1

4

7

2

3

9

8

6

5

1

4

7

2

3

9

8

6

5

1

4

7

2

3

9

8

6

5

1

4

7

2

3

9

8

6

5

1

4

7

2

3

9

8

6

5

niedopuszczalne

{1 2}

{1 2 3 5 8 7}

{1 2 3 5 8}

{1 2 3 5}

{1 2 3}

{1 2 3 5 8 7 4 }

Dalej nie ma
wyboru:
Cykl Eulera
{1 2 3 5 8 7 4}

∪

{2 5 7 9 8 6 3 1}

drogi i cykle w grafach

5

Drugi algorytm wyznaczania cyklu Eulera
Założenie:
Graf spójny, wszystkie wierzchołki są stopnia parzystego
Algorytm II (z wykorzystaniem stosu)
1. Wybieramy wierzchołek początkowy v; stos:= {v} CE = ∅

(cykl Eulera pusty)

2. dopóki stos ≠ ∅ wykonuj:

a) v:= front (stos)
b) jeżeli z v wychodzą nie odwiedzone krawędzie, to

wybieramy jedną z nich, przechodzimy wzdłuż niej do
sąsiedniego wierzchołka w. Krawędź (v, w) zaznaczamy
jako odwiedzoną oraz

stos = stos + {w}

c) jeżeli wszystkie krawedzie wychodzące z v już były

odwiedzone, to usuwamy v ze stosu, dokładając do cyklu
Eulera CE. Przechodzimy do następnego wierzchołka na
stosie.

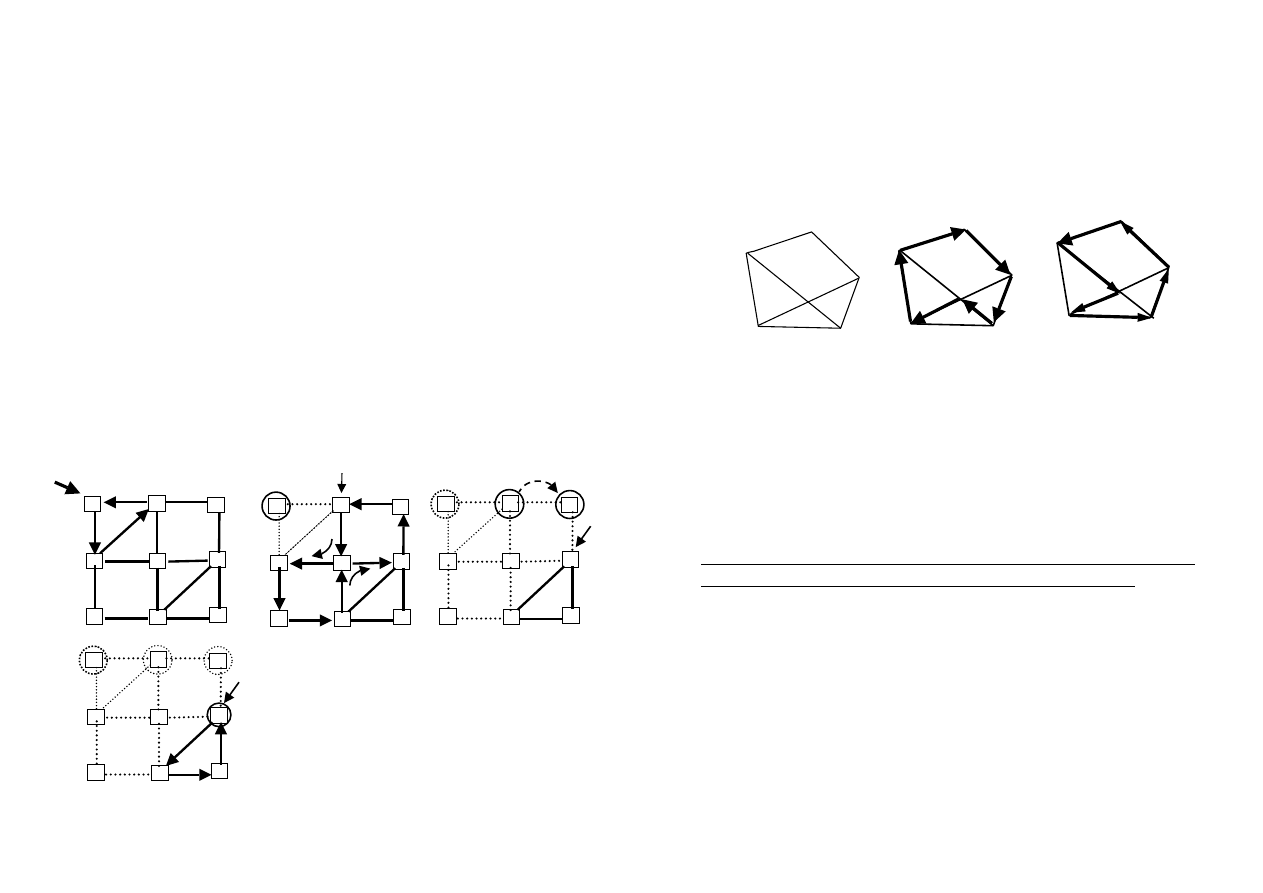
Przykład:
Graf 9 wierzchołków – start 1 – algorytm II (ze stosem)

1

4

7

2

3

9

8

6

5

1

4

7

2

3

9

8

6

5

1

4

7

2

3

9

8

6

5

1

4

7

2

3

9

8

6

5

Wynik – cykl Eulera:

{1 3 6 8 9 7 8 5 7 4 2 5 3 2 1}

drogi i cykle w grafach

6

Droga Hamiltona

Droga Hamiltona jest to droga, która przechodzi dokładnie

raz przez każdy wierzchołek grafu. Cykl Hamiltona – zamknięta

droga Hamiltona.

Rys. Cykle Hamiltona w grafie

Grafem pełnym - graf, w którym każde dwa wierzchołki są
połączone krawędzia.
Graf pełny o n wierzchołkach jest oznaczany prze K

n

.

Własność: Każdy graf pełny o n ≥ 3 wierzchołkach ma cykl
Hamiltona.
Nie jest znane żadne kryterium na istnienie cyklu Hamiltona, ani
tez żaden algorytm działający w czasie wielomianowym.
Algorytm naiwny – sprawdzanie wszystkich permutacji
wierzchołków (n! permutacji dla n wierzchołków).

Algorytm szukania drogi Hamiltona (algorytm z nawrotami).

Zasada; idziemy pierwszą możliwą ścieżką tak daleko jak to
możliwe, odkładając kolejne wierzchołki na stos. Gdy nie ma już
dokąd iść, zdejmujemy bieżący wierzchołek ze stosu i
próbujemy iść inną drogą, od następnego na stosie.

1

2

5

6

3

4

1

2

5

6

3

4

5

1

2

6

3

4

drogi i cykle w grafach

7

Algorytm z nawrotami.
1. wybieramy wierzchołek początkowy v; stos = {v}
2. Powtarzamy do skutku
a) jeżeli u = front (stos), to wybieramy w taki ,że

- w połączony z u krawędzią
- w nie należy do stosu
- w spełnia dodatkowe kryterium wyboru – np. ma najniższy

numer ze spełniających w/w warunki

b) jeżeli istnieje wierzchołek spełniający warunki z p. a, to stos

= stos +{w}. Sprawdzamy, czy wierzchołki na stosie tworzą
drogę Hamiltona. Jeżeli tworzą, to koniec.

c) jeżeli wierzchołek w o własnościach podanych w p. a nie

istnieje, to stos = stos – {u} (u = front(stos))

Przykład:







Start z 4
droga 4 1 2 3 6 5

dalej nie ma dokąd bo 1 zamyka a 7 nie było

5 ze stosu

droga 4 1 2 3 6

dokładamy 7

droga 4 1 2 3 6 7

znowu nie ma dokąd ( 3 i 1 były, 5 brak)

7 ze stosu

droga 4 1 2 3 6

6 ze stosu

(obie drogi, do 5 i 7 wycofane)

droga 4 1 2 3

dokładamy 7

(druga z możliwych, do 6, już była )

droga 4 1 2 3 7 dalej przez 6, 5 – razem 7 wierzchołków
droga 4 1 2 3 7 6 5 droga Hamiltona, wszystkie wierzchołki

(ale z tej drogi nie można utworzyć
cyklu Hamiltona)

2

3

4

6

5

7

1