TEMAT:
Drgania wymuszone o wielu stopniach swobody
(nietłumione)
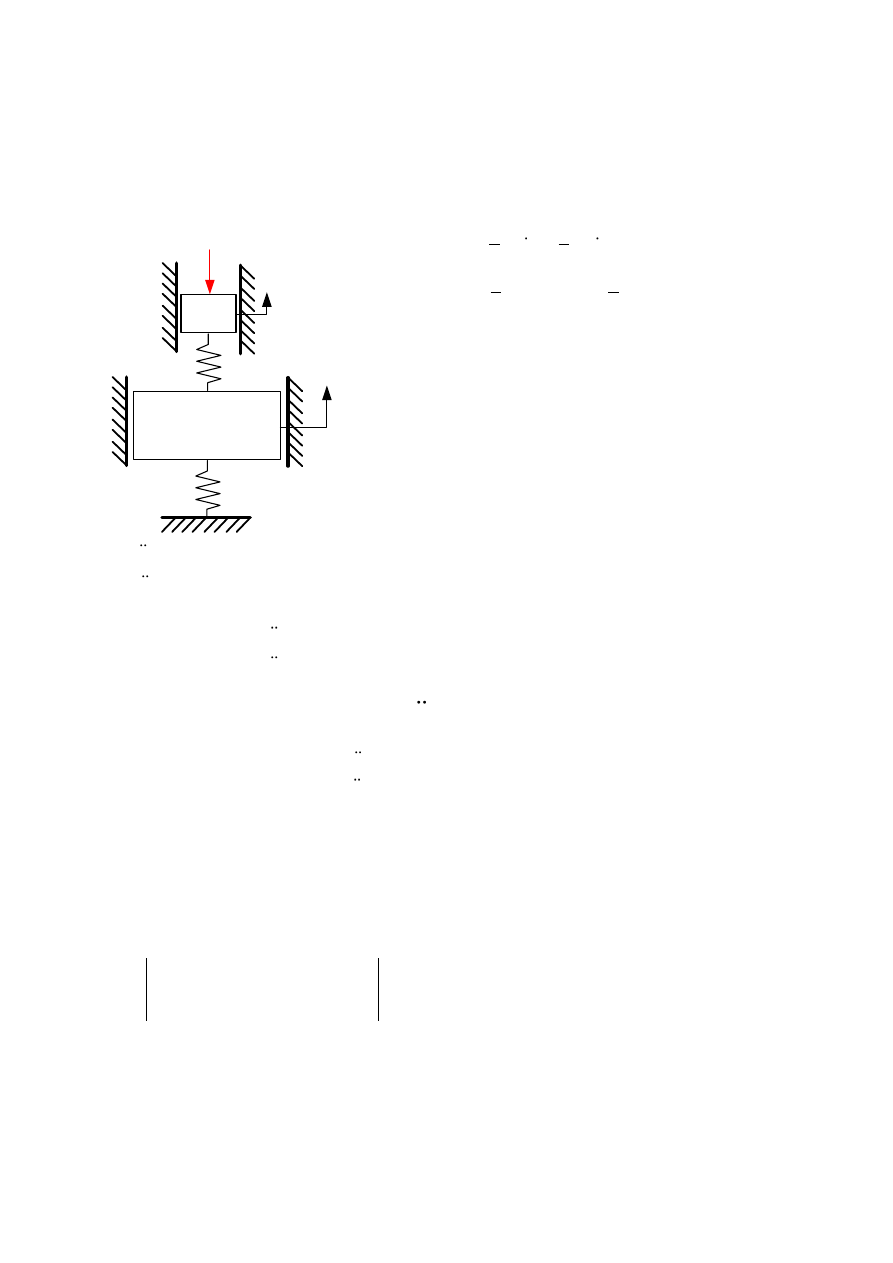
Przykład 1.
1
m
2
m
1
k
2
k
1
x
2
x
0
sin
F t
F
t
2
2
1 1
2
2
2
2
1
1
2
2
2
1
1
2
2
1
1
2
2
E
m x
m x
U
k
x
x
k x
1 1
1
1
2
0
2
2
2
2
1
1
2
sin
0
m x
k x
x
F
t
m x
k x
k x
x
1
1
2
2
sin
sin
x
A
t
x
A
t
2
1
1
2
2
2
sin
sin
x
A
t
x
A
t
0
Mx Kx
1
1
1
1
1
0
2
2
1
2
1
2
0
sin
0
0
m
x
k
k
x
F
t
m
x
k
k
k
x
1
1
1
1
1
0
2
2
2
1
2
1
2
0
0
0
m
A
k
k
A
F
m
A
k
k
k
A
2
1
1
1
1
2
0
2
1
1
2
1
2
2
0
m
k
A
k A
F
k A
m
k
k
A
2
1
1
1
2
2
2
1
1
2
1
2
1
2
1
2
1
2
0
m
k
k
W
m
k
m
k
k
k
k
m
k
k
4
2
2
2
1
2
1
1
2
1
1
2
1
1 2
1
4
2
2
1
2
1
1
2
1
1
2
1 2
1
2
2
2
1
2
1
1
2
1
1
2
1 2
2
1
2
1
1
2
1 2
0
0 /
0
4
m m
k m
k m
k m
k
k k
k
m m
k m
k m
k m
k k
m m
z
m m z
z
k m
k m
k m
k k
k
k
m
k m
k k m
2
2
2
2
1
2
1
2
1
1
2
1
1
2
1
2
1 2
1
2
2
2
2
2
2
2
1
1
2
1 2
1
2
1
1
1 2
1
2
1
2
4
2
2
2
m
k
k
m
k
k
k m m
k m
k k m m
k m m
k k m m
k m
k k m
k m
1
1
2
1
1
2
1
1
2
2
k m
k m
k m
z
m m
1
1
2
1
1
2
2
1
2
2
k m
k m
k m
z
m m
1
1
2
1
1
2
2
1
1
2
2
k m
k m
k m
m m
1
1
2
1
1
2
2
2
1
2
2
k m
k m
k m
m m
+
+
-
1
2
W
0
1
2
1
0
2
1
2
2
2
1
2
0
F
k
W
F
m
k
k
m
k
k
2
1
1
0
2
0 1
1
0
m
k
F
W
F k
k
2
0
2
1
2
1
1
2
2
2
1
1
2
1
2
1
F
m
k
k
W
A
W
m
k
m
k
k
k
2
0 1
2
2
2
2
1
1
2
1
2
1
W
F k
A
W
m
k
m
k
k
k
0
1
2
0
1
2
1
2
1
1
2
1
1 2
0
F k
k
F k
k
A
k k
k
k
k k
0 1
2
1 2
0
F k
A
k k
2
0
2
1
2
1
2
2
0
- antyrezonans
ar
F
m
k
k
k
k
m
1
2
1
A
0
1
2
1 2
F k
k
k k
ar
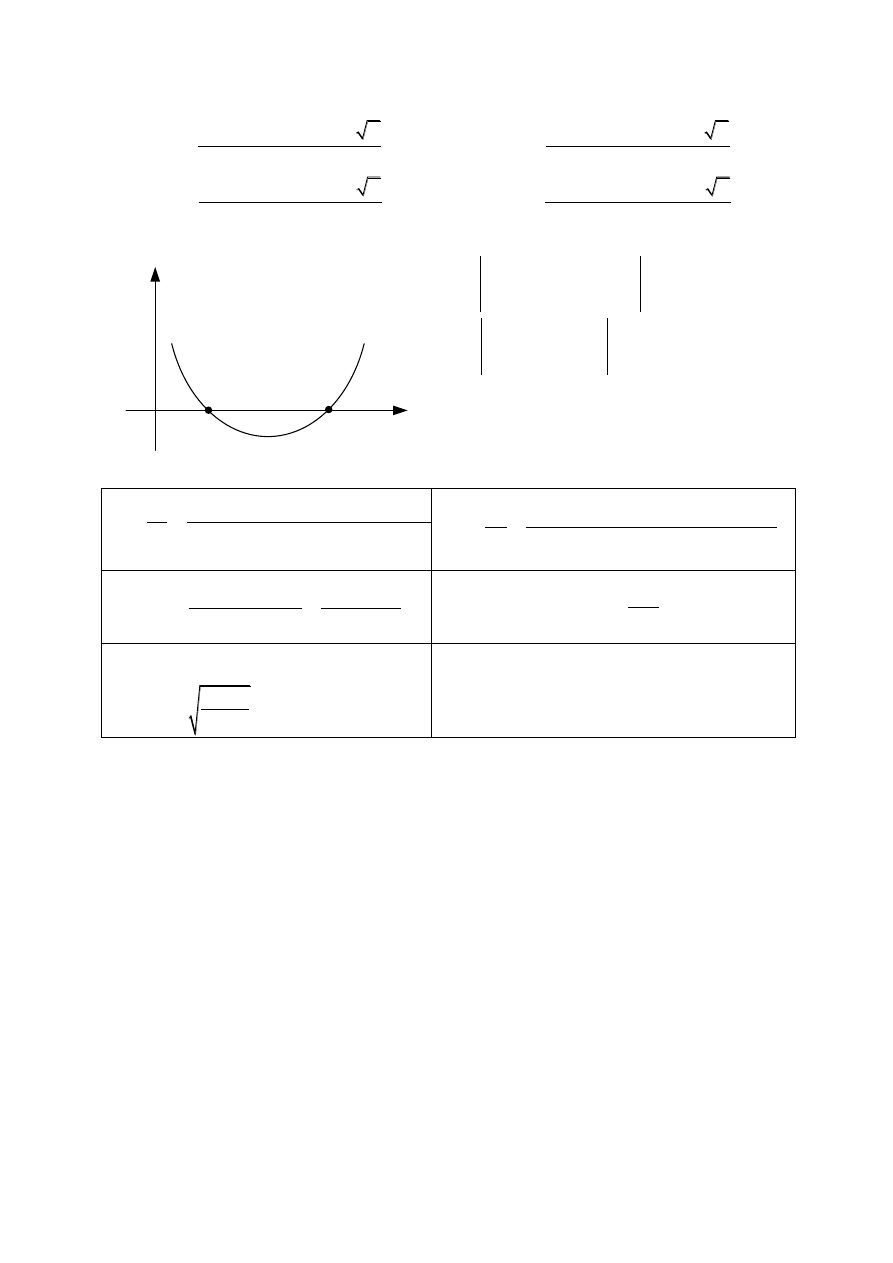
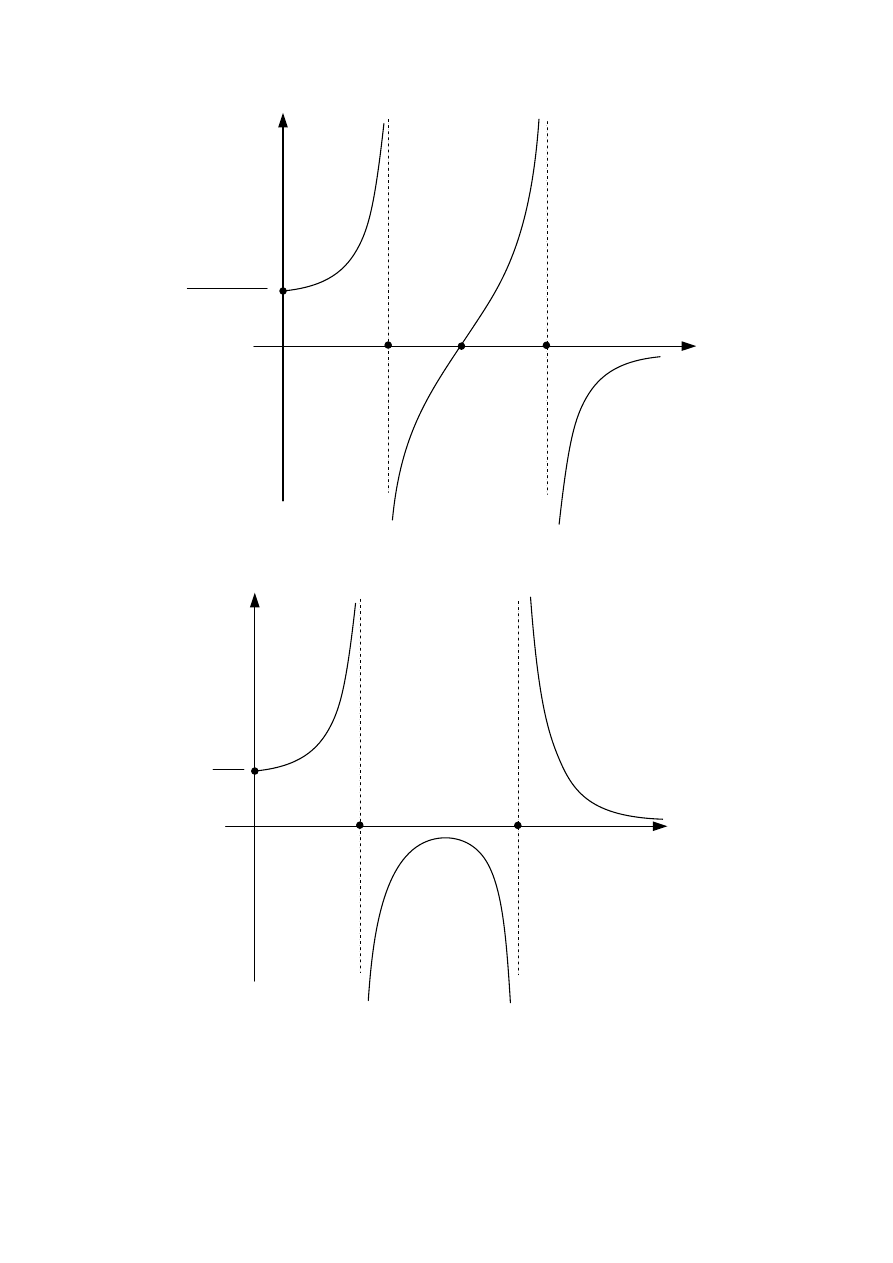
Rys. 1 Charakterystyka amplitudowo - częstotliwościowa masy pierwszej
1
2
2
A
0 1
1 2
F k
k k
Rys. 2 Charakterystyka amplitudowo - częstotliwościowa drugiej masy
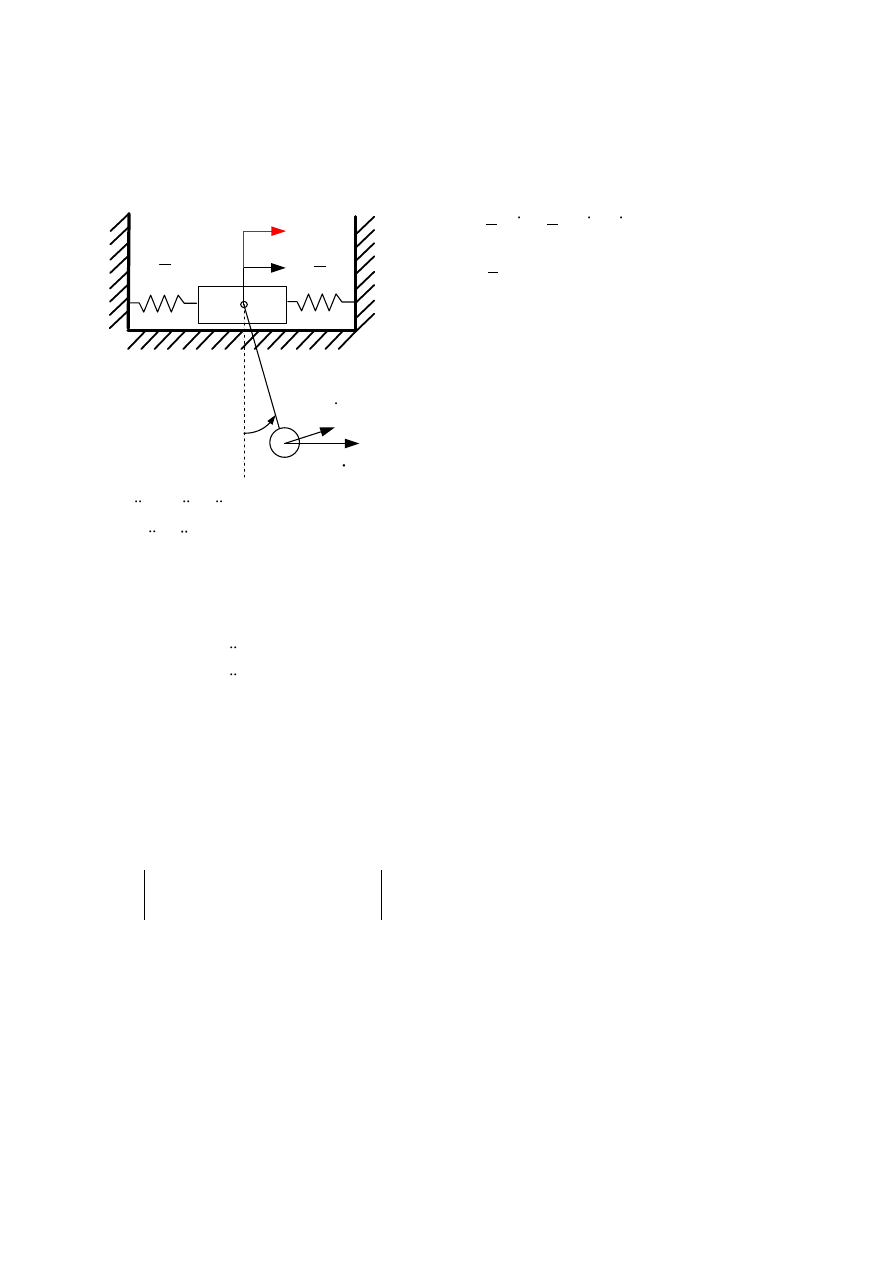
Przykład 2.
Wyznacz częstość drgań własnych oraz charakterystyki amplitudowo częstotliwościowe dla
ruchomego wahadła przedstawionego na rysunku. Przyjąc M=5m.
m
M
x
l
0
sin
F t
F
t
l
x
2
k
2
k
2
2
2
1
1
2
2
1
cos
2
E
Mx
m
l
x
U
kx
mgl
0
sin
0
Mx
m
l
x
kx
F
t
ml
l
x
mgl
1
2
sin
sin
x
A
t
A
t
0
2
0
sin
0
0
M
m
ml
x
k
x
F
t
ml
ml
mgl
1
1
0
2
2
2
2
0
0
0
A
A
M
m
ml
k
F
A
A
ml
ml
mgl
2
2
1
0
2
2
2
2
0
A
F
M
m
k
ml
A
ml
ml
mgl
2
2
2
2
2
4
2 2
2
2
2
0
M
m
k
ml
W
M
m
k
ml
mgl
m l
ml
ml
mgl
4
2
2 2
2
2
2
2
0
Mml
m l
m l
Mmgl
m gl
mkl
mkgl
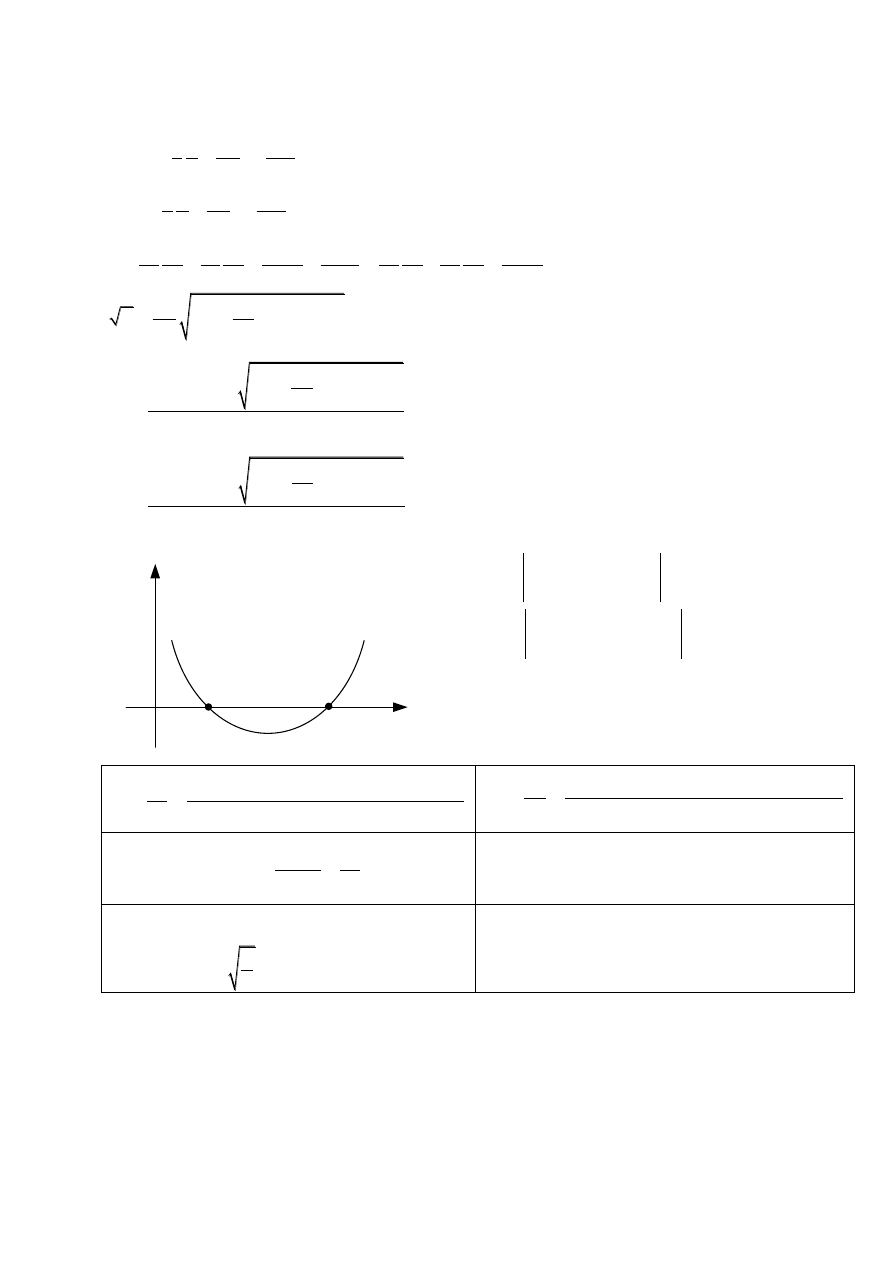
4
2 2
2
2
2
4
2
2
2
2
2
2
2
2
2
2
2
2
2
2
5
6
0
6
0
5
5
5
6
0
5
5
5
36
12
20
36
8
25
25
25
25
25
25
25
1
36
8
5
m l
m gl
mkl
mkgl
g
k
kg
l
m
ml
g
k
kg
z
z
l
m
ml
g
kg
k
kg
g
kg
k
ml
ml
ml
l
m
l
m
g
m
kgm
k
m
l
2
2
2
2
2
1
6
36
8
10
g
gm
k
m
kgm
k
l
m
2
2
2
2
2
2
6
36
8
10
g
gm
k
m
kgm
k
l
m
+
+
-
1
2
W
2
2
2
0
1
0
2
2
0
F
ml
W
F
ml
mgl
ml
mgl
2
2
0
2
0
2
0
M
m
k
F
W
F ml
ml
2
0
1
1
4
2 2
2
2
2
5
6
F ml
l
g
W
A
W
m l
m gl
mkl
mkgl
2
0
2
2
4
2 2
2
2
2
5
6
F ml
W
A
W
m l
m gl
mkl
mkgl
0
0
1
0
F mgl
F
A
mkgl
k
2
0
0
A
2
0
0
- antyrezonans
ar
F ml
l
g
g
l
1
2
1
A
0
1
F
k
ar
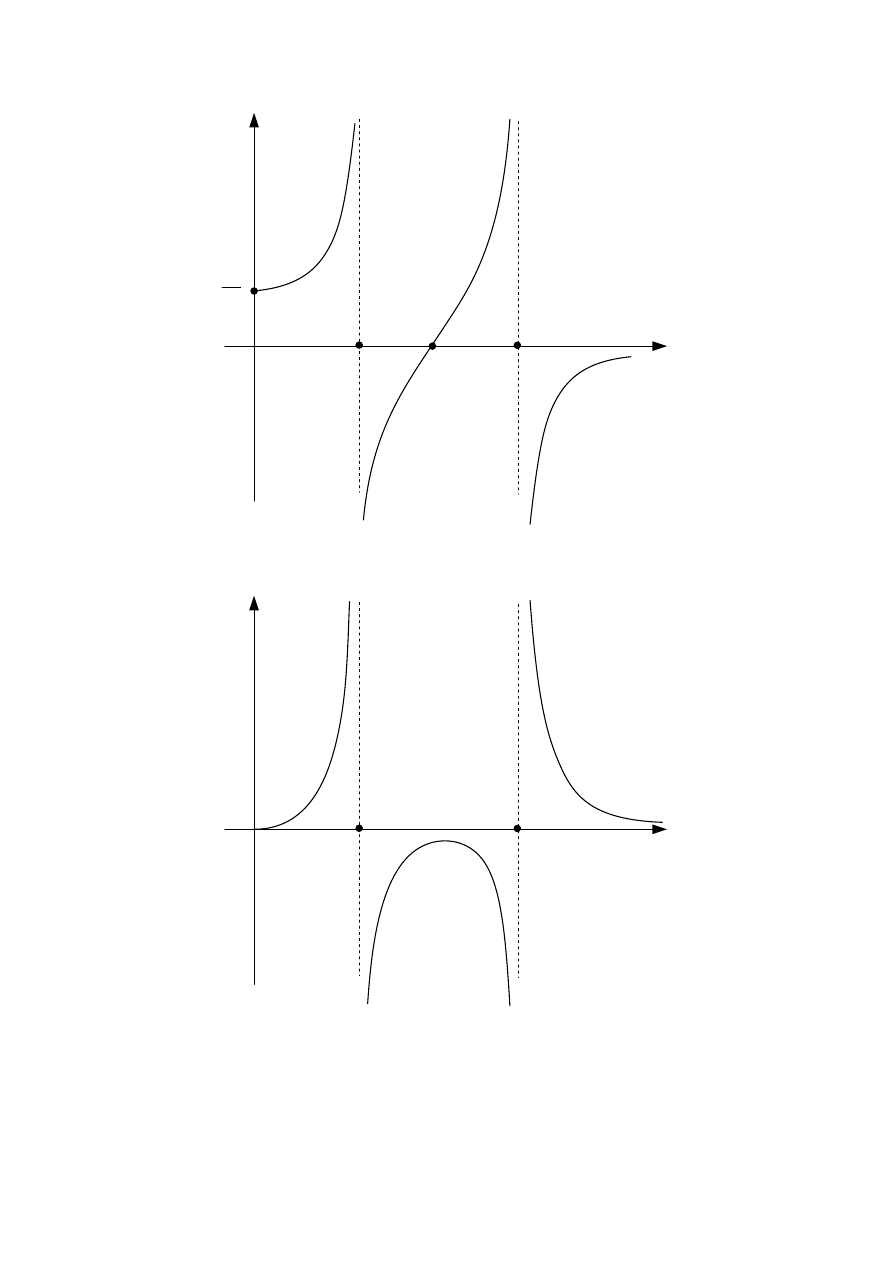
Rys. 3 Charakterystyka amplitudowo - częstotliwościowa suwaka
1
2
2
A
Rys. 4 5 Charakterystyka amplitudowo - częstotliwościowa wahadła
Zadania do rozwiązania!
Analizujemy drgania od położenia równowagi, dlatego nie uwzględniamy w energii
potencjalnej pola grawitacyjnego.
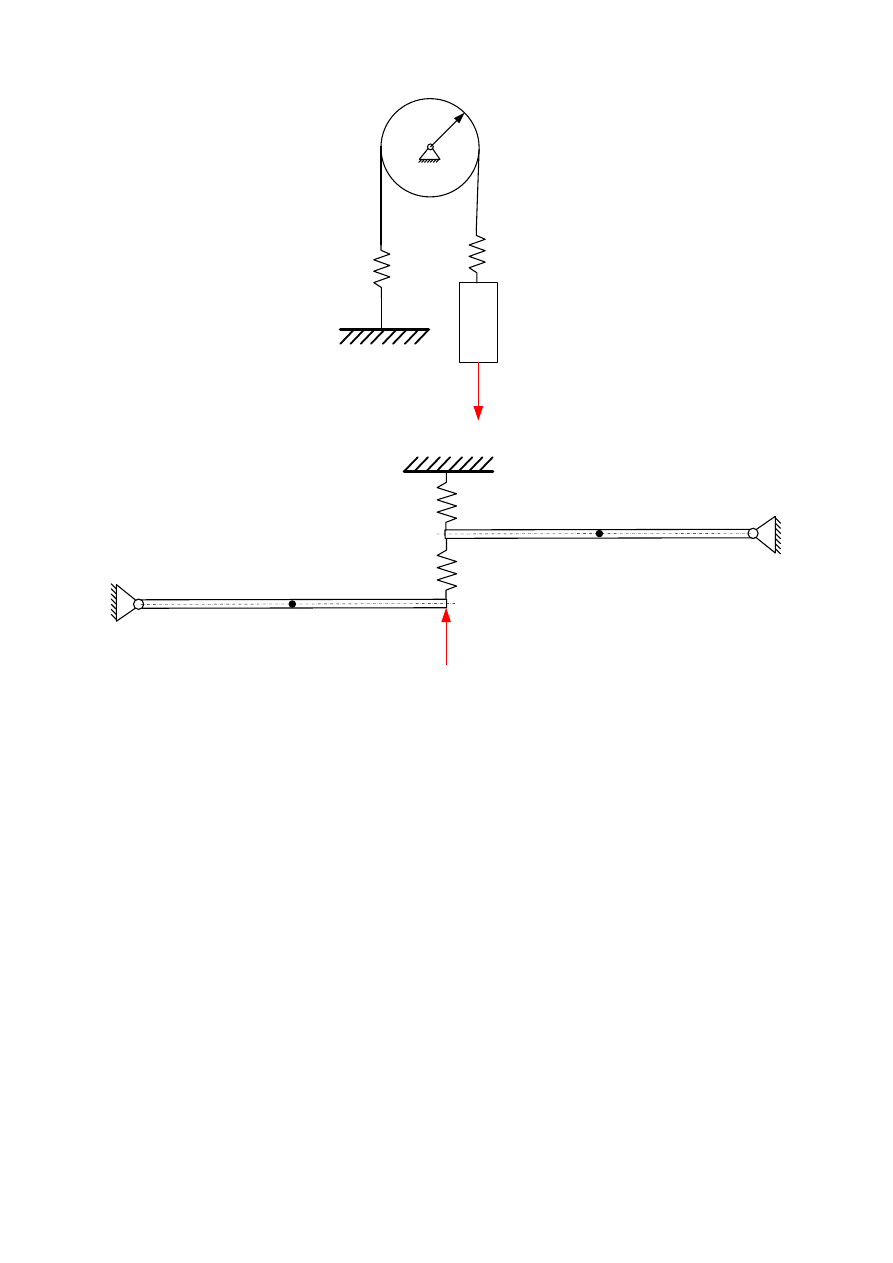
Zadanie.
Narysować charakterystyki amplitudowo częstotliwościowe. Zaznaczyć i obliczyć punkty
charakterystyczne na wykresie w tym częstości drgań własnych, częstości antyrezonansowe
itp..
,
m r
4 , 2
m r
k
k
0
sin
F
t
k
k
,
m r
m
0
sin
F
t
,
m r
k
2k
0
sin
F
t
,
m r
k
r
r
k
2k
2k
m
m
sin
M
t
0
sin
F
t
m
k
k
m r
, 2
m l
, 2
m l
k
k
0
sin
F
t
Wyszukiwarka
Podobne podstrony:
Konwekcja wymuszona id 247087 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
pedagogika ogolna id 353595 Nieznany
Misc3 id 302777 Nieznany
cw med 5 id 122239 Nieznany
D20031152Lj id 130579 Nieznany
więcej podobnych podstron