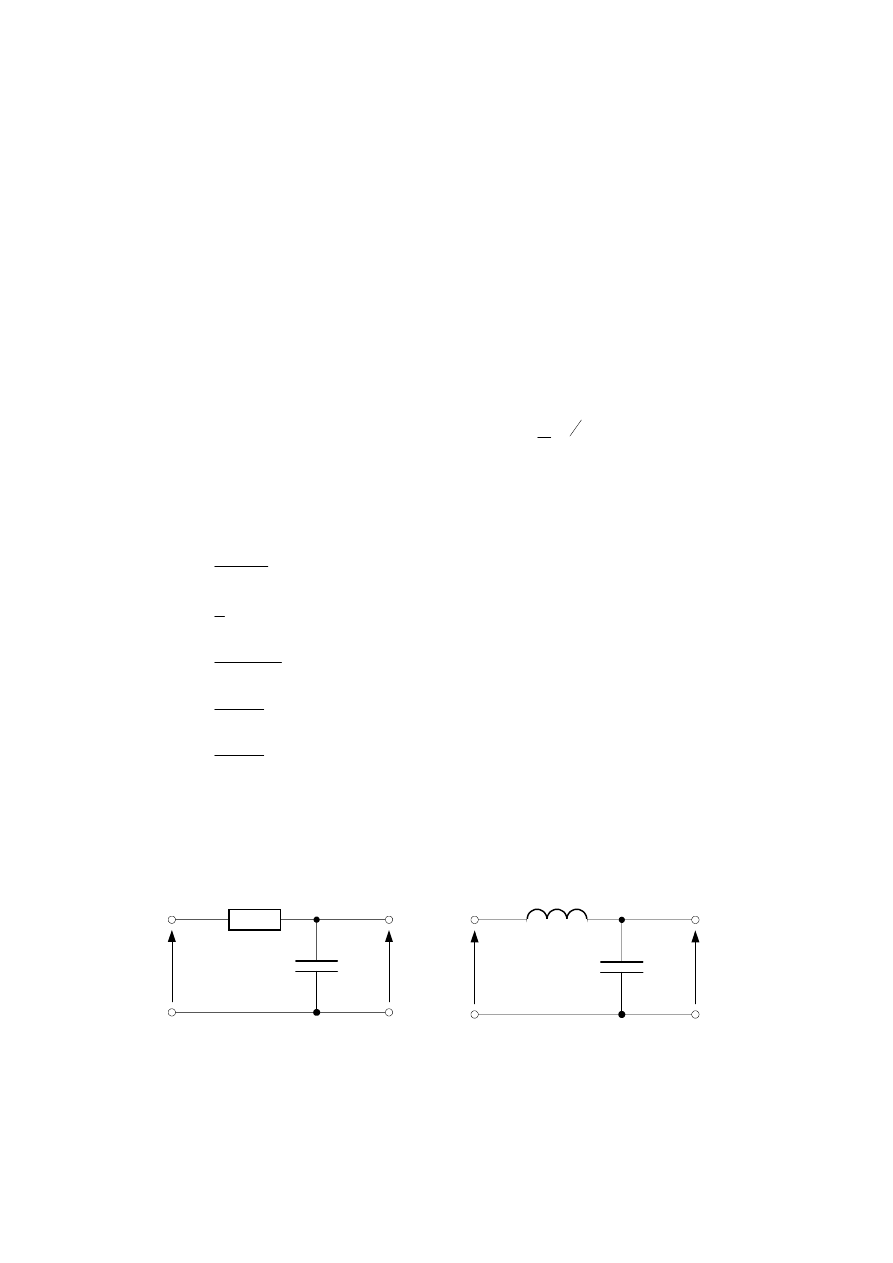
PODSTAWY AUTOMATYKI I – ĆWICZENIA
LISTA ZADAŃ NR 1
Zad. 1. Znaleźć transmitancję operatorową członu dynamicznego, którego charakterystyka impulsowa
ma postać
(
)
)
(
1
50
10
5
t
e
e
t
t
−
−
−
.
Zad. 2. Obliczyć transmitancje, funkcje wagi i odpowiedzi skokowe układów opisanych równaniami
różniczkowymi:
a)
u
u
y
y
y
4
'
2
'
3
''
+
=
+
+
b)
u
u
y
y
+
=
+
'
2
'
c)
u
u
y
y
y
y
3
'
2
'
3
''
3
''
'
−
=
+
+
+
Zad. 3. Odpowiedź pewnego układu na deltę Diraca jest równa
T
t
e
T
−
1
. Obliczyć odpowiedź tego
układu na skok położenia.
Zad. 4. Obliczyć odpowiedzi skokowe i impulsowe układów danych transmitancjami:
a)
)
1
(
1
)
(
+
=
s
s
s
G
b)
s
s
G
1
)
(
=
c)
1
10
)
(
2
+
+
=
s
s
s
G
d)
1
10
1
)
(
+
=
s
s
G
e)
s
e
s
s
G
5
.
0
1
10
1
)
(
−
+
=
Zad. 5. Obliczyć transmitancje układów względem zaznaczonych sygnałów u oraz y. Obliczyć
odpowiedzi układów na pobudzenia deltą Diraca, skokiem położenia i skokiem prędkości:
a)
b)
u
y
R
C
u
y
L
C
LISTA ZADAŃ NR 2
Zad. 1. Narysować charakterystyki amplitudową, fazową i amplitudowo-fazową elementu inercyjnego
rzędu pierwszego (
1
)
(
+
=
Ts
k
s
G
). Udowodnić, że charakterystyka amplitudowo-fazowa tego
układu jest półokręgiem o środku w punkcie (k/2, j0).
Zad. 2. Narysować charakterystyki amplitudową, fazową i amplitudowo-fazową dla układów o
transmitancjach:
a)
)
1
5
)(
1
10
(
10
)
(
+
+
=
s
s
s
G
b)
)
1
(
1
)
(
+
=
s
s
s
G
c)
)
1
1
.
0
)(
1
10
(
)
1
100
)(
1
(
)
(
+
+
+
+
=
s
s
s
s
s
G
d)
s
e
s
s
G
5
.
0
1
10
100
)
(
−
+
=
e)
s
e
s
s
s
s
G
1
.
0
)
1
10
(
)
1
(
10
)
(
−
+
+
=
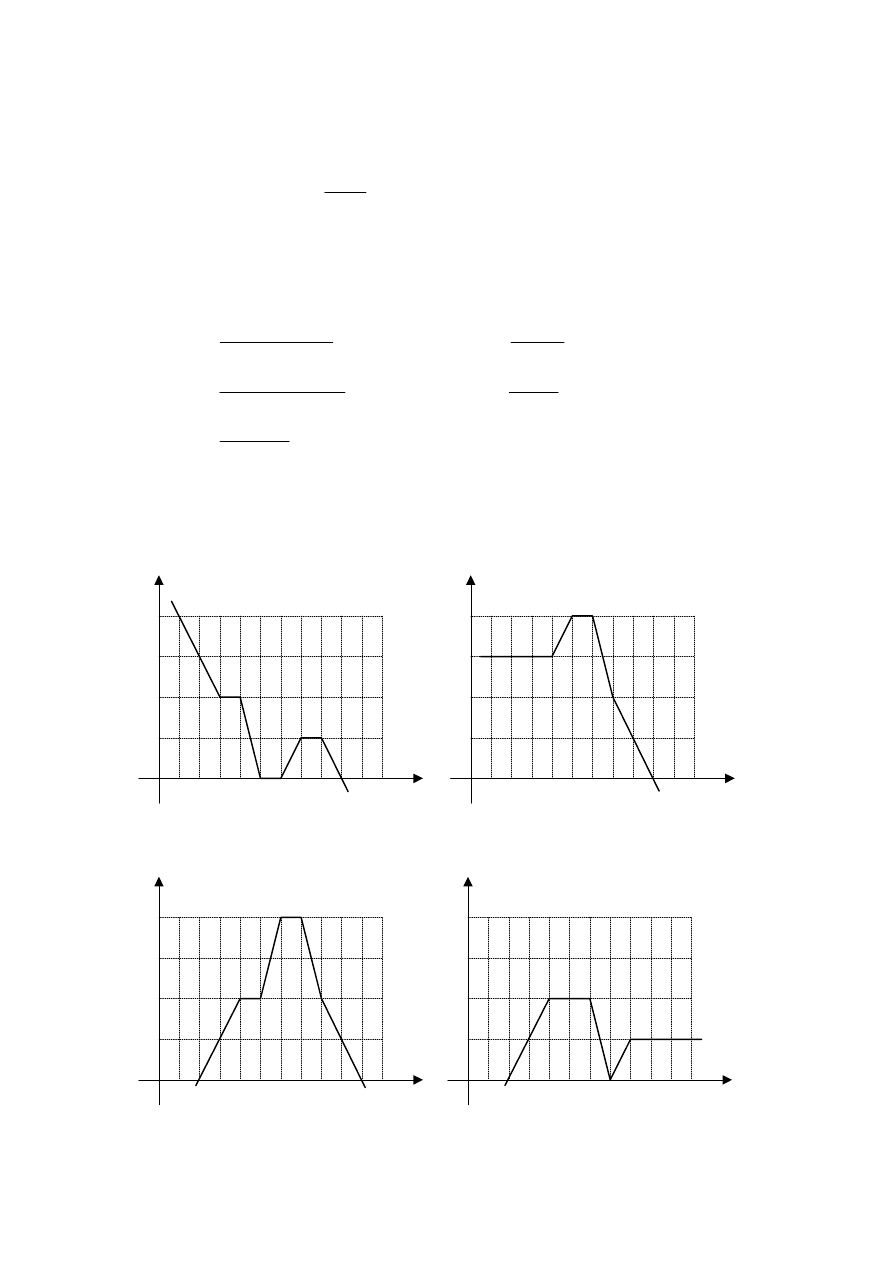
Zad. 3. Wyznaczyć transmitancje i narysować charakterystyki fazową i amplitudowo-fazową dla
układów, których charakterystyki amplitudowe dane są na rysunkach:
a)
b)
ω
10
0
20
40
60
80
0
|G(j
ω)| [dB]
10
-2
10
-4
10
2
10
4
ω
10
0
20
40
60
80
0
|G(j
ω)| [dB]
10
-2
10
-4
10
2
10
4
c)
d)
ω
10
0
20
40
60
80
0
|G(j
ω)| [dB]
10
-2
10
-4
10
2
10
4
ω
10
0
20
40
60
80
0
|G(j
ω)| [dB]
10
-2
10
-4
10
2
10
4
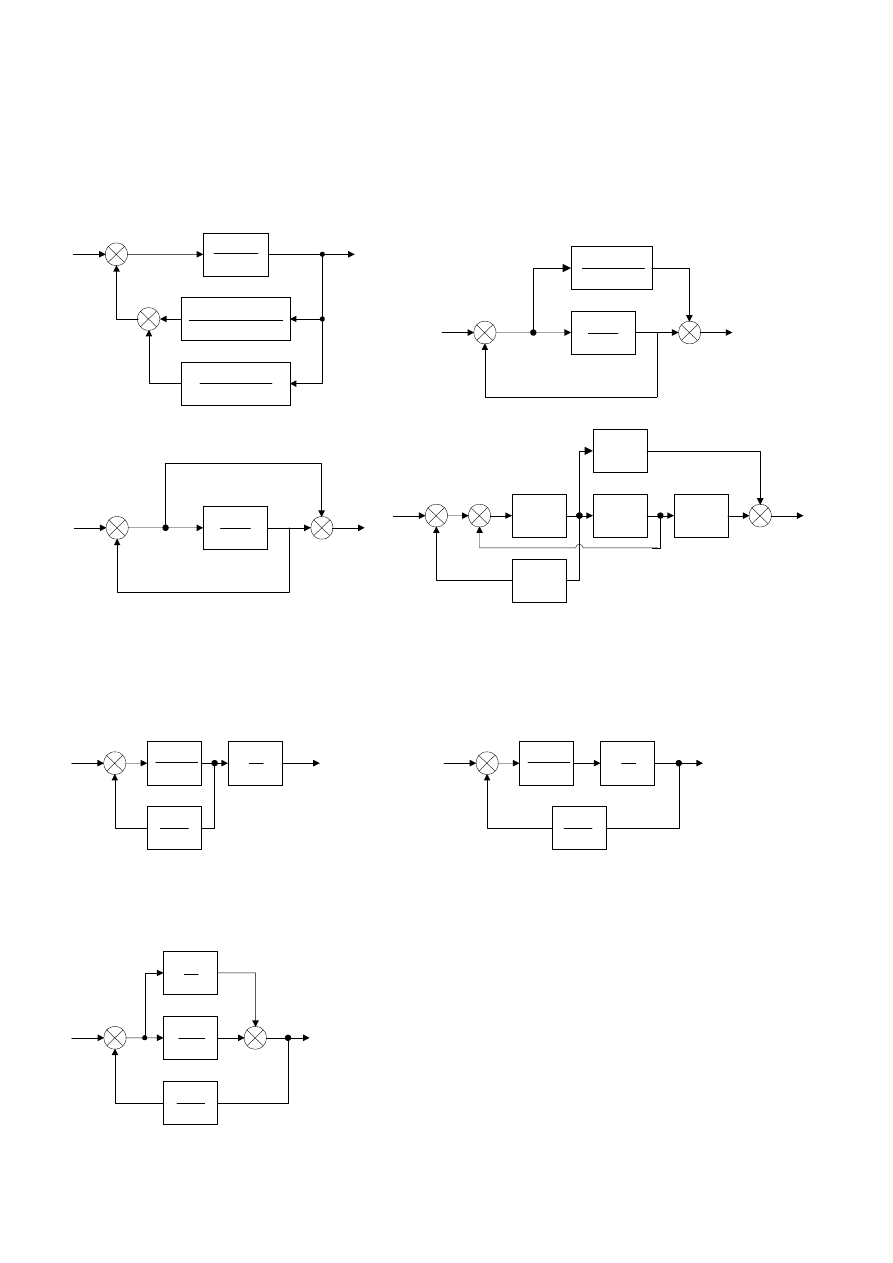
LISTA ZADAŃ NR 3
Zad. 1. Stosując metody przekształcania schematów blokowych „zwinąć” (obliczyć transmitancję
zastępczą) następujące schematy blokowe:
a)
b)
-
-
)
3
(
1
+
+
s
s
s
1
3
3
7
2
3
2
+
+
+
+
s
s
s
s
)
3
)(
1
(
+
+ s
s
s
u
y
u
y
-
7
1
+
+
s
s
7
8
2
+
+ s
s
s
c)
d)
u
y
-
7
1
+
+
s
s
u
y
-
)
(
1
s
G
)
(
2
s
G
)
(
3
s
G
)
(
5
s
G
-
)
(
2
s
G
Zad. 1. Obliczyć transmitancję układu otwartego i zamkniętego oraz uchyby regulacji e
p
, e
v
, e
a
dla
układów regulacji danych schematami blokowymi:
a)
b)
u
y
-
)
1
(
10
+
s
s
s
10
2
1
+
s
u
y
-
)
1
(
10
+
s
s
s
10
2
1
+
s
Zad. 3. W układzie jak na rysunku wyznaczyć wartość k wzmocnienia w układzie tak, aby uchyb
prędkości był mniejszy niż 0.01.
u
y
-
1
1
+
s
s
10
5
+
s
k
LISTA ZADAŃ NR 4
Zad. 1. Wykorzystując kryterium Ruth’a zbadać stabilność układów o transmitancjach:
a)
1
20
10
10
4
10
)
(
2
3
4
5
2
+
+
+
+
+
+
+
=
s
s
s
s
s
s
s
s
G
b)
1
2
5
3
)
(
2
3
+
+
+
+
=
s
s
s
s
s
G
c)
2
7
5
)
(
2
3
4
+
+
+
+
+
=
s
s
s
s
s
s
G
d)
4
8
8
8
5
2
3
2
3
)
(
2
3
4
5
6
2
+
+
+
+
+
+
+
+
=
s
s
s
s
s
s
s
s
s
G
e)
3
6
2
1
2
)
(
2
3
4
5
+
+
+
+
+
+
=
s
s
s
s
s
s
s
G
Zad. 2. Wykorzystując kryterium Hurwitz’a zbadać stabilność układów z zad. 1, punkty b, c, e.
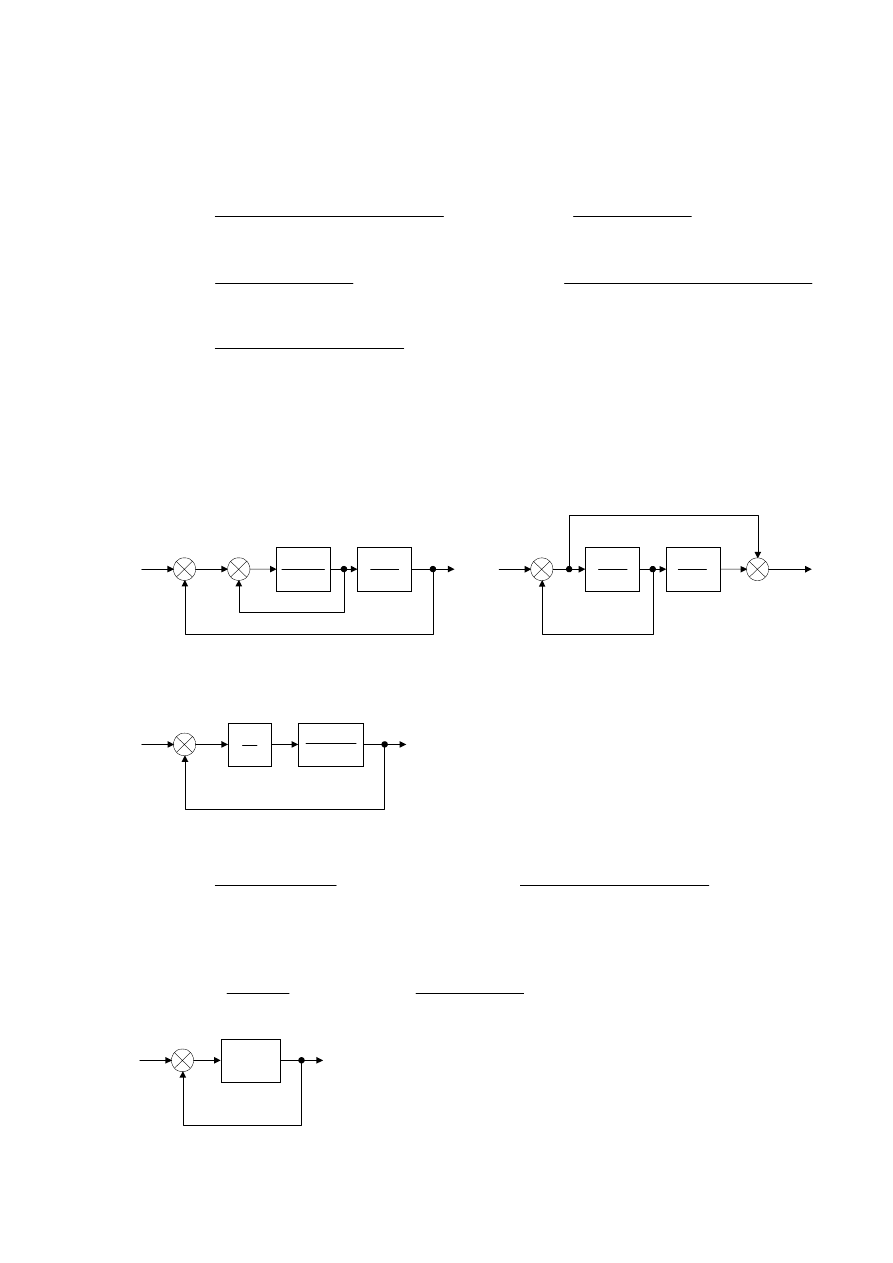
Zad. 3. Zbadać stabilność układów danych schematami blokowymi:
a)
b)
u
y
-
2
)
1
(
5
+
+
s
s
2
10
+
s
-
u
y
2
+
s
s
4
3
+
+
s
s
-
Zad. 4. Znaleźć warunek stabilności układu z regulatorem całkującym. Wykreślić obszar stabilności w
układzie współrzędnych (T, k
r
).
u
y
s
k
r
2
)
1
(
2
+
Ts
-
Zad. 5. Określić, ile biegunów transmitancji układu leży na lewo od prostej Re(s) = p, jeśli:
a)
7
6
5
1
)
(
2
3
+
+
+
+
=
s
s
s
s
s
G
, p = -2
b)
3
6
2
3
)
(
2
3
4
5
+
+
+
+
+
+
=
s
s
s
s
s
s
s
G
, p = -1
Zad. 6. Zbadać stabilność układu zamkniętego, jeżeli transmitancja układu otwartego wynosi:
a)
)
1
(
1
2
)
(
2
12
+
+
=
s
s
s
s
G
, b)
)
10
(
)
1
(
10
)
(
2
12
+
+
=
s
s
s
G
u
y
)
(
12
s
G
-
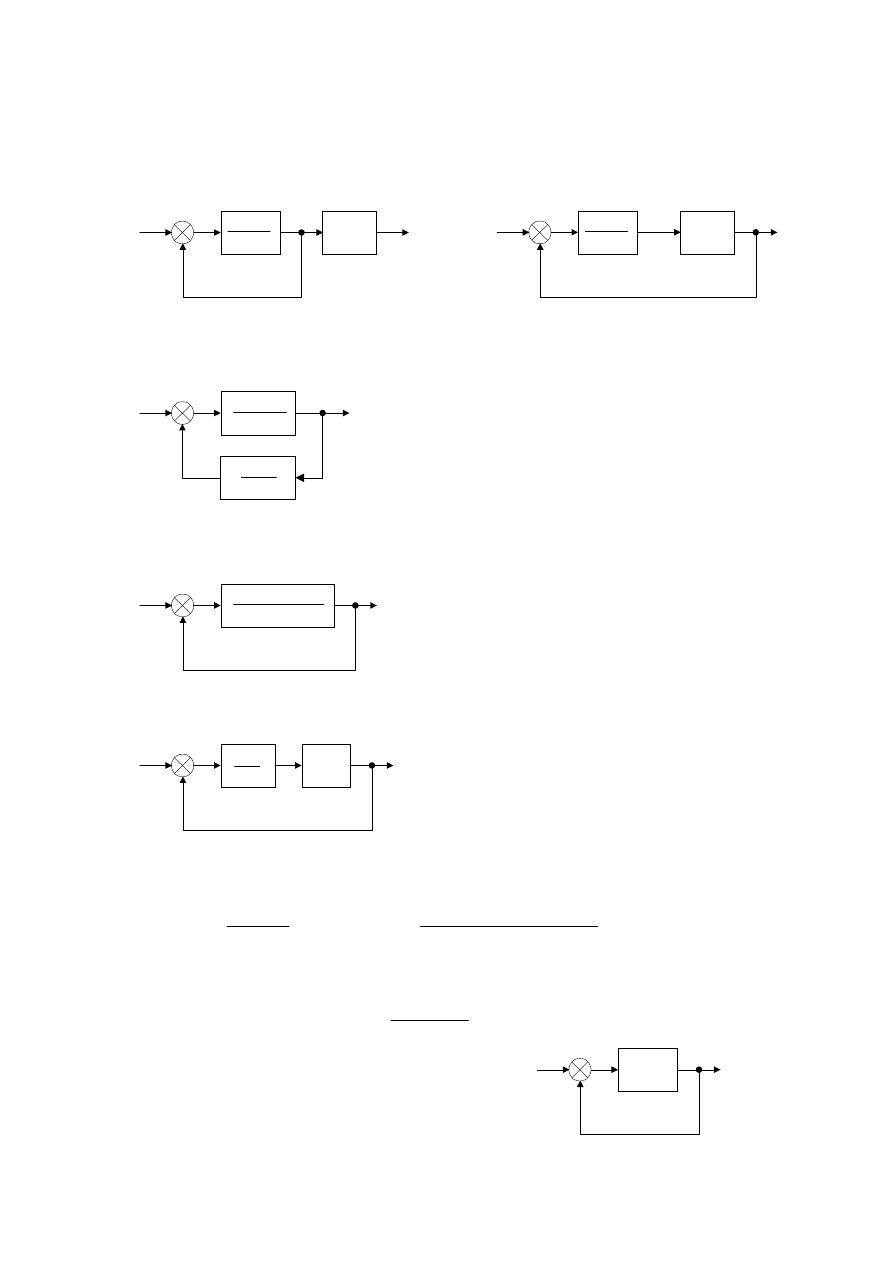
LISTA ZADAŃ NR 5
Zad. 1. Wykorzystując pełną wersję kryterium Nyquista zbadać stabilność układów:
a) b)
s
e
01
.
0
−
u
y
-
2
)
1
(
5
+
s
s
e
01
.
0
−
u
y
-
2
)
1
(
5
+
s
Zad. 2. Wykorzystując kryterium Nyquista wyznaczyć zależność między parametrami k, T i T
1
, dla
której układ przedstawiony na rysunku jest stabilny.
u
y
-
)
1
(
+
Ts
s
k
1
1
1
+
s
T
Zad. 3. Dla jakiej wartości parametru k zapas wzmocnienia w układzie wynosi 10 dB? Dla szukanej
wartości k obliczyć także zapas fazy i uchyb położenia.
u
y
-
)
1
10
(
)
1
(
2
+
+
s
s
k
Zad. 4. Dla jakiej wartości T
o
układ jest stabilny? Obliczyć zapas wzmocnienia i fazy dla T
o
=0.01.
u
y
-
1
100
+
s
s
T
o
e
−
Zad. 5. Określić zapas wzmocnienia i fazy dla układów o transmitancjach:
a)
)
1
(
3
2
)
(
2
12
+
+
=
s
s
s
s
G
, b)
)
1
10
)(
1
)(
1
01
.
0
(
)
1
1
.
0
(
100
)
(
12
+
+
+
+
=
s
s
s
s
s
G
Zad. 6. Określić obszar stabilności układu zamkniętego (we współrzędnych (T
1
, T
2
)), jeśli transmitancja
układu otwartego wynosi:
)
1
(
)
1
(
10
)
(
2
2
1
12
+
+
=
s
T
s
s
T
s
G
.
(rys. do zad. 5 i 6):
u
y
)
(
12
s
G
-
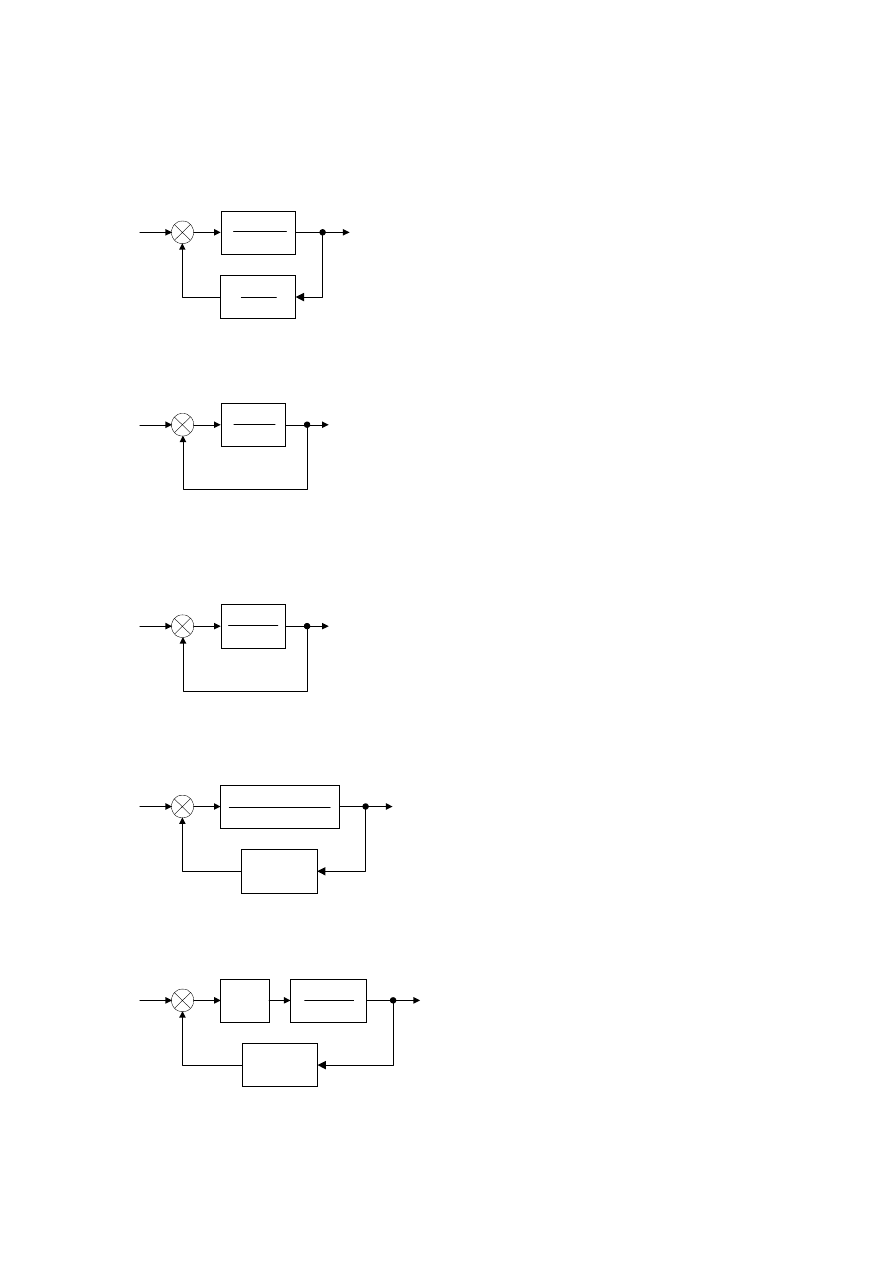
LISTA ZADAŃ NR 6
Zad. 1. Wykorzystując algebraiczno-graficzne kryterium Michajłowa określić warunek stabilności
układu:
u
y
-
)
1
(
+
Ts
s
k
1
1
1
+
s
T
Zad. 2. Korzystając z kryterium Michajłowa wyznaczyć, dla jakiej wartości parametru k układ
przedstawiony na rysunku jest stabilny.
u
y
-
3
)
1
(
+
s
k
Zad. 3. Dokonać analizy układu jak na rysunku (k=10, T=0.01) w dziedzinie czasu i częstotliwości.
Narysować charakterystyki częstotliwościowe układu, obliczyć zapas fazy, zapas wzmocnienia,
uchyby regulacji, przeregulowanie i 2%-wy czas ustalenia.
u
y
-
)
1
(
+
Ts
s
k
Zad. 4. Zbadać stabilność układu: a) otwartego (po otwarciu pętli sprzężenia zwrotnego), b)
zamkniętego. Określić uchyby regulacji w układzie zamkniętym.
u
y
-
1
2
2
3
10
2
3
+
+
+
s
s
s
1
2
+
s
Zad. 5. Dobrać wartości parametrów regulatorów typu P i PI zastosowanych w układzie, aby uzyskać:
przeregulowanie
∆y ≤ 25%, czas ustalenia t
2%
≤ 0.05 s, uchyb prędkości e
v
≤ 0.1.
u
y
-
)
1
5
(
10
+
s
s
)
1
(
+
s
T
k
i
i
p
k
Wyszukiwarka
Podobne podstrony:
Podstawy automatyki zadania1
ZADANIA Z KOLOKWIUM Z PODST automatyki A[1]. Kochan, Semestr IV, Wspólne, Podstawy automatyki
zadania 17.02, Energetyka, sem5, sem5, automaty, podstawy automatyki i robotyki
zadania na egzamin, PWr W9 Energetyka stopień inż, III Semestr, Podstawy automatyki
Podstawy automatyki egzamin zadania
FESTO Podstawy automatyzacji
12 Podstawy automatyki Układy sterowania logicznego
podstawy automatyki ćwiczenia lista nr 4b
Podstawy automatyki cz1
Podstawy Telekomunikacji zadania, problemy
Z2, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
automaty, PWr W9 Energetyka stopień inż, IV Semestr, Podstawy automatyki - laboratorium, Podsatwy au
Podstawy automatyki 2
podstawy automatyki
Podstawy automatyki (w 5) elementy wykonawcze i pomiarowe ppt [tryb zgodnosci]
podstawy automatyki ćwiczenia lista nr 4c
więcej podobnych podstron