Autor: Martin Slota

Zdroj: http://www.zones.sk

Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú

č

ely a akéko

ľ

vek verejné

publikovanie je bez predchádzajúceho súhlasu zakázané.

1/3

MATURITNÉ PRÍKLADY Z MATEMATIKY

M

ATURITNÝ OKRUH

9:

F

UNKCIE

1. príklad (103/3)

Zadanie: Ur

č

te intervaly monotónnosti a obor funk

č

ných hodnôt funkcie

2

2

:

x

e

y

f

−

=

.

Riešenie:

( )

2

2

2

2

2

2

'

x

x

e

x

e

x

x

f

−

−

⋅

−

=

−

=

Ke

ď

že

2

2

x

e

−

je vždy kladné, funkcia

f

je rastúca, ke

ď

je

0

<

x

(vtedy je

0

>

−

x

a

'

f

je teda

kladná), a klesajúca, ke

ď

je

0

>

x

(vtedy je

0

<

−

x

a

'

f

je teda záporná).

Funkcia

f

je rastúca na intervale

(

0

,

∞

−

a klesajúca na intervale

)

∞

,

0

.

Funkcia

f

má lokálne (aj globálne) maximum v bode

[ ]

1

,

0

. Preto jej funk

č

ná hodnota nestúpa nad

bod

1

a neklesá pod bod

0

, pretože

0

2

2

>

−

x

e

.

Obor funk

č

ných hodnôt funkcie

f

je teda

( ) (

1

,

0

=

f

H

.

2. príklad (103/8)

Zadanie: Nájdite intervaly monotónnosti funkcie

x

x

y

f

ln

2

:

2

−

=

.

Riešenie:

( )

+

=

R

f

D

( )

(

) (

)

x

x

x

x

x

x

x

x

f

1

2

1

2

1

4

1

4

'

2

+

⋅

−

=

−

=

−

=

Ke

ď

že berieme do úvahy iba kladné hodnoty, je funkcia rastúca na intervale







∞

,

2

1

a klesajúca na

intervale







2

1

,

0

.

3. príklad (103/10)

Zadanie: Je daná funkcia

(

)

5

2

:

2

−

⋅

−

=

x

x

y

f

. Na základe grafu

f

rozhodnite, pre ktoré reálne

p

má

rovnica

(

)

p

x

x

=

−

⋅

−

5

2

2

práve štyri korene.

Riešenie:

Nulové body má funkcia

f

v bodoch

2

a

5

.

(

5

,

∞

−

∈

x

:

(

)

(

)

20

24

9

4

4

20

20

5

5

4

4

:

2

3

2

3

2

2

+

−

+

−

=

−

+

−

+

−

=

−

⋅

+

−

=

x

x

x

x

x

x

x

x

x

x

x

y

f

( )

(

)

(

) (

)

2

4

3

8

6

3

24

18

3

'

2

2

−

⋅

−

⋅

−

=

+

−

⋅

−

=

−

+

−

=

x

x

x

x

x

x

x

f

Funkcia

f

je rastúca na intervale

4

,

2

a klesajúca na intervaloch

(

2

,

∞

−

a

5

,

4

.

2

+

–

4

5

–

2

1

+

–

0

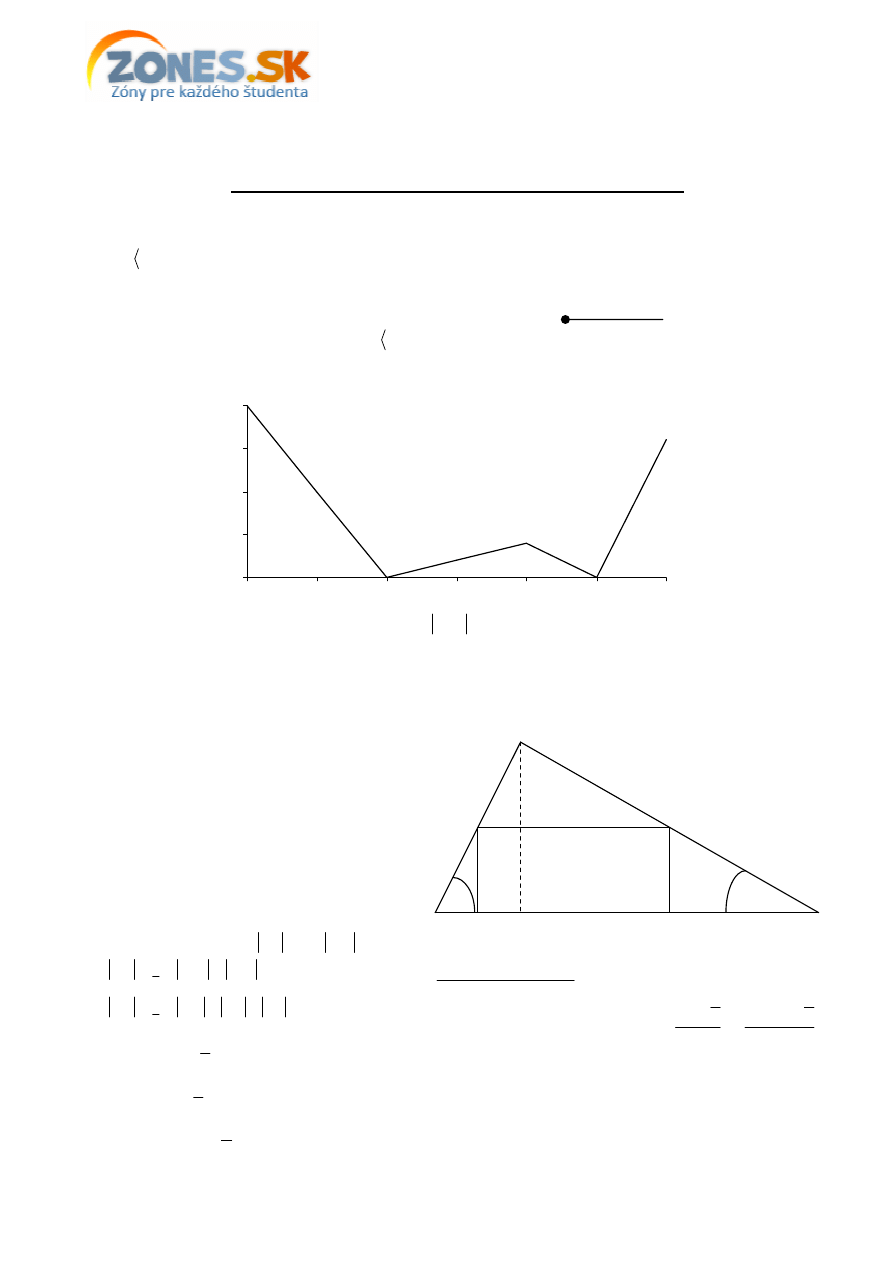
Autor: Martin Slota

Zdroj: http://www.zones.sk

Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú

č

ely a akéko

ľ

vek verejné

publikovanie je bez predchádzajúceho súhlasu zakázané.

2/3

MATURITNÉ PRÍKLADY Z MATEMATIKY

M

ATURITNÝ OKRUH

9:

F

UNKCIE

)

∞

∈

,

5

x

:

(

)

(

)

20

24

9

20

20

5

4

4

5

4

4

:

2

3

2

2

3

2

−

+

−

=

−

+

−

+

−

=

−

⋅

+

−

=

x

x

x

x

x

x

x

x

x

x

x

y

f

( )

(

)

(

) (

)

2

4

3

8

6

3

24

18

3

'

2

2

−

⋅

−

⋅

=

+

−

⋅

=

+

−

=

x

x

x

x

x

x

x

f

Funkcia

f

je rastúca na intervale

)

∞

,

5

.

Funkcia

f

má v bodoch

[ ]

0

,

2

a

[ ]

0

,

5

lokálne minimá a v bode

[ ]

4

,

4

lokálne maximum.

Približný graf funkcie

f

(bez konvexnosti a konkávnosti):

Z grafu môžeme vy

č

íta

ť

, že rovnica

(

)

p

x

x

=

−

⋅

−

5

2

2

má práve štyri korene pre

( )

4

,

0

∈

p

.

4. príklad (103/11)

Zadanie: Z trojuholníka, ktorého základ

ň

a je

c

, výška na základ

ň

u je

v

a uhly pri základni sú ostré, má

by

ť

vystrihnutý obd

ĺ

žnik, pri

č

om jedna strana obd

ĺ

žnika je

č

as

ť

ou základne. Ur

č

te rozmery obd

ĺ

žnika

tak, aby mal maximálny obsah.

Riešenie:

Rozmery obd

ĺ

žnika:

x

KL

=

,

y

LM

=

(

)

β

α

β

α

cotg

cotg

cotg

cotg

1

1

+

⋅

=

⋅

+

⋅

=

+

=

=

v

v

v

BC

AC

c

AB

(

)

v

c

y

c

x

v

c

y

x

y

x

y

x

y

LB

KL

AK

c

AB

−

=

⇒

+

=

+

⋅

+

=

⋅

+

+

⋅

=

+

+

=

=

β

α

β

α

cotg

cotg

cotg

cotg

( )

v

y

y

v

c

cy

xy

S

,

0

2

∈

−

=

=

( )

y

v

c

c

y

S

2

'

−

=

( )

2

0

'

v

y

y

S

=

⇔

=

+

5

α

β

A

B

C

K

L

M

N

1

C

v

x

y

0

5

10

15

20

0

1

2

3

4

5

6

x

y

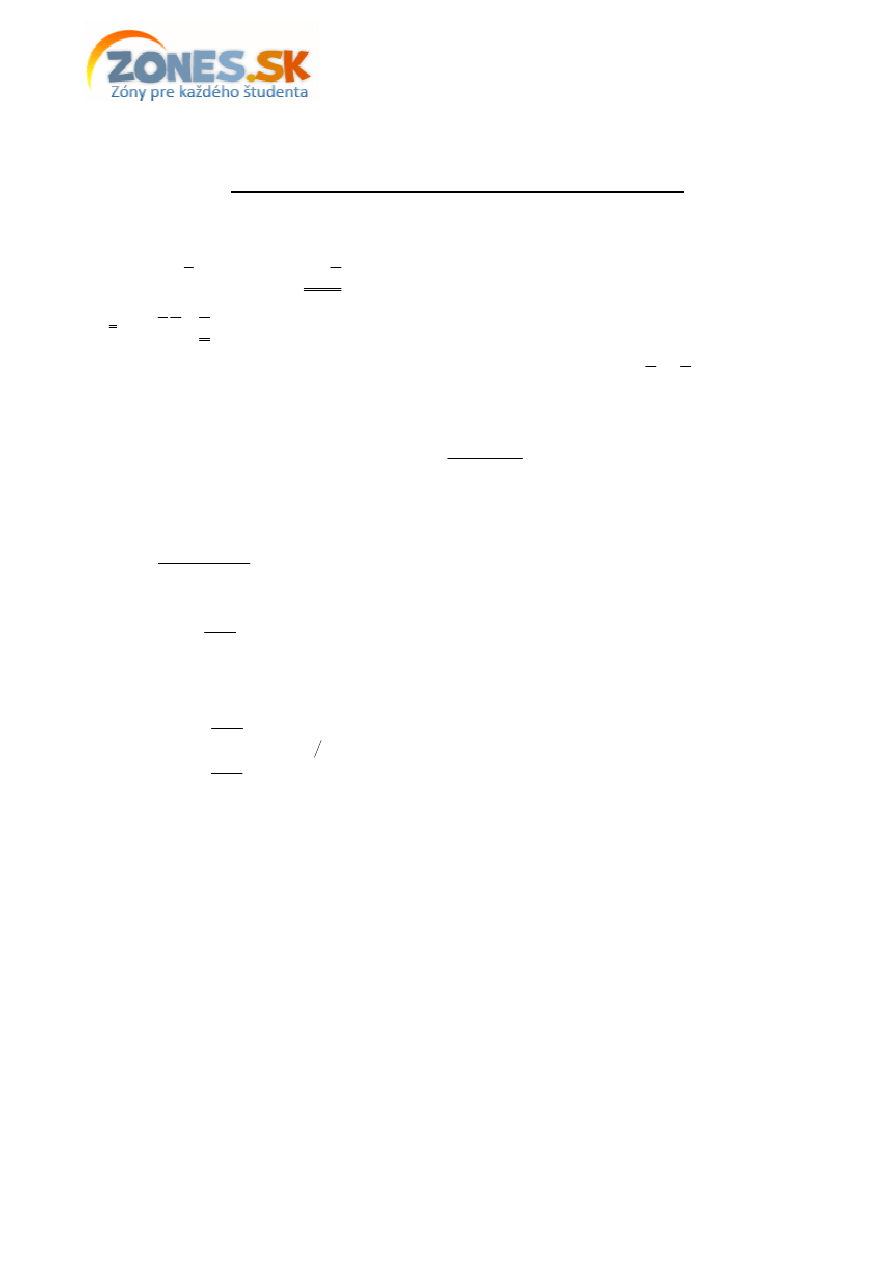
Autor: Martin Slota

Zdroj: http://www.zones.sk

Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú

č

ely a akéko

ľ

vek verejné

publikovanie je bez predchádzajúceho súhlasu zakázané.

3/3

MATURITNÉ PRÍKLADY Z MATEMATIKY

M

ATURITNÝ OKRUH

9:

F

UNKCIE

( )

⇒

<

−

=

0

2

''

v

c

y

S

v bode

2

v

y

=

je lokálne (a na danom intervale aj globálne) maximum.

2

2

c

v

v

c

c

x

=

−

=

Rozmery obd

ĺ

žnika s najvä

č

ším obsahom vystrihnutého z trojuholníka sú

2

c

a

2

v

.

5. príklad (104/18)

Zadanie: Nájdite body nespojitosti funkcie

2

3

2

:

2

2

+

−

−

−

=

x

x

x

x

y

f

a pokúste sa dodefinova

ť

v týchto bodoch

funkciu

f

tak, aby v nich bola spojitá.

Riešenie:

(

) (

)

(

) (

)

1

2

1

2

:

−

⋅

−

+

⋅

−

=

x

x

x

x

y

f

Body nespojitosti funkcie

f

:

2

a

1

.

( )

3

1

1

lim

lim

2

2

=

−

+

=

→

→

x

x

x

f

x

x

( )

( )

2

lim

2

2

⇒

∃

∧

∉

→

x

f

f

D

x

je odstránite

ľ

ný bod nespojitosti funkcie

f

a funk

č

nú hodnotu v bode

2

by

sme mohli dodefinova

ť

hodnotou

3

.

( )

( )

( )

⇒

∃

⇒












−∞

=

−

+

=

∞

=

−

+

=

→

→

→

→

→

−

−

+

+

x

f

x

x

x

f

x

x

x

f

x

x

x

x

x

1

1

1

1

1

lim

1

1

lim

lim

1

1

lim

lim

bod

1

nie je odstránite

ľ

ným bodom nespojitosti funkcie

f

.