Ćwiczenie 5

Fala płaska w ośrodkach stratnych.

Autorzy: R. Lech i P. Kowalczyk, Katedra In

ż

ynierii Mikrofalowej i Antenowej

Pola i fale elektromagnetyczne

=

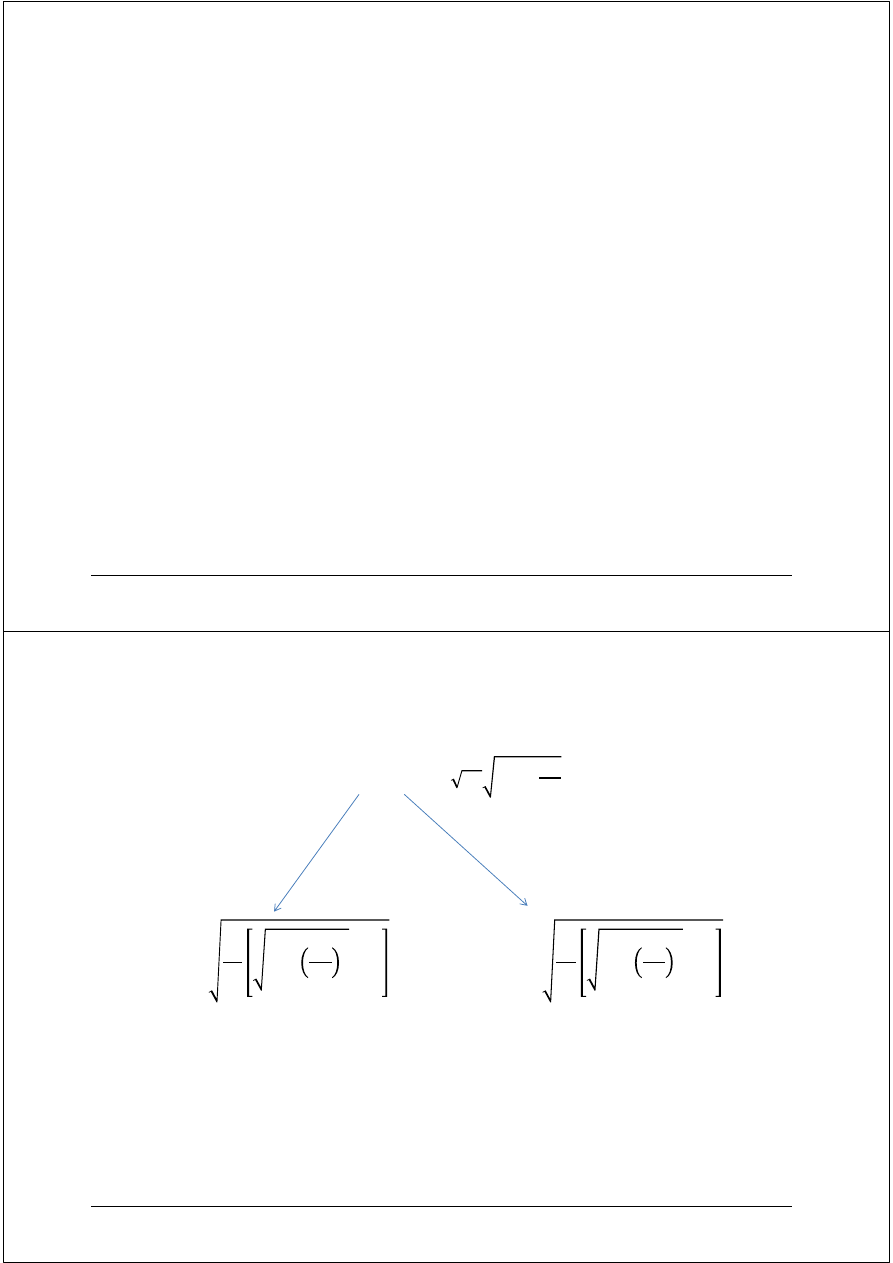
2

1 +

− 1

=

2

1 +

+ 1

Autorzy: R. Lech i P. Kowalczyk, Katedra In

ż

ynierii Mikrofalowej i Antenowej

=

+ β = j

1 −

Zespolony współczynnik propagacji:

współczynnik tłumienia

współczynnik fazowy

Autorzy: R. Lech i P. Kowalczyk, Katedra In

ż

ynierii Mikrofalowej i Antenowej

Wzory na długość i prędkość fali oraz relacje impedancyjne, które wyprowadzone
były dla ośrodków bezstratnych, pozostają prawdziwe!

Dla materiału silnie stratnego (metalu), czyli gdy

≫ 1 uproszczone wyrażenia na

impedancję i powyższe współczynniki mają postać

≈

≈

≈

Dla materiału mało stratnego (dielektryka), czyli gdy

≪1

≈

≈

≈

!

"#$

Autorzy: R. Lech i P. Kowalczyk, Katedra In

ż

ynierii Mikrofalowej i Antenowej

Korzyść praktyczna tego zjawiska jest taka, że aby uzyskać niskie straty komponentów mikrofalowych
(np. prowadnic, falowodów) wystarczy pokryć je cienką warstwą bardzo dobrego przewodnika (np.
srebro, złoto, miedź).

Zadanie:

Wyznacz głębokość wnikania fali elektromagnetycznej o częstotliwości % = 2.4 GHz w miedź (przyjąć: = 6 ⋅ 10

+

S/m,

,

= 1 i

,

= 1).

Odp: .

/

=

0

1

=

≅ 1.33 ⋅ 10

45

m

Autorzy: R. Lech i P. Kowalczyk, Katedra In

ż

ynierii Mikrofalowej i Antenowej

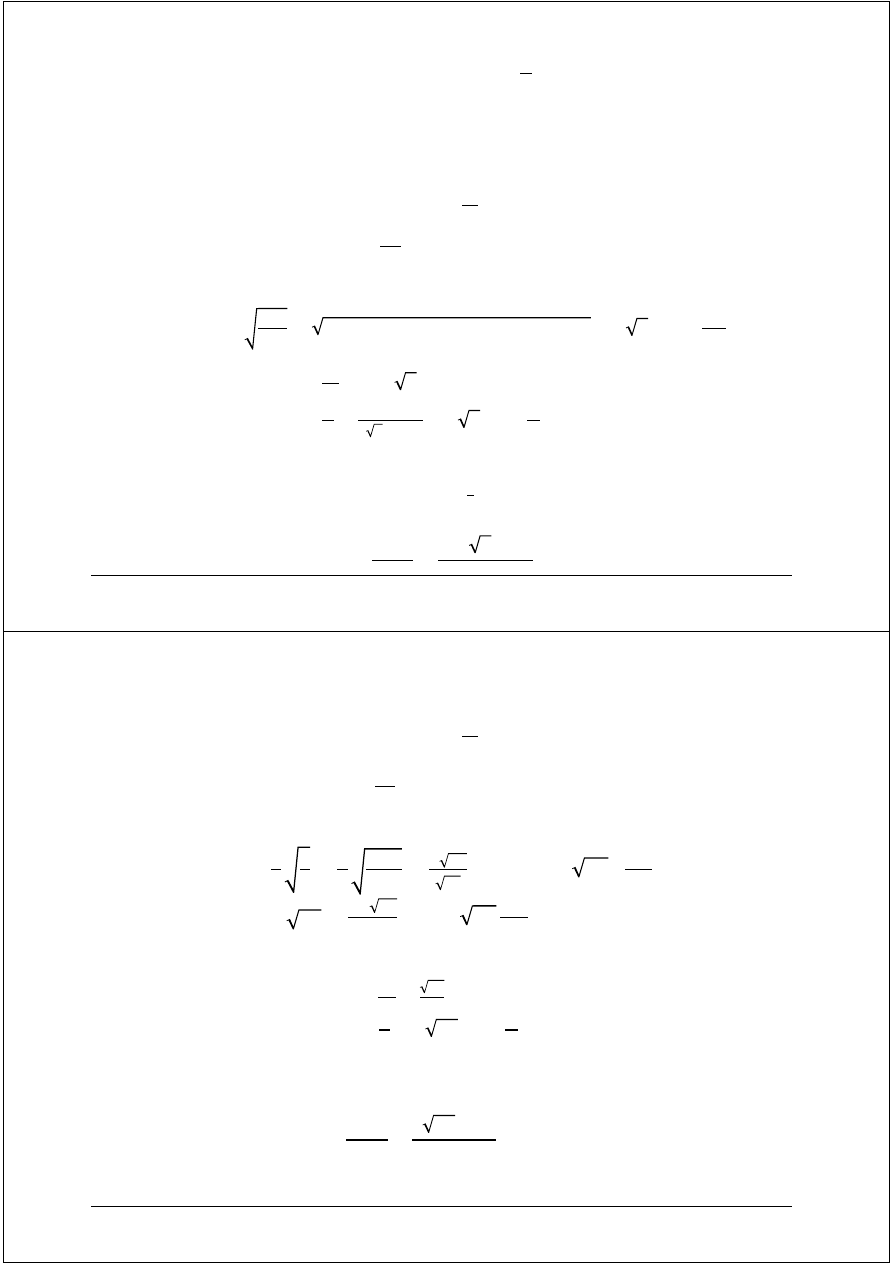
Rozwiązanie (a):

Zatem współczynnik fazowy i współczynnik tłumienia wyznaczyć można ze wzoru:

Stąd:

w celu ustaleniu typu ośrodka należy określić wartość

= 10

6

≫ 1

=

=

=

7 · 10

6

· 4 · 7 · 10

4+

· 10 · 2 · 10

46

= 2 2710

46 ,9:

;

.

< =

=

>

= 500 2@,

A =

>

=

=·0B

C

=0B

DC

= 5 2 · 10

E ;

/

.

Odległość d, na której amplituda pola zmaleje pięciokrotnie wyznaczyć można z relacji

F

B

41:

=

0

E

F

B

.

Zatem

1:

= 5 i ostatecznie

G =

ln (5)

=

250 2ln (5)

7

@.

W ośrodku o parametrach

,

= 10,

,

= 36 i

= 2 · 10

46 L

;

rozchodzi się elektromagnetyczna

fala płaska. Wyznacz długość i prędkość fazową fali oraz odległość, na której jej amplituda
zmaleje pięciokrotnie. Przyjmij, ze częstotliwość wynosi:
(a) f = 1kHz, (b) f = 1GHz.

Zadanie:

Autorzy: R. Lech i P. Kowalczyk, Katedra In

ż

ynierii Mikrofalowej i Antenowej

Rozwiązanie (b):

zatem

Stąd:

w celu ustaleniu typu ośrodka należy określić wartość

= 10

46

≪ 1

=

=

M N

M

N

=

N

N

607 = 0.02 107

,9:

;

=

=

5 0B

O

= 407 10

,9:

;

.

< =

=

>

=

0B

BB

@,

A =

>

= 5 10 · 10

5 ;

/

.

Odległość d, tak jak w punkcie (a), wyznaczamy z relacji

G =

ln (5)

=

5 10ln (5)

7

@.

Autorzy: R. Lech i P. Kowalczyk, Katedra In

ż

ynierii Mikrofalowej i Antenowej

Ostatecznie

zatem

Zadanie:

Ω

Autorzy: R. Lech i P. Kowalczyk, Katedra In

ż

ynierii Mikrofalowej i Antenowej

Głębokość wnikania dla ośrodka o przenikalności elektrycznej

,

= 4 i przewodności = 1 S/m przy częstotliwości

% = 30 MHz wynosi G =

0

5=

m. Określ przenikalność magnetyczną ośrodka oraz długość i prędkość rozważanej fali.

Zakładając, że pole elektryczne w ośrodku ma postać F P, R, S, T = 607

41U

cos

T − P Y

Z

V/m wyznacz

towarzyszące mu pole magnetyczne.

Zadanie:

Odp.:

,

= 3,

< =

0

6

m,

A = 10

+

m/s,

[ P, R, S, T = − 5 2

41U

cos

T − P − \ Y

]

A/m,

gdzie

= 6710

+

rad/s,

=

= 67 rad/m,

\ =

7

4

Autorzy: R. Lech i P. Kowalczyk, Katedra In

ż

ynierii Mikrofalowej i Antenowej

Dodatek 1

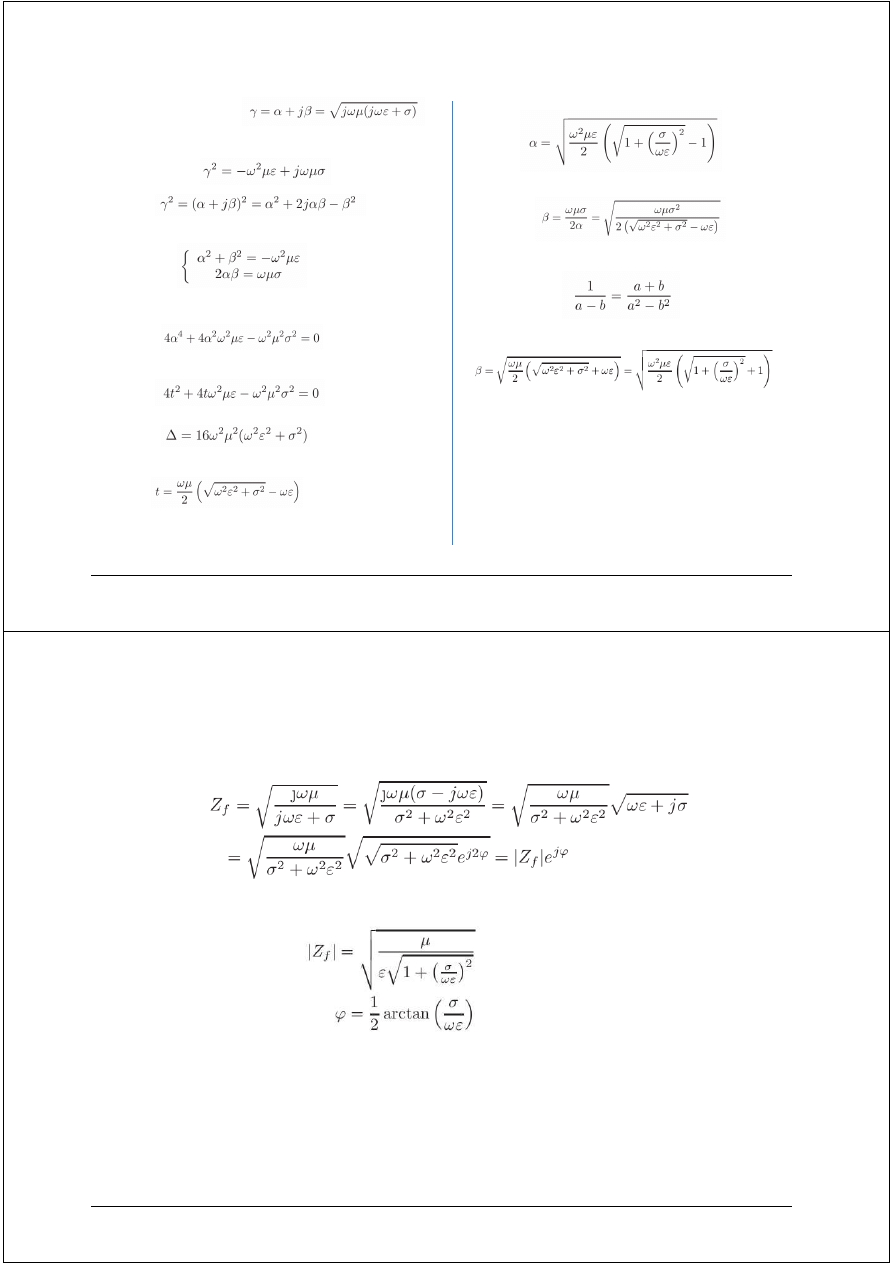
Wyprowadzenie wyrażeń ogólnych na i

Wychodzimy ze wzoru na :

Podnosząc równanie do kwadratu i wymnażając wyrażenie w nawiasie
otrzymujemy

Ponieważ:

możemy zapisać następujący układ równań:

Wyznaczając β z drugiego równania i podstawiając do pierwszego
otrzymujemy:

Podstawiając T =

2

≥ 0 otrzymujemy równanie kwadratowe:

dla którego wyróżnik wynosi:

i rozwiązanie (nieujemne):

W związku z tym współczynnik tłumienia wyznaczamy korzystając z
wyrażenia:

Wstawiając powyższą zależność do układu równań otrzymujemy:

Korzystając ze wzoru skróconego mnożenia:

otrzymujemy:

Autorzy: R. Lech i P. Kowalczyk, Katedra In

ż

ynierii Mikrofalowej i Antenowej

Dodatek 2

Aby wyznaczyć moduł i fazę impedancji falowej dla ośrodka stratnego wychodzimy ze wzoru:

gdzie

Wyprowadzenie wyrażeń ogólnych na |S | i \

Dodatek 3

Wyprowadzenie wyrażeń na i w ośrodku słabo stratnym

≪ 1

Autorzy: R. Lech i P. Kowalczyk, Katedra In

ż

ynierii Mikrofalowej i Antenowej

Uwzględniając przyjęte założenie

≪ 1 we wzorach wyprowadzonych w Dodatku 1 czynnik ten może zostać pominięty. Jednakże w

przypadku współczynnika tłumienia oraz fazy impedancji falowej taki krok prowadziłby do całkowitego wyzerowania tych elementów.

Wówczas w przypadku współczynnika tłumienia korzystamy z rozwinięcia funkcji w szereg Taylora 1 + P ≈ 1 +

U

dla |P| << 1

i otrzymujemy:

Współczynnik fazowy redukuje się do postaci:

Moduł impedancji falowej:

Do wyznaczenia fazy impedancji falowej korzystamy z założenia tan P ≈ P dla P << 1 i otrzymujemy:

Dodatek 4

Wyprowadzenie wyrażeń na i w ośrodku silnie stratnym

≫ 1

Autorzy: R. Lech i P. Kowalczyk, Katedra In

ż

ynierii Mikrofalowej i Antenowej

Uwzględniając przyjęte założenie

≪ 1 we wzorach wyprowadzonych w Dodatku 1 w przypadku współczynnika

tłumienia otrzymujemy:

W ten sam sposób redukuje się współczynnik fazowy:

Moduł i faza impedancji falowej wynoszą odpowiednio: