DYFUZJA
Rozważymy ustalony przepływ masy w układach, w których zarówno koncentracja jak i
strumień masy są funkcjami jednej zmiennej przestrzennej. Ze względu na ustalony przepływ
masy, koncentracja w danym punkcie przestrzeni nie zmienia się, czyli
jest równa
zeru. Pominiemy w tych rozważaniach reakcję chemiczną.
t
c
A
∂
∂ /
Z czterech strumieni masy N
A
, n
A
, J
A
i j
A
używać będziemy jedynie molowego strumienia
masy względem ustalonego układu odniesienia, który dla zagadnienia jednowymiarowego o
współrzędnej z, dla składnika A w mieszaninie binarnej, wyraża się:
)]
(
)
(
)[
(
)
(
)
(
z
N
z
N
z
y
dz
z
dy
cD
z
N
B
A
A
A
AB
A
+
+
−
=
(1)
Współczynnik dyfuzji dla gazów można wyznaczyć eksperymentalnie w komorze dyfu-
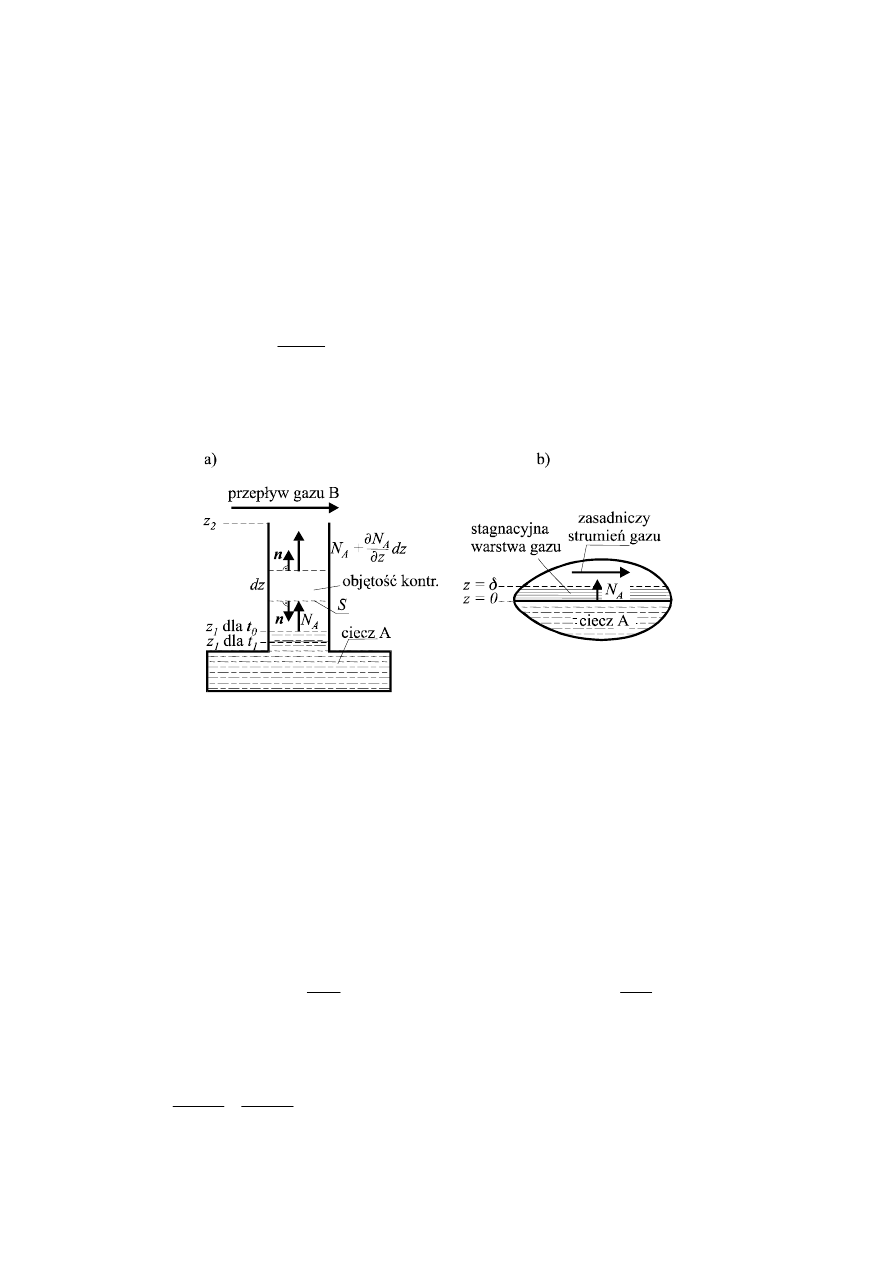
zyjnej, której schemat przedstawiony jest na rysunku 1a.
Rys.1. Model dyfuzji składnika A do przepływającego strumie-
Wąski cylinder, wypełniony u dołu fazą ciekłą składnika A, jest umieszczony w otoczeniu o
stałym ciśnieniu i temperaturze. Gaz B, który przepływa nad wylotem z cylindra, posiada zni-
komą rozpuszczalność w cieczy A i jest także chemicznie obojętny wobec pary składnika A,
który po odparowaniu z lustra cieczy dyfunduje do gazu B. Prędkość parowania może być
fizycznie zmierzona i wyrażona w formie molowego strumienia masy.
Rozważmy objętość kontrolną Sdz, gdzie S oznacza pole przekroju cylindra. Bilans masy
składnika A wpływającego i wypływającego z objętości kontrolnej, przy ustalonym procesie
przedstawia się następująco
∫
∫
=
⋅
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
+
⋅
S
S
A
A
A
dS
dz
z
dS
0
n
N
N
n
N
, czyli
0
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
+
−
dz
z
N
N
S
SN
A
A
A
Po dokonaniu uproszczeń, otrzymamy
0
)
(
)
(
=
≡
∂
∂
dz
z
dN
z
z
N
A
A
(2)
1
Powyższe równanie wskazuje, że molowy strumień składnika A w cylindrze jest stały. W cy-
lindrze znajduje się również gaz B. Ponieważ nie jest on wchłaniany do cieczy A, jego ilość w
cylindrze jest cały czas stała. Jest to więc stagnacyjna warstwa gazu B, a więc strumień N
B
(z)
jest równy zeru.
B
Wzór (1), określający strumień gazu składnika A, możemy obecnie zapisać jak następuje
const
dz
dy
y
cD
N
A
A
AB
A
=
−
−
=
1
(3)
Równanie (3) można scałkować przyjmując poniższe warunki brzegowe
y
A
= y
A1
dla z = z
1
oraz y
A
= y
A2
dla z = z
2
Dokonamy operacji całkowania przy założeniu, że współczynnik dyfuzji jest niezależny od
koncentracji oraz uwzględnieniu, że strumień masy N
A
jest stały
∫
∫
−
−
=
2
1
2
1
1
)
1
(
z
z
y
y
A
A
AB
A
A
A
y
y
d
cD
dz
N
(4)
Po scałkowaniu i wstawieniu granic całkowania otrzymamy
)
1
(
)
1
(
ln
)
(
1
2
1
2
A
A
AB
A
y
y
z
z
cD
N
−
−
−
=
(5)
Rozkład koncentracji składnika A wzdłuż wysokości cylindra opisuje równanie różnicz-
kowe, które otrzymuje się przez podstawienie strumienia masy do równania bilansu masy. W
naszym przypadku równanie bilansu określa wzór (2), a strumień masy wzór (3). W wyniku
wspomnianego podstawienia otrzymujemy następujące równanie różniczkowe
0
)
1
ln(
1
2
2
=
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
A
AB
A
A
AB
y
dz
d
cD
dz
dy
y
cD
dz
d
(6)
W wyniku dwukrotnego całkowania otrzymujemy
2
1
)
1
ln(
C
z
C
y
A
+
=
−
(7)
Po wykorzystaniu wyżej wymienionych warunków brzegowych w równaniu (7) otrzymuje się
układ równań, z którego wyznacza się stałe C
1
i C
2
. Wynoszą one
1
2
1
2
1
1
1
ln
1
A
A
y
y
z
z
C
−
−
−
=
oraz
1
2
1
2
1
1
2
1
1
ln
)
1
ln(
A
A
A
y
y
z
z
z
y
C
−
−
−
−
−
=
Po podstawieniu tych stałych do wzoru (7) oraz wykonaniu oczywistych redukcji i prze-
kształceń, otrzymamy
2
1
2
1
1
2
1
1
1
1
)
(
1
z
z
z
z
A
A
A
A
y
y
y
z
y
−
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
=
−
−
(8)
Zauważmy, że dla mieszaniny binarnej wypełniającej cylinder suma udziałów molowych wy-
nosi
1
)
(
)
(
=
+
z
y
z
y
B
A
(9)
Po wykorzystaniu tej zależności we wzorze (8), otrzymamy rozkład udziału molowego skład-
nika B w cylindrze
1
2
1
1
2
1
)
(
z
z
z
z
B
B
B
B
y
y
y
z
y
−
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
(10)
Określimy średni udział molowy składnika B w cylindrze, określony jak następuje
)
1
/(
)
1
ln(
)
/
ln(
/
)
(
1
2
2
1
1
2
1
2
2
1
2
1
A
A
A
A
B
B
B
B
z
z
z
z
B
Bśr
y
y
y
y
y
y
y
y
dz
dz
z
y
y
−
−
−
=
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∫
∫
(11)
Po wykorzystaniu powyższej zależności we wzorze (5), otrzymamy
Bśr
A
A
AB
A
y
y
y
z
z
cD
N
)
(
)
(
2
1
1
2
−
−
=
(12)
Jeśli przyjąć, że rozważane gazy spełniają równania gazu doskonałego, czyli
T
p
V
n
c
ℜ
=
=
oraz
p
p
y
A
A
=
to molowy strumień składnika A wynosi
Bśr
A
A
AB
A
y
p
p
z
z
T
pD
N
)
(
)
(
2
1
1
2
−
−
ℜ
=
(13)
Równania (12) i (13) opisują dyfuzję jednego gazu poprzez drugi gaz będący w stanie sta-
gnacyjnym (nieruchomym). W praktyce spotyka się szereg przykładów dyfuzji jednego gazu
poprzez inny, na przykład, absorpcja, nawilżanie powietrza.
Równanie (13) może posłużyć do określenia konwekcyjnego współczynnika wymiany ma-
sy, przez wykorzystanie koncepcji tzw. międzyfazowej warstwy stagnacyjnej, rys.1b. Według
tej koncepcji, główny opór dyfuzji cząstek pary cieczy do przepływającego strumienia gazu
ma miejsce w laminarnej warstwie (filmie) o stałej grubości
δ
.
Prędkość konwekcyjnej wymiany masy można zapisać w postaci
)
(
)
(
2
1
2
1
A
A
k
A
A
k
A
p
p
T
k
c
c
k
N
−
ℜ
=
−
=
(14)
3
Jeśli przyjąć, że
δ
= z
2
−
z
1
, to z porównania wzorów (14) i (13) mamy
δ
śr
AB
k
y
pD
k
B
=
(15)
Otrzymany wynik wskazuje, że konwekcyjny współczynnik wymiany masy k
k
jest wprost
proporcjonalny do współczynnika dyfuzji D
AB
.
Ruch powierzchni cieczy spowodowany emisją pary. Istnieją technicznie problemy, w
których występuje przemieszczanie się powierzchni brzegowej lub międzyfazowej. Jednym z
nich jest problem zagłębiania się powierzchni parowania cieczy w ośrodku porowatym pod-
czas procesu suszenia. W czasie tego procesu wydłuża się droga dyfuzji cząstek pary od
zwierciadła wody do powierzchni brzegowej materiału suszonego.
Ośrodek porowaty często modeluje się za pomocą zbioru kapilar. Niech cylinder na rysun-
ku 1a przedstawia kapilarę, częściowo wypełnioną cieczą. Pokazane są dwa położenia lustra
cieczy, odpowiadające odpowiednio chwili t
o
i t
1
. Jeśli różnica położeń lustra cieczy A, w
stosunkowo długim przedziale czasu t
1
–t
o
, jest jedynie małym ułamkiem całkowitej drogi
dyfuzji cząstek pary, to molowy strumień pary do otoczenia może być obliczany ze wzoru
(12), czyli
Bśr
A
A
AB
A
y
z
y
y
cD
N
−
=
)
(
2
1
(16)
gdzie z= z
2
– z
1
jest drogą dyfuzji cząstki pary w chwili t procesu.
Strumień N
A
jest równy prędkości ubywania cieczy
dt
dz
c
N
A
A
=
(17)
gdzie c
A
=
ρ
A
/M
A
jest molową koncentracją składnika A w fazie ciekłej. Z porównania (17) i
(16), obliczenia dt i scałkowania, otrzymuje się
∫
∫
−
=
)
(
)
(
2
1
)
(
t
z
t
z
A
A
A
AB
Bśr
A
t
t
o
o
zdz
y
y
M
cD
y
dt
ρ
(18)
Po wykonaniu operacji całkowania znajdujemy
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
=
−
2
)
(
)
(
)
(
2
2
2
1
o
A
A
A
AB
Bśr
A
o
t
z
t
z
y
y
M
cD
y
t
t
ρ
(19)
Powyższy wzór może służyć do wyznaczania współczynnika dyfuzji
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
−
=
)
(
2
)
(
)
(
)
(
2
2
2
1
o
o
A
A
A
Bśr
A
AB
t
t
t
z
t
z
y
y
cM
y
D
ρ
(20)
Poniższy przykład ilustruje sposób wyznaczania współczynnika dyfuzji na podstawie da-
nych doświadczalnych
4
Przykład
Używając cylindra jak na rysunku 1 zmierzono dyfuzyjność trójchlorometanu w powietrzu
przy temperaturze 25
o
C i ciśnieniu 1 atm. Gęstość cieczy trójchlorometanu w temperaturze
25
o
C wynosi 1,485 g/cm
3
, a ciśnienie jego pary nad powierzchnią parowania przy 25
o
C jest
200 mmHg. W chwili t = 0 powierzchnia cieczy trójchlorometanu była oddalona od górnej
krawędzi cylindra o 7,40 cm, a po 10 godzinach powierzchnia cieczy opadła o 0,44 cm. Ile
wynosi współczynnik dyfuzji trójchlorometanu do powietrza, jeśli przyjąć, że koncentracja
trójchlorometanu nad górną krawędzią cylindra wynosi zero.
Przyjmując, że para trójchlorometanu oraz powietrze są gazami idealnymi, możemy obli-
czyć ich udziały molowe nad powierzchnią cieczy
263
.
0
760
200
1
1
=
=
=
mmHg
mmHg
p
p
y
A
A
oraz
737
,
0
1
1
1
=
−
=
A
B
y
y
Nad górną krawędzią cylindra udziały obu gazów wynoszą odpowiednio
0
2
=
A
y
oraz
stąd
0
2
=
B
y
263
,
0
2
1
=
−
A
A
y
y
Na podstawie wzoru (11) określamy średni molowy udział składnika B w cylindrze
862
,
0
)
737
,
0
/
1
ln(
737
,
0
1
)
/
ln(
1
2
1
2
=
−
=
−
=
B
B
B
B
Bśr
y
y
y
y
y
Masa drobinowa trójchlorometanu wynosi M
A
= 119,39 g/mol. Koncentracja molowa trój-
chlorometanu, określona na podstawie wzoru, ma wartość
0124
,
0
39
,
119
485
,
1
=
=
=
A
A
A
M
c
ρ
Gęstość molowa mieszaniny c w cylindrze:
przy czym
K
mol
cm
atm
K
mol
J
o
o
=
=
ℜ
3
06
,
86
314
,
8
zatem
3
5
10
09
,
4
298
06
,
82
1
cm
mol
T
p
c
−
⋅
=
⋅
=
ℜ
=
Początkowa odległość powierzchni cieczy od górnej krawędzi cylindra wynosiła z(t
o
) =
7,40 cm, a po czasie t – t
o
= 10 godz. = 36000 s odległość ta była z(t) = 7,84 cm.
Po podstawieniu powyższych wartości do wzoru (20) otrzymamy
5
s
m
s
cm
D
AB
2
6
2
2
2
5
10
3
,
9
093
,
0
36000
2
40
,
7
84
,
7
263
,
0
10
09
,
4
862
,
0
0124
,
0
−
−
⋅
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
−
⋅
⋅
⋅
=
.
PRZEBIEG POMIARÓW
Na podstawie przykładu obliczyć współczynnik dyfuzji alkoholu etylowego do powie-
trza.
6
Document Outline