GRUPA {G, *} ∀ a , b∈G a∗b∈G
(G - zbiór, * - działanie łączne w G spełniające poniższe warunki)
1. Istnieje element neutralny

∃

e∈G ∀ a∈G a∗e=e∗a=a

2. Każdy element G posiada element odwrotny/przeciwny

∀

a∈G ∃b∈G a∗b=b∗a=e

3. Działania * na zbiorze G są łączne

∀

a , b , c∈G a∗b∗c = a∗b∗c

Jeżeli występuje przemienność działań to grupa jest abelowa (przemienna)

∀

a , b∈G a∗b=b∗a

CIAŁO {F, +, . }
(F - zbiór, działania wewnętrzne „+” - dodawanie
i „.” - mnożenie, spełniające poniższe warunki)
1. {F,+} jest grupą abelową (przemienną)
2. {F\{0}, . } jest grupą abelową (przemienną)
3. ∀ a , b , c∈F

a⋅bc =abac (prawo

rozdzielności mnożenia względem dodawania)

W ciele zachodzą następujące warunki:

∀

a , b∈F

1.1≠0
2. 0⋅a=a⋅0=0
3.−1⋅a=−a
4. jeżeli ab=0, to a=0 lub b=0
5. jeżeli a≠0 i b≠0, to ab

−

1

=

b

−

1

a

−

1

LICZBY ZESPOLONE
(a) Postać kanoniczna z =xiy
(b) Postać sprzężona z=x−iy

(c) Postać trygonometryczna

z =∣z∣

x

∣

z∣



i

y

∣

z∣

=∣

z∣cosi sin 

(d) Wzory:

z=∣z∣cos −i sin −

z

1

⋅

z

2

=∣

z

1

∣⋅∣

z

2

∣

cos

1



2



i sin

1



2



z

1

z

2

=

∣

z

1

∣

∣

z

2

∣



cos

1

−

vaphi

2



i sin

1

−

2



z

n

=∣

z∣

n



cos nisin n 

W

k

=

z

1
n

=∣

z∣

1
n



cos



2k 

n



isin 



2k 

n



, k =0, 1, ... , n−1

PRZESTRZENIE LINIOWE {V(F), +, . } (też przestrzenie wektorowe)
(V - zbiór, F - ciało)
(a) Przestrzenią liniową V nad ciałem F nazywamy układ {V(F), +, . } gdzie „+” jest działaniem
wewnętrznym w zbiorze V a „.”

F ×V V

działaniem zewnętrznym

1. {V, + } jest grupą abelową
2. ∀ x∈V ∀ a∈F a⋅x ∈V , x - wektor
3. a) ∀ a , b∈F ∀ x∈V a⋅b⋅x=a⋅b ⋅x

b) ∀ x∈V 1⋅x= x

c) ∀ a , b∈F ∀ x ∈V ab⋅x=axbx
d) ∀ a ∈F ∀ x , y ∈V a⋅ x y =axay

(b) Podprzestrzeń liniowa zawarta W ⊂V nazywamy każdy taki podzbiór w przestrzeni V, że W
jest przestrzenią liniową nad F

∀ 

, ∈F ∀ W

1,

W

2

∈

W



W

1



W

2

∈

W

(c) baza: Zbiór

{

x

i

}

jest bazą przestrzeni liniowej V(F) jeżeli

1. Jest zbiorem wektorów liniowo niezależnych
2. ∀ x∈V x=

∑



i

x

i

każdy wektor da się przedstawić jako kombinację liniową wektorów ze

zbioru (napina przestrzeń wektorową)

[

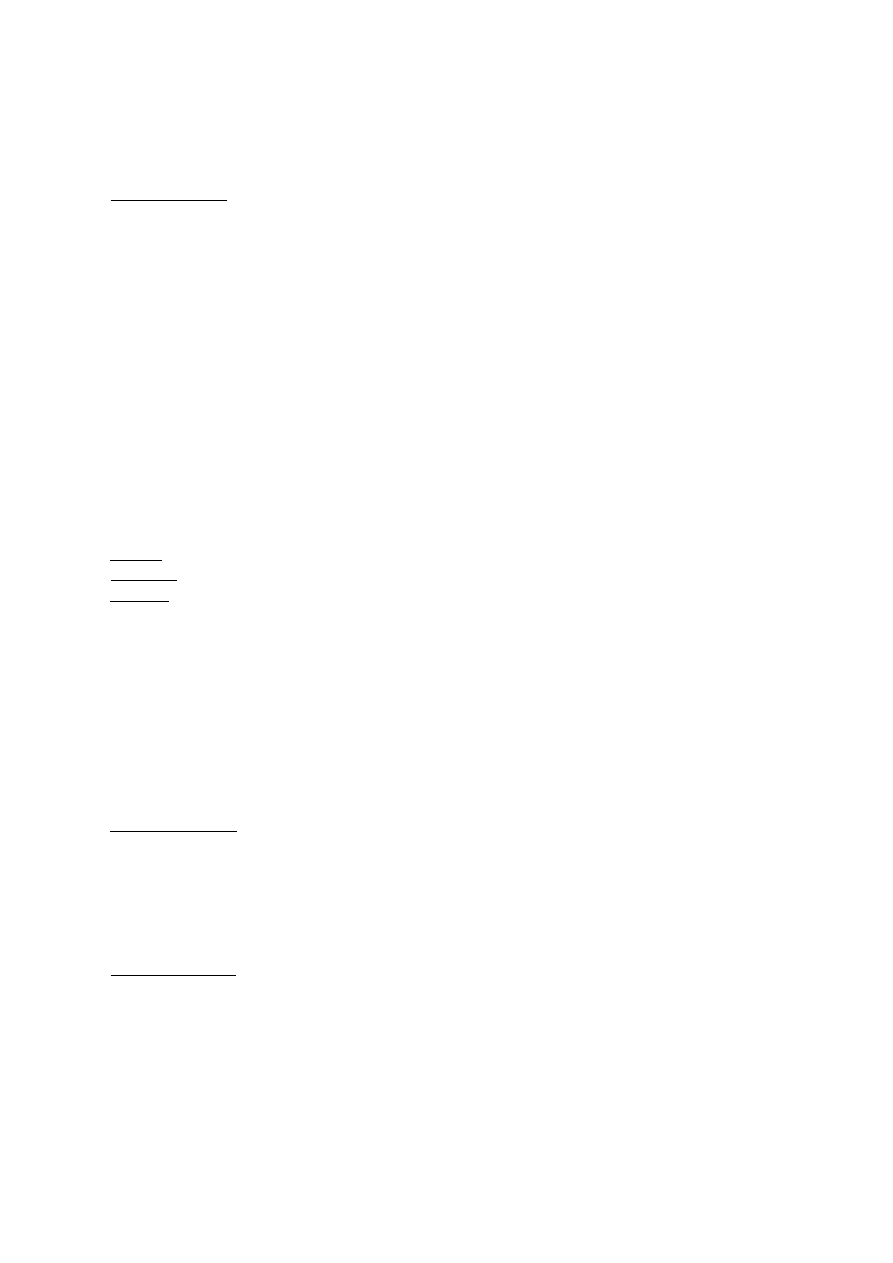
4,3]z bazy B do B ' , B= 

b

1

, 

b

2



, B '=b

1

' , b

2

' , b

1

' =2b

1

−

b

2,

b

2

' =b

2



b

1

4b

1



3b

2

=

xb

1

' yb

2

'=x  2b

1

−

b

2



y b

2



b

2

=

b

1



2x yb

2

−

x y 

{

2x y=4

−

x y=3

(d) układ wektorów

{

x

i

}

i =1

n

nazywamy układem wektorów liniowo niezależnych jeżeli dla

dowolnego układu skalarów

k

i

∈

F

spełniony jest warunek

∑

i=1

n

k

i

x

i

=

0 ⇒ k

i

=

0 dla i∈{1, ... , n }

PRZEKSZTAŁCENIA LINIOWE A :V V ' (też odwzorowania liniowe)
(A - przekształcenie liniowe, V i V' - przestrzenie liniowe nad ciałem F)
(a) A jest przekształceniem liniowym ⇔ ∀ x , y∈V ∀ ,∈F A x y=⋅A x⋅A y

a nie przypadkiem A x y = A x A y?

poprawcie mnie jeśli się mylę

można rozpisać na * przekształcenia liniowego:
*addytywność ∀ x , y ∈V A xb =Ax Ab
*jednorodność ∀ x∈V ∀ ∈F A x=⋅Ax

(b) 

1

,... , 

n

= 

1

,... , 

m

 

:ℝ

n

ℝ

m

i=1, ... , m

j=1, ... , n

B

i

=

∑

j=1

n

a

ij



j

a

ij

∈ℝ



i



i

∈ℝ

(c) Jądrem A nazywamy zbiór {x∈V : Ax=0} . Ker A jest podprzestrzenią V
(d) Obrazem A nazywamy zbiór { y∈V ' : ∃ x ∈V y= Ax} . Im A jest podprzestrzenią V
(e) Rzędem przekształcenia A nazywamy wymiar obrazu A

rk A=dim im A

(f) Macierz przekształcenia jest to zapis przekształcenia liniowego dwóch skończenie wymiarowych
przestrzeni liniowych nad tym samym ciałem

Ax

i

=

∑

j =1

n

a

ij

y

j

i=1, ... , n a

ij

∈

F

A :V V '

[

a

11

⋯

a

1n

⋮

⋱ ⋮

a

m1

⋯

a

mn

]

x∈V

y ∈V '

PRZEJŚCIE Z JEDNEJ BAZY DO INNEJ BAZY
(a) Macierz przejścia jest to macierz odwracalna, zwana macierzą przejścia z bazy B do bazy B'
(b) 

V =V

1



e

1



...V

n



e

n

=

V

1

' 

e

1

' ...V

n

' 

e

n

'

[

V

1

⋮

V

n

]

=

p

−

1

[

V

1

'

⋮

V

n

'

]

(c) A ' =D

−

1

⋅

A⋅C (co jest w miejscu „?”)

(d) Macierz podobna. Dwie macierze (

n×n

) A, B są podobne, jeżeli istnieje macierz C (

n×n

)

nieosobliwa, że

B=C

−

1

AC

. Własności: det B=det C , Tr A=Tr B (Tr - ślad macierzy, suma

elementów na diagonalnej (przekątnej) )

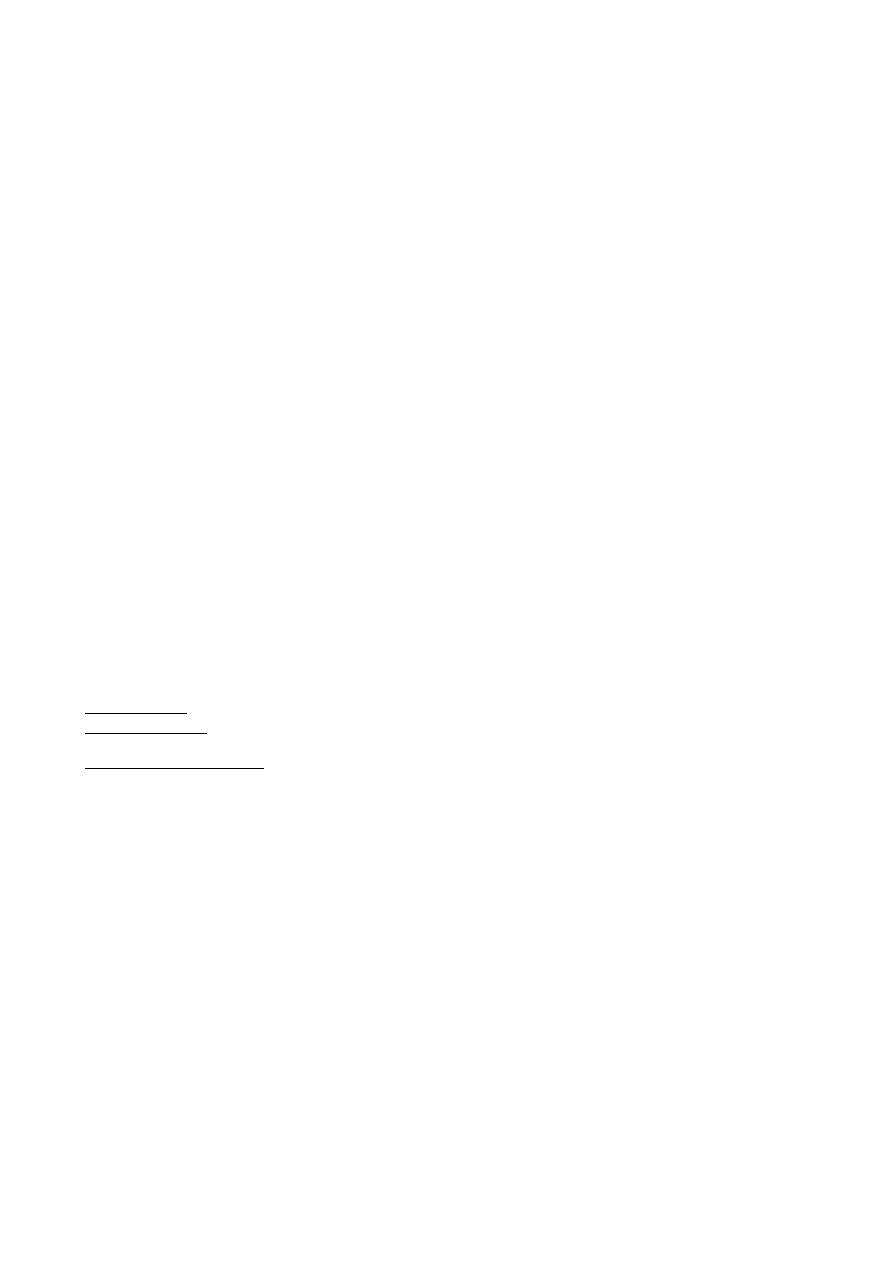
MACIERZE

- macierz zerowa [ ]

ij

=

0

- macierz jednostkowa (tylko "1" na przekątnej) I
- macierz diagonalna (nie ma zer tylko na przekątnej) [ ]

ij

=

0 dla i≠ j

- macierz odwrotna A

−

1

- macierz ortogonalna A

T

=

A

−

1

- macierz indepotentna A

2

=

A

[

1 −1
0

0

]

⋅

[

1 −1
0

0

]

=

[

1 −1
0

0

]

- macierz transponowana

A

T

jest macierzą transponowaną do A ⇔[ A

T

]

ij

=[

A]

ji

A=

[

1 2
3 4

]

⇒

A

T

=

[

1 3
2 4

]

1. B= A

T

⇒

B

T

=

A

2.  AB

T

=

A

T



B

T

3. A⋅B

T

=

B

T

⋅

A

T

- macierz symetryczna

A jest symetryczna ⇔ A= A

T

[

1 5 4
5 2 6
4 6 3

]

- macierz sprzężona hermitowsko[ A

+

]

ij

=[

A]

ji

*

- macierz samosprzężona hermitowsko A=A

+

[

1

i

1−i

−

i

2

2i

1i −2i

3

]

rząd macierzy - ilość niezależnych liniowo kolumn
macierz skalarna z przekątną główną (a, …, a)

sprzężenie hermitowskie np.

[

i

2−i

3−4i

5

]

+

=

[

−

i

34i

2i

5

]

WYZNACZNIK MACIERZY KWADRATOWEJ detA
(A - macierz)
(a) Wyznacznik to funkcja określona na macierzach kwadratowych, związana z mnożeniem i
dodawaniem odpowiednich elementów dużej macierzy, by otrzymać pojedynczą liczbę

det A=

∑

i =1

n

−

1

i j

a

ij

det M

ij

(z Laplace'a)

(b) Własności:
1. detA=detA

T

2. Wyznacznik macierzy, w której jeden z wierszy został pomnożony przez liczbę



jest równy

iloczynowi



i wyznacznika wyjściowej macierzy

det

[

a

11

⋯

a

1n



a

21

⋯ 

a

2n

⋮

⋱

⋮

a

mn

⋯

a

mn

]

=

det

[

a

11

⋯

a

1n

a

21

⋯

a

2n

⋮

⋱

⋮

a

mn

⋯

a

mn

]

3. Wyznacznik macierzy, której kolumna lub wiersz zawiera same zera = 0
4. Przy zamianie dwóch kolumn lub wierszy znak wyznacznika zmienia się na przeciwny

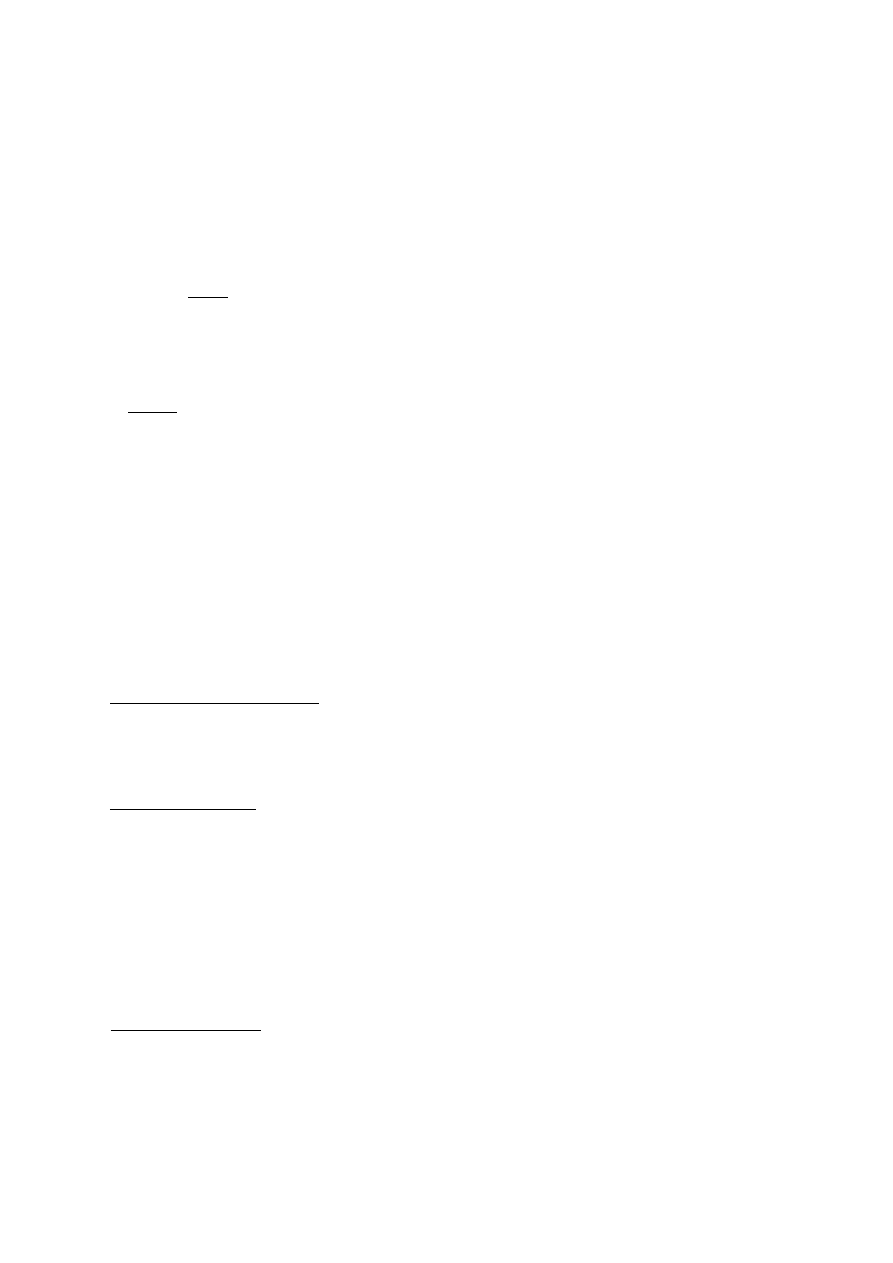
det

[

1 2
3 4

]

=

4−6=−2 det

[

3 4
1 2

]

=

6−4=2

5. Wyznacznik macierzy jednostkowej = 1
6. Jeżeli w macierzy są identyczne dwa wiersze lub kolumny to wyznacznik jest równy 0

det A=−det A

7. det  A⋅B=det A⋅det B
8. Wyznacznik nie ulega zmianie jeśli do jednego z jego wierszy dodamy drugi pomnożony przez
liczbę
9. Wyznacznik macierzy, w której wiersze lub kolumny są liniowo zależne jest równy 0

10. det A

−

1

=

1

det A

det A≠0

(c) Rozwinięcie Laplace'a det A=

∑

i =1

n

−

1

i j

a

ij

⋅

det M

ij

(d) Układ Cramera

det A≠0

x

i

=

det A

xi

det A

x= A

−

1

⋅

b b−wyrazy wolne

Ax

i

- powstaje poprzez zastąpienie i-tej kolumny wyrazem wolnym

układ jednorodny gdy



b=0

(e) niezależność liniowa wektora jako kolumny, jeżeli det = 0 to zależne liniowo

WARTOŚCI I WEKTORY WŁASNE PRZEKSZTAŁCEŃ LINIOWYCH
(a) M −NieMogęSięOdczytać  x=0

det M −NieMogęSięOdczytać =0

My

[

x

1

x

2

]

=

[

x

1

x

2

]

[

My−]

[

x

1

x

2

]

=

0

(b) Transformacja podobieństwa
macierz diagonalizująca (P), wektory własne jako kolumny
macierz diagonalna, wartości własne na przekątnej D=P

−

1

AP

PRZESTRZENIE Z ILOCZYNEM WEWNĘTRZNYM (iloczyn skalarny)
(a) Iloczyn wewnętrzny: operator na przestrzeni liniowej przypisujący dwóm argumentom tej
przestrzeni wartość skalarną
Iloczyn skalarny:  x , y ∈F

x , y ∈V

1.  x , y=u , x 

*

2.  x ,  y z = z , y x , z



y  z , z =z ,  y z

¿

*

=

*



x , y 

*



*



z , z

*

=

*



y , z

*



z , x

3. ∀ x∈V



x , x0



x , x =0 ⇒ x=0



x , x ∈ℝ , bo :⇒ x , x= x , x

*



x , x − x , x 

*

=

0⇒ 2 Im x , x=0

(b) Zbiory ortonormalne

{

x

i

}

i

n

=

1

jest zbiorem ortonormalnym ⇔ x

i

, x

j

=

ij



x

i

, x

j

=

ij

{

1 i= j
0 !! i≠ j

(c) Zupełność zbioru ortonormalnego nie zawiera się z żadnym większym zbiorze ortonormalnym
(d) Własności:

X ={x

i

}

i

n

=

1 w przestrzeni V

x - jest zbiorem ortonormalnym zupełnym

1.  x

i

, x=0 i=1, ... , n to x =0 Ortogonalne dla wszystkich elementów

2. x napina przestrzeń wektorową

3. x ∈V

x=

∑

i=1

n



i

x

i



i



x

i

, x 

4. Jeżeli x , y ∈V to  x , y =

∑

i=1

n



x , x

i



x

i

, y

5. Jeżeli x ∈V ∥x∥=

∑

i =1

n



x

i

, x

2

(e) Ortogonalizacja Grama-Schmidta

y

k

=

x

k

−

y

1

, x

k



y

1

−

...− y

k−1

, x

k



y

k −1

∥

x

k

−

y

1

, x

k



y

1

−

...− y

k−1

, x

k



y

k −1

∥

PRZEKSZTAŁCENIA SPRZĘŻONE DO DANEGO PRZEKSZTAŁCENIA
Przekształcenia B jest sprzężone do A jeśli  A x , y =x , B y
Zazwyczaj przekształcenie sprzężone do

A : A

+

Samosprzężone A

+

=

A (rzeczywiste wartości własne)

Macierz unitarna A

−

1

=

A *

T

det A=1