Opis dwiczenia

„Symulacja komputerowa przepływu cieczy lepkiej nieściśliwej

w kanale o zmiennym przekroju”

Przeczytad należy całą instrukcję, a nie losowo wybrane zdania lub wyrazy!

Zadanie opisane jest równaniem Naviera-Stokesa

𝐷𝐯

𝐷𝑡

= 𝐛 −

1
ρ

grad 𝑝 + ν ∇

2

𝐯 +

1
3

grad(div 𝐯)

v

– wektor prędkości,

b

– siły masowe,

p

– ciśnienie,

ν - lepkośd,

oraz

𝐷

𝐷𝑡

=

𝜕

𝜕𝑡

+ (𝐯 ∙ ∇)

W przypadku nieściśliwego płynu narzucamy warunek div 𝐯 = 0 i mamy

𝐷𝐯

𝐷𝑡

= 𝐛 −

1
ρ

grad 𝑝 + ν ∇

2

𝐯

Przypomnienie

Zachodzą zależności

∇ ∙ ∇ 𝑓 = ∇

2

𝑓 = ∆ 𝑓

Δ - operator Laplace’a,

∆𝑓 = div 𝐠𝐫𝐚𝐝 𝑓

W przypadku przepływu ustalonego (niezależnego od czasu) pochodna

𝜕

𝜕𝑡

= 0.

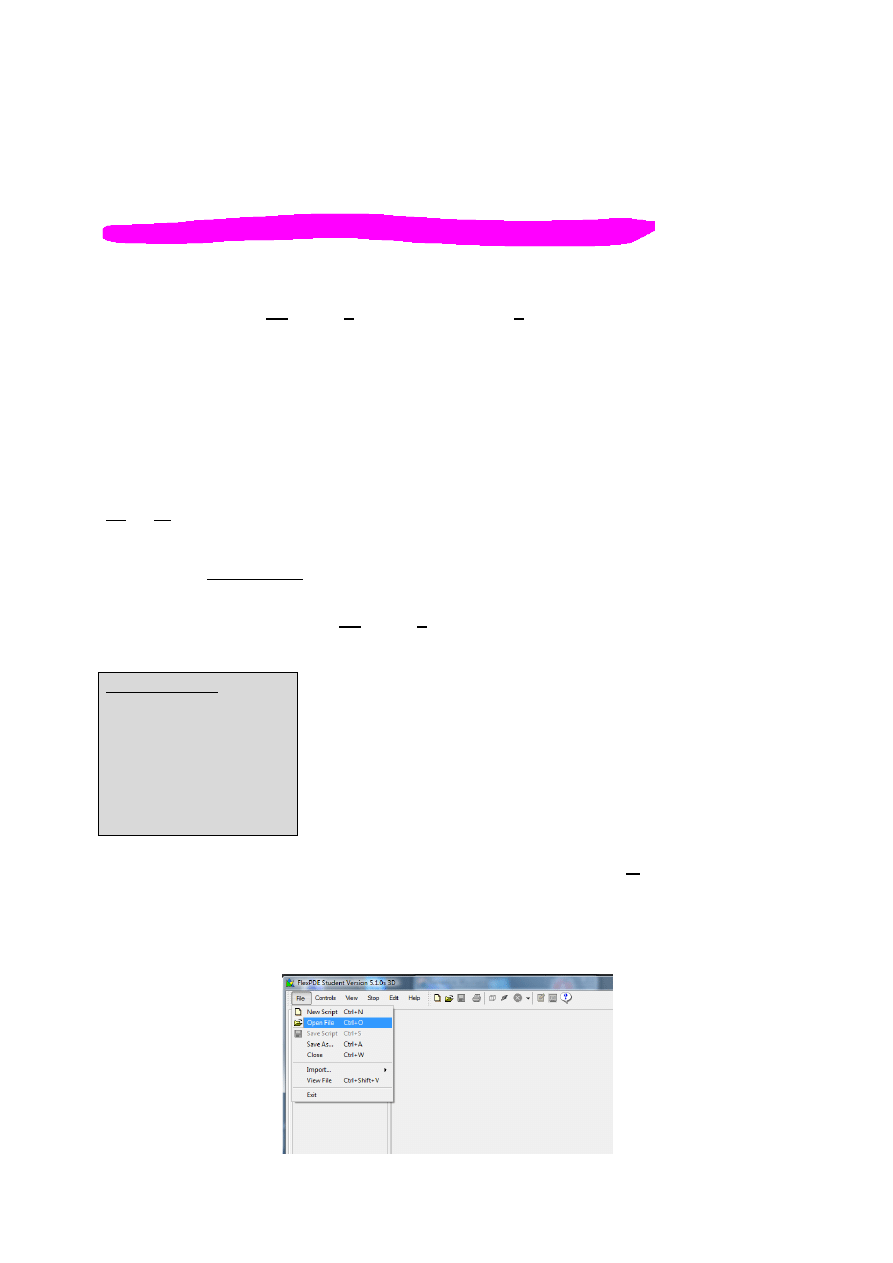
Do obliczeo numerycznych używamy studenckiej wersji programu FlexPDE (flexpde5s). Po
uruchomieniu programu wprowadzamy przygotowany wcześniej program źródłowy

lub uruchamiamy edytor

CTRL-n

i po ukazaniu się szkieletu programu wpisujemy potrzebne

informacje. Możemy skorzystad z gotowego źródła programu i zmodyfikowad go. Dostęp do
edytora uzyskujemy przez

CTRL-e

. Poniżej przedstawiono przykładowy program do dwiczeo:

{ PRZEPLYW.PDE }
title 'Przeplyw cieczy lepkiej w kanale 2-wymiarowym, Re > 40'
select errlim = 0.005
variables
u(0.1)
v(0.00)
p(1)
definitions
Lx = 5 Ly = 1.5
Gx = 0 Gy = 0
p0 = 2
speed2 = u^2+v^2
speed = sqrt(speed2)
dens = 1
visc = 0.04
vxx = (p0/(2*visc*(2*Lx)))*(Ly-y)^2 { open-channel x-velocity }

rball=0.25
cut = 0.05

{ bevel the corners of the obstruction }

n=1

penalty = 100*visc/rball^2
Re = globalmax(speed)*(Ly/2)/visc
initial values
u = 0.5*vxx v = 0 p = p0*x/(2*Lx)
equations
u: visc*div(grad(u)) - dx(p) = dens*(u*dx(u) + v*dy(u))
v: visc*div(grad(v)) - dy(p) = dens*(u*dx(v) + v*dy(v))
p: div(grad(p)) = penalty*(dx(u)+dy(v))
Boundaries
region 1
start(-Lx,0)
load(u) = 0 value(v) = 0 load(p) = 0
line to (Lx/2-rball,0)

value(u)=0 value(v)=0 load(p)= 0
line to (Lx/2-rball,rball*n) bevel(cut)
to (Lx/2+rball,rball*n) bevel(cut)
to (Lx/2+rball,0)

load(u) = 0 value(v) = 0 load(p) = 0
line to (Lx,0)

load(u) = 0 value(v) = 0 value(p) = p0
line to (Lx,Ly)

value(u) = 0 value(v) = 0 load(p) = 0
line to (-Lx,Ly)

load(u) = 0 value(v) = 0 value(p) = 0
line to close

monitors
contour(speed)

plots
contour(u) report(Re)
contour(v) report(Re)
contour(speed) painted report(Re)
vector(u,v) as "flow" report(Re)
contour(p) as "Pressure" painted
contour(dx(u)+dy(v)) as "Continuity Error"
elevation(u) from (-Lx,0) to (-Lx,Ly)
elevation(u) from (0,0) to (0,Ly)
elevation(u) from (Lx/2,0) to (Lx/2,Ly)
elevation(p) from (Lx,0) to (Lx,Ly)
elevation(p) from (Lx/2+rball,0) to (Lx/2+rball,rball*n)
end

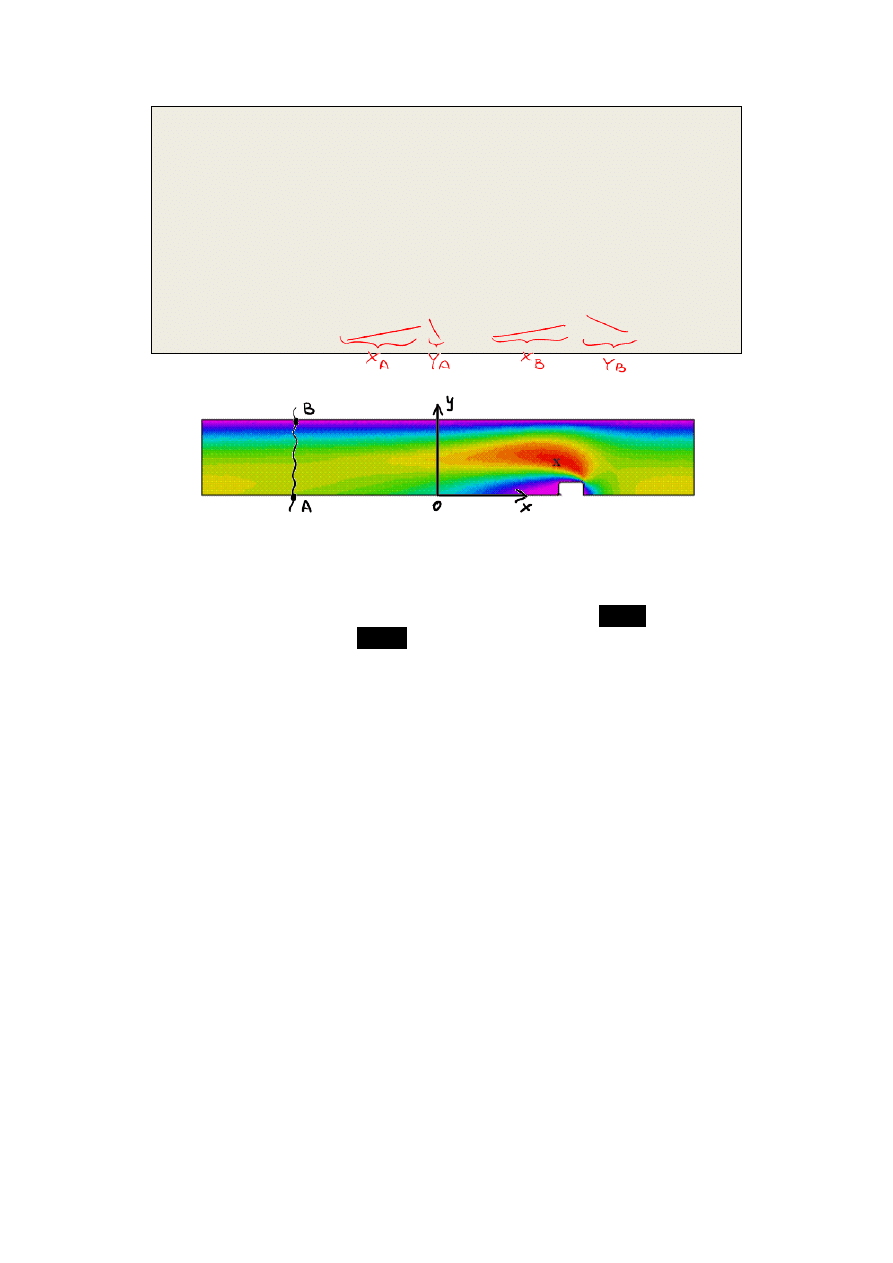
Program opisuje obiekt o kształcie jak poniżej:

Jest to połowa symetrycznego kształtu o wymiarach 2Lx, 2Ly (połówka ma zatem wysokośd
Ly). Na górnej krawędzi zadana jest zerowa prędkośd pozioma (u=0). Prawa krawędź ma
zadane stałe cośnienie P

0

.

Obliczenia uruchamiamy wykorzystując menu lub skrót klawiszowy

CTRL-r

. Dostęp do

edytora danych uzyskujemy przez

CTRL-e

.

W wyniku otrzymujemy zestaw wykresów. Wskazanie jednego z nich powiększa obraz.
Ponowne kliknięcie przywraca poprzedni widok.

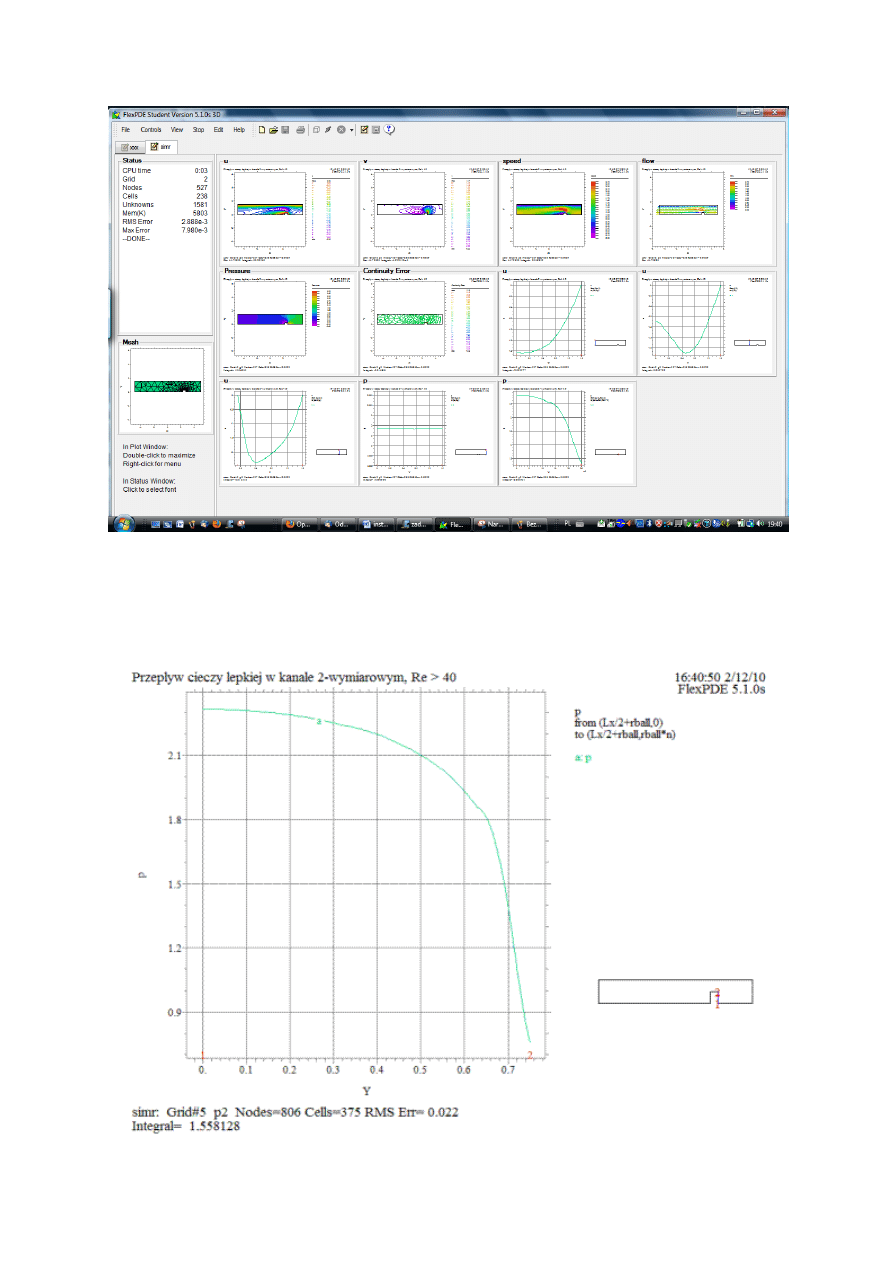
Oprócz graficznych postaci wyników podawane są wielkości liczbowe, w tym całki wybranych
krzywych (patrz: ostatni wiersz na wykresie poniżej):

Opis analizowanego równania

equations
u: visc*div(grad(u)) - dx(p) = dens*(u*dx(u) + v*dy(u))
v: visc*div(grad(v)) - dy(p) = dens*(u*dx(v) + v*dy(v))
p: div(grad(p)) = penalty*(dx(u)+dy(v))

u, v – składowe wektora prędkości v.
Jest to odpowiednik równania

𝜇 ∇

2

𝐯 − ∇ 𝑝 = 𝜌 grad 𝐯

(tutaj współczynnik lepkości ν = ρµ)
uzupełniony warunkiem

∇

2

𝑝 = 𝑘 div 𝐯

wprowadzonym metodą funkcji kary ze współczynnikiem k.

Instrukcja działania programu FlexPDE wraz z przykładami znajduje się na stronie opisu
programu: http://www.pdesolutions.com/help/index.html .

Modyfikowad możemy kształt karbu oraz prędkośd wlotową:

Boundaries
region 1
start(-Lx,0)
load(u) = 0 value(v) = 0 load(p) = 0
line to (Lx/2-0.5,0) {lewy dolny rog}

value(u)=0 value(v)=0 load(p)= 0
line to (Lx/2-0.25,0.25) bevel(cut) {lewy gorny rog}
to (Lx/2+0.25,0.25) bevel(cut) {prawy gorny rog}
to (Lx/2+.25,0) {prawy dolny rog}

load(u) = 0 value(v) = 0 load(p) = 0
line to (Lx,0)

load(u) = 0 value(v) = 0 value(p) = p0 {cisnienie na prawej krawedzi}

Do programu wprowadzamy bezwymiarowe dane. Przyjmujemy, że wartości podawane są
w układzie jednostek [cm, g, s]. W związku z tym prędkośd uzyskujemy w [cm/s], gęstośd w
[g/cm

3

], a siłę konsekwentnie w [g cm/s

2

= 10

-5

N].

Rozpatrujemy zadanie dwuwymiarowe. Przyjmujemy, że głębokośd zadanego obiektu
wynosi 1 cm. Dzięki temu możemy badad obiekt trójwymiarowy.

Zadanie obliczeniowe

 wprowadzamy własne zmienne wykorzystywane do opisu geometrii oraz nadajemy

im wartości,

 modyfikujemy geometrię, wykorzystując wprowadzone zmienne,
 modyfikujemy instrukcje służące do wyświetlenia wyników; w szczególności

dodajemy instrukcję pozwalającą wykreślid funkcję ciśnienia w pionowym przekroju
za przeszkodą.

Wprowadzid przewężenie kanału przepływu o zadanym kształcie. Wyznaczyd:



rozkład prędkości i ciśnienia w obszarze,



rozkład ciśnienia w przekrojach skrajnych oraz całki tych rozkładów,



oraz obliczyd siłę oporu na krawędzi (powierzchni) zadanej przeszkody oraz opór
przepływu przez kanał.

Wyniki w formie graficznej możemy zapisywad wybierając na wykresie prawym guzikiem
myszy „export” oraz właściwy do zapisu format.