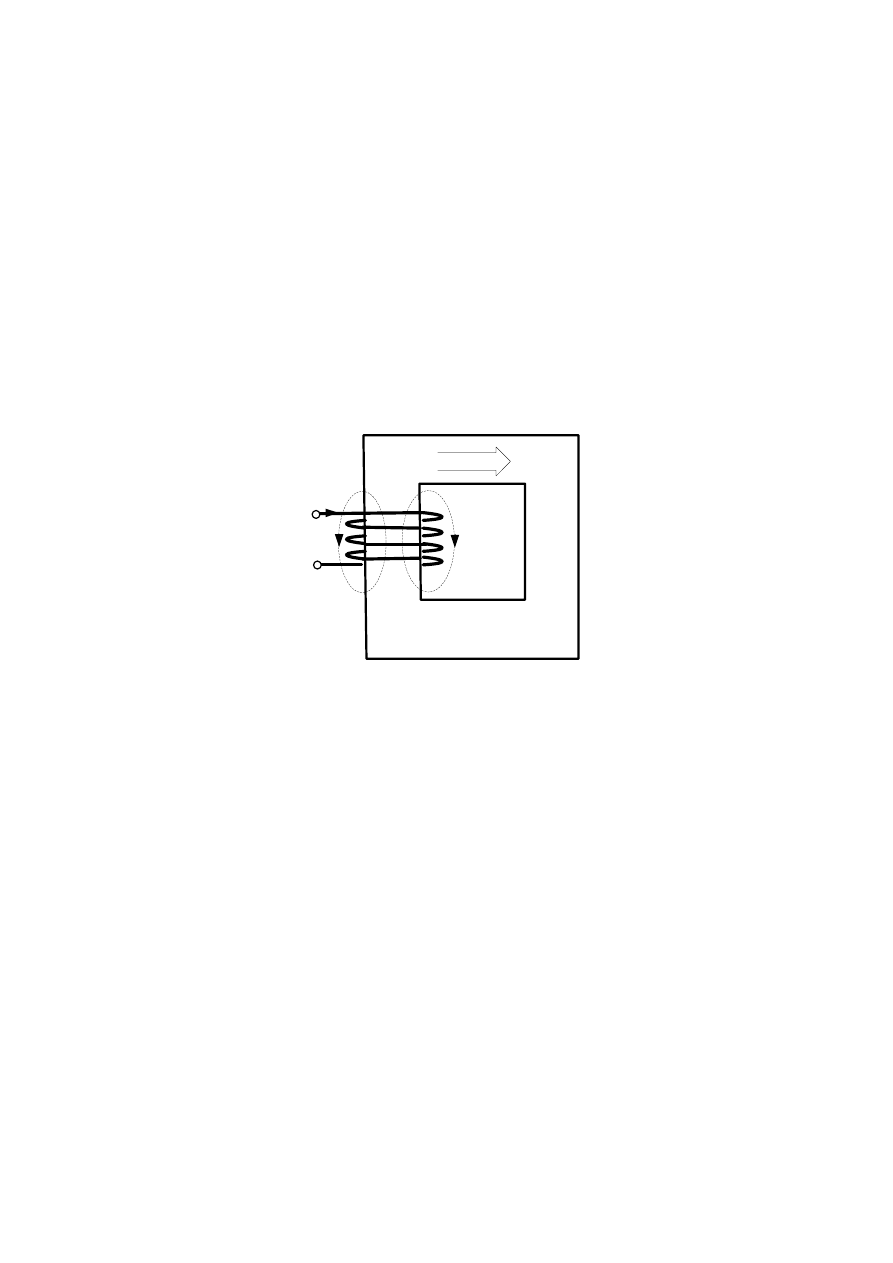
Dodatek 1- Uzupełnienie wiadomości o obwodach

magnetycznych

D.1. Wprowadzenie

Obwodem magnetycznym nazywamy przestrzeń, w której zamyka się strumień magnetyczny.

Przykładem takiego obwodu może być stalowy rdzeń, na którym nawinięto cewkę o liczbie zwojów

w

(Rys. D.1.). Pod wpływem wymuszonego prądu płynącego w cewce powstaje w rdzeniu pole

magnetyczne. Linie sił pola magnetycznego przebiegające w rdzeniu tworzą strumienie główne

Φ

(zamykające się przez rdzeń) oraz rozproszenia

σ

Φ

(zamykający się przez powietrze). Zazwyczaj

strumień rozproszenia stanowi kilka procent strumienia głównego i często w rozważaniach bywa
pomijany.

i

Φ

σ

Φ

σ

Φ

w

Rys. D.1. Przykład obwodu magnetycznego

W dalszej kolejności rozważać będziemy jedynie strumienie główne, więc założymy, że strumień

całkowity wytworzony przez prąd w cewce równa się strumieniowi głównemu, który przenika przez
przekroje elementów rdzenia. Dla obwodów magnetycznych występują pewne analogie z obwodami
elektrycznymi, a wielkość

i

⋅

=

Θ

w

nazywa się siłą magnetomotoryczną lub przepływem.

D.2. Prawo Ohma dla obwodów magnetycznych

Rozważania dotyczące analiz obwodów magnetycznych rozpoczniemy od postawienia zadania

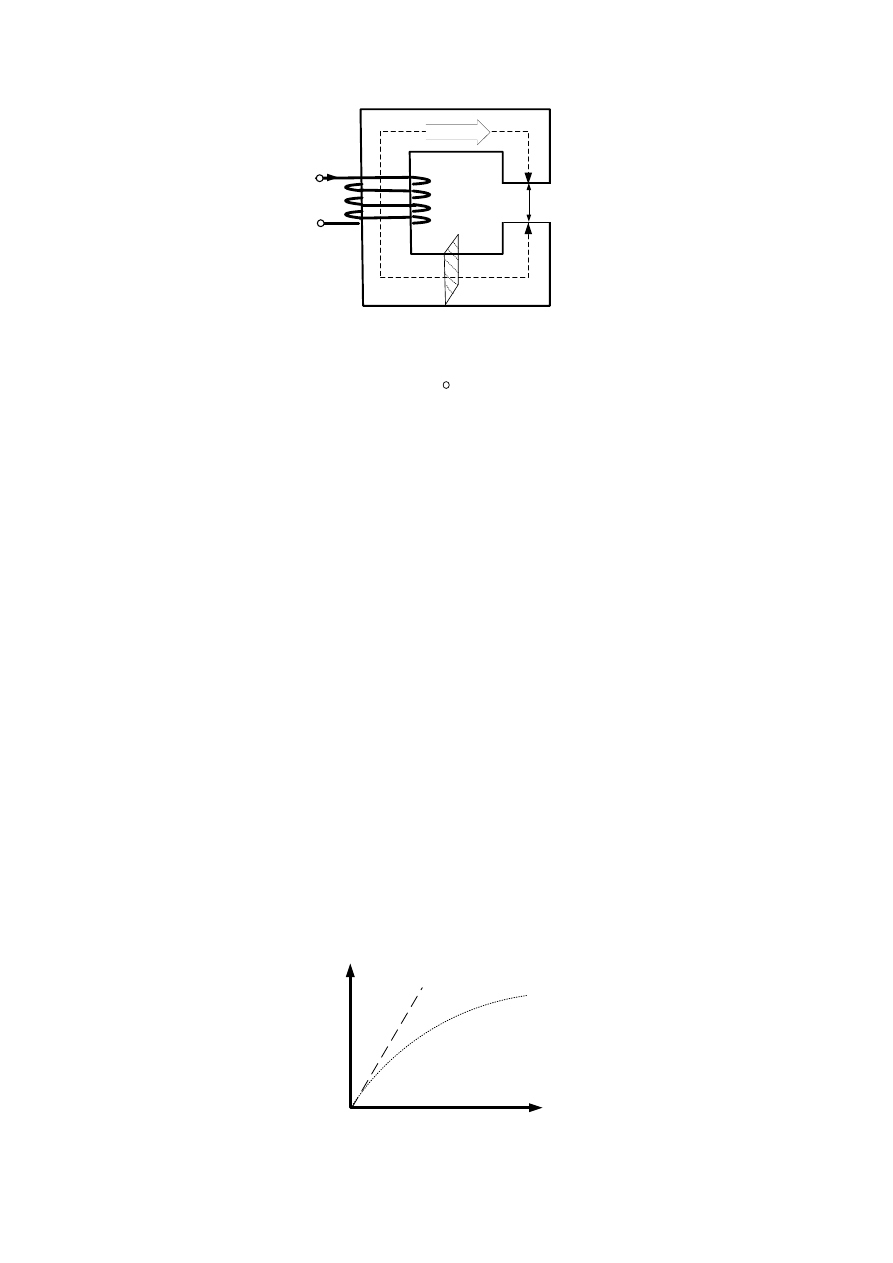
polegającego na określeniu strumienia głównego cewki nawiniętej na stalowym rdzeniu (Rys. D.2.) o
przekroju S zawierającą szczelinę powietrzną

δ

.

i

Φ

Fe

l

S

δ

l

w

Rys. D.2. Obwód magnetyczny ze szczeliną powietrzną

Zapisując prawo przepływu (Ampera)

∫

=

Θ

=

⋅

→

→

i

dl

H

w dla rozpatrywanego obwodu

magnetycznego z Rys. D.2. otrzymamy

Θ

=

⋅

+

⋅

δ

δ

l

l

H

H

Fe

Fe

(D.1)

gdzie

Fe

H

- natężenie pola magnetycznego w żelazie [A/m]

Fe

l

- długość linii sił pola magnetycznego w żelazie [m]

δ

H - natężenie pola magnetycznego w szczelinie powietrznej [A/m]

δ

l

- długość linii sił pola magnetycznego w szczelinie powietrznej [m]

Ponieważ obwód magnetyczny jest nierozgałęziony, dlatego ogólna formuła określająca strumień

magnetyczny

∫∫

→

→

⋅

=

Φ

S

s

B d może zostać zastąpiona wyrażeniem

Φ

=

Φ

=

Φ

δ

Fe

(D.2)

gdzie

S

⋅

=

Φ

Fe

Fe

B

[Wb]

S

⋅

=

Φ

δ

δ

B

[Wb]

a zależność określającą indukcję

Fe

B należy określić zgodnie z charakterystykami magnesowania stali

(Rys. D.3.), gdzie

Fe

µ

nosi nazwę przenikalności magnetycznej. Jednostką indukcji magnetycznej jest

tesla [T]

Fe

Fe

Fe

H

B

µ

=

(3)

Fe

H

Fe

B

Rys. D.3. Przykładowa charakterystyka magnesowania żelaza

Jeżeli założyć, że uwzględniamy liniową aproksymację magnesowania to wówczas będziemy

rozważać cewkę o charakterystyce liniowej, czyli

i

~

Φ

.

Dokonując przekształceń po zdefiniowaniu zależności na indukcję w szczelinie powietrznej

δ

δ

µ

=

H

B

0

(

7

0

10

4

−

⋅

π

=

µ

[V][s]/[A][m]) otrzymamy

S

Fe

Fe

Fe

Fe

B

H

µ

Φ

=

µ

=

(D.4)

S

0

0

µ

Φ

=

µ

=

δ

δ

B

H

(D.5)

Podstawiając wyrażenia (D.4), (D.5) do zależności opisującej prawo przepływu (D.1) dostaje się

następujące wyrażenie

Θ

=

µ

Φ

+

µ

Φ

δ

S

l

S

l

0

Fe

Fe

(D.6)

Definiując reluktancję

µ

R

(opór magnetyczny) dla elementów obwodu magnetycznego

S

l

R

Fe

Fe

Fe

µ

=

µ

(D.7)

S

l

R

0

µ

=

δ

µδ

(D.8)

dostaje się dla wyrażenia (D.6) postać prawa Ohma dla obwodów magnetycznych w następującej
formie

Θ

=

+

Φ

µδ

µ

)

R

R

(

Fe

(D.9)

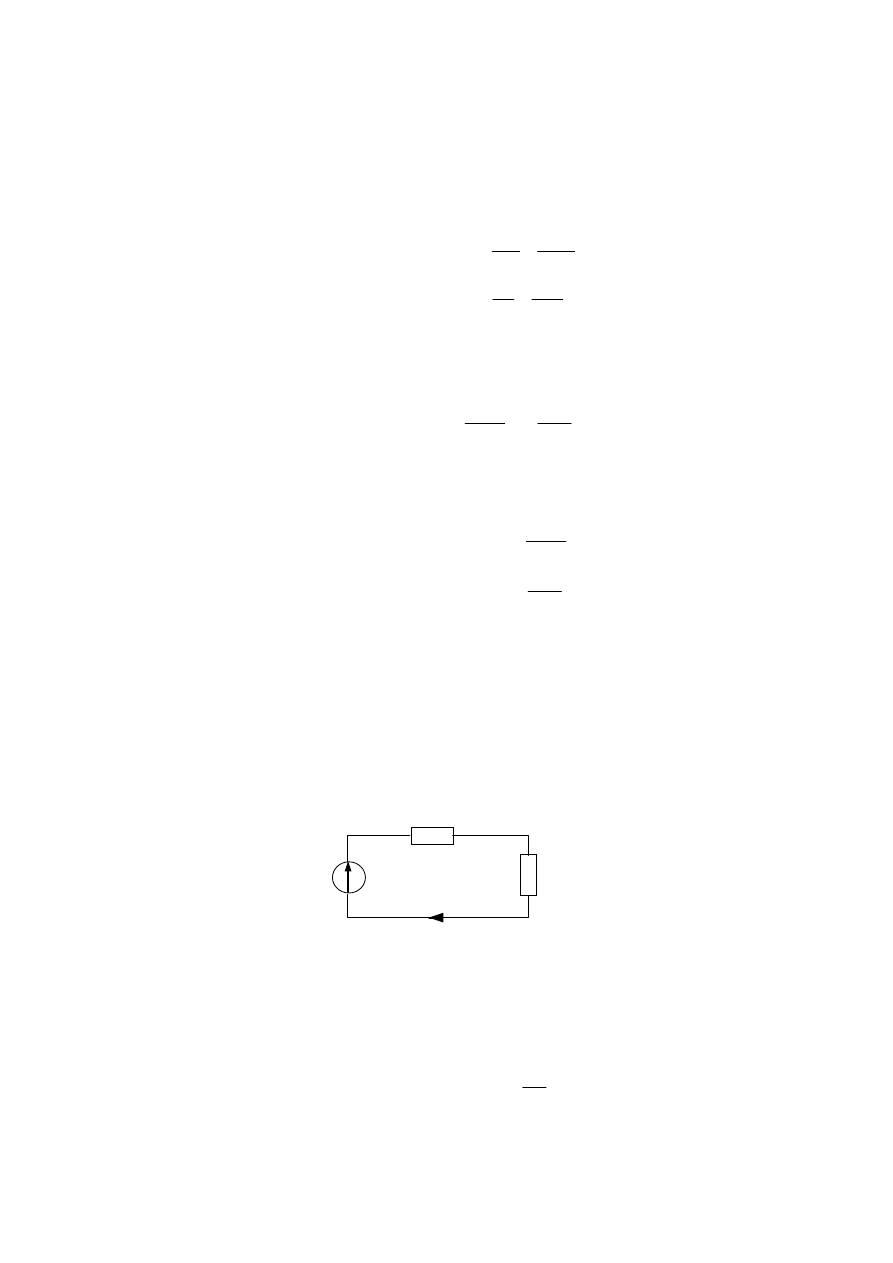
Można, więc obwód magnetyczny z Rys. D.2. Zastąpić równoważnym obwodem elektrycznym

(Rys. D.4.)

Fe

µ

R

i

w

=

Θ

µδ

R

Φ

Rys. D.4. Schemat zastępczy obwodu magnetycznego z Rys. D.2.

Podobnie jak dla obwodów elektrycznych w obwodach magnetycznych istnieje pojęcie

przewodności tylko magnetycznej, będącej odwrotnością reluktancji i nazywa się ją permeancją.
Jednostką permeancji jest Henr [H].

µ

=

Λ

R

1

(D.10)

Prawo Ohma dla obwodów magnetycznych może mieć również postać

µ

Λ

=

Φ

U

(D.11)

gdzie

µ

U

jest tzw. napięciem magnetycznym.

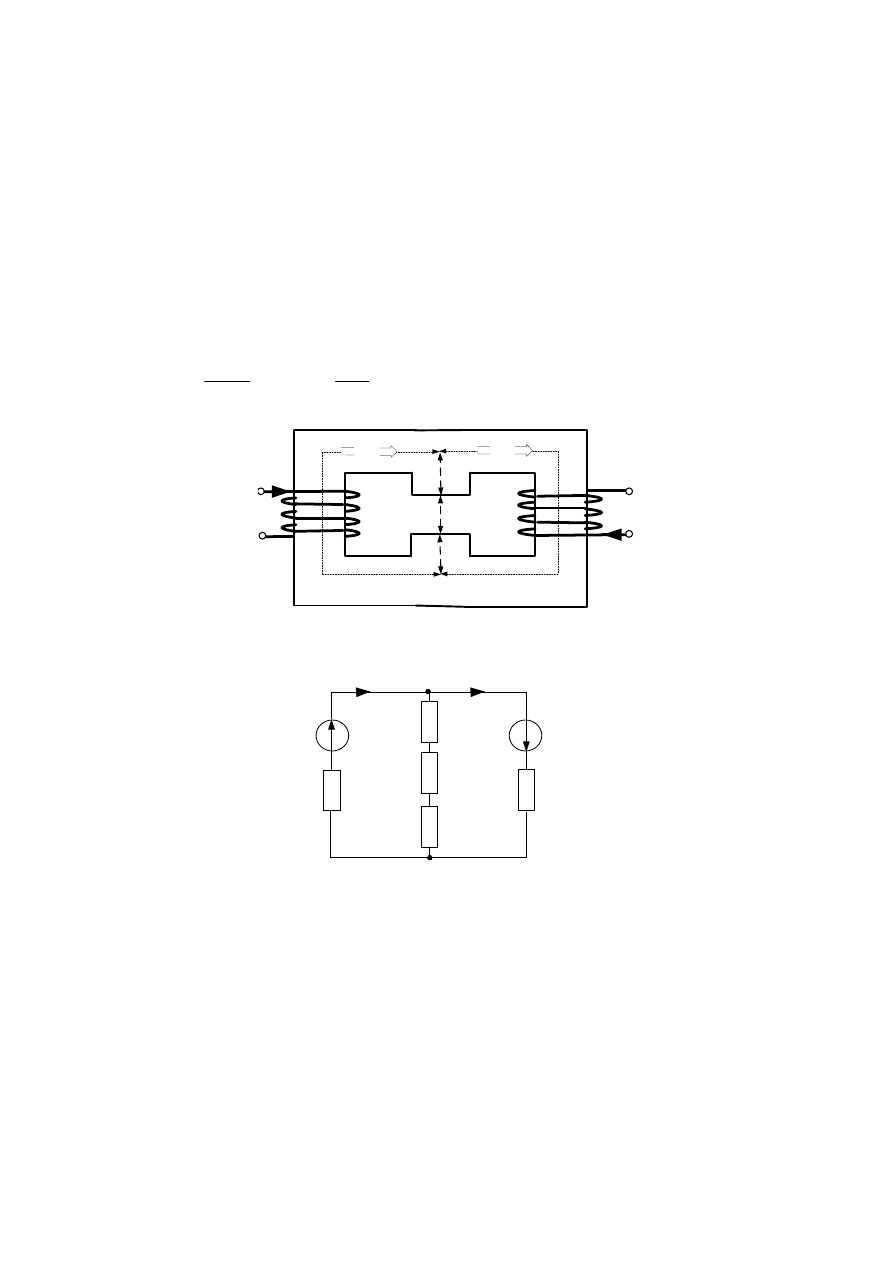
D.3. Rozgałęzione obwody magnetyczne

Poprzez analogię obwodów magnetycznych do obwodów elektrycznych można tworzyć zastępcze

równoważne obwody i dla nich zastosować prawa Kirchhoffa w celach analiz rozpływu strumieni w
obwodach magnetycznych. Ilustruje to następujący przykład rozgałęzionego obwodu magnetycznego
(Rys. D.5.) i odpowiadający temu obwodowi równoważny schemat elektryczny (Rys. D.6), dla

którego

i

Fe

i

i

S

l

R

µ

=

µ

oraz

S

l

R

0

µ

=

δ

µδ

.

1

i

Fe

µ

2

i

1

w

1

l

2

l

3

l

s

2

w

δ

l

4

l

2

Φ

1

Φ

s

s

s

Rys. D.5. Przykładowy rozgałęziony obwód magnetyczny

1

R

µ

1

1

1

w i

=

Θ

µδ

R

1

Φ

2

2

2

w i

=

Θ

2

R

µ

3

R

µ

4

R

µ

2

Φ

Rys. D.6. Schemat zastępczy obwodu magnetycznego z Rys. D.5.

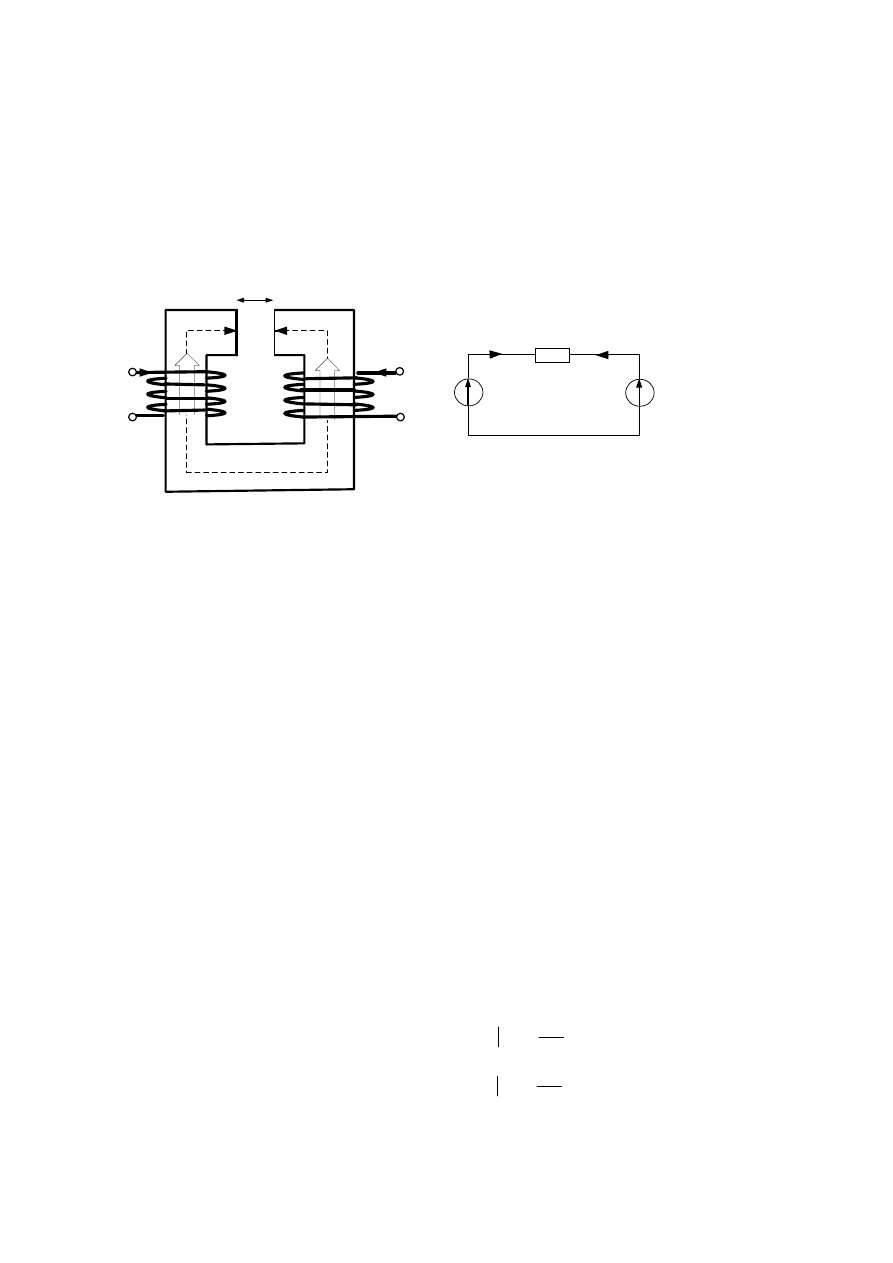
D.4. Indukcyjności własne i wzajemne cewek

Dla ilustracji analiz głównych strumieni sprzężonych cewek zostanie rozpatrzony układ dwóch

cewek nawiniętych na wspólnym rdzeniu ze szczeliną powietrzną (Rys. D.7. – Dla uproszczenia
przyjęto

∞

→

µ

rFe

).

1

1

1

w i

=

Θ

µδ

R

1

Φ

2

2

2

w i

=

Θ

2

Φ

1

i

1

w

1

Φ

Fe

l

δ

l

S

∞

→

µ

Fe

r

2

i

S

2

w

2

Φ

⇔

Rys. D.7. Układ dwóch cewek sprzężonych i odpowiadający im schemat zastępczy

Strumieniem skojarzonym cewki nazywać będziemy iloczyn strumienia i liczby zwojów

1

1

1

w

Φ

=

Ψ

,

2

2

2

w

Φ

=

Ψ

(D.12)

Ponieważ strumienie

1

Φ

i

2

Φ

mogą być wzbudzane zarówno przez prądy cewek 1 i 2, dlatego

można dokonać superpozycji strumieni pochodzących od tych prądów

12

11

1

Φ

+

Φ

=

Φ

(D.13)

22

21

2

Φ

+

Φ

=

Φ

(D.14)

gdzie

11

Φ

- strumień zamykający się przez cewkę 1, wzbudzony przez cewkę 1

12

Φ

- strumień zamykający się przez cewkę 1, wzbudzony przez cewkę 2

21

Φ

- strumień zamykający się przez cewkę 2, wzbudzony przez cewkę 1

22

Φ

- strumień zamykający się przez cewkę 2, wzbudzony przez cewkę 2

Zależność określająca strumienie skojarzone przybiera, zatem formę

12

1

11

1

1

w

w

Φ

+

Φ

=

Ψ

, (D.15)

22

2

21

2

2

w

w

Φ

+

Φ

=

Ψ

(D.16)

Zgodnie ze schematem zastępczym z Rys. D.7.

Λ

Θ

=

Θ

=

Φ

=

Φ

µδ

=

1

1

0

1

11

2

R

i

(D.17)

Λ

Θ

=

Θ

=

Φ

=

Φ

µδ

=

2

2

0

1

12

1

R

i

(D.18)

Λ

Θ

=

Θ

=

Φ

=

Φ

µδ

=

1

1

0

2

21

2

R

i

(D.19)

Λ

Θ

=

Θ

=

Φ

=

Φ

µδ

=

2

2

0

2

22

1

R

i

(D.20)

więc

2

12

1

11

2

2

1

1

2

1

1

L

L

)

w

w

(

)

w

(

i

i

i

i

+

=

Λ

+

Λ

=

Ψ

, (D.21)

2

22

1

21

2

2

2

1

2

1

2

L

L

)

w

(

)

w

w

(

i

i

i

i

+

=

Λ

+

Λ

=

Ψ

(D.22)

Z powyższej zależności widać, że dla liniowego obwodu magnetycznego strumienie sprzężone są

liniową kombinacją prądów, a współczynniki

11

L

i

22

L

noszą nazwę indukcyjności własnych,

natomiast

21

12

L

L

=

nazywa się indukcyjnościami wzajemnymi cewek.

D.5. Obwody magnetyczne z magnesem trwałym

Magnesy trwałe charakteryzuje się za pomocą krzywej odmagnesowania, czyli części pętli

histerezy z II ćwiartki wykresu

)

(

H

f

B

=

. Dla magnesów z ziem rzadkich typu NdFeB oraz SmCo

można przyjmować liniową aproksymację ch-ki odmagnesowania (Rys. D.8.), gdzie

r

B

jest indukcją

remanentu (rzędu 1.0÷1,3[T]), natomiast

c

H

jest natężeniem koercji (rzędu 800÷1000[kA/m]).

m

H

m

B

r

B

c

H

Rys. D.8. Charakterystyka demagnesowania magnesów z ziem rzadkich

Do analizy przypadku obwodu magnetycznego z magnesem trwałym rozważymy przykład rdzenia

stalowego, na którym nawinięto cewkę (dla rdzenia zaniedbamy spadki napięć magnetycznych) w
obwodzie, którego znajduje się magnes trwały o przekroju

S

oraz szczelina powietrzna

δ

.

i

Φ

Fe

l

δ

l

S

∞

→

µ

Fe

r

m

l

w

Rys. D.9. Obwód magnetyczny z magnesem trwałym

Zapisując prawo przepływu dla analizowanego obwodu magnetycznego z Rys. D.9. otrzymujemy

Θ

=

⋅

+

⋅

+

⋅

δ

δ

l

l

l

H

H

H

m

m

Fe

Fe

(D.23)

gdzie

m

H - natężenie pola magnetycznego w magnesie [A/m]

m

l

- długość linii sił pola magnetycznego w magnesie [m]

Ponieważ zakładaliśmy, że

∞

→

µ

Fe

więc zależność (D.23) upraszcza się do postaci

Θ

=

⋅

+

⋅

δ

δ

l

l

H

H

m

m

(D.23)

Charakterystykę odmagnesowania z Rys. D.8. można aproksymować następującą zależnością

m

rm

r

m

H

B

µ

µ

+

=

0

B

lub

m

r

m

H

B

)

1

(

B

0

χ

+

µ

+

=

(D.24)

gdzie

rm

µ

- przenikalność magnetyczna względna magnesu (dla magnesów z ziem rzadkich wynosi ona

1.02 ÷ 1.1 przez co objętość magnesu może być z pewnym przybliżeniem traktowana jak
powietrze)

χ

- podatność magnetyczna

Po przekształceniach zależności

)

(

H

f

B

=

dla szczeliny i magnesu otrzymuje się wyrażenia

opisujące natężenia pola magnetycznego

0

µ

=

δ

δ

B

H

(D.25)

rm

r

m

m

B

H

µ

µ

−

=

0

B

(D.26)

Ponieważ obwód magnetyczny (Rys. D.9) jest nierozgałęziony, więc

Φ

=

Φ

=

Φ

δ

m

. Ze względu

na jednakowy przekrój dla szczeliny i magnesu również indukcje w szczelinie i magnesie są sobie
równe (

B

B

B

m

=

=

δ

). Można, zatem prawo przepływu (D.23) dla tego obwodu magnetycznego,

zapisać w następującej formie

Θ

=

µ

+

µ

µ

−

δ

l

l

0

0

B

B

B

m

rm

r

(D.27)

Wprowadzając oznaczenie

rm

m

m

µ

=

l

l

'

można zapisać zależność na indukcję w szczelinie i magnesie

następująco

δ

δ

+

+

+

µ

Θ

=

l

l

l

B

l

l

'

'

'

0

m

m

r

m

B

(D.28)

Po wprowadzeniu zależności na strumień

S

⋅

=

Φ

B

do (D.28) i wykonaniu formalnych

przekształceń matematycznych otrzymamy prawo Ohma dla obwodu magnetycznego, w którym
umieszczony jest magnes trwały

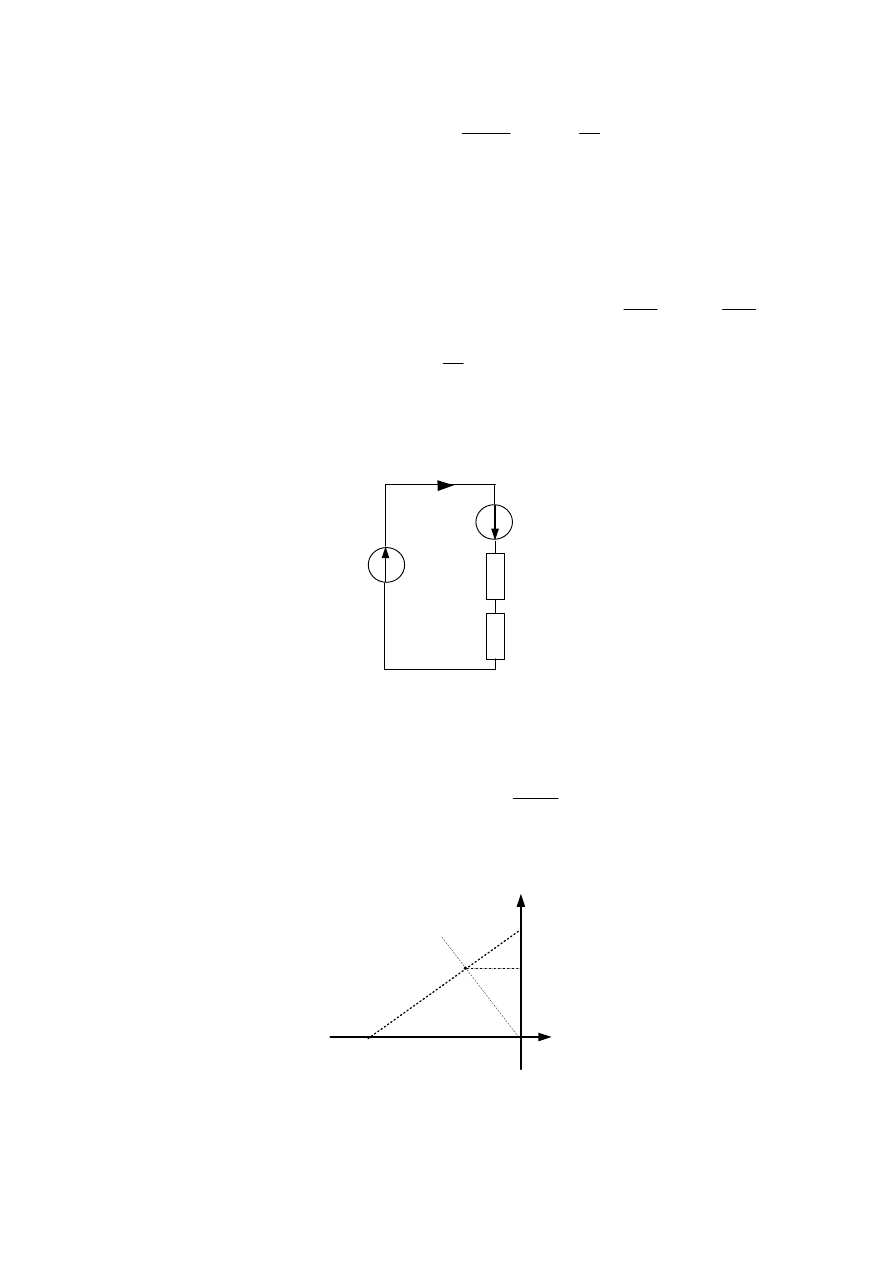
0

'

0

'

l

B

S

l

l

µ

+

Θ

=

µ

+

Φ

δ

m

r

m

(D.29)

co można również przedstawić następująco

m

F

R

+

Θ

=

Φ

µ

(D.30)

gdzie

µ

R - zastępcza reluktancja obwodu magnetycznego (

m

µ

µδ

µ

+

=

R

R

R

;

S

l

R

0

µ

=

δ

µδ

;

S

l

R

0

'

µ

=

µ

m

m

)

m

F

- siła magnetomotoryczna magnesu (

0

'

l

B

F

µ

=

m

r

m

)

Zastępczy schemat obwodu magnetycznego z magnesem trwałym z Rys. D.9. wygląda, więc

następująco

i

w

=

Θ

µδ

R

Φ

m

F

m

µ

R

Rys. D.10. Schemat zastępczy obwodu magnetyczny z magnesem trwałym

W stanie bezprądowym indukcja

0

B

=

B

i przedstawia się następująco

δ

+

=

l

l

l

B

B

'

'

0

m

m

r

(D.31)

Z zależności (D.31) wynika tzw. punkt pracy magnesu trwałego

m

H

m

B

r

B

c

H

0

B

Rys. D.11. Położenie punktu pracy magnesu trwałego

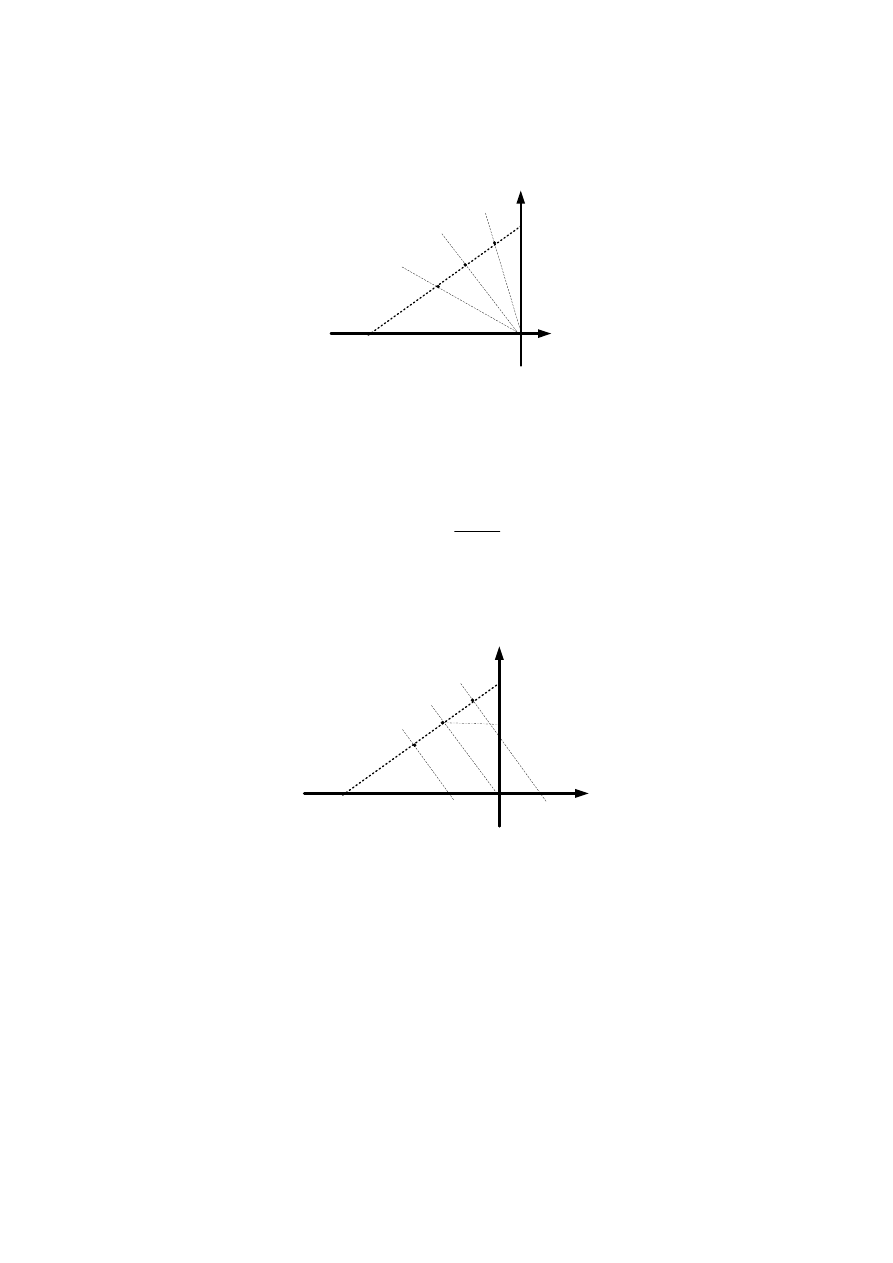
Dla zmieniającej się szczeliny punkt pracy

0

B

przesuwa się w zależności od wielkości szczeliny

δ

l

zgodnie z poniższym rysunkiem

m

H

m

B

r

B

c

H

0

l

δ

=

δ

0

l

δ

>

δ

0

l

δ

<

δ

Rys. D.12. Przesunięcie punktu pracy magnesu trwałego wskutek zmian szczeliny powietrznej

Poddając magnes trwały zewnętrznemu oddziaływaniu pola magnetycznego wytworzonego przez

cewkę z prądem możemy, również doprowadzić do zmiany położenia punktu pracy wskutek
domagnesowania (

0

>

i

) lub odmagnesowania (

0

<

i

) magnesu.

Zgodnie z wcześniej wyprowadzoną zależnością (D.28)

0

0

'

0

B

k

B

l

l

w

+

=

+

+

µ

=

δ

i

i

B

m

(D.32)

widać, że punkt pracy będzie się również przesuwał pod wpływem zewnętrznego pola magnetycznego
wzbudzanego przez prąd cewki.

m

H

m

B

r

B

c

H

0

=

i

0

B

0

>

i

0

<

i

Rys. D.13. Przesunięcie punktu pracy magnesu trwałego wskutek oddziaływania cewki z prądem

Z Rys. D.13. można zauważyć, że pod wpływem oddziaływania demagnesujacego zewnętrznego

pola magnetycznego wytworzonego przez cewkę z prądem może dojść nawet do całkowitego
odmagnesowania magnesu, co będzie skutkować jego zniszczeniem.

D.6. Energia pola magnetycznego

Poprzednie rozważania, w których określono wartości indukcji oraz natężenia pola magnetycznego

dla elementów obwodu magnetycznego były zależnościami uwzględniającymi jednowymiarowy (1-D)
rozkład pola magnetycznego, co dla prostych obwodów magnetycznych jest wystarczającym
przybliżeniem z technicznego punktu widzenia. Na podstawie znajomości rozkładu indukcji oraz
natężenia pola magnetycznego, można wyznaczyć gęstość energii pola magnetycznego (

g

w ) zawartej

w jednostce objętości dowolnej przestrzeni g

∫

=

B

g

B

H

w

0

d

(D.33)

Energia pola magnetycznego będzie, więc zależna od objętości

g

V dla przestrzeni g i w ogólnym

przypadku wyrażać się będzie zależnością

V

B

H

V

w

E

g

g

V

B

V

g

d

)

d

(

d

0

∫ ∫

∫

=

=

(D.34)

Na podobnej zasadzie można zdefiniować gęstość objętościową ko-energii, jako

∫

=

H

g

H

B

w

0

0

d

(D.35)

oraz ko-energię

V

H

B

V

w

E

g

g

V

H

V

g

d

)

d

(

d

0

0

0

∫ ∫

∫

=

=

(D.36)

O ile definicja gęstości energii jest zawsze poprawna o tyle definicja gęstości objętościowej ko-

energii jest słuszna jedynie dla elementów obwodu magnetycznego posiadających swe charakterystyki
w I ćwiartce zależności

)

(

H

f

B

=

. Charakterystyki magnesów trwałych są opisywane funkcjami z II

ćwiartki zależności

)

(

m

m

H

f

B

=

, dlatego wiec należy dla magnesów trwałych zmodyfikować

definicję gęstości objętościowej ko-energii do postaci

∫

=

m

c

H

m

m

m

H

B

w

H

0

d

(D.37)

Ko-energia pola magnetycznego zawarta w magnesie o objętości

m

V wyrażać się będzie

następującą zależnością

V

H

B

V

w

E

m

m

c

m

V

H

m

m

V

m

d

)

d

(

d

H

0

0

∫ ∫

∫

=

=

(D.38)

W celu przeprowadzenia dalszych analiz zależności energetycznych dla pola magnetycznego

podeprzemy się obwodem magnetycznym z Rys. D.9. Zgodnie z założeniami do tego przykładu w
przestrzeni rdzenia stalowego nie ma spadków napięć magnetycznych, więc cała energia pola
magnetycznego koncentrować się będzie w przestrzeni magnesu trwałego oraz szczeliny powietrznej.

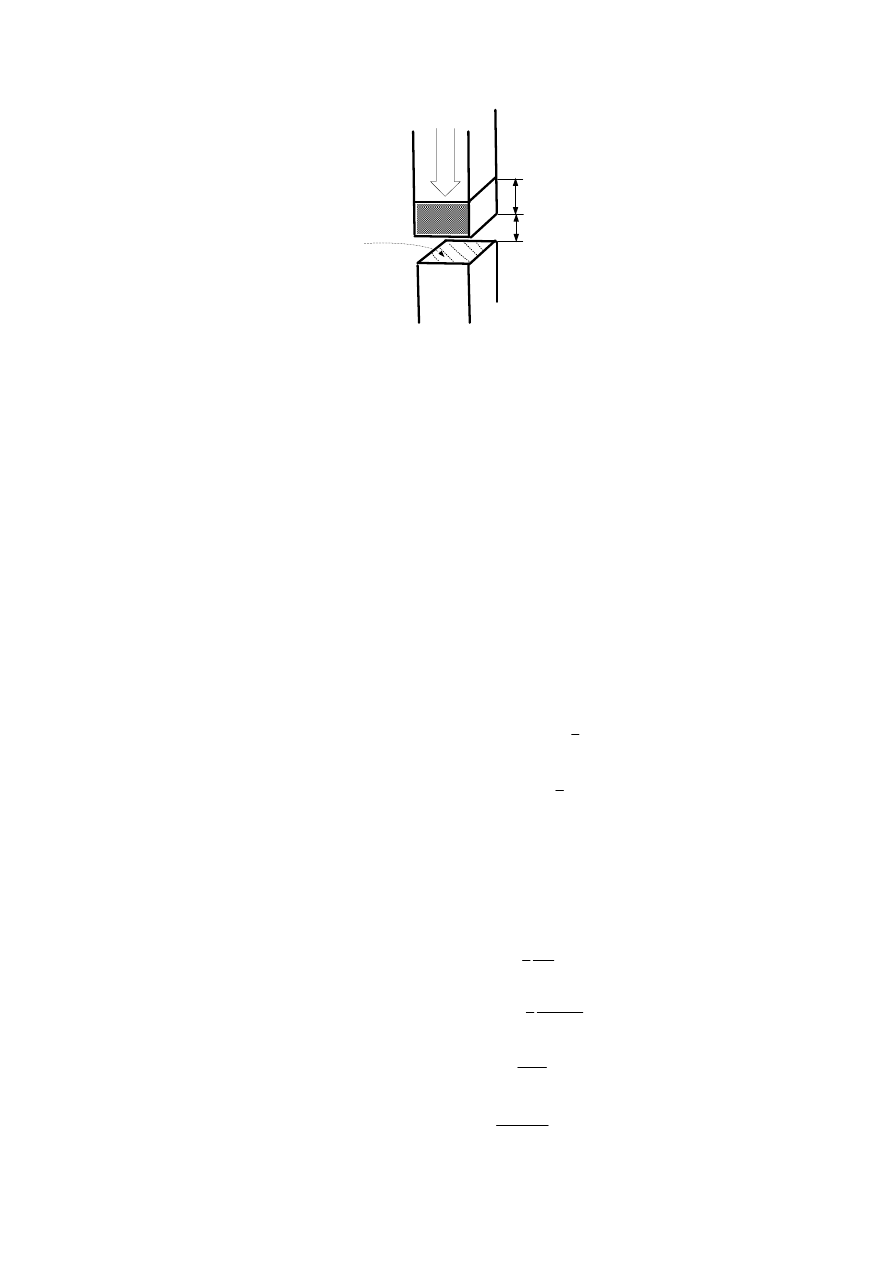
Φ

δ

l

S

Fe

m

l

N

S

Fe

Rys. D.14. Przestrzenie szczeliny powietrznej oraz magnesu trwałego

Ko-energię dla tego przypadku można, zatem przedstawić, jako sumę ko-energii szczeliny i

magnesu

m

E

E

E

0

0

0

+

=

δ

(D.39)

gdzie

∫

δ

δ

δ

=

V

dV

w

E

0

0

(D.40)

∫

=

m

V

m

m

dV

w

E

0

0

(D.41)

Ponieważ indukcje w szczelinie i magnesie można zapisać zgodnie z wcześniejszymi założeniami

następująco

δ

δ

µ

=

H

B

0

;

m

rm

r

m

H

B

µ

µ

+

=

0

B

, więc gęstości ko-energii dla rozważanego przypadku

przybierają formę

2

0

2

1

0

0

d

δ

δ

δ

δ

µ

=

=

∫

δ

H

H

B

w

H

(D.42)

)

H

(

)

H

(

d

2

2

0

2

1

H

0

c

m

rm

c

m

r

H

m

m

m

H

H

B

H

B

w

m

c

−

µ

µ

+

−

=

=

∫

(D.43)

Zależności (D.42) oraz (D.43) opisujące gęstości ko-energii w szczelinie i magnesie można

również wyrazić, jako funkcje indukcji. Po formalnych przekształceniach matematycznych otrzymuje
się następujące ogólne formuły przedstawiające gęstości objętościowe ko-energii oraz funkcje ko-
energii dla szczeliny i magnesu

0

2

2

1

0

µ

=

δ

δ

B

w

(D.44)

rm

m

m

B

w

µ

µ

=

0

2

2

1

0

(D.45)

∫

δ

δ

δ

µ

=

V

V

B

E

d

2

1

2

0

0

(D.46)

∫

µ

µ

=

m

V

m

rm

m

V

B

E

d

2

1

2

0

0

(D.47)

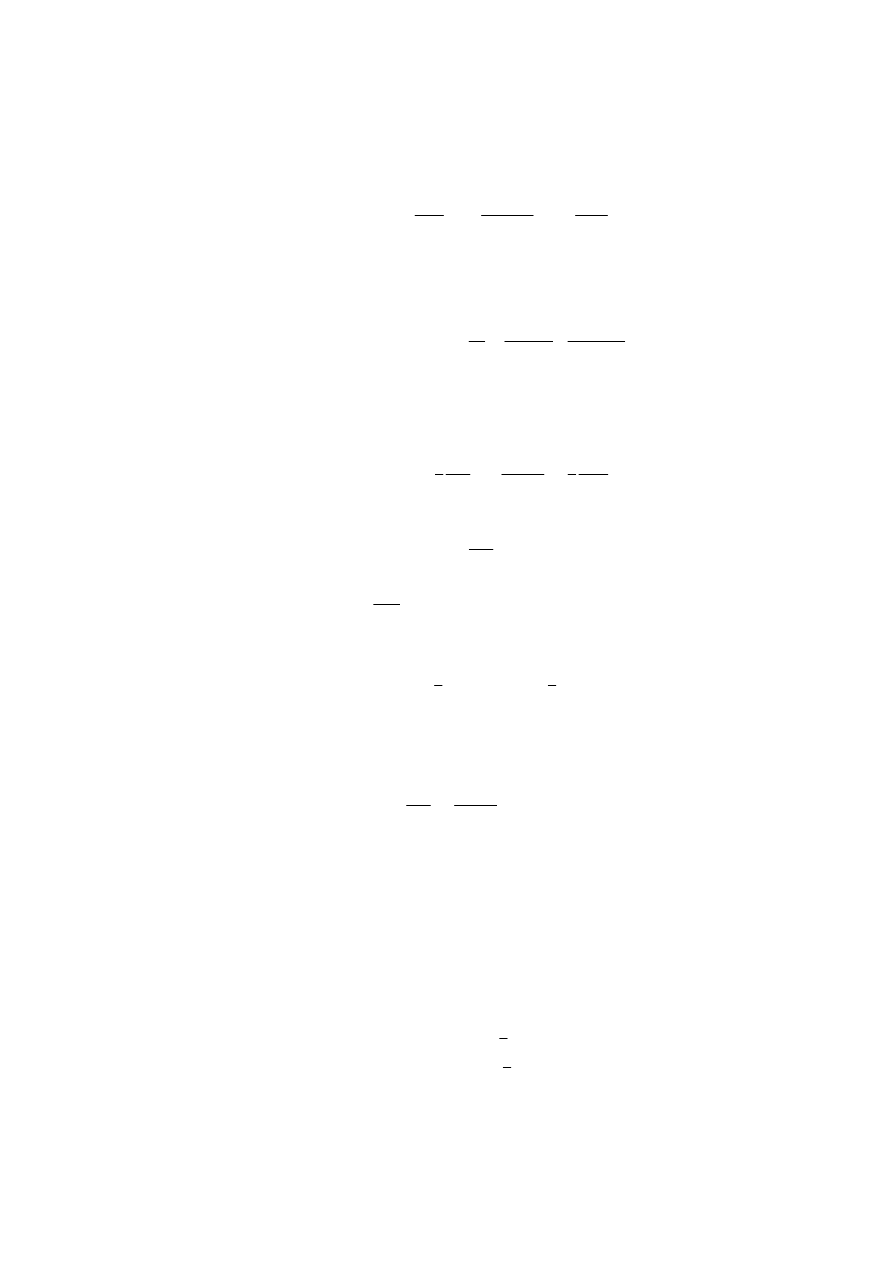
Dla rozważanego przykładu z Rys. D.9., gdzie indukcje w szczelinie i magnesie są sobie równe

(

B

B

B

m

=

=

δ

) zależność (D.39) opisująca ko-energie upraszcza się do następującej formuły

)

l

l

(

2

S

V

2

V

2

'

0

2

0

2

0

2

0

m

m

rm

B

B

B

E

+

µ

=

µ

µ

+

µ

=

δ

δ

(D.48)

Wyznaczając strumień zgodnie z formułą (D.30) obowiązującą dla schematu zastępczego z Rys.

D.10., można indukcje dla tego przypadku przedstawić następująco

S

R

F

w

S

R

F

µ

µ

+

=

+

Θ

=

Φ

=

m

m

i

S

B

(D.49)

Po podstawieniu zależności (D.49) do wzoru (D.48) i wykonaniu formalnych przekształceń,

otrzymujemy zależność na ko-energię w następującej formie

µ

µ

µ

+

+

=

R

F

R

F

w

R

w

2

2

1

2

2

2

1

0

m

m

i

i

E

(D.50)

Definiując indukcyjność dla cewki, jako

µ

=

R

w

L

2

oraz strumień w stanie bezprądowym

(pochodzący od magnesu), jako

µ

=

Φ

R

F

0

m

, ko-energię opisaną zależnością (D.50) można zapisać

również następująco

2
0

2

1

0

2

2

1

0

R

w

L

Φ

+

Φ

+

=

µ

i

i

E

(D.51)

Na podstawie zależności na strumień z formuły (D.30) można zdefiniować tzw. charakterystykę

cewki, czyli zależność strumienia skojarzonego z cewką (

Ψ

) od prądu ( i )

0

0

2

L

w

L

R

F

w

R

w

)

(

Ψ

+

=

Φ

+

=

+

=

Φ

=

Ψ

µ

µ

i

i

i

w

i

m

(D.52)

gdzie

0

Ψ

jest strumieniem skojarzonym z cewka w stanie bezprądowym

Analizując zależność (D.51) zauważamy, że ko-energia układu złożonego z cewki oraz magnesu

trwałego posiada dwa człony, jeden zależny, a drugi niezależny od prądu odpowiadający ko-energii
zgromadzonej w układzie w stanie bezprądowym

m

E

i

E

E

0

0

0

)

(

+

=

Θ

(D.53)

gdzie

i

i

E

0

2

2

1

0

L

Ψ

+

=

Θ

(D.54)

2
0

2

1

0

R

Φ

=

µ

m

E

(D.55)

Zależność (D.54) może zostać również uogólniona do postaci jak jest używana do opisu

energetycznego cewek nie zawierających w swym obwodzie magnetycznym magnesów trwałych

∫

Ψ

=

Θ

i

di

i

E

0

0

)

(

(D.56)

przy czym

)

(i

Ψ

określa się używając formuły (D.52).

Przedstawione wyprowadzenie może zostać, więc rozszerzone i wykorzystane do opisu

energetycznego układów złożonych z większej liczby cewek sprzężonych, zawierających w swym
obwodzie magnetycznym magnesy trwałe.

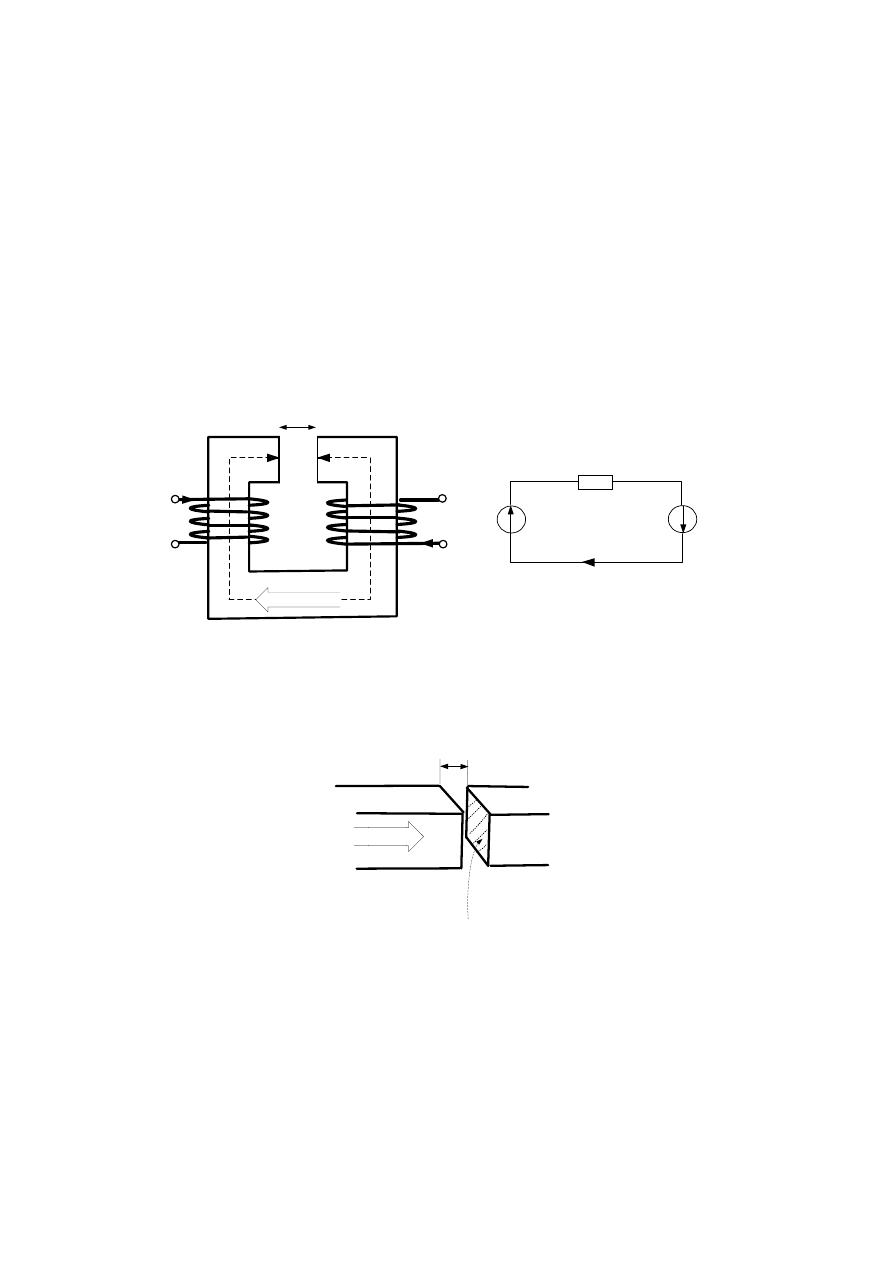
D.7. Zależności energetyczne dla układu cewek liniowych

W celu przeprowadzenia analiz zależności energetycznych dla pola magnetycznego wzbudzanego

przez układ cewek podeprzemy się obwodem magnetycznym z dwoma cewkami z Rys. D.15.

1

1

1

w i

=

Θ

µδ

R

Φ

2

2

2

w i

=

Θ

1

i

1

w

Fe

l

δ

l

S

∞

→

µ

Fe

r

2

i

S

2

w

Φ

⇔

Rys. D.15. Układ dwóch cewek sprzężonych i odpowiadający im schemat zastępczy

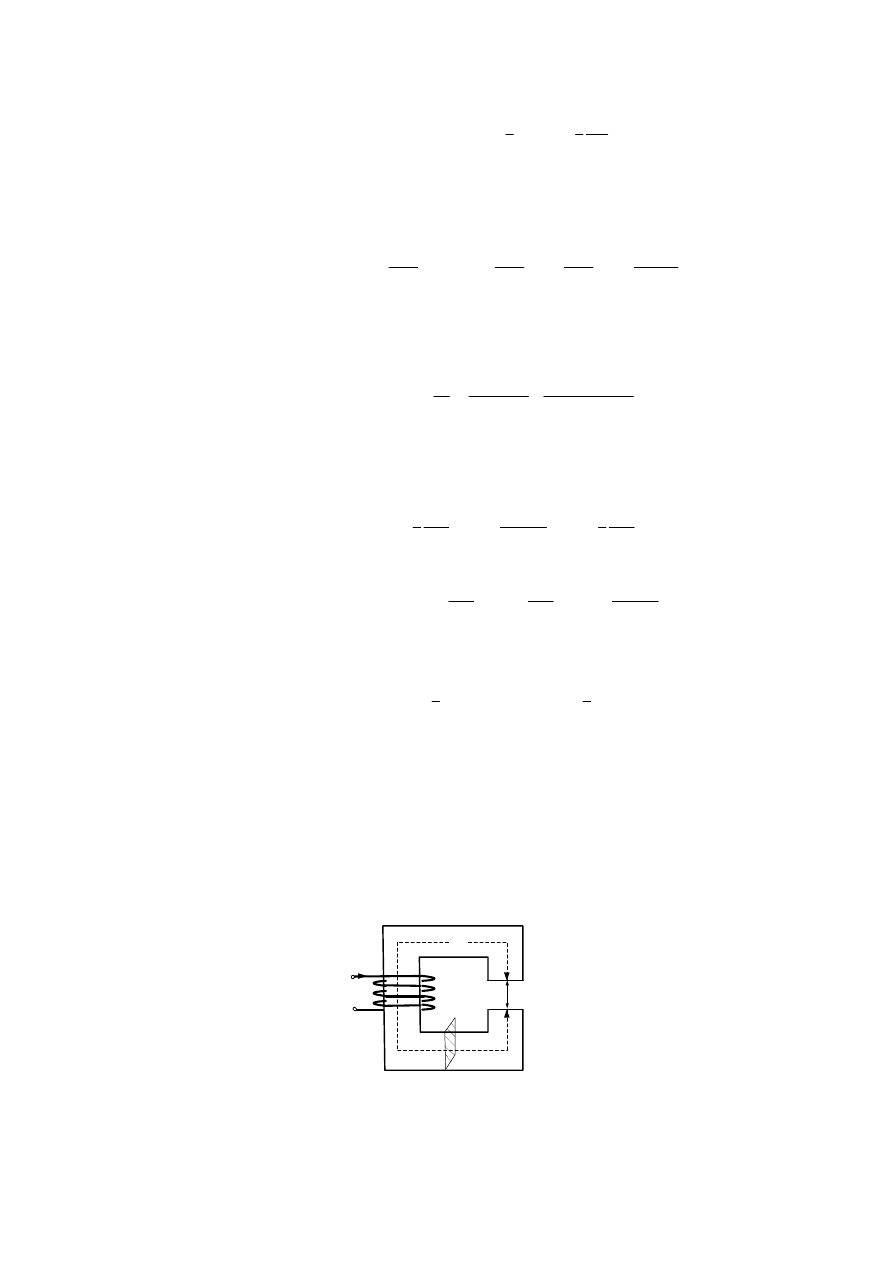
Zakładając, że w przestrzeni rdzenia stalowego nie ma spadków napięć magnetycznych

(

∞

→

µ

Fe

r

), więc cała energia pola magnetycznego koncentrować się będzie w przestrzeni szczeliny

powietrznej.

Φ

δ

l

S

Fe

Fe

Rys. D.16. Przestrzeń szczeliny powietrznej

Ko-energię dla tego przypadku można, zatem przedstawić, jako

∫

δ

δ

δ

=

=

V

V

w

E

E

d

0

0

0

(D.57)

Ponieważ indukcja w szczelinie

B

H

B

=

µ

=

δ

δ

0

, więc gęstość ko-energii w szczelinie będzie

równa również gęstości energii i przybiera formę

0

2

2

1

2

0

2

1

0

0

µ

=

µ

=

=

δ

δ

δ

δ

∫

δ

B

H

dH

B

w

H

(D.58)

Zależności przedstawiająca funkcje ko-energii w tym przypadku będzie również tożsama z funkcją

energii

µδ

δ

δ

δ

=

µ

=

µ

=

µ

=

=

∫

δ

R

2

S

S

l

2

V

2

d

2

1

2

2

0

2

0

2

2

0

0

0

B

B

B

V

B

E

E

V

(D.59)

Wyznaczając strumień zgodnie z formułą (D.9), można indukcje dla tego przypadku przedstawić

następująco

S

R

w

w

S

R

2

2

1

1

2

1

µδ

µδ

+

=

Θ

+

Θ

=

Φ

=

i

i

S

B

(D.60)

Po podstawieniu zależności (D.60) do wzoru (D.59) i wykonaniu formalnych przekształceń,

otrzymujemy zależność na ko-energię

2

2

2
2

2

1

1

1

2

1

2

1

2

1

2

1

0

)

(

R

w

)

(

R

w

w

)

(

R

w

i

i

i

i

E

µ

µ

µ

+

+

=

(D.61)

Definiując indukcyjność dla cewek, jako

µ

=

R

w

L

2

1

11

,

µ

=

R

w

L

2
2

22

,

µ

=

R

w

w

L

2

1

12

można ko-energię

opisaną zależnością (D.61), zapisać zgodnie z dobrze znaną klasyczną postacią energii dla dwóch
cewek linowych w następującej formie

2

2

22

2

1

1

1

12

2

1

11

2

1

0

)

(

L

)

(

L

)

(

L

i

i

i

i

E

+

+

=

(D.62)

Zadania

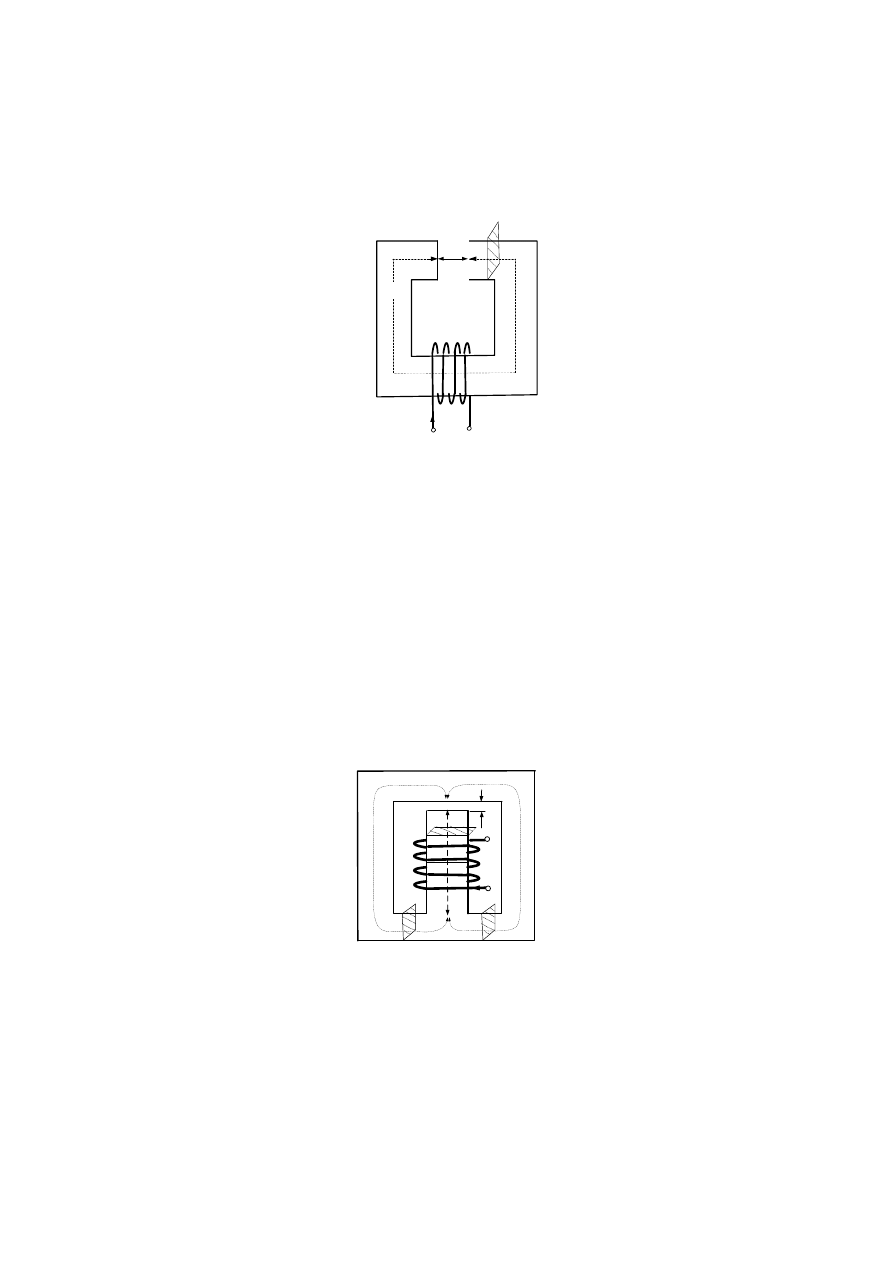
D.1
Podać wzór na indukcyjność cewki nawiniętej (zgodnie z poniższym rysunkiem) na stalowym rdzeniu
o przekroju S. Jak zmieni się ta indukcyjność, jeżeli zaniedbujemy spadki napięć magnetycznych w
żelazie (

∞

→

µ

Fe

r

)? Jak wpływa powiększenie szczeliny powietrznej

δ

l

na wartość indukcyjności?

Zapisać zależność na ko-energie zgromadzona w układzie.

i

Fe

l

S

Fe

µ

δ

l

w

D.2
Cewka o

w

=500 zwojach przewodzi prąd

=

=

I

i

2A. Przekrój rdzenia wynosi S=0.8 10

-4

m

2

a

średnia długość linii sił pola magnetycznego w stalowym rdzeniu o przenikalności względnej

800

=

µ

Fe

r

wynosi

Fe

l

=0.15 m. Wyznaczyć wartość indukcji w szczelinie powietrznej o długości

δ

l

=0.5 mm.

i

Fe

l

δ

l

S

Fe

µ

w

D.3
Dla cewki o

=

w

800 zwojach nawiniętej na stalowym rdzeniu o

Fe

l

=0.3 m i

1000

=

µ

Fe

r

(przedstawionej na rysunku do zad. D.2), wyznaczyć wartość prądu potrzebnego do wytworzenia
indukcji w szczelinie powietrznej na poziomie 1 T, gdy efektywny przekrój szczeliny powietrznej

wynosi S=2500 mm

2

, a jej długość

δ

l

=2 mm. Jak zmieniłyby się ten prąd, gdyby założyć, że

∞

→

µ

Fe

r

?

D.4
Obwód magnetyczny z poniższego rysunku ma na środkowej części o przekroju

=

1

S

800 mm

2

nawiniętą cewkę o

w

=600 zwojach. Zakładając, że przekroje pozostałych gałęzi obwodu

magnetycznego maja przekroje

=

2

S

500 mm

2

, a szczelina powietrzna wynosi

δ

l

=1 mm, obliczyć

prąd wymagany do wzbudzenia strumienia magnetycznego w szczelinie powietrznej o wartości

Φ

=1

Wb. Założyć

600

=

µ

Fe

r

. Sprawdzić, jaki musiałby być ten prąd gdyby założyć, że

∞

→

µ

Fe

r

.

Fe

r

µ

i

w

1

l

2

l

1

S

2

S

2

S

2

l

δ

l

D.5
Dla cewki nawiniętej (jak na rysunku) na niemagnetycznym karkasie o wymiarach: d= 200 mm,
D=300 mm, h= 30 mm i 200 zwojach, obliczyć natężenie pola wewnątrz cewki, wartość indukcji oraz
strumień skojarzony z cewką, jeżeli prąd cewki wynosi 5 A. Jak zmienią się te wielkości, jeżeli karkas
zastąpimy rdzeniem stalowym o przenikalności względnej

400

=

µ

Fe

r

.

D.6
Dla obwodu magnetycznego, w którym umieszczono magnes trwały typu NdFeB o parametrach
B

r

=1.2 T; H

c

=1000 kA/m, dobrać długości magnesu l

m

oraz szczeliny

δ

l

(przy założeniu

jednorodnego przekroju dla szczeliny i magnesu S

δ

=S

m

=S=2000 mm

2

) takie, aby indukcja w

szczelinie wynosiła 0.6 T. Podać wartość oraz kierunek przepływu cewki taki by doprowadzić do
całkowitego odmagnesowania magnesu trwałego (

∞

→

µ

Fe

r

). Wyznaczyć ko-energie zgromadzoną w

układzie oraz strumień skojarzony z cewką dla stanu bezprądowego.

i

Φ

δ

l

S

∞

→

µ

Fe

r

m

l

w

D.7
Wyznaczyć indukcyjności własne i wzajemne cewek nawiniętych (zgodnie z poniższym rysunkiem)
na stalowym rdzeniu o jednorodnym przekroju S w którym występują szczeliny powietrzne o
wymiarach

δ

l

(zaniedbać spadki napięć magnetycznych w żelazie

∞

→

µ

Fe

r

)

1

i

∞

→

µ

Fe

2

i

1

w

S

2

w

δ

l

S

S

∞

→

µ

Fe

δ

l

δ

l

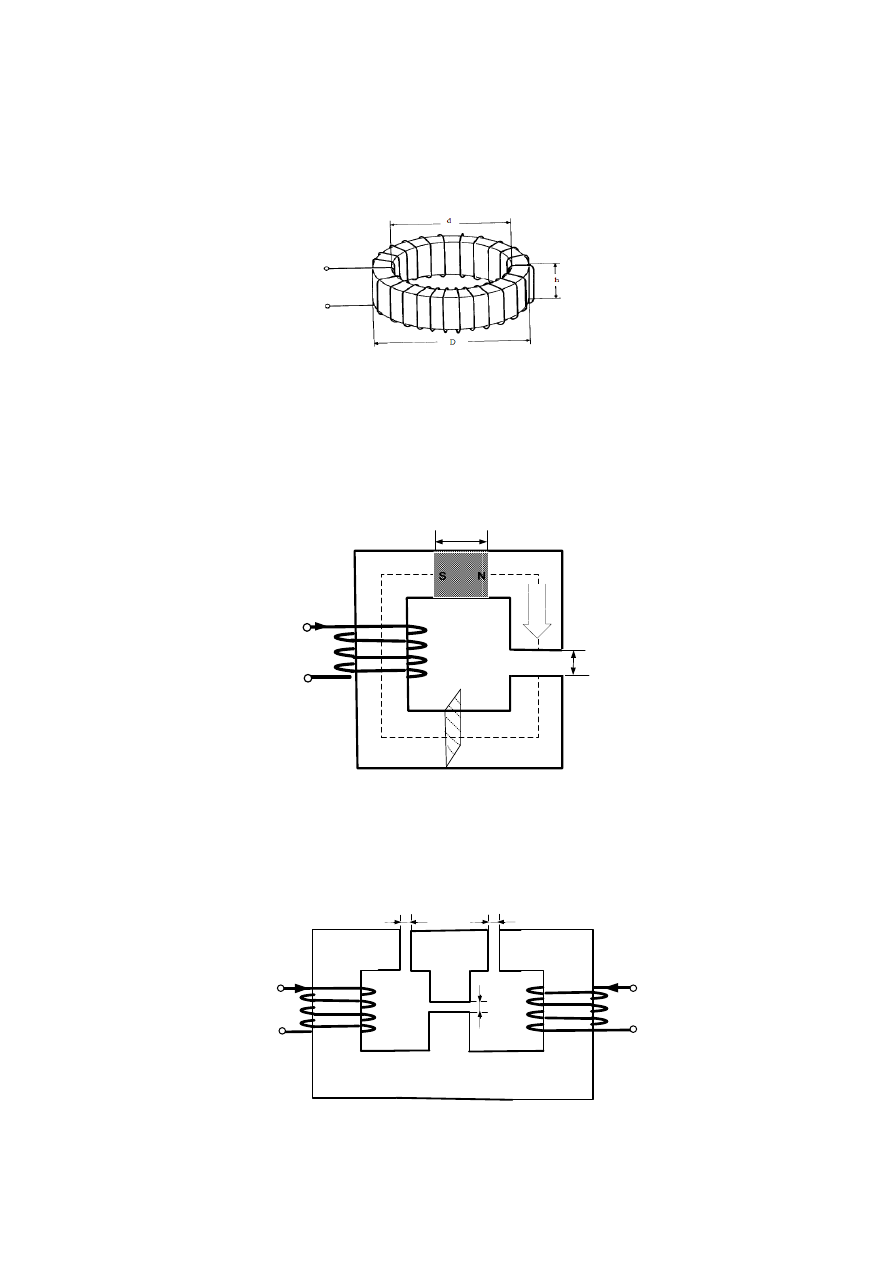
D.8
Wyznaczyć indukcyjności własne i wzajemne cewek nawiniętych na żelaznym rdzeniu (zgodnie z
poniższym rysunkiem) o nieskończenie dużej przenikalności magnetycznej (

∞

→

µ

Fe

r

) w którym

znajdują się trzy szczeliny o przekrojach

3

2

1

S

,

S

,

S

oraz długościach

3

2

1

l

,

l

,

l

wypełnione materiałami

o różnych przenikalnościach magnetycznych

3

2

1

,

,

µ

µ

µ

.

1

i

∞

→

µ

Fe

r

∞

→

µ

Fe

r

2

i

1

w

2

w

1

µ

2

µ

3

µ

1

l

2

l

3

l

1

S

2

S

3

S

3

i

3

w

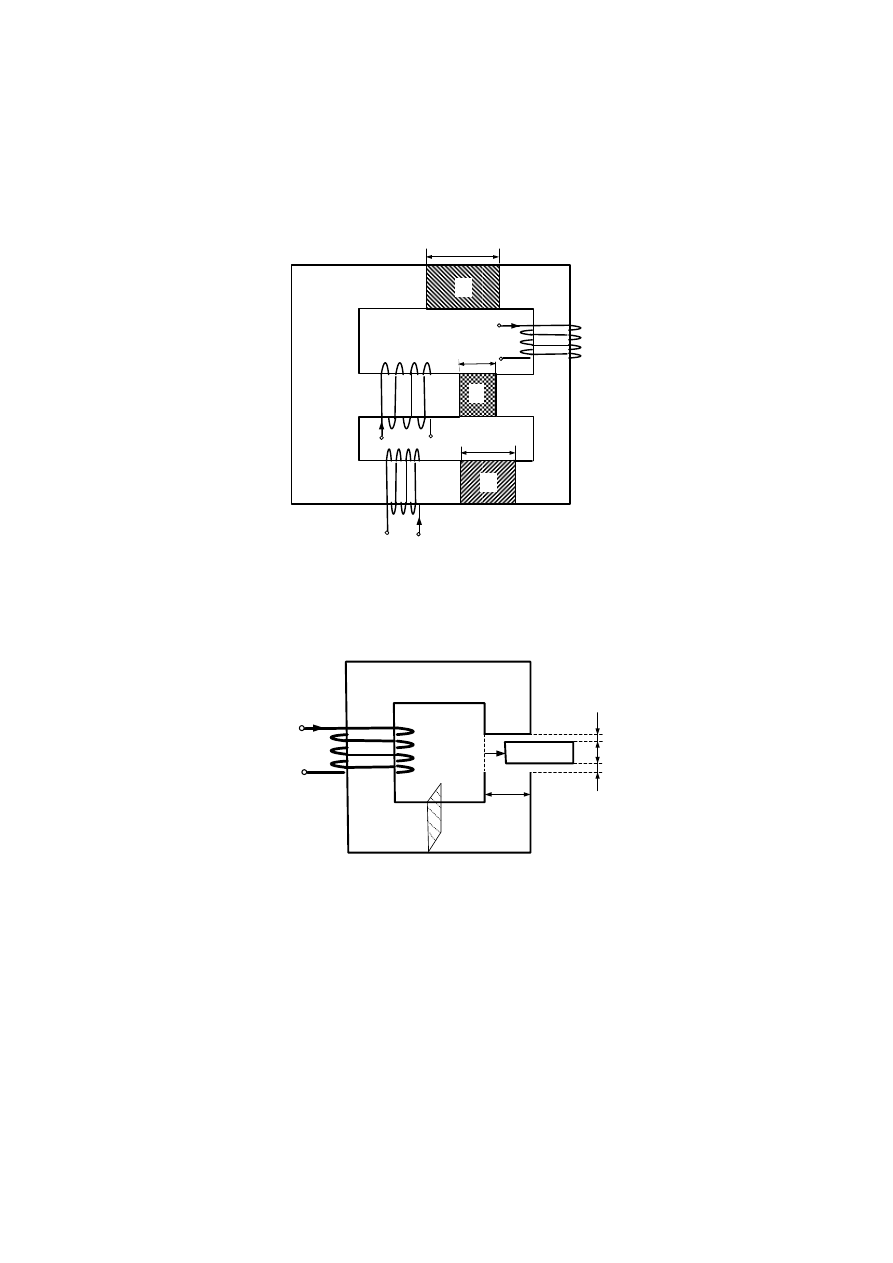
D.9
Wyznaczyć funkcję indukcyjność cewki od położenia

x ruchomego rdzenia, jeżeli cewka nawinięta

jest (zgodnie z poniższym rysunkiem) na stalowym rdzeniu o nieskończonej przewodności
magnetycznej (

∞

→

µ

Fe

r

).

i

δ

l

2

d

S

=

h

d

x

δ

l

0

µ

>>

µ

Fe

0

µ

>>

µ

Fe

w