3. Funkce
157
3.10. Goniometrické funkce
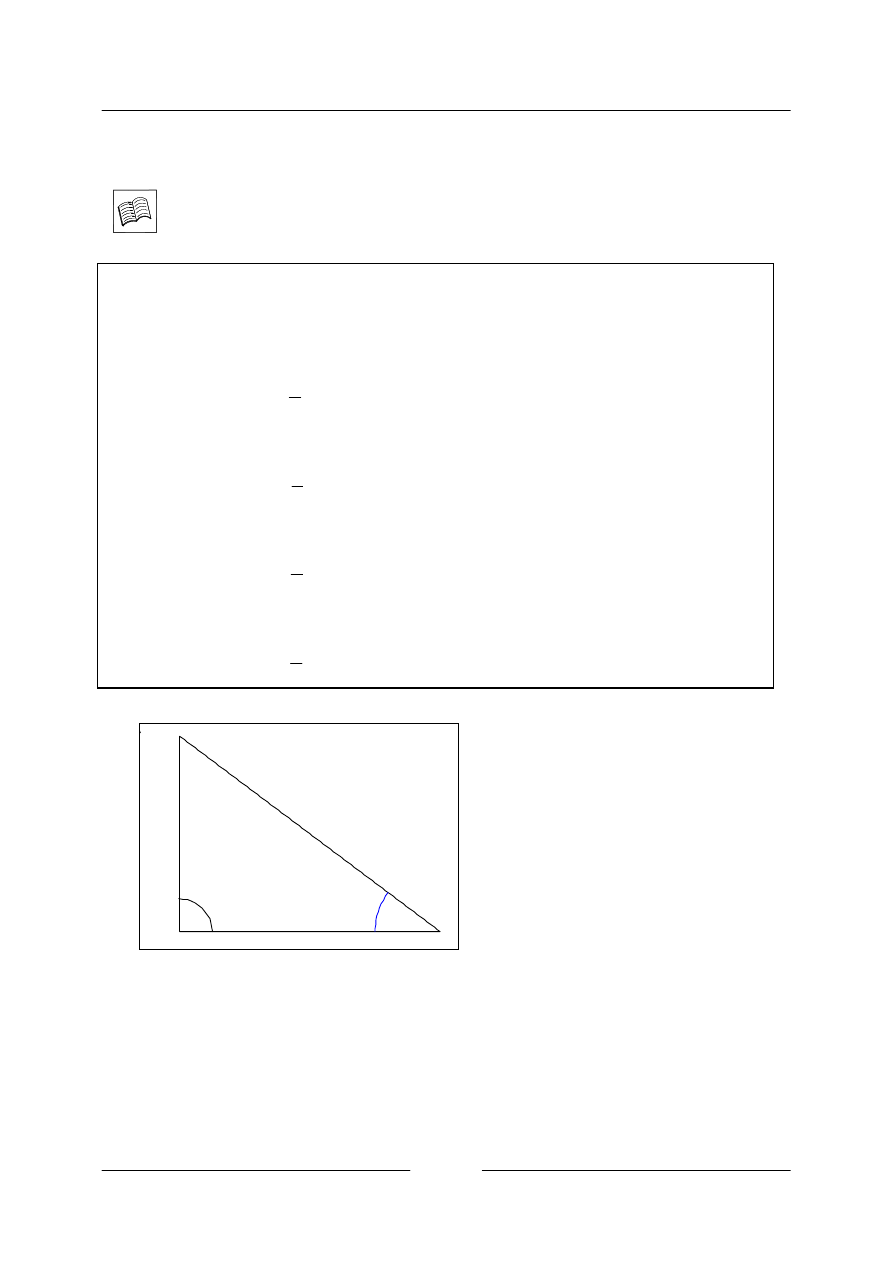
Goniometrické funkce ostrého úhlu definujeme pomocí pravoúhlého trojúhelníku. Mějme
pravoúhlý trojúhelník s odvěsnami b
a, a přeponou
c
. Pak definujeme:
Sinus
α je poměr délky odvěsny protilehlé k úhlu α a délky přepony pravoúhlého
trojúhelníku.
c
a
=
α
sin
.
Kosinus
α je poměr délky odvěsny přilehlé k úhlu α a délky přepony pravoúhlého
trojúhelníku.
c
b
=
α
cos
.
Tangens
α je poměr délek odvěsny protilehlé k úhlu α a odvěsny přilehlé k úhlu α
pravoúhlého trojúhelníku.
b
a
=
α
tan
.
Kotangens
α je poměr délek odvěsny přilehlé k úhlu α a odvěsny protilehlé k úhlu α
pravoúhlého trojúhelníku
a
b
=
α
cot
.
C
A
B
α
c
a
b
.
3. Funkce
158
Velikost úhlu – oblouková a stupňová míra
Uvažujme jednotkovou kružnici
k
se středem
S
, tj. kružnici o poloměru
1
. Délka této kružnice je
π
2
. Délka kružnicového oblouku, je-li velikost úhlu
°
1
, je
360
2
π
nebo
180
π
. Jestliže velikosti úhlů
zapisujeme ve stupních, říkáme, že používám stupňovou míru. Kromě jednotky
1
stupeň, ozn.
°
1
,
používáme i menší jednotky:
1
minuta, ozn.
'
1
, pro šedesátinu stupně a
1
vteřina, ozn.
''
1
, pro jednu
šedesátinu minuty.
Jeden radián je středový úhel, který přísluší na jednotkové kružnici oblouku o délce
1
. Radián je
jednotkový úhel v obloukové míře, ozn. rad.
Převodní vztah mezi stupni a radiány dostaneme z přímé úměrnosti
π
2
rad………………..
360
stupňů
x
rad………………...
α
stupňů
180
.
π
α
=
x
π
α
180
.
x
=
Funkce sinus, kosinus, tangens a kotangens
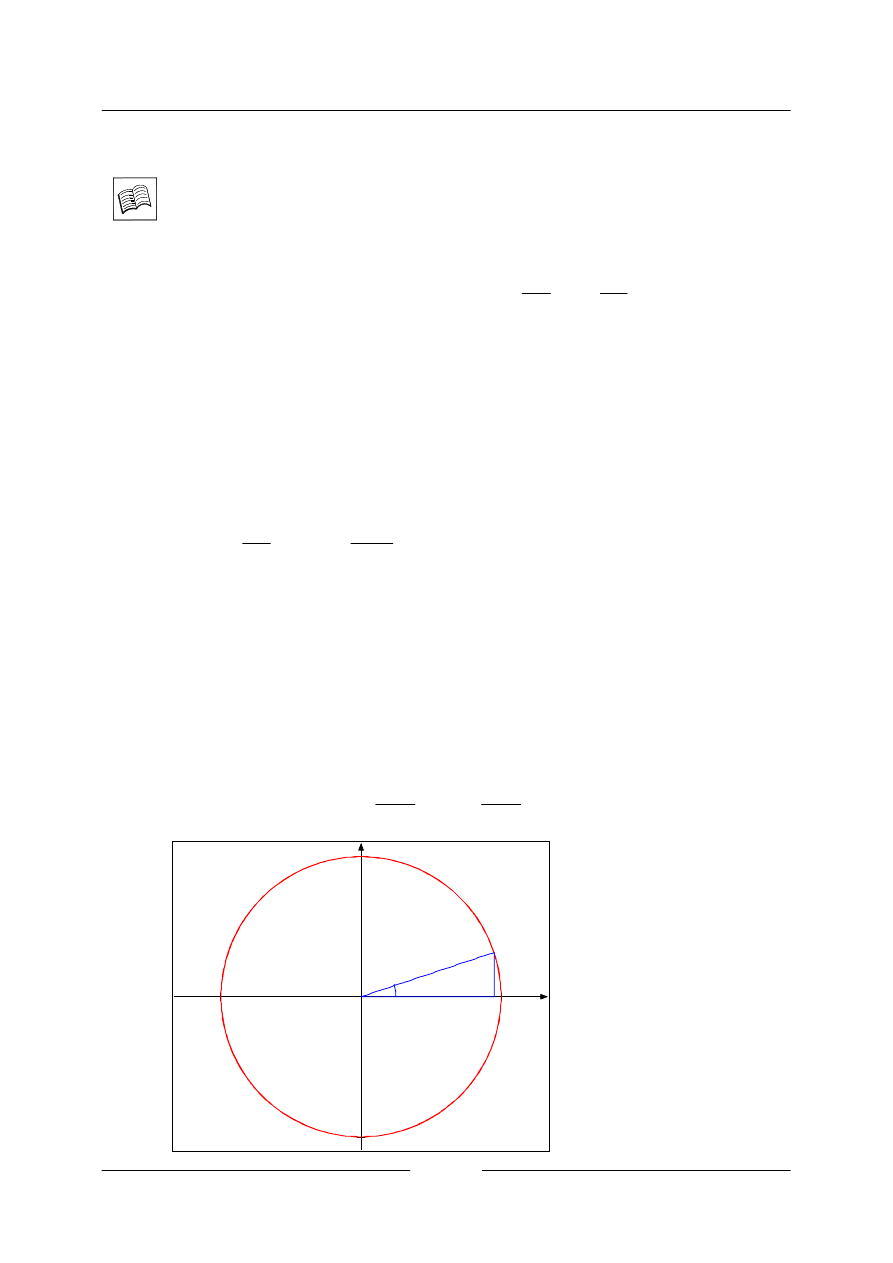
Goniometrické funkce obecného úhlu definujeme pomocí jednotkové kružnice. V kartézské soustavě
souřadnic sestrojíme kružnici se středem v počátku a o poloměru jedna. Každému reálnému číslu
α
můžeme přiřadit orientovaný úhel velikosti
α
( v obloukové míře), jehož počáteční rameno je kladná
osa
x
. Průsečík koncového ramene s kružnicí označme
[
]
M
M
y
x
M
,
. Funkce sinus, kosinus, tangens a
kotangens definujeme takto:
M
y
=
α
sin
M
x
=
α
cos
α
α
α
cos
sin
tan
=
α
α
α
sin
cos
cot
=
-1
1
-1
0
x
y
-1
1
-1
0
x
y
1
M[x
M
,y
M
]
x
M
y
M
α
3. Funkce
159
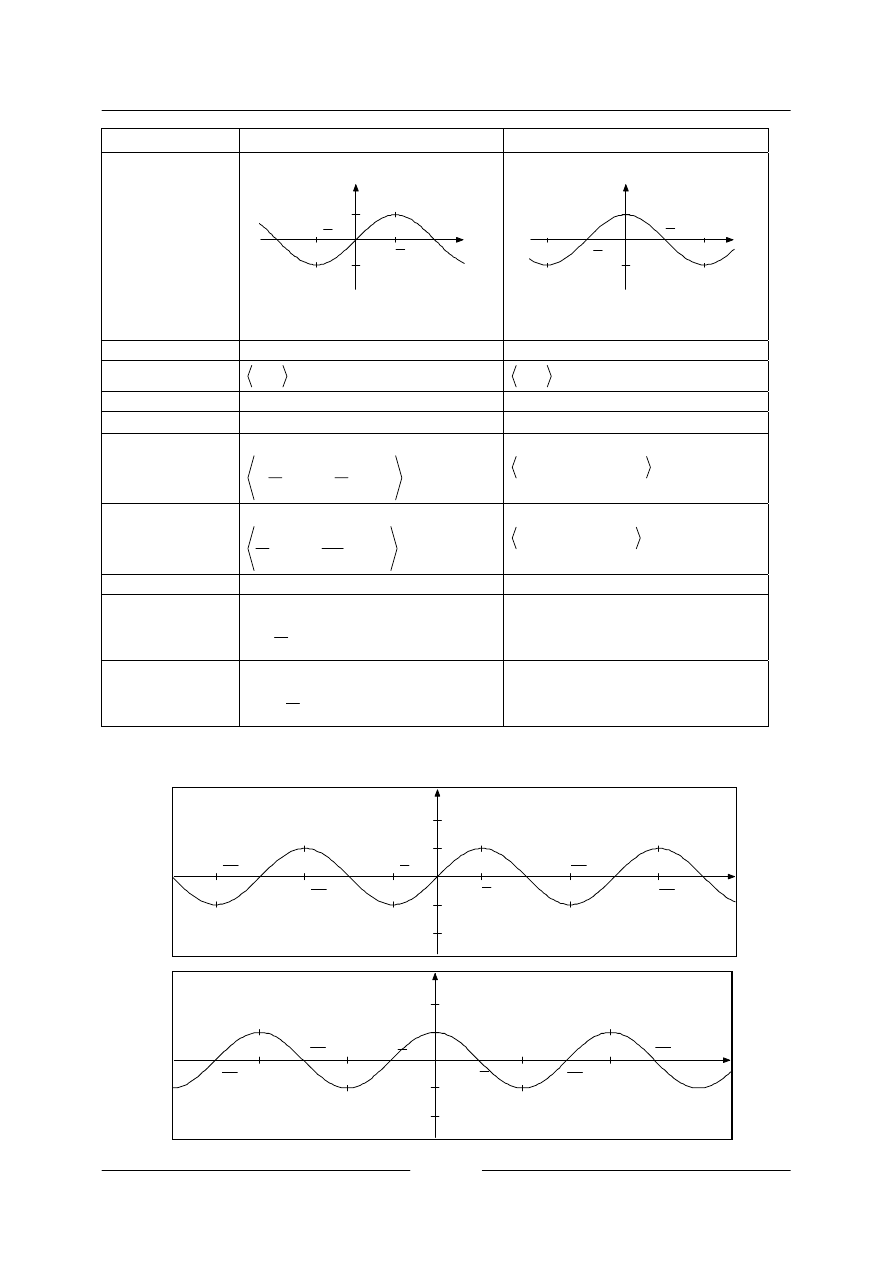
x
y
sin
=
x
y
cos
=
Definiční obor
R
R
Obor hodnot
1
,
1
−
1
,
1
−
Parita
lichá
sudá
Perioda
π
2
π
2
Rostoucí
V každém intervalu
π
π
π
π
k
k
2
2
,
2
2
+
+
−
V každém intervalu
π
π
π
π
k
k
2
2
,
2
+
+
Klesající
V každém intervalu
π
π
π
π
k
k
2
2
3
,
2
2
+
+
V každém intervalu
π
π
π
k
k
2
,
2
0
+
+
Omezená
Shora i zdola omezená
Shora i zdola omezená
Maximum
V každém bodě
π
π
k
x
2
2
+
=
V každém bodě
π
k
x
2
=
Minimum
V každém bodě
π
π
k
x
2
2
+
−
=
V každém bodě
π
π
k
x
2
+
=
Písmeno k v tabulce jako označuje libovolné celé číslo.
-1
1
0
x
y
-1
1
0
x
y
π
-π
π
2
- π
2
-1
1
0
x
y
-1
1
0
x
y
π
-π
π
2
- π
2
-1
-2
1
2
0
x
y
-1
-2
1
2
0
x
y
π
-π
π
2
-
π
2
y=sinx
3π
2
-
3π
2
5π
2
-
5π
2
2π
-2π
-1
-2
1
2
0
x
y
-1
-2
1
2
0
x
y
π
-π
π
2
-
π
2
y=cosx
3π
2
-
3π
2
5π
2
-
5π
2
2π
-2π
3. Funkce
160
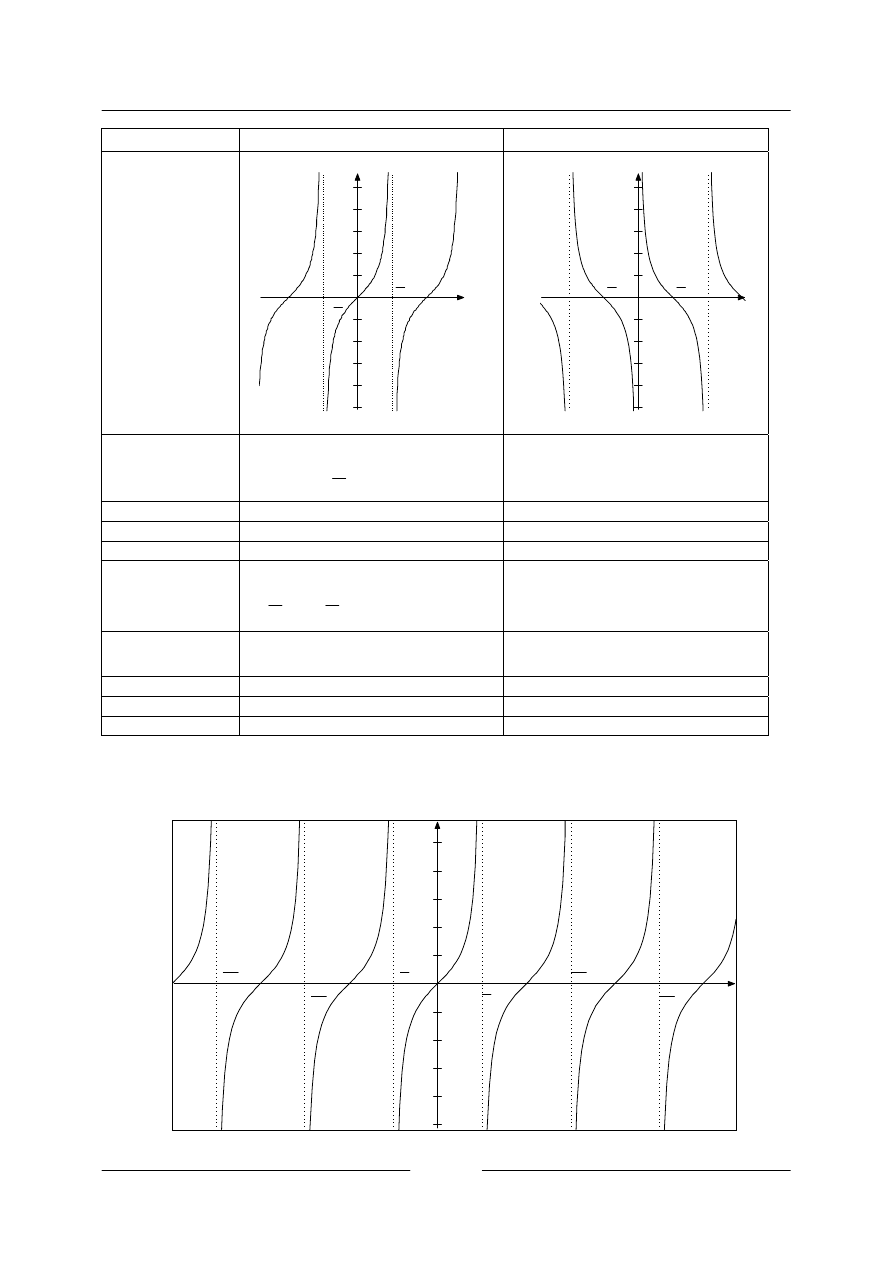
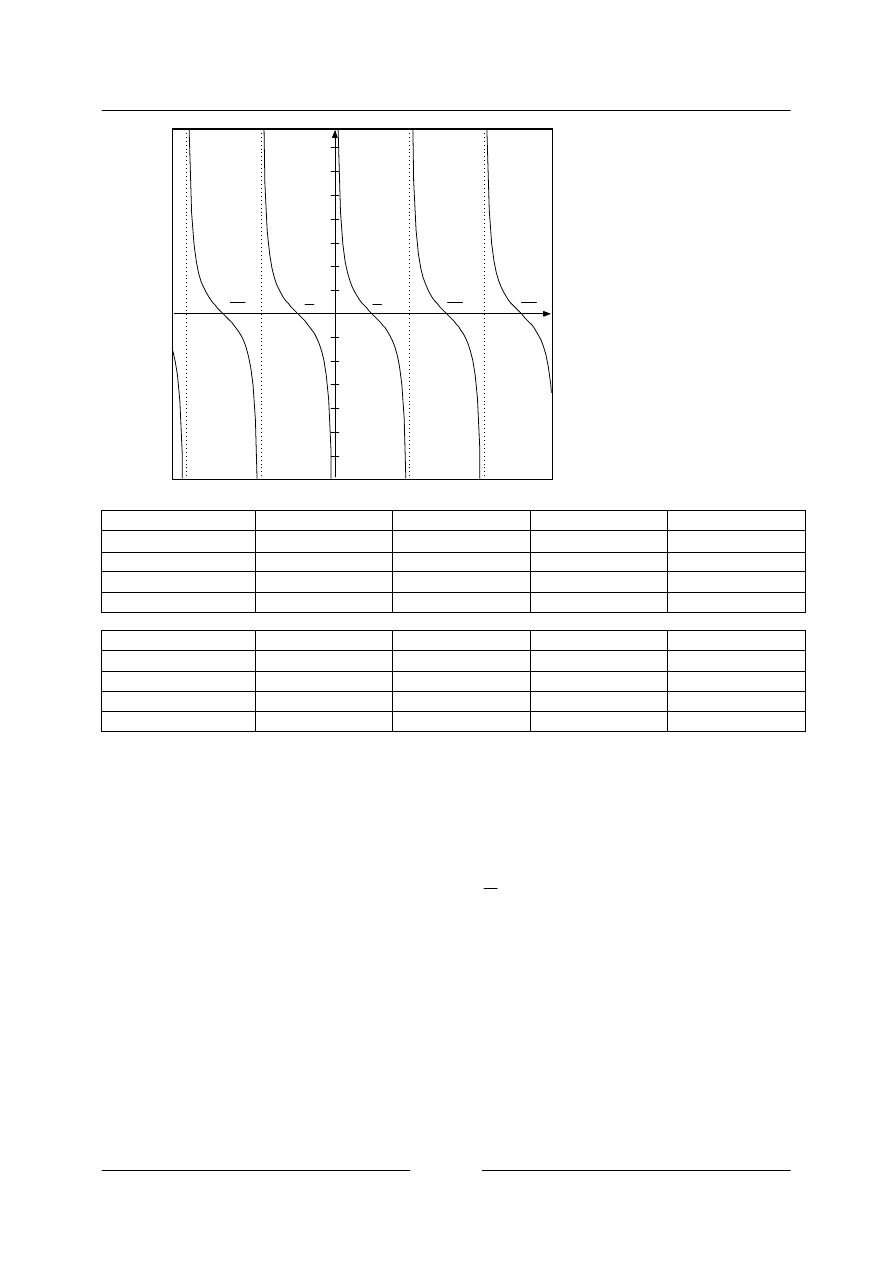
x
y
tan
=
x
y
cot
=
Definiční obor
Množina všech
(
)
2
1
2
π
+
≠ k
x
Množina všech
π
k
x
≠
Obor hodnot
R
R
Parita
lichá
lichá
Perioda
π
π
Rostoucí
V každém intervalu
+
+
−
π
π
π
π
k
k
2
,
2
_________________
Klesající
_________________________
V každém intervalu
(
)
π
π
π
k
k
+
+
,
0
Omezená
Shora i zdola neomezená
Shora i zdola neomezená
Maximum
Neexistuje
Neexistuje
Minimum
Neexistuje
Neexistuje
Písmeno
k
v tabulce jako označuje libovolné celé číslo.
-1
-2
-3
-4
1
2
3
4
0
x
y
-1
-2
-3
-4
1
2
3
4
0
x
y
π
-π
π
2
-
π
2
-1
-2
-3
-4
1
2
3
4
0
x
y
-1
-2
-3
-4
1
2
3
4
0
x
y
π
-π
π
2
-
π
2
-1
-2
-3
-4
1
2
3
4
0
x
y
-1
-2
-3
-4
1
2
3
4
0
x
y
π
-π
π
2
- π
2
y=tanx
3π
2
-
3π
2
5π
2
-
5π
2
2π
-2π
3. Funkce
161
Znaménko funkce
I. kvadrant
II. kvadrant
III. kvadrant
IV. kvadrant
x
sin
+
+
-
-
x
cos
+
-
-
+
x
tan
+
-
+
-
x
cot
+
-
+
-
Monotónnost funkce
I. kvadrant
II. kvadrant
III. kvadrant
IV. kvadrant
x
sin
roste
klesá
klesá
roste
x
cos
klesá
klesá
roste
roste
x
tan
roste
roste
roste
roste
x
cot
klesá
klesá
klesá
klesá
Goniometrické funkce jsou periodické.
Platí: Pro každé
Z
∈
k
a pro každé
R
∈
x
je
x
k
x
cos
)
2
.
cos(
=
+
π
x
k
x
sin
)
2
.
sin(
=
+
π
.
Pro každé
Z
∈
k
a pro každé
(
)
+
−
∈
2
1
2
π
k
x
R
je
x
k
x
tan
)
.
tan(
=
+
π
.
Pro každé
Z
∈
k
a pro každé
{ }
π
k
x
−
∈ R
je
x
k
x
cot
)
.
cot(
=
+
π
.
Funkce sinus je lichá, platí tedy
x
x
sin
)
sin(
−
=
−
.
Funkce kosinus je sudá, platí tedy
x
x
cos
)
cos(
=
−
.
Funkce tangens je lichá, platí tedy
x
x
tan
)
tan(
−
=
−
.
Funkce kotangens je lichá, platí tedy
x
x
cot
)
cot(
−
=
−
.
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
0
x
y
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
0
x
y
π
-π
π
2
- π
2
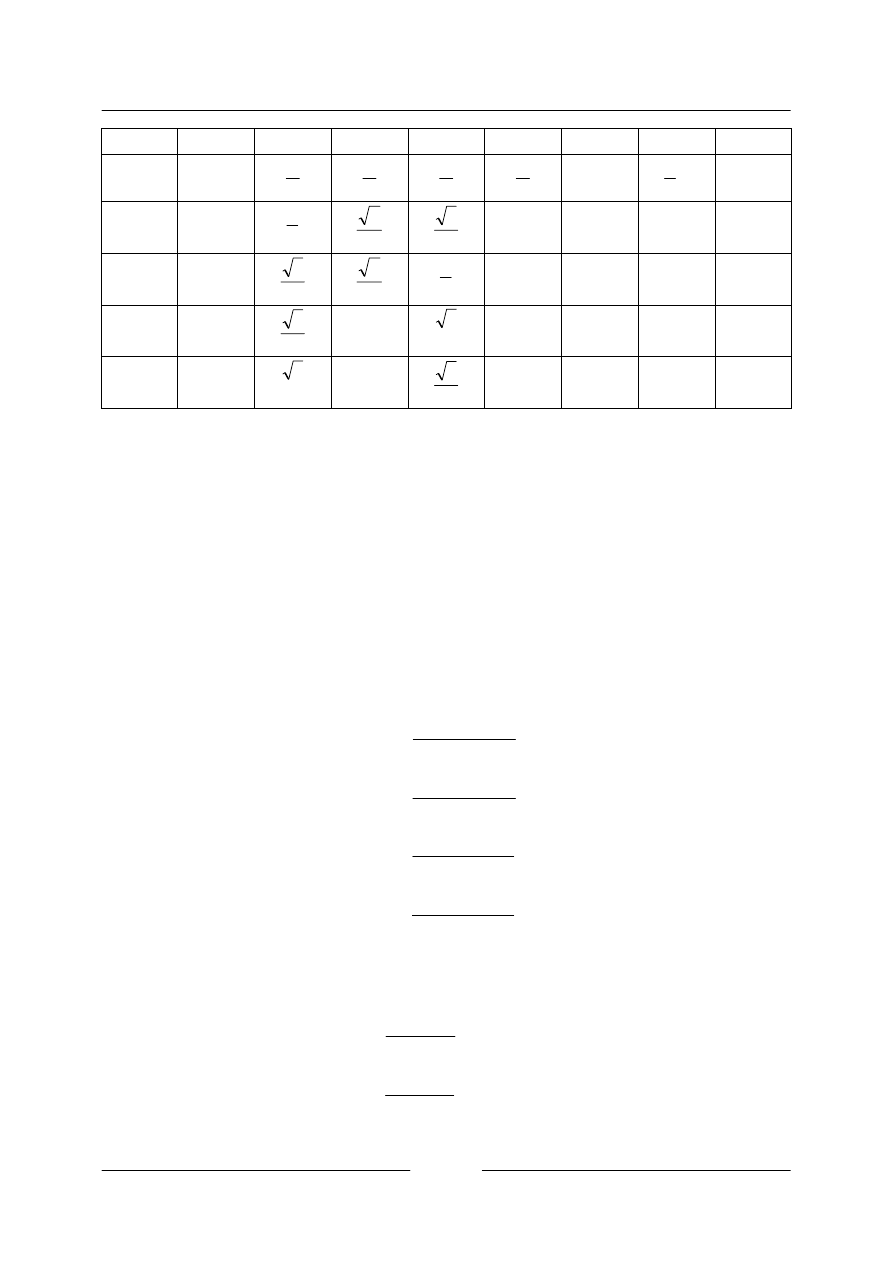
y=cotx
3π
2
-
3π
2
5π
2
2π
-2π
3. Funkce
162
°
α
°
0
30°
45°
60°
90°
180°
270°
360°
x rad
0
6
π
4
π
3
π
2
π
π
π
2
3
π
2
x
sin
0
2
1
2
2
2
3
1
0
-1
0
x
cos
1
2
3
2
2
2
1
0
-1
0
1
x
tan
0
3
3
1
3
ND
0
ND
0
x
cot
ND
3
1
3
3
0
ND
0
ND
ND značí není definována, body nepatří definičnímu oboru.
Goniometrické vzorce
Pro každé
( )
f
D
x
∈
platí:
1
cos
sin
2
2
=
+
x
x
1
cot
.
tan
=
x
x
Součtové vzorce:
(
)
y
x
y
x
y
x
sin
cos
cos
sin
sin
+
=
+
(
)
y
x
y
x
y
x
sin
cos
cos
sin
sin
−
=
−
(
)
y
x
y
x
y
x
sin
sin
cos
cos
cos
−
=
+
(
)
y
x
y
x
y
x
sin
sin
cos
cos
cos
+
=
−
(
)
y
x
y
x
y
x
tan
.
tan
1
tan
tan
tan
−
+
=
+
(
)
y
x
y
x
y
x
tan
.
tan
1
tan
tan
tan
+
−
=
−
(
)
y
x
y
x
y
x
cot
cot
1
cot
.
cot
cot
+
−
=
+
(
)
x
y
y
x
y
x
cot
cot
1
cot
.
cot
cot
−
+
=
−
Vzorce pro dvojnásobný úhel:
x
x
x
cos
sin
2
2
sin
=
x
x
x
2
2
sin
cos
2
cos
−
=
x
x
x
2
tan
1
tan
2
2
tan
−
=
x
x
x
cot
2
1
cot
2
cot
2
−
=
3. Funkce
163
Řešený příklad
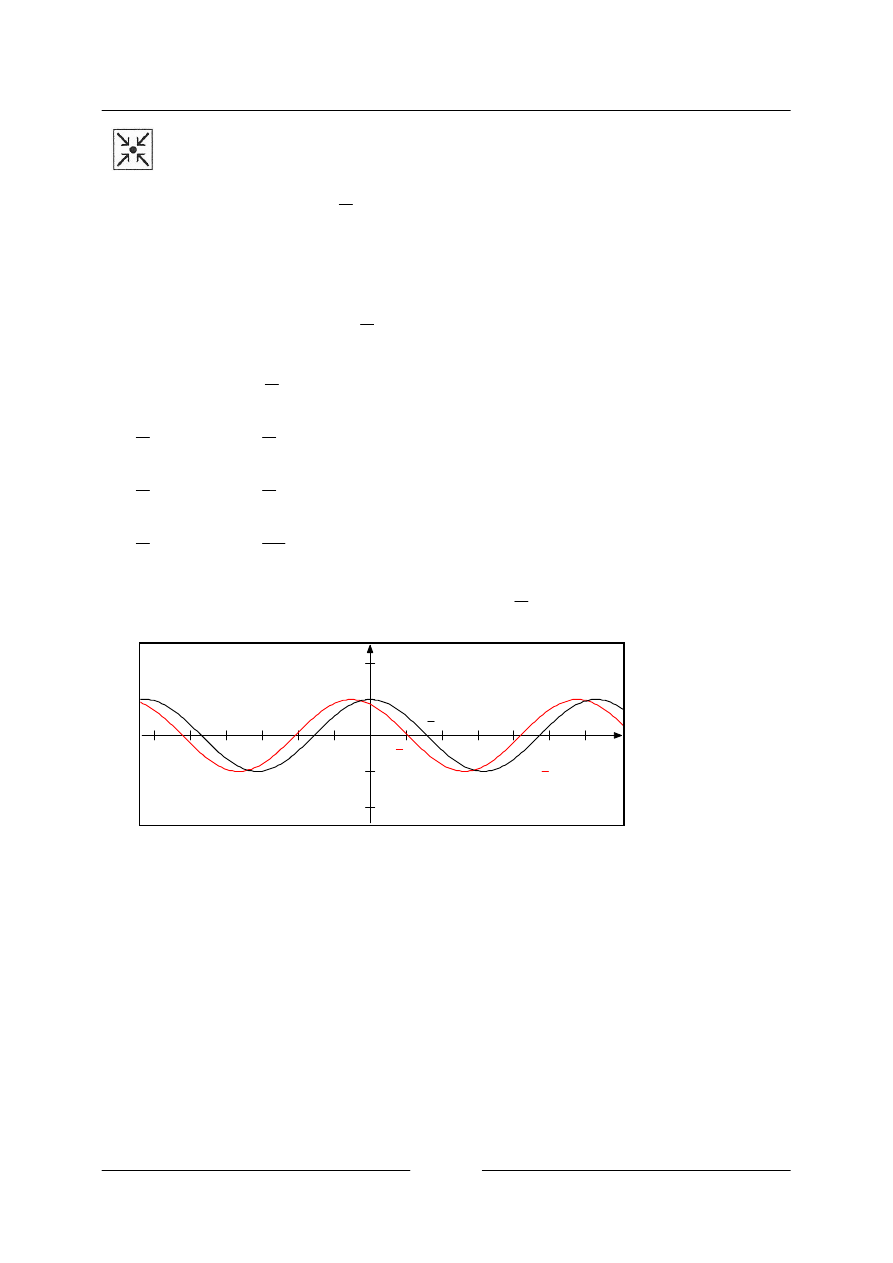
• Sestrojte graf funkce
+
=
x
y
6
cos
π
.
Řešení
Budeme postupovat od jednoduššího grafu. Tím je graf funkce
x
y
cos
=
.
Nyní sestrojíme graf funkce
+
=
x
y
6
cos
π
.
=
=
=
=
=
=
=
=
3
2
cos
.
..........
2
2
cos
.
..........
3
3
cos
.
..........
6
6
cos
...
..........
0
π
π
π
π
π
π
π
y
x
y
x
y
x
y
x
Posuneme graf funkce
x
y cos
=
ve směru záporné osy
x
o
6
π
.
• Sestrojte graf funkce
x
y
2
sin
=
.
Řešení
Budeme postupovat od jednoduššího grafu. Tím je graf funkce
x
y sin
=
.
Nyní sestrojíme graf funkce
x
y
2
sin
=
.
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
-1
-2
1
0
x
y
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
-1
-2
1
0
x
y
y=cos(
π
6
+ x)
y=cos(x)
π
2
π
3
3. Funkce
164
π
π
π
π
π
π
π
π
2
sin
..
..........
sin
.
..........
2
3
2
sin
.
..........
3
3
sin
.
..........
6
0
sin
...
..........
0
=
=
=
=
=
=
=
=
=
=
y
x
y
x
y
x
y
x
y
x
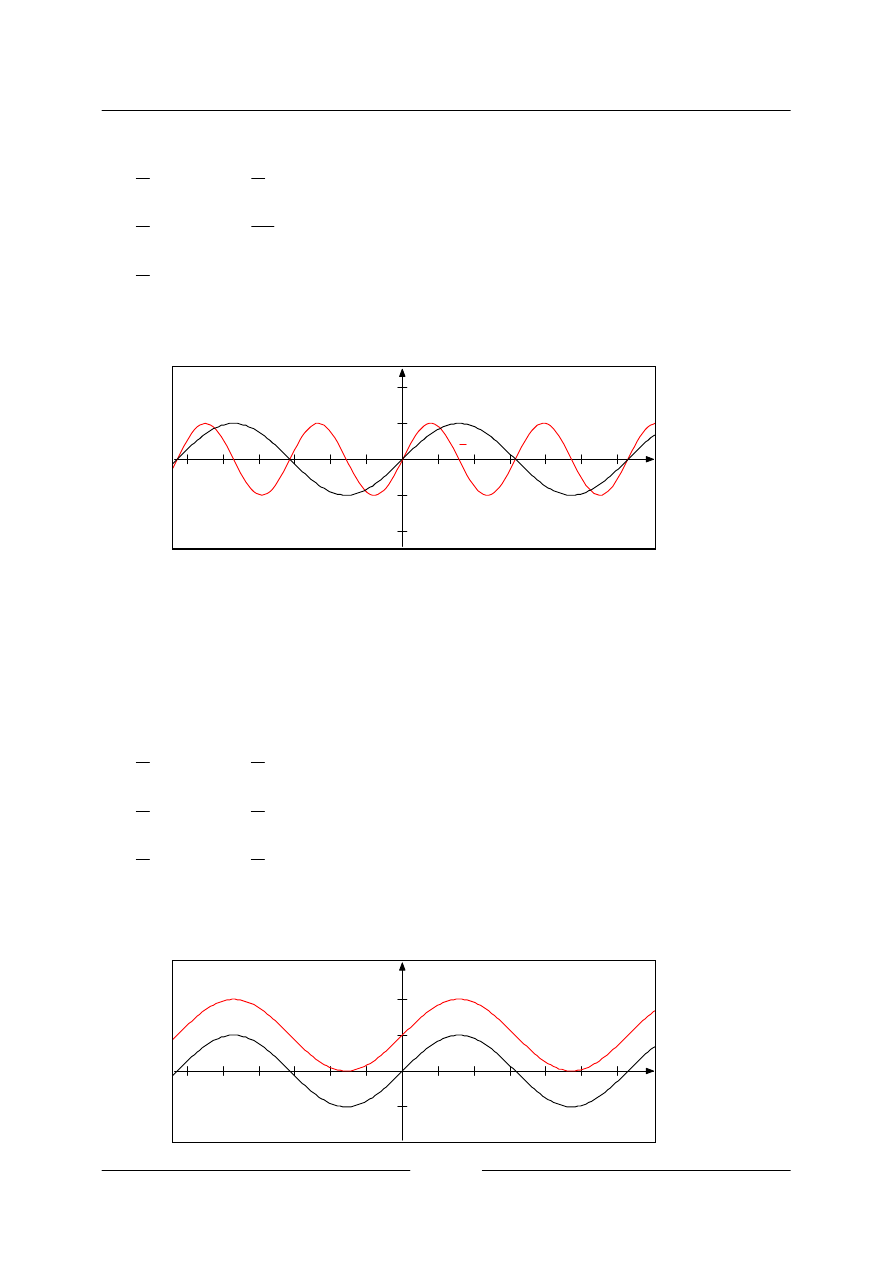
Průběh grafu se 2x „zrychlí“, perioda se zkrátí na polovinu.
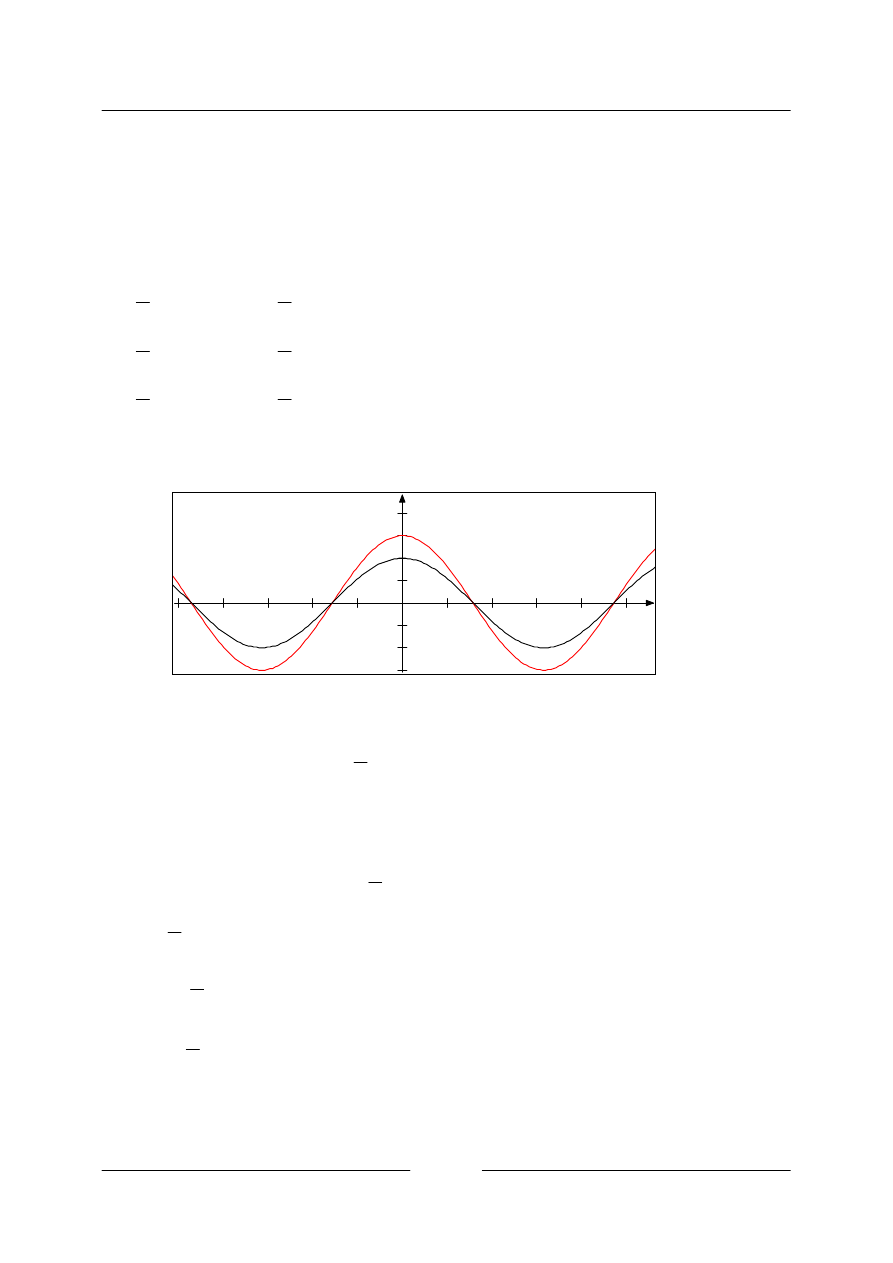
• Sestrojte graf funkce
1
sin
+
=
x
y
.
Řešení
Budeme postupovat od jednoduššího grafu. Tím je graf funkce
x
y sin
=
.
Nyní sestrojíme graf funkce
1
sin
+
=
x
y
.
1
sin
..
..........
1
2
sin
.
..........
2
1
3
sin
.
..........
3
1
6
sin
.
..........
6
1
0
sin
...
..........
0
+
=
=
+
=
=
+
=
=
+
=
=
+
=
=
π
π
π
π
π
π
π
π
y
x
y
x
y
x
y
x
y
x
Funkční hodnoty se zvětší o 1, posuneme tedy graf funkce
x
y sin
=
o 1 ve kladném směru osy y.
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
-1
-2
1
0
x
y
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
-1
-2
1
0
x
y
y=sin2x
y=sinx
π
2
π
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
-1
1
2
0
x
y
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
-1
1
2
0
x
y
y=sinx+1
y=sinx
3. Funkce
165
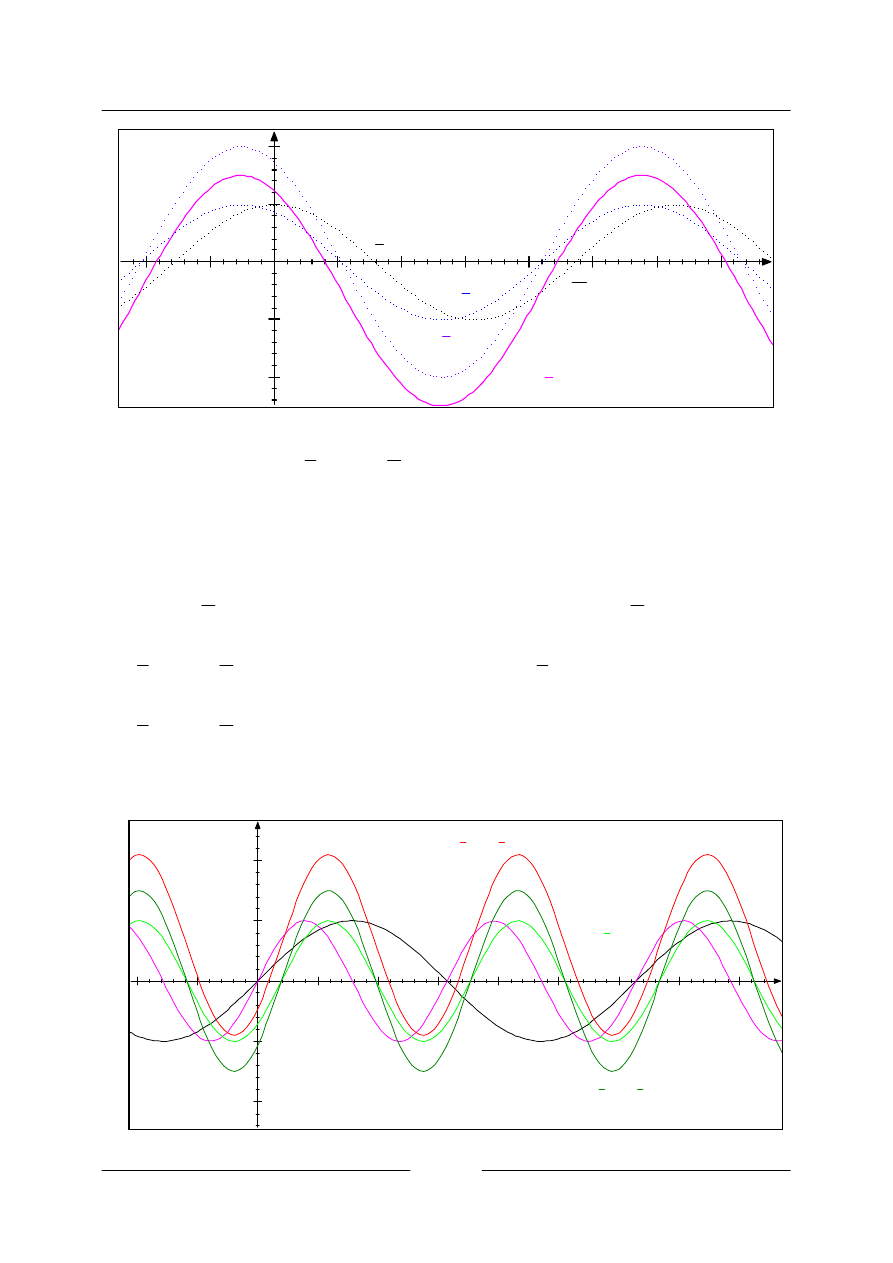
• Sestrojte graf funkce
x
y
cos
.
5
,
1
=
.
Řešení
Budeme postupovat od jednoduššího grafu. Tím je graf funkce
x
y
cos
=
.
Nyní sestrojíme graf funkce
x
y
cos
.
5
,
1
=
.
π
π
π
π
π
π
π
π
cos
.
5
,
1
..
..........
2
cos
.
5
,
1
.
..........
2
3
cos
.
5
,
1
.
..........
3
6
cos
.
5
,
1
.
..........
6
0
cos
.
5
,
1
...
..........
0
=
=
=
=
=
=
=
=
=
=
y
x
y
x
y
x
y
x
y
x
Funkční hodnoty se zvětší 1,5krát.
• Sestrojte graf funkce
5
,
0
6
cos
.
2
−
+
=
x
y
π
.
Řešení
Budeme postupovat od nejjednoduššího grafu. Tím je graf funkce
x
y cos
=
.
Nyní sestrojíme graf funkce
+
=
x
y
6
cos
π
. Posuneme graf funkce
x
y cos
=
ve směru záporné
osy
x
o
6
π
.
+
=
x
y
6
cos
.
2
π
Nyní každou funkční hodnotu zdvojnásobíme.
5
,
0
6
cos
.
2
−
+
=
x
y
π
od předchozí funkční hodnoty odečteme
5
,
0
tzn. posuneme graf o
5
,
0
ve
směru záporné osy
y
.
-1
-2
-3
-4
-5
1
2
3
4
5
-0.5
-1
0.5
1
1.5
0
x
y
-1
-2
-3
-4
-5
1
2
3
4
5
-0.5
-1
0.5
1
1.5
0
x
y
y=1.5cosx
y=cosx
3. Funkce
166
-1
-2
1
2
3
4
5
6
7
-1
-2
1
0
x
y
-1
-2
1
2
3
4
5
6
7
-1
-2
1
0
x
y
y=2.cos(
π
6
+ x) - 0.5
y=2.cos(
π
6
+ x)
y=cos(
π
6
+ x)
y=cos(x)
π
2
π
3
π
2
2π
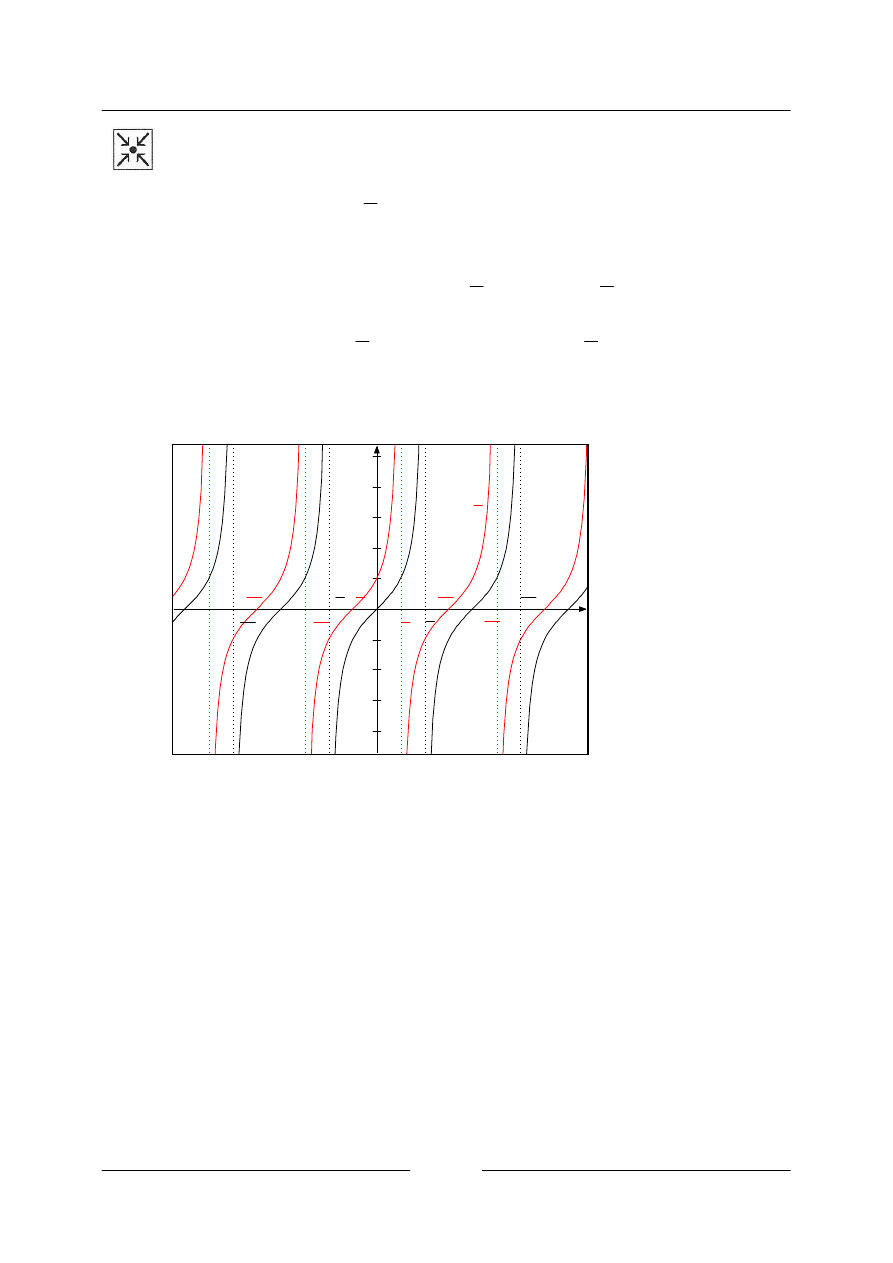
• Sestrojte graf funkce
6
,
0
4
2
sin
.
2
3
+
−
=
π
x
y
.
Řešení
Budeme postupovat od nejjednoduššího grafu. Tím je graf funkce
x
y sin
=
.
Nyní sestrojíme graf funkce
x
y
2
sin
=
. Perioda funkce se zkrátí na polovinu, tedy
π
.
−
=
4
2
sin
π
x
y
Posuneme graf funkce
x
y
2
sin
=
ve směru kladné osy
x
o
4
π
.
−
=
4
2
sin
.
2
3
π
x
y
Nyní každou funkční hodnotu vynásobíme
2
3
.
6
,
0
4
2
sin
.
2
3
+
−
=
π
x
y
K předchozí funkční hodnotě přičteme
6
,
0
tzn. posuneme graf o
6
,
0
ve
směru kladné osy
y
.
-1
-2
1
2
3
4
5
6
7
8
-1
-2
1
2
0
x
y
-1
-2
1
2
3
4
5
6
7
8
-1
-2
1
2
0
x
y
y=
3
2
.sin(2.x-
π
4
)+0.6
y=
3
2
.sin(2.x-
π
4
)
y=sin(2.x-
π
4
)
y=sin(2.x)
y=sin(x)
3. Funkce
167
Řešený příklad
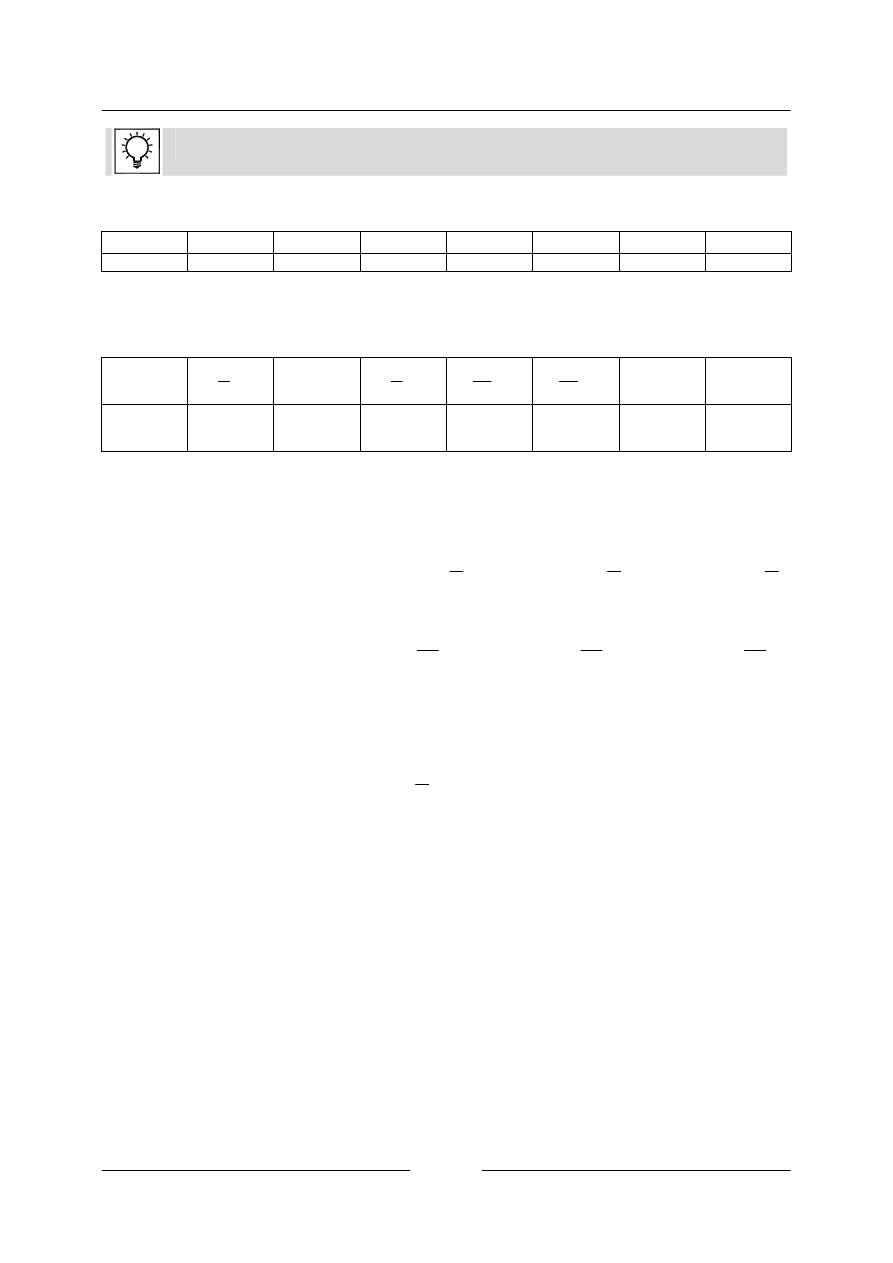
• Sestrojte graf funkce
)
4
tan(
π
+
=
x
y
.
Řešení
Nejdříve musíme určit definiční obor funkce:
0
)
4
cos(
≠
+
π
x
odtud
π
π
k
x
+
≠
4
.
Graf funkce
x
y
tan
=
posuneme o
4
π
v záporném směru osy x,
π
π
k
x
+
=
4
jsou asymptoty grafu
funkce.
-1
-2
-3
-4
1
2
3
4
0
x
y
-1
-2
-3
-4
1
2
3
4
0
x
y
π
-π
π
2
- π
2
y=tanx
3π
2
-
3π
2
2π
-2π
y=tan(x+
π
4
)
- π
4
-
3π
4
π
4
-
5π
4
3π
4
5π
4
3. Funkce
168
Úlohy k řešení
Úloha 3.14.
Velikosti úhlů ve stupňové míře vyjádřete v míře obloukové:
α
°
0
°
30
°
135
'
30
12
°
°
330
°
154
'
18
317
°
x
♦
Úloha 3.15.
Velikosti úhlů v obloukové míře vyjádřete v míře stupňové:
x
π
3
4
π
π
5
4
π
9
17
π
10
1
75
,
0
2
,
4
α
♦
Úloha 3.16.
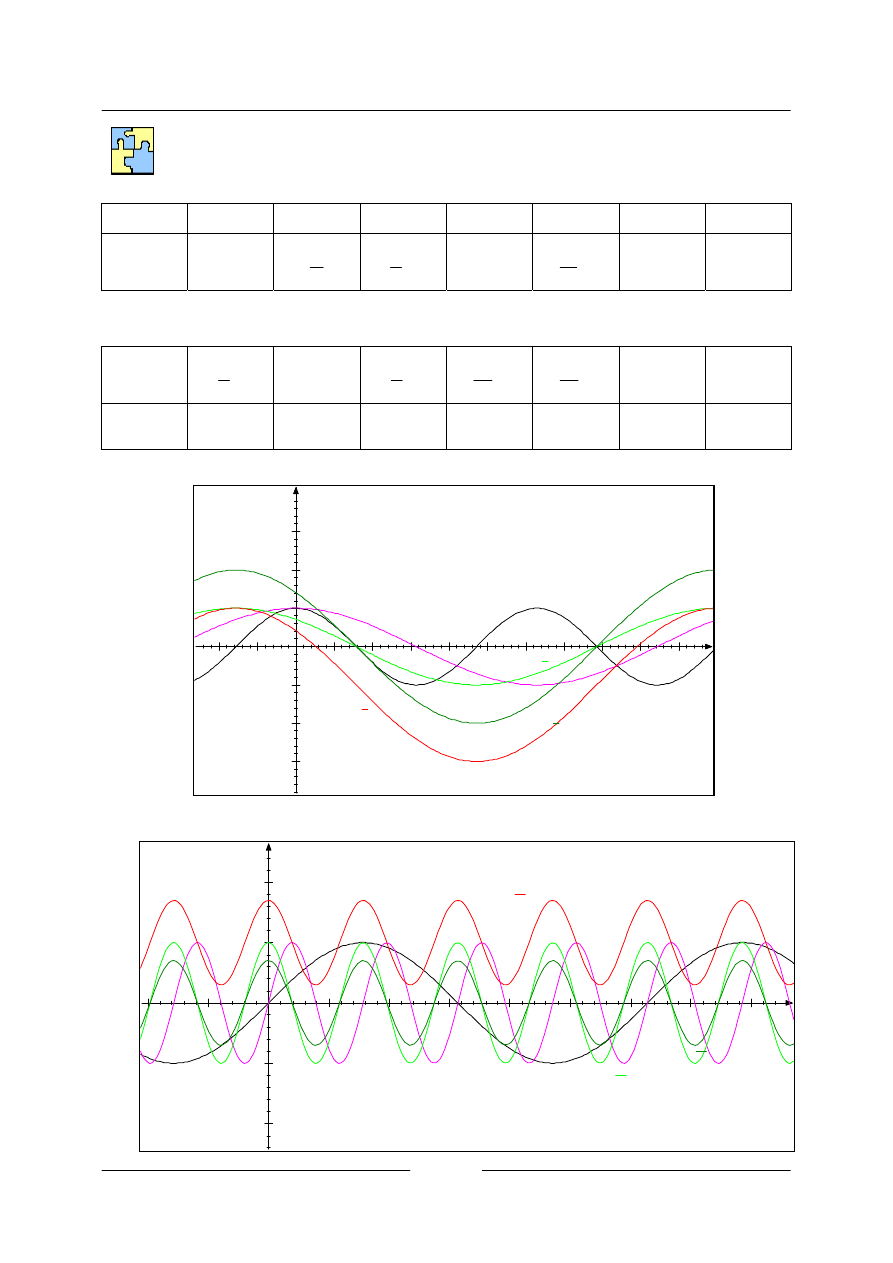
Postupně zakreslete do téže soustavy souřadnic grafy těchto funkcí
a)
1
4
5
,
0
cos
.
2
;
4
5
,
0
cos
.
2
;
4
5
,
0
cos
;
5
,
0
cos
;
cos
−
+
=
+
=
+
=
=
=
π
π
π
x
y
x
y
x
y
x
y
x
y
b)
1
2
3
4
sin
.
7
,
0
;
2
3
4
sin
.
7
,
0
;
2
3
4
sin
;
4
sin
;
sin
+
−
=
−
=
−
=
=
=
π
π
π
x
y
x
y
x
y
x
y
x
y
♦
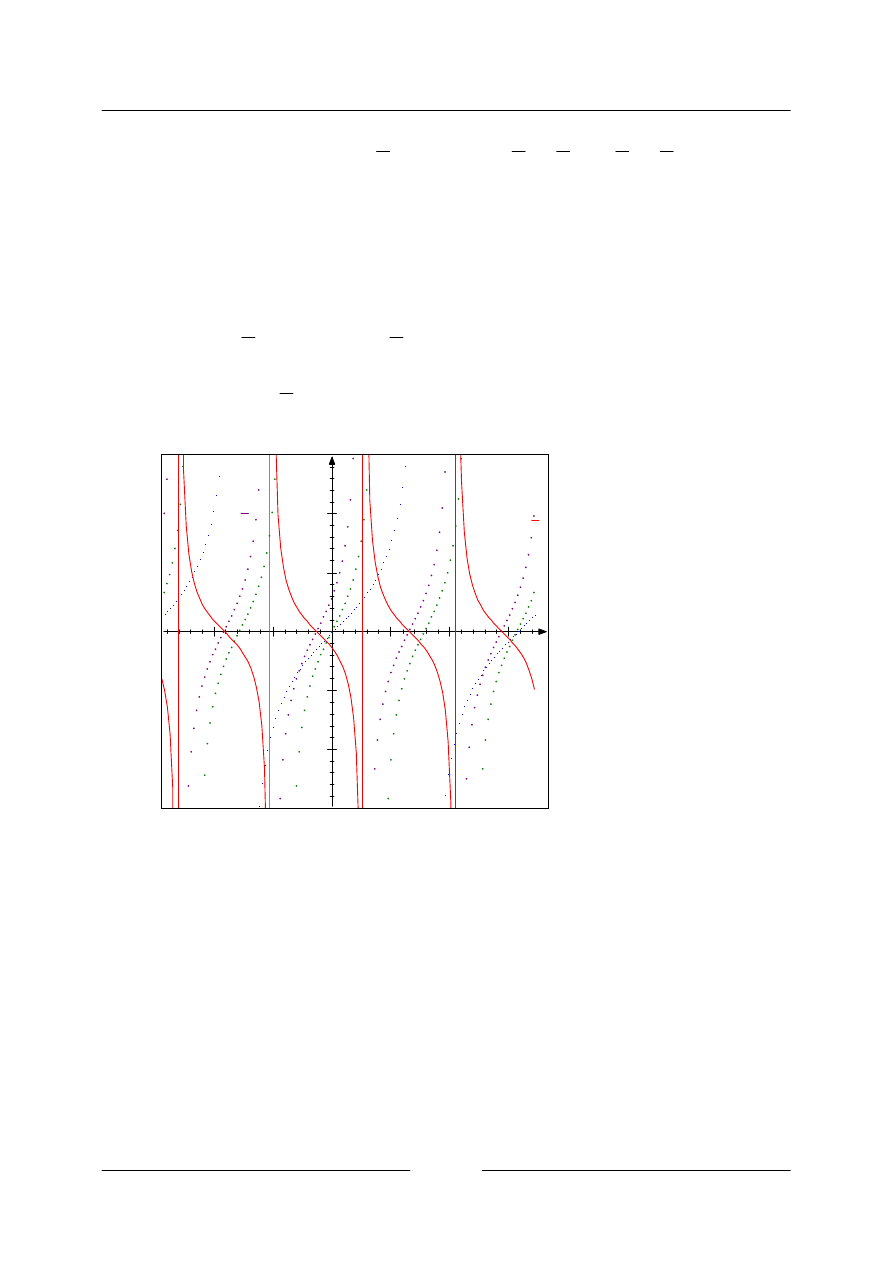
Úloha 3.17.
Sestrojte graf funkce
)
6
2
tan(
.
5
,
0
π
+
−
=
x
y
♦
3. Funkce
169
Výsledky
3.14. Velikosti úhlů ve stupňové míře vyjádřete v míře obloukové:
α
°
0
°
30
°
135
'
30
12
°
°
330
°
154
'
18
317
°
x
0
6
π
π
4
3
0,48
π
6
11
69
,
2
1,76
3.15. Velikosti úhlů v obloukové míře vyjádřete v míře stupňové:
x
π
3
4
π
π
5
4
π
9
17
π
10
1
75
,
0
2
,
4
α
240°
180°
144°
340°
18°
135°
756°
3.16.
a)
b)
-1
-2
1
2
3
4
5
6
7
8
-1
-2
1
2
0
x
y
-1
-2
1
2
3
4
5
6
7
8
-1
-2
1
2
0
x
y
y=0,7.sin(4.x-
3π
2
)+1
y=0,7.sin(4.x-
3π
2
)
y=sin(4.x-
3π
2
)
y=sin(4.x)
y=sin(x)
-1
-2
1
2
3
4
5
6
7
8
9
10
-1
-2
-3
1
2
3
0
x
y
-1
-2
1
2
3
4
5
6
7
8
9
10
-1
-2
-3
1
2
3
0
x
y
y=2.cos(0,5.x+
π
4
)+1
y=2.cos(0,5.x+
π
4
)
y=cos(0,5.x+
π
4
)
y=cos0,5x
y=cosx
3. Funkce
170
3.17. Určíme definiční obor:
0
)
6
2
cos(
≠
+
π
x
odtud
2
6
π
π
k
x
+
≠
.
2
6
π
π
k
x
+
=
jsou asymptoty
grafu.
Budeme postupovat opět od nejjednoduššího grafu, jako v předchozích příkladech s funkcemi
sinus a kosinus.
x
y
tan
=
x
y
2
tan
=
Zkrátíme periodu na polovinu tedy na
π
.
)
6
2
tan(
π
+
=
x
y
Graf posuneme o
6
π
v záporném směru osy
x
.
)
6
2
tan(
.
5
,
0
π
+
−
=
x
y
Funkční hodnoty vynásobíme
5
,
0
−
.
-1
-2
1
2
3
-1
-2
1
2
0
x
y
-1
-2
1
2
3
-1
-2
1
2
0
x
y
tgx
tg2x
tg(2x+
π
6
)
-0,5.tg(2x+
π
6
)
Wyszukiwarka
Podobne podstrony:
10 Metody otrzymywania zwierzat transgenicznychid 10950 ppt
10 dźwigniaid 10541 ppt
wyklad 10 MNE
Kosci, kregoslup 28[1][1][1] 10 06 dla studentow
10 budowa i rozwój OUN
10 Hist BNid 10866 ppt
POKREWIEŃSTWO I INBRED 22 4 10
Prezentacja JMichalska PSP w obliczu zagrozen cywilizacyjn 10 2007
Mat 10 Ceramika
BLS 10
10 0 Reprezentacja Binarna
10 4id 10454 ppt
więcej podobnych podstron