TERMOCHEMIA

1. Podstawowe definicje i równania

Układ jest to część przyrody, której właściwości lub zachodzące w niej zjawiska

badamy. Pozostała część przestrzeni to otoczenie.

Energia wewnętrzna układu, U [J], całkowita ilość energii w układzie, jest

sumą energii kinetycznej i potencjalnej wszystkich atomów, jonów, cząsteczek w
układzie. Nie można zmierzyć wartości bezwzględnej energii wewnętrznej układu,
można natomiast mierzyć różnicę energii wewnętrznej układu, ΔU, w różnych
stanach, np. w stanie 1, początkowym, i w stanie 2, końcowym, czyli

.

1

2

U

U

U

−

=

Δ

Całkowitą ilość energii w układzie można scharakteryzować za pomocą

entalpii, H [J], którą definiuje następujące równanie:

pV

U

H

+

=

Nie można zmierzyć bezwzględnej wartości entalpii, można natomiast zmierzyć
różnicę entalpii układu ΔH, w różnych stanach, np. w stanie 1, początkowym, i w
stanie 2, końcowym, czyli

1

2

H

H

H

−

=

Δ

Energia wewnętrzna i entalpia są funkcjami stanu, co oznacza, że ich

wartość zależy tylko od stanu układu, który określają parametry stanu, takie jak
temperatura, ciśnienie, objętość, liczba składników itp. Wartość funkcji stanu nie
zależy od sposobu (drogi) osiągnięcia danego stanu.

Ciepło, q [J] jest jednym ze sposobów przeniesienia energii między układem

a otoczeniem. Wymiana ciepła jest spowodowana różnicą temperatur pomiędzy
układem i otoczeniem. Z molekularnego punktu widzenia wymiana ciepła jest
skutkiem bezładnych ruchów termicznych cząsteczek.

Ciepło dostarczone do układu z otoczenia oznaczamy jako dodatnie, a

proces, w którym ciepło pobierane jest od otoczenia nazywamy procesem
endotermicznym. Ciepło przeniesione od układu do otoczenia jest ujemne, a proces,
w którym ciepło oddawane jest do otoczenia jest procesem egzotermicznym.

Praca, w [J] jest innym sposobem wymiany energii pomiędzy układem i

otoczeniem. Pracę wykonaną przez układ na otoczeniu oznaczamy ją jako dodatnią.
Pracę wykonanej przez otoczenie na układzie oznaczamy jako ujemną.

Ciepło i praca są funkcjami drogi, co oznacza, że ich wartości zależą od

sposobu osiągnięcia przez układ danego stanu.

Pierwsza zasada termodynamiki jest specyficznym sformułowaniem zasady

zachowania energii, która mówi, że zmiana energii wewnętrznej układu jest skutkiem
wymiany ciepła i/lub pracy z otoczeniem. Zapisujemy to następującym równaniem:

ΔU = q – w

Jeśli w układzie możliwa jest jedynie praca zmiany objętości, zwana pracą
objętościową pierwsza zasada termodynamiki przyjmuje postać:

∫

−

=

Δ

2

1

V

V

pdV

q

U

Widać stąd, że w przemianie izochorycznej (V = const) zmiana energii wewnętrznej
układu jest równa ciepłu wymienionemu z otoczeniem:

V

q

U

=

Δ

Pierwszą zasadę termodynamiki można zapisać za pomocą entalpii:

∫

+

=

Δ

2

1

p

p

Vdp

q

H

Łatwo wykazać, że ciepło wymienione z otoczeniem w przemianie izobarycznej
(p=const) jest równe zmianie entalpii układu:

p

q

H

=

Δ

Pojemność cieplna jest to ilość ciepła niezbędna do ogrzania układu o

jeden stopień pod stałym ciśnieniem

p

p

T

H

c

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

=

lub w stałej objętości

V

v

T

U

c

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

=

.

Ilość ciepła niezbędna do ogrzania 1 mola składnika pod stałym ciśnieniem

nazywamy molową pojemnością cieplną pod stłym ciśnieniem,

[J/(mol · K)] lub w

stałej objętości

p

_

c

V

_

c

[J/(mol · K)].

Praktycznym zastosowaniem pierwszej zasady termodynamiki w chemii jest

możliwość obliczania ciepła wymienionego w reakcjach chemicznych i procesach
fizykochemicznych na podstawie zmierzonych doświadczalnie ciepeł innych
procesów i reakcji. Możliwość taka, wynika z pierwszej zasady termodynamiki, gdyż
w procesach izochorycznych lub izobarycznych ilość ciepła wymieniona pomiędzy
układem i otoczeniem jest równa zmianie funkcji stanu i nie zależy od drogi procesu.
Zależność ta została zaobserwowana doświadczalnie i jest znana jako prawo Hessa,
które można sformułować na przykład tak: ”Jeśli proces jest izochoryczny lub
izobaryczny i gdy nie ma pracy innej niż praca zmiany objętości, wówczas efekty
cieplne procesu nie zależą od drogi procesu ale tylko od stanu początkowego i
końcowego”.

Inną konsekwencją pierwszej zasady termodynamiki jest prawo Kirchhoffa,

umożliwiające obliczanie ciepła reakcji w dowolnej temperaturze. Dla reakcji
izobarycznych, w których ciepło jest równe zmianie entalpii, ΔH, prawo Kirchhoffa
zapisujemy w postaci równania:

∫ Δ

+

Δ

=

Δ

2

1

1

2

T

T

p

T

T

dT

c

H

H

gdzie:

są entalpiami reakcji odpowiednio w temperaturach T

2

1

T

T

H

i

H

Δ

Δ

1

i T

2

natomiast Δc

p

jest różnicą pojemności cieplnych produktów i substartów reakcji,

wyrażonych zależnością:

∑ ν

−

∑

ν

=

Δ

substraty

p

_

i

produkty

p

_

j

p

c

c

c

2. Pomiary kalorymetryczne

Pomiary ilości ciepła wydzielanego lub pobieranego podczas przemian

fizykochemicznych dokonywane są w za pomocą kalorymetrów. Najczęściej
stosowane kalorymetry diatermiczne składają się z izolowanego cieplnie naczynia
napełnionego wodą zaopatrzonego w termometr i mieszadło.
Wymianę ciepła pomiędzy naczyniem, w którym zachodzi proces, którego efekt
cieplny badamy a otaczającym medium, np. wodą, można opisać równaniem bilansu
cieplnego:

(

)

ϑ

Σ

+

Δ

=

T

K

q

gdzie q jest ciepłem wymienionym pomiędzy naczyniem kalorymetrycznym i
otaczającym je medium, K jest pojemnością cieplną kalorymetru, natomiast

jest różnicą temperatur, uwzględniającą poprawkę

, związaną z

niedoskonałą izolacją kalorymetru.

(

ϑ

Δ

+

ΔT

)

ϑ

Δ

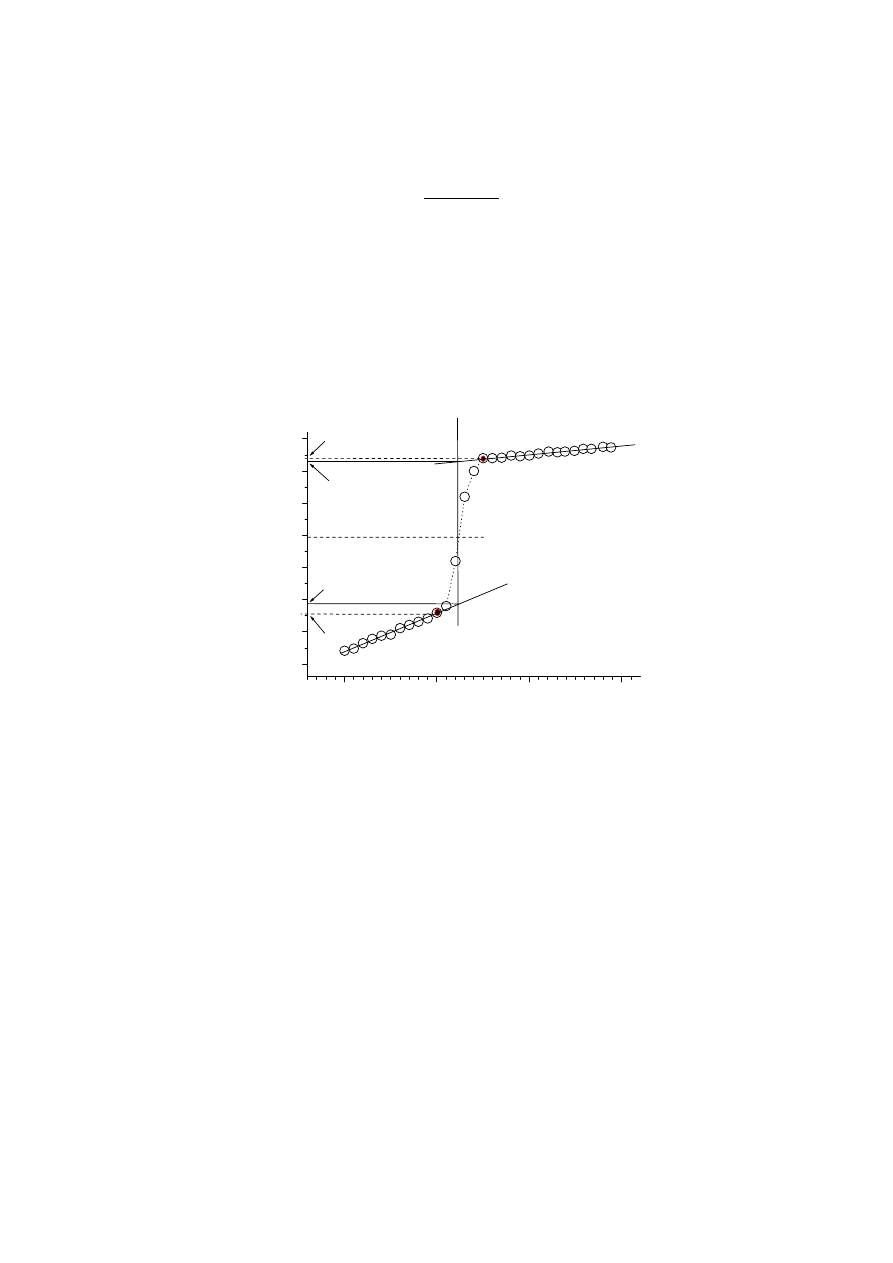
W celu wyznaczenia pojemności cieplnej (kalibracji) kalorymetru należy zatem
zmierzyć zmianę temperatury wraz z poprawką,

(

)

ϑ

Δ

+

ΔT

, dla znanej ilości ciepła, q,

i obliczyć pojemność cieplna kalorymetru ze wzoru:

)

T

(

q

K

ϑ

Σ

+

Δ

=

Graficzne wyznaczanie

(

)

ϑ

Δ

+

ΔT

Stosowane powszechnie kalorymetry diatermiczne nie są idealnie izolowane

cieplnie od otoczenia. Możliwa jest zatem wymiana ciepła między kalorymetrem a
otoczeniem powodująca zmianę temperatury kalorymetru nawet wtedy, gdy żaden
proces w nim nie zachodzi. Na rysunku pokazano przebieg zmian temperatury
kalorymetru dla procesu egzotermicznego, gdy temperatura otoczenia jest wyższa od
temperatury kalorymetru.

0

5

10

15

22,00

22,25

22,50

22,75

23,00

23,25

23,50

23,75

Δ

T = T

B'

- T

A'

B'

A'

T

A'

T

B'

C

T

B

T

A

B

A

te

m

pe

ratur

a

,

o

C

Czas, min

Jak widać w okresie początkowym, czyli przed zapoczątkowaniem badanego

procesu temperatura kalorymetru powoli rośnie. Po zapoczątkowaniu procesu (punkt
A) wzrost temperatury jest szybki aż do zakończenia procesu (punkt B). Następnie, w
okresie końcowym temperatura znowu powoli rośnie. Aby z takiego wykresu
poprawnie odczytać przyrost temperatury związany wyłącznie z badanym procesem
należy przeprowadzić następującą procedurę graficzną:

1. Rysujemy prostą przechodzącą przez punkty pomiarowe odpowiadające

okresowi początkowemu i przedłużamy (ekstrapolujemy) ją w kierunku
wzrastającego czasu.

2. Analogicznie rysujemy prostą przechodzącą przez punkty okresu końcowego i

ekstrapolujemy ją w kierunku przeciwnym.

3. Następnie przez punkt C, którego rzędna leży w środku pomiędzy

temperaturami odpowiadającymi początkowi, T

A

, i końcowi, T

B

, okresu

głównego, prowadzimy prostą prostopadłą do osi odciętych.

B

4.

Prosta ta przecina proste ekstrapolowane w punktach A’ i B’. Różnica
temperatur odpowiadających tym punktom jest poszukiwanym przyrostem
temperatury, czyli

(

)

'

A

'

B

T

T

T

−

=

ϑ

Δ

+

Δ

.

ĆWICZENIE NR 15

WYZNACZANIE CIEPŁA SPALANIA

Celem ćwiczenia jest wyznaczenie ciepła spalania krystalicznej substancji

organicznej. Eksperyment przeprowadza się w tzw. bombie kalorymetrycznej

umieszczonej

w kalorymetrze diatermicznym. Ćwiczenie obejmuje następujące etapy, które należy

przeprowadzić w tym samym kalorymetrze:

1. Wyznaczenie

pojemności cieplnej kalorymetru (kalibracja) w oparciu o ciepło

spalania substancji wzorcowej.

2. Wyznaczenie

ciepła spalania substancji nieznanej.

Reakcja spalania

W termochemii przez reakcję spalania rozumie się reakcję łączenia pierwiastka lub

związku chemicznego z tlenem, w wyniku czego powstają produkty nie mogące ulec

dalszemu spaleniu. Dla związków organicznych zawierających wodór i węgiel

produktami tymi są woda i CO

2

(ale nie CO). Jeżeli spalany związek organiczny

zawiera także azot i siarkę, to powstają azot cząsteczkowy, N

2

oraz SO

3

(ale nie

SO

2

). Z powyższej definicji wynika, że termochemiczne spalenie powinno odbywać

się w nadmiarze tlenu.

Bomba kalorymetryczna

Spalanie substancji badanej, przygotowanej w formie tabletki, przeprowadza się

w ciśnieniowej bombie kalorymetrycznej w atmosferze tlenu. Schemat bomby

pokazano na poniższym rysunku.

z1

z2

d

t

k

g

el

p

p

Bomba kalorymetryczna składa się ona z korpusu (k) i głowicy (g) zamknietych

pierścieniem. Z głowicą połączone są dwie elektrody (p), pomiędzy którymi

umieszcza się w tyglu (t) pastylkę wykonaną z badanej substancji. W pastylkę

wprasowany jest drut zapłonowy (d), którego wystające końce łączy się z elektrodami

(p). Elektrody przechodzą przez głowicę, a ich końce zaopatrzone są w gniazda do

przyłączania kabla zapłonowego. Ponadto w głowicy znajdują się zawory wlotowy

(z1) i wylotowy (z2). Korpus, głowica i pierścień są numerowane. Przy montażu

bomby należy zwrócić uwagę, by wszystkie jej części miały ten sam numer.

Jak wynika z powyższego opisu spalanie w kalorymetrze przebiega w warunkach

stałej objętości, czyli wydzielone w tym procesie ciepło oznaczymy – q

v

.

Wykonanie ćwiczenia

I. Sporządzanie tabletek

W środkowej części drutu zapłonowego należy wykonać 3 – 4 zwojową spiralkę i

wprasować ją w tabletkę z badanej substancji krystalicznej. Masa tabletki powinna

wynosić 0,7 – 0,9 g. Prasa do sporządzania tabletek znajduje się w sali

laboratoryjnej.

II. Przygotowanie bomby kalorymetrycznej do pomiaru

1. Umieścić przygotowaną i dokładnie zważoną pastylkę między elektrodami głowicy

bomby kalorymetrycznej.

2. Głowicę umieścić w korpusie, tak by końcówki drutu zapłonowego nie stykały się

z nim. Zakręcić pierścień zamykający.

3. Bombę napełnić tlenem (czynność tę wykonuje laborant w pokoju

przygotowawczym). Napełnienie bomby tlenem ma na celu zapewnienie

całkowitego spalenia badanej substancji, usunięcie azotu oraz wytworzenie

nadciśnienia zapobiegającego dostaniu się wody do jej wnętrza. Po napełnieniu

tlenem należy sprawdzić czy przez drut zapłonowy płynie prąd.

4. Wstawić bombę do kalorymetru wypełnionego wodą. Temperatura wody powinna

być zbliżona do temperatury otoczenia, a jej ilość tak dobrana, by ponad jej

powierzchnię wystawały tylko końcówki elektrod, do których dołączamy kabelki

zapłonowe. Bombę należy ustawić centralnie, a następnie sprawdzić, czy

mieszadło może się swobodnie obracać.

5. Nałożyć pokrywę kalorymetru wyprowadzając kabelki, tak by nie stykały się z osią

mieszadła. Uruchomić mieszadło.

III.

Wyznaczanie pojemności cieplnej kalorymetru (kalibrowanie kalorymetru)

1. Umocować w bombie kalorymetrycznej pastylkę o znanej masie wykonaną z

substancji wzorcowej (kwas benzoesowy,(q

v,sp

)

wz

= 26,476 kJ/g w temp. 20

o

C).

2. Ostrożnie umieścić termometr w przewidzianym dla niego gnieździe.

3. Uruchomić mieszadło i odczekać 5 minut. Następnie w odstępach 30

sekundowych dokonać 10 - 15 odczytów temperatury z dokładnością 0,005

o

C

(okres początkowy).

4. Nacisnąć przycisk zapłonu (trzymaj wciśnięty przez 5 s), aby zapalić pastylkę. Nie

przerywać odczytywania temperatury. Zaobserwuje się wyraźny wzrost

temperatury (5 – 10 odczytów).

5.

Gdy temperatura przestanie wyraźnie wzrastać dokonać kolejnych 10 – 15

odczytów.

IV.

Wyznaczanie ciepła spalania nieznanej substancji

1. Wykonać pastylkę z substancji wskazanej przez asystenta. Należy pamiętać, że

masa pastylki powinna zawierać się w przedziale 0,7 – 0,9 g. Ręczna prasa do

sporządzania pastylek znajduje się na sali.

2. Następnie postępować analogicznie jak przy wyznaczaniu pojemności cieplnej

kalorymetru.

Opracowanie wyników

1. Na podstawie wyników pomiarów wykonać wykresy zmian temperatury w czasie

dla spalania substancji wzorcowej i badanej.

2. Metodą graficzną wyznaczyć przyrosty temperatury z poprawkami,

, dla

obu substancji.

ϑ

Σ

+

ΔT

3. Obliczyć pojemność cieplną kalorymetru z zależności:

ϑ

Σ

+

Δ

⋅

=

T

)

q

(

m

K

wz

sp

,

v

kw

gdzie m

kw

jest masą kwasu benzoesowego, natomiast (q

v,sp

)

wz

jest gramowym

ciepłem spalania kwasu benzoesowego.

4. Obliczyć gramowe ciepło spalania nieznanej substancji:

subst

sp

,

v

m

)

T

(

K

)

q

(

ϑ

Σ

+

Δ

⋅

=

5. Zwrócić uwagę na odpowiednie znakowanie ciepła spalania.

6. Porównać otrzymany wynik z ciepłem spalania substancji wzorcowej. Znaleźć w

tablicach ciepła spalania kilku związków organicznych różniących się wyraźnie

masami cząsteczkowymi. Czy zauważa się jakąś prawidłowość?