Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
1
CZWÓRNIKI PASYWNE
3.1. Okre
ś
lenie i wła
ś
ciwo
ś
ci n-wrotnika
Metody badania obwodu elektrycznego można podzielić na metody sieciowe i metody zaciskowe.
Metody sieciowe charakteryzują się tym, że dana jest pełna struktura obwodu i parametry elementów,
a poszukujemy rozpływu prądów w obwodzie oraz rozkładu napięć na poszczególnych elementach.
W metodach zaciskowych obwód traktowany jest jako dwójnik, czwórnik lub ogólniej obwód
o n-parach zacisków (n-wrotnik). Przy badaniu obwodu metodami zaciskowymi określa się zależności
pomiędzy wielkościami związanymi z zaciskami obwodu bez wnikania w strukturę wewnętrzną.
Wielkości zaciskowe pozwalają na badanie własności rozpatrywanego obwodu.
Część obwodu elektrycznego scharakteryzowana przez parametry konieczne i dostateczne do
sformułowania związków między napięciem i prądami na zaciskach tego obwodu nazywamy
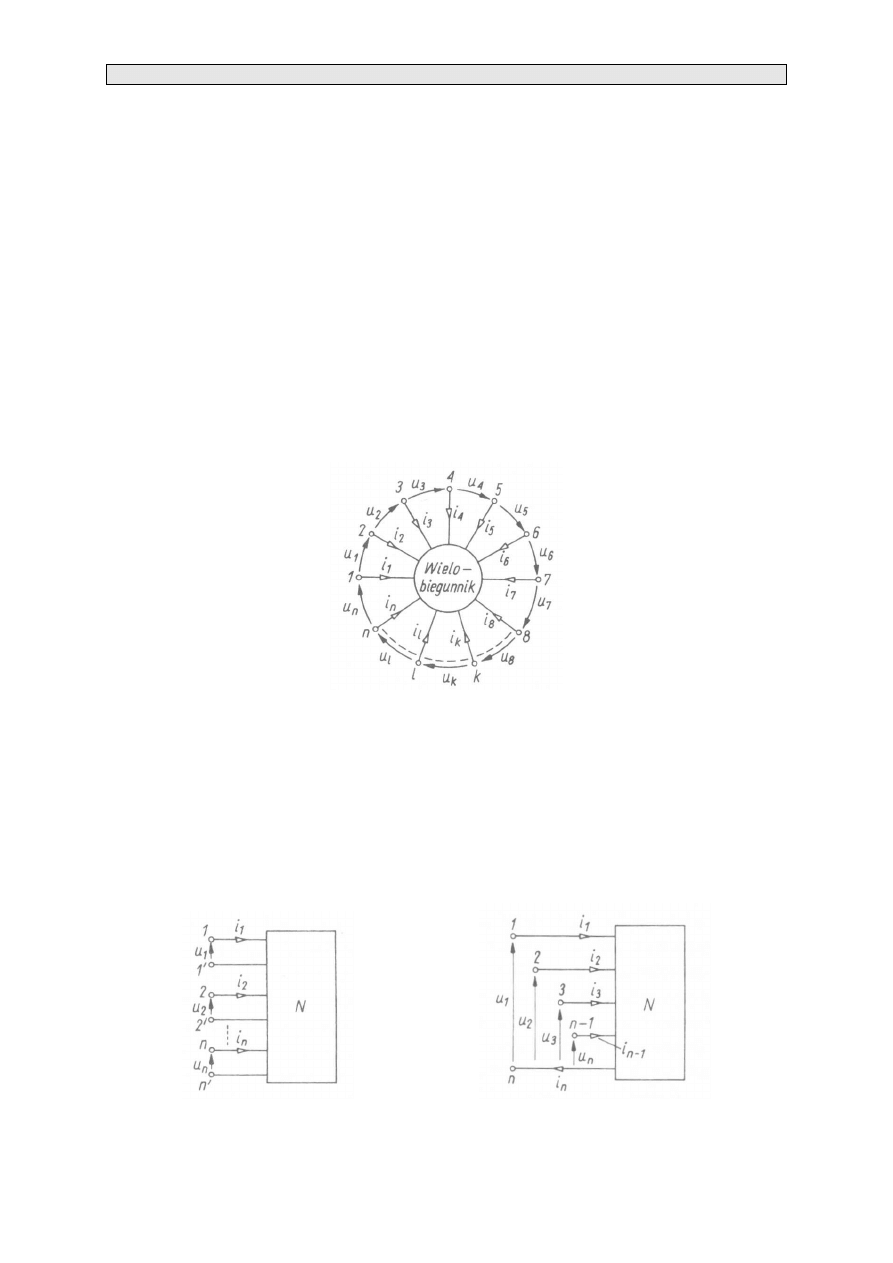
wielobiegunnikiem.
Rys. 3.1. Wielobiegunnik o n zaciskach [1]
W ogólnym przypadku wielobiegunnik jest scharakteryzowany przez n zacisków (przy
2
≥
n
)
(rys. 3.1)
Jako przykład wielobiegunników można wymienić transformator (zwłaszcza wielouzwojeniowy),
wzmacniacz, tranzystor, linię przesyłową wielotorową itp.
Jeśli zaciski wielobiegunnika tworzą pary uporządkowane, przy czym można wyróżnić n-par takich
zacisków, to wielobiegunnik nazywamy n-wrotnikiem.
W szczególnym przypadku, gdy wszystkie pary mają jeden wspólny zacisk, n-wrotnik nazywamy
niezrównoważonym lub uziemionym.
Rys. 3.2. Schemat ogólny n-wrotnika [1]
Rys. 3.3. Schemat n-wrotnika niezrównoważonego [1]

Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
2
Model matematyczny n-wrotnika wyraża związki między n wymiarowym wektorem napięć u na
zaciskach n-wrotnika i n wymiarowym wektorem prądów i związanych z poszczególnymi zaciskami.
Często wektor napięć traktujemy jako wektor wymuszeń, a wektor prądów jako wektor odpowiedzi.
W ogólnym przypadku związek pomiędzy wymuszeniem x a odpowiedzią y wyrażamy zależnością
x
y
⋅
=
N
(3.1)
przy czym: N - pewien operator; y - wektor odpowiedzi; x - wektor wymuszeń (zarówno
napięciowych jak i prądowych).
Przy badaniu n-wrotnika, sygnały związane z jego wrotami mogą być wyrażone w postaci czasowej,
w postaci zespolonej lub w postaci operatorowej. Opis operatorowy jest najbardziej ogólny i pozwala
na badanie n-wrotnika w warunkach dynamicznych (w stanach nieustalonych).
Podstawowe własno
ś
ci wielobiegunnika
•
Liniowość
Wielobiegunnik N nazywamy liniowym jeśli spełnia własności:
a) addytywności:
N
∈
+
)
,
(
)
,
(
2
2
1
1
y
x
y
x
dla wszystkich
N
∈
)
,
(
),
,
(
2
2
1
1
y
x
y
x
Jeśli
1
y
jest odpowiedzią układu na wymuszenie
1
x
, a
2
y
jest odpowiedzią układu na wymuszenie
2
x
, to
2
1
y
y
+
jest odpowiedzią na wymuszenie
2
1
x
x
+
.
b) jednorodności
N
a
∈
)
,
(
y
x
dla wszystkich
N
∈
)
,
(
y
x
Jeśli
y
jest odpowiedzią układu na wymuszenie
x
, to
y
a
jest odpowiedzią na wymuszenie
x
a
(
a
- stała rzeczywista).
•
Stacjonarność
Wielobiegunnik N nazywamy stacjonarnym jeśli przy dowolnej, rzeczywistej wartości
τ
spełniona
jest zależność
[
] [
]
)
(
),
(
)
(
),
(
τ
τ
τ
τ
+
+
=
t
t
t
t
y
x
y
x
dla wszystkich
N
∈
)
,
( y
x
oraz
N
τ
τ
∈
)
,
(
y
x
Wielobiegunnik N jest stacjonarny, jeśli jego parametry są niezależne od czasu.
•
Pasywność
Wielobiegunnik N nazywamy pasywnym jeśli dla dowolnej chwili
t
energia doprowadzona do
wielobiegunnika jest nieujemna. (wewnątrz nie zawiera źródeł napięcia ani prądu)
0
)
(
)
(
≥
=
∫
∞
−
τ
τ
d
p
t
W
t
•
Wzajemność (odwracalność)
Wielobiegunnik N nazywamy wzajemnym (odwracalnym) jeśli.
)
(
*
)
(
)
(
*
)
(
1
2
2
1
t
t
t
t
t
t
y
x
y
x
=
dla wszystkich
N
∈
)
,
(
),
,
(
2
2
1
1
y
x
y
x
Wielobiegunnik, który spełnia zasadę wzajemności nazywamy wzajemnym lub odwracalnym.
Twierdzenie o wzajemności (oczkowe): jeżeli w obwodzie liniowym rozgałęzionym, jedyne
ź
ródło napięcia znajdujące się w gałęzi k-tej wywołuje w gałęzi l-tej tego obwodu prąd I,
to po przeniesieniu tego źródła do gałęzi l-tej w gałęzi k-tej popłynie również prąd I.
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
3
3.2. Podstawowe poj
ę
cia dotycz
ą
ce czwórników
Czwórnik jest szczególnym przypadkiem n-wrotnika, o n=2. Jest zatem elementem czterozaciskowym
mającym dwie pary uporządkowanych zacisków zwanych wrotami; jedną parę zacisków nazywamy
wejściem, a drugą parę wyjściem czwórnika. Czwórniki pobierają energię przez zaciski wejściowe
(pierwotne), a oddają ją przez zaciski wyjściowe (wtórne). Wobec tego czwórniki służą do
przekazywania energii, przy czym przepływ energii odbywa się w kierunku od zacisków wejściowych
do zacisków wyjściowych. Przykładem czwórników są np. dwuprzewodowe linie przesyłowe (dwa
zaciski na początku linii i dwa zaciski na jej końcu) albo transformatory (dwa zaciski uzwojenia
pierwotnego i dwa zaciski uzwojenia wtórnego).
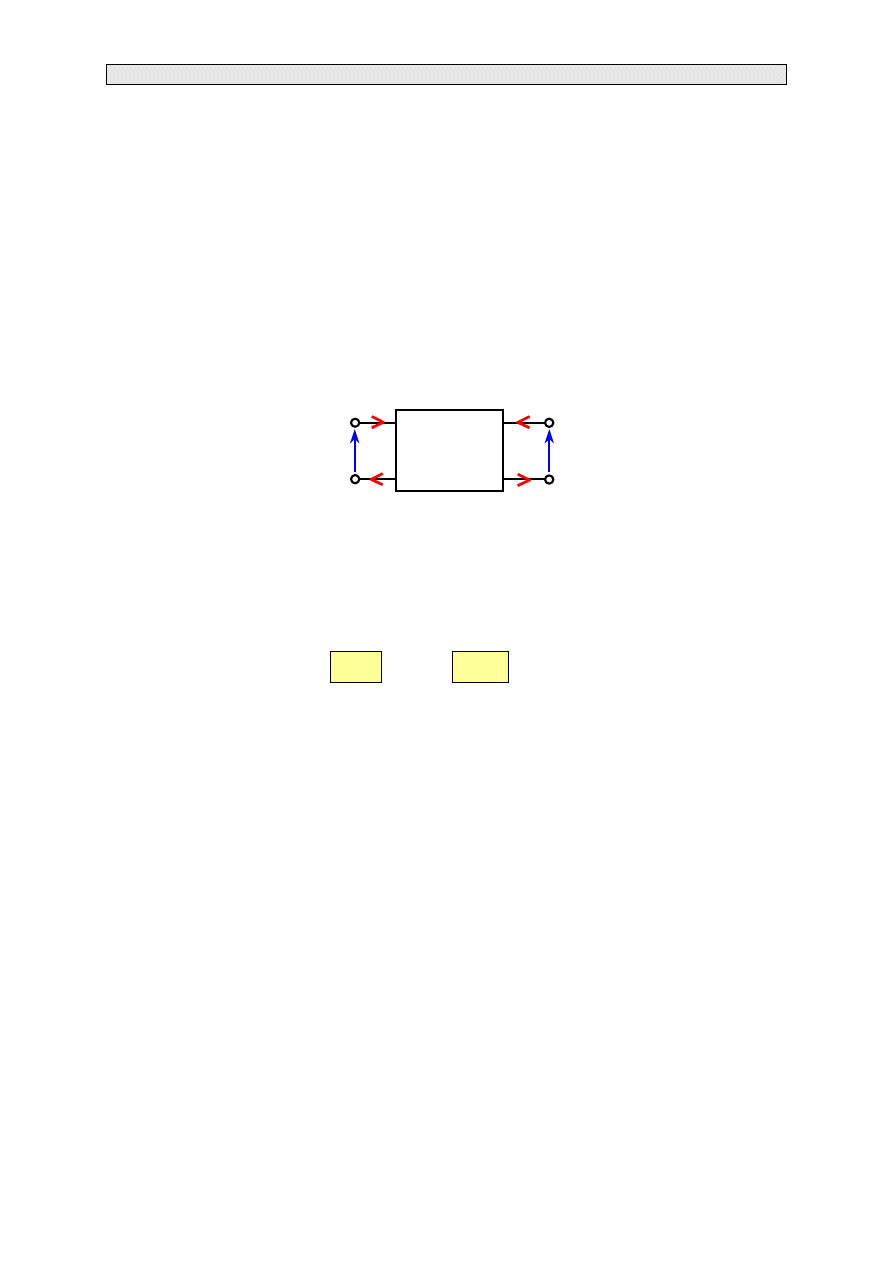
Schemat ogólny czwórnika ma postać prostokąta z wyprowadzonymi dwiema parami zacisków. Prąd
i napięcie wrót wejściowych oznaczamy indeksem „1”, a wrót wyjściowych indeksem „2”.
I
1
I
2
U
1
U
2
Wejście
Wyjście
1
1’
2
2’
I
1
’
I
2
’
Rys. 3.4. Schemat ogólny czwórnika (prądy zwrócone do prostokąta)
Ze względu na to, że czwórniki pobierają energię przez zaciski wejściowe, prądy w przewodach
połączonych z tymi zaciskami są jednakowe. Biorąc pod uwagę, że czwórnik oddaje energię przez
zaciski wyjściowe, otrzymujemy równość prądów w przewodach połączonych z tymi zaciskami.
W odniesieniu do wejścia i wyjścia czwórnika musi być spełniony następujący warunek równości
prądów:
'
1
1
I
I
=
oraz
'
2
2
I
I
=
(3.2)
Czwórniki dzielimy na
liniowe (składające się z elementów liniowych) i nieliniowe, stacjonarne
(o parametrach niezależnych od czasu) i
niestacjonarne, symetryczne (jeśli przy zamianie miejscami
wejścia i wyjścia, nie zmieni się rozpływ prądów i rozkład napięć w obwodzie poza czwórnikiem) i
niesymetryczne, odwracalne (spełniające zasadę wzajemności)
i
nieodwracalne, pasywne (wszystkie
gałęzie połączeń w czwórniku są pasywne albo gałęzie aktywne występujące w połączeniach
wewnętrznych wzajemnie się kompensują) i
aktywne.
Teoria czwórników umożliwia badanie ich własności zaciskowych na podstawie ogólnych równań
algebraicznych wiążących prądy i napięcia na wejściu i wyjściu czwórnika. Badanie tych własności
dokonuje się bez konieczności wnikania do wnętrza czwórnika.
3.3. Równania czwórników
Równania czwórnika określają związki pomiędzy prądami i napięciami na wejściu i wyjściu
czwórnika. W przypadku rozważania czwórników liniowych do rozwiązywania zagadnień można
stosować metody rozwiązywania obwodów, a więc metodę klasyczną, metodę oczkową, węzłową,
zasadę superpozycji, twierdzenie o zastępczym źródle napięcia i zastępczym źródle prądu, metodę
transfiguracji obwodu itp. Napięcia i prądy na zaciskach czwórnika mogą być wielkościami
skalarnymi (przy prądzie stałym), mogą być wyrażone jako wartości skuteczne zespolone (w stanie
ustalonym przy wymuszeniu sinusoidalnym) i mogą być wielkościami operatorowymi. Opis
operatorowy jest najbardziej ogólny i pozwala badać czwórniki w stanie nieustalonym.

Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
4
Związek między czterema wielkościami U
1
, U
2
, I
1
, I
2
, ujmujemy za pomocą dwóch równań liniowych.
W zależności od zastosowań wyróżniamy sześć typów równań wiążących prądy i napięcia czwórnika
(nie tylko pasywnego): postać impedancyjna, admitancyjna, łańcuchowa, łańcuchowa odwrócona,
hybrydowa, hybrydowa odwrócona.
Typy równa
ń
opisuj
ą
cych czwórniki
•
Równanie impedancyjne
⋅
+
⋅
=
⋅
+
⋅
=
2
22
1
21
2
2
12
1
11
1
I
z
I
z
U
I
z
I
z
U
(3.3)
lub w postaci macierzowej
⋅
=
2
1
22
21
12
11
2
1
I
I
z
z
z
z
U
U
(3.4)
w której
=
22
21
12
11
z
z
z
z
Z
(3.5)
jest macierzą impedancyjną, a
11
z
,
12
z
,
21
z
,
22
z
nazywane są parametrami impedancyjnymi.
Wielkości występujące w równaniu (3.4) wyrażane są w następujących jednostkach
⋅
=
A
A
Ω
Ω
Ω
Ω
V
V
(3.6)
•
Równanie admitancyjne
⋅
+
⋅
=
⋅
+
⋅
=
2
22
1
21
2
2
12
1
11
1
U
y
U
y
I
U
y
U
y
I
(3.7)
lub w postaci macierzowej
⋅
=
2
1
22
21
12
11
2
1
U
U
y
y
y
y
I
I
(3.8)
w której
=
22
21
12
11
y
y
y
y
y
(3.9)
jest macierzą admitancyjną, a
11
y ,
12
y
,
21
y
,
22
y
nazywane są parametrami admitancyjnymi.
Wielkości występujące w równaniu (3.8) wyrażane są w następujących jednostkach
⋅
=
V
V
S
S
S
S
A
A
(3.10)
•
Równanie łańcuchowe
⋅
+
⋅
=
⋅
+
⋅
=
2
2
1
2
2
1
I
D
U
C
I
I
B
U
A
U
(3.11)
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
5
lub w postaci macierzowej
⋅
=
2
2
1
1
I
U
D
C
B
A
I
U
(3.12)
w której
=
D
C
B
A
A
(3.13)
jest macierzą łańcuchową, a A, B , C , D nazywane są parametrami łańcuchowymi.
Wielkości występujące w równaniu (3.12) wyrażane są w następujących jednostkach
⋅
=
A
V
1
S
Ω
1
A
V
(3.14)
•
Równanie łańcuchowe odwrócone
⋅
+
⋅
=
⋅
+
⋅
=
1
1
2
1
1
2
'
'
'
'
I
D
U
C
I
I
B
U
A
U
(3.15)
lub w postaci macierzowej
⋅
=
1
1
2
2
'
'
'
'
I
U
D
C
B
A
I
U
(3.16)
w której
=
=
A
C
B
D
D
C
B
A
A
B
det
1
'
'
'
'
(3.17)
jest macierzą łańcuchową odwróconą, a
'
A ,
'
B ,
'
C ,
'
D nazywane są parametrami łańcuchowymi
odwróconymi. Wielkości występujące w równaniu (3.16) wyrażane są w następujących jednostkach
⋅
=
A
V
1
S
Ω
1
A
V
(3.18)
•
Równanie hybrydowe
⋅
+
⋅
=
⋅
+
⋅
=
2
22
1
21
2
2
12
1
11
1
U
h
I
h
I
U
h
I
h
U
(3.19)
lub w postaci macierzowej
⋅
=
2
1
22
21
12
11
2
1
U
I
h
h
h
h
I
U
(3.20)
w której
=
22
21
12
11
h
h
h
h
h
(3.21)
jest
macierzą hybrydową, a
11
h ,
12
h
,
21
h
,
22
h
nazywane są
parametrami hybrydowymi.
Wielkości występujące w równaniu (3.20) wyrażane są w następujących jednostkach
⋅
=
V
A
S
1
1
Ω
A
V
(3.22)
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
6
•
Równanie hybrydowe odwrócone
⋅
+
⋅
=
⋅
+
⋅
=
2
22
1
21
2
2
12
1
11
1
I
g
U
g
U
I
g
U
g
I
(3.23)
lub w postaci macierzowej
⋅
=
2
1
22
21
12
11
2
1
I
U
g
g
g
g
U
I
(3.24)
w której
=
22
21
12
11
g
g
g
g
g
(3.25)
jest macierzą hybrydową odwróconą, a
11
g ,
12
g
,
21
g
,
22
g
nazywane są parametrami hybrydowymi
odwróconymi
. Wielkości występujące w równaniu (3.24) wyrażane są w następujących jednostkach
⋅
=
A
V
Ω
1
1
S
V
A
(3.26)
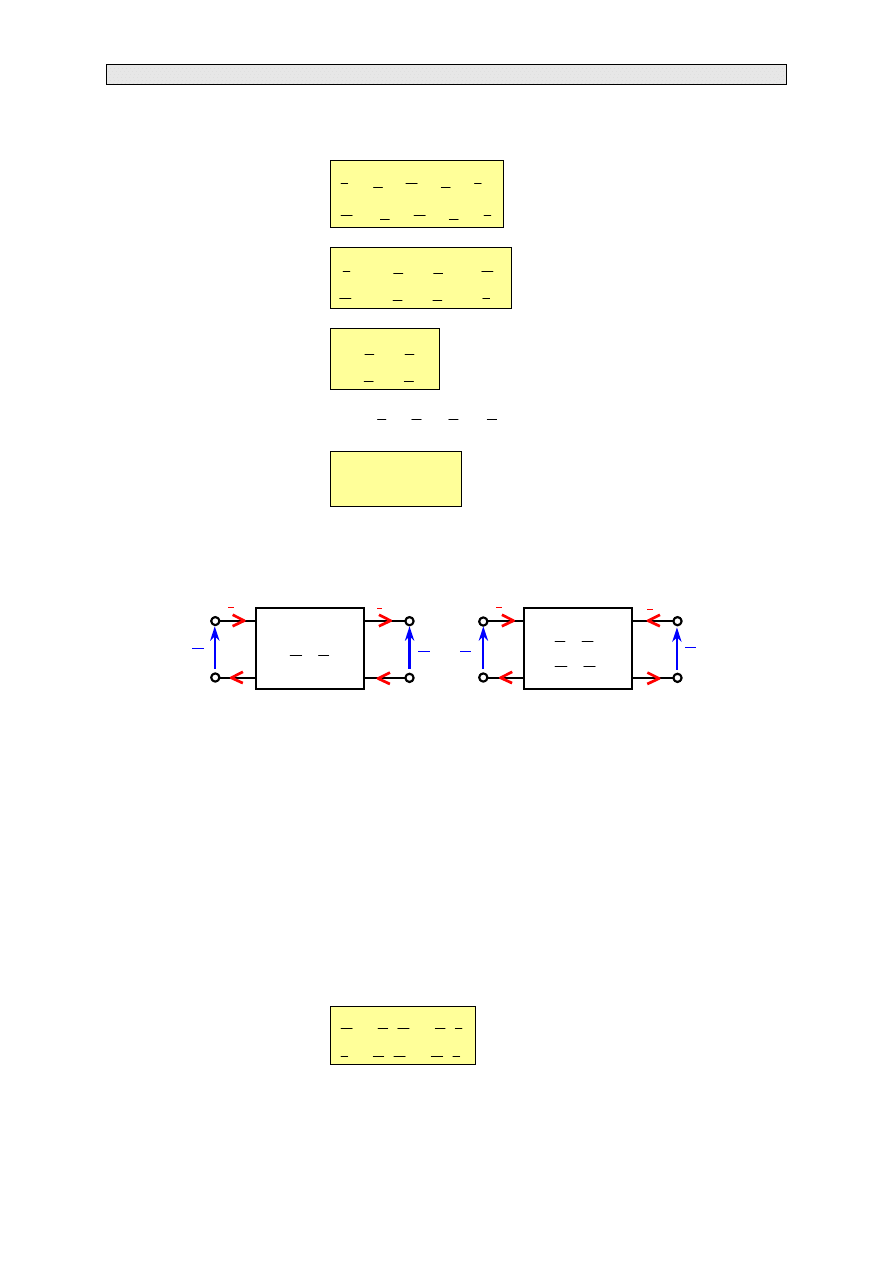
W zależności od wyboru postaci równań opisujących dany czwórnik stosuje się różne zwroty prądów
na wyjściu czwórnika (zasady strzałkowania przedstawiono na rys. 3.5).
B
A
I
1
I
2
U
1
U
2
G
H
Y
Z
I
1
I
2
U
1
U
2
a)
b)
Rys. 3.5. Zasady strzałkowania czwórników w zależności od macierzy opisującej
Ustalenie związku pomiędzy napięciami i prądami wejścia i wyjścia jest możliwe wówczas, gdy
znane są parametry jednej z postaci. W celu wyznaczenia parametrów równania określonej postaci
należy zastosować jedną z metod rozwiązywania obwodów rozgałęzionych liniowych.
Do opisów czwórników pasywnych najczęściej stosuje się równania łańcuchowe, natomiast przy
połączeniach czwórników stosuje się równania o niemal wszystkich postaciach wybieranych w
zależności od sposobów połączenia czwórników.
3.4. Warunki symetrii i odwracalno
ś
ci czwórnika
Rozważmy czwórnik pasywny, którego schemat przedstawiony jest na rys. 3.5a. Równania
łańcuchowe (3.11)
⋅
+
⋅
=
⋅
+
⋅
=
2
2
1
2
2
1
I
D
U
C
I
I
B
U
A
U
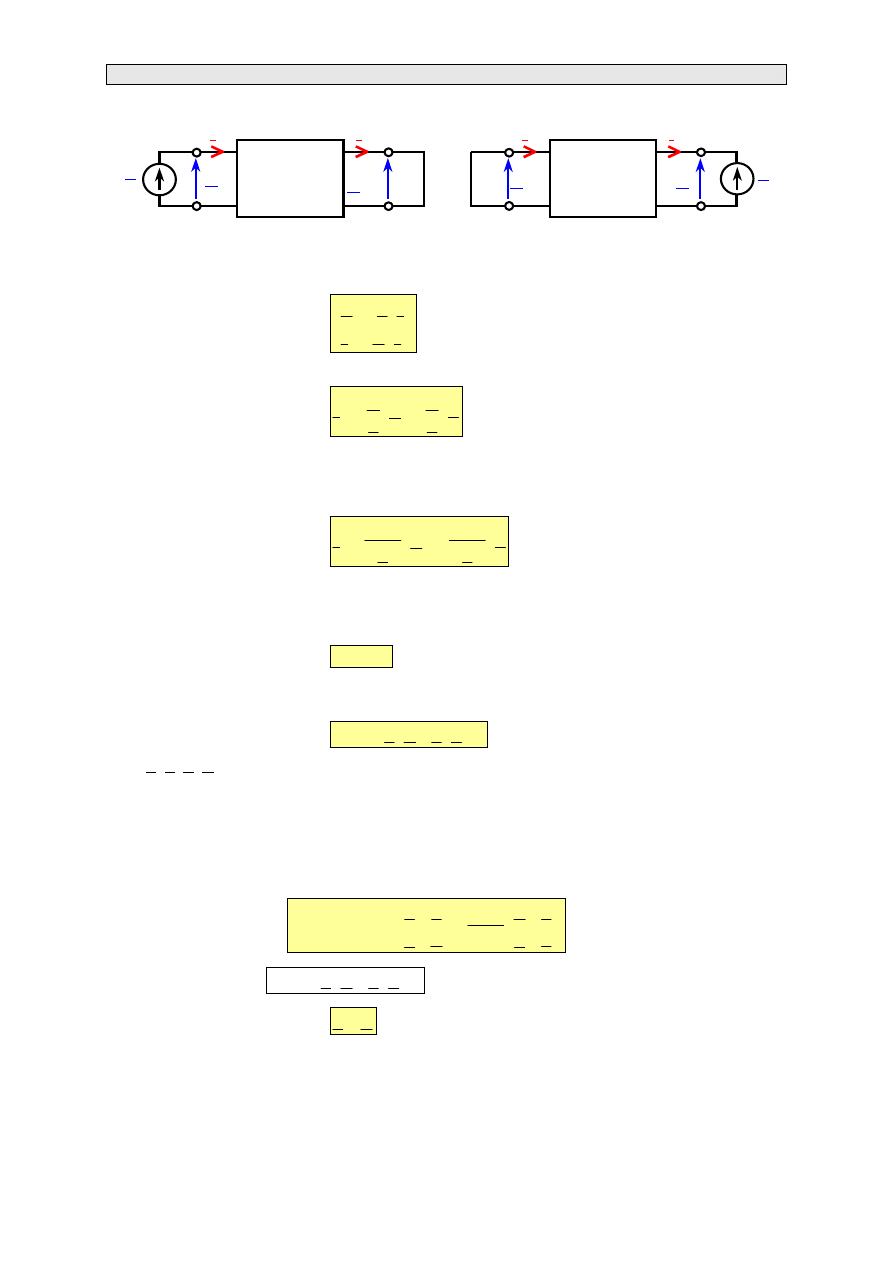
Załóżmy, że czwórnik jest zasilany od strony zacisków wejściowych napięciem U
1
=E, natomiast
zaciski wyjściowe są zwarte (U
2
=0) (rys. 3.6a)
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
7
I
1
I
2
U
1
U
2
=0
E
a)
I
1
I
2
U
1
=0
U
2
E
b)
Rys. 3.6. Czwórnik zasilany od strony zacisków wejściowych, o zwartych zaciskach wyjściowych
Równania łańcuchowe (3.11) przyjmą postać:
⋅
=
⋅
=
2
1
2
1
I
D
I
I
B
U
(3.27)
Wobec czego prąd I
2
(płynący w zwartym obwodzie wyjścia) wyznaczony zostanie z zależności
E
B
U
B
I
⋅
=
⋅
=
1
1
1
2
(3.28)
Załóżmy także sytuację odwrotną - czwórnik jest zasilany od strony zacisków wyjściowych napięciem
U
2
=E, natomiast zaciski wejściowe są zwarte (U
1
=0) (rys. 3.6b). W zwartym obwodzie wejścia
popłynie wówczas prąd I
1
(prąd I
1
zmieni zwrot)
E
B
U
B
I
⋅
=
⋅
=
A
A
det
det
2
1
(3.29)
Jeśli prąd I
2
określony równaniem (3.28) jest równy prądowi I
1
określonemu równaniem (3.29), to
wówczas spełniona zostaje zasada wzajemności. Równość tych prądów zachodzi wtedy, gdy
spełniony zostaje warunek
1
det
=
A
(3.30)
Warunek (3.30) jest jednocześnie warunkiem odwracalności czwórnika. Równanie (3.30) można
zapisać też w równoważnej postaci
1
det
=
⋅
−
⋅
=
C
B
D
A
A
(3.31)
gdzie A, B, C, D- parametry macierzy łańcuchowej.
Wspomniano powyżej, że czwórnik nazywamy symetrycznym jeżeli przy zamianie miejscami wejścia i
wyjścia, nie zmieni się rozpływ prądów i rozkład napięć w obwodzie poza czwórnikiem, tzn. w
obwodzie dołączonym do wejścia i w obwodzie dołączonym do wyjścia czwórnika. Wynika z tego, że
dla czwórnika symetrycznego macierze A (macierz łańcuchowa) i B (macierz łańcuchowa odwrócona)
muszą być sobie równe. Porównując zależności (3.13) oraz (3.17) otrzymamy
=
⇒
=
A
C
B
D
D
C
B
A
A
B
A
det
1
(3.32)
Zatem A=B jeżeli przy
1
det
=
⋅
−
⋅
=
C
B
D
A
A
, parametr
D
A
=
(3.33)
Równania (3.31) oraz (3.33) są warunkami symetryczności czwórnika.
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
8
Podsumowując, i uwzględniając relacje
pomiędzy elementami różnych macierzy czwórnika (relacje te
opublikowano np. w [2], str. 393 lub w [5] str. 90), można stwierdzić co następuje
•
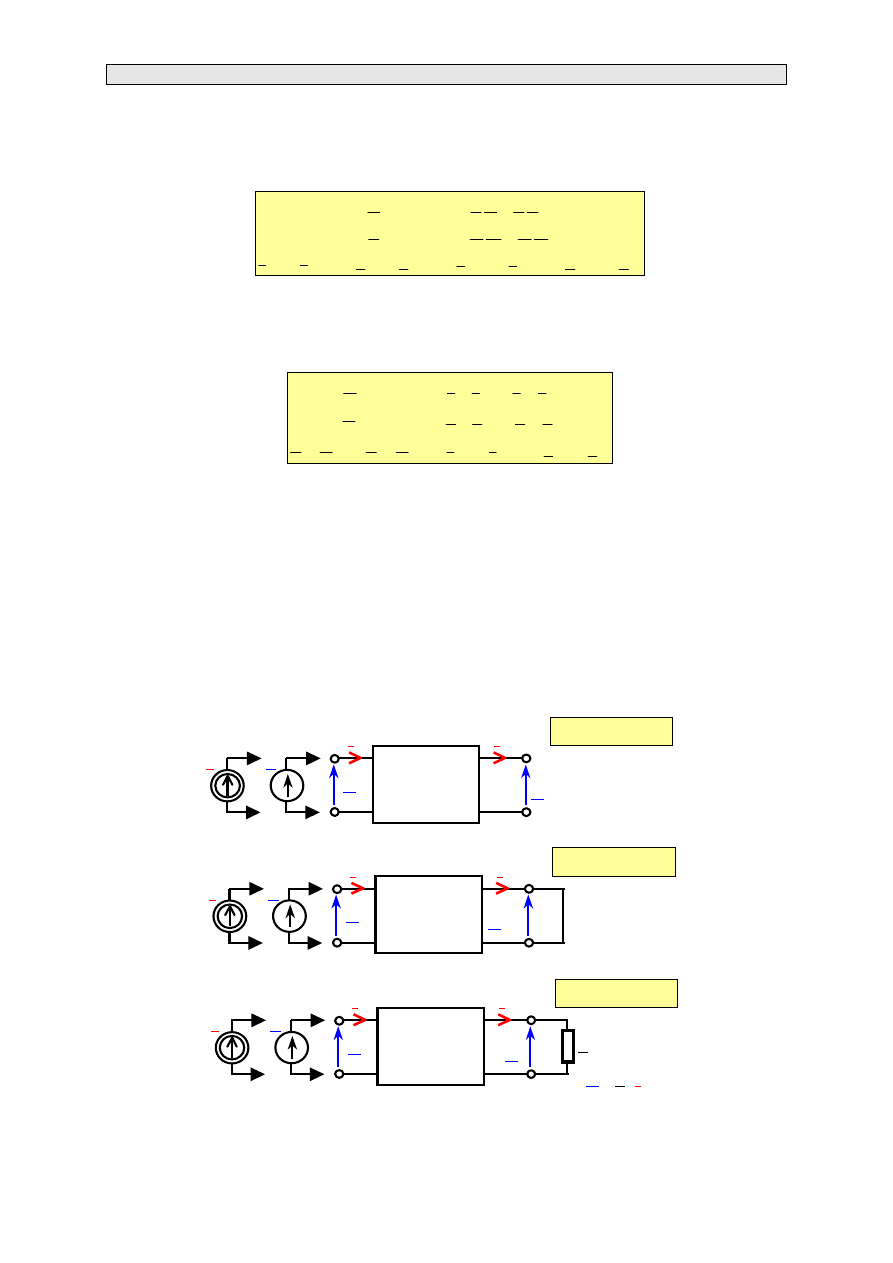
Czwórnik jest odwracalny jeżeli spełnione są zależności
12
21
12
21
12
21
12
21
1
'
'
'
'
1
)
(
det
1
1
)
(
det
g
g
h
h
y
y
z
z
C
B
D
A
C
B
D
A
−
=
−
=
=
=
=
−
⇔
=
=
−
⇔
=
B
A
(3.34)
•
Czwórnik jest symetryczny wtedy i tylko wtedy, gdy jest odwracalny i gdy po zamianie strony
zasilania prądy i napięcia nie zmieniają się zarówno po stronie wejściowej jak i wyjściowej. Dla
czwórników symetrycznych prawdziwe są związki
11
22
11
22
21
12
22
11
21
12
22
11
'
'
1
1
)
(
det
1
1
)
(
det
y
y
z
z
D
A
D
A
g
g
g
g
h
h
h
h
=
=
=
=
=
−
⇔
=
=
−
⇔
=
G
H
(3.35)
Do opisu czwórnika pasywnego symetrycznego wystarczą tylko dwa niezależne parametry, gdyż
czwórniki pasywne są jednocześnie odwracalne.
3.5. Stany pracy czwórnika
Po dołączeniu do zacisków wejściowych czwórnika źródła napięcia lub źródła prądu możliwe są
następujące stany pracy czwórnika:
•
stan jałowy - zaciski wyjściowe czwórnika są rozwarte (rys. 3.7a)
•
stan zwarcia - zaciski wyjściowe czwórnika są zwarte (rys. 3.7b)
•
stan obciążenia – do zacisków wyjściowych dołączony jest odbiornik (rys. 3.7c)
I
1
I
2
=0
U
1
U
2
E
J
Stan jałowy
a)
I
1
I
2
U
1
U
2
=0
E
J
Stan zwarcia
b)
c)
I
1
I
2
U
1
U
2
E
J
Stan obciążenia
Z
2
U
2
=
Z
2
·
I
2
Rys. 3.7. Stany pracy czwórnika: stan jałowy (rys. a), stan zwarcia (rys. b), stan obciążenia (rys. c)
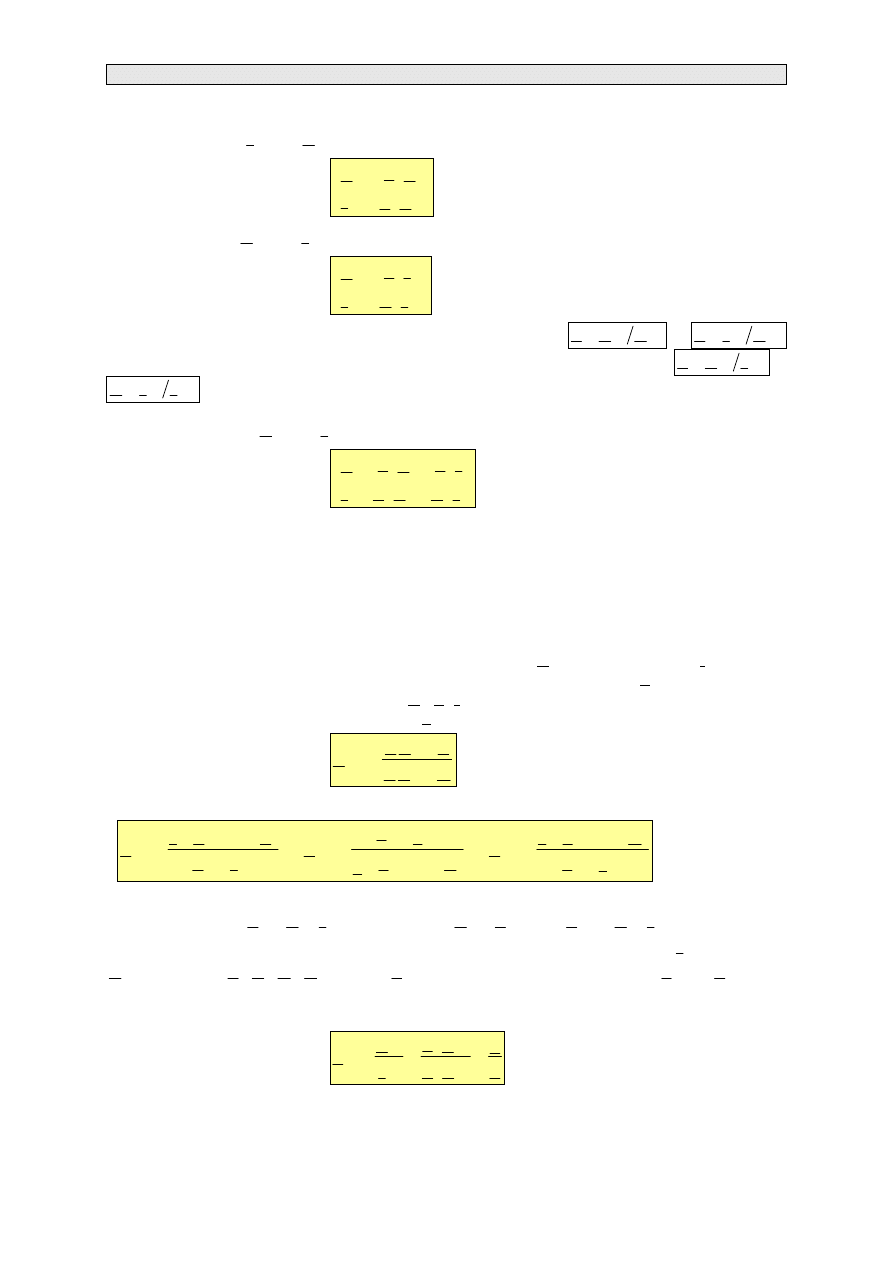
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
9
W stanie jałowym (
0
2
=
I
,
0
2
≠
U
) równania łańcuchowe (3.13) przyjmą postać
⋅
=
⋅
=
20
10
20
10
U
C
I
U
A
U
(3.36)
W stanie zwarcia (
0
2
=
U
,
0
2
≠
I
) równania łańcuchowe przyjmą postać
⋅
=
⋅
=
k
k
k
k
I
D
I
I
B
U
2
1
2
1
(3.37)
Zauważmy, że w stanie jałowym można wyznaczyć parametry
20
10
U
U
A
=
i
20
10
U
I
C
=
(równania 3.36), natomiast w stanie zwarcia można wyznaczyć parametry
k
k
I
U
B
2
1
=
i
k
k
I
I
D
2
1
=
czwórnika (równ. 3.37), i w ten sposób uzyskać pełną postać macierzy łańcuchowej
A
W stanie obciążenia (
0
2
≠
U
,
0
2
≠
I
) równania łańcuchowe mają pełną postać (3.13)
⋅
+
⋅
=
⋅
+
⋅
=
2
2
1
2
2
1
I
D
U
C
I
I
B
U
A
U
W stanie zwarcia i w stanie jałowym uproszczeniu ulegają także i pozostałe typy równań czwórnika,
a więc równania impedancyjne, admitancyjne i hybrydowe.
3.6. Impedancja wej
ś
ciowa czwórnika
Impedancja wejściowa czwórnika jest to stosunek napięcia U
1
na wejściu do prądu I
1
na wejściu
czwórnika. Oczywiście impedancja wejściowa czwórnika zależy od obciążenia Z
2
. Uwzględniając, że
po stronie wtórnej spełniona jest równość U
2
=Z
2
·I
2
możemy napisać wzór ogólny na impedancję
wejściową czwórnika obciążonego impedancją Z
2
w zależności od elementów macierzy łańcuchowej
D
Z
C
B
Z
A
Z
we
+
+
=
2
2
(3.38)
Jeżeli znana jest macierz inna niż łańcuchowa, wówczas stosowane są zależności
22
2
2
11
2
11
22
2
22
2
2
11
)
(
det
,
)
(
det
,
)
(
det
h
Y
Y
h
Z
Y
y
y
Y
Z
z
Z
Z
z
Z
we
we
we
+
+
=
+
+
=
+
+
=
H
Y
Z
(3.39)
Wzory (3.39) można uzyskać w oparciu o ogólne równania czwórnika w różnych postaciach, przy
uwzględnieniu, że
2
2
2
/ I
U
Z
=
dla macierzy
B
A i
, oraz
2
2
2
/
I
U
Z
−
=
dla pozostałych
macierzy. Znak minus wynika z nieodbiornikowego (zgodnego) strzałkowania prądu
2
I oraz napięcia
2
U dla macierzy
G
H
Y
Z
,
,
,
. Symbol
2
Y oznacza admitancję obciążenia, tzn.
2
2
/
1
Z
Y
=
.
Impedancja wejściowa czwórnika w stanie jałowym wyznaczana jest z zależności (3.36)
C
A
U
C
U
A
I
U
Z
=
⋅
⋅
=
=
20
20
10
10
10
(3.40)
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
10
Dla innych równań macierzowych czwórnika impedancja wejściowa w stanie jałowym wyznaczana
jest z zależności
22
10
22
10
11
10
)
(
det
)
(
det
h
Z
y
Z
z
Z
H
Y
=
=
=
(3.41)
Impedancja wejściowa czwórnika w stanie zwarcia wyznaczana jest z zależności (3.37)
D
B
I
D
I
B
I
U
Z
k
k
k
k
k
=
⋅
⋅
=
=
2
2
1
1
1
(3.42)
Dla innych równań macierzowych czwórnika impedancja wejściowa w stanie zwarcia wyznaczana
jest z zależności
11
1
11
1
22
1
1
)
(
det
h
Z
y
Z
z
Z
k
k
k
=
=
=
Z
(3.43)
3.7. Schematy zast
ę
pcze czwórników pasywnych
Czwórniki, jako schematy zastępcze wielu urządzeń, można prawie zawsze przedstawić za pomocą
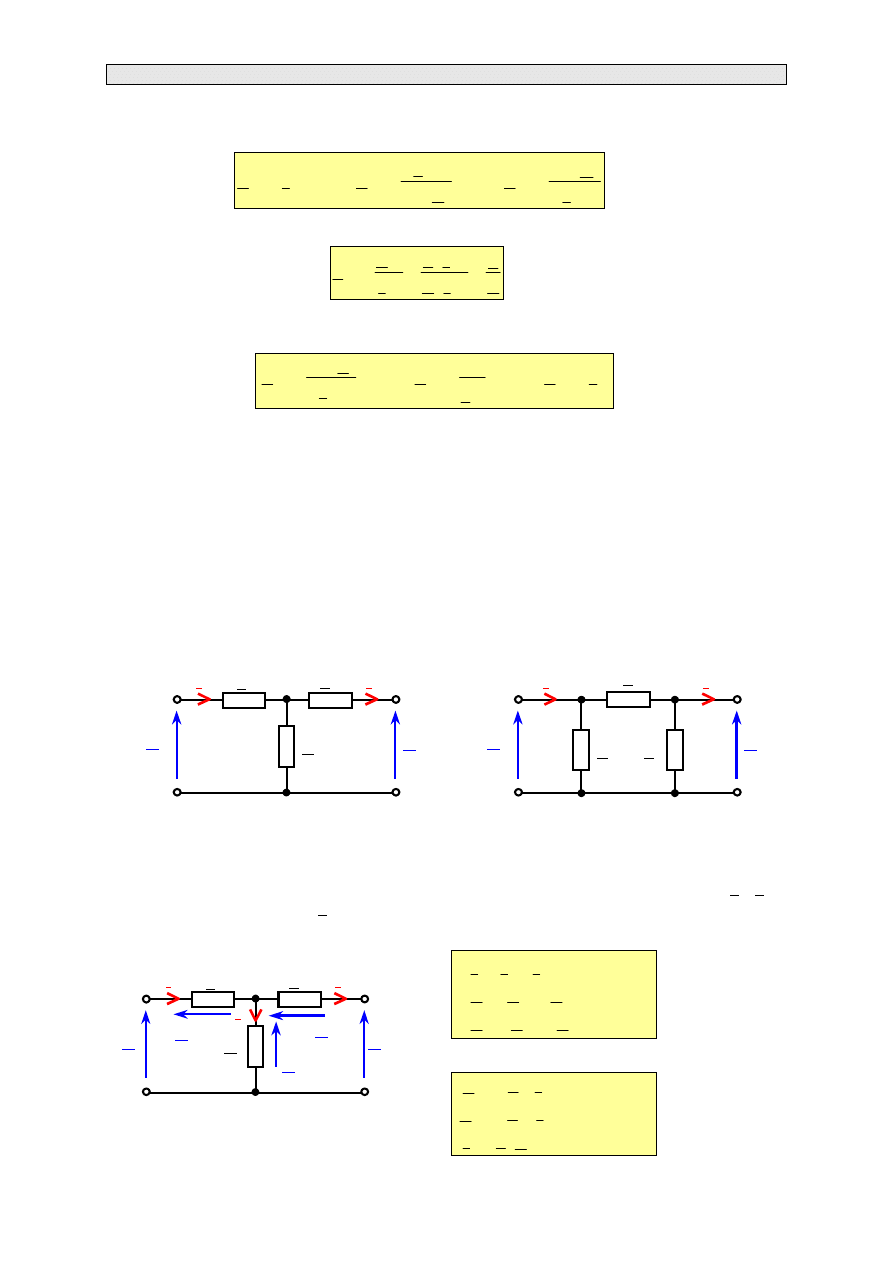
trzech impedancji tworzących strukturę jak pokazano na rys. 3.8. Czwórnik przedstawiony na
rys. 3.8a nazywamy czwórnikiem typu (kształtu) T, a czwórnik przedstawiony na rys. 3.8b
nazywamy czwórnikiem typu (kształtu) Π. Pierwszy z tych czwórników nazywany jest także
czwórnikiem gwiazdowym, gdyż jego gałęzie tworzą gwiazdę, a drugi nazywany jest czwórnikiem
trójkątowym, gdyż połączenie elementów odpowiada połączeniu w trójkąt. W praktyce czwórniki o
bardziej złożonej strukturze, można dzięki stosowaniu reguł przekształcania doprowadzić do jednej z
podanych struktur.
I
1
I
2
U
1
U
2
a)
Z
1
Z
2
Y
I
1
I
2
U
1
U
2
b)
Z
Y
1
Y
2
Rys. 3.8. Schematy zastępcze czwórników typu T (rys. a) i typu Π (rys. b)
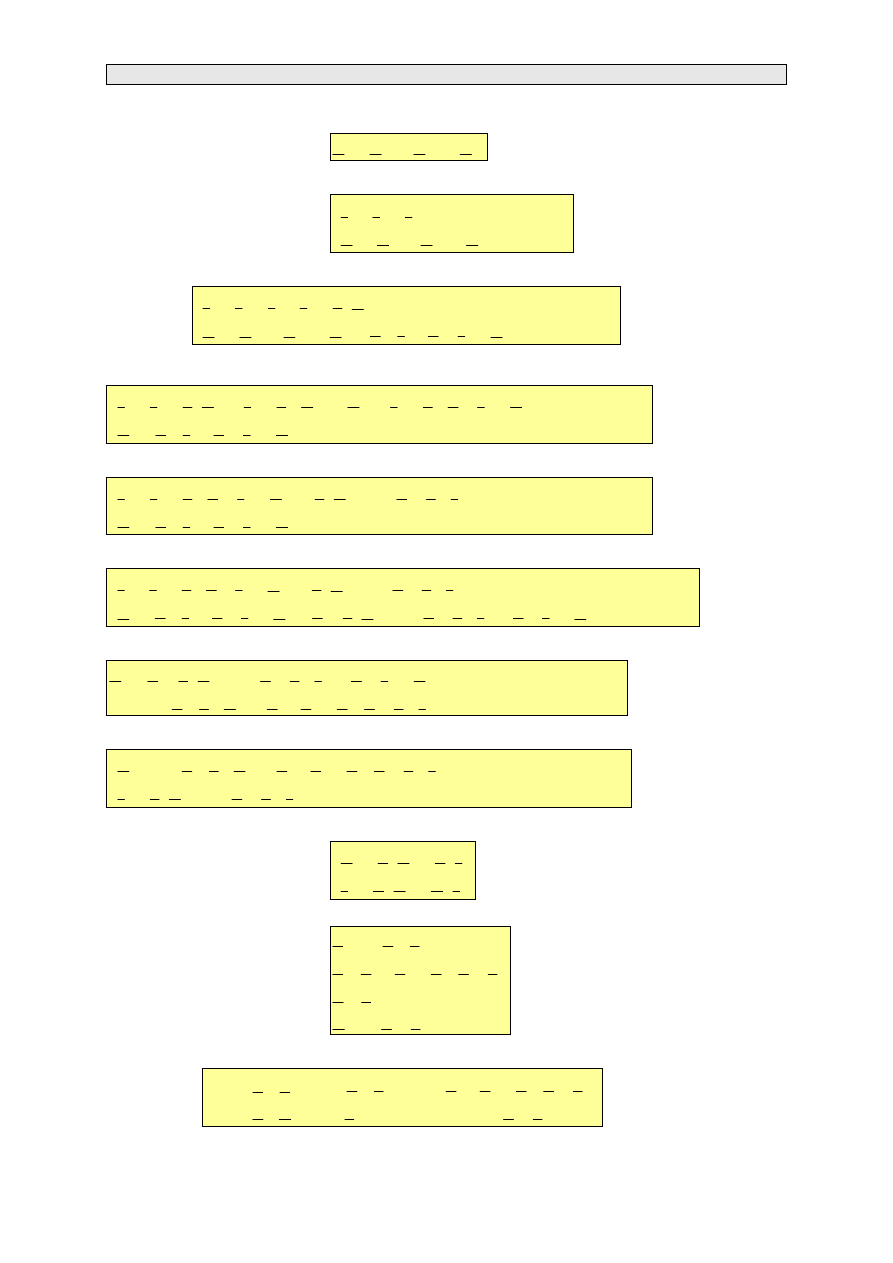
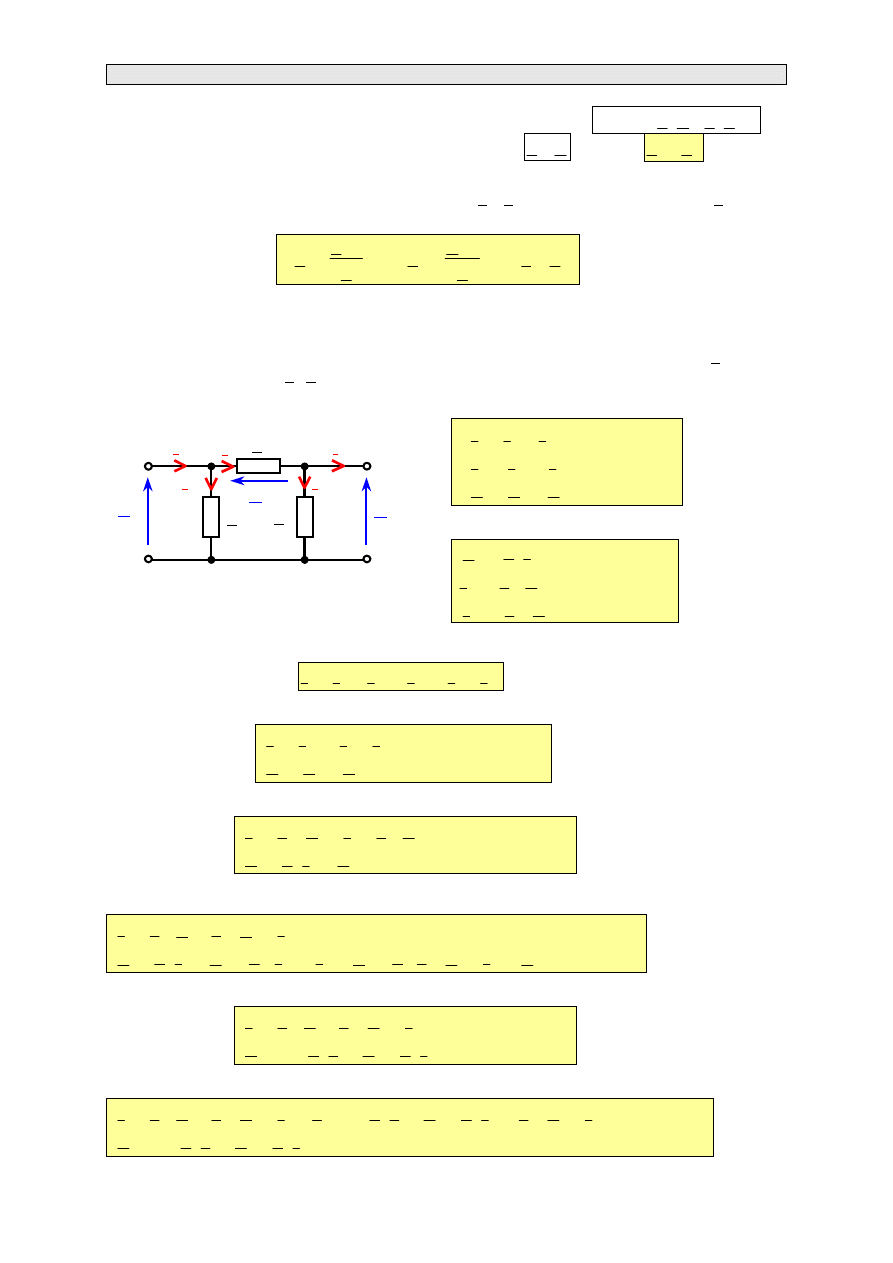
Czwórnik typu T
Przedstawiony na rys. 3.8a czwórnik typu T składa się z dwóch impedancji podłużnych (Z
1
, Z
2
) i
jednej admitancji poprzecznej (Y). Zależność pomiędzy napięciami i prądami na wejściu i na wyjściu
czwórnika znajdujemy na podstawie praw Kirchhoffa
+
=
+
=
=
−
−
)
3
(
)
2
(
)
1
(
0
2
2
1
1
3
2
1
T
U
U
U
T
U
U
U
T
I
I
I
Z
Y
Y
Z
(3.44)
Prawo Ohma wyrażają równania
)
6
(
)
5
(
)
4
(
3
2
2
2
1
1
1
T
U
Y
I
T
I
Z
U
T
I
Z
U
Y
Z
Z
⋅
=
⋅
=
⋅
=
(3.45)
I
1
I
2
U
1
U
2
Z
1
Z
2
Y
U
Z1
U
Z2
U
Y
I
3
Rys. 3.9. Zwroty napięć i prądów
w czwórniku typu T
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
11
Podstawmy równanie (T3) do równania (T2)
2
2
1
1
U
U
U
U
Z
Z
+
+
=
(3.46)
Otrzymamy układ równań postaci
+
+
=
+
=
)
8
(
)
7
(
2
2
1
1
3
2
1
T
U
U
U
U
T
I
I
I
Z
Z
(3.47)
Do układu równań (3.47) podstawny równania (T4), (T5) oraz (T6)
+
⋅
+
⋅
=
+
+
=
⋅
+
=
+
=
)
10
(
)
9
(
2
2
2
1
1
2
2
1
1
2
3
2
1
T
U
I
Z
I
Z
U
U
U
U
T
U
Y
I
I
I
I
Z
Z
Y
(3.48)
Do równania (T9) w układzie równań (3.48) podstawny równania (T3) oraz (T5)
+
⋅
+
⋅
=
+
⋅
⋅
+
=
+
⋅
+
=
⋅
+
=
)
12
(
)
11
(
)
(
)
(
2
2
2
1
1
1
2
2
2
2
2
2
2
2
1
T
U
I
Z
I
Z
U
T
U
I
Z
Y
I
U
U
Y
I
U
Y
I
I
Z
Y
(3.49)
Po przekształceniach
+
⋅
+
⋅
=
⋅
⋅
+
+
⋅
=
+
⋅
⋅
+
=
)
12
(
)
13
(
)
1
(
)
(
2
2
2
1
1
1
2
2
2
2
2
2
2
1
T
U
I
Z
I
Z
U
T
I
Y
Z
U
Y
U
I
Z
Y
I
I
(3.50)
Do równania (T12) w układzie równań (3.50) podstawny równanie (T13)
[
]
+
⋅
+
⋅
⋅
+
+
⋅
⋅
=
+
⋅
+
⋅
=
⋅
⋅
+
+
⋅
=
+
⋅
⋅
+
=
)
14
(
)
1
(
)
13
(
)
1
(
)
(
2
2
2
2
2
2
1
2
2
2
1
1
1
2
2
2
2
2
2
2
1
T
U
I
Z
I
Y
Z
U
Y
Z
U
I
Z
I
Z
U
T
I
Y
Z
U
Y
U
I
Z
Y
I
I
(3.51)
Równanie (T14), po przekształceniach, przyjmie postać
[
]
)
15
(
)
(
)
1
(
)
1
(
2
2
1
2
1
2
1
2
2
2
2
2
2
1
1
T
I
Y
Z
Z
Z
Z
U
Y
Z
U
I
Z
I
Y
Z
U
Y
Z
U
⋅
⋅
⋅
+
+
+
⋅
⋅
+
=
=
+
⋅
+
⋅
⋅
+
+
⋅
⋅
=
(3.52)
Ostatecznie otrzymamy układ równań
⋅
⋅
+
+
⋅
=
⋅
⋅
⋅
+
+
+
⋅
⋅
+
=
)
17
(
)
1
(
)
16
(
)
(
)
1
(
2
2
2
1
2
2
1
2
1
2
1
1
T
I
Y
Z
U
Y
I
T
I
Y
Z
Z
Z
Z
U
Y
Z
U
(3.53)
Porównując układ równań (3.53) z układem (3.11)
⋅
+
⋅
=
⋅
+
⋅
=
2
2
1
2
2
1
I
D
U
C
I
I
B
U
A
U
zauważamy, że parametry łańcuchowe
Y
Z
D
Y
C
Y
Z
Z
Z
Z
B
Y
Z
A
⋅
+
=
=
⋅
⋅
+
+
=
⋅
+
=
2
2
1
2
1
1
1
1
(3.54)
zatem macierz łańcuchowa ma postać
⋅
+
⋅
⋅
+
+
⋅
+
=
=
Y
Z
Y
Y
Z
Z
Z
Z
Y
Z
D
C
B
A
2
2
1
2
1
1
T
1
1
A
(3.55)
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
12
Nietrudno wykazać, że spełniony jest warunek odwracalności czwórnika
1
A
det
T
=
⋅
−
⋅
=
C
B
D
A
.
Czwórnik typu T jest symetryczny, gdy spełniony jest warunek
D
A
=
, czyli gdy
2
1
Z
Z
=
Jeżeli dane są parametry łańcuchowe, to na podstawie równań (3.54) można wyprowadzić zależności
na elementy czwórnika, czyli impedancje podłużne (Z
1
, Z
2
) i admitancję poprzeczną (Y), a więc
rozwiązać zagadnienie odwrotne w stosunku do zagadnienia rozważanego powyżej.
C
Y
C
D
Z
C
A
Z
=
−
=
−
=
1
1
2
1
(3.56)
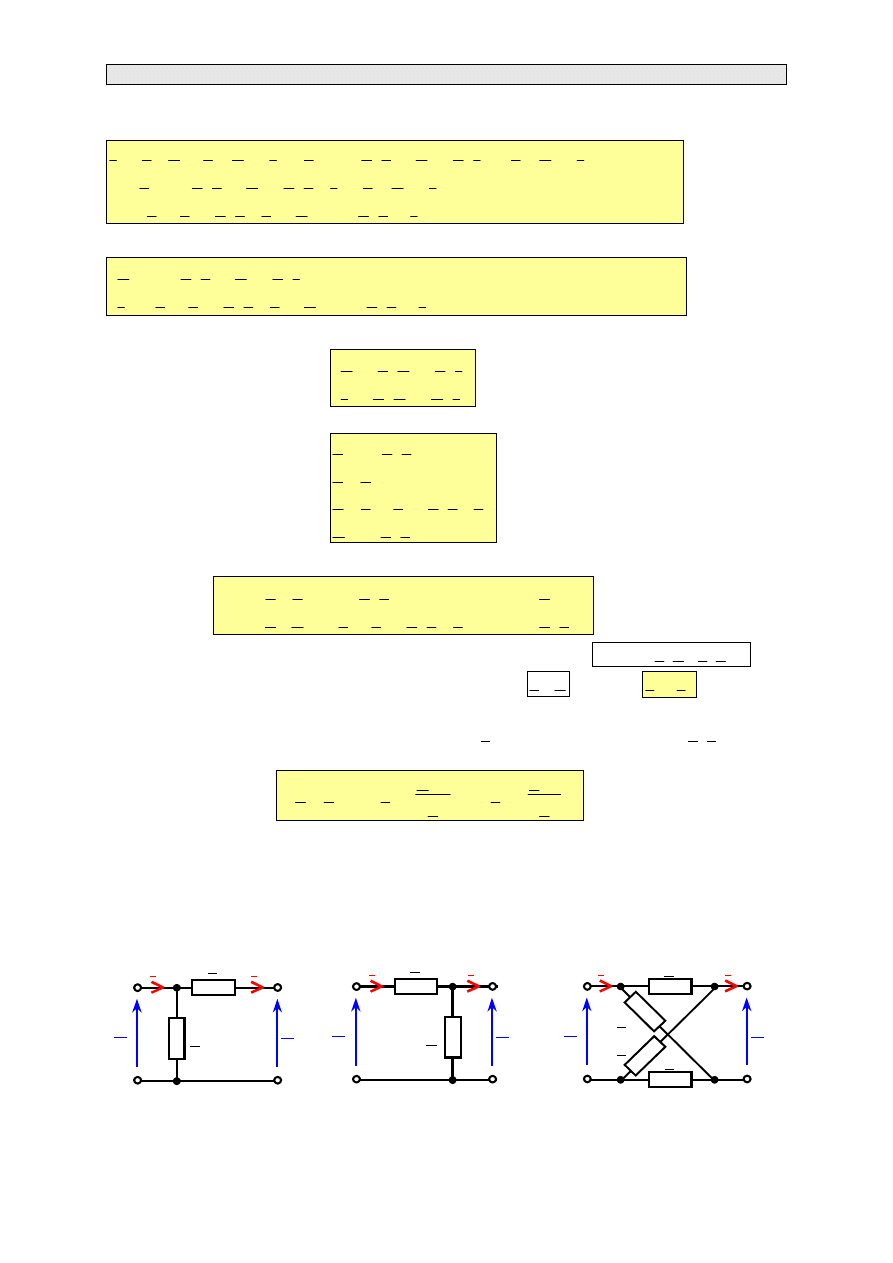
Czwórnik typu
Π
Przedstawiony na rys. 3.8b czwórnik typu Π składa się z jednej impedancji podłużnej (Z) i dwóch
admitancji poprzecznych (Y
1,
Y
2
). Zależność pomiędzy napięciami i prądami na wejściu i na wyjściu
czwórnika znajdujemy na podstawie praw Kirchhoffa
Π
+
=
Π
+
=
Π
+
=
)
3
(
)
2
(
)
1
(
2
1
2
2
1
1
U
U
U
I
I
I
I
I
I
Z
Y
Z
Y
Z
(3.57)
Prawo Ohma wyrażają równania
)
6
(
)
5
(
)
4
(
2
2
2
1
1
1
Π
⋅
=
Π
⋅
=
Π
⋅
=
U
Y
I
U
Y
I
I
Z
U
Y
Y
Z
Z
(3.58)
Podstawmy równanie (Π2) do równania (Π1)
1
2
2
1
1
Y
Y
Y
Z
I
I
I
I
I
I
+
+
=
+
=
(3.59)
Otrzymamy układ równań postaci
Π
+
=
Π
+
+
=
)
8
(
)
7
(
2
1
1
2
2
1
U
U
U
I
I
I
I
Z
Y
Y
(3.60)
Do układu równań (3.60) podstawny równania (Π4), (Π5) oraz (Π6)
Π
+
⋅
=
Π
⋅
+
+
⋅
=
)
10
(
)
9
(
2
1
1
1
2
2
2
1
U
I
Z
U
U
Y
I
U
Y
I
Z
(3.61)
Do równania (Π10) w układzie równań (3.61) podstawny równania (Π2) oraz (Π6)
Π
+
+
⋅
⋅
=
+
+
⋅
=
+
⋅
=
Π
+
⋅
+
⋅
=
)
12
(
)
(
)
(
)
11
(
2
2
2
2
2
2
2
2
1
2
2
2
1
1
1
U
I
U
Y
Z
U
I
I
Z
U
I
Z
U
I
U
Y
U
Y
I
Y
Z
(3.62)
Po przekształceniach
Π
⋅
+
⋅
⋅
+
=
Π
+
⋅
+
⋅
=
)
13
(
)
1
(
)
11
(
2
2
2
1
2
2
2
1
1
1
I
Z
U
Y
Z
U
I
U
Y
U
Y
I
(3.63)
Do równania (Π11) w układzie równań (3.63) podstawny równanie (Π13)
{
}
Π
⋅
+
⋅
⋅
+
=
Π
+
⋅
+
⋅
+
⋅
⋅
+
⋅
=
+
⋅
+
⋅
=
)
13
(
)
1
(
)
14
(
)
1
(
2
2
2
1
2
2
2
2
2
2
1
2
2
2
1
1
1
I
Z
U
Y
Z
U
I
U
Y
I
Z
U
Y
Z
Y
I
U
Y
U
Y
I
(3.64)
I
1
I
2
U
1
U
2
Z
Y
1
Y
2
U
Z
I
Y1
I
Z
I
Y2
Rys. 3.10. Zwroty napięć i prądów
w czwórniku typu Π
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
13
Równanie (Π14), po przekształceniach, przyjmie postać
{
}
)
15
(
)
1
(
)
(
)
1
(
)
1
(
2
1
2
2
1
2
1
2
2
2
2
1
2
2
1
2
2
2
2
2
2
1
2
2
2
1
1
1
Π
⋅
⋅
+
+
⋅
⋅
⋅
+
+
=
=
+
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
=
=
+
⋅
+
⋅
+
⋅
⋅
+
⋅
=
+
⋅
+
⋅
=
I
Y
Z
U
Y
Y
Z
Y
Y
I
U
Y
I
Y
Z
U
Y
Z
Y
I
U
Y
I
Z
U
Y
Z
Y
I
U
Y
U
Y
I
(3.65)
Ostatecznie otrzymamy układ równań
Π
⋅
⋅
+
+
⋅
⋅
⋅
+
+
=
Π
⋅
+
⋅
⋅
+
=
)
17
(
)
1
(
)
(
)
16
(
)
1
(
2
1
2
2
1
2
1
1
2
2
2
1
I
Y
Z
U
Y
Y
Z
Y
Y
I
I
Z
U
Y
Z
U
(3.66)
Porównując układ równań (3.66) z układem (3.11)
⋅
+
⋅
=
⋅
+
⋅
=
2
2
1
2
2
1
I
D
U
C
I
I
B
U
A
U
zauważamy, że parametry łańcuchowe
1
2
1
2
1
2
1
1
Y
Z
D
Y
Y
Z
Y
Y
C
Z
B
Y
Z
A
⋅
+
=
⋅
⋅
+
+
=
=
⋅
+
=
(3.67)
zatem macierz łańcuchowa ma postać
⋅
+
⋅
⋅
+
+
⋅
+
=
=
Π
1
2
1
2
1
2
1
1
A
Y
Z
Y
Y
Z
Y
Y
Z
Y
Z
D
C
B
A
(3.68)
Nietrudno wykazać, że spełniony jest warunek odwracalności czwórnika
1
A
det
=
⋅
−
⋅
=
Π
C
B
D
A
.
Czwórnik typu Π jest symetryczny, gdy spełniony jest warunek
D
A
=
, czyli gdy
2
1
Y
Y
=
Jeżeli dane są parametry łańcuchowe, to na podstawie równań (3.67) można wyprowadzić zależności
na elementy czwórnika, czyli impedancję podłużną (
Z) i admitancje poprzeczne (Y
1
,
Y
2
), a więc
rozwiązać zagadnienie odwrotne w stosunku do zagadnienia rozważanego powyżej.
B
A
Y
B
D
Y
B
Z
1
1
2
1
−
=
−
=
=
(3.69)
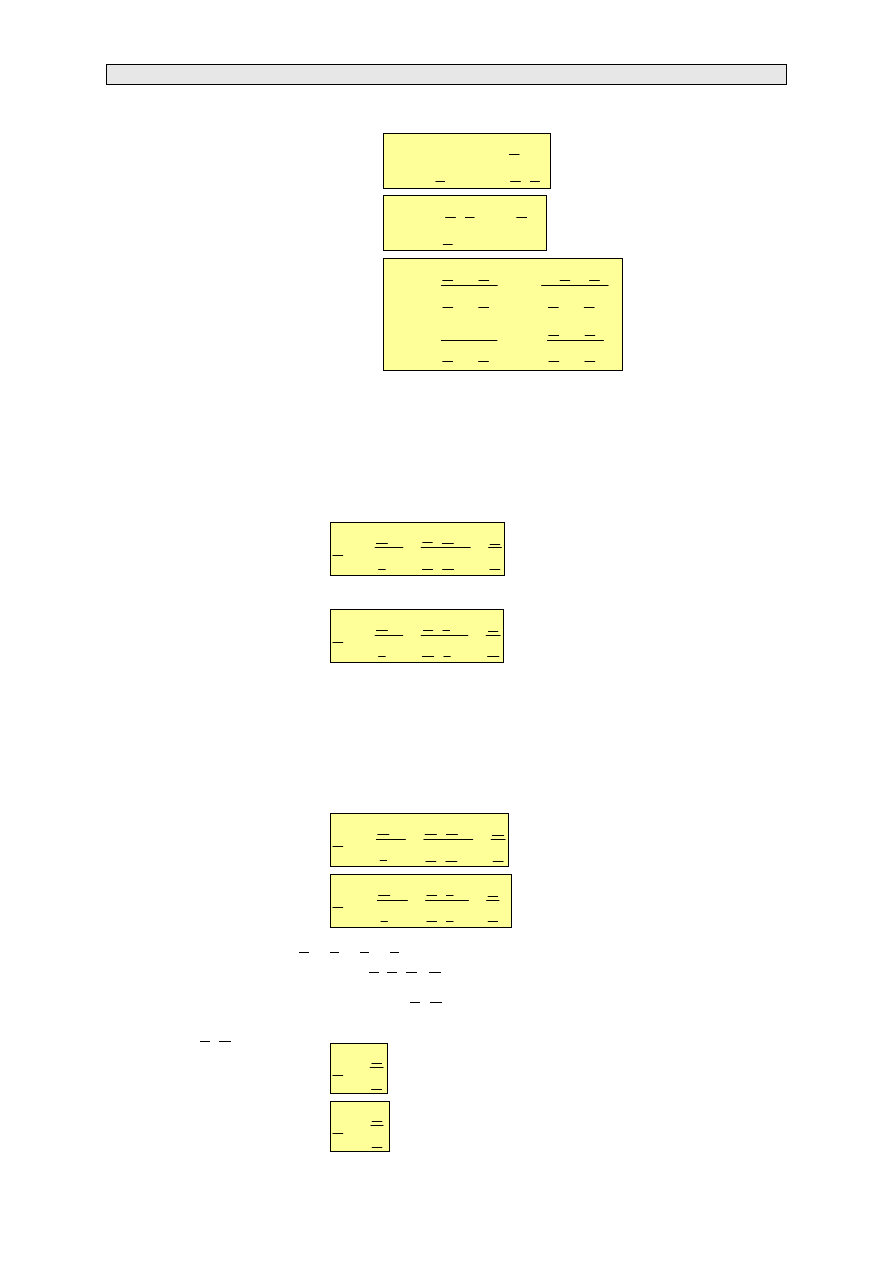
Czwórniki typu
Γ
,
T
, Χ
Na rys. 3.11. przedstawiono inne schematy spotykanych czwórników. Czwórniki przedstawione na
rys. 3.11a oraz rys. 3.11b stanowią szczególne przypadki, gdy jedna z impedancji czwórnika typu
T
lub jedna z admitancji czwórnika typu Π jest równa zeru.
I
1
I
2
U
1
U
2
a)
Z
Y
I
1
I
2
U
1
U
2
b)
Z
Y
I
1
I
2
U
1
U
2
c)
Z
1
Z
1
Z
2
Z
2
Rys. 3.11. Schematy zastępcze czwórników typu Γ (rys. a), typu T (rys. b) i typu X (rys. c)
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
14
Macierze łańcuchowe czwórników przedstawionych na rys. 3.11 są następujące
•
dla czwórnika typu Γ (rys. 3.11a)
⋅
+
=
Γ
Y
Z
Y
Z
1
1
A
(3.70)
•
dla czwórnika typu T (rys. 3.11b)
⋅
+
=
1
1
A
Y
Z
Y
Z
(3.71)
•
dla czwórnika
typu X (rys. 3.11c)
−
+
−
−
⋅
⋅
−
+
=
1
2
1
2
1
2
1
2
1
2
1
2
1
2
X
2
2
A
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
(3.72)
3.8. Zwi
ą
zki pomi
ę
dzy parametrami ła
ń
cuchowymi a impedancjami
w stanie jałowym i w stanie zwarcia czwórnika
Jak wspomniano wyżej impedancja wejściowa czwórnika w stanie jałowym wyznaczana jest z
zależności (3.40)
C
A
U
C
U
A
I
U
Z
=
⋅
⋅
=
=
20
20
10
10
10
a impedancja wejściowa czwórnika w stanie zwarcia wyznaczana jest z zależności (3.42)
D
B
I
D
I
B
I
U
Z
k
k
k
k
k
=
⋅
⋅
=
=
2
2
1
1
1
Zależności te otrzymujemy w wyniku dołączenia do zacisków wejściowych czwórnika źródła napięcia
lub źródła prądu i rozważania wspomnianych stanów pracy czwórnika (stan jałowy, stan zwarcia) w
oparciu o równania łańcuchowe.
Jeżeli źródło napięcia lub źródło prądu dołączymy do zacisków wyjściowych czwórnika, a zaciski
wejściowe będą odpowiednio rozwarte (stan jałowy) lub zwarte (stan zwarcia), to w podobny sposób
jak to przedstawiono w punkcie 3.5 otrzymamy wzory na impedancję w stanie jałowym (3.73) i w
stanie zwarcia (3.74), przy zasilaniu czwórnika od strony wyjścia (indeksy „2” w zależnościach)
C
D
U
C
U
D
I
U
Z
=
⋅
⋅
=
=
10
10
20
20
20
(3.73)
A
B
I
A
I
B
I
U
Z
k
k
k
k
k
=
⋅
⋅
=
=
1
1
2
2
2
(3.74)
Jeżeli znane są impedancje Z
10
, Z
1k
, Z
20
, Z
2k
to korzystając z równań (3.40), (3.42), (3.73) i (3.74)
można obliczyć parametry łańcuchowe A, B, C i D.
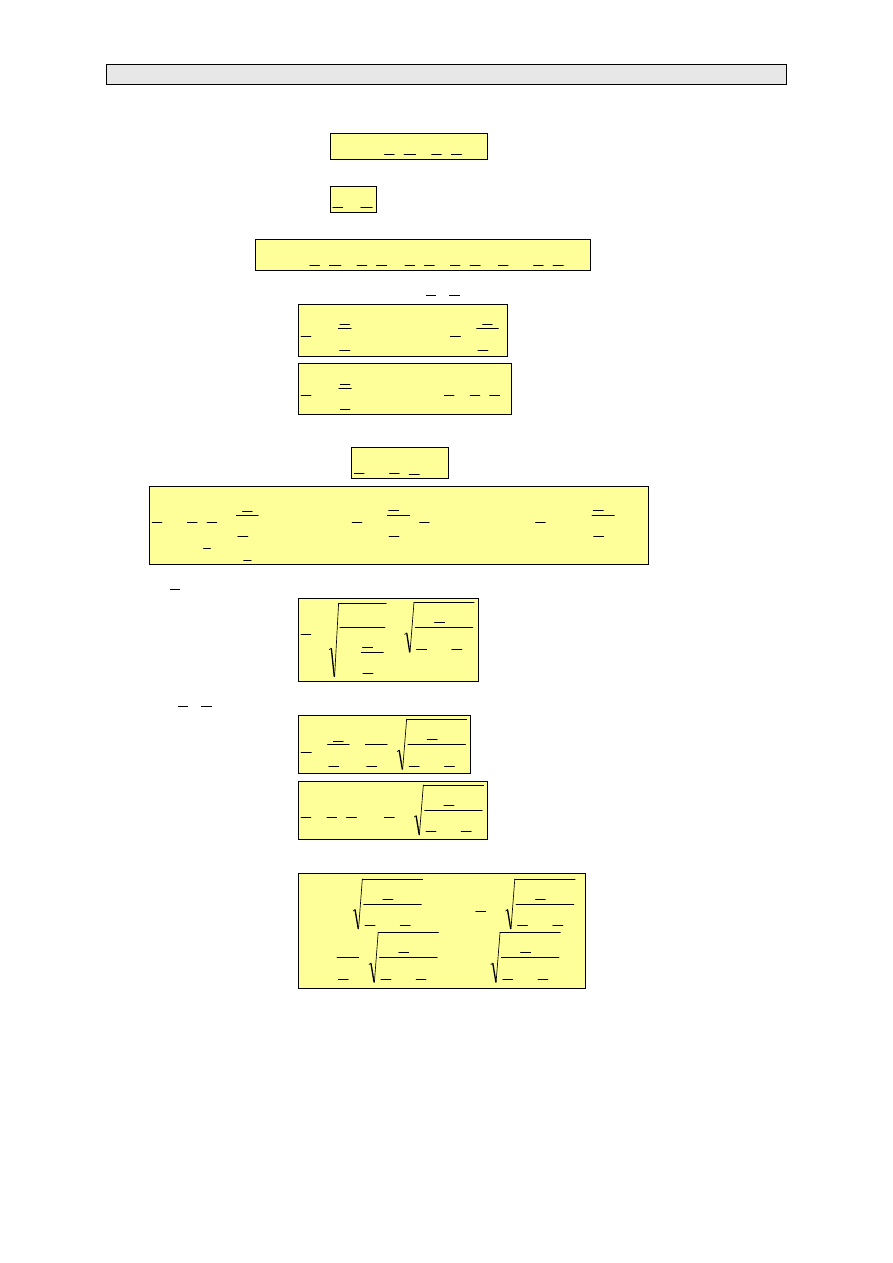
W przypadku czwórników symetrycznych (A=D) impedancje stanu jałowego i stanu zwarcia nie
zależą od tego, z której strony zasilono czwórnik. Jeżeli w równaniach (3.40), (3.42), (3.73) i (3.74)
uwzględnimy A=D to otrzymamy
C
A
Z
=
0
(3.75)
A
B
Z
k
=
(3.76)
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
15
Czwórnik jest odwracalny jeżeli spełniony jest warunek (3.31)
1
det
=
⋅
−
⋅
=
C
B
D
A
A
Wstawiając warunek symetryczności czwórnika (3.33)
D
A
=
do równania (3.31) otrzymamy
1
A
det
2
=
⋅
−
=
⋅
−
⋅
=
⋅
−
⋅
=
C
B
A
C
B
A
A
C
B
D
A
(3.77)
Wyznaczmy z równań (3.75) i (3.76) parametry B i C
0
0
Z
A
C
C
A
Z
=
⇒
=
(3.78)
k
k
Z
A
B
A
B
Z
⋅
=
⇒
=
(3.79)
i podstawny równania (3.78) i (3.79) do równania (3.77)
1
2
=
⋅
−
C
B
A
(3.80)
{
1
1
1
1
0
2
2
0
2
0
2
=
−
⋅
⇒
=
⋅
−
⇒
=
⋅
⋅
−
Z
Z
A
A
Z
Z
A
Z
A
Z
A
A
k
k
C
B
k
3
2
1
Parametr A ma zatem postać
k
k
Z
Z
Z
Z
Z
A
−
=
−
=
0
0
0
1
1
(3.81)
Parametry B i C wyznaczymy wstawiając równania (3.81) do równań (3.78) i (3.79)
k
Z
Z
Z
Z
Z
A
C
−
⋅
=
=
0
0
0
0
1
(3.82)
k
k
k
Z
Z
Z
Z
Z
A
B
−
⋅
=
⋅
=
0
0
(3.83)
Macierz łańcuchowa A ma zatem postać
−
−
⋅
−
⋅
−
=
k
k
k
k
k
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
0
0
0
0
0
0
0
0
0
1
A
(3.84)
Tak więc, w przypadku czwórnika symetrycznego, na podstawie znajomości impedancji stanu
jałowego i impedancji stanu zwarcia na podstawie równań (3.84) możemy wyznaczyć parametry
macierzy łańcuchowej.
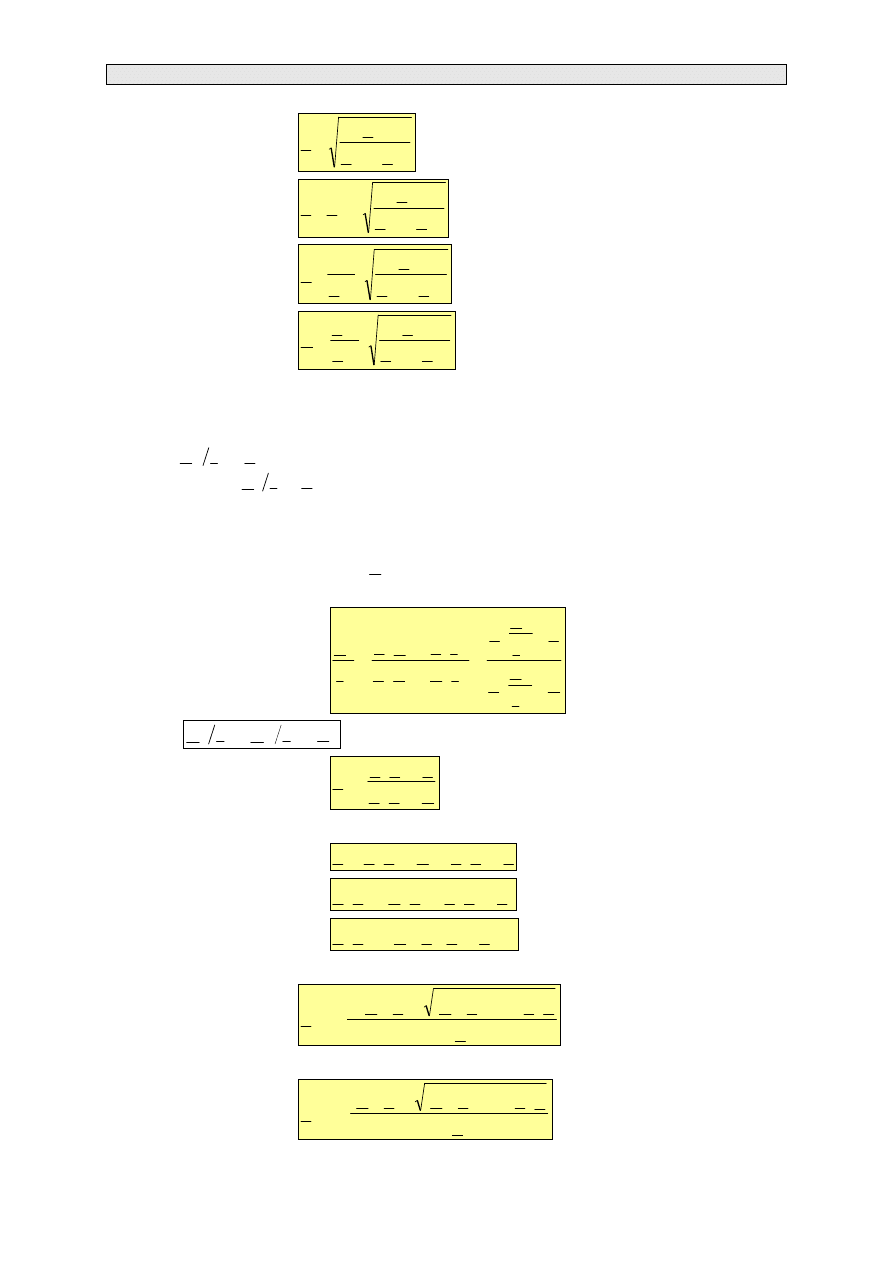
W celu wyznaczenia parametrów macierzy łańcuchowej dowolnego czwórnika należy skorzystać z
zależności wynikających z równań (3.1), (3.40), (3.42), (3.73) oraz (3.74). Po przekształceniu
wymienionych zależności otrzymamy równania, z których wyznaczyć można parametry łańcuchowe
dowolnego czwórnika
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
16
k
Z
Z
Z
A
2
20
10
−
=
(3.85)
k
k
Z
Z
Z
Z
B
2
20
10
2
−
⋅
=
(3.86)
k
Z
Z
Z
Z
C
2
20
10
10
1
−
⋅
=
(3.87)
k
Z
Z
Z
Z
Z
D
2
20
10
10
20
−
⋅
=
(3.88)
3.9. Impedancja falowa czwórnika symetrycznego
Stosunek
2
2
2
Z
I
U
=
oznacza impedancję na wyjściu czwórnika, tj. impedancję odbiornika,
natomiast stosunek
1
1
1
Z
I
U
=
przedstawia impedancję na wejściu , tj. impedancję czwórnika wraz
z odbiornikiem.
Powstaje pytanie, czy możliwy jest taki dobór odbiornika, aby impedancja wyjściowa była równa
impedancji wejściowej? Impedancję spełniającą ten warunek nazywamy impedancją iterowaną
(z łac. powtórną) i oznaczamy przez
i
Z
. Impedancję iterowaną wyznaczamy dzieląc, w układzie
równań (3.11), równanie pierwsze przez drugie
D
I
U
C
B
I
U
A
I
D
U
C
I
B
U
A
I
U
+
⋅
+
⋅
=
⋅
+
⋅
⋅
+
⋅
=
2
2
2
2
2
2
2
2
1
1
(3.89)
Podstawny
i
Z
I
U
I
U
=
=
2
2
1
1
do równania (3.89)
D
Z
C
B
Z
A
Z
i
i
i
+
⋅
+
⋅
=
(3.90)
Przekształcając równanie (3.90) otrzymamy
(
)
B
Z
A
D
Z
C
Z
i
i
i
+
⋅
=
+
⋅
⋅
B
Z
A
Z
D
Z
C
i
i
i
+
⋅
=
⋅
+
⋅
2
0
)
(
2
=
−
⋅
−
+
⋅
B
Z
A
D
Z
C
i
i
(3.91)
Rozwiązanie równania (3.91)
(
) (
)
C
C
B
A
D
A
D
Z
i
⋅
⋅
⋅
+
−
±
−
−
=
2
4
2
2
,
1
(3.92)
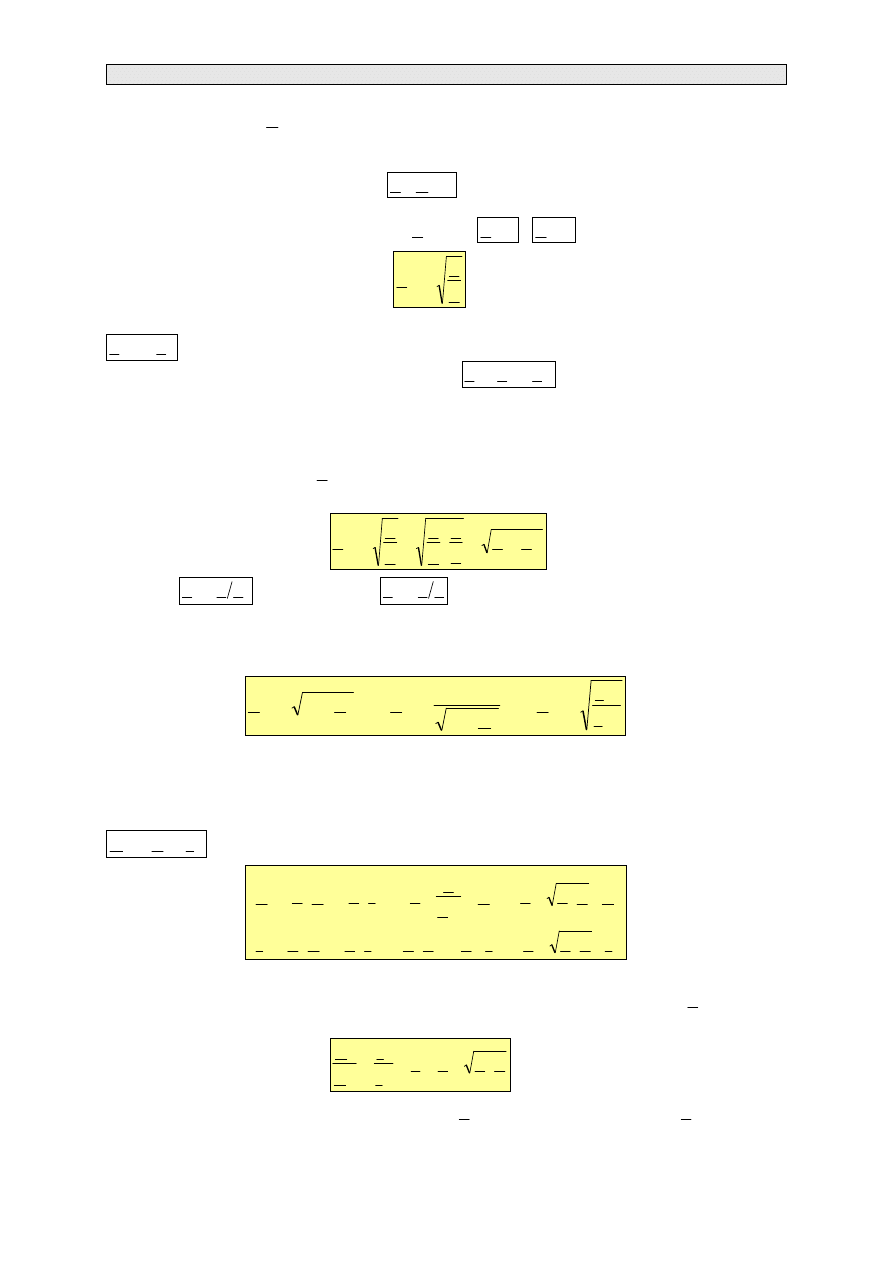
Obliczając impedancję iterowaną przy zasilaniu czwórnika od strony przeciwnej otrzymujemy
(
) (
)
C
C
B
A
D
A
D
Z
i
⋅
⋅
⋅
+
−
±
−
=
2
4
2
4
,
3
(3.93)
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
17
Dwie z tych wartości
i
Z
(wzory 3.92 i 3.93) mają część rzeczywistą dodatnią i te uważamy za
fizycznie realne.
W przypadku czwórnika symetrycznego
0
=
−
D
A
, otrzymujemy więc tylko jedno rozwiązanie na
impedancję iterowaną. Nazywamy ją
impedancją falową lub impedancją charakterystyczną
czwórnika symetrycznego i oznaczamy przez
C
Z . Gdy
0
≠
B
i
0
≠
C
C
B
Z
C
=
(3.94)
Impedancją charakterystyczną (falową) czwórnika symetrycznego nazywamy taką impedancję
2
Z
Z
odb
=
odbiornika dołączonego do zacisków wyjściowych czwórnika, że impedancja mierzona na
wejściu czwórnika jest równa impedancji odbiornika
C
Z
Z
Z
=
=
2
1
.
Odbiornik, którego impedancja jest równa impedancji falowej czwórnika, nazywamy
odbiornikiem
dopasowanym falowo do czwórnika.
Pomiędzy impedancją falową
C
Z
czwórnika a jego impedancjami stanu jałowego i stanu zwarcia
zachodzi zależność
k
C
Z
Z
A
B
C
A
C
B
Z
⋅
=
⋅
=
=
0
(3.95)
przy czym
C
A
Z
=
0
(równanie 3.78),
A
B
Z
k
=
(3.79)
Zależność (3.95) pozwala na wyznaczenie impedancji falowej na podstawie znajomości (pomiarów)
impedancji stanu jałowego i stanu zwarcia.
Impedancję falową można również wyznaczyć z zależności
22
11
)
(
det
1
)
(
det
h
h
Z
Z
Z
f
f
f
=
=
=
Y
Z
(3.96)
3.10. Przekładnia i współczynnik przenoszenia
Równania czwórnika symetrycznego obciążonego impedancją falową przybierają przy uwzględnieniu
2
2
I
Z
U
C
⋅
=
następującą postać
(
)
(
)
(
)
⋅
⋅
+
=
⋅
+
⋅
=
⋅
+
⋅
=
⋅
⋅
+
=
⋅
+
=
⋅
+
⋅
=
2
2
2
2
1
2
2
2
2
1
I
C
B
A
I
A
Z
C
I
A
U
C
I
U
C
B
A
U
Z
B
A
I
B
U
A
U
C
C
(3.97)
Z równań (3.97) wynika, że przy obciążeniu impedancją falową stosunek napięć na wejściu i na
wyjściu jest równy stosunkowi prądów na wejściu i na wyjściu. Oznaczamy go literą
ϑ
i nazywamy
przekładnią czwórnika symetrycznego
C
B
A
I
I
U
U
⋅
+
=
=
=
ϑ
2
1
2
1
(3.98)
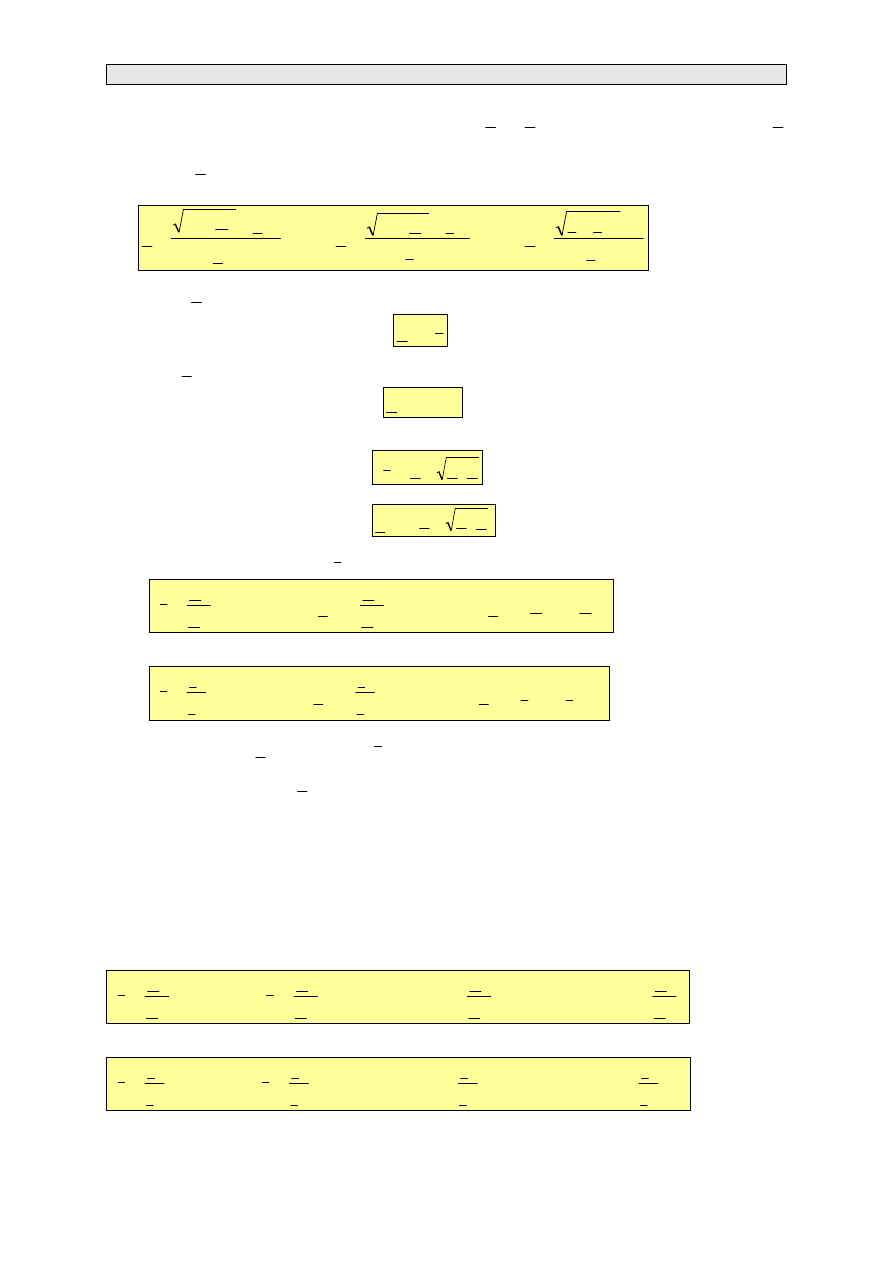
Można oddzielnie mówić o przekładni napięciowej
u
ϑ
jak i o przekładni prądowej
i
ϑ
. Przekładnie
te ulegają zmianom wraz ze zmianą obciążenia czwórnika, dlatego nie są w praktyce stosowane.
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
18
Jedynie w przypadku obciążenia impedancją falową
i
u
ϑ
ϑ
=
, tak że mówimy o przekładni
ϑ
czwórnika nie dodając określenia: napięciowa lub prądowa.
Przekładnia
ϑ
czwórnika jest wielkością zespoloną. Jeżeli znana jest inna macierz niż macierz
łańcuchowa, to do obliczenia przekładni możemy skorzystać ze wzorów
21
22
11
21
11
21
22
1
)
(
det
)
(
det
h
h
h
z
z
y
y
−
=
+
=
−
=
ϑ
ϑ
ϑ
Z
Y
(3.99)
Przekładnię
ϑ
można zapisać w postaci wykładniczej
g
e
=
ϑ
(3.100)
przy czym g jest wykładnikiem zespolonym
jb
a
g
+
=
(3.101)
Z zależności (3.98) wynika, że
C
B
A
e
g
⋅
+
=
(3.102)
czyli
(
)
C
B
A
g
⋅
+
=
ln
(3.103)
Wygodniej jest wyrazić wartość
g
e
ze stosunku napięć lub prądów (3.97)
2
1
2
1
2
1
ln
ln
ln
U
U
g
U
U
g
U
U
e
g
−
=
⇒
=
⇒
=
(3.104)
lub
2
1
2
1
2
1
ln
ln
ln
I
I
g
I
I
g
I
I
e
g
−
=
⇒
=
⇒
=
(3.105)
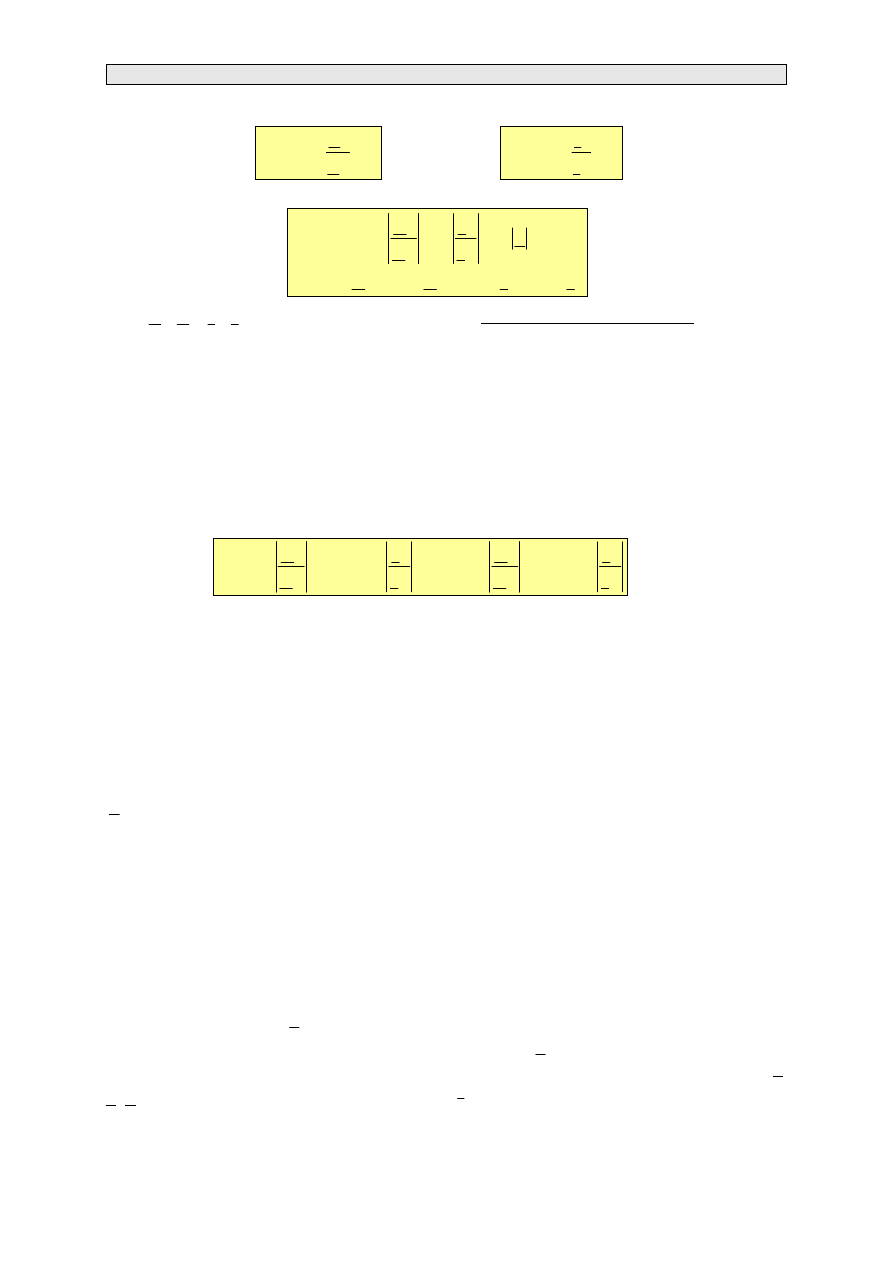
Wykładnik potęgowy g w wyrażeniu
g
e
nazywamy współczynnikiem przenoszenia czwórnika
Współczynnik przenoszenia g czwórnika symetrycznego jest równy różnicy logarytmów naturalnych
wektora napięcia skutecznego na wejściu i wektora napięcia skutecznego na wyjściu czwórnika przy
jego obciążeniu odbiornikiem dopasowanym falowo, czyli impedancją falową
. Analogicznie można
określić współczynnik przenoszenia jako różnicę logarytmów wektorów prądu.
Występujące w zależności (3.101) wyrażenia
a
i
b
noszą nazwę
a
- współczynnik tłumienia czwórnika
b
- współczynnik fazowy (współczynnik przesunięcia fazowego) czwórnika
Znaczenie fizyczne współczynników
a
i
b
wynika z zależności (3.104) i (3.105)
2
1
2
1
2
1
2
1
U
U
e
e
U
U
e
U
U
e
U
U
e
jb
a
jb
a
g
g
=
⋅
⇒
=
⇒
=
⇒
=
+
(3.106)
lub
2
1
2
1
2
1
2
1
I
I
e
e
I
I
e
I
I
e
I
I
e
jb
a
jb
a
g
g
=
⋅
⇒
=
⇒
=
⇒
=
+
(3.107)
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
19
Ze wzorów
2
1
U
U
e
e
jb
a
=
⋅
oraz
2
1
I
I
e
e
jb
a
=
⋅
wynika
2
1
2
1
2
1
2
1
faza
faza
faza
faza
ln
ln
ln
I
I
U
U
b
I
I
U
U
a
−
=
−
=
=
=
=
ϑ
(3.108)
gdzie
2
1
2
1
,
,
,
I
I
U
U
- napięcia i prądy wrót czwórnika obciążonego impedancją falową.
Współczynnik tłumienia
a
czwórnika symetrycznego jest równy różnicy logarytmów naturalnych
napięć skutecznych (lub prądów skutecznych) na wejściu i na wyjściu przy jego obciążeniu
odbiornikiem dopasowanym do niego falowo.
Współczynnik a jest miarą tłumienia napięcia lub prądu przy przejściu od zacisków wejściowych do
zacisków wyjściowych czwórnika, zaś b jest miarą zmiany fazy napięcia lub prądu. Jednostką
współczynnika a jest neper (1 Np).
Tłumienie o wartości jednego nepera oznacza zmniejszenie amplitudy napięcia lub prądu
e razy, czyli
około 2.72 raza. Często wygodniej jest podawać tłumienie w decybelach. Wówczas należy obliczyć
jedną z poniższych wartości
2
1
2
1
2
1
10
2
1
10
ln
686
.
8
ln
686
.
8
log
20
log
20
I
I
U
U
I
I
U
U
=
=
=
(3.109)
Jednemu neperowi odpowiada tłumienie równe 8.686 dB.
Współczynnik fazowy
b
czwórnika symetrycznego jest równy kątowi przesunięcia fazowego w
radianach pomiędzy napięciem na wejściu a napięciem na wyjściu czwórnika przy jego obciążeniu
odbiornikiem dopasowanym falowo. Jest zatem miarą zmiany fazy napięcia lub prądu przy przejściu
od zacisków wejściowych do zacisków wyjściowych czwórnika.
Oba współczynniki (współczynnik tłumienia
a
i współczynnik fazowy
b
) łącznie wskazują sposób
przenoszenia sygnału w czwórniku, czyli zmianę jego wartości (modułu) i fazy. Dlatego współczynnik
g
nazywany jest współczynnikiem przenoszenia czwórnika.
W teletransmisji przewodowej wymienione wyżej współczynniki znane są pod nazwami:
g
-
tamowność
a
-
tłumienność
b
-
przesuwność
3.11. Równania hiperboliczne czwórnika
Wprowadzenie parametru g ma ważną zaletę, pozwala uzależnić równania łańcuchowe czwórnika
symetrycznego od funkcji hiperbolicznych zmiennej zespolonej g .
Równanie (3.102) uzależnia współczynnik przenoszenia czwórnika od parametrów łańcuchowych A,
B
, C. Na podstawie równania (3.102) wyznaczmy
g
e
−
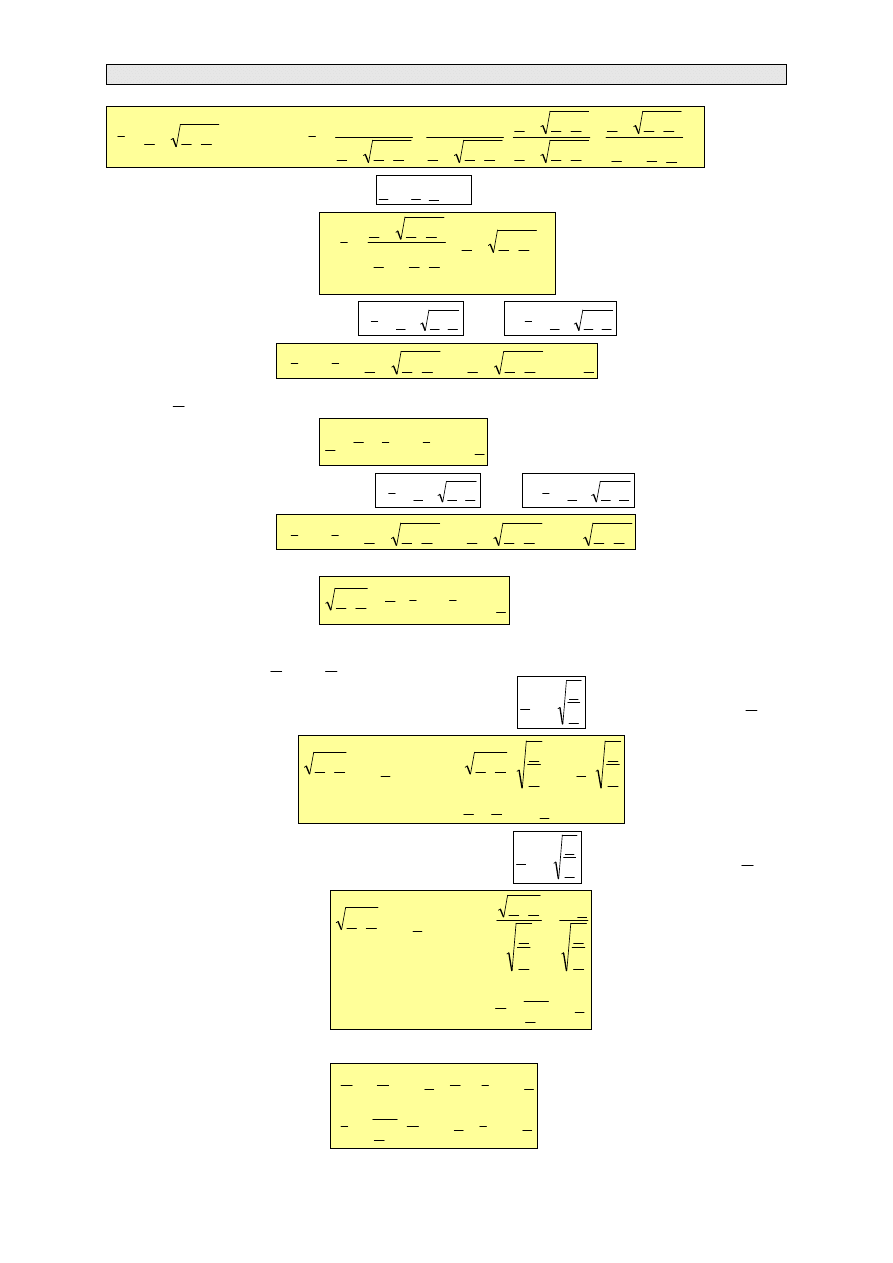
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
20
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
e
C
B
A
e
g
g
⋅
−
⋅
−
=
⋅
−
⋅
−
⋅
⋅
+
=
⋅
+
=
⇒
⋅
+
=
−
2
1
1
(3.110)
Ponieważ dla czwórnika symetrycznego
1
2
=
⋅
−
C
B
A
to zależność (3.110) przyjmie postać
C
B
A
C
B
A
C
B
A
e
g
⋅
−
=
⋅
−
⋅
−
=
=
−
4
3
42
1
1
2
(3.111)
Dodając do siebie stronami równania
C
B
A
e
g
⋅
+
=
oraz
C
B
A
e
g
⋅
−
=
−
otrzymamy
A
C
B
A
C
B
A
e
e
g
g
⋅
=
⋅
−
+
⋅
+
=
+
−
2
)
(
)
(
(3.112)
Parametr
A
wyraża się zależnością
g
ch
e
e
A
g
g
=
+
=
−
2
1
(3.113)
Odejmując od siebie stronami równania
C
B
A
e
g
⋅
+
=
oraz
C
B
A
e
g
⋅
−
=
−
otrzymamy
C
B
C
B
A
C
B
A
e
e
g
g
⋅
⋅
=
⋅
−
−
⋅
+
=
−
−
2
)
(
)
(
(3.114)
a po przekształceniu
(
)
g
sh
e
e
C
B
g
g
=
−
=
⋅
−
2
1
(3.115)
Podstawiając do równania (3.115) zależność na impedancję falową czwórnika symetrycznego (3.94)
wyznaczymy parametry
B
oraz
C
•
w wyniku pomnożenia obu stron równania (3.115) przez
C
B
Z
C
=
wyznaczymy parametr
B
g
sh
Z
B
C
B
g
sh
C
B
C
B
g
sh
C
B
C
⋅
=
⋅
=
⋅
⋅
⇒
=
⋅
(3.116)
•
w wyniku podzielenia obu stron równania (3.115) przez
C
B
Z
C
=
wyznaczymy parametr
C
g
sh
Z
C
C
B
g
sh
C
B
C
B
g
sh
C
B
C
⋅
=
=
⋅
⇒
=
⋅
1
(3.117)
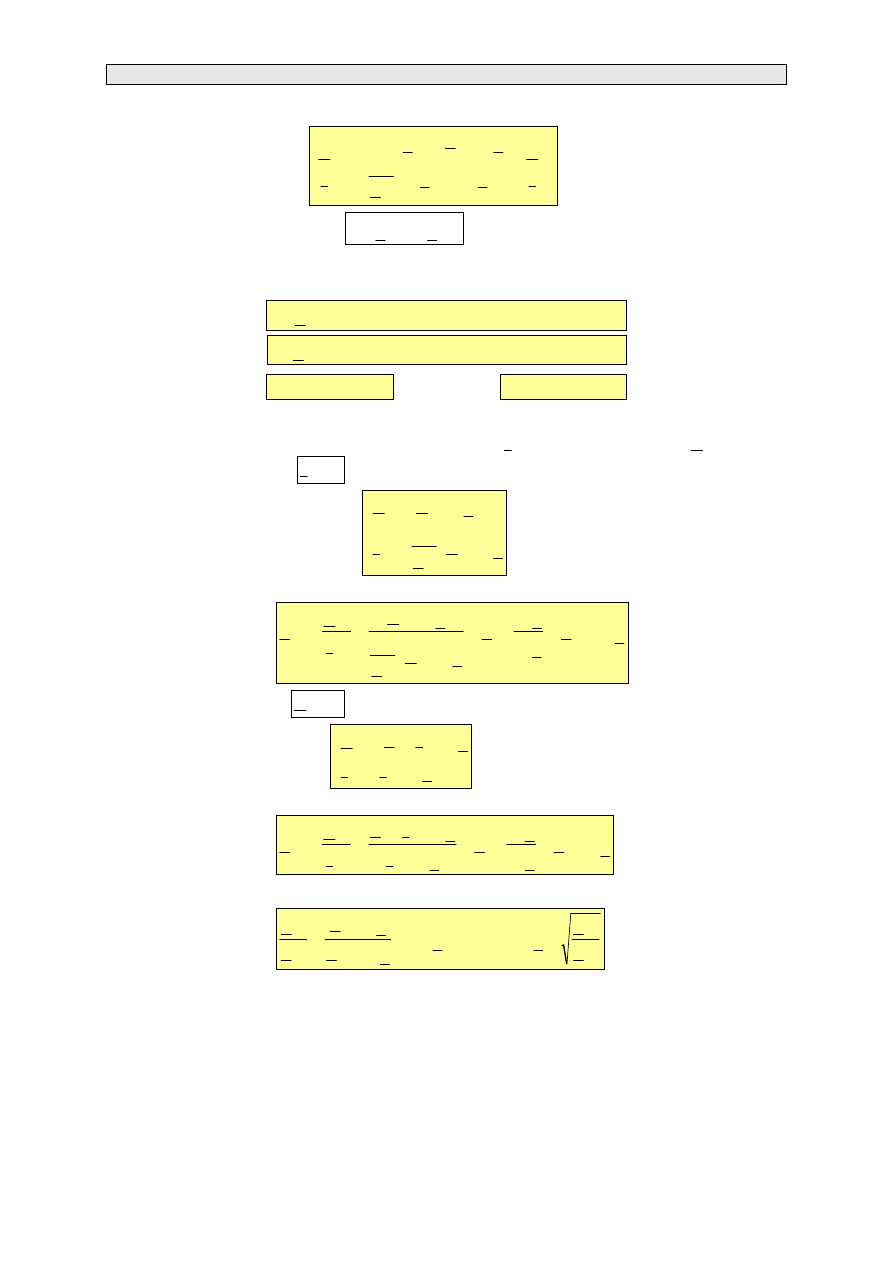
Po podstawieniu wyrażeń (3.113), (3.116) oraz (3.117) do układ równań (3.11) otrzymamy
⋅
+
⋅
⋅
=
⋅
⋅
+
⋅
=
g
ch
I
g
sh
U
Z
I
g
sh
I
Z
g
ch
U
U
C
C
2
2
1
2
2
1
1
(3.118)
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
21
lub w postaci macierzowej
⋅
⋅
⋅
=
2
2
1
1
1
I
U
g
ch
g
sh
Z
g
sh
Z
g
ch
I
U
C
C
(3.119)
Wyznacznik macierzy łańcuchowej
1
2
2
=
−
g
sh
g
ch
W przypadku korzystania z powyższych równań niezbędna jest umiejętność obliczania wartości
funkcji sinus i cosinus hiperboliczny z liczby zespolonej. Pomocne są w tym przypadku tożsamości
)
sin(
)
(
j
)
(
cos
)
(
)
j
(
)
(
b
a
sh
b
a
ch
b
a
ch
g
ch
+
=
+
=
(3.120)
)
sin(
)
(
j
)
cos(
)
(
)
j
(
)
(
b
a
ch
b
a
sh
b
a
sh
g
sh
+
=
+
=
(3.121)
przy czym
)
sin(
)
(
a
a
sh
j
j
=
oraz
)
cos(
)
(
a
a
ch
=
j
Powyższe równania (3.120, 3.121) są słuszne przy dowolnych obciążeniach czwórnika, a więc
również w przypadkach granicznych, tj. w stanie jałowym (
0
2
=
I
) i w stanie zwarcia (
0
2
=
U
)
•
w stanie jałowym, przy
0
2
=
I
równania (3.118) przyjmą postać
⋅
⋅
=
⋅
=
g
sh
U
Z
I
g
ch
U
U
C
2
10
2
10
1
(3.122)
Impedancja wejściowa w stanie jałowym
g
cth
Z
g
sh
g
ch
Z
g
sh
U
Z
g
ch
U
I
U
Z
C
C
C
⋅
=
⋅
=
⋅
⋅
⋅
=
=
2
2
10
10
10
1
(3.123)
•
w stanie zwarcia, przy
0
2
=
U
równania (3.118) przyjmą postać
⋅
=
⋅
⋅
=
g
ch
I
I
g
sh
I
Z
U
k
C
k
2
1
2
1
(3.124)
Impedancja wejściowa w stanie zwarcia
g
th
Z
g
ch
g
sh
Z
g
ch
I
g
sh
I
Z
I
U
Z
C
C
C
k
k
k
⋅
=
⋅
=
⋅
⋅
⋅
=
=
2
2
1
1
1
(3.125)
W wyniku podzielenia stronami równania (3.125) przez równanie (3.123) otrzymujemy
10
1
2
10
1
Z
Z
g
th
g
th
g
cth
Z
g
th
Z
Z
Z
k
C
C
k
=
⇒
=
⋅
⋅
=
(3.126)
Wzór (3.126) pozwala na wyznaczenie współczynnika przenoszenia czwórnika na podstawie
znajomości impedancji wejściowej w stanie jałowym i impedancji wejściowej w stanie zwarcia.
3.12. Poł
ą
czenia czwórników
Czwórnik złożony może być rozpatrywany jako połączenie odpowiedniej liczby czwórników
prostych. Takie czwórniki muszą przy tym spełniać warunki regularności. Oznacza to, że po
połączeniu zachodzi warunek równości prądów w parach końcówek czwórników. Dzięki temu
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
22
obowiązują wówczas równania czwórników i możliwe jest związane z tym uproszczenie analizy.
Podstawowe typy połączeń czwórników to: połączenie łańcuchowe, połączenie szeregowe,
połączenie równoległe, połączenie równoległo-szeregowe i połączenie równoległo-szeregowe.
•
Połączenie łańcuchowe czwórników
Połączeniem łańcuchowym (inaczej nazywanym kaskadowym) czwórników nazywamy taki układ
czwórników, w którym zaciski wyjściowe pierwszego czwórnika są połączone z zaciskami
wejściowymi drugiego czwórnika, zaciski wyjściowe drugiego czwórnika z zaciskami wejściowymi
trzeciego czwórnika itd.
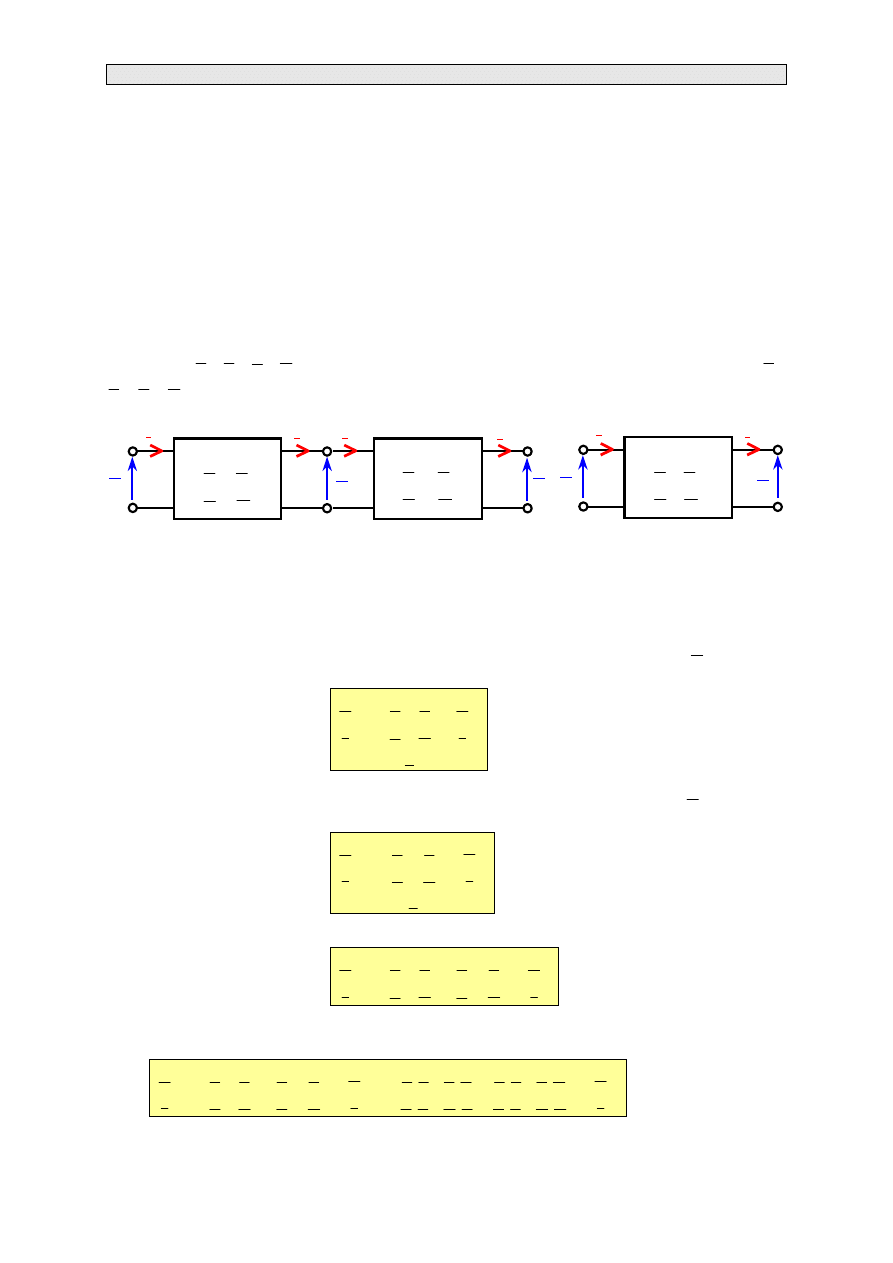
Rozważmy układ składający się z dwóch czwórników połączonych kaskadowo jak to przedstawiono
na rys. 3.12. Takie połączenie bardzo często występuje w praktyce. Przykładowo czwórnik o
parametrach
'
A
,
'
B
,
'
C
,
'
D
może zastępować transformator, natomiast czwórnik o parametrach
"
A
,
"
B
,
"
C
,
"
D
linię przesyłową.
'
'
'
'
D
C
B
A
I
1
I
2
U
1
U
2
I
3
U
3
1
I
2
"
"
"
"
D
C
B
A
1’
2
2’
3
3’
a)
D
C
B
A
I
1
I
3
U
1
U
3
1
1’
3
3’
b)
Rys. 3.12. Połączenie łańcuchowe dwóch czwórników (rys. a); schemat zastępczy (rys. b)
Do rozważań zastosujemy macierzową postać równań łańcuchowych czwórnika (3.12). Wskaźniki
„ ’ ” (prim) dotyczą parametrów pierwszego czwórnika, zaś wskaźniki „ ” „ (bis) dotyczą parametrów
drugiego czwórnika.
Równania łańcuchowe pierwszego czwórnika w postaci macierzowej mają postać (
1
A
– macierz
łańcuchowa pierwszego czwórnika)
⋅
=
2
2
1
1
1
'
'
'
'
I
U
D
C
B
A
I
U
4
3
42
1
A
(3.127)
Równania łańcuchowe drugiego czwórnika w postaci macierzowej mają postać (
2
A
– macierz
łańcuchowa drugiego czwórnika)
⋅
=
3
3
2
2
2
"
"
"
"
I
U
D
C
B
A
I
U
4
3
42
1
A
(3.128)
Podstawiając równanie (3.128) do równania (3.127) otrzymujemy
⋅
⋅
=
3
3
1
1
"
"
"
"
'
'
'
'
I
U
D
C
B
A
D
C
B
A
I
U
(3.129)
Po dokonaniu operacji mnożenia macierzy łańcuchowych czwórników otrzymujemy równanie
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
=
⋅
⋅
=
3
3
3
3
1
1
"
'
"
'
"
'
"
'
"
'
"
'
"
'
"
'
"
"
"
"
'
'
'
'
I
U
D
D
B
C
C
D
A
C
D
B
B
A
C
B
A
A
I
U
D
C
B
A
D
C
B
A
I
U
(3.130)
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
23
Zapiszmy równanie (3.130) w prostszej postaci
⋅
=
3
3
1
1
I
U
D
C
B
A
I
U
(3.131)
gdzie
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
=
"
'
"
'
"
'
"
'
"
'
"
'
"
'
"
'
D
D
B
C
C
D
A
C
D
B
B
A
C
B
A
A
D
C
B
A
(3.132)
Zatem parametry łańcuchowej wypadkowej macierzy łańcuchowej połączenia kaskadowego
(łańcuchowego) dwóch czwórników
"
'
"
'
C
B
A
A
A
⋅
+
⋅
=
"
'
"
'
D
B
B
A
B
⋅
+
⋅
=
"
'
"
'
C
D
A
C
C
⋅
+
⋅
=
"
'
"
'
D
D
B
C
D
⋅
+
⋅
=
czyli macierz łańcuchowa czwórnika zastępczego jest równa iloczynowi macierzy łańcuchowych
czwórników składowych
"
'
A
A
A
⋅
=
(3.133)
W analogiczny sposób można rozważać układ połączonych ze sobą kaskadowo
n
czwórników.
Należy jednak pamiętać, że mnożenie macierzy nie jest przemienne (wynika to z rachunku
macierzowego), dlatego przy połączeniu łańcuchowych czwórników nie wolno czwórników zamieniać
miejscami czyli
k
k
k
k
A
A
A
A
⋅
≠
⋅
+
+
1
1
(3.134)
gdzie
k
A
– macierz łańcuchowa k-tego czwórnika, a
1
+
k
A
– macierz łańcuchowa
1
+
k
czwórnika w
układzie
n
czwórników połączonych kaskadowo.
W ogólnym przypadku przy połączeniu dwóch czwórników symetrycznych, czwórnik zastępczy jest
niesymetryczny. By zastępczy czwórnik był symetryczny, czwórniki wchodzące w skład połączenia
muszą mieć równe impedancje falowe (charakterystyczne), czyli w przypadku połączenia dwóch
czwórników spełniony powinien być warunek
2
1
C
C
Z
Z
=
Przy połączeniu łańcuchowym
n
jednakowych czwórników, macierz czwórnika zastępczego jest
równa
n
A
, gdzie
A
jest macierzą pojedynczego czwórnika.
Przykład
Jako przykład połączenia łańcuchowego czwórników złożonych z elementów pojemnościowych może
służyć łańcuch izolatorów linii napowietrznej wysokiego napięcia (rys. 3.13a). Łańcuch jest
zawieszony na stalowej konstrukcji słupa. Przewód o napięciu
1
U
względem ziemi jest umocowany
do dolnego izolatora. Okucia izolatorów oraz słup stalowy traktujemy jak okładziny kondensatorów.
Na schemacie zastępczym (rys. 3.13b) C - oznacza pojemność pomiędzy dwoma okuciami, a
0
C
-
pojemność okucia względem słupa. Jeżeli rozdzielimy pojemność
0
C
na dwie pojemności równoległe
2
0
C
, to schemat zastępczy sprowadzi się do szeregowego połączenia
n
czwórników w kształcie Π
(rys. 3.13c). [4]
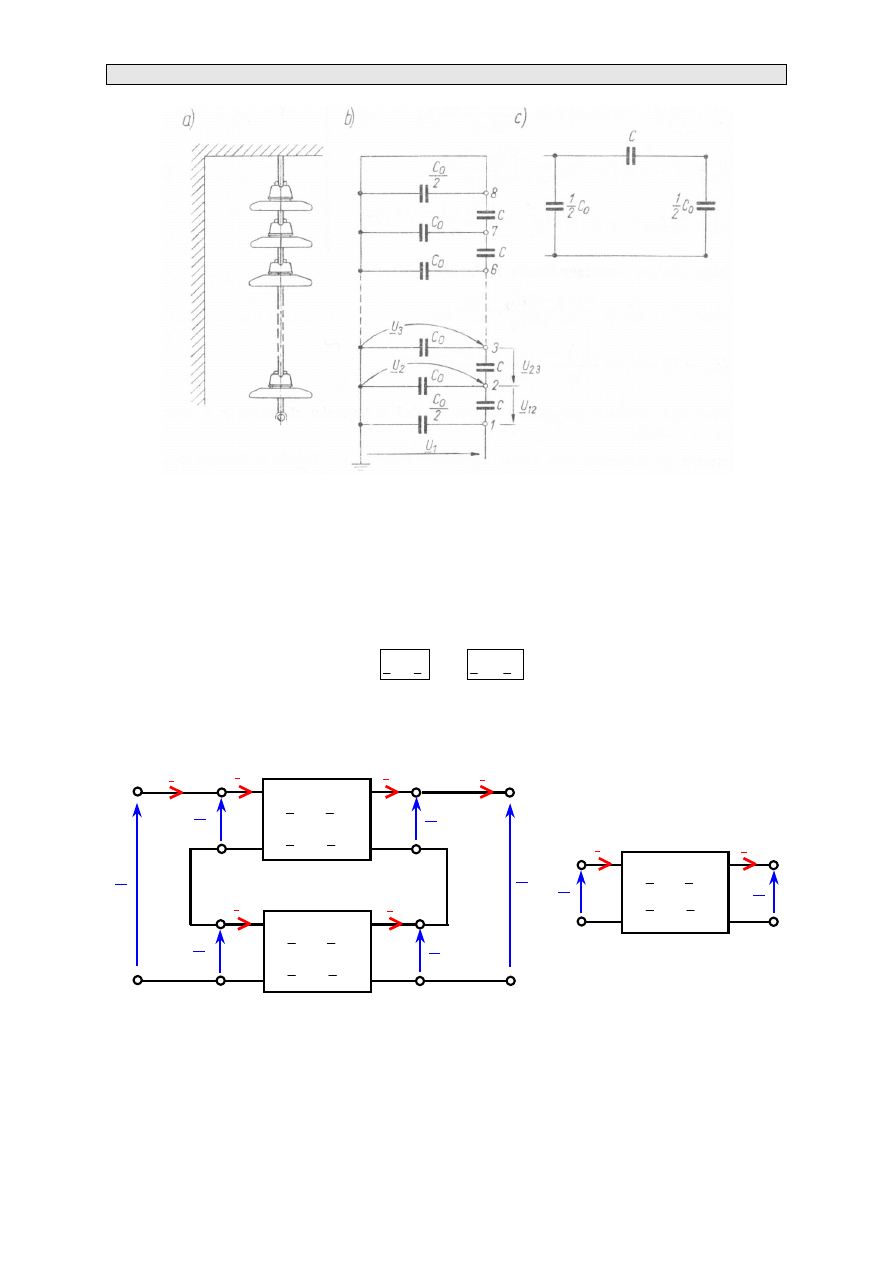
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
24
Rys. 3.13. Łańcuch izolatorów linii wysokiego napięcia: a) izolatory; b) schemat zastępczy
łańcucha izolatorów; c) schemat zastępczy jednego ogniwa [4]
•
Połączenie szeregowe czwórników
Połączeniem szeregowym czwórników nazywamy układ, w którym są spełnione następujące warunki:
•
zacisk 1’ pierwszego czwórnika jest połączony bezimpedancyjnie z zaciskiem 1 drugiego
czwórnika, a zacisk 2’ pierwszego czwórnika z zaciskiem 2 drugiego czwórnika;
•
jest spełniony warunek (3.2), czyli
'
1
1
I
I
=
oraz
'
2
2
I
I
=
Rozważmy układ składający się z dwóch czwórników połączonych szeregowo jak to przedstawiono
na rys. 3.14.
,
22
,
21
,
12
,
11
z
z
z
z
I
1
’
I
2
’
U
1
’
U
2
’
I
2
U
2
1
,
,
22
,
,
21
,
,
12
,
,
11
z
z
z
z
1’
2
2’
2
2’
a)
I
1
”
U
1
”
1
1’
I
2
”
U
2
”
2
2’
I
1
U
1
1
1’
22
21
12
11
z
z
z
z
I
1
I
2
U
1
U
2
1
1’
2
2’
b)
Rys. 3.14. Połączenie szeregowe dwóch czwórników (rys. a); schemat zastępczy (rys. b)
Do rozważań zastosujemy macierzową postać równań impedancyjnych czwórnika (3.4).
Wskaźniki „
’ ” (prim) dotyczą parametrów pierwszego czwórnika, zaś wskaźniki „ ” „ (bis) dotyczą
parametrów drugiego czwórnika.
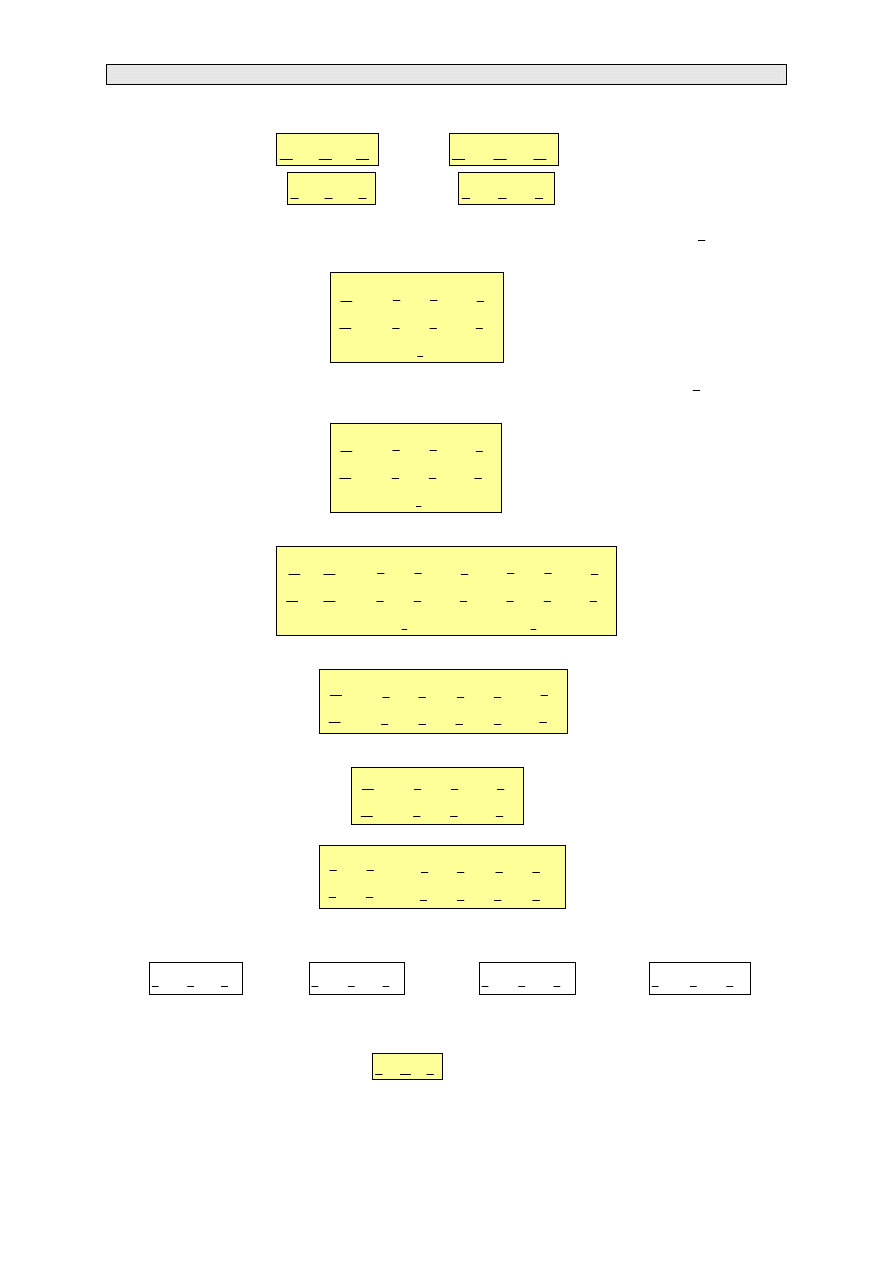
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
25
Przy połączeniu szeregowym czwórników zachodzą następujące równania napięć i prądów
"
1
'
1
1
U
U
U
+
=
oraz
"
2
'
2
2
U
U
U
+
=
(3.135)
1
"
1
'
1
I
I
I
=
=
oraz
2
"
2
'
2
I
I
I
=
=
(3.136)
Równania impedancyjne pierwszego czwórnika w postaci macierzowej mają postać (
1
z
– macierz
impedancyjna pierwszego czwórnika)
⋅
=
'
2
'
1
,
22
,
21
,
12
,
11
'
2
'
1
1
I
I
z
z
z
z
U
U
43
42
1
z
(3.137)
Równania impedancyjne drugiego czwórnika w postaci macierzowej mają postać (
2
z
– macierz
impedancyjna drugiego czwórnika)
⋅
=
"
2
"
1
,
,
22
,
,
21
,
,
12
,
,
11
"
2
"
1
2
I
I
z
z
z
z
U
U
43
42
1
z
(3.138)
Dodając do siebie stronami równania (3.137) i (3.138) otrzymujemy
⋅
+
⋅
=
+
+
"
2
"
1
,
,
22
,
,
21
,
,
12
,
,
11
'
2
'
1
,
22
,
21
,
12
,
11
"
2
'
2
"
1
'
1
2
1
I
I
z
z
z
z
I
I
z
z
z
z
U
U
U
U
43
42
1
43
42
1
z
z
(3.139)
a po uwzględnieniu równań (3.135) i (3.136)
⋅
+
+
+
+
=
2
1
,
,
22
,
22
,
,
21
,
21
,
,
12
,
12
,
,
11
,
11
2
1
I
I
z
z
z
z
z
z
z
z
U
U
(3.140)
Zapiszmy równanie (3.140) w prostszej postaci
⋅
=
2
1
22
21
12
11
2
1
I
I
z
z
z
z
U
U
(3.141)
gdzie
+
+
+
+
=
,
,
22
,
22
,
,
21
,
21
,
,
12
,
12
,
,
11
,
11
22
21
12
11
z
z
z
z
z
z
z
z
z
z
z
z
(3.142)
Zatem parametry impedancyjne wypadkowej macierzy impedancyjnej połączenia szeregowego dwóch
czwórników
,
,
11
,
11
11
z
z
z
+
=
,
,
12
,
12
12
z
z
z
+
=
,
,
21
,
21
21
z
z
z
+
=
,,
22
,
22
22
z
z
z
+
=
czyli macierz impedancyjna czwórnika zastępczego jest równa sumie macierzy impedancyjnych
czwórników składowych
"
z
z'
z
+
=
(3.143)
W analogiczny sposób można rozważać układ połączonych ze sobą szeregowo
n
czwórników.
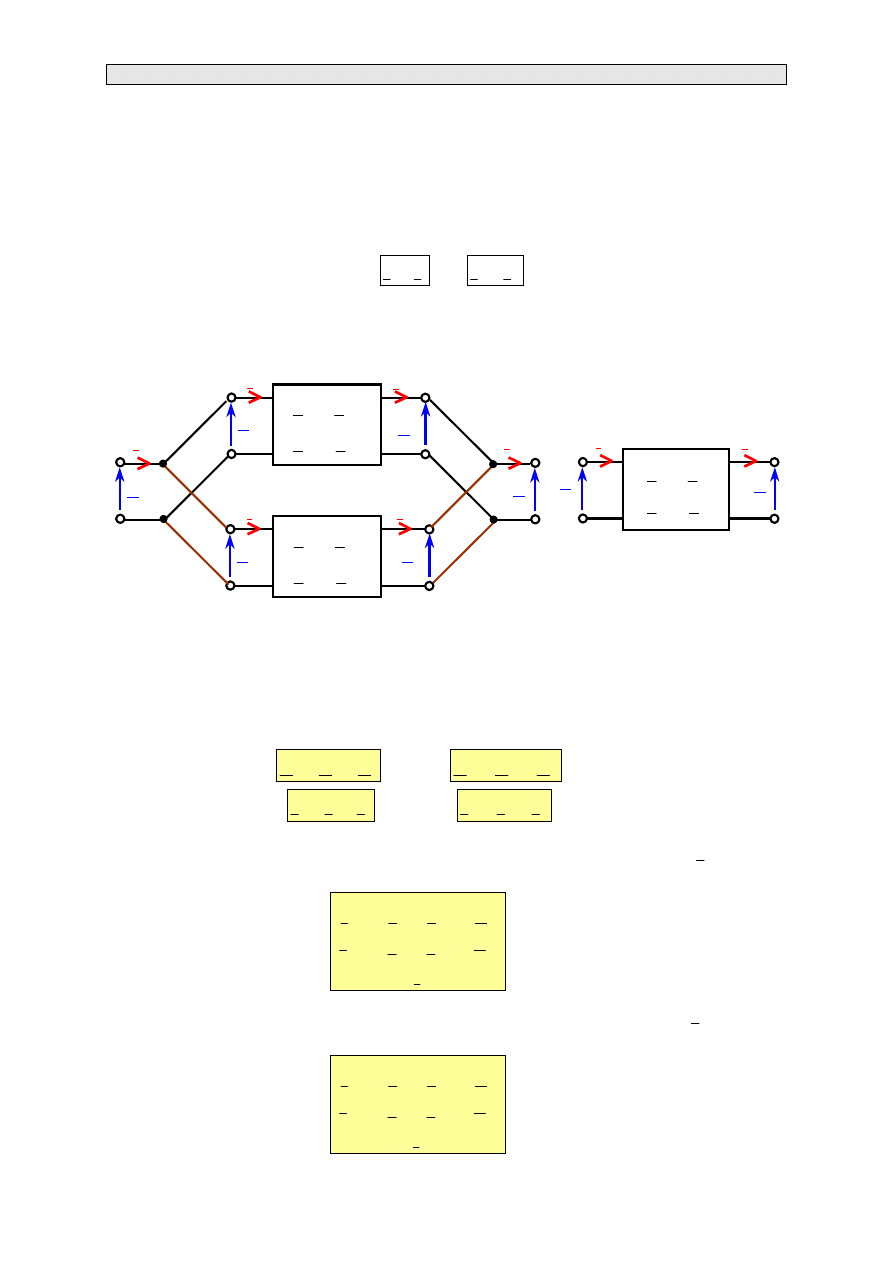
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
26
•
Połączenie równoległe czwórników
Połączeniem równoległym czwórników nazywamy układ, w którym są spełnione następujące
warunki:
•
Pary zacisków 1-1, 1’-1’ oraz 2-2, 2’-2’ czwórników są ze sobą połączone
bezimpedancyjnie(przy jednakowym oznaczeniu zacisków wejściowych i wyjściowych każdego z
czwórników);
•
jest spełniony warunek (3.2), czyli
'
1
1
I
I
=
oraz
'
2
2
I
I
=
Rozważmy układ składający się z dwóch czwórników połączonych równolegle jak to przedstawiono
na rys. 3.15.
,
22
,
21
,
12
,
11
y
y
y
y
I
1
’
I
2
’
U
1
’
U
2
’
1
,
,
22
,
,
21
,
,
12
,
,
11
y
y
y
y
1’
2
2’
a)
I
1
”
U
1
”
1
1’
I
2
”
U
2
”
2
2’
I
1
U
1
1
1’
I
2
U
2
2
2’
22
21
12
11
y
y
y
y
I
1
I
2
U
1
U
2
1
1’
2
2’
b)
Rys. 3.15. Połączenie równoległe dwóch czwórników (rys. a); schemat zastępczy (rys. b)
Do rozważań zastosujemy macierzową postać równań admitancyjnych czwórnika (3.8).
Wskaźniki „
’ ” (prim) dotyczą parametrów pierwszego czwórnika, zaś wskaźniki „ ” „ (bis) dotyczą
parametrów drugiego czwórnika.
Przy połączeniu równoległym czwórników zachodzą następujące równania napięć i prądów
1
"
1
'
1
U
U
U
=
=
oraz
2
"
2
'
2
U
U
U
=
=
(3.144)
"
1
'
1
1
I
I
I
+
=
oraz
"
2
'
2
2
I
I
I
+
=
(3.145)
Równania admitancyjne pierwszego czwórnika w postaci macierzowej mają postać (
1
y
– macierz
admitancyjna pierwszego czwórnika)
⋅
=
'
2
'
1
,
22
,
21
,
12
,
11
'
2
'
1
1
U
U
y
y
y
y
I
I
43
42
1
y
(3.146)
Równania admitancyjne drugiego czwórnika w postaci macierzowej mają postać (
2
y
– macierz
admitancyjna drugiego czwórnika)
⋅
=
"
2
"
1
,
,
22
,
,
21
,
,
12
,
,
11
"
2
"
1
2
U
U
y
y
y
y
I
I
43
42
1
y
(3.147)
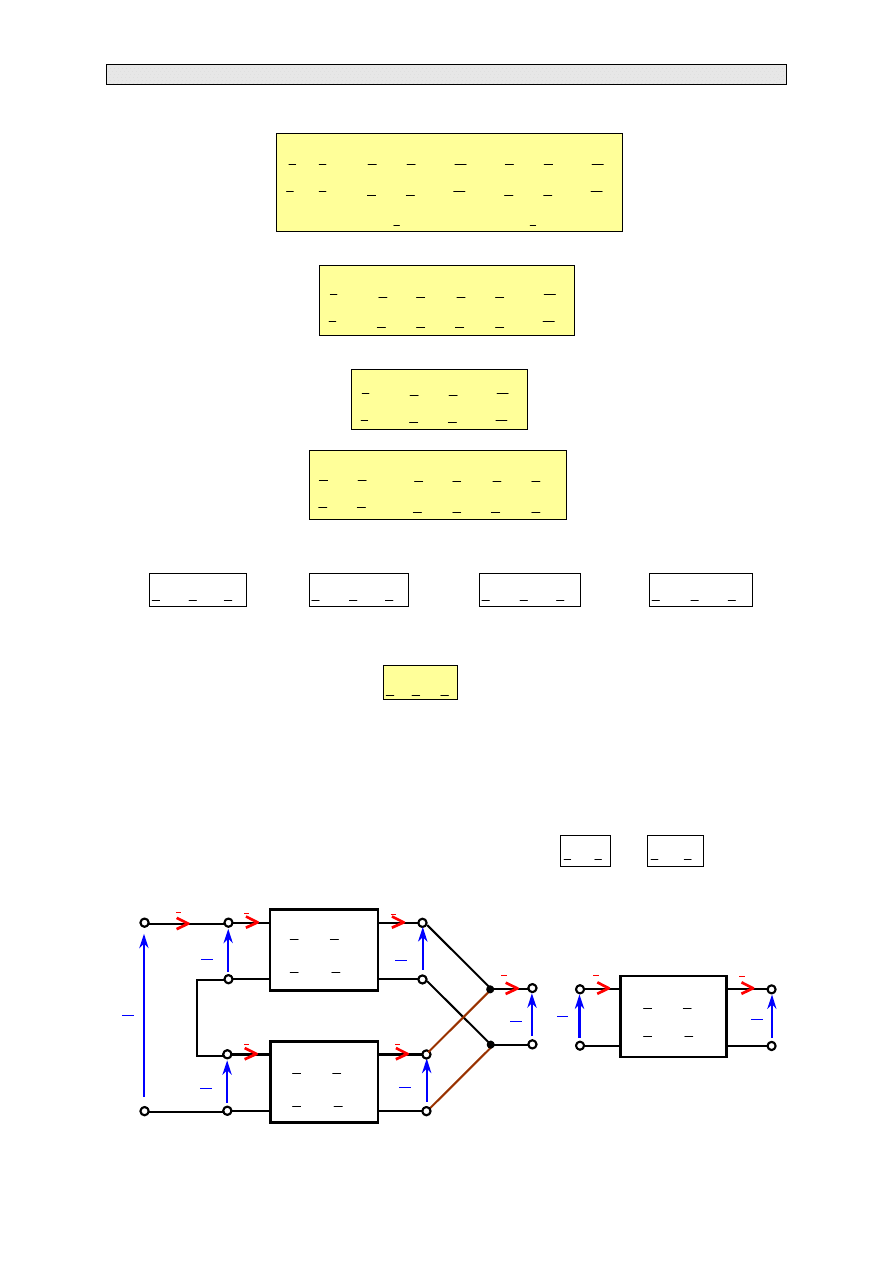
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
27
Dodając do siebie stronami równania (3.146) i (3.147) otrzymujemy
⋅
+
⋅
=
+
+
"
2
"
1
,
,
22
,
,
21
,
,
12
,
,
11
'
2
'
1
,
22
,
21
,
12
,
11
"
2
'
2
"
1
'
1
2
1
U
U
y
y
y
y
U
U
y
y
y
y
I
I
I
I
43
42
1
43
42
1
y
y
(3.148)
a po uwzględnieniu równań (3.144) i (3.145)
⋅
+
+
+
+
=
2
1
,
,
22
,
22
,
,
21
,
21
,
,
12
,
12
,
,
11
,
11
2
1
U
U
y
y
y
y
y
y
y
y
I
I
(3.149)
Zapiszmy równanie (3.149) w prostszej postaci
⋅
=
2
1
22
21
12
11
2
1
U
U
y
y
y
y
I
I
(3.150)
gdzie
+
+
+
+
=
,
,
22
,
22
,
,
21
,
21
,
,
12
,
12
,
,
11
,
11
22
21
12
11
y
y
y
y
y
y
y
y
y
y
y
y
(3.151)
Zatem parametry admitancyjne wypadkowej macierzy admitancyjnej połączenia równoległego dwóch
czwórników
,
,
11
,
11
11
y
y
y
+
=
,
,
12
,
12
12
y
y
y
+
=
,
,
21
,
21
21
y
y
y
+
=
,
,
22
,
22
22
y
y
y
+
=
czyli macierz admitancyjna czwórnika zastępczego jest równa sumie macierzy admitancyjnych
czwórników składowych
"
'
y
y
y
+
=
(3.152)
W analogiczny sposób można rozważać układ połączonych ze sobą równolegle
n
czwórników.
•
Połączenie szeregowo-równoległe czwórników
Połączeniem szeregowo-równoległym czwórników nazywamy układ, w którym czwórniki na wejściu
są połączone szeregowo, a na wyjściu równolegle.
Dla każdego z czwórników musi być spełniony warunek (3.2), czyli
'
1
1
I
I
=
oraz
'
2
2
I
I
=
'
22
'
21
'
12
'
11
h
h
h
h
I
1
’
I
2
’
U
2
’
1
"
22
"
21
"
12
"
11
h
h
h
h
1’
2
2’
a)
I
1
”
1
1’
I
2
”
U
2
”
2
2’
I
2
U
2
2
2’
U
1
’
U
1
”
I
1
U
1
1
1’
22
21
12
11
h
h
h
h
I
1
I
2
U
1
U
2
1
1’
2
2’
b)
Rys. 3.16. Połączenie szeregowo-równoległe dwóch czwórników (rys. a); schemat zastępczy (rys. b)
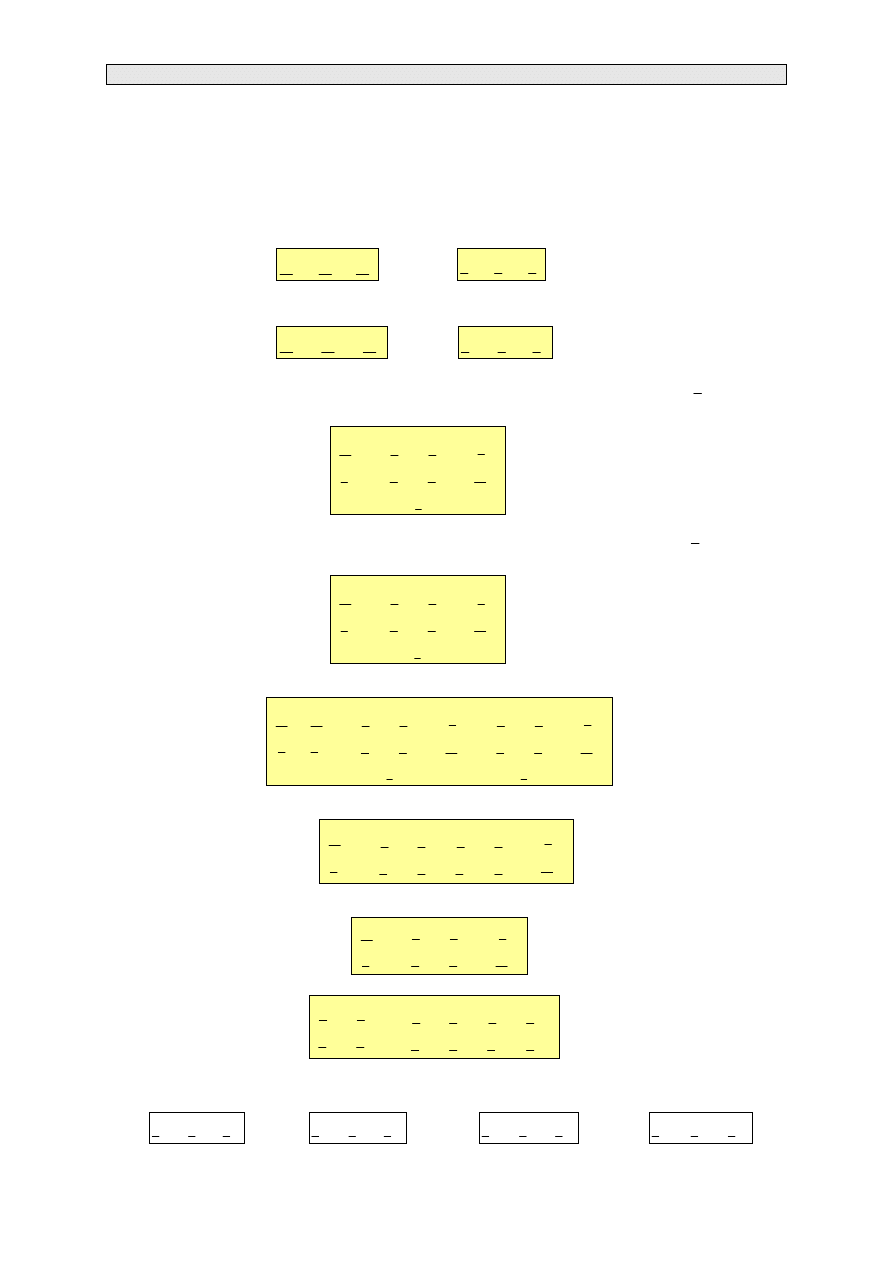
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
28
Rozważmy układ składający się z dwóch czwórników połączonych szeregowo-równolegle jak to
przedstawiono na rys. 3.16.
Do rozważań zastosujemy macierzową postać równań hybrydowych czwórnika (3.20).
Wskaźniki „ ’ ” (prim) dotyczą parametrów pierwszego czwórnika, zaś wskaźniki „ ” „ (bis) dotyczą
parametrów drugiego czwórnika.
Przy połączeniu szeregowym na wejściu czwórników zachodzą następujące równania napięć i prądów
"
1
'
1
1
U
U
U
+
=
oraz
1
"
1
'
1
I
I
I
=
=
(3.153)
Przy połączeniu równoległym na wyjściu czwórników zachodzą następujące równania napięć i
prądów
2
"
2
'
2
U
U
U
=
=
oraz
"
2
'
2
2
I
I
I
+
=
(3.154)
Równania hybrydowe pierwszego czwórnika w postaci macierzowej mają postać (
1
h
– macierz
hybrydowa pierwszego czwórnika)
⋅
=
'
2
'
1
'
22
'
21
'
12
'
11
'
2
'
1
1
U
I
h
h
h
h
I
U
43
42
1
h
(3.155)
Równania hybrydowe pierwszego czwórnika w postaci macierzowej mają postać (
2
h
– macierz
hybrydowa pierwszego czwórnika)
⋅
=
"
2
"
1
"
22
"
21
"
12
"
11
"
2
"
1
2
U
I
h
h
h
h
I
U
43
42
1
h
(3.156)
Dodając do siebie stronami równania (3.155) i (3.156) otrzymujemy
⋅
+
⋅
=
+
+
"
2
"
1
"
22
"
21
"
12
"
11
'
2
'
1
'
22
'
21
'
12
'
11
"
2
'
2
"
1
'
1
2
1
U
I
h
h
h
h
U
I
h
h
h
h
I
I
U
U
43
42
1
43
42
1
h
h
(3.157)
a po uwzględnieniu równań (3.153) i (3.154)
⋅
+
+
+
+
=
2
1
"
22
'
22
"
21
'
21
"
12
'
12
"
11
'
11
2
1
U
I
h
h
h
h
h
h
h
h
I
U
(3.158)
Zapiszmy równanie (3.158) w prostszej postaci
⋅
=
2
1
22
21
12
11
2
1
U
I
h
h
h
h
I
U
(3.159)
gdzie
+
+
+
+
=
"
22
'
22
"
21
'
21
"
12
'
12
"
11
'
11
22
21
12
11
h
h
h
h
h
h
h
h
h
h
h
h
(3.160)
Zatem parametry hybrydowe wypadkowej macierzy hybrydowej połączenia szeregowo-równoległego
dwóch czwórników
"
11
'
11
11
h
h
h
+
=
"
12
'
12
12
h
h
h
+
=
"
21
'
21
21
h
h
h
+
=
"
22
'
22
22
h
h
h
+
=
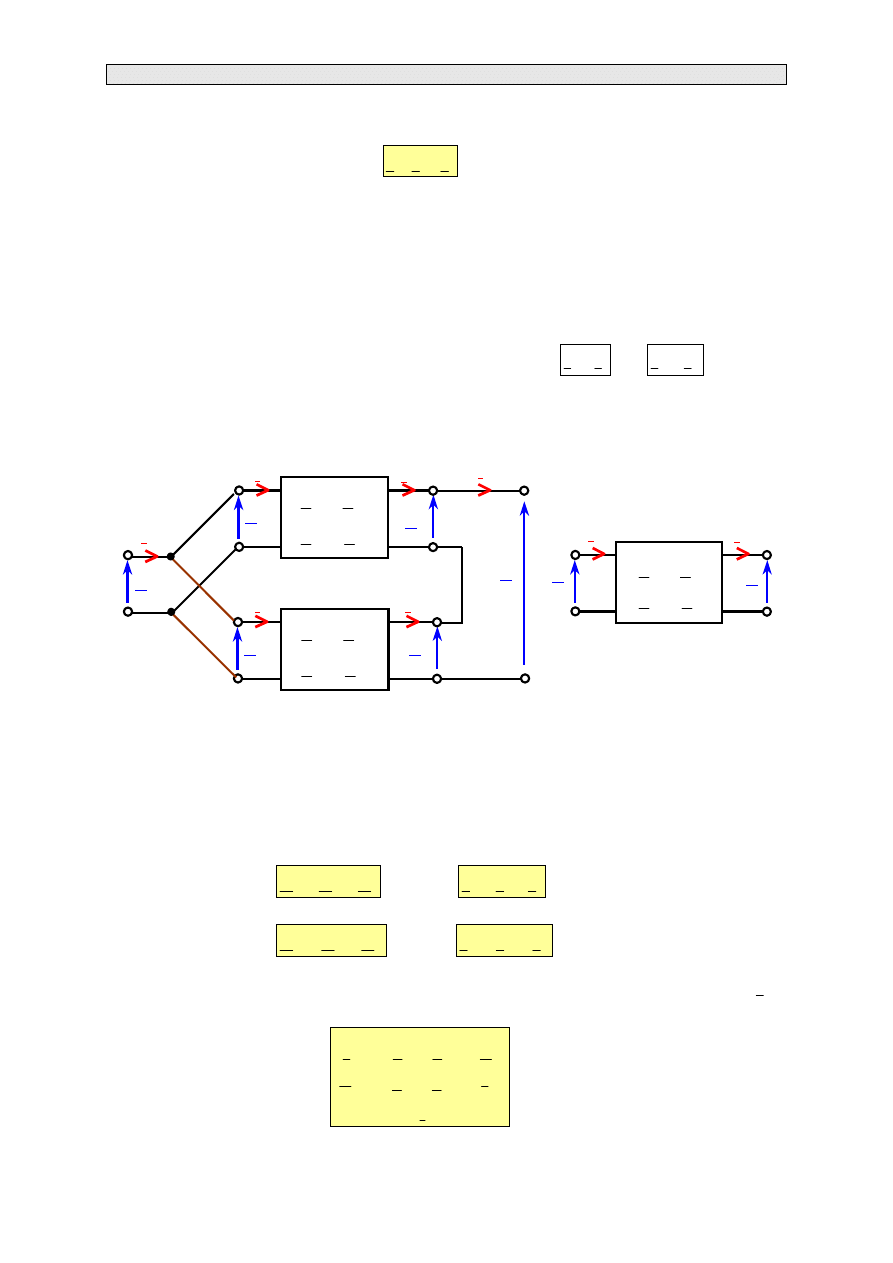
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
29
czyli macierz hybrydowa czwórnika zastępczego jest równa sumie macierzy hybrydowych czwórników
składowych
"
'
h
h
h
+
=
(3.161)
W analogiczny sposób można rozważać układ połączonych ze sobą szeregowo-równolegle
n
czwórników.
•
Połączenie równoległo-szeregowe czwórników
Połączeniem równoległo-szeregowym czwórników nazywamy układ, w którym czwórniki na wejściu
są połączone równolegle, a na wyjściu szeregowo.
Dla każdego z czwórników musi być spełniony warunek (3.2), czyli
'
1
1
I
I
=
oraz
'
2
2
I
I
=
Rozważmy układ składający się z dwóch czwórników połączonych równoległo-szeregowo jak to
przedstawiono na rys. 3.17.
,
22
,
21
,
12
,
11
g
g
g
g
I
1
’
I
2
’
U
1
’
U
2
’
1
,
,
22
,
,
21
,
,
12
,
,
11
g
g
g
g
1’
2
2’
a)
I
1
”
U
1
”
1
1’
I
2
”
U
2
”
2
2’
I
1
U
1
1
1’
I
2
U
2
2
2’
22
21
12
11
g
g
g
g
I
1
I
2
U
1
U
2
1
1’
2
2’
b)
Rys. 3.17. Połączenie równoległo-szeregowe dwóch czwórników (rys. a); schemat zastępczy (rys. b)
Do rozważań zastosujemy macierzową postać równań hybrydowych odwróconych czwórnika (3.24).
Wskaźniki „
’ ” (prim) dotyczą parametrów pierwszego czwórnika, zaś wskaźniki „ ” „ (bis) dotyczą
parametrów drugiego czwórnika.
Przy połączeniu równoległym na wejściu czwórników zachodzą następujące równania napięć i
prądów
1
"
1
'
1
U
U
U
=
=
oraz
"
1
'
1
1
I
I
I
+
=
(3.162)
Przy połączeniu szeregowym na wyjściu czwórników zachodzą następujące równania napięć i prądów
"
2
'
2
2
U
U
U
+
=
oraz
2
"
2
'
2
I
I
I
=
=
(3.163)
Równania hybrydowe odwrócone pierwszego czwórnika w postaci macierzowej mają postać (
1
g
–
macierz hybrydowa odwrócona pierwszego czwórnika)
⋅
=
'
2
'
1
,
22
,
21
,
12
,
11
'
2
'
1
1
I
U
g
g
g
g
U
I
43
42
1
g
(3.164)
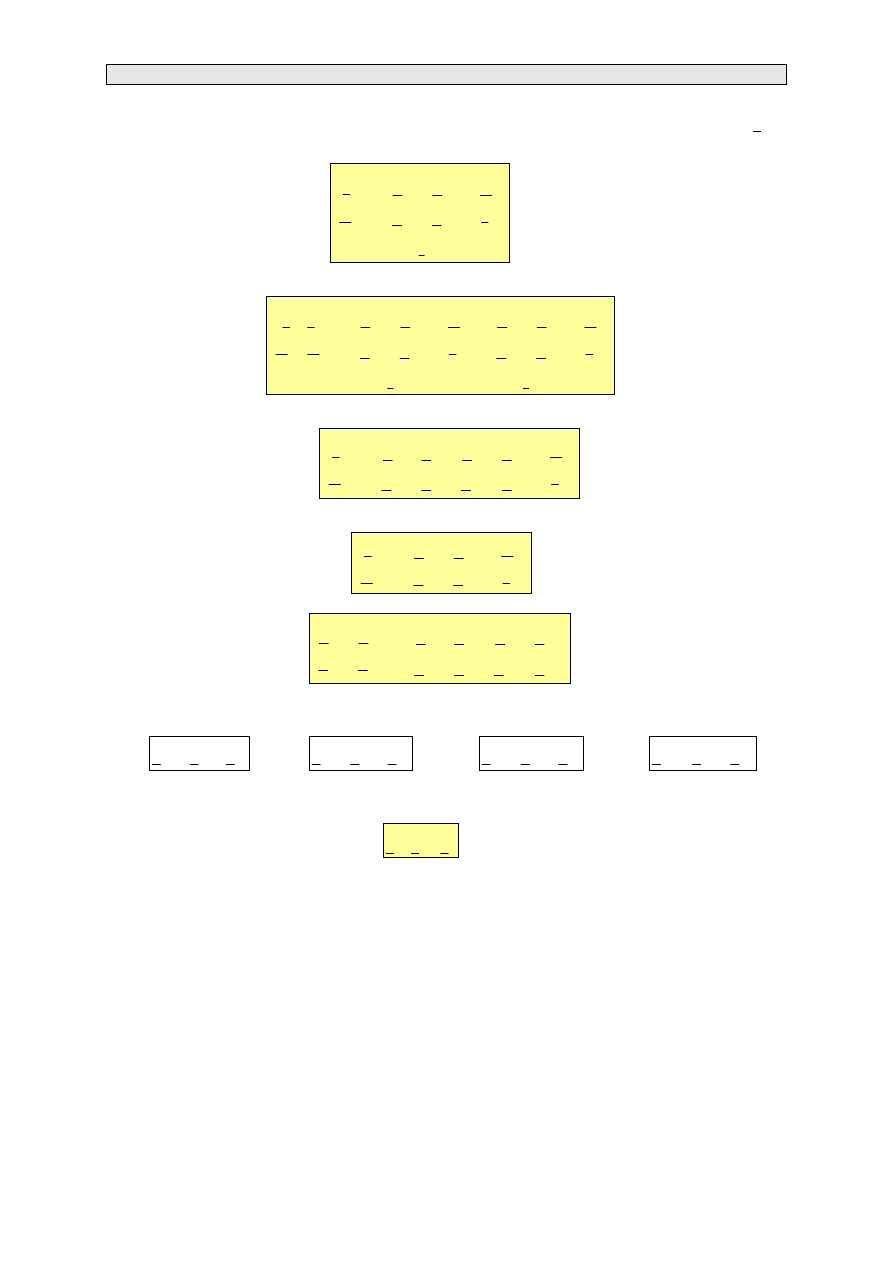
Dr inż. Mariusz Trojnar
Obwody i Sygnały 2
Wykład nr 6,7
30
Równania hybrydowe odwrócone drugiego czwórnika w postaci macierzowej mają postać (
2
g
–
macierz hybrydowa odwrócona drugiego czwórnika)
⋅
=
"
2
"
1
,
,
22
,
,
21
,
,
12
,
,
11
"
2
"
1
2
I
U
g
g
g
g
U
I
43
42
1
g
(3.165)
Dodając do siebie stronami równania (3.164) i (3.165) otrzymujemy
⋅
+
⋅
=
+
+
"
2
"
1
,
,
22
,
,
21
,
,
12
,
,
11
'
2
'
1
,
22
,
21
,
12
,
11
"
2
'
2
"
1
'
1
2
1
I
U
g
g
g
g
I
U
g
g
g
g
U
U
I
I
43
42
1
43
42
1
g
g
(3.166)
a po uwzględnieniu równań (3.162) i (3.163)
⋅
+
+
+
+
=
2
1
,
,
22
,
22
,
,
21
,
21
,
,
12
,
12
,
,
11
,
11
2
1
I
U
g
g
g
g
g
g
g
g
U
I
(3.167)
Zapiszmy równanie (3.167) w prostszej postaci
⋅
=
2
1
22
21
12
11
2
1
I
U
g
g
g
g
U
I
(3.168)
gdzie
+
+
+
+
=
,
,
22
,
22
,
,
21
,
21
,
,
12
,
12
,
,
11
,
11
22
21
12
11
g
g
g
g
g
g
g
g
g
g
g
g
(3.169)
Zatem parametry hybrydowe odwrócone wypadkowej macierzy hybrydowej odwróconej połączenia
równoległo- szeregowego dwóch czwórników
,
,
11
,
11
11
g
g
g
+
=
,
,
12
,
12
12
g
g
g
+
=
,
,
21
,
21
21
g
g
g
+
=
,
,
22
,
22
22
g
g
g
+
=
czyli macierz hybrydowa odwrócona czwórnika zastępczego jest równa sumie macierzy hybrydowych
odwróconych czwórników składowych
,
,
,
g
g
g
+
=
(3.170)
W analogiczny sposób można rozważać układ połączonych ze sobą w sposób równoległo-szeregowy
n
czwórników.
Wykorzystano następujące materiały:
1.
J. Bajorek, L. Gołębiowski, W. Posiewała, Obwody elektryczne. Laboratorium mikrokomputerowe,
Oficyna Wydawnicza Politechniki Rzeszowskiej, 1996.
2.
S. Bolkowski, Teoria obwodów elektrycznych, WNT, Warszawa, 1995.
3.
M. Krakowski, Elektrotechnika teoretyczna. Tom I. Obwody liniowe i nieliniowe, Państwowe
Wydawnictwo Naukowe, Warszawa, 1983.
4.
R. Kurdziel, Podstawy elektrotechniki, Wydawnictwa Naukowo-Techniczne, Warszawa, 1973.
5.
A. Szczepański, M. Trojnar, Obwody i Sygnały, Oficyna Wydawnicza Politechniki Rzeszowskiej,
2006.
Wyszukiwarka
Podobne podstrony:
ET DI2 ObwodySygnaly2 wyklad nr 9 10 czworniki aktywne
ET DI2 ObwodySygnaly2 wyklad nr 1 5 2014 w1
wykład nr 2 - 7.03.2009, WSAP, WSAP, Nuka o administracji, Nuka o administracji
Wykład nr 3 2009 - enzymologia kliniczna, materiały medycyna SUM, biochemia, wykłady
Wykład nr 2 1.12.2009, biomechanika
0205 25.03.2009, wykład nr 5.,, Jądro komórkowe
6.A Wykład OiSE CZWÓRNIK, Wojskowa Akademia Techniczna (WAT), Obwody i Sygnały, Materiały 2013
0203 11 03 2009, wykład nr 3 , Białka powierzchni komórkowej Cząsteczki adhezyjne
0202 04 03 2009, wykład nr 2 , Budowa i funkcje błony komórkowej oraz transport przez błony(1)
0201 25 02 2009, wykład nr 1 , Rys historyczny rozwoju wiedzy o komórce Podstawowe techniki stosowa
0214 13 10 2009, wykład nr 14 , Układ pokarmowy, cześć II Paul Esz(1)
0212 20 05 2009, wykład nr 12 , Krew i limfa Paul Esz(1)
0209 29 04 2009, wykład nr 9 , Tkanka nabłonkowa Paul Esz(1)
0215 20 10 2009, wykład nr 15 , Układ pokarmowy, cześć III Paul Esz(1)
0216 27 10 2009, wykład nr 16 , Układ dokrewny, cześć I Paul Esz(1)
więcej podobnych podstron