Przedmiot, cel i zasady prognozowania

Wstęp
1. Prognozowanie gospodarcze — podstawowe pojęcia i problemy
2. Metody prognozowania. Metody heurystyczne
3. Standardy i zasady prognozowania
4. Weryfikacja i trafność prognoz — podstawy teoretyczne
5. Wstępna analiza danych
Bibliografia

Wstęp

Nauka o formułowaniu prognoz tworzy zbiór zasad i standardów powszechnie wykorzystywanych do określe-
nia (wyznaczenia) tego, co nieznane. Może to dotyczyć zarówno warunków gospodarowania w kolejnym roku
kalendarzowym, wielkości zapotrzebowania na nowo wprowadzane towary, przyszłego poziomu cen produk-
tów na rynku, wolumenu zawartych transakcji, jak i efektów oddziaływania reklamy, prowadzonej polityki go-
spodarczej czy stanu koniunktury na rynku. O tym, jak taka wiedza jest doceniana w warunkach gospodarki
rynkowej, niech świadczy prestiż i uznanie będące udziałem największych firm doradczych i najbardziej znanych
ośrodków prognostycznych.

Wiedza o kształtowaniu się zjawisk gospodarczych w przyszłości oparta jest na ogół na ich dotychczasowym za-
chowaniu się. Wykorzystujemy w tym celu dobrze znaną regułę mówiącą, że „przyszłość jest podobna do prze-
szłości”. Badając wariantowo efekty oddziaływania różnych czynników rynkowych lub planowanych działań
przedsiębiorstwa, korzystamy z kolei ze związków korelacyjnych zachodzących między cechami podmiotów go-
spodarczych lub między zmiennymi opisującymi ich zachowanie się. Zakładając lub sprawdzając, że dostrzeżo-
ne zależności są stabilne w próbie, wnioskujemy, że przez analogię będą dobrze sprawdzały się w przyszłości lub
dla innych podobnych obiektów.

Na początek zapoznamy się z podstawowymi pojęciami i problemami związanymi z prognozowaniem. W dru-
gim temacie przedstawione zostaną najważniejsze metody prognozowania i ich klasyfikacje. Z trzeciego tematu
dowiemy się, że istnieje spisany zbiór zasad i standardów, którymi powinien posługiwać się każdy prognostyk
w trakcie poszczególnych etapów procesu prognozowania. Następnie poznamy podstawy teoretyczne związane
z weryfikacją trafności prognozy i dowiemy się, co sprzyja „dobrym” prognozom. Na koniec zajmiemy się przy-
gotowaniem porównywalnych danych umożliwiających podjęcie zadania prognostycznego w sytuacji, gdy wy-
magają tego dostępne dane.

4

1. Prognozowanie gospodarcze

— podstawowe pojęcia i problemy

Prognozowaniem gospodarczym

(predykcją ekonomiczną) nazywamy formułowanie

sądów (jakościowych i ilościowych) o kształtowaniu się pewnych cech w obiektach
gospodarczych lub o występowaniu zjawisk gospodarczych w określonych momen-
tach lub okresach czasu. Niektórzy autorzy podkreślają, że prognoza powinna od-
nosić się jedynie do przyszłości (Czerwiński 1992, s. 220), a przynajmniej do tego,
co nieznane na podstawie tego, co znane

1

. Owszem, taki jest rezultat budowy pro-

gnoz, ale prognozowanie jest złożonym procesem, w którym wyznaczanie prognoz
na przeszłość stanowi regułę, a nie wyjątek. To właśnie ocena sprawdzalności pro-
gnoz ex post (po fakcie, czyli po zajściu zdarzenia) przez ich zrealizowane błędy de-
terminuje wybór metody prognozowania. Dla prognozowania ex ante (przed fak-
tem, czyli przed wystąpieniem zjawiska) zarezerwujemy termin projekcja.

Na tym kursie ograniczymy się jedynie do prognozowania ilościowych aspektów
gospodarowania, pomijając prognozy o charakterze jakościowym (typu: dana ce-
cha wystąpi w badanym obiekcie lub nie, czy wystąpi zdarzenie a, b lub c w danym
okresie czasu). Prognozy takie mogą mieć charakter punktowy, gdy ich efektem
jest pojedyncza liczba lub przedziałowy, kiedy podajemy zakres prawdopodobnej
realizacji prognozy. W przeciwieństwie do wróżek i fałszywych proroków nie bę-
dziemy natomiast zajmować się przewidywaniem, czy badany obiekt (na przykład
klient wróżki lub współwyznawca) odniesie sukces (majątkowy, zawodowy, uczu-
ciowy czy wiekuisty), chociaż w kręgu naszego zainteresowania możemy umieścić
prognozy dotyczące prawdopodobieństwa wzrostu ceny akcji lub szans pracownika
na otrzymanie podwyżki.

Z korzystaniem z wyników procesu prognozowania mamy stale do czynienia. I nie
dotyczy to tylko prognoz pogody podawanych po wiadomościach przez najpopu-
larniejszych synoptyków w kraju, a o sytuacje z codziennego życia ekonomiczne-
go. Udając się do sklepu na zakupy z określoną kwotą pieniędzy, zaciągając kre-
dyt w obcej walucie, decydując się na studia wyższe, organizując posezonową wy-
przedaż kolekcji, zatrudniając osobę na stanowisku prezesa banku czy kupując ak-
cje na giełdzie, świadomie lub nieświadomie formułujemy prognozy i dokonujemy
ich wyboru. Nieważne czy przedmiotem prognoz są koszty codziennych zakupów,
przyszłe raty kredytowo-odsetkowe, korzyści finansowe płynące z wykształcenia,
przychody ze sprzedaży, czy wymierne korzyści finansowe, jakie może przynieść
akcjonariuszom nowy prezes, a inwestorom nabyte akcje spółki. We wszystkich
tych sytuacjach występują podobne przesłanki do formułowania ocen ilościowych,
a zatem można zastosować podobne podejście do ich rozwiązywania.

Jakie są te wspólne elementy w prognozowaniu zjawisk gospodarczych? Zacznijmy
od

przesłanek prognozowania

, czyli od określenia celów, dla których duże przedsię-

biorstwa tworzą komórki zajmujące się tylko prognozowaniem przyszłej sytuacji
finansowej firmy, a decydenci — podejmując ryzykowne decyzje inwestycyjne —
są gotowi słono płacić za porady i ekspertyzy. U podstaw tych zachowań leżą nie
tylko wymogi prawa, takie jak przepisy dotyczące podawania do publicznej wia-
domości planów finansowych spółek giełdowych i ich zmian. Równie ważne, je-
śli nie ważniejsze, są wewnętrzne motywy takiego postępowania, w tym koniecz-
ność podejmowania decyzji często w bardzo skomplikowanych sytuacjach bizneso-

1

Cieślak (1996: 14–15) na-

zywa takie działanie prze-

widywaniem, rezerwując

nazwę prognozowanie je-

dynie do metod korzysta-

jących z aparatu nauko-

wego i ścisłego rozumo-

wania.

5

wych. Podmioty gospodarcze funkcjonują bowiem w środowisku przepełnionym
niepewnością. W szczególności dotyczy ona przyszłej sytuacji ekonomicznej firmy:
przychodów ze sprzedaży, kosztów działalności, cen produktów i materiałów do
produkcji czy wreszcie zapotrzebowania na wytwarzane produkty. Stąd biorą się
działania oparte na jasno określonych zasadach (tj. regułach prognozowania), pro-
wadzące do porządkowania otoczenia i kształtowania uproszczonego obrazu rze-
czywistości. Modele decyzyjne, które temu służą, wymagają zarówno parametrów
pozyskanych za pomocą metod statystycznych, jak i prostych prognoz danych wej-
ściowych, które warunkują wynik procesu podejmowania decyzji. Dotyczy to za-
równo unikalnych sytuacji występujących w planowaniu strategicznym, jak i po-
wtarzalnych decyzji w codziennych działaniach operacyjnych firmy. Wykorzysta-
nie modeli ekonometrycznych w formułowaniu takich prognoz pozwala ponadto
udzielać odpowiedzi warunkowych typu „co by było, gdyby”. Pomagają one przy
wyborze wariantu działania spośród kilku możliwych. Oparcie decyzji na przejrzy-
stych regułach ilościowych sprzyja sprawności funkcjonowania przedsiębiorstwa
i tworzy pozytywny obraz w oczach inwestorów. Również prowadząc na mniej-
szą skalę działalność gospodarczą, staramy się śledzić nie tylko zmiany w przepi-
sach, ale również dokładnie obserwujemy rynek, na którym działamy, starając się
zmniejszyć obszar niepewności. Określenie charakteru trendu i zmian sezonowych
sprzedaży poszczególnych towarów i ich cen może bowiem stanowić o sukcesie
czy przetrwaniu na lokalnym rynku. Podsumowując, prognozowanie koniunktury
w gospodarce, tendencji na rynku i własnych działań ma na celu zamianę niepew-
ności w funkcjonowaniu firmy na formalnie opisane sytuacje ryzyka. Modele pro-
gnostyczne korzystające z dotychczas zdobytych doświadczeń empirycznych mogą
wyznaczać prawdopodobieństwa wystąpienia tych zjawisk lub określać przeciętne
efekty planowanych przez firmę działań.

Bez wątpienia zatem prognozy spełniają ważne

funkcje informacyjne

(wyjaśniające).

Informują nas o przyszłych prawdopodobnych stanach systemów gospodarczych
czy konsekwencjach podjętych decyzji. Funkcje informacyjne prognozy związane
są z celami, dla których dokonuje się projekcji. Jeżeli są to cele badawcze, to wte-
dy zadaniem prognozy jest wszechstronne rozpoznanie przyszłości i ukazanie wie-
lu możliwych jej wersji (prognozy wariantowe), w tym wskazanie tej najbardziej
prawdopodobnej. Analizy typu „co by było, gdyby” są chętnie wykorzystywane
przez decydentów do symulacji efektów polityki gospodarczej.

W praktyce prognoza jest niekiedy jedynym źródłem wiedzy o nieznanych para-
metrach rachunku ekonomicznego. Wiedza ta sama w sobie nie jest celem progno-
zowania gospodarczego. Prognoza ma na ogół przygotować lub wspomagać inne
działanie — najczęściej podjęcie jednej z wielu możliwych decyzji w przedsiębior-
stwie. Taką funkcję prognoz nazywamy

preparacyjną

, czyli przygotowującą i wspo-

magającą podjęcie tej decyzji. Prognoza może również pełnić funkcję

ostrzegaw-

czą

, gdy zwraca uwagę na niekorzystne dla odbiorcy kształtowanie się zjawiska.

Ostrzeżenie o niekorzystnym rozwoju sytuacji jest wówczas zachętą do podjęcia
dodatkowych działań, które mogą zapobiec katastrofie. Bardzo często prognozy
pełnią również funkcję

aktywizująca

, czyli pobudzającą do podejmowania działań

sprzyjających realizacji prognozy (w przypadku zdarzeń korzystnych) lub zachęca-
jącą do podjęcia czynności przeciwdziałających realizacji prognozy (w przypadku
zdarzeń niekorzystnych). Niekiedy samo ogłoszenie prognozy w przypadku jej du-
żej wiarygodności sprzyja jej realizacji. Mówimy wówczas o samospełniających się
przepowiedniach, które są skrajnym przypadkiem przejawiania się aktywizującej
funkcji prognoz. Ich przeciwieństwem są samounicestwiające się przepowiednie,
które z chwilą ujrzenia światła dziennego automatycznie wywołują działania zapo-
biegające realizacji prognozy. Mniej popularne, ale niekiedy równie użyteczne są
tak zwane prognozy kontrfaktyczne. Pokazują one prawdopodobne przeszłe stany
przedsiębiorstwa lub gospodarki w przypadku wystąpienia sytuacji, które nie mia-

6

ły miejsca w rzeczywistości. Służą one uzasadnieniu poprawności podjętych decy-
zji lub obrazują rozmiary ryzyka, na jakie narażony był decydent w sytuacji nieko-
rzystnego ukształtowania się czynników zewnętrznych.

Jedną z przesłanek prognozowania jest horyzont prognozy.

Horyzontem prognozy

nazywamy najdalszy okres, dla którego formułujemy prognozę właściwą. Wybór
horyzontu prognozy jest kluczową sprawą z punktu widzenia możliwości zastoso-
wania prognoz w decyzjach gospodarczych. Rozróżniamy na ogół prognozy krót-
ko-, średnio- i długookresowe

2

. Za

prognozę krótkookresową

uważa się prognozę na

taki okres, w którym zachodzą tylko zmiany ilościowe.

Prognoza długookresowa

do-

tyczy horyzontu prognozy, w którym mogą zachodzić zarówno zmiany ilościowe,
jak i jakościowe.

Prognoza średniookresowa

jest czymś pomiędzy wymienionymi sy-

tuacjami. Wyróżnia ją to, że zmiany ilościowe przeważają nad występującymi śla-
dowo zmianami jakościowymi. Oczywiście podział ten jest umowny i nie określa
precyzyjnie okresów, dla których można go stosować. Dla porównania na rynku
kapitału fizycznego zmiany do roku to zmiany krótkookresowe, powyżej roku do
5 lat to zmiany średniookresowe, a powyżej 5 lat — długookresowe, ale już na ryn-
ku akcyjnym, charakteryzującym się dużą zmiennością warunków gospodarowa-
nia, prognozy powyżej roku można uznać za długookresowe. Zmiany w trakcie
kolejnej sesji giełdowej na notowaniach ciągłych dotyczą w tym przypadku bardzo
krótkiego okresu. Nawet dla stabilnego inwestora giełdowego tydzień może przy-
nieść informacje, które wpłyną na jego decyzje, choć „twarde” informacje o wyni-
kach finansowych, które mogą zweryfikować sposób spojrzenia na kondycję spół-
ek, podawane są miesięcznie i kwartalnie (średni okres). Tak naprawdę jednak do-
piero wyniki roczne i wieloletnie plany restrukturyzacji spółek można traktować
jako znaczącą informację o zmianie warunków ich funkcjonowania w długim okre-
sie. W praktyce prognozy dotyczące tego samego horyzontu prognozy możemy na-
zwać krótko-, średnio- lub długookresowymi w zależności od przedmiotu, celu
i podmiotu prognozy.

Przykład 1

W grudniu 2006 roku dokonano prognozy dotyczącej sytuacji finansowej pewnego
przedsiębiorstwa na następny rok, wykorzystując w tym celu dane miesięczne z po-
przedniego roku. Prognoza dotyczyła wielkości produkcji, popytu na produkowa-
ne towary, przepływów finansowych, zatrudnienia i wielkości importu. Dokonamy
klasyfikacji tej prognozy.
Ponieważ horyzont prognozy wynosi rok, to prognozę tę zaliczymy do średnio-
okresowych, gdyż w tym okresie można dokonać zmiany części aparatu produk-
cyjnego.
Na podstawie danych miesięcznych uzyskamy 12 wyprognozowanych wartości dla
każdej z kategorii. Jest to więc prognoza wielookresowa. Ponieważ wszystkie pro-
gnozowane wielkości są mierzalne i wyrażone w jednostkach fizycznych, to pro-
gnozę zaliczymy do ilościowych, ale może być to prognoza zarówno punktowa, jak
i przedziałowa (nie mamy dokładnej informacji na ten temat). Można byłoby za cel
prognozy podać rozpoznanie prawdopodobnej sytuacji finansowej i w tej sytuacji
byłaby to prognoza badawcza, ale może także pełnić rolę prognozy ostrzegawczej,
pasywnej lub aktywizującej (w zależności od otrzymanego rezultatu).

Ważną rolę w procesie prognozowania spełnia

prognostyk

(synoptyk) — osoba lub

grupa osób formułująca prognozy. Dobrze, jeśli prognostyk w procesie formuło-
wania prognoz jest niezależny od decydentów i niepowiązany z konkretną sytu-
acją decyzyjną (np. nie jest beneficjentem planowanych działań). W takiej roli do-
brze wypadają niezależne instytucje audytorskie albo niezależni doradcy. Z drugiej
strony dobra znajomość materii prognozowania i konieczność zachowania pouf-
ności w dostępie do informacji sprzyjają powodzeniu całego procesu. Warunki te
spełniają pracownicy lub te komórki funkcjonujące w firmie, które w sposób ciągły

2

Podział w tej klasyfikacji

przyjęto za Cieślak,

1996: 26.

7

i profesjonalny zajmują się analizowaniem danych i projektowaniem rozwoju firmy.
Pracownicy pozostają jednak w stosunkach zależności z decydentami (zarządem,
dyrekcją lub właścicielami firmy), co ogranicza niezależność ich poglądów i obiek-
tywizm ich ocen. Ważne jest zatem znalezienie konsensusu między niezależnością
podmiotu wykonującego prognozy a dobrą znajomością przedmiotu analizy i do-
stępem do odpowiednich danych.

W tym miejscu warto jeszcze rozróżnić typowe

eksperckie prognozowanie

otoczenia

rynkowego firmy od projektowania jej działalności przez

planowanie gospodarcze

.

Te pierwsze prognozy, często wykonywane na zamówienie lub oficjalnie publiko-
wane, mogą dotyczyć uznanych kategorii rynkowych i powinny być formułowane
z zachowaniem obiektywizmu. Planowanie gospodarcze jest z kolei czynnością ce-
lową czynioną na potrzeby konkretnego przedsiębiorstwa. Plan ma bowiem zmobi-
lizować jego wykonawców, zaprezentować potencjalnym inwestorom ambitne za-
miary bez ujawniania wszystkich szczegółów konkurentom. A więc z natury rzeczy
jest subiektywną oceną przyszłości. Prognozowanie wynika wówczas z założenia,
że podejmowane działania mogą kształtować przedmiot analizy na przykład zmie-
niać kierunki rozwoju firmy, wpływać na zachowania konkurencji i sytuację na
rynku. Z kolei ekspert powinien wyrażać opinie i osądy w sposób niezależny od
osób i podmiotów podejmujących decyzje i nie mieć wpływu ani na prognozowa-
ną rzeczywistość, ani na decydentów. Ta niezależność nie tylko może wpływać na
formułowanie poprawnych ocen dotyczących przyszłości, ale stanowi warunek ko-
nieczny ich wiarygodności. Służy temu również jawne formułowanie zastosowa-
nych metod prognozowania, które można poddać statystycznej ocenie i weryfika-
cji. W planowaniu regułą jest podawanie do wiadomości tylko wyników prognoz
finansowych i projekcji makroekonomicznych, a ukrywanie wykorzystywanych
w planie szczegółowych założeń dotyczących funkcjonowania firmy.

Oczywiście obie wymienione sytuacje prognostyczne nie występują w czystej for-
mie. Zawsze istnieją jacyś odbiorcy prognoz, więc eksperci nie są kompletnie nie-
zależni od ocen otoczenia i własnych przekonań. Zupełnie obiektywne prognozy
słabo spełniają funkcje społeczne (np. ostrzegawczą). Niektóre wyniki takich pro-
gnoz mogą być ponadto społecznie nieakceptowane, a zbyt sformalizowane pro-
gnozy po prostu słabo się sprzedają. Często to sami eksperci decydują się nie poka-
zywać całego warsztatu wykorzystywanego do tworzenia prognoz, więc nie można
go w pełni zweryfikować. Z kolei planista uzależniający wszystkie prognozy jedy-
nie od intencji i celów przedsiębiorstwa szybko straci wiarygodność, czyniąc z pla-
nu bezwartościowy dokument nieakceptowany przez jego wykonawców. Poszuki-
wanie „złotego środka” jest konieczne w nieustannym przetargu między odbior-
cami prognoz a ich wykonawcami. Reasumując, w prognozowaniu formułujemy
sądy na temat tego, jaka jest lub jaka będzie rzeczywistość, a w planowaniu, jaka
powinna ona być. Intencja stojąca za planistą może powodować, że plan jako su-
biektywna prognoza nie będzie spełniał wielu funkcji, które wiążemy z procesem
prognozowania.

8

2. Metody prognozowania.

Metody heurystyczne

Istnieje wiele sposobów przejścia od posiadanych, czyli znanych informacji do pro-
gnozy. Te sposoby nazywamy metodami prognozowania. Według Czerwińskiego
i Guzik (1980) metody obejmują kolejno przetworzenie informacji o przeszłości
zjawiska, a następnie sposób przejścia od informacji przetworzonej do prognozy.
O tym pierwszym technicznym elemencie metody prognozowania powiemy więcej
w ostatnim temacie tego modułu. Ten drugi element, zwany regułą prognozowania,
zajmuje najwięcej miejsca w dyskusjach na temat wyboru odpowiednich metod.

Dane zjawisko można prognozować za pomocą różnych reguł prognozowania, ko-
rzystając z odpowiedniego przepisu generującego prognozę. Na przykład prognozę
zmiennej można przyjąć na poziomie ostatniej dostępnej w próbie informacji o tej
zmiennej — taką metodę nazywamy naiwną. Informacje z kilku ostatnich okresów
można uśredniać, co daje regułę średniej ruchomej. Niektóre z tych formuł (wzór
na metodę naiwną, średnią ruchomą k-okresowa) są dobrze znane i powszechnie
stosowane. Na ogół nie trzeba ich więc przytaczać przy prezentacji wyników pro-
gnozy. Na podstawie metod podstawowych konstruować można różne modyfikacje
przydatne w określonej sytuacji (np. metoda Holta z multiplikatywnym trendem).
Jest tu miejsce na inwencję prognostyka i twórcze wykorzystanie znajomości me-
tod podstawowych. Wówczas należy wyraźnie określić regułę, za pomocą której
uzyskano prognozę. Stanowi to o wiarygodności badania i daje okazję do odtwo-
rzenia wyników procesu prognozowania. Formułę wyliczenia prognozy nazywamy

predykatorem

i zapisujemy za pomocą wzoru

3

:

(...).

*

f

y

t



Predykator jest zatem matematyczną funkcją, która może dostarczać punktową
prognozę zmiennej, gdy prognoza przyjmuje określoną pojedynczą wartość (jak
powyżej). Predykator może również wyznaczać prognozę przedziałową, gdy po-
daje przedział liczbowy realizacji prognozy z określonym poziomem prawdopodo-
bieństwa, zwanym poziomem ufności prognozy 1 – α:

.

1

)}

,

(

{

*

*

*









G

t

D

t

t

y

y

y

P

Do najpopularniejszych predykatorów należą formuły oparte na statystycznej ana-
lizie regresji:

)).

,

,...,

,

(

2

1

t

kt

t

t

t

x

x

x

f

y





Zmienne objaśniające x

1t

, x

2t

, …, x

kt

z takiej regresji nazywamy predyktorami

zmiennej prognozowanej. Predykatorem jest w tym modelu warunkowa wartość
oczekiwana, czyli regresja zmiennej prognozowanej (objaśnianej) względem zmien-
nych objaśniających:

.

...,

2,

1,

dla

)

...

,

,

(

2

1

*

T

t

x

x

y

E

y

t

t

t

t





3

Potrójny znak równości

oznacza, że w tym miejscu

tożsamościowo definiu-

jemy predykator y* okre-

ślony za pomocą funkcji

f(…).

9

Prognozę z modelu ekonometrycznego można traktować jako prognozę

według

wartości oczekiwanej

. Reguła dostarczania prognoz opartych na wartości oczekiwa-

nej rozkładu daje prognozę nieobciążoną, czyli systematycznie poprawną. Ozna-
cza to, że przeciętnie rzecz biorąc nie mylimy się ani in plus ani in minus w ocenie
zjawiska. Prognozy otrzymane w ten sposób obarczone są pewnym błędem, czyli
różnią się od przyszłej realizacji zmiennej. Należy oczekiwać, że powtarzanie pro-
cesu prognozowania danego zjawiska w tych samych warunkach da średni błąd
otrzymanych prognoz równy zero. Regułę tę można stosować przy założeniu, że
model trafnie opisujący przeszłość będzie równie dobrze opisywał kształtowanie
się zmiennej w przyszłości. Jest to założenie dość mocne. W rzeczywistości trudno
jest mówić o wielokrotnym prognozowaniu zjawiska w tych samych warunkach.
Na wyniki takiej prognozy wpływ mają również nietypowe wartości predyktorów
w okresie próby.

Prognoza przedziałowa wymaga na ogół zdefiniowania rozkładu zmiennej losowej

ε

t

w modelu. Prognozę punktową według wartości oczekiwanej możemy stosować,

jeżeli zdefiniujemy jedynie pierwszy moment centralny rozkładu zmiennej losowej
(tj. wartość oczekiwaną). Chcąc wyznaczyć prognozę na podstawie predykatora
według pozostałych reguł, musimy określić więcej parametrów rozkładu. I tak mo-
żemy wyróżnić następujące reguły prognozowania:
—

Według dominanty (mody) rozkładu prognoz (prognoza najbardziej prawdopo-
dobna):

.

...,

2,

1,

dla

)}

(

)

(

:

{

0

T

t

y

P

y

P

y

y

t

D

t

D

t

t















gdzie

)

(

0



t

y

P

oznacza prawdopodobieństwo, z jakim zmienna prognozowana y

t

przyjmie dowolną wartość

0



t

y

, a

D

t

y



najbardziej prawdopodobna wartość zmien-

nej y

t

.

Jeżeli interesuje nas prognoza najbardziej prawdopodobna, to należy posłużyć się
tą regułą.
—

Według mediany rozkładu prognoz (prognoza według wartości środkowej roz-
kładu):

,

...,

2,

1,

dla

}

5

,

0

)

(

5

,

0

)

(

:

{

0

0

T

t

y

y

P

y

y

P

y

y

t

M

t

t

M

t

M

t

t



























gdzie

M

t

y



— wartość zmiennej y

t

równa medianie.

Ta prognoza dzieli zbiór możliwych wartości prognoz na dwie części. Równie praw-
dopodobne są wartości prognoz mniejsze i większe od mediany. Metoda ta jest bar-
dziej odporna na występowanie nietypowych obserwacji w okresie próby.
— Minimalizacji straty:

.

...,

2,

1,

dla

)}

(

)

(

:

{

0

T

t

y

W

y

W

y

y

t

S

t

S

t

t















Zasada ta polega na przyporządkowaniu błędowi prognozy określonej straty

)

(

S

t

y

W



i wyborze takiej prognozy zmiennej, z którą związana jest najmniejsza stra-

ta. W szczególności metoda bazująca na minimalizacji sumy kwadratów reszt, czyli
MNK może być uważana za tego typu prognozę, jeśli pojedynczą stratę zdefiniu-
jemy jako kwadrat reszty. Również dla reguły dominanty minimalizujemy funkcję
strat:



















}

|

{|

max

0

D

t

t

y

y

P

S

, która przyjmuje wartość najmniejszą dla

D

t

t

y

y 



.

Opisanych powyżej metod możemy użyć również do wyboru prognozy na podsta-
wie zbioru konkurencyjnych prognoz. Przedstawia to poniższy przykład.

10

Przykład 2

Agencja Reuters regularnie pyta o zdanie na tematy gospodarcze analityków ryn-
kowych (przede wszystkim głównych ekonomistów największych banków komer-
cyjnych). Spośród uzyskanych za pomocą e-mailowych ankiet odpowiedzi na ten
temat prezentuje średnią, medianę, najmniejszą i największą wartość. Oto przykła-
dowe odpowiedzi 16 niezależnych ekspertów polskiego rynku finansowego na te-
mat decyzji o zmianie stóp procentowych na bieżącym i najbliższym posiedzeniu
Rady Polityki Pieniężnej:

Stopa referencyjna

Styczeń

Luty

Wzrośnie o 200 punktów bazowych

1

0

Wzrośnie o 100 punktów bazowych

0

1

Wzrośnie o 50 punktów bazowych

2

2

Wzrośnie o 25 punktów bazowych

3

7

Bez zmian

6

3

Spadnie o 25 punktów bazowych

1

1

Spadnie o 50 punktów bazowych

2

1

Spadnie o 100 punktów bazowych

1

0

Spadnie o 150 punktów bazowych

0

1

Uwaga:

punkt bazowy w skrócie bp (ang. base point) to 0,01 punktu procentowego.

W tabelce podano liczbę wybranych wariantów poszczególnych odpowiedzi.

Ponieważ pojedynczych ocen serwis na ogół nie publikuje, syntetyczna informa-
cja o wysokości przewidywanej zmiany stopy ujawniana zainteresowanym mogła-
by wyglądać następująco:

Stopa referencyjna

Styczeń

Luty

Średnia

9,375

9,375

Mediana

0

25

Max

200

100

Min

–100

–150

Wynika z niej, że stopy procentowe w styczniu i lutym według przewidywań anali-
tyków wzrosną przeciętnie o tyle samo (o ok. 9 bp). Na ogół przyjęlibyśmy, że tak
mała zmiana jest mało prawdopodobna w ocenie ekspertów, ponieważ jest prawie
znikoma (stopy banku centralnego zmieniają się o wielokrotność 25 bp). Wartość
średnia nie odróżnia obydwóch prognoz w wystarczającym stopniu. Więcej infor-
macji niesie mediana. Mówi ona, że przynajmniej połowa analityków wypowiedzia-
ła się, że w styczniu stopy nie wzrosną oraz że w lutym nie wzrosną o więcej niż
25 bp. Podobnie bardziej jednoznaczną informację uzyskalibyśmy, gdyby Reuter eli-
minował przed wyliczeniem średniej informacje nietypowe, na przykład odrzucał
skrajne prognozy (najmniejszą i największą). Zwróćmy uwagę, że taki zabieg nie
zmieniłby wartości mediany. Czytelnikowi zostawiamy sprawdzenie, że prognoza
według wartości oczekiwanej na styczeń wciąż byłaby na znikomym poziomie, a na
luty przekroczyłaby poziom graniczny 12,5 bp, co mogłoby świadczyć o nieznacznej
przewadze poglądów o minimalnym wzroście stóp procentowych w lutym.

Różne są klasyfikacje metod prognozowania. Do najważniejszych należy wyróżnia-
nie metod prognozowania według rodzaju szeregu, który prognozujemy. W prak-
tyce do najczęściej stosowanych z tych metod zaliczamy

metody prognozowania sze-

regów czasowych

. Ze względu na to, że można w nich używać specjalnych narzędzi

konstrukcji prognozy, zyskały one w ostatnich latach pewną odrębność i dużą po-
pularność. Do najprężniej rozwijających się współcześnie metod w tej klasie nale-

11

żą

modele szeregów niestacjonarnych

. Wiele metod dla szeregów czasowych dopiero

ostatnio znajduje zastosowanie w prognozowaniu szeregów przestrzennych i prze-
strzenno-czasowych. Mówi się o wykorzystaniu autokorelacji w szeregach prze-
strzennych czy niestacjonarności w szeregach przestrzenno-czasowych. Są to nadal
metody słabo poznane i złożone obliczeniowo.

Drugi z omawianych podziałów dotyczy stosowanych reguł prognozowania wyni-
kających z przesłanek formułowanych przez prognostyka. Ze względu na przesłan-
ki prognozowania metody możemy podzielić na dwie klasy:
—

metody niestrukturalne, czyli opisujące zjawisko przez odkrywanie tzw. proce-
su generującego dane, czyli statystycznej reprezentacji szeregu czasowego, gene-
rującej wartości prognoz odpowiadające cechom statystycznym prognozowane-
go szeregu, do tej grupy zaliczamy przede wszystkim metody mechaniczne,

—

metody strukturalne, wykorzystujące mechanizm opisu zjawiska za pomocą
czynników mających nań wpływ, na przykład przez formułowanie zależności
przyczynowo-skutkowych; w tej klasie metod dominują metody oparte na mo-
delowaniu ekonometrycznym.

W podejściu

niestrukturalnym

przyjmuje się, że w przeszłości prognozowanej zmien-

nej zawarta jest informacja o mechanizmie, który generuje przyszłe wartości zmien-
nej. Sprawdzając funkcjonowanie mechanizmu w przeszłości, weryfikujemy sku-
teczność odtwarzania przez niego zmienności szeregu. Takie postępowanie nazy-
wamy również mechanicznym, gdyż nie uwzględnia ono żadnych merytorycznych
przesłanek przebiegu procesu. Aby odkryć i potwierdzić kształtowanie się procesu
według określonego mechanizmu, należy korzystać z dość licznej próby. Do metod
niestrukturalnych zaliczamy modele (metody) naiwne oraz modele wyrównywania
wykładniczego, modele tendencji rozwojowej. Tę klasę metod stosujemy najczę-
ściej do prognozowania szeregów czasowych, w których za pomocą modelu naj-
łatwiej opisać wewnętrzny mechanizm generujący przyszłe wartości, pod warun-
kiem, że przeszłe wartości prognozowanej zmiennej wpływają na przyszłe jej reali-
zacje. Mówimy wówczas, że takie procesy charakteryzuje duża inercja zachowań.
Można je opisać na przykład za pomocą modelu autoregresyjnego.

W podejściu

strukturalnym

instrumentem prognozowania jest model strukturalny

(najczęściej model ekonometryczny), czyli taki, który odzwierciedla pewną teorię,
opisuje mechanizm generujący dane zjawisko przez czynniki strukturalne. Zmien-
ność czynników objaśniających kształtowanie się danego zjawiska w przeszłości
determinuje jego przyszłe realizacje. Regułą w tej klasie metod jest estymacja para-
metrów modelu na podstawie próby. Pod warunkiem zgodności ocen parametrów
z teorią ekonomiczną lub założeniami teoretycznymi modelu dokonujemy prognoz
danego zjawiska. W przypadku prognozowania na podstawie modeli ekonome-
trycznych prognozę nazwiemy ex post, jeżeli oparta będzie na znanych wartościach
zmiennych egzogenicznych, a ex ante, jeżeli wartości te musiały zostać uprzednio
wyprognozowane, czyli były nieznane.

Różnicę między tymi klasami metod obrazuje przykład rozwijający analizę odpo-
wiedzi specjalistów na ankietę Reutera.

Przykład 3

Na rozwiniętym rynku finansowym analitycy są w stanie w sposób nieobciążony
przewidzieć zachowania władz monetarnych. Zatem kluczem do prognozowania
działań władz monetarnych jest odkrycie sposobu generowania prognoz przez ana-
lityków. Zajmijmy się prognozowaniem prawdopodobieństwa wzrostu stóp pro-
centowych w marcu na podstawie prognoz analityków w styczniu i lutym. W tym
celu możemy użyć zarówno metod niestrukturalnych, jak i strukturalnych.

12

Niech p

t

będzie zmienną z przedziału (0,1), oznaczającą prawdopodobieństwo

wzrostu stóp procentowych w miesiącu t. Wówczas możemy wyznaczyć następują-
cą regułę prognozowania:

,

*

t

t

t

N

k

p 

gdzie k

t

oznacza liczbę pozytywnych odpowiedzi analityków na pytanie, że stopy

wzrosną w miesiącu t, a N

t

liczbę ankietowanych analityków.

Bez przeprowadzenia kolejnej ankiety nie umiemy jednak zastosować tej reguły dla
prognozowania na przyszłość. Możemy przyjąć jednak, że ci spośród ankietowa-
nych analityków, którzy odpowiedzieli twierdząco w danym miesiącu, odpowiedzą
tak samo za miesiąc (metoda naiwna) k

t + 1

= k

t

. Moglibyśmy łatwo sprawdzić, czy

ta metoda sprawdziła się w lutym i zastosować ją dla marca na podstawie odpo-
wiedzi udzielonych w lutym. Takie myślenie byłoby jednak zbyt naiwne i mogłoby
oznaczać, że część analityków cały czas generuje takie same prognozy (ich opinie
nie byłyby więc nieobciążone). Jeżeli uznamy, że stopy procentowe nie będą bez
końca rosnąć, to lepszą regułą mogłaby okazać się następująca reguła dla każdego
z k analityków oddzielnie:









0

1

*

,k

t

y

dla

dla

0

1

,

1

,

1









k

t

k

t

y

y

lub

i

1

0

,

2

,

2









k

t

k

t

y

y

,

gdzie y

t,k

oznacza odpowiedź k-tego analityka na pytanie o podwyżkę stóp procen-

towych w miesiącu t. Odpowiedź „1” oznacza podwyżkę, „0” — brak podwyżki.

Reguła ta oznacza, że analityk oczekuje podwyżek najwyżej dwa miesiące z rzę-
du. Aby obliczyć prognozę liczby odpowiedzi pozytywnych, sumujemy odpowiedzi

(







16

1

*

,

*

k

k

t

t

y

k

) i dzielimy je przez stałą liczbę ankietowanych osób (N

k

= N). Oby-

dwie te metody (naiwną i indywidualną) nazywamy metodami niestrukturalnymi
i mechanicznymi. Jednak drugiej z nich nie możemy sprawdzić, dysponując tylko
odpowiedziami z dwóch miesięcy. Ta druga reguła wymaga więc większej liczby
okresów do przeprowadzenia jej weryfikacji.

Metody strukturalne moglibyśmy wprowadzić do tego modelu, dołączając do niego
zmienną opisującą zachowanie władz monetarnych. Na przykład można to uczynić
w następujący sposób:

)

,

)

(

,

)

(

(

1

1

*

t

t

t

t

I

p

f

p













,

gdzie f(…) oznacza funkcję regresji, I

t – 1

oznacza zmienną zerojedynkową (binar-

ną) przyjmującą wartość 1, jeżeli w ostatnim miesiącu stopy wzrosły i 0, jeżeli nie
wzrosły, ε

t

to składnik losowy, a znaki (+) ponad zmiennymi oznaczają dodatni

kierunek wpływu predyktorów na zmienną prognozowaną.

Dla tak określonych predyktorów powstałby jednak problem z określeniem ich
wpływu w okresie t w sytuacji, gdyby prognozy analityków sprawdziły się w okre-
sie t – 1. Wówczas bowiem zrealizowanie podwyżki zmniejszałoby szansę jej wy-
stąpienia w następnym okresie, czego nie wyraża ten model. Właściwa modyfikacja
w sytuacji, gdy stopy „nie rosną bez końca” (tj. są generowane przez stacjonarny
proces) mogłaby przyjąć taką postać:

13

)

,

)

(

,

)

(

,

)

(

(

1

1

1

1

*

t

t

t

t

t

t

I

p

I

p

f

p



















.

Zrealizowanie się oczekiwań dotyczących wzrostu stóp procentowych obniża wów-
czas prawdopodobieństwo wystąpienia kolejnej podwyżki w następnym miesiącu
(znak minus nad zmienną interakcyjną p

t – 1

I

t – 1

, która jest iloczynem zmiennej bi-

narnej i prawdopodobieństwa).

Oprócz estymacji parametrów takiego modelu na wystarczająco długiej próbie,
metoda taka wymagałaby statystycznego sprawdzenia jej poprawności w okresie
ex post. Generuje ona prognozy według bardziej ogólnej i określonej w sposób jaw-
ny teoretycznej reguły postępowania analityków niż metody niestrukturalne. Pa-
rametry modelu strukturalnego są tak określane, aby dawały w okresie próby war-
tości prawdopodobieństw zbliżone do obserwowanych odpowiedzi na ankiety. Dla
metod mechanicznych nie jest to dominującą zasadą.

Odpowiedzi analityków na ankietę stanowią jednocześnie przykład innej klasy nie-
matematycznych metod prognozowania, zwanych

metodami heurystycznymi

. Znane

są one również jako metody twórczego rozwiązywania problemów. Wobec ogra-
niczonej liczby danych empirycznych lub zbyt dużej ilości informacji, którą nale-
ży wziąć pod uwagę, metody te w dużej mierze opierają się na intuicji, wyobraźni
czy też zdrowym rozsądku. Wykorzystywane są różne techniki pozyskiwania in-
formacji. Oprócz ankiety są to bezpośrednie wypowiedzi i opinie ekspertów oraz
metoda panelowa, zwana burzą mózgów. Prognozowanie heurystyczne jest wyni-
kiem świadomego „wymyślania” wariantów przyszłości oraz zbierania, obserwo-
wania i łączenia informacji dotyczących interesującego nas fragmentu rzeczywisto-
ści. Na podstawie zebranych opinii ustala się możliwe warianty i wybiera najbar-
dziej prawdopodobny. W ten sposób uzyskujemy uśrednioną grupową opinię doty-
czącą prawdopodobnych przyszłych zjawisk czy wydarzeń. Stosowanie tej metody
opiera się na założeniu, że opinie dużej liczby obserwatorów lub uczestników gry
rynkowej są adekwatne dla opinii ogółu, a trafność sądu grupowego jest większa
niż indywidualnego.

Najbardziej popularną metodą heurystyczną jest metoda delficka. Polega ona na
wykorzystaniu opinii dużej liczby ekspertów, ich doświadczenia i intuicji. Popraw-
ność polegania na opinii ekspertów i niezależnych obserwatorów jest potwierdzo-
na empirycznie. Z doświadczenia wiemy bowiem, że opinia eksperta bywa często
bardziej trafna niż prognoza na podstawie niejednego formalnego modelu. Ponad-
to z uwagi na koszty pozyskiwania opinii u dużej grupy osób, jak również z uwa-
gi na długi czas trwania zbierania takich informacji, preferuje się zebranie panelu
ekspertów w jednym miejscu i czasie. Metoda delficka opiera się na badaniu opi-
nii ekspertów posiadających podobną wiedzę, sposób myślenia czy osobowość, ale
pracujących niezależnie od siebie, komunikujących się przez ankiety. Oczywiście,
aby prognoza była trafna, należy zadbać, aby grono ekspertów było odpowiednio
dobrane. Grupa powinna być liczna i w miarę możliwości reprezentować różna po-
glądy. Eksperci powinni tworzyć grupę uniwersalną, posiadać wiedzę na temat
prognozowanego zjawiska, ale także wszechstronną wiedzę ogólną. Metoda del-
ficka jest metodą ankietową z pytaniami zamkniętymi. Tym samym zapewnia ano-
nimowość, gdyż albo ankiety dostarczane są drogą korespondencji, albo osoby je
wypełniające robią to niezależnie, w odizolowaniu.

Prognozowanie analogowe jest alternatywą dla podejścia strukturalnego, gdyż ideą
tej metody jest konstruowanie prognoz danego zjawiska na podstawie informacji
o zjawiskach innego rodzaju występujących w innych obiektach. Nie zakłada się
tu, w przeciwieństwie do metod strukturalnych, że ustalona zależność czy związek
jest niezmienny w czasie. Do metod analogowych zaliczamy: metodę analogii bio-

14

logicznych, przestrzennych, historycznych i przestrzenno-czasowych. Zakłada się
w nich, że podobieństwo rozważanych obiektów determinuje podobne ich zacho-
wanie. Z uwagi na mało formalne postępowanie nie będziemy się tymi metodami
szczegółowo zajmować.

15

3. Standardy i zasady prognozowania

Proces przewidywania przyszłości oparty na naukowych podstawach wymaga for-
mułowania reguł i zasad, jakimi należy się kierować, stosując metody prognozowa-
nia. W przeciwnym razie na podstawie tych samych informacji za każdym razem
można byłoby uzyskać inny wynik prognozy, a prognozowanie byłoby w większym
stopniu czynnością przypadkową niż naukową. Stosowanie tych zasad służy nie
tylko sformalizowaniu metod prognozowania, ale przede wszystkim są empiryczne
dowody, że prognozy tworzone za pomocą tych reguł są dokładniejsze, mniej ob-
ciążone, ale także mniej kosztowne i bardziej odpowiednie do prognozowanej sy-
tuacji, wiarygodne i użyteczne.

Zbiór zasad ewoluował od stadium dobrych obyczajów do dobrze określonych stan-
dardów i procedur

4

. Całkiem niedawno zostały one zebrane, spisane i poddane na-

ukowej dyskusji w czasopiśmie ‘Journal of Forecasting’. Publikacja z 2001 roku
o nazwie Standardy i praktyka prognozowania określa zestaw 139 zasad poprawne-
go postępowania w trakcie realizacji procesu prognostycznego uporządkowanych
w 16 kategorii odpowiadających różnym etapom procesu budowy i wykorzystania
prognoz. W zamyśle jej autora J. Scotta Armstronga poszczególne zasady odnoszą
się do różnych aspektów i etapów prognozowania i nie sposób stosować wszystkich
na raz. Duża ich liczba wynika raczej ze złożoności sytuacji, jakie można napotkać,
formułując prognozę, niż z faktu, że prognozowanie jest bardzo sformalizowaną
dziedziną nauki. Standardy… mają za zadanie wskazać prognozującemu właści-
wą metodę postępowania, a decydentom korzystającym z prognoz pomóc w oce-
nie jakości procesu prognozowania (a nie tylko jego wyników). Kilka z tych zasad
pokażemy na tle poszczególnych etapów prognozowania. Bazują one na zdrowo-
rozsądkowym postępowaniu, doświadczeniu ekspertów lub na bogatym materiale
empirycznym.

Prognozowanie to złożony i powtarzalny proces decyzyjny, w którym można
uwzględnić pewne podstawowe etapy

5

. Należy je realizować w następującej kolej-

ności:

Etap 1. Sformułowanie zadania prognostycznego

Na tym etapie określamy obiekt lub zjawisko, którego prognozowanie dotyczy,
formułujemy cel prognozy, możliwości jego realizacji i wykorzystania wyników,
niekiedy określamy horyzont oraz wymaganą dokładność prognozy. Jedna z re-
guł dotyczących tego etapu mówi o tym, że przed wykonaniem prognozy należy
opisać, w jaki sposób decyzja, którą wspomagamy prognozą, może zmieniać się
w zależności od wyniku tej prognozy. Zdrowy rozsądek wskazuje, że jeśli pro-
gnoza nie ma wpływu na decyzję, to nie warto jej stosować, chyba że prognoza
ma charakter rozrywkowy (jak na przykład prognozy wyników wyborów po za-
mknięciu lokali wyborczych).

Etap 2. Sformułowanie przesłanek prognozy

Formułujemy tu sposób patrzenia na zjawisko przez mechanizm „czarnej skrzyn-
ki” (tak zwany proces generujący dane) albo przez czynniki je kształtujące (ma-
jące wpływ na obiekt)

6

.

Na tym etapie eksperci radzą rozkładać problem na czynniki pierwsze, w tym:
—

znajdować wszystkie czynniki sprzyjające rozwojowi lub zanikaniu zjawiska,
wspierające lub hamujące jego rozwój,

4

Zapewne z czasem zbiór

tych standardów stanie się

ogólnie przyjętą metody-

ką postępowania w kon-

strukcji i wykorzystaniu

prognoz.

5

Etapy wyróżniono za

Armstrong (2001).

6

Dobrze, jak nasz wybór

dominującej metody pro-

gnozowania jest ustalony

z odbiorcami prognoz.

16

— prognozować zmienną na podstawie prognoz jej składowych,
—

wyróżniać wszystkie zależności przyczynowo-skutkowe i ich złożenia, tj. wie-
lopoziomowe łańcuchy przyczynowe,

— dekomponować proces na trend i odchylenia od niego.

Etap 3. Pozyskanie potrzebnych do prognozowania informacji

Etap ten składa się ze zidentyfikowania źródeł danych, zebrania odpowiednich
danych i ich przygotowania. Możliwie pełne, potrzebne i najbardziej aktualne
dane powinny: pochodzić z wiarygodnych i ogólnie uznanych źródeł, być ze-
brane według tej samej metodyki, być wstępnie przetworzone, czyli oczyszczo-
ne z błędów, zmian metodologicznych, zmian systematycznych i jednorazowych
oraz wpływu inflacji, poddane odpowiednim transformacjom (np. logarytmy lub
stopy zmian oryginalnych wielkości), odpowiednio zagregowane, a na koniec za-
prezentowane na wykresie, który umożliwi rozpoznanie charakteru ich przebie-
gu. Omówimy niektóre z tych czynności w ostatnim temacie tego modułu.

Etap 4. Dokonanie wyboru predyktorów i metod prognozowania

Zaleca się raczej stosowanie prognoz opartych na modelach ilościowych i przy-
czynowych zamiast na mechanicznych, jakościowych i naiwnych ujęć. Standar-
dem jest:
— dopasowywanie metod do sytuacji prognostycznej,
—

porównywanie wyników prognoz ex ante na podstawie różnych metod w jak
najbardziej podobnych sytuacjach prognostycznych,

—

ocenianie stopnia akceptacji i zrozumienia wykorzystanych metod przez od-
biorców.

Etap 5. Zastosowanie (określonych w poprzednim etapie) metod prognozowania

Na tym etapie najtrudniejsze jest pogodzenie różnych przeciwstawnych potrzeb.
Z jednej strony użyte modele prognostyczne powinny być możliwie proste,
a z drugiej powinny być realistyczną reprezentacją rzeczywistości (czyli wystar-
czająco złożone). Należy brać pod uwagę planowane duże zmiany sytuacji go-
spodarczej, ale w sytuacji dużej niepewności (np. co do danych) należy zachować
konserwatywną postawę (małe zmiany). Niektóre z wykorzystywanych tu zasad
są specyficzne w określonych grupach metod. Na przykład w metodach heury-
stycznych zaleca się dobieranie ekspertów z różnych — związanych z prognozą
— dziedzin i wielokrotne proszenie ich o podanie na piśmie opinii na określony
temat. W metodach ilościowych zaleca się:
— starannie dopasowywać model do horyzontu prognozy i charakteru danych,
—

rozwijać model przez głębsze rozpoznanie teorii, a nie lepsze dopasowanie
danych do modelu,

—

zwracać większą uwagę na najnowsze okresy lub obiekty najbardziej zbliżone
do badanego,

— często uaktualniać model,
— łączyć różnorodne podejścia w jednej prognozie.

Etap 6. Ocena dokładności prognozy, czyli analiza błędów prognoz (błędów ex
post, gdy prognoza wygaśnie lub oczekiwanych błędów w przypadku prognoz
ex ante

)

Regułą w prognozowaniu na tym etapie jest:
— porównywanie jakości uzasadnionych teoretycznie prognoz,
—

testowanie hipotez dotyczących jawnych założeń wybranej metody progno-
zowania,

—

projektowanie sytuacji, w której porównujemy prognozy w sposób zbliżony
do sytuacji, którą chcemy prognozować i do sytuacji, w której podejmowana
będzie na podstawie tej prognozy decyzja ekonomiczna,

17

—

opisywanie potencjalnych przyczyn obciążeń prognozy, wynikających z wy-
branej metody prognozowania oraz użytych danych,

—

udostępnianie danych oraz pełnego opisu metod w celu umożliwienia replika-
cji wyników prognoz przez zainteresowane osoby,

—

ocenianie zasadności poczynionych założeń, wyjaśnianie znaczenia zastoso-
wanych metod,

—

używanie rozszerzeń zarówno zakresu ewaluacji, jak i użytych metod w celu
potwierdzenia, że sposoby testowania prognoz i uzyskane metody są wystar-
czające w bardziej ogólnych sytuacjach,

—

wybór ważnych kryteriów sprawdzenia prognozy przed wyliczeniem prognoz
i ich zastosowanie dla wszystkich metod, wybór przynajmniej kilku miar do-
kładności prognozy,

—

stosowanie nieobciążonych miar błędów, odpornych na nietypowe obserwa-
cje i odpowiednich do danej sytuacji i charakteru porównań,

— wykorzystanie błędów predykcyjnych (tzw. błędów spoza próby),

— wykorzystanie błędów ex post (w obrębie próby), aby poznać ich przyczyny,
—

unikanie niektórych miar dopasowania (jak współczynnik determinacji) w po-
równywaniu prognoz dla szeregów czasowych,

— dokonywanie porównań metod dla długich okresów prognoz
— przeprowadzanie analizy kosztów i korzyści alternatywnych metod.

Etap 7. Wykorzystanie prognoz

Aby dobrze i zgodnie z założonym celem wykorzystać prognozy, należy po
pierwsze w prosty i zrozumiały sposób je przedstawić (wraz z wyjaśnieniem za-
stosowanych metod i założeń) oraz zaprezentować prognozy przedziałowe i sce-
nariuszowe, jeśli to możliwe. Prognostyk, który zdobywa doświadczenie, wyko-
rzystując procedury prognozowania, jednocześnie adaptuje je i rozwija. A zatem
prognozowanie to nieustanny proces uczenia się na własnych błędach i dostoso-
wywania narzędzi do wnioskowania na przyszłość.

Jak wspomniano wcześniej, na kursie będziemy zajmować się głównie prognoza-
mi ilościowymi, dlatego interesować nas będą głównie reguły matematyczno-sta-
tystyczne, w tym również te oparte na specjalnie budowanych modelach staty-
styczno-ekonomicznych. Do budowy i estymacji tych ostatnich modeli stosujemy
wszystkie znane zasady konstrukcji i estymacji modelu ekonometrycznego, takie
jak założenia konstrukcji estymatorów, warunki stosowania metod estymacji czy
zasada interpretacji parametrów modelu (zasada ceteris paribus)

7

. W prognozowa-

niu korzystamy ponadto z zasady o stałości relacji określonej przez model, przy
czym — w odróżnieniu od estymacji — zasadę tę rozciągamy również na okresy
wybiegające w przyszłość, tj. poza próbę, dla której dokonaliśmy estymacji.

W poszukiwaniu odpowiednich metod prognozowania nie możemy stosować tylko
kryteriów ilościowych, których omówienie znajduje się w czwartym temacie tego
modułu. Stosowany model powinniśmy dostosować do rozważanego problemu.
I tak, gdy naszym celem jest określenie ceny wybranego artykułu w osiedlowym
sklepie w następnym dniu, wygodnie posłużyć się metodami możliwie prostymi,
takimi jak metoda naiwna. Nie ma nic niepoprawnego w twierdzeniu, że cena ju-
tro będzie taka sama jak dzisiaj. Co więcej, wydaje się to zdroworozsądkowym po-
dejściem w sytuacji, gdy inflacja jest niska, a rynek konkurencyjny. Jeżeli natomiast
naszym zadaniem jest określenie budżetu firmy na kolejny rok, to prognoza w myśl
zasady „będzie tak jak było” z dużym prawdopodobieństwem doprowadzi firmę do
utraty rynku, klientów, przewagi konkurencyjnej, a może nawet do bankructwa.
Dla tak złożonego zagadnienia jak budżet firmy czy państwa należy wykorzysty-
wać modele strukturalne, które umożliwią sformułowanie prognoz warunkowych
w powiązaniu z większością ważnych aspektów funkcjonowania przedsiębiorstwa.

7

Przypomnijmy, że oznacza

ona interpretację poszcze-

gólnych parametrów przez

ocenę efektów zmian po-

jedynczych zmiennych

objaśniających przy zało-

żeniu, że pozostałe czyn-

niki nie ulegną zmianie

(w szczególności nie zmie-

nią się wartości pozosta-

łych zmiennych objaśnia-

jących).

18

Taki wielorównaniowe model nigdy nie znajdzie zastosowania w prognozie cen na
następny dzień, chociażby dlatego, że jego zbudowanie zajęłoby więcej czasu niż
jest to możliwe. To właśnie mamy na myśli, mówiąc o modelu „odpowiednim”,
o czym nie należy zapominać, poświęcając czas na formułowanie własnych — czę-
sto bardzo złożonych i pomysłowych — modeli prognozowania.

19

4. Weryfikacja i trafność prognoz

— podstawy teoretyczne

Celem prognosty jest trafne określenie tego, jak dane zjawisko będzie kształtowało
się w czasie. Od tego zależy powodzenie prognosty, wiarygodność, a także możli-
wość uzyskania kolejnych zamówień lub podtrzymania współpracy. Podobnie jak
w innych dziedzinach życia najlepiej uczyć się tego „fachu” na własnych błędach.
Dlatego popularne powiedzenie mówi: „Jeśli już musisz prognozować, to rób to
często”.

Formułując ilościowe prognozy różnych zmiennych gospodarczych, nie możemy
ocenić ich trafności dopóki nie będziemy mieć informacji o realizacji zmiennej pro-
gnozowanej. Ponieważ prognoza dotyczy przyszłości, nie umiemy jej ocenić dopóki
ta przyszłość się nie zrealizuje. Nie mając możliwości oceny, czy i o ile się mylimy,
prognosta często poszukuje innych informacji zastępczych. Takimi są właśnie pro-
gnozy wygasłe.

Prognozy wygasłe

to prognozy dokonywane na okres, dla których

znamy już wartości (realizacje) zmiennej prognozowanej. Prognozy takie są sfor-
mułowane na podstawie informacji pochodzących z okresów wcześniejszych. Na-
zywamy je również

prognozami

ex post

8

. Chociaż prognozowanie docelowo dotyczy

tego, co nieznane lub jeszcze niepoznane, to w procesie poszukiwania najlepszych
metod prognozowania wykonuje się setki prognoz zmiennej dla tych okresów lub
dla tych obiektów, dla których wartości znamy w momencie prognozowania. Dzię-
ki temu możemy testować różne metody i wskazać wśród nich metodę uznaną za
najlepszą i za jej pomocą dokonać prognoz na przyszłość.

Przewidywania dotyczące tych obserwacji, których wartości jeszcze nie znamy,
czyli

prognozy

ex ante

(inaczej prognozy właściwe), są ostatecznym rezultatem ana-

lizy wyników prognozowania i wyboru najlepszego narzędzia do przewidywania
danego zjawiska. Sam wybór odpowiedniego modelu prognozowania ex ante jest
kwestią ilościowej oceny zrealizowanych błędów prognoz wygasłych, a znajomość
i zastosowanie odpowiednich technik prognozowania można uczynić bardzo uży-
teczną sztuką inwencji i dedukcji.

W zasadzie wybierając najlepszą prognozę, zajmujemy się przede wszystkim jej błę-
dami w okresie ex post. Sprawdzając, jak duże błędy niosło zastosowanie określo-
nej metody w okresie ex post, spodziewamy się, że ta sama metoda da podobne wy-
niki przy jej wykorzystaniu do prognozy właściwej (w okresie ex ante). Czymże jest
zatem błąd prognozy ex post, czyli zrealizowany błąd prognozy?

Błąd prognozy

ex post

(zrealizowany błąd prognozy) e

t

definiujemy jako różnicę mię-

dzy wartością empiryczną (rzeczywistą) zmiennej y

t

a jej wartością prognozowaną

(czyli prognozą) y*

t

:

E

t

= y

t

– y*

t

.

Zauważmy, że dodatni błąd prognozy oznacza prognozę

niedoszacowaną

, gdyż:

e

t

> 0 ⇔ y*

t

< y

t

,

8

W metodach struktural-

nych warto brać pod uwa-

gę rozróżnienie między

obydwoma pojęciami.

Gdy zmienna objaśniana

nie jest znana, ale znane

są zmienne objaśniające,

to taką prognozę nazy-

wamy wciąż prognozą ex

post, a określenie progno-

za wygasła rezerwujemy

tylko dla przypadku, gdy

możemy wyznaczyć błędy

prognozy ex post — por.

dyskusja u Gajdy (2001:

143 i nast.).

20

a ujemy błąd prognozy — prognozę

przeszacowaną

, gdyż:

e

t

< 0 ⇔ y*

t

> y

t

.

Otrzymaną wartość błędu nazywamy

dopuszczalną

, jeżeli wartość bezwzględna

z błędu (moduł błędu | e

t

|) jest mniejsza od poziomu z góry określonego przez

prognostyka lub odbiorcę prognoz. Prognozę możemy również nazywać dopusz-
czalną, gdy prawdopodobieństwo jej realizacji jest co najmniej równe z góry zada-
nemu.

O ile błąd prognozy ex post po upływie czasu lub przeprowadzeniu dokładnego
badania możemy policzyć, to prawdopodobieństwo realizacji konkretnej progno-
zy jest wielkością subiektywną. Czasem staramy się je częściowo obiektywizować
przez stosowanie metod statystycznych, konstruując prognozy przedziałowe, lub
przez opisywanie prawdopodobieństwa zdarzenia za pomocą czynników sprzyja-
jących lub utrudniających zrealizowanie danego zdarzenia (modele probitowe i lo-
gitowe). Prognozowanie w okresie ex ante jest jednak tylko formułowaniem praw-
dopodobnych zdań o przyszłości. Nie umiemy powiedzieć, czy zrealizowanie pro-
gnozy jest potwierdzeniem trafnego określenia prawdopodobieństwa jej realizacji,
mimo że po upływie czasu hipotezy badawcze zmieniają się w zdania logiczne, któ-
re mogą być albo prawdziwe albo fałszywe. Oczywiście realizacja prognozy, która
była mało prawdopodobna w okresie jej formułowania, jest ważnym argumentem
za tym, aby podważyć zasadność metody prognozowania. Jak mówi zasada wia-
rygodności, mało prawdopodobne zdarzenia realizują się stosunkowo rzadko. Ist-
nieje jednak ryzyko wystąpienia mało prawdopodobnych zdarzeń (w ekonometrii
zwane poziomem istotności). Zbyt częsta realizacja zdarzeń mało prawdopodob-
nych jest sprzeczna z częstościową definicją prawdopodobieństwa. Jednak ostatecz-
nie prognozę weryfikuje się tylko przez pomiar jej błędów ex post (tj. błędów wy-
gasłych).

Chociaż staramy się unikać błędów w prognozowaniu, to ich popełnianie jest nie-
odłącznym elementem procesu prognozowania. Niska dokładność metod pro-
gnozowania powinna skłaniać do szukania przyczyn błędów i ich eliminowania.
W modelach strukturalnych możemy wskazać ex post, które przyczyny spowodo-
wały niską trafność prognozy, w modelach niestrukturalnych na ogół należy szu-
kać metody, która lepiej się sprawdzała ex post. Zwracanie uwagi na źródła błę-
dów sprzyja ulepszaniu procesu prognozowania, choć całkowita eliminacja błędów
w prognozowaniu nie jest możliwa. Z błędami prognozy należy się zatem oswoić
i poddawać je częstej analizie.

Są jednak czynniki, które sprzyjają generowaniu trafnych prognoz. Warto mieć
świadomość ich istnienia już na etapie projektowania zadania prognostycznego.
Elementy sprzyjające „dobrym”, czyli trafnym prognozom, to:
— Krótki horyzont czasowy

Łatwiej na ogół określać wystąpienie zjawisk w krótkim okresie od momentu
formułowania prognozy, czyli o krótkim horyzoncie. Realizacja prognoz długo-
okresowych poddana jest silniejszemu oddziaływaniu tych samych czynników
oraz oddziaływaniu większej liczby czynników. Tak zresztą definiowaliśmy długi
okres w tym module (możliwość wystąpienia zmian jakościowych w prognozo-
wanym zjawisku).

— Niektóre cechy prognozowanego procesu

Duża inercja zachowań podmiotów gospodarczych oznacza powolne zmiany
prognozowanych zmiennych. Sprzyja to lepszej przewidywalności kształtowania
się zmiennych w przyszłości. Systemy gospodarcze, które zachowują się w spo-
sób stabilny na ogół nie są poddane zmianom jakościowym, które najtrudniej
przewidzieć.

21

—

Autonomiczny charakter prognozowanej wielkości (zmienna w niewielkim stop-
niu zależy od arbitralnych decyzji)

Łatwiej jest przewidzieć zachowania większych zbiorowości niż pojedynczych
osób podejmujących decyzje na podstawie intuicyjnych przesłanek. Do opisu za-
chowań większej grupy ludzi można również stosować metody statystyczne.

— Współzależność zmiennych

Zmienne, które kształtują się wokół wspólnych trendów, w podobnym kierunku
czy z podobną siłą i są wzajemnie powiązane, można użyć do konstrukcji jedno-
lub wielorównaniowego modelu ekonometrycznego, w którym jedne ze zmien-
nych będą predyktorami innych.

22

5. Wstępna analiza danych

Ważny etap prac prognostycznych to pozyskanie danych statystycznych. Na ich
podstawie następuje wybór metody prognozowania i klasy modelu prognostycz-
nego (predykcji). Przy kompletowaniu danych należy zwrócić uwagę, aby liczbowe
dane statystyczne były jednorodne, rzetelne, jednoznaczne, porównywalne w cza-
sie i przestrzeni, kompletne, aktualne. Informacja statystyczna dotyczy na ogół
części badanej zbiorowości lub fragmentu badanej rzeczywistości, a ponieważ po-
chodzi ona z niepełnych badań statystycznych, to nie jest wolna od błędów, uprosz-
czeń, ominięć i innych niedoskonałości. Czasem błędy wynikające z mało dokład-
nych badań ankietowych lub niedoskonałych systemów ewidencji społeczno-go-
spodarczej dają fałszywe wyobrażenie o rzeczywistości. Podstawowe źródła błę-
dów w trakcie zbierania i opracowywania danych to:
— niedokładność,
— trudności z określeniem (zmierzeniem) badanej wielkości,
— opuszczenie lub wielokrotne ujęcie tych samych wielkości,
—

niejasne lub zbyt ogólne pytania w formularzu pytań lub zła interpretacja od-
powiedzi,

— świadome lub nieświadome udzielanie fałszywych informacji,
— niedokładność pomiarów lub obliczeń,
— błędy w czasie przepisywania (przepływie danych),
— błędy klasyfikacji, segregacji, tabulacji.

Błędy te możemy podzielić na dwa rodzaje: błędy systematyczne (nielosowe) i przy-
padkowe (losowe). We wszelkiego typu analizach najbardziej niebezpieczne są błę-
dy systematyczne, gdyż mogą sfałszować obraz rzeczywistości w jednym kierunku.
Błędy losowe z kolei zmniejszają dokładność prognoz formułowanych na podstawie
błędnych danych, ale na ogół nie powodują systematycznego obciążenia prognoz.
W ekonomii przyjęło się stosować zasadę, że jeśli źródło danych jest wiarygodne
(np. publikacja krajowego urzędu statystycznego), a nie ma poważnych zastrzeżeń
co do jakości danych, to warto przyjąć zasadę: „z faktami się nie dyskutuje”. Mimo
takiego założenia, kompletując dane należy zachować ostrożność, zwłaszcza gdy
korzystamy ze źródeł nieoficjalnych, takich jak serwisy internetowe, oraz zwrócić
uwagę na porównywalność danych zbieranych w różnych okresach.

Opracowane zbiory danych uzyskane w wyniku obserwacji statystycznej lub po-
miaru tworzą materiał statystyczny zwany próbą statystyczną. Dane liczbowe do-
tyczące (ilościowych lub jakościowych) cech badanej części populacji generalnej
mogą być pogrupowane i uporządkowane według niektórych z tych cech, tworząc
szeregi statystyczne. Mogą to być

szeregi czasowe

— opisujące wartości określo-

nej cechy X dla pojedynczego obiektu w kolejnych okresach lub momentach czasu
t = 1, 2, …, T (np. poziom inflacji średniorocznej w gospodarce polskiej w kolej-
nych latach). Szeregi czasowe będziemy oznaczać wielką literą z subskryptem czasu
Y

t

, a ich realizacje pochodzące z okresów t małymi literami y

t

. Zebrane dane mogą

dotyczyć tych samych cech obserwowanych u wielu obiektów w jednym okresie lub
momencie czasu. Takie dane nazywamy

danymi przekrojowymi

. Opisują one proce-

sy zróżnicowania obiektów pochodzących z próby statystycznej pod względem wy-
branych cech X w jednym okresie (momencie) czasu. Dla zmiennych określających
miarę danego procesu dla poszczególnych obiektów i = 1, 2, … I przyjmujemy
oznaczenie X

i

, a ich realizacje oznaczamy jako x

i

.

23

Po zebraniu odpowiednich danych reprezentujących prognozowane zjawisko i jego
predyktory należy poddać te dane wstępnej obróbce numerycznej. W szczególno-
ści należy:
1.

Zaprezentować dane na wykresie, co pozwoli na wstępne określenie charakteru
ich przebiegu

Ze wstępnych obserwacji surowego szeregu czasowego można wysnuć pierwsze
wnioski dotyczące zakresu czynności, które należy wykonać, aby uzyskać po-
równywalne dane, zgodne z celem badania. Po oczyszczeniu danych i ich obrób-
ce statystycznej warto jeszcze raz zaprezentować szereg na wykresie i dokonać
wstępnego wyboru klasy metod prognozowania i reguły odpowiedniej do pro-
gnozowanego szeregu. Przykład poniższy pokazuje, jakie wnioski można wysnuć
z analizy danych nieoczyszczonych.

Przykład 4

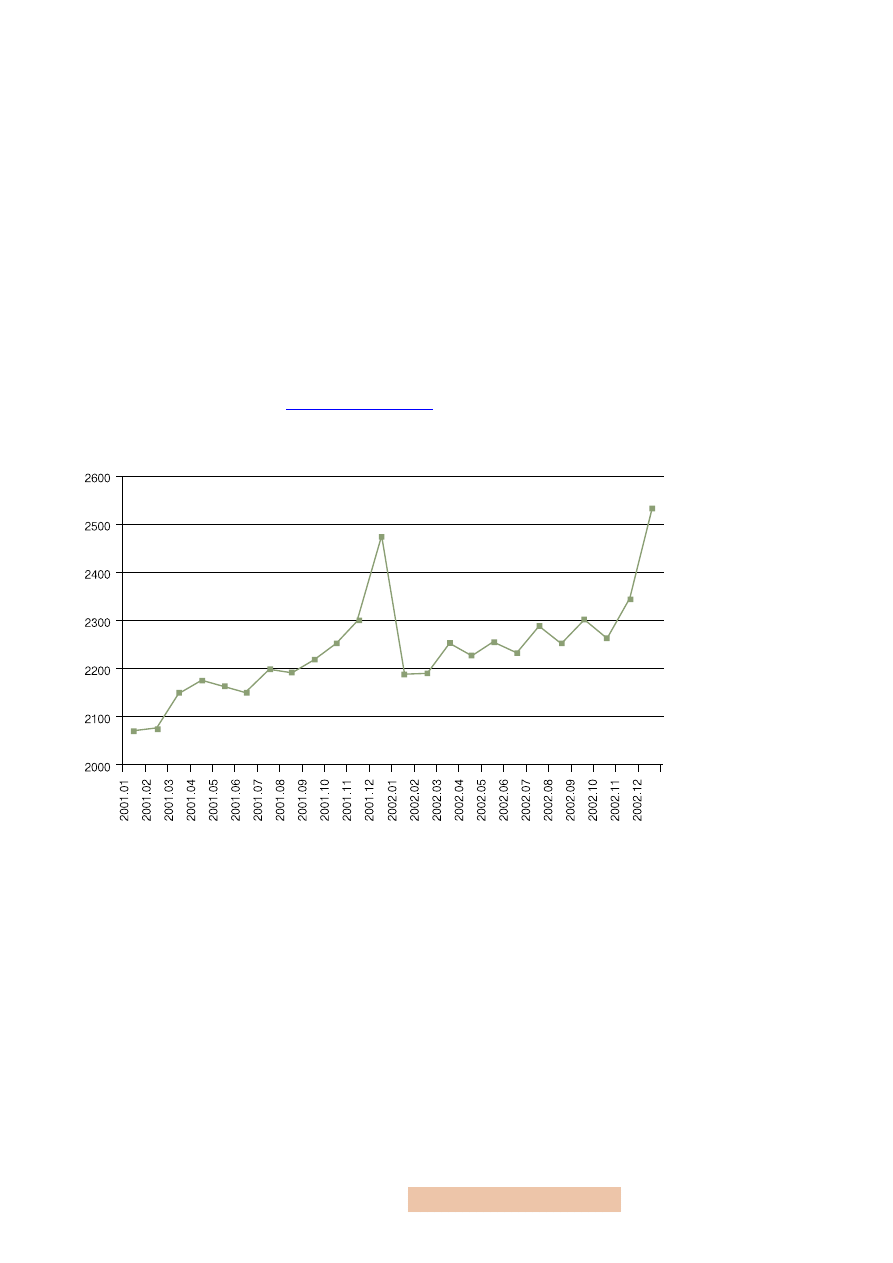
Dane na temat przeciętnych miesięcznych wynagrodzeń brutto w gospodarce
polskiej uzyskane z publikacji GUS (np. Biuletynu Statystycznego lub jego elek-
tronicznego odpowiednika

http://www.stat.gov.pl

) i dostępne w pliku Excela

wynagrodzenia.xls

prezentuje poniższy wykres:

2.

Zagregować dane dla wybranych grup obiektów (na przykład dla grupy krajów)
lub dla wybranej częstotliwości (na przykład zamienić dane miesięczne na kwar-
talne)

Przesłanki do agregacji danych wynikają ze sposobu ich prezentacji w oficjalnych
statystykach odbiegającego od potrzeb prognostyka. Aby uzyskać odpowiednie
dane, dokonujemy ich przeliczenia według pewnych ustalonych sposobów — na
przykład z danych dziennych o wielkości stopy WIBOR uzyskujemy dane mie-
sięczne, wyliczając je jako średnią arytmetyczną ze wszystkich dostępnych (tylko
dni robocze) obserwacji w danym miesiącu. Dane o wyższej częstotliwości (np.
dane miesięczne) zamieniamy na dane o niższej częstotliwości (np. dane kwar-
talne) oraz dane jednostkowe (dla obiektów) na dane zagregowane (np. dane dla
powiatów na dane dla województw) w zależności od ich treści ekonomicznej, tj.
przez ich sumowanie (dla zmiennych ekonomicznych wyrażających strumienie),
uśrednianie (dla zasobów) lub inne transformacje odpowiednie do konstrukcji
zmiennych (np. dla wskaźników w postaci ilorazów oddzielnie sumujemy skła-
dowe licznika i mianownika, a następnie dzielimy przez siebie te wielkości).

Rysunek 1

Przeciętne wynagrodzenie

brutto w sektorze

przedsiębiorstw w okresie

styczeń 2001 – grudzień 2002

Źródło: GUS, Biuletyn Statystycz-

ny, 01/2003.

24

3.

Ujednolicić dane, w tym uzupełnić brakujące dane, oczyścić dane z efektów sys-
tematycznych i jednorazowych, a także zmian metodologicznych, jeżeli jest to
wskazane

Zmiany metodologiczne należy eliminować przez zastosowanie proporcji (tzw.
metoda nawiązania łańcuchowego) z jednego lub kilku okresów, dla których do-
stępne są dane przed i po wystąpieniu zmiany metodologicznej. Dane zawsze
przelicza się na dane porównywalne w stosunku do obecnie obowiązującej (a nie
poprzednio obowiązującej) metodyki prezentacji (zbierania) szeregów. Jeżeli bra-
kuje podstaw dla uzyskania porównywalnych danych, można zostawić je bez
zmian (pod warunkiem, że zmiany nie były znaczące dla kształtowania się pro-
gnozowanej zmiennej) lub zrezygnować z danych za poprzedni okres (jeśli liczba
obserwacji po zmianach metodyki szeregu jest wystarczająca do wnioskowania).
W każdym z tych przypadków należy robić wyraźne zastrzeżenia dotyczące pro-
blemów z porównywalnością danych i sposobów ich rozwiązania.
Oczyszczanie danych ze zmian systematycznych i jednorazowych odbywa się na
ogół przez ich uprzednie wygładzenie znanymi metodami mechanicznymi (na
ogół są to średnie ruchome i ich kombinacje). Można jednak zrezygnować ze
wstępnego oczyszczania szeregów czasowych z efektów zmian metodologicz-
nych, systematycznych (powtarzalnych) i jednorazowych (nietypowe obserwa-
cje), jeżeli do prognozowania stosujemy model ekonometryczny

9

. Przykład 5

pokazuje jak postępować w sytuacji, gdy brakuje danych dla niektórych okre-
sów i co rozumiemy przez zmiany metodologiczne w konstrukcji szeregów cza-
sowych.

Przykład 5

W Polsce badania aktywności ekonomicznej ludności (BAEL) są ankietowymi
badaniami reprezentacyjnymi członków losowo wybranych gospodarstw domo-
wych, prowadzonymi od maja 1992 roku. Dzięki zastosowaniu kryterium wy-
konywania, posiadania lub poszukiwania pracy zawartość informacyjna tego
wskaźnika jest bardziej przydatna do określenia statusu osoby na rynku pracy
niż informacje pochodzące z rejestrów osób bezrobotnych i zatrudnionych. Jest
kilka przyczyn, dla których do danych tych należy podchodzić ostrożnie. Po
pierwsze, od pierwszego kwartału 2000 roku zmieniono sposób dokonywania
obserwacji

10

. Aby uzyskać porównywalne dane, w pierwszym etapie przyporząd-

kowujemy obserwacje z środkowych miesięcy dla lat 1998–1999 do kwartałów,
w których te miesiące występują, czyniąc zastrzeżenie, że dane sprzed 1999 r.
mogą nie być w pełni porównywalne z obserwacjami dla lat 2000 i 2001.

9

Efekty systematycznych

zmian sezonowych można

wówczas uwzględnić

w modelu za pomocą od-

powiednich zmiennych

zerojedynkowych (sezo-

nowych) lub sezonowej

autoregresji, a obserwacje

nietypowe wyeliminować

za pomocą impulsowych

zmiennych zerojedynko-

wych.

10

Od tego okresu obserwa-

cja prowadzona jest meto-

dą ciągłą, tj. 1/13 losowej

próby w każdym

z 13 tygodni danego

kwartału, do tego okresu

stosowano badanie wy-

branego tygodnia w środ-

kowym miesiącu danego

kwartału.

25

Aktywni zawodowo w tys. osób

Bierni zawodowo

okres

ogółem

zatrudnieni

bezrobotni

I kw. 1998

17012

15116

1896

12794

II kw. 1998

17116

15362

1754

12770

III kw. 1998

17394

15607

1787

12669

IV kw. 1998

17162

15335

1827

12899

I kw. 1999

17082

14941

2141

13055

II kw. 1999

17126

14818,33

2307,67

13094,67

III kw. 1999

17170

14695,67

2474,33

13134,33

IV kw. 1999

17214

14573

2641

13174

I kw. 2000

17198

14317

2881

13290

II kw. 2000

17344

14518

2826

13193

III kw. 2000

17401

14727

2674

13292

IV kw. 2000

17300

14540

2760

13289

I kw. 2001

17305

14148

3157

13445

II kw. 2001

17459

14251

3208

13335

III kw. 2001

17511

14385

3126

13421

IV kw. 2001

17229

14043

3186

13664

Po drugie, aby uzyskać obserwacje dotyczące BAEL za pełen okres 1998–2001,
wyliczamy (uśredniamy) dane dla II i III kwartału 1999 roku, gdyż w tym okre-
sie badania nie były prowadzone

11

. Oczywiście można zrezygnować z uwzględ-

niania w badaniu brakujących okresów. Jeśli jednak dla predyktorów dyspo-
nujemy wartościami za te kwartały, to powinniśmy dokonać tych przeliczeń
— w przeciwnym razie byłaby to znacząca strata zarówno liczby stopni swobody,
jak i ogólności uzyskanych wyników.

4. Uwzględnić wpływ inflacji

Typowym problemem spotykanym w analizie szeregów czasowych jest przedsta-
wienie wielkości nominalnych określanych przy aktualnym układzie cen w po-
staci wielkości wyrażonych w tak zwanych cenach stałych. Eliminowanie wpły-
wu zmian cen w analizie dynamiki procesów gospodarczych jest uzasadnione
tym, że ceny kształtują jedynie wielkość nominalnych wydatków, a nie rzeczywi-
ste zadowolenie konsumenta z konsumpcji dobra. Ceny określają wartość przy-
chodów ze sprzedaży, a nie ilość wytworzonej produkcji, adekwatną do ilości
zaangażowanych zasobów. Wyrażenie danych w postaci wielkości realnych ma
bardzo duże znaczenie ze względu na ich porównywalność. Sposób uwzględnia-
nia wpływu inflacji i wyrażenia danych w cenach stałych prezentuje poniższy
przykład.

Przykład 6

Przyrost nominalny dochodów nie zawsze jest równoznaczny ze wzrostem ich
siły nabywczej. Jeżeli procentowy przyrost cen w tym samym czasie był więk-
szy niż procentowy przyrost dochodów, to mimo nominalnego wzrostu dochodu
nie jesteśmy w stanie kupić za niego większej ilości dóbr. Aby stwierdzić, czy za
wynagrodzenia z przykładu 4 w kolejnych miesiącach można kupić większą ilość
dóbr, musimy je urealnić za pomocą deflatora według wzoru:

Q = QP/P,

gdzie Q oznacza wielkości realne (dane w cenach stałych), QP — wielkości no-
minalne (w cenach bieżących), a P — wskaźnik cen o wybranej (stałej) podsta-
wie, zwany deflatorem.

11

Hipotetyczne wielkości

dla tych kwartałów moż-

na wyliczyć w różny spo-

sób. Najprostszym spo-

sobem jest równomier-

ne rozłożenie dynamiki

zmian liczby zatrudnio-

nych, bezrobotnych

i biernych zawodowo

w okresie I kwartał 1999

– IV kwartał 1999. Od-

powiednie wyliczenia

prowadzące do wyników

pokazanych w tabeli 1

zawarte są w pliku

BAEL.xls.

Tabela 1

Aktywność ekonomiczna

ludności w wieku 15 lat i więcej

— dane źródłowe i przeliczone

Źródło: GUS, Badania Aktywności

Ekonomicznej Ludności, 1/2001,

tabl. 1, obliczenia własne kursywą.

26

Dostępny w oficjalnych źródłach GUS miesięczny wskaźnik cen towarów i usług
konsumpcyjnych jest odpowiednim indeksem łańcuchowym do wyliczenia de-
flatora dla porównań wartości nominalnych z różnych okresów, z punktu wi-
dzenia typowego konsumenta, a w szczególności w ocenie siły nabywczej jego
wynagrodzenia. W arkuszu deflatory w pliku wynagrodzenia.xls przypominamy
jak uzyskać indeks jednopodstawowy o wybranej podstawie na podstawie indek-
su łańcuchowego. Kolejne kolumny arkusza realne pokazują sposób wyliczenia
wielkości wynagrodzeń w cenach stałych dla wybranego okresu (stycznia 2001,
grudnia 2002 lub według średnich cen 2002 roku — odpowiednio kolumny H, I,
J). Uzyskujemy je, dzieląc wielkości nominalne (w cenach bieżących) przez odpo-
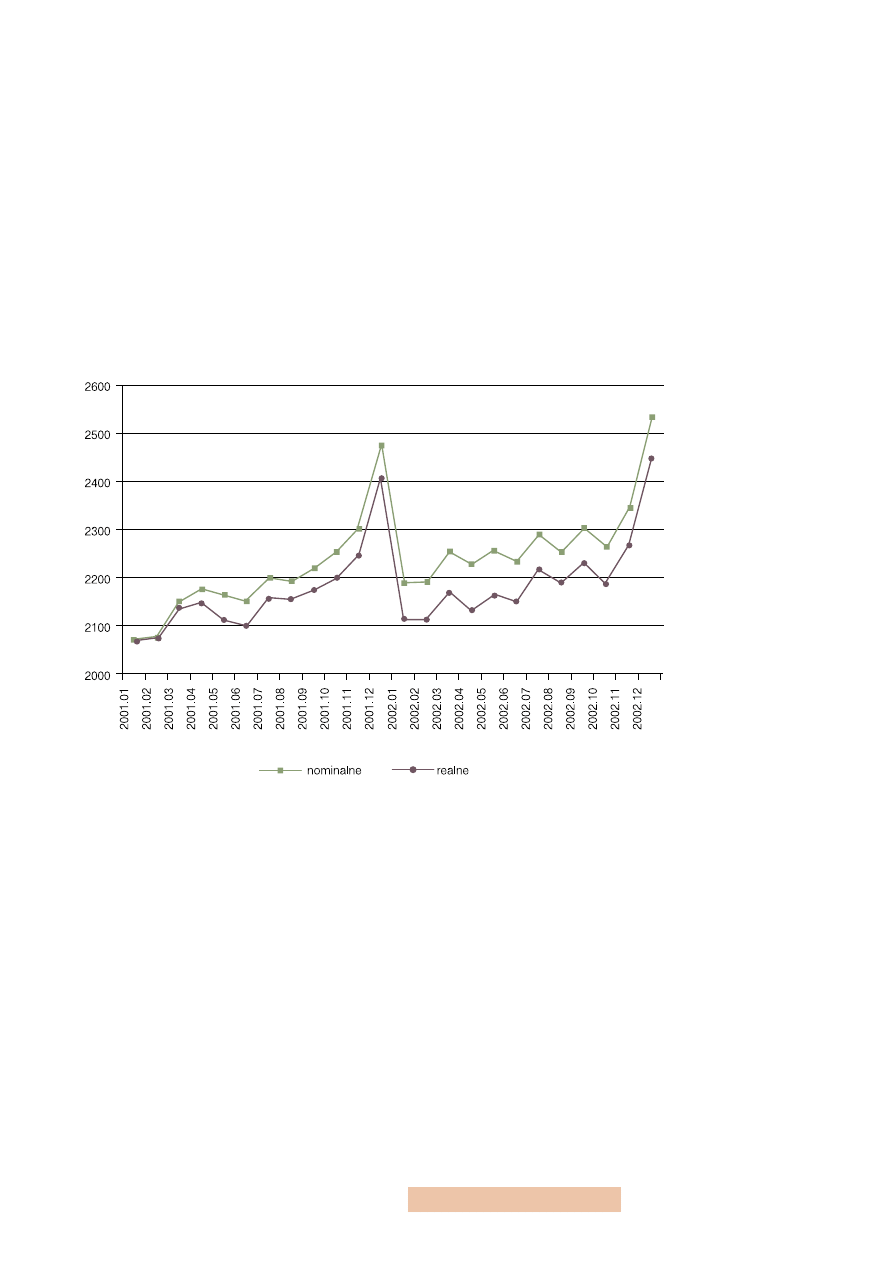
wiednie deflatory wyznaczone w arkuszu deflatory. Poniższy wykres prezentuje
skutki urealnienia wielkości wynagrodzeń. Uważny czytelnik powinien odgad-
nąć, że dane realne prezentowane są w cenach stałych stycznia 2001 roku (war-
tość nominalna jest równa wartości realnej w tym okresie).

5.

Ujednolicić dane pod względem merytorycznym (na przykład wszystkie wyra-
zić jako strumienie lub jako zasoby) i poddać odpowiednim transformacjom (na
przykład wyliczyć ich tempa zmian, logarytmy, ilorazy), jeżeli jest to konieczne
ze względu na przedmiot lub cel badania

Wśród szeregów czasowych możemy wyróżnić szeregi zasobów ekonomicz-
nych i strumieni ekonomicznych oraz wskaźników. W przypadku zasobów dane
dla momentów czasu opisują najczęściej wartości podawane na określoną datę
— moment czasu (np. wg stanu na ostatni dzień każdego miesiąca). Nawet gdy
podawane są one jako wartości średnie w okresie, to zawsze dotyczą one war-
tości przeciętnej, liczonej z kilku wyróżnionych momentów czasu. Dlatego poje-
dyncze dane o zasobach są na ogół obarczone błędem pomiaru. Strumienie eko-
nomiczne dotyczą z kolei przebiegu procesu ekonomicznego w okresach czasu
— zwykle o równych długościach. Mając na myśli czas trwania tych okresów,
mówimy o danych o częstotliwości miesięcznej, kwartalnej, rocznej, tygodnio-
wej, dziennej lub jeszcze większej. W ekonomii oprócz danych o strumieniach
i zasobach są jeszcze dane w postaci

wskaźników

, czyli ilorazów poszczególnych

wielkości.

Rysunek 2

Przeciętne wynagrodzenia

nominalne i realne w okresie

styczeń 2001 – grudzień 2002

Źródło: Obliczenia własne na pod-

stawie danych GUS.

27

Bibliografia

1.

Armstrong J. S., 2001: Standards and Practices for Forecasting, [in:] Principles
of Forecasting: A Handbook for Researchers and Practitioners, Kluwer Academic
Publishers, Norwell.

2.

Cieślak M., 1996: Prognozowanie gospodarcze, Wydawnictwo Akademii Ekono-
micznej im. Oskara Langego, Wrocław.

3. Czerwiński Z., 1992: Dylematy ekonomiczne, PWE, Warszawa.
4.

Czerwiński Z., Guzik B., 1980: Prognozowanie ekonometryczne, PWE, Warsza-
wa.

5.

Gajda J., 2001: Prognozowanie i symulacja a decyzje gospodarcze, Wydawnictwo
C.H. Beck, Warszawa, rozdział 4.

6. Zeliaś A., 1997: Teoria prognozy, PWE, Warszawa, rozdział 1.